Среди обыкновенных дробей различают два разных вида.
Правильные и неправильные дроби
Рассмотрим дроби.
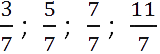
Обратите внимание, что в двух первых дробях (
и
)
числители меньше знаменателей. Такие дроби называют правильными.
Запомните!
![]()
У правильной дроби числитель меньше знаменателя. Поэтому правильная дробь
всегда меньше единицы.
Рассмотрим две оставшиеся дроби.
Дробь
имеет числитель равный знаменателю (такие дроби
равны единицы), а дробь
имеет числитель больший знаменателя. Такие
дроби называют неправильными.
Запомните!
![]()
У неправильной дроби числитель равен или больше знаменателя.
Поэтому неправильная дробь или равна единице или больше единицы.
Любая неправильная дробь всегда больше правильной.
Как выделить целую часть
У неправильной дроби можно выделить целую часть. Рассмотрим, как это можно сделать.
Чтобы из неправильной дроби выделить целую часть надо:
- разделить с остатком числитель на знаменатель;
- полученное неполное частное записываем в целую часть дроби;
- остаток записываем в числитель дроби;
- делитель записываем в знаменатель дроби.
Пример. Выделим целую часть из неправильной дроби
.
- Разделим в столбик числитель на знаменатель.
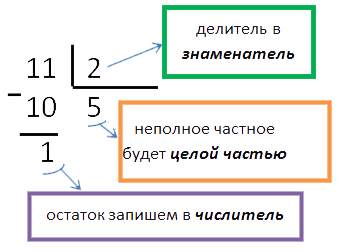
- Теперь запишем ответ.
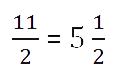
Запомните!
![]()
Полученное число выше, содержащее целую и дробную часть, называют смешанным числом.
Мы получили смешанное число из неправильной дроби, но можно
выполнить и обратное действие, то есть представить смешанное число в виде неправильной дроби.
Чтобы представить смешанное число в виде неправильной дроби надо:
- умножить его целую часть на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- записать полученную сумму из пункта 2 в числитель дроби, а знаменатель дробной части оставить прежним.
Пример. Представим смешанное число в виде неправильной дроби.
- Умножаем целую часть на знаменатель.
3 · 5 = 15
- Прибавляем числитель.
15 + 2 = 17
- Записываем полученную сумму в числитель новой дроби, а знаменатель оставляем прежним.
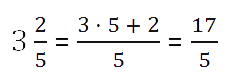
Любое смешанное число можно представить как сумму целой и дробной части.
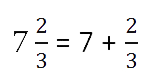
Запомните!
![]()
Любое натуральное число можно записать дробью с любым натуральным знаменателем.
Частное от деления числителя на знаменатель такой дроби будет равно данному натуральному числу.
Примеры.
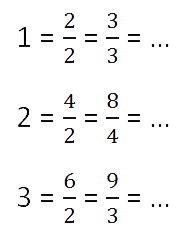
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
7 сентября 2020 в 18:33
Ксюша Островская

Профиль
Благодарили: 0
Сообщений: 1

Ксюша Островская
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
7 сентября 2020 в 20:33
Ответ для Ксюша Островская
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
= 55 : 66 = 5 : 6.
0
Спасибо
Ответить
14 декабря 2016 в 16:32
Руслан Потапов

Профиль
Благодарили: 0
Сообщений: 2

Руслан Потапов
Профиль
Благодарили: 0
Сообщений: 2
50
найдите числитель неправильной обыкновенной
дроби.равной смешанному числу.
помогите пожалуйста решением.
0
Спасибо
Ответить
15 декабря 2016 в 16:45
Ответ для Руслан Потапов
Амина Гилазиева

Профиль
Благодарили: 0
Сообщений: 2

Амина Гилазиева
Профиль
Благодарили: 0
Сообщений: 2
я думаю что это дродь
0
Спасибо
Ответить
15 декабря 2016 в 16:46
Ответ для Руслан Потапов
Амина Гилазиева

Профиль
Благодарили: 0
Сообщений: 2

Амина Гилазиева
Профиль
Благодарили: 0
Сообщений: 2
а числитель 71
0
Спасибо
Ответить
16 декабря 2016 в 19:33
Ответ для Руслан Потапов
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Чушь полная, конечно.
0
Спасибо
Ответить
18 октября 2016 в 10:44
Светлана Черемисова

Профиль
Благодарили: 0
Сообщений: 1

Светлана Черемисова
Профиль
Благодарили: 0
Сообщений: 1
Найдите целые значения а, при которых дробь принимает целые значения:
0
Спасибо
Ответить
18 октября 2016 в 18:00
Ответ для Светлана Черемисова
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
±2.
0
Спасибо
Ответить
2 апреля 2016 в 19:01
Валерия Аралушкина

Профиль
Благодарили: 0
Сообщений: 1

Валерия Аралушкина
Профиль
Благодарили: 0
Сообщений: 1
Вычитание дроби из единицы и вычитание дроби из натурального числа.
5-7/10 10-3/5 9-5/9 7-5/11 8-2/5
Помогите я не очень понимаю как это делать!
0
Спасибо
Ответить
3 апреля 2016 в 12:22
Ответ для Валерия Аралушкина
Марина Доценко

Профиль
Благодарили: 0
Сообщений: 1

Марина Доценко
Профиль
Благодарили: 0
Сообщений: 1
5-7/10=5/1-7/10=50/10-7/10=43/10=4 целых и 3/10.
10-3/5=10/1-3/5=50/5-3/5=47/5=9 целых 2/5
9-5/9=9/1-5/9=81/9-5/9=76/9=8 целых 4/9
7-5/11=7/1-5/11=77/11-5/11=72/11=6 целых 6/11
8-2/5=8/1-2/5=40/5-2/5=38/5=7целых 3/5
0
Спасибо
Ответить
11 января 2016 в 23:48
Алинчик Плышевская

Профиль
Благодарили: 0
Сообщений: 1

Алинчик Плышевская
Профиль
Благодарили: 0
Сообщений: 1
Привет, помогите понять как сложить и вычетать смешаные числа?
0
Спасибо
Ответить
12 января 2016 в 19:05
Ответ для Алинчик Плышевская
Janina Kutovska

Профиль
Благодарили: 0
Сообщений: 2

Janina Kutovska
Профиль
Благодарили: 0
Сообщений: 2
смотри:
Сложение дробейСложение дробей с одинаковыми знаменателями.Определение. Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений:
| a | + | б | = | + б |
| С | С | С |
Примеры сложения дробей с одинаковыми знаменателямиПример 1. Найти сумму двух дробей с одинаковыми знаменателями:
| 1 | + | 2 | = | 1 + 2 | = | 3 |
| 5 | 5 | 5 | 5 |
Пример 2. Найти сумму двух дробей с одинаковыми знаменателями:
| 3 | + | 2 | = | 3 + 2 | = | 5 |
| 7 | 7 | 7 | 7 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание дробей с равными знаменателями
Сложение обыкновенных дробей.Определение. Чтобы сложить две обыкновенные дроби, следует:привести дроби к наименьшему общему знаменателю;сложить числители дробей, а знаменатель оставить без изменений;сократить полученную дробь;Если получилась неправильная дробь преобразовать неправильную дробь в смешанную.Примеры сложения обыкновенных дробейПример 3. Найти сумму двух дробей:
| 1 | + | 1 | = | 1·2 | + | 1 | = | 2 | + | 1 | = | 2 + 1 | = | 3 | = | 3 | = | 1 |
| 3 | 6 | 3·2 | 6 | 6 | 6 | 6 | 6 | 3·2 | 2 |
Пример 4. Найти сумму двух дробей:
| 29 | + | 44 | = | 29·3 | + | 44·2 | = | 87 | + | 88 | = | 87 + 88 | = |
| 30 | 45 | 30·3 | 45·2 | 90 | 90 | 90 |
| = | 175 | = | 35·5 | = | 35 | = | 18 + 17 | = 1 | 17 |
| 90 | 18·5 | 18 | 18 | 18 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание двух обыкновенных дробей
Сложение смешанных чиселОпределение. Чтобы сложить смешанные дроби, надо:привести дробные части этих чисел к наименьшему общему знаменателю;отдельно сложить целые части и отдельно дробные части;если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части;сократить полученную дробь.Примеры сложения смешанных чиселПример 5. Найти сумму двух смешанных чисел:
| 2 | + | 1 | 1 | = | 2·2 | + | 1 | 1·3 | = | 4 | + | 1 | 3 | = | 1 + | 4 + 3 | = |
| 3 | 2 | 3·2 | 2·3 | 6 | 6 | 6 |
| = | 1 + | 7 | = | 1 + | 6 + 1 | = | 1 + 1 | 1 | = 2 | 1 |
| 6 | 6 | 6 | 6 |
Пример 6. Найти сумму двух смешанных чисел:
| 1 | 5 | + | 2 | 3 | = | 1 | 5·4 | + | 2 | 3·3 | = | 1 | 20 | + | 2 | 9 | = | 3 + | 20 + 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 | 24 |
| = | 3 + | 29 | = | 3 + | 24 + 5 | = | 3 + 1 | 5 | = 4 | 5 |
| 24 | 24 | 24 | 24 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание двух смешанных чисел
Вычитание дробейВычитание дробей с одинаковыми знаменателями.Определение. Чтобы найти разницу двух дробей с одинаковыми знаменателями, нужно вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений:
| a | – | б | = | – б |
| С | С | С |
Примеры вычитания дробей с одинаковыми знаменателямиПример 7. Найти разность двух дробей с одинаковыми знаменателями:
| 3 | – | 1 | = | 3 — 1 | = | 2 |
| 5 | 5 | 5 | 5 |
Пример 8. Найти разность двух дробей с одинаковыми знаменателями:
| 8 | – | 5 | = | 8 — 5 | = | 3 |
| 41 | 41 | 41 | 41 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание дробей с равными знаменателями
Вычитание обыкновенных дробей.Определение. Чтобы вычесть из одной обыкновенной дроби другую, следует:привести дроби к наименьшему общему знаменателю;из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменений;сократить полученную дробь.
Примеры вычитания обыкновенных дробейПример 9. Найти разность двух дробей:
| 5 | – | 1 | = | 5 | – | 1·3 | = | 5 | – | 3 | = | 5 — 3 | = | 2 | = | 2 | = | 1 |
| 6 | 2 | 6 | 2·3 | 6 | 6 | 6 | 6 | 2·3 | 3 |
Пример 10. Найти разность двух дробей:
| 3 | – | 1 | = | 3·3 | – | 1·5 | = | 9 | – | 5 | = | 9 — 5 | = | 4 | = | 2·2 | = | 2 |
| 10 | 6 | 10·3 | 6·5 | 30 | 30 | 30 | 30 | 15·2 | 15 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание двух обыкновенных дробей
Вычитание смешанных чисел.Определение. Чтобы выполнить вычитание смешанных чисел, надо:привести дробные части этих чисел к наименьшему общему знаменателю;если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу, целую часть;отдельно выполнить вычитание целых частей и отдельно дробных частей;сократить полученную дробь.
Примеры вычитания смешанных чиселПример 11. Найти разность двух смешанных чисел:
| 2 | 1 | – | 1 | 1 | = | 2 | 1·3 | – | 1 | 1·2 | = | (2 — 1) | + | 3 | – | 2 | = |
| 2 | 3 | 2·3 | 3·2 | 6 | 6 |
| = | 1 | + | 3 -2 | = | 1 | + | 1 | = | 1 | 1 |
| 6 | 6 | 6 |
Пример 12. Найти разность двух смешанных чисел:
| 3 | 1 | – | 1 | 3 | = | 3 | 1·4 | – | 1 | 3·3 | = | 3 | 4 | – | 1 | 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 |
| = | 2 | 24 + 4 | – | 1 | 9 | = | 1 + | 28 — 9 | = | 1 + | 19 | = 1 | 19 |
| 24 | 24 | 24 | 24 | 24 |
Пример 13. Найти разность двух смешанных чисел:
| 1 | 1 | – | 3 | 2 | = | 1 | 1 | – | 3 | 2·2 | = | 1 | 1 | – | 3 | 4 | = | (1-3) | + | 1 — 4 | = |
| 6 | 3 | 6 | 3·2 | 6 | 6 | 6 |
| = -2 | – | 3 | = | -2 | – | 3 | = | -2 | – | 1 | = | -2 | 1 |
| 6 | 2·3 | 2 | 2 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание двух смешанных чиселДробиВиды дробей (обыкновенная правильная, неправильная, смешанная, десятичная)Основное свойство дробиСокращение дробиПриведение дробей к общему знаменателюПреобразование неправильной дроби в смешанное числоПреобразование смешанного числа в неправильную дробьСложение и вычитание дробейУмножение дробейДеление дробейСравнение дробейПреобразование десятичной дроби в обыкновенную дробьОнлайн калькуляторы дробейОнлайн упражнения с дробями
0
Спасибо
Ответить
12 января 2016 в 19:06
Ответ для Алинчик Плышевская
Janina Kutovska

Профиль
Благодарили: 0
Сообщений: 2

Janina Kutovska
Профиль
Благодарили: 0
Сообщений: 2
![]()
0
Спасибо
Ответить
8 сентября 2015 в 23:36
Лариса Краснова

Профиль
Благодарили: 0
Сообщений: 1

Лариса Краснова
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
5 сентября 2016 в 14:12
Ответ для Лариса Краснова
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
=25 ? + = 25 ? = 25 ? = 24=24,25
0
Спасибо
Ответить
8 сентября 2015 в 18:48
Никита Парфёнов

Профиль
Благодарили: 0
Сообщений: 1

Никита Парфёнов
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
5 сентября 2016 в 9:14
Ответ для Никита Парфёнов
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
В таком виде не ясна задача и решить её не возмонжо.
0
Спасибо
Ответить
8 сентября 2015 в 0:32
Sparkiss Princess

Профиль
Благодарили: 0
Сообщений: 1

Sparkiss Princess
Профиль
Благодарили: 0
Сообщений: 1
Всем привет! Помогите пожалуйста в решении примеров со смешанными дробями!
1.) 2
? 51
:11 · (21
? 9,8 : 2,8 · 4
) +
2.) 48
? ( 66,4 — 66,25) · (1
+
) + 28, 2: 5 ? 44, 2
3.) 12
? 0,5 ? 5
· 1
: (
+ 1
· 1,5) · 0,62
4.) 7, 025 ? (11
+ 22
? 33
) · 7,8 + (65
? 64) : 0,5
5.) 97
? 3
? 8,5 ? ( 2
+ 28,2 : 2) · 0,2 ·
22,5
Заранее спасибо! ![]()
0
Спасибо
Ответить
5 сентября 2016 в 14:21
Ответ для Sparkiss Princess
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Принцип решения таких примеров сводится к большой внимательности и применения нескольких простейших правил:
1) Последовательность действий в первую очередь действие в скобках, далее умножение/деление, далее сложение/вычитание
2) Правила перевода обыкновенных дробей в десятичные. Подробно можно почитать вот здесь: http://math-prosto.ru/index.php?page=pages/convert-decimal/convert-decimal2.php
3)Действия с десятичными дробями. О них можно подробнее почитать здесь: math-prosto.ru/index.php?page=pages/decimal/decimal1.php
В случаях, когда решение осложняется периодическими дробями, можно воспользоваться обратными действиями и перевести десятичные дроби в обыкновенные. Подробнее можно прочесть здесь http://math-prosto.ru/index.php?page=pages/decimal/decimal1.php
0
Спасибо
Ответить
5 апреля 2015 в 12:10
Кристина Тишина

Профиль
Благодарили: 0
Сообщений: 1

Кристина Тишина
Профиль
Благодарили: 0
Сообщений: 1
[1
*0,27-3
*0,15] ? 1500*[ ? 0,1]3
0
Спасибо
Ответить
14 апреля 2016 в 10:27
Ответ для Кристина Тишина
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Преобразуем и решим.
(1 · -3 · ) ?1500 · (-0,001)=( ?) +1,5=( ? )+1,5= ? +1,5= ?0,14+1,5=1,36
Ответ:1,36
0
Спасибо
Ответить
14 апреля 2016 в 10:28
Ответ для Кристина Тишина
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Решил пойти с конца форума и ответить на неотвеченные задачи =) Камни не кидайте, что так долго отвечал =)
0
Спасибо
Ответить

Влад Тихонов
30.07.2019 14:33:09
Математика 5-6 класс

10 баллов
Как найти целую и дробную части неправильной дроби?

Alex
30.07.2019 14:33:20
Нужно разделить с остатком числитель на знаменатель, неполное частное будет целой частью, остаток дает числитель, а знаменатель – делимое, на которое делили.
Все предметы

Рейтинг пользователей
Как найти целую и дробную часть неправильной дроби
-

Марлеша
2 января, 15:03
0
Целая часть находится левее дробной в то же время как и дробь справа.
- Комментировать
- Жалоба
- Ссылка
-

Делишь числитель на знаменатель, то что делится пишешь в целую часть, а остаток в числитель, но а знаменатель остаётся прежним:
пример:
43/12=3 7/12
43:12=3 целых и 7 в остатке
102/11=9 3/11
102:11=9 целых и 3 в остатке
- Комментировать
- Жалоба
- Ссылка
Найди верный ответ на вопрос ✅ «Как найти целую и дробную часть неправильной дроби …» по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Новые вопросы по математике
Перейти к содержанию
Правильная и неправильная дроби
Опубликовано 04.06.2021
Дадим определение правильной и неправильной дроби. Эти понятия часто используются в математике. Как понять – какая дробь правильная, а какая неправильная – даем определения. Пример правильной дроби и пример неправильной дроби – в этом материале.
Правильная дробь
Определение правильной дроби:
Дробь, в которой числитель меньше знаменателя, называется правильной. Например,
– правильная дробь.
Неправильная дробь
Определение неправильной дроби:

Дробь, в которой числитель равен знаменателю или больше его, называется неправильной дробью. Например,
,
– неправильные дроби.
Обращение числа с целой и дробной частями в неправильную дробь
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Например, ![]() .
.
![]() .
.
Вообще, чтобы записать число в виде неправильной дроби, нужно умножить его целую часть на знаменатель дробной части и к произведению прибавить числитель дробной части. Полученная сумма будет числителем дроби, а знаменателем будет знаменатель дробной части.

Как выделить целую часть из неправильной дроби
Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления будет целой частью числа, остаток – числителем, а делитель – знаменателем. Например, .

( 8 оценок, среднее 4.25 из 5 )
Выделение целой части из неправильной дроби
Дробями называют одну или несколько равных долей целого. Записывают дроби двумя
![]()
называется числителем дроби. Число n, записанное под чертой, называется знаменателем дроби.
Дробь, в которой числитель больше или равен знаменателю, называют неправильной дробью. .
![]()
![]()
![]()
13 показывает, что взяли 13 таких частей. Покажем это на рисунке.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
Можем сделать вывод: чтобы из неправильной дроби выделить целую часть, можно ее числитель разделить с остатком на знаменатель. Неполное частное будет целой частью полученного смешанного числа, остаток – числителем дробной части смешанного числа, а делитель – знаменателем дробной части.
![]()
![]()
знаменатель 16. Выполним деление столбиком:
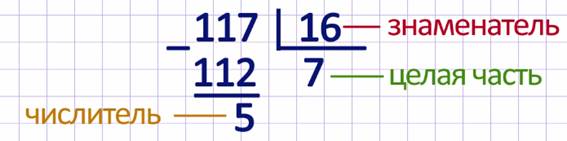
![]()
![]()
![]()
Чтобы из неправильной дроби выделить целую часть, можно ее числитель разделить с остатком на знаменатель. Неполное частное будет целой частью полученного смешанного числа, остаток – числителем дробной части, а делитель – ее знаменателем.
Список использованной литературы:
- Петерсон Л.Г. Математика. 4 класс. Часть 1. / Л.Г. Петерсон. – М.: Ювента, 2014. – 96 с.: ил.
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса. / Л.Г. Петерсон. – М.: Ювента, 2014. – 280 с.: ил.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
- CD-ROM. Математика. 4 класс. Сценарии уроков к учебнику к 1 части Петерсон Л.Г. – М.: Ювент, 2013.
