Корень и его свойства
 Тема в математике «Корень и его свойства» нередко вызывает затруднения у школьников, особенно при решении примеров. В данной статье описаны основные свойства корней, а также правила сложения, вычитания, умножения и деления. Наглядные примеры помогаю понять, как решать задания с корнями.
Тема в математике «Корень и его свойства» нередко вызывает затруднения у школьников, особенно при решении примеров. В данной статье описаны основные свойства корней, а также правила сложения, вычитания, умножения и деления. Наглядные примеры помогаю понять, как решать задания с корнями.
Определение «Корень»
Корень второй степени (квадратный корень) из числа a — это число, которое становится равным a, если число a возвести во вторую степень (в квадрат).
Например, √ 64 = 8 (√ 64 равно числу 8).
Формула: √ a 2 = a
Число, стоящее под знаком корня, называется подкоренным числом. Если под знаком корня стоит целое выражение, то его называют подкоренным выражением.
Свойство квадратного корня: для действительных чисел не существует квадратный корень из отрицательного числа, так как возведение числа в квадрат будет всегда неотрицательным числом.
Извлечение корней: примеры
Извлечь корень — значит найти значение корня (то есть найти число, при возведении которого в степень, получается подкоренное значение).
Например, извлечь корень из 64 – значит найти √ 64 .
Найти корень из числа можно одним из следующих способов:
- Использование таблицы квадратов, таблицы кубов и т.д. В данном случае нужно просто найти нужное число в таблице и посмотреть, какому значению оно соответствует.
Приведение корней с разными показателями
Для того, чтобы упростить выражение с корнями, которое содержит корни разных степеней, необходимо привести все корни к одной степени.
Для этого воспользуемся следующим свойством дроби: a = n √ a n .
Например, есть квадратный корень (второй степени √ 2 ) и кубический корень (третьей степени 3 √ 3 ).
Во-первых, необходимо найти наименьшее общее кратное (НОК) для степеней. В нашем примере НОК=6 (2х3).
Во-вторых, применим свойство a = n √ a n : √ 2 = 2 √ 2 = 6 √ 2 3 = 6 √ 8 ; 3 √ 3 = 6 √ 3 2 = 6 √ 9
Получилось два корня одинаковой степени, с которыми можно совершать различные математические действия.
Корень: сложение и вычитание корней
Основное правила сложения и вычитания квадратных корней: сложение и вычитание квадратного корня возможны только при условии одинакового подкоренного выражения.
Примеры:
2√ 3 + 3√ 3 = 5√ 3
2√ 3 + 2√ 4 – не выполняется.
При этом, нужно рассмотреть возможность упростить выражения.
Пример: 2√ 3 + 3√ 12 = 2√ 3 + 3√ 2х2х3 = 2√ 3 + 3√ 2 2 х3 = 2√ 3 + 6√ 3 = 8√ 3 .
Алгоритм действия:
1. Упростить подкоренное выражение путем разложения на простые множители.
2. Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня.
3. После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
4. У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Корень: умножение
Умножение корней без множителей
Произведение корней из чисел равно корню из произведения этих чисел.
√ a*b =√ a *√ b
Важно: между собой можно умножать только одинаковые степени корней, то есть можно умножить один квадратный корень на другой, но нельзя умножить квадратный корень на корень кубической степени.
Примеры:
√ 2 х √ 3 = √ 6
√ 6 х √ 3 = √ 18 = √ 3х3х2 = 3√ 2
Умножение корней с множителями
При умножении корней с множителями нужно отдельно перемножить множители и подкорневые выражения (числа). Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице.
Примеры:
3√ 2 х √ 5 = (3х1) √ (2*5) = 3√ 10
4√ 2 х 3√ 3 = (3х4) √ (2х3) = 12√ 6
Корень: деление
Основной правило деления — подкоренные выражения делятся на подкоренные выражения, а множители на множители.
√ a:b =√ a :√ b
В процессе деления квадратных корней дроби упрощаются.
Деление корней без множителей
Частное корней из чисел равно корню из частного этих чисел.
Важно: между собой можно делить только одинаковые степени корней, то есть можно делить один квадратный корень на другой, но нельзя делить квадратный корень на корень кубической степени.
Пример. √ 21 :√ 3 =√ 21:3 =√ 7
Деление квадратных корней с множителями
При делении корней с множителями нужно отдельно разделить множители и подкорневые выражения (числа). Подкорневые числа можно делить между собой только в том случае, если они имеют одинаковые степени. В случае отсутствия множителя, он равен единице.
Пример. 12√ 32 : 6√ 16 = (12:6) √ (32:16) = 2√ 2 .
Примеры для практики
Чтобы попрактиковаться решать примеры на вычисление квадратный корней, можно скачать программу «Корни квадратные«
Решение №903 Сколько целых чисел расположено между числами √13 и √130?
Сколько целых чисел расположено между числами √13 и √130?
Решение:
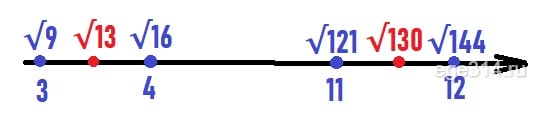
Видим, что в данном промежутке расположены числа от 4 до 11, это:
4, 5, 6, 7, 8, 9, 10, 11
Получаем 8 целых чисел.
Ответ: 8.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.6 / 5. Количество оценок: 40
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.
Вычисление квадратного корня из числа: как вычислить вручную
При решении различных задач из курса математики и физики ученики и студенты часто сталкиваются с необходимостью извлечения корней второй, третьей или n-ой степени. Конечно, в век информационных технологий не составит труда решить такую задачу при помощи калькулятора. Однако возникают ситуации, когда воспользоваться электронным помощником невозможно.
К примеру, на многие экзамены запрещено приносить электронику. Кроме того, калькулятора может не оказаться под рукой. В таких случаях полезно знать хотя бы некоторые методы вычисления радикалов вручную.
Извлечение квадратного корня при помощи таблицы квадратов
Один из простейших способов вычисления корней заключается в использовании специальной таблицы. Что же она собой представляет и как ей правильно воспользоваться?
При помощи таблицы можно найти квадрат любого числа от 10 до 99. При этом в строках таблицы находятся значения десятков, в столбах — значения единиц. Ячейка на пересечении строки и столбца содержит в себе квадрат двузначного числа. Для того чтобы вычислить квадрат 63, нужно найти строку со значением 6 и столбец со значением 3. На пересечении обнаружим ячейку с числом 3969.

Поскольку извлечение корня — это операция, обратная возведению в квадрат, для выполнения этого действия необходимо поступить наоборот: вначале найти ячейку с числом, радикал которого нужно посчитать, затем по значениям столбика и строки определить ответ. В качестве примера рассмотрим вычисление квадратного корня 169.
Находим ячейку с этим числом в таблице, по горизонтали определяем десятки — 1, по вертикали находим единицы — 3. Ответ: √169 = 13.
Аналогично можно вычислять корни кубической и n-ой степени, используя соответствующие таблицы.

Преимуществом способа является его простота и отсутствие дополнительных вычислений. Недостатки же очевидны: метод можно использовать только для ограниченного диапазона чисел (число, для которого находится корень, должно быть в промежутке от 100 до 9801). Кроме того, он не подойдёт, если заданного числа нет в таблице.
Разложение на простые множители
Если таблица квадратов отсутствует под рукой или с её помощью оказалось невозможно найти корень, можно попробовать разложить число, находящееся под корнем, на простые множители. Простые множители — это такие, которые могут нацело (без остатка) делиться только на себя или на единицу. Примерами могут быть 2, 3, 5, 7, 11, 13 и т. д.

Рассмотрим вычисление корня на примере √576. Разложим его на простые множители. Получим следующий результат: √576 = √(2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3) = √(2 ∙ 2 ∙ 2)² ∙ √3². При помощи основного свойства корней √a² = a избавимся от корней и квадратов, после чего подсчитаем ответ: 2 ∙ 2 ∙ 2 ∙ 3 = 24.
Что же делать, если у какого-либо из множителей нет своей пары? Для примера рассмотрим вычисление √54. После разложения на множители получаем результат в следующем виде: √54 = √(2 ∙ 3 ∙ 3 ∙ 3) = √3² ∙ √(2 ∙ 3) = 3√6. Неизвлекаемую часть можно оставить под корнем. Для большинства задач по геометрии и алгебре такой ответ будет засчитан в качестве окончательного. Но если есть необходимость вычислить приближённые значения, можно использовать методы, которые будут рассмотрены далее.
Метод Герона
Как поступить, когда необходимо хотя бы приблизительно знать, чему равен извлечённый корень (если невозможно получить целое значение)? Быстрый и довольно точный результат даёт применение метода Герона. Его суть заключается в использовании приближённой формулы:
где R — число, корень которого нужно вычислить, a — ближайшее число, значение корня которого известно.
Рассмотрим, как работает метод на практике, и оценим, насколько он точен. Рассчитаем, чему равен √111. Ближайшее к 111 число, корень которого известен — 121. Таким образом, R = 111, a = 121. Подставим значения в формулу:
√111 = √121 + (111 — 121) / 2 ∙ √121 = 11 — 10 / 22 ≈ 10,55.

Теперь проверим точность метода:
Погрешность метода составила приблизительно 0,3. Если точность метода нужно повысить, можно повторить описанные ранее действия:
√111 = √111,3025 + (111 — 111,3025) / 2 ∙ √111,3025 = 10,55 — 0,3025 / 21,1 ≈ 10,536.
Проверим точность расчёта:
После повторного применения формулы погрешность стала совсем незначительной.
Вычисление корня делением в столбик
Этот способ нахождения значения квадратного корня является чуть более сложным, чем предыдущие. Однако он является наиболее точным среди остальных методов вычисления без калькулятора.
Допустим, что необходимо найти квадратный корень с точностью до 4 знаков после запятой. Разберём алгоритм вычислений на примере произвольного числа 1308,1912.
- Разделим лист бумаги на 2 части вертикальной чертой, а затем проведём от неё ещё одну черту справа, немного ниже верхнего края. Запишем число в левой части, разделив его на группы по 2 цифры, двигаясь в правую и левую сторону от запятой. Самая первая цифра слева может быть без пары. Если же знака не хватает в правой части числа, то следует дописать 0. В нашем случае получится 13 08,19 12.
- Подберём самое большое число, квадрат которого будет меньше или равен первой группе цифр. В нашем случае это 3. Запишем его справа сверху; 3 — первая цифра результата. Справа снизу укажем 3×3 = 9; это понадобится для последующих расчётов. Из 13 в столбик вычтем 9, получим остаток 4.
- Припишем следующую пару чисел к остатку 4; получим 408.
- Число, находящееся сверху справа, умножим на 2 и запишем справа снизу, добавив к нему _ x _ =. Получим 6_ x _ =.
- Вместо прочерков нужно подставить одно и то же число, меньшее или равное 408. Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.
- Повторим шаги 3—6. Поскольку снесённые вниз цифры находятся в дробной части числа, необходимо поставить десятичную запятую справа сверху после 6. Запишем удвоенный результат с прочерками: 72_ x _ =. Подходящей цифрой будет 1: 721×1 = 721. Запишем её в ответ. Выполним вычитание 1219 — 721 = 498.
- Выполним приведённую в предыдущем пункте последовательность действий ещё три раза, чтобы получить необходимое количество знаков после запятой. Если не хватает знаков для дальнейших вычислений, у текущего слева числа нужно дописать два нуля.
В результате мы получим ответ: √1308,1912 ≈ 36,1689. Если проверить действие при помощи калькулятора, можно убедиться, что все знаки были определены верно.
Поразрядное вычисление значения квадратного корня
Метод обладает высокой точностью. Кроме того, он достаточно понятен и для него не требуется запоминать формулы или сложный алгоритм действий, поскольку суть способа заключается в подборе верного результата.
Извлечём корень из числа 781. Рассмотрим подробно последовательность действий.
- Выясним, какой разряд значения квадратного корня будет являться старшим. Для этого возведём в квадрат 0, 10, 100, 1000 и т. д. и выясним, между какими из них находится подкоренное число. Мы получим, что 10² < 781 < 100², т. е. старшим разрядом будут десятки.
- Подберём значение десятков. Для этого будем по очереди возводить в степень 10, 20, …, 90, пока не получим число, превышающее 781. Для нашего случая получим 10² = 100, 20² = 400, 30² = 900. Значение результата n будет находиться в пределах 20 < n <30.
- Аналогично предыдущему шагу подбирается значение разряда единиц. Поочерёдно возведём в квадрат 21,22, …, 29: 21² = 441, 22² = 484, 23² = 529, 24² = 576, 25² = 625, 26² = 676, 27² = 729, 28² = 784. Получаем, что 27 < n < 28.
- Каждый последующий разряд (десятые, сотые и т. д. ) вычисляется так же, как было показано выше. Расчёты проводятся до тех пор, пока не будет достигнута необходимая точность.
Видео
Из видео вы узнаете, как извлекать квадратные корни без использования калькулятора.
Сколько целых чисел расположено между числами √13 и √130?
Решение:
Найдём к числам √13 и √130 ближайшие числа из которых извлекается корень нацело:
√9 < √13 < √16
3 < √13 < 4
√121 < √130 < √144
11 < √130 < 12
Расположим их на координатной прямой:
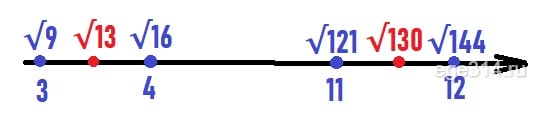
Видим, что в данном промежутке расположены целые числа от 4 до 11, это:
4, 5, 6, 7, 8, 9, 10, 11
Получаем 8 целых чисел.
Ответ: 8.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.8 / 5. Количество оценок: 73
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Можно например методом натуральных границ. Он заключается в том, что наши числа заключаются в интервалы, границы которых есть ближайшие натуральные числа. В наше случае имеем корень из 3,5, т. е. число √(3,5) и корень из 5, т. е. √(5). Число 3,5 можно ограничить следующим образом:
3 < 3,5 < 4, тогда кв. корень из нашего числа будет ограничен, как:
√(3) < √(3,5) < 2. Пять ограничим, как: 4 < 5 < 6, тогда её корень будет ограничен:
2 < √(5) < √(6), заметим, что границы в ограничении корня из 3,5 и 5 совпадают, а именно совпадает верхняя грань корня из 3,5 и нижняя грань кв. корня 5, т. е. двойка. Совмести эти границы:
√(3) < √(3,5) < 2 < √(5) < √(6) или √(3,5) < 2 < √(5), т. е. между нашими границами оказалось одно натуральное число 2.
433
Комментировать ответ…Комментировать…
Задания
Версия для печати и копирования в MS Word
Тип 8 № 401223 

Сколько целых чисел расположено между и
?
Спрятать решение
Решение.
Заметим, что а
Далее оценим:
Следовательно, между исходными числами расположено единственное целое число — 12.
Ответ: 1.
Аналоги к заданию № 401223: 401447 401580 401665 … Все
Спрятать решение
·
Помощь
Ответ: 2 целых числа .
Решение:
Сначала немного преобразуем эти числа:
Также заметим, что (между получившимися корнями есть только два числа, корень из которых извлекается нацело – это 196 и 225):
То есть, между 5√7 и 7√5 расположены целые числа 14 и 15 – всего 2 целых числа.
