Найти целые решения системы неравенств
В алгебре часто требуется не просто решить систему неравенств, но выбрать из полученного множества решений решения, удовлетворяющие некоторым дополнительным условиям.
Найти целые решения системы неравенств — одно из заданий такого рода.
1) Найти целые решения системы неравенств:
Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:
После упрощения разделим обе части каждого неравенства на
Отмечаем решения неравенств на числовых прямых. Решением системы является пересечение решений (то есть та часть, где штриховка есть на обеих прямых).
Оба неравенства строгие, поэтому -4 и 2 изображаются выколотыми точками и в решение не входят:
Из промежутка (-4;2) выбираем целые решения.
Ответ: -3; -2; -1; 0; 1.
2) Какие целые решения имеет система неравенств?
Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком
Упрощаем и делим обе части на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не меняется, второе — на отрицательное число, поэтому знак неравенства изменяется на противоположный:
Отмечаем решения неравенств на числовых прямых. Первое неравенство нестрогое, поэтому -2 изображаем закрашенной точкой. Второе неравенство нестрогое, соответственно, 5 изображается выколотой точкой:
Целые решения на промежутке [-2;5) — это -2; -1; 0; 1; 2; 3; 4.
Ответ: -2; -1; 0; 1; 2; 3; 4.
В некоторых примерах не требуется перечислять целые решения, нужно лишь указать их количество.
3) Сколько целых решений имеет система неравенств?
Переносим неизвестные в одну сторону, известные — в другую:
Обе части первого неравенства делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Обе части второго неравенства делим на положительное число, знак неравенства при этом не меняется:
Решение неравенств отмечаем на числовых прямых. Оба неравенства нестрогие, поэтому -3,5 и 1,7 изображаем закрашенными точками:
Решением системы является промежуток [-3,5; 1,7]. Целые числа, которые входят в данный промежуток — это -3; -2; -1; 0; 1. Всего их 5.
Ответ: 5.
4) Сколько целых чисел являются решениями системы неравенств?
Неизвестные — в одну сторону, известные — в другую с противоположным знаком:
При делении обеих частей неравенства на положительное число знак неравенства не изменяется, при делении на отрицательное число — меняется на противоположный:
Решение неравенств отмечаем на числовых прямых.
Множество решений системы состоит из единственного элемента — {2}. 2 — целое число, следовательно, решением данной системы является одно целое число.
Ответ: 1.
Сколько целых решений имеет неравенство -18
Для того, чтобы определить сколько целых решений имеет неравенство — 18 < х < 174 выполним следующие действия.
Алгоритм решения задачи
- вспомним определение целого числа;
- выясним входят ли концы отрезка в решение неравенства;
- найдем число отрицательных решений неравенства;
- найдем число положительных решений неравенства;
- найдем количество целых решений неравенства.
Определение целого числа
Давайте вспомним определение целого числа в математике.
Натуральные числа, противоположные им числа и 0 называются целыми числами.
Теперь выясним входят ли концы отрезка в решение неравенства.
Знаки в заданном неравенстве — 18 < х < 174 строгие и при изображении этих точек на координатной прямой они будут выколотыми и не будут являться решением неравенства.
Найдем количество целых решений неравенства — 18 < х < 174
Чтобы посчитать число целых решений неравенства можно поступить двумя способами:
1) выписать все целые числа удовлетворяющие неравенству и сосчитать их;
2) методом логических рассуждений вычислить число отрицательных решений, число положительных решений и не забыть про ноль.
Давайте решим наше задание вторым способом.
Рассмотрим отрезок (- 18; 0). На нем целых чисел, удовлетворяющих нашему неравенству будет 17 (так как -18 не входит и число 0 мы посчитаем отдельно).
0 будем считать за 1 решение неравенства.
Рассмотрим отрезок (0; 174). На нем целых чисел, удовлетворяющих неравенству 173.
Сложим число всех найденных решений на каждом из рассмотренных отрезков и получим:
Что значит найти целые решения системы неравенств. Найти целые цешения системы неравенств. Соблюдение вашей конфиденциальности на уровне компании
В алгебре часто требуется не просто решить систему неравенств, но выбрать из полученного множества решений решения, удовлетворяющие некоторым дополнительным условиям.
Найти целые решения системы неравенств — одно из заданий такого рода.
1) Найти целые решения системы неравенств:
Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:
Title=»Rendered by QuickLaTeX.com»>
После упрощения разделим обе части каждого неравенства на . При делении на положительное число знак неравенства не меняется:
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.com»>
Отмечаем решения неравенств на числовых прямых. является пересечение решений (то есть та часть, где штриховка есть на обеих прямых).
Оба неравенства строгие, поэтому -4 и 2 изображаются выколотыми точками и в решение не входят:
Из промежутка (-4;2) выбираем целые решения.
Ответ: -3; -2; -1; 0; 1.
2) Какие целые решения имеет система неравенств?
Title=»Rendered by QuickLaTeX.com»>
Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком
Title=»Rendered by QuickLaTeX.com»>
Упрощаем и делим обе части на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не меняется, второе — на отрицательное число, поэтому знак неравенства изменяется на противоположный:
Title=»Rendered by QuickLaTeX.com»>
Отмечаем решения неравенств на числовых прямых. Первое неравенство нестрогое, поэтому -2 изображаем закрашенной точкой. Второе неравенство нестрогое, соответственно, 5 изображается выколотой точкой:
Целые решения на промежутке [-2;5) — это -2; -1; 0; 1; 2; 3; 4.
Ответ: -2; -1; 0; 1; 2; 3; 4.
В некоторых примерах не требуется перечислять целые решения, нужно лишь указать их количество.
3) Сколько целых решений имеет система неравенств?
Переносим неизвестные в одну сторону, известные — в другую:
Title=»Rendered by QuickLaTeX.com»>
Обе части первого неравенства делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Обе части второго неравенства делим на положительное число, знак неравенства при этом не меняется:
Решение неравенств отмечаем на числовых прямых. Оба неравенства нестрогие, поэтому -3,5 и 1,7 изображаем закрашенными точками:
Решением системы является промежуток [-3,5; 1,7]. Целые числа, которые входят в данный промежуток — это -3; -2; -1; 0; 1. Всего их 5.
4) Сколько целых чисел являются решениями системы неравенств?
Неравенство это выражение с, ≤, или ≥. Например, 3x — 5 Решить неравенство означает найти все значения переменных, при которых это неравенство верно. Каждое из этих чисел является решением неравенства, а множество всех таких решений является его множеством решений . Неравенства, которые имеют то же множество решений, называются эквивалентными неравенствами .
Линейные неравенства
Принципы решения неравенств
Для любых вещественных чисел a, b, и c :
Принцип прибавления неравенств : Если a Принцип умножения для неравенств : Если a 0 верно, тогда ac Если a bc также верно.
Подобные утверждения также применяются для a ≤ b.
Когда обе стороны неравенства умножаются на отрицательное число, необходимо полностью изменить знак неравенства.
Неравенства первого уровня, как в примере 1 (ниже), называются линейными неравенствами .
Пример 1 Решите каждое из следующих неравенств. Затем изобразите множество решений.
a) 3x — 5 b) 13 — 7x ≥ 10x — 4
Решение
Любое число, меньше чем 11/5, является решением.
Множество решений есть Чтобы сделать проверку, мы можем нарисовать график y 1 = 3x — 5 и y 2 = 6 — 2x. Тогда отсюда видно, что для x
Множеством решений есть , или (-∞, 1]. График множества решений изображён ниже.
Двойные неравенства
Когда два неравенства соединены словом и , или , тогда формируется двойное неравенство . Двойное неравенство, как
-3 и 2x + 5 ≤ 7
называется соединённым , потому что в нём использовано и . Запись -3 Двойные неравенства могут быть решены с использованием принципов прибавления и умножения неравенств.
Пример 2 Решите -3 Решение У нас есть
Множество решений или x > 3>. Мы можем также написать решение с использованием обозначения интервала и символ для объединения или включения обоих множеств: (-∞ -1] (3, ∞). График множества решений изображен ниже.
Для проверки, нарисуем y 1 = 2x — 5, y 2 = -7, и y 3 = 1. Заметьте, что для или x > 3>, y 1 ≤ y 2 или y 1 > y 3 .
Неравенства с абсолютным значением (модулем)
Неравенства иногда содержат модули. Следующие свойства используются для их решения.
Для а > 0 и алгебраического выражения x:
|x| |x| > a эквивалентно x или x > a.
Подобные утверждения и для |x| ≤ a и |x| ≥ a.
Например,
|x| |y| ≥ 1 эквивалентно y ≤ -1 или y ≥ 1;
и |2x + 3| ≤ 4 эквивалентно -4 ≤ 2x + 3 ≤ 4.
Пример 4 Решите каждое из следующих неравенств. Постройте график множества решений.
a) |3x + 2| b) |5 — 2x| ≥ 1
Решение
a) |3x + 2|
Множеством решением есть
b) |5 — 2x| ≥ 1
Множеством решением есть или x ≥ 3>, или (-∞, 2] .
Весь выше прописанный алгоритм записывается так:
3 · x + 12 ≤ 0 ; 3 · x ≤ − 12 ; x ≤ − 4 .
Ответ: x ≤ − 4 или (− ∞ , − 4 ] .
Указать все имеющиеся решения неравенства − 2 , 7 · z > 0 .
Решение
Из условия видим, что коэффициент a при z равняется — 2 , 7 , а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.
Производим деление обеих частей уравнения на число — 2 , 7 . Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что (− 2 , 7 · z) : (− 2 , 7) 0 ; z , ≥) :
Числовое неравенство вида b , ≥) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.
Решить неравенство 0 · x + 7 > 0 .
Решение
Данное линейное неравенство 0 · x + 7 > 0 может принимать любое значение x . Тогда получим неравенство вида 7 > 0 . Последнее неравенство считается верным, значит любое число может быть его решением.
Ответ : промежуток (− ∞ , + ∞) .
Найти решение неравенства 0 · x − 12 , 7 ≥ 0 .
Решение
При подстановке переменной x любого числа получим, что неравенство получит вид − 12 , 7 ≥ 0 . Оно является неверным. То есть 0 · x − 12 , 7 ≥ 0 не имеет решений.
Ответ: решений нет.
Рассмотрим решение линейных неравенств, где оба коэффициента равняется нулю.
Определить не имеющее решение неравенство из 0 · x + 0 > 0 и 0 · x + 0 ≥ 0 .
Решение
При подстановке любого числа вместо x получим два неравенства вида 0 > 0 и 0 ≥ 0 . Первое является неверным. Значит, 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет бесконечное количество решений, то есть любое число.
Ответ : неравенство 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет решения.
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0 . Иначе придется вычислять при помощи другого метода.
Метод интервалов – это:
- введение функции y = a · x + b ;
- поиск нулей для разбивания области определения на промежутки;
- определение знаков для понятия их на промежутках.
Соберем алгоритм для решения линейных уравнений a · x + b , ≥) при a ≠ 0 с помощью метода интервалов:
- нахождение нулей функции y = a · x + b , чтобы решить уравнение вида a · x + b = 0 . Если a ≠ 0 , тогда решением будет единственный корень, который примет обозначение х 0 ;
- построение координатной прямой с изображением точки с координатой х 0 , при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
- определение знаков функции y = a · x + b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
- решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, 0 .
Решение
Из алгоритма следует, что для начала нужно найти корень уравнения − 3 · x + 12 = 0 . Получаем, что − 3 · x = − 12 , x = 4 . Необходимо изобразить координатную прямую, где отмечаем точку 4 . Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.
Нужно определить знаки на промежутках. Чтобы определить его на промежутке (− ∞ , 4) , необходимо произвести вычисление функции y = − 3 · x + 12 при х = 3 . Отсюда получим, что − 3 · 3 + 12 = 3 > 0 . Знак на промежутке является положительным.
Определяем знак из промежутка (4 , + ∞) , тогда подставляем значение х = 5 . Имеем, что − 3 · 5 + 12 = − 3 , причем штриховка выполняется над положительным промежутком. Рассмотрим чертеж, приведенный ниже.
Из чертежа видно, что искомое решение имеет вид (− ∞ , 4) или x 0 и 0 , 5 · x − 1 ≥ 0 . Их решениями будут значения x 2 и x ≥ 2 . Для этого изобразим график линейной функции y = 0 , 5 · x − 1 , приведенный ниже.
- решением неравенства 0 , 5 · x − 1 0 считается промежуток, гре функция располагается выше О х;
- решением 0 , 5 · x − 1 ≥ 0 считается промежуток, где график выше О х или совпадает.
Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике. В данном случае получаем, что левая часть имеет y = a · x + b , а правая – y = 0 , причем совпадает с О х.
Построение графика функции y = a · x + b производится:
- во время решения неравенства a · x + b 0 производится определение промежутка, где график изображается выше О х;
- во время решения неравенства a · x + b ≥ 0 производится определение промежутка, где график находится выше О х или совпадает.
Решить неравенство — 5 · x — 3 > 0 при помощи графика.
Решение
Необходимо построить график линейной функции — 5 · x — 3 > 0 . Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с О х — 5 · x — 3 > 0 получим значение — 3 5 . Изобразим графически.
Решение неравенства со знаком > , тогда необходимо обратить внимание на промежуток выше О х. Выделим красным цветом необходимую часть плоскости и получим, что
Необходимый промежуток является частью О х красного цвета. Значит, открытый числовой луч — ∞ , — 3 5 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки — 3 5 также являлось бы решением неравенства. И совпадало бы с О х.
Ответ : — ∞ , — 3 5 или x 0 , 7 · (x − 1) + 3 ≤ 4 · x − 2 + x , x — 3 5 — 2 · x + 1 > 2 7 · x .
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
При сведении неравенства 5 − 2 · x > 0 к линейному, представляем его таким образом, чтобы оно имело вид − 2 · x + 5 > 0 , а для приведения второго получаем, что 7 · (x − 1) + 3 ≤ 4 · x − 2 + x . Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
7 · x − 7 + 3 ≤ 4 · x − 2 + x 7 · x − 4 ≤ 5 · x − 2 7 · x − 4 − 5 · x + 2 ≤ 0 2 · x − 2 ≤ 0
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
- раскрыть скобки;
- слева собрать переменные, а справа числа;
- привести подобные слагаемые;
- разделить обе части на коэффициент при x .
Решить неравенство 5 · (x + 3) + x ≤ 6 · (x − 3) + 1 .
Решение
Производим раскрытие скобок, тогда получим неравенство вида 5 · x + 15 + x ≤ 6 · x − 18 + 1 . После приведения подобных слагаемых имеем, что 6 · x + 15 ≤ 6 · x − 17 . После перенесения слагаемых с левой в правую, получим, что 6 · x + 15 − 6 · x + 17 ≤ 0 . Отсюда имеет неравенство вида 32 ≤ 0 из полученного при вычислении 0 · x + 32 ≤ 0 . Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Ответ : нет решений.
Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 5 2 · x − 1 ≥ 1 является показательным уравнением, которое сводится к решению линейного вида 2 · x − 1 ≥ 0 . Эти случаи будут рассмотрены при решении неравенств данного вида.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Решение целых и дробно рациональных неравенств
Продолжаем разбирать способы решения неравенств, имеющих в составе одну переменную. Мы уже изучили линейные и квадратные неравенства, которые представляют из себя частные случаи рациональных неравенств. В этой статье мы уточним, неравенства какого типа относятся к рациональным, расскажем, на какие виды они делятся (целые и дробные). После этого покажем, как правильно их решать, приведем нужные алгоритмы и разберем конкретные задачи.
Понятие рациональных равенств
Когда в школе изучают тему решения неравенств, то сразу берут рациональные неравенства. На них приобретаются и оттачиваются навыки работы с этим видом выражений. Сформулируем определение данного понятия:
Рациональное неравенство представляет из себя такое неравенство с переменными, которое содержит в обоих частях рациональные выражения.
Отметим, что определение никак не затрагивает вопрос количества переменных, значит, их может быть сколь угодно много. Следовательно, возможны рациональные неравенства с 1 , 2 , 3 и более переменными. Чаще всего приходится иметь дело с выражениями, содержащими всего одну переменную, реже две, а неравенства с большим количеством переменных обычно в рамках школьного курса не рассматривают вовсе.
Таким образом, мы можем узнать рациональное неравенство, посмотрев на его запись. И с правой, и с левой стороны у него должны быть расположены рациональные выражения. Приведем примеры:
x > 4 x 3 + 2 · y ≤ 5 · ( y − 1 ) · ( x 2 + 1 ) 2 · x x — 1 ≥ 1 + 1 1 + 3 x + 3 · x 2
А вот неравенство вида 5 + x + 1 < x · y · z не относится к рациональным, поскольку слева у него есть переменная под знаком корня.
Все рациональные неравенства делятся на целые и дробные.
Целое рациональное равенство состоит из целых рациональных выражений (в обеих частях).
Дробно рациональное равенство – это такое равенство, которое содержит дробное выражение в одной или обеих своих частях.
Например, неравенства вида 1 + x — 1 1 3 2 2 + 2 3 + 2 11 — 2 · 1 3 · x — 1 > 4 — x 4 и 1 — 2 3 5 — y > 1 x 2 — y 2 являются дробно рациональными, а 0 , 5 · x ≤ 3 · ( 2 − 5 · y ) и 1 : x + 3 > 0 – целыми.
Мы разобрали, что из себя представляют рациональные неравенства, и выделили их основные типы. Можем переходить дальше, к обзору способов их решения.
Как решать целые неравенства
Допустим, что нам требуется найти решения целого рационального неравенства r ( x ) < s ( x ) , которое включает в себя только одну переменную x . При этом r ( x ) и s ( x ) представляют собой любые целые рациональные числа или выражения, а знак неравенства может отличаться. Чтобы решить это задание, нам нужно преобразовать его и получить равносильное равенство.
Начнем с перенесения выражения из правой части в левую. Получим следующее:
вида r ( x ) − s ( x ) < 0 ( ≤ , > , ≥ )
Мы знаем, что r ( x ) − s ( x ) будет целым значением, а любое целое выражение допустимо преобразовать в многочлен. Преобразуем r ( x ) − s ( x ) в h ( x ) . Это выражение будет тождественно равным многочленом. Учитывая, что у r ( x ) − s ( x ) и h ( x ) область допустимых значений x одинакова, мы можем перейти к неравенствам h ( x ) < 0 ( ≤ , > , ≥ ) , которое будет равносильно исходному.
Зачастую такого простого преобразования будет достаточно для решения неравенства, поскольку в итоге может получиться линейное или квадратное неравенство, значение которого вычислить несложно. Разберем такие задачи.
Условие: решите целое рациональное неравенство x · ( x + 3 ) + 2 · x ≤ ( x + 1 ) 2 + 1 .
Решение
Начнем с переноса выражения из правой части в левую с противоположным знаком.
x · ( x + 3 ) + 2 · x − ( x + 1 ) 2 − 1 ≤ 0
Теперь, когда мы выполнили все действия с многочленами слева, можно переходить к линейному неравенству 3 · x − 2 ≤ 0 , равносильному тому, что было дано в условии. Решить его несложно:
Ответ: x ≤ 2 3 .
Условие: найдите решение неравенства ( x 2 + 1 ) 2 − 3 · x 2 > ( x 2 − x ) · ( x 2 + x ) .
Решение
Переносим выражение из левой части в правую и выполняем дальнейшие преобразования с помощью формул сокращенного умножения.
( x 2 + 1 ) 2 − 3 · x 2 − ( x 2 − x ) · ( x 2 + x ) > 0 x 4 + 2 · x 2 + 1 − 3 · x 2 − x 4 + x 2 > 0 1 > 0
В итоге наших преобразований мы получили неравенство, которое будет верным при любых значениях x , следовательно, решением исходного неравенства может быть любое действительное число.
Ответ: любое действительно число.
Условие: решите неравенство x + 6 + 2 · x 3 − 2 · x · ( x 2 + x − 5 ) > 0 .
Решение
Из правой части мы ничего переносить не будем, поскольку там 0 . Начнем сразу с преобразования левой части в многочлен:
x + 6 + 2 · x 3 − 2 · x 3 − 2 · x 2 + 10 · x > 0 − 2 · x 2 + 11 · x + 6 > 0 .
Мы вывели квадратное неравенство, равносильное исходному, которое легко решить несколькими методами. Применим графический способ.
Начнем с вычисления корней квадратного трехчлена − 2 · x 2 + 11 · x + 6 :
D = 11 2 — 4 · ( — 2 ) · 6 = 169 x 1 = — 11 + 169 2 · — 2 , x 2 = — 11 — 169 2 · — 2 x 1 = — 0 , 5 , x 2 = 6
Теперь на схеме отметим все необходимые нули. Поскольку старший коэффициент меньше нуля, ветви параболы на графике будут смотреть вниз.
Нам будет нужна область параболы, расположенная над осью абсцисс, поскольку в неравенстве у нас стоит знак > . Нужный интервал равен ( − 0 , 5 , 6 ) , следовательно, эта область значений и будет нужным нам решением.
Ответ: ( − 0 , 5 , 6 ) .
Бывают и более сложные случаи, когда слева получается многочлен третьей или более высокой степени. Чтобы решить такое неравенство, рекомендуется использовать метод интервалов. Сначала мы вычисляем все корни многочлена h ( x ) , что чаще всего делается с помощью разложения многочлена на множители.
Условие: вычислите ( x 2 + 2 ) · ( x + 4 ) < 14 − 9 · x .
Решение
Начнем, как всегда, с переноса выражения в левую часть, после чего нужно будет выполнить раскрытие скобок и приведение подобных слагаемых.
( x 2 + 2 ) · ( x + 4 ) − 14 + 9 · x < 0 x 3 + 4 · x 2 + 2 · x + 8 − 14 + 9 · x < 0 x 3 + 4 · x 2 + 11 · x − 6 < 0
В итоге преобразований у нас получилось равносильное исходному равенство, слева у которого стоит многочлен третьей степени. Применим метод интервалов для его решения.
Сначала вычисляем корни многочлена, для чего нам надо решить кубическое уравнение x 3 + 4 · x 2 + 11 · x − 6 = 0 . Имеет ли оно рациональные корни? Они могут быть лишь в числе делителей свободного члена, т.е. среди чисел ± 1 , ± 2 , ± 3 , ± 6 . Подставим их по очереди в исходное уравнение и выясним, что числа 1 , 2 и 3 будут его корнями.
Значит, многочлен x 3 + 4 · x 2 + 11 · x − 6 может быть описан в виде произведения ( x − 1 ) · ( x − 2 ) · ( x − 3 ) , и неравенство x 3 + 4 · x 2 + 11 · x − 6 < 0 может быть представлено как ( x − 1 ) · ( x − 2 ) · ( x − 3 ) < 0 . С неравенством такого вида нам потом будет легче определить знаки на промежутках.
Далее выполняем оставшиеся шаги интервального метода: рисуем числовую прямую и точки на ней с координатами 1 , 2 , 3 . Они разбивают прямую на 4 промежутка, в которых нужно определить знаки. Заштрихуем промежутки с минусом, поскольку исходное неравенство имеет знак < .
Нам осталось только записать готовый ответ: ( − ∞ , 1 ) ∪ ( 2 , 3 ) .
Ответ: ( − ∞ , 1 ) ∪ ( 2 , 3 ) .
В некоторых случаях выполнять переход от неравенства r ( x ) − s ( x ) < 0 ( ≤ , > , ≥ ) к h ( x ) < 0 ( ≤ , > , ≥ ) , где h ( x ) – многочлен в степени выше 2 , нецелесообразно. Это распространяется на те случаи, когда представить r ( x ) − s ( x ) как произведение линейных двучленов и квадратных трехчленов проще, чем разложить h ( x ) на отдельные множители. Разберем такую задачу.
Условие: найдите решение неравенства ( x 2 − 2 · x − 1 ) · ( x 2 − 19 ) ≥ 2 · x · ( x 2 − 2 · x − 1 ) .
Решение
Данное неравенство относится к целым. Если мы перенесем выражение из правой части влево, раскроем скобки и выполним приведение слагаемых, то получим x 4 − 4 · x 3 − 16 · x 2 + 40 · x + 19 ≥ 0 .
Решить такое неравенство непросто, поскольку придется искать корни многочлена четвертой степени. Оно не имеет ни одного рационального корня (так, 1 , − 1 , 19 или − 19 не подходят), а искать другие корни сложно. Значит, воспользоваться этим способом мы не можем.
Но есть и другие способы решения. Если мы перенесем выражения из правой части исходного неравенства в левую, то сможем выполнить вынесение за скобки общего множителя x 2 − 2 · x − 1:
( x 2 − 2 · x − 1 ) · ( x 2 − 19 ) − 2 · x · ( x 2 − 2 · x − 1 ) ≥ 0 ( x 2 − 2 · x − 1 ) · ( x 2 − 2 · x − 19 ) ≥ 0 .
Мы получили неравенство, равносильное исходному, и его решение даст нам искомый ответ. Найдем нули выражения в левой части, для чего решим квадратные уравнения x 2 − 2 · x − 1 = 0 и x 2 − 2 · x − 19 = 0 . Их корни – 1 ± 2 , 1 ± 2 5 . Переходим к равенству x — 1 + 2 · x — 1 — 2 · x — 1 + 2 5 · x — 1 — 2 5 ≥ 0 , которое можно решить методом интервалов:
Согласно рисунку, ответом будет — ∞ , 1 — 2 5 ∪ 1 — 2 5 , 1 + 2 ∪ 1 + 2 5 , + ∞ .
Ответ: — ∞ , 1 — 2 5 ∪ 1 — 2 5 , 1 + 2 ∪ 1 + 2 5 , + ∞ .
Добавим, что иногда нет возможности найти все корни многочлена h ( x ) , следовательно, мы не можем представить его в виде произведения линейных двучленов и квадратных трехчленов. Тогда решить неравенство вида h ( x ) < 0 ( ≤ , > , ≥ ) мы не можем, значит, решить исходное рациональное неравенство тоже нельзя.
Как решать дробно рациональные неравенства
Допустим, надо решить дробно рационально неравенств вида r ( x ) < s ( x ) ( ≤ , > , ≥ ) , где r ( x ) и s ( x ) являются рациональными выражениями, x – переменной. Хотя бы одно из указанных выражений будет дробным. Алгоритм решения в этом случае будет таким:
- Определяем область допустимых значений переменной x .
- Переносим выражение из правой части неравенства налево, а получившееся выражение r ( x ) − s ( x ) представляем в виде дроби. При этом где p ( x ) и q ( x ) будут целыми выражениями, которые являются произведениями линейных двучленов, неразложимых квадратных трехчленов, а также степеней с натуральным показателем.
- Далее решаем полученное неравенство методом интервалов.
- Последним шагом является исключение точек, полученных в ходе решения, из области допустимых значений переменной x , которую мы определили в начале.
Это и есть алгоритм решения дробно рационального неравенства. Большая часть его понятна, небольшие пояснения требуются только для п. 2 . Мы перенесли выражение из правой части налево и получили r ( x ) − s ( x ) < 0 ( ≤ , > , ≥ ) , а как потом привести его к виду p ( x ) q ( x ) < 0 ( ≤ , > , ≥ ) ?
Сначала определим, всегда ли можно выполнить данное преобразование. Теоретически, такая возможность имеется всегда, поскольку в рациональную дробь можно преобразовать любое рациональное выражение. Здесь же у нас есть дробь с многочленами в числителе и знаменателе. Вспомним основную теорему алгебры и теорему Безу и определим, что любой многочлен n -ной степени, содержащий одну переменную, может быть преобразован в произведение линейных двучленов. Следовательно, в теории мы всегда можем преобразовать выражение таким образом.
На практике разложение многочленов на множители зачастую оказывается довольно трудной задачей, особенно если степень выше 4 . Если мы не сможем выполнить разложение, то не сможем и решить данное неравенство, однако в рамках школьного курса такие проблемы обычно не изучаются.
Далее нам надо решить, будет ли полученное неравенство p ( x ) q ( x ) < 0 ( ≤ , > , ≥ ) равносильным по отношению к r ( x ) − s ( x ) < 0 ( ≤ , > , ≥ ) и к исходному. Есть вероятность, что оно может оказаться и неравносильным.
Равносильность неравенства будет обеспечена тогда, когда область допустимых значений p ( x ) q ( x ) совпадет с областью значений выражения r ( x ) − s ( x ) . Тогда последний пункт инструкции по решению дробно рациональных неравенств выполнять не нужно.
Но область значений для p ( x ) q ( x ) может оказаться шире, чем у r ( x ) − s ( x ) , например, за счет сокращения дробей. Примером может быть переход от x · x — 1 3 x — 1 2 · x + 3 к x · x — 1 x + 3 . Либо это может происходить при приведении подобных слагаемых, например, здесь:
x + 5 x — 2 2 · x — x + 5 x — 2 2 · x + 1 x + 3 к 1 x + 3
Для таких случаев и добавлен последний шаг алгоритма. Выполнив его, вы избавитесь от посторонних значений переменной, которые возникают из-за расширения области допустимых значений. Возьмем несколько примеров, чтобы было более понятно, о чем идет речь.
Условие: найдите решения рационального равенства x x + 1 · x — 3 + 4 x — 3 2 ≥ — 3 · x x — 3 2 · x + 1 .
Решение
Действуем по алгоритму, указанному выше. Сначала определяем область допустимых значений. В данном случае она определяется системой неравенств x + 1 · x — 3 ≠ 0 x — 3 2 ≠ 0 x — 3 2 · ( x + 1 ) ≠ 0 , решением которой будет множество ( − ∞ , − 1 ) ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) .
Далее нам надо сделать так, чтобы в правой части неравенства получился 0 . Выполняем перенос выражения из правой части влево с противоположным знаком и получаем неравенство, равносильное исходному:
x x + 1 · x — 3 + 4 ( x — 3 ) 2 + 3 · x ( x — 3 ) 2 · ( x + 1 ) ≥ 0
После этого нам нужно преобразовать его так, чтобы было удобно применить метод интервалов. Первым делом приводим алгебраические дроби к наименьшему общему знаменателю ( x − 3 ) 2 · ( x + 1 ) :
x x + 1 · x — 3 + 4 ( x — 3 ) 2 + 3 · x ( x — 3 ) 2 · ( x + 1 ) = = x · x — 3 + 4 · x + 1 + 3 · x x — 3 2 · x + 1 = x 2 + 4 · x + 4 ( x — 3 ) 2 · ( x + 1 )
Сворачиваем выражение в числителе, применяя формулу квадрата суммы:
x 2 + 4 · x + 4 x — 3 2 · x + 1 = x + 2 2 x — 3 2 · x + 1
Областью допустимых значений получившегося выражения является ( − ∞ , − 1 ) ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) . Мы видим, что она аналогична той, что была определена для исходного равенства. Заключаем, что неравенство x + 2 2 x — 3 2 · x + 1 ≥ 0 является равносильным исходному, значит, последний шаг алгоритма нам не нужен.
Используем метод интервалов:
Видим решение ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) , которое и будет решением исходного рационального неравенства x x + 1 · x — 3 + 4 x — 3 2 ≥ — 3 · x ( x — 3 ) 2 · ( x + 1 ) .
Ответ: ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) .
Условие: вычислите решение x + 3 x — 1 — 3 x x + 2 + 2 x — 1 > 1 x + 1 + 2 · x + 2 x 2 — 1 .
Решение
Определяем область допустимых значений. В случае с этим неравенством она будет равна всем действительным числам, кроме − 2 , − 1 , 0 и 1 .
Переносим выражения из правой части в левую:
x + 3 x — 1 — 3 x x + 2 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 > 0
Далее выполняем преобразование левой части. Сначала преобразуем первую дробь:
x + 3 x — 1 — 3 x x + 2 = x + 3 — x — 3 x x + 2 = 0 x x + 2 = 0 x + 2 = 0
Учитывая получившийся результат, запишем:
x + 3 x — 1 — 3 x x + 2 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 0 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 2 x — 1 — 1 x + 1 — 2 · x + 2 ( x + 1 ) · x — 1 = = — x — 1 ( x + 1 ) · x — 1 = — x + 1 ( x + 1 ) · x — 1 = — 1 x — 1
Для выражения — 1 x — 1 областью допустимых значений будет множество всех действительных чисел, за исключением единицы. Мы видим, что область значений расширилась: в нее были добавлены − 2 , − 1 и 0 . Значит, нам нужно выполнить последний шаг алгоритма.
Поскольку мы пришли к неравенству — 1 x — 1 > 0 , можем записать равносильное ему 1 x — 1 < 0 . С помощью метода интервалов вычислим решение и получим ( − ∞ , 1 ) .
Исключаем точки, которые не входят в область допустимых значений исходного равенства. Нам надо исключить из ( − ∞ , 1 ) числа − 2 , − 1 и 0 . Таким образом, решением рационального неравенства x + 3 x — 1 — 3 x x + 2 + 2 x — 1 > 1 x + 1 + 2 · x + 2 x 2 — 1 будут значения ( − ∞ , − 2 ) ∪ ( − 2 , − 1 ) ∪ ( − 1 , 0 ) ∪ ( 0 , 1 ) .
Ответ: ( − ∞ , − 2 ) ∪ ( − 2 , − 1 ) ∪ ( − 1 , 0 ) ∪ ( 0 , 1 ) .
В заключение приведем еще один пример задачи, в котором окончательный ответ зависит от области допустимых значений.
Условие: найдите решение неравенства 5 + 3 x 2 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≥ 0 .
Решение
Область допустимых значений неравенства, заданного в условии, определяет система x 2 ≠ 0 x 2 — x + 1 ≠ 0 x — 1 ≠ 0 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≠ 0 .
Решений у этой системы нет, поскольку
x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 = = ( x + 1 ) · x 2 — x + 1 x 2 — x + 1 — ( x — 1 ) · x + 1 x — 1 = = x + 1 — ( x + 1 ) = 0
Значит, исходное равенство 5 + 3 x 2 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≥ 0 не имеет решения, поскольку нет таких значений переменной, при которой оно имело бы смысл.
Содержание
- Найти целые цешения системы неравенств
- Метод интервалов, решение неравенств
- Определение квадратного неравенства
- Решение неравенства графическим методом
- Решение неравенства методом интервалов
- Плюс или минус: как определить знаки
- Решение линейных неравенств
- Как решить линейное неравенство
- Правило переноса в неравенствах
- Правило умножения или деления неравенства на число
Найти целые цешения системы неравенств
В алгебре часто требуется не просто решить систему неравенств, но выбрать из полученного множества решений решения, удовлетворяющие некоторым дополнительным условиям.
Найти целые решения системы неравенств — одно из заданий такого рода.
1) Найти целые решения системы неравенств:

Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:

После упрощения разделим обе части каждого неравенства на b» href=»http://www.algebraclass.ru/axb/» target=»_blank»>число, стоящее перед иксом. При делении на положительное число знак неравенства не меняется:


Отмечаем решения неравенств на числовых прямых. Решением системы является пересечение решений (то есть та часть, где штриховка есть на обеих прямых).
Оба неравенства строгие, поэтому -4 и 2 изображаются выколотыми точками и в решение не входят:
Из промежутка (-4;2) выбираем целые решения.
Ответ: -3; -2; -1; 0; 1.
2) Какие целые решения имеет система неравенств?

Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком

Упрощаем и делим обе части на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не меняется, второе — на отрицательное число, поэтому знак неравенства изменяется на противоположный:

Отмечаем решения неравенств на числовых прямых. Первое неравенство нестрогое, поэтому -2 изображаем закрашенной точкой. Второе неравенство нестрогое, соответственно, 5 изображается выколотой точкой:
Целые решения на промежутке [-2;5) — это -2; -1; 0; 1; 2; 3; 4.
Ответ: -2; -1; 0; 1; 2; 3; 4.
В некоторых примерах не требуется перечислять целые решения, нужно лишь указать их количество.
3) Сколько целых решений имеет система неравенств?
Переносим неизвестные в одну сторону, известные — в другую:

Обе части первого неравенства делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Обе части второго неравенства делим на положительное число, знак неравенства при этом не меняется:
Решение неравенств отмечаем на числовых прямых. Оба неравенства нестрогие, поэтому -3,5 и 1,7 изображаем закрашенными точками:
Решением системы является промежуток [-3,5; 1,7]. Целые числа, которые входят в данный промежуток — это -3; -2; -1; 0; 1. Всего их 5.
4) Сколько целых чисел являются решениями системы неравенств?
Неизвестные — в одну сторону, известные — в другую с противоположным знаком:

При делении обеих частей неравенства на положительное число знак неравенства не изменяется, при делении на отрицательное число — меняется на противоположный:
Решение неравенств отмечаем на числовых прямых.
Множество решений системы состоит из единственного элемента — <2>. 2 — целое число, следовательно, решением данной системы является одно целое число.
Источник
Метод интервалов, решение неравенств
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
где x — переменная,
Квадратное неравенство можно решить двумя способами:
- графический метод;
- метод интервалов.
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два корня;
- D
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.
Если неравенство со знаком
Плюс или минус: как определить знаки
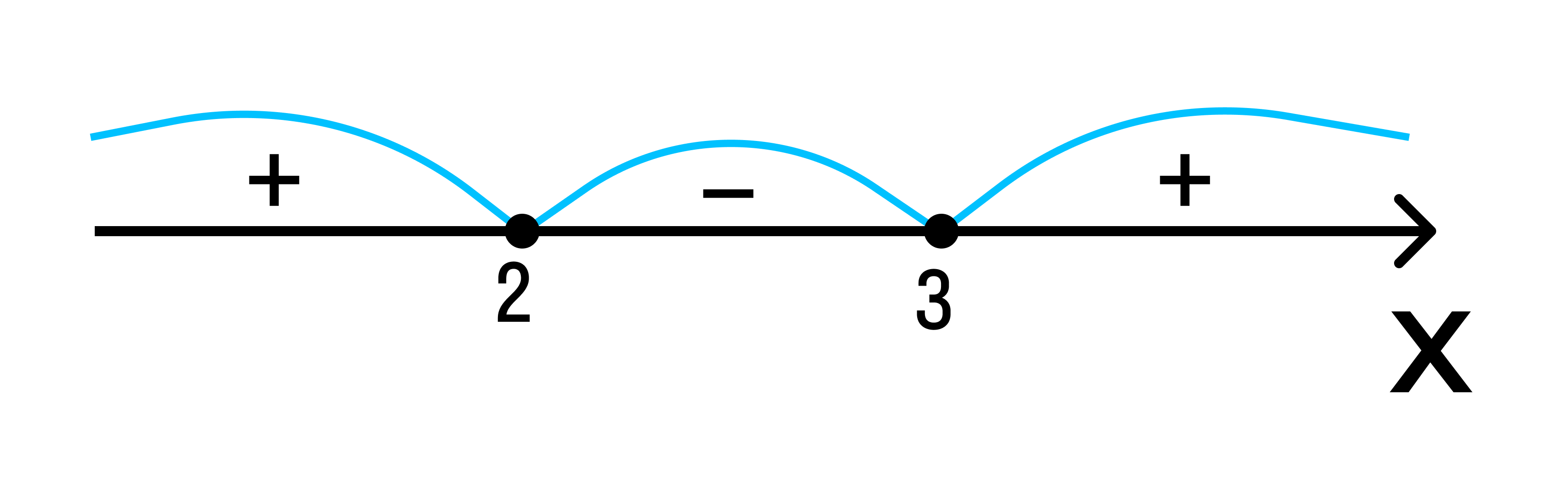
Можно сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, −, +,
если a 0, последовательность знаков: +, +,
если a 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.
Пример 1. Решить неравенство методом интервалов: x^2 — 5x + 6 ≥ 0.
Разложим квадратный трехчлен на множители.
Неравенство примет вид:
Проанализируем два сомножителя:
Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х — 3 > 0.
Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.
Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.
В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.
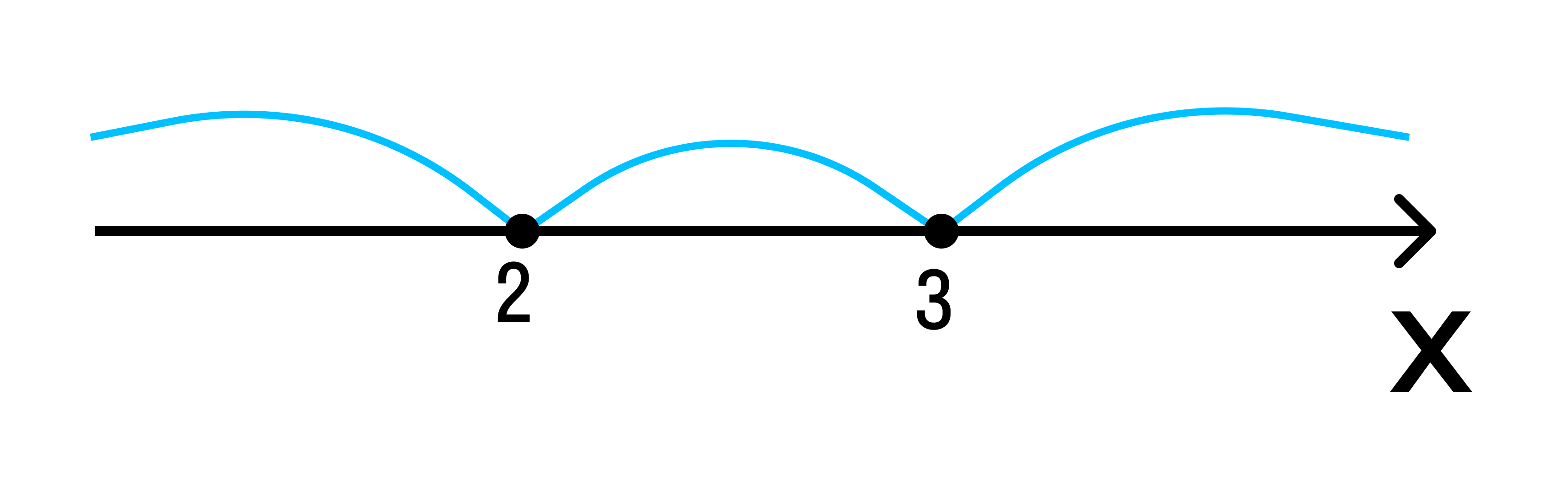
Отобразим эти данные на чертеже:
2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
- (25 — 3) (25 — 2) = 22*23 = 506 > 0
Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.
Исходное неравенство: (х — 3) * (х — 2) ≥ 0.
Если (х — 3) * (х — 2) > 0:
Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.
Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Ответ: х ≤ 0, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3
Источник
Решение линейных неравенств
Прежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для сравнения величин.
| Символ | Название | Тип знака |
|---|---|---|
| > | больше | строгий знак (число на границе не включается ) |
| строгий знак (число на границе не включается ) |
||
| ≥ | больше или равно | нестрогий знак (число на границе включается ) |
| ≤ | меньше или равно | нестрогий знак (число на границе включается ) |
Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство отличается от уравнения.
В отличии от уравнения в неравенстве вместо знака равно « = » используют любой знак сравнения: « > », « », « ≤ » или « ≥ ».
Линейным неравенством называют неравенство, в котором неизвестное стоит только в первой степени.
Рассмотрим пример линейного неравенства.
Как решить линейное неравенство
Чтобы решить неравенство, нужно чтобы в левой части осталось только неизвестное в первой степени с коэффициентом « 1 ».
При решении линейных неравенств используют правило переноса и правило деления неравенства на число.
Правило переноса в неравенствах
Также как и в уравнениях, в неравенствах можно переносить любой член неравенства из левой части в правую и наоборот.
При переносе из левой части в правую (и наоборот) член неравенства меняет свой знак на противоположный .
Вернемся к нашему неравенству и используем правило переноса.
Для того, чтобы понять, что получается при решении неравенства, нам нужно вспомнить, понятие числовой оси.
Нарисуем числовую ось для неизвестного « x » и отметим на ней число « 14 ».
При нанесении числа на числовую ось соблюдаются следующие правила:
- если неравенство строгое, то число отмечается как «пустая» точка.
Это означает, что число не входит в область решения;
- если неравенство нестрогое, то число отмечается как «заполненная» точка.
Это означает, что число входит в область решения.
Заштрихуем на числовой оси по полученному ответу « x » все решения неравенства, то есть область слева от числа « 14 ».
Рисунок выше говорит о том, что любое число из заштрихованной области при подстановке в исходное неравенство « x − 6 » даст верный результат.
Возьмем, например число « 12 » из заштрихованной области и подставим его вместо « x » в исходное неравенство « x − 6 ».
Другими словами, можно утверждать, что любое число из заштрихованной области будет являться решением неравенства.
Решить неравенство — это значит найти множество чисел, которые при подстановке в исходное неравенство дают верный результат.
Решением неравенства называют множество чисел из заштрихованной области на числовой оси.
В нашем примере ответ « x » можно понимать так: любое число из заштрихованной области (то есть любое число меньшее « 14 ») будет являться решением неравенства « x − 6 ».
Правило умножения или деления неравенства на число
Рассмотрим другое неравенство.
Используем правило переноса и перенесём все числа без неизвестного, в правую часть.
Теперь нам нужно сделать так, чтобы при неизвестном « x » стоял коэффициент « 1 ». Для этого достаточно разделить и левую, и правую часть на число « 2 ».
При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть.
- Если неравенство умножается (делится) на положительное число, то
знак самого неравенства остаётся прежним . - Если неравенство умножается (делится) на отрицательное число, то
знак самого неравенства меняется на противоположный .
Разделим « 2x > 16 » на « 2 ». Так как « 2 » — положительное число, знак неравенства останется прежним.
Рассмотрим другое неравенство.
Разделим неравенство на « −3 ». Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный.
Источник
В алгебре часто требуется не просто решить систему неравенств, но выбрать из полученного множества решений решения, удовлетворяющие некоторым дополнительным условиям.
Найти целые решения системы неравенств — одно из заданий такого рода.
1) Найти целые решения системы неравенств:
7x – 5\ 5 – x
Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:
Title=”Rendered by QuickLaTeX.com”>
После упрощения разделим обе части каждого неравенства на . При делении на положительное число знак неравенства не меняется:
Title=”Rendered by QuickLaTeX.com”>
Title=”Rendered by QuickLaTeX.com”>
Отмечаем решения неравенств на числовых прямых. является пересечение решений (то есть та часть, где штриховка есть на обеих прямых).
Оба неравенства строгие, поэтому -4 и 2 изображаются выколотыми точками и в решение не входят:
Из промежутка (-4;2) выбираем целые решения.
Ответ: -3; -2; -1; 0; 1.
2) Какие целые решения имеет система неравенств?
Title=”Rendered by QuickLaTeX.com”>
Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком
Title=”Rendered by QuickLaTeX.com”>
Упрощаем и делим обе части на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не меняется, второе — на отрицательное число, поэтому знак неравенства изменяется на противоположный:
Title=”Rendered by QuickLaTeX.com”>
Отмечаем решения неравенств на числовых прямых. Первое неравенство нестрогое, поэтому -2 изображаем закрашенной точкой. Второе неравенство нестрогое, соответственно, 5 изображается выколотой точкой:
Целые решения на промежутке [-2;5) — это -2; -1; 0; 1; 2; 3; 4.
Ответ: -2; -1; 0; 1; 2; 3; 4.
В некоторых примерах не требуется перечислять целые решения, нужно лишь указать их количество.
3) Сколько целых решений имеет система неравенств?
Переносим неизвестные в одну сторону, известные — в другую:
Title=”Rendered by QuickLaTeX.com”>
Обе части первого неравенства делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Обе части второго неравенства делим на положительное число, знак неравенства при этом не меняется:
Решение неравенств отмечаем на числовых прямых. Оба неравенства нестрогие, поэтому -3,5 и 1,7 изображаем закрашенными точками:
Решением системы является промежуток [-3,5; 1,7]. Целые числа, которые входят в данный промежуток — это -3; -2; -1; 0; 1. Всего их 5.
4) Сколько целых чисел являются решениями системы неравенств?
Неравенство
это выражение с, ≤, или ≥. Например, 3x – 5 Решить неравенство означает найти все значения переменных, при которых это неравенство верно.
Каждое из этих чисел является решением неравенства, а множество всех таких решений является его множеством решений
. Неравенства, которые имеют то же множество решений, называются эквивалентными неравенствами
.
Линейные неравенства
Принципы решения неравенств аналогичны принципам решения уравнений.
Принципы решения неравенств
Для любых вещественных чисел a, b,
и c
:
Принцип прибавления неравенств
: Если a
Принцип умножения для неравенств
: Если a 0 верно, тогда ac
Если a bc также верно.
Подобные утверждения также применяются для a ≤ b.
Когда обе стороны неравенства умножаются на отрицательное число, необходимо полностью изменить знак неравенства.
Неравенства первого уровня, как в примере 1 (ниже), называются линейными неравенствами
.
Пример 1
Решите каждое из следующих неравенств. Затем изобразите множество решений.
a) 3x – 5
b) 13 – 7x ≥ 10x – 4
Решение
Любое число, меньше чем 11/5, является решением.
Множество решений есть {x|x
Чтобы сделать проверку, мы можем нарисовать график y 1 = 3x – 5 и y 2 = 6 – 2x. Тогда отсюда видно, что для x
Множеством решений есть {x|x ≤ 1}, или (-∞, 1]. График множества решений изображён ниже.
Двойные неравенства
Когда два неравенства соединены словом и
, или
, тогда формируется двойное неравенство
.
Двойное неравенство, как
-3
и
2x + 5 ≤ 7
называется соединённым
, потому что в нём использовано и
. Запись -3
Двойные неравенства могут быть решены с использованием принципов прибавления и умножения неравенств.
Пример 2
Решите -3
Решение
У нас есть
Множество решений {x|x ≤ -1 или
x > 3}. Мы можем также написать решение с использованием обозначения интервала и символ для объединения
или включения обоих множеств: (-∞ -1] (3, ∞). График множества решений изображен ниже.
Для проверки, нарисуем y 1 = 2x – 5, y 2 = -7, и y 3 = 1. Заметьте, что для {x|x ≤ -1 или
x > 3}, y 1 ≤ y 2 или
y 1 > y 3 .
Неравенства с абсолютным значением (модулем)
Неравенства иногда содержат модули. Следующие свойства используются для их решения.
Для а > 0 и алгебраического выражения x:
|x|
|x| > a эквивалентно x или x > a.
Подобные утверждения и для |x| ≤ a и |x| ≥ a.
Например,
|x|
|y| ≥ 1 эквивалентно y ≤ -1 или
y ≥ 1;
и |2x + 3| ≤ 4 эквивалентно -4 ≤ 2x + 3 ≤ 4.
Пример 4
Решите каждое из следующих неравенств. Постройте график множества решений.
a) |3x + 2|
b) |5 – 2x| ≥ 1
Решение
a) |3x + 2|
Множеством решением есть {x|-7/3
b) |5 – 2x| ≥ 1
Множеством решением есть {x|x ≤ 2 или
x ≥ 3}, или (-∞, 2] .
Весь выше прописанный алгоритм записывается так:
3 · x + 12 ≤ 0 ; 3 · x ≤ − 12 ; x ≤ − 4 .
Ответ:
x ≤ − 4 или (− ∞ , − 4 ] .
Пример 2
Указать все имеющиеся решения неравенства − 2 , 7 · z > 0 .
Решение
Из условия видим, что коэффициент a при z равняется – 2 , 7 , а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.
Производим деление обеих частей уравнения на число – 2 , 7 . Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что (− 2 , 7 · z) : (− 2 , 7) < 0: (− 2 , 7) , и дальше z < 0 .
Весь алгоритм запишем в краткой форме:
− 2 , 7 · z > 0 ; z < 0 .
Ответ:
z < 0 или (− ∞ , 0) .
Пример 3
Решить неравенство – 5 · x – 15 22 ≤ 0 .
Решение
По условию видим, что необходимо решить неравенство с коэффициентом a при переменной x , которое равняется – 5 , с коэффициентом b , которому соответствует дробь – 15 22 . Решать неравенство необходимо, следуя алгоритму, то есть: перенести – 15 22 в другую часть с противоположным знаком, разделить обе части на – 5 , изменить знак неравенства:
5 · x ≤ 15 22 ; – 5 · x: – 5 ≥ 15 22: – 5 x ≥ – 3 22
При последнем переходе для правой части используется правило деления числе с разными знаками 15 22: – 5 = – 15 22: 5 , после чего выполняем деление обыкновенной дроби на натурально число – 15 22: 5 = – 15 22 · 1 5 = – 15 · 1 22 · 5 = – 3 22 .
Ответ:
x ≥ – 3 22 и [ – 3 22 + ∞) .
Рассмотрим случай, когда а = 0 . Линейное выражение вида a · x + b < 0 является неравенством 0 · x + b < 0 , где на рассмотрение берется неравенство вида b < 0 , после чего выясняется, оно верное или нет.
Все основывается на определении решения неравенства. При любом значении x получаем числовое неравенство вида b < 0 , потому что при подстановке любого t вместо переменной x , тогда получаем 0 · t + b < 0 , где b < 0 . В случае, если оно верно, то для его решения подходит любое значение. Когда b < 0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.
Все суждения рассмотрим в виде алгоритма решения линейных неравенств 0 · x + b < 0 (≤ , > , ≥) :
Определение 5
Числовое неравенство вида b < 0 (≤ , > , ≥) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.
Пример 4
Решить неравенство 0 · x + 7 > 0 .
Решение
Данное линейное неравенство 0 · x + 7 > 0 может принимать любое значение x . Тогда получим неравенство вида 7 > 0 . Последнее неравенство считается верным, значит любое число может быть его решением.
Ответ
: промежуток (− ∞ , + ∞) .
Пример 5
Найти решение неравенства 0 · x − 12 , 7 ≥ 0 .
Решение
При подстановке переменной x любого числа получим, что неравенство получит вид − 12 , 7 ≥ 0 . Оно является неверным. То есть 0 · x − 12 , 7 ≥ 0 не имеет решений.
Ответ:
решений нет.
Рассмотрим решение линейных неравенств, где оба коэффициента равняется нулю.
Пример 6
Определить не имеющее решение неравенство из 0 · x + 0 > 0 и 0 · x + 0 ≥ 0 .
Решение
При подстановке любого числа вместо x получим два неравенства вида 0 > 0 и 0 ≥ 0 . Первое является неверным. Значит, 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет бесконечное количество решений, то есть любое число.
Ответ
: неравенство 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет решения.
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0 . Иначе придется вычислять при помощи другого метода.
Определение 6
Метод интервалов – это:
- введение функции y = a · x + b ;
- поиск нулей для разбивания области определения на промежутки;
- определение знаков для понятия их на промежутках.
Соберем алгоритм для решения линейных уравнений a · x + b < 0 (≤ , > , ≥) при a ≠ 0 с помощью метода интервалов:
- нахождение нулей функции y = a · x + b , чтобы решить уравнение вида a · x + b = 0 . Если a ≠ 0 , тогда решением будет единственный корень, который примет обозначение х 0 ;
- построение координатной прямой с изображением точки с координатой х 0 , при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
- определение знаков функции y = a · x + b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
- решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, < или ≤ над отрицательным промежутком.
Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.
Пример 6
Решить неравенство − 3 · x + 12 > 0 .
Решение
Из алгоритма следует, что для начала нужно найти корень уравнения − 3 · x + 12 = 0 . Получаем, что − 3 · x = − 12 , x = 4 . Необходимо изобразить координатную прямую, где отмечаем точку 4 . Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.
Нужно определить знаки на промежутках. Чтобы определить его на промежутке (− ∞ , 4) , необходимо произвести вычисление функции y = − 3 · x + 12 при х = 3 . Отсюда получим, что − 3 · 3 + 12 = 3 > 0 . Знак на промежутке является положительным.
Определяем знак из промежутка (4 , + ∞) , тогда подставляем значение х = 5 . Имеем, что − 3 · 5 + 12 = − 3 < 0 . Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.
Мы выполняем решение неравенства со знаком > , причем штриховка выполняется над положительным промежутком. Рассмотрим чертеж, приведенный ниже.
Из чертежа видно, что искомое решение имеет вид (− ∞ , 4) или x < 4 .
Ответ
: (− ∞ , 4) или x < 4 .
Чтобы понять, как изображать графически, необходимо рассмотреть на примере 4 линейных неравенства: 0 , 5 · x − 1 < 0 , 0 , 5 · x − 1 ≤ 0 , 0 , 5 · x − 1 > 0 и 0 , 5 · x − 1 ≥ 0 . Их решениями будут значения x < 2 , x ≤ 2 , x > 2 и x ≥ 2 . Для этого изобразим график линейной функции y = 0 , 5 · x − 1 , приведенный ниже.
Видно, что
Определение 7
- решением неравенства 0 , 5 · x − 1 < 0 считается промежуток, где график функции y = 0 , 5 · x − 1 располагается ниже О х;
- решением 0 , 5 · x − 1 ≤ 0 считается промежуток, где функция y = 0 , 5 · x − 1 ниже О х или совпадает;
- решением 0 , 5 · x − 1 > 0 считается промежуток, гре функция располагается выше О х;
- решением 0 , 5 · x − 1 ≥ 0 считается промежуток, где график выше О х или совпадает.
Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике. В данном случае получаем, что левая часть имеет y = a · x + b , а правая – y = 0 , причем совпадает с О х.
Определение 8
Построение графика функции y = a · x + b производится:
- во время решения неравенства a · x + b < 0 определяется промежуток, где график изображен ниже О х;
- во время решения неравенства a · x + b ≤ 0 определяется промежуток, где график изображается ниже оси О х или совпадает;
- во время решения неравенства a · x + b > 0 производится определение промежутка, где график изображается выше О х;
- во время решения неравенства a · x + b ≥ 0 производится определение промежутка, где график находится выше О х или совпадает.
Пример 7
Решить неравенство – 5 · x – 3 > 0 при помощи графика.
Решение
Необходимо построить график линейной функции – 5 · x – 3 > 0 . Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с О х – 5 · x – 3 > 0 получим значение – 3 5 . Изобразим графически.
Решение неравенства со знаком > , тогда необходимо обратить внимание на промежуток выше О х. Выделим красным цветом необходимую часть плоскости и получим, что
Необходимый промежуток является частью О х красного цвета. Значит, открытый числовой луч – ∞ , – 3 5 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки – 3 5 также являлось бы решением неравенства. И совпадало бы с О х.
Ответ
: – ∞ , – 3 5 или x < – 3 5 .
Графический способ решения используется, когда левая часть будет отвечать функции y = 0 · x + b , то есть y = b . Тогда прямая будет параллельна О х или совпадающей при b = 0 . Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.
Пример 8
Определить из неравенств 0 · x + 7 < = 0 , 0 · x + 0 ≥ 0 то, которое имеет хотя бы одно решение.
Решение
Представление y = 0 · x + 7 является y = 7 , тогда будет задана координатная плоскость с прямой, параллельной О х и находящейся выше О х. Значит, 0 · x + 7 < = 0 решений не имеет, потому как нет промежутков.
График функции y = 0 · x + 0 , считается y = 0 , то есть прямая совпадает с О х. Значит, неравенство 0 · x + 0 ≥ 0 имеет множество решений.
Ответ
: второе неравенство имеет решение при любом значении x .
Неравенства, сводящиеся к линейным
Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.
Данные неравенства были рассмотрены в школьном курсе, так как они являлись частным случаем решения неравенств, что приводило к раскрытию скобок и приведению подобных слагаемых. Для примера рассмотрим, что 5 − 2 · x > 0 , 7 · (x − 1) + 3 ≤ 4 · x − 2 + x , x – 3 5 – 2 · x + 1 > 2 7 · x .
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
При сведении неравенства 5 − 2 · x > 0 к линейному, представляем его таким образом, чтобы оно имело вид − 2 · x + 5 > 0 , а для приведения второго получаем, что 7 · (x − 1) + 3 ≤ 4 · x − 2 + x . Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
7 · x − 7 + 3 ≤ 4 · x − 2 + x 7 · x − 4 ≤ 5 · x − 2 7 · x − 4 − 5 · x + 2 ≤ 0 2 · x − 2 ≤ 0
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
Определение 9
- раскрыть скобки;
- слева собрать переменные, а справа числа;
- привести подобные слагаемые;
- разделить обе части на коэффициент при x .
Пример 9
Решить неравенство 5 · (x + 3) + x ≤ 6 · (x − 3) + 1 .
Решение
Производим раскрытие скобок, тогда получим неравенство вида 5 · x + 15 + x ≤ 6 · x − 18 + 1 . После приведения подобных слагаемых имеем, что 6 · x + 15 ≤ 6 · x − 17 . После перенесения слагаемых с левой в правую, получим, что 6 · x + 15 − 6 · x + 17 ≤ 0 . Отсюда имеет неравенство вида 32 ≤ 0 из полученного при вычислении 0 · x + 32 ≤ 0 . Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Ответ
: нет решений.
Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 5 2 · x − 1 ≥ 1
является показательным уравнением, которое сводится к решению линейного вида 2 · x − 1 ≥ 0 . Эти случаи будут рассмотрены при решении неравенств данного вида.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Слайд 1
7. Методы решения уравнений и неравенств в целых числах Выполнила: ученица 11 «А» класса Устименко О.Д. Учитель математики: Кукса Б.И. 2014г. МОУ – СОШ № 3 г. Можайск Презентация на тему:
Слайд 2
7.1. Линейные уравнения Метод прямого перебора Использование неравенств Использование отношения делимости Метод «спуска» Использование формул 7.2. Нелинейные уравнения Метод разложения на множители Вынесение общих множителей за скобку Применение формул сокращенного умножения Использование параметра Метод решения относительно одной переменной выделение целой части Метод «спуска» метод конечного «спуска» Параметризация уравнения Функционально-графический метод 7.3. Неравенства Использование области определения Использование монотонности Использование ограниченности 7.4. Уравнения и неравенства Уравнение с одной неизвестной Показательные уравнения Неравенства Уравнения, содержащие функцию «целая часть числа» [ x ]
Слайд 3
Пример 74. В клетке сидят кролики и фазаны. Всего у них 18 ног. Узнать сколь- ко в клетке тех и других. Укажите все решения. Решение. Пусть х – количество кроликов , у – количество фазанов, тогда имеем уравнение 4 x + 2y = 18 или 2x + y = 9 Если х =1, то у=7. Если х=2, то у=5. Если х = 3, то у = 3. Если х = 4, то у = 1. При х = 5 получаем 2 ∙ 5 = 10 > 9. Ответ: (1 ;7), (2;5), (3;3), (4;1). 7.1. Линейные уравнения Метод прямого перебора
Слайд 4
Использование неравенств Пример 75. Решить в натуральных числах уравнение 5х + 8у = 39 Решение. Для уменьшения перебора вариантов рассмотрим неравенства 5х = 39 – 8у ≥ 0 8у = 39 – 5х ≥ 0 у ≤ 4 х ≤ 7 Проведем перебор по неизвестной у. Если у = 1, то х = 6,2 не является натуральным числом. Если у = 2, то х = 4,6 не является натуральным числом. Если у = 3, то х = 3. Если у = 4, то х = 1,4 не является натуральным числом. Ответ: (3; 3)
Слайд 5
Использование отношения делимости Пример 76. Имеются контейнеры двух видов: по 130 кг и 160 кг. Сколько было контейнеров первого и сколько второго вида, если вместе они весят 3 тонны? Укажите все решения Решение. Обозначим количество контейнеров первого вида через х , второго – через у . Получаем уравнение 130х + 160у = 3000 или 13х + 16у = 300. Далее имеем : 13х + 13у + 3у = 13 ∙ 23 + 1, 3у – 1 = 13 ∙ (23 – х – у). Отсюда следует, что разность 3у – 1 делится на 13. Если 3у – 1 = 0, то у не является натуральным числом. Если 3у – 1 = 13, то у не является натуральным числом. Если 3у – 1 = 26, то у = 9 и х = 12. Если 3у – 1 = 39, то у не является натуральным числом. Если 3у – 1 = 52, то у не является натуральным числом. Если 3у – 1 = 65, то у = 22 но 16 ∙ 22 = 352 > 300. Ответ: 12 контейнеров по 130 кг и 9 по 160 кг.
Слайд 6
Метод «спуска» Пример 79. Решить в целых числах уравнение 5х – 7у = 3. Решение. Выразим из уравнения то не- известное, коэффициент при котором меньше по модулю: Дробь должна быть равна целому числу. где z – целое число. Тогда 2у + 3 = 5 z . Из последнего уравнения выразим то неизвестное, коэффициент при котором меньше по модулю, и проделаем аналогичные преобразования: Дробь должна быть целым числом. Обозначим , г де t – целое число . Отсюда z = 2t – 3. Последовательно возвращаемся к неизвестным x и y . y = 3∙(2t – 3) – t = 5t – 9, x = y + z = 5t – 9 + 2t – 3 = 7t – 12. Ответ: x = 7t – 12, y = 5t – 9, где t Z . Положим ,
Слайд 7
Использование формул Теорема. Уравнение a 1 x 1 + a 2 x 2 + … + a n x n = b разрешимо в целых числах тогда и только тогда, когда d │ b , где d = НОД ( a 1, a 2 ,…, a n ). Теорема. Пусть уравнение ax + by= c разрешимо в Z и пара ( x 0 ; y 0 ) является частным решением этого уравнения. Тогда множеством всех решений в Z данного уравнения является множество пар ( x; y ) , где Следствие. Пусть а и b взаимно просты и ( x 0 y 0 ) какое-нибудь решение уравнения ax + by = c (*) Тогда формулы x = x 0 – b ∙ t , y = y 0 + a ∙ t при t є Z дают все решения уравнения (*).
Слайд 8
Пример 81. (МГУ, 1969). Остаток от деления некоторого натурального числа n на 6 равен 4, остаток от деления n на 15 равен 7. Чему равен остаток от деления n на 30? Решение. Из условия задачи следует, что существует натуральное число k такое, что n = 6k + 4. 2 k – 5l = 1. (*) Для решения этого уравнения найдем какое-нибудь частное решение в целых (не обязательно неотрицательных) числах. Подбором в качестве такого частного решения можно взять, например, k = -2 , l = -1 . Согласно следствия уравнение (*) имеет решения k = -2 +5t, l = -1 + 2t, где t є Z. Чтобы числа k и l были неотрицательными, параметр t должен принимать натуральные значения. Теперь имеем n = 6 ∙ (5t – 2) +4 = Ответ: 22. Аналогично имеем , n = 15l + 7, где l є N. Исключая из этих двух равенств n , получим уравнение 30t – 8 = 30(t – 1) + 22.
Слайд 9
Пример 83. Решить в целых числах уравнение 127 x – 52y + 1 = 0. Решение. Преобразуем отношение коэффициентов при неизвестных. Прежде всего, выделим целую часть неправильной дроби Правильную дробь заменим равной ей дробью Тогда получим Проделаем такие же преобразования с полученной в знаменателе неправильной дробью . Повторяя те же рассуждения для дроби , получим
Слайд 10
Мы получили выражение, которое называется конечной цепной или непрерывной дробью. Отбросив последнее звено этой цепной дроби – одну пятую, превратим получающуюся при этом новую цепную дробь в простую и вычтем ее из исходной дроби Приведем полученное выражение к общему знаменателю и отбросим его 127 ∙ 9 – 52 ∙ 22 + 1 = 0. 127 x -52y + 1 = 0 x = 9, y = 22 x = 9 +52t , y = 22 + 127 t , где t є Z . Ответ: x = 9 +52t , y = 22 + 127 t , где t є Z .
Слайд 11
7.2. Нелинейные уравнения Метод разложения на множители вынесение общих множителей за скобку Пример 84. Решить в целых числах уравнение 2 x 3 + xy – 7 = 0 . Решение. Приведем данное уравнение к виду x(2x 2 + y) = 7 Так как 7= 1 ∙ 7 = 7 ∙ 1 = -1 ∙ (-7) = -7 ∙ (-1), то рассмотрим четыре системы уравнений: Из каждой системы получаем решения. Ответ: (1; 5); (-1; -9); (7; -97); (-7; -99).
Слайд 12
Применение формул сокращенного умножения Пример 85. Найти все пары натуральных чисел, разность квадратов которых равна 55. Решение. Запишем условие задачи в виде уравнения n 2 – k 2 = 55 или (n – k)(n + k) = 55. Так как n + k > 0 , то n – k > 0 , причем n + k > n – k. Поскольку 55 = 1 ∙ 55 = 5 ∙ 11 то возможны два случая Решая эти уравнения, получим два ответа: n = 28, k = 27 и n = 8, k = 3. Ответ: (28; 27); (8; 3).
Слайд 13
Использование параметра Пример 88. Решить в целых числах уравнение 2 x 2 – 2yx + 9x + y = 2. Решение. Перепишем уравнение в виде 2 x 2 – x(2y – 9) + y – 2 + a = a и разложим левую часть уравнения на множители как квадратный трехчлен относительно х . Находим дискриминант D = 4y 2 – 44y + 97 – 8a. Очевидно, если , 97 – 8a = 121 , то дискриминант будет полным квадратом. При этом a = -3 и Отсюда x 1 = 0,5 и x 2 = y – 5 . Уравнение принимает вид (2x – 1)(x – y + 5) = -3 . Рассмотрите самостоятельно решение последнего уравнения. Ответ: (1; 9); (-1; 3); (2; 8); (0; 2).
Слайд 14
Метод решения относительно одной переменной выделение целой части Пример 89. (МГУ, 1997). Найти все пары целых чисел x и у, удовлетворяющие уравнению 3xy + 14x + 17y + 71 = 0. Решение. Выразим из данного уравнения у через х: При этом следует отметить, что величина 3x + 17 ≠ 0 (так как x – целое число). Выделим из дроби в правой части этого равенства правильную алгебраическую дробь (у которой степень числителя меньше степени знаменателя): Умножим обе части последнего равенства на 3:
Слайд 15
Метод «спуска» метод конечного «спуска» Пример 96. Решить в целых числах уравнение 2x 2 – 5y 2 = 7. Решение. Так как 2x 2 – четное число, а 7 – нечетное, то 5y 2 должно быть нечетным, т.е. у – нечетное. Пусть , y = 2z + 1, где z є Z , тогда данное уравнение можно переписать в виде x 2 – 10z 2 – 10z = 6. Отсюда видно, что x должно быть четным. Пусть , x = 2m , тогда последнее уравнение примет вид 2m 2 – 5z(z + 1) = 3 , что невозможно, так как число z(z + 1) – четно, а разность двух четных чисел не может быть равна нечетному числу. Таким образом, данное уравнение не имеет решений в целых числах. Ответ: нет решений.
Слайд 16
Поскольку числа 3у и 14 – целые, то 3x +17 должно быть делителем числа 25 : 3x + 17 = ±1; ±5; ±25 – всего 6 возможностей. Отсюда для x получаем три возможных значения: –4, –6, –14 (в остальных трех случаях x не является целым). Соответствующие значения у равны –3, –13, –5. Ответ: (-4; -3); (-6; -13); (-14; -5). Замечание. В данном примере суть выделения целой части состоит в избавлении переменной x из числителя (сравните с примером 77). В решении был использован прием домножения обеих частей равенства на коэффициент при x в знамена- теле. Этот прием домножения также удобно использовать при решении уравнений методом разложения на множители.
Слайд 17
Параметризация уравнения Пример 99. Решить в целых числах уравнение x 3 + y 3 + z 3 = 2 . Решение. Положим x = a + b, y = a – b. Так как x 3 + y 3 = 2a 3 + 6ab 2 , то исходное уравнение принимает вид 2a 3 + 6ab 2 + z 3 = 2. Положив a = 1, получим z 3 = -6b 2 . Считаем теперь b = 6t 2 Отсюда x = 1 + 6t 2 , y = 1 -6t 2 , z = -6t 2 . Таким образом, получено бесконечное множество решений исходного уравнения, соответствующих целочисленным значениям параметра t . Ответ: x = 1 + 6t 2 , y = 1 -6t 2 , z = -6t 2 , где t є Z
Слайд 18
Функционально-графический метод Пример 100. (МИОО 2010). Найти все пары натуральных k и n таких, что k < n и ( n ) k = ( k ) n . Решение. 1 . Преобразуем исходное равенство: k ln n = n ln k 2.
Слайд 19
откуда следует k = 1 или , k = 2, причем для каждого k может найтись не более одного значения n , удовлетворяющего уравнению в паре с этим значением k . 3. В случае k = 1 из данного уравнения получаем n = 1, ч то не соответствует условию k < n . 4. В случае k = 2 получаем уравнение , n 2 = 2 n , решение которого легко находится подбором: n = 4, причем в силу выше- сказанного это единственное решение n > e . Ответ: k = 2 , n = 4 .
Слайд 20
7.3. Неравенства Использование области определения Пример 102. (МГУ, 1973). Найти все целые числа x , удовлетворяющие неравенству Решение. Допустимые значения x определяются системой неравенств Подставляем последовательно найденные значения x в неравенство, предварительно его упростив.
Слайд 21
1. x = 1. Тогда 2. х = 2. Тогда 3. х = 3. Тогда Ответ: 2; 3.
Слайд 22
Использование монотонности Пример 103. (МГУ, 1976). Найти все целые z , удовлетворяющие неравенству Решение. Допустимые значения z определяются из системы Заметим, что левая часть неравенства увеличивается с ростом z , а правая – уменьшается. Это обстоятельство позволяет упростить перебор. В силу сделанного выше замечания, необходимости в проверке значений z = 3, 4, 5, 6 нет. Эти числа решениями не являются. Ответ: -1, 0, 1.
Слайд 23
Использование ограниченности Пример 104. (МГУ, 1996). Найти все целочисленные решения неравенства Решение. Целые решения будем искать из двух ограничений системы Первое неравенство выполняется при x = 3, 4, 5, 6. Но из этих значений исходному неравенству удовлетворяет только x = 3 . При x = 0, 1, 2 первое неравенство не выполняется. При x = -1 выполняется как первое не- равенство, так и исходное неравенство. При x = -2 первое неравенство не выполняется. При остальных значениях x = -3, -4, … первое неравенство не разрешимо, так как левая часть неравенства x(x 2 – 5) ≥ 3 будет отрицательной. Ответ: -1; 3.
Слайд 24
Метод интервалов Пример 105. (МГУ, 1972). Определить, сколько целочисленных решений имеет неравенство Решение. Методом интервалов по 2 n определяем решения (см. рис. 2): Дальше подбором находим n = ± 2, ± 3, ±4 или n = ±8, ±9,±10, ±11, ±12. Ответ: 16 решений.
Слайд 25
7.4. Уравнения и неравенства Уравнение с одной неизвестной Пример 107. Может ли квадратное уравнение ax 2 + bx + c = 0 с целыми коэффициентами иметь дискриминант, равный 23? Первое решение. Рассмотрим уравнение b 2 – 4ac = 23. Так как 23 – нечетное число, а 4 ac – четное, то b 2 и, следовательно, b – нечетное число, т.е . b = 2k – 1, k є Z . Тогда (2k – 1) 2 – 4ac = 23; 4(k 2 – k -ac) = 22. Последнее уравнение не имеет решений, так как 22 не делится на 4. Второе решение. Перепишем уравнение b 2 – 4ac = 23 в виде b 2 – 25 = 4ac – 2 и разложим обе части уравнения на множители: (b – 5)(b + 5) = 2(2ac – 1). (*) Так как в правой части уравнения – число четное, то и в левой – тоже четное, следовательно, b – 5 и b + 5 одновременно четные (докажите), т.е. b – 5 =2m, b – 5 = 2k. Левая часть уравнения (*) делится на 4 , а правая – нет, поэтому уравнение b 2 -4ac = 23 не имеет решений в целых числах. Третье решение. Перепишем уравнение b 2 -4ac = 23 в виде b 2 = 4ac + 23 или b 2 = 4(ac + 5) + 3. Получили, что квадрат натурального числа при делении на 4 дает остаток 3 , что невозможно (докажите). Ответ: не может.
Слайд 26
Показательные уравнения Теорема. Если остаток от деления a 1 на b равен r 1 , а остаток от деления a 2 на b равен r 2 , то остаток от деления a 1 +a 2 на b равен остатку от деления r 1 + r 2 на b . Опорная задача. Докажите, что оста- ток от деления на 3 числа 5 k равен 1 , если k четно, и 2 , если k нечетно.
Слайд 27
Неравенства Пример 121. (МИОО 2010). Найти все пары (x; y) целых чисел, удовлетворяющие системе неравенств : Решение. Выделяя полные квадраты, получаем: Из первого и второго неравенства системы: Подставляя x = 12 в систему, получаем: Ответ: (12; -8).
Слайд 28
Уравнения, содержащие функцию «целая часть числа» [ x ] Целой частью числа x называется наибольшее целое число, не превосходящее х . Свойства целой части числа: 1) Из равенства [y] = n следует, что a) n – целое число; б) y = n + α , где 0 ≤ α < 1; в) 0 ≤ y – n < 1. 2) Если [ u ] = [ v ] то u = m + α , v = m+ β , где 0 ≤ α < 1 и 0 ≤ β <1 , поэтому u – v = α – β и -1 < u – v < 1. 3 ) Если [ x + y ] = x то x – целое число и 0 ≤ y < 1. 4) Если n – целое число, то [ n + x ] = n + [ x ].






















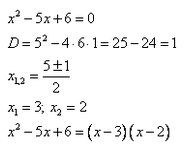


 Это означает, что число не входит в область решения;
Это означает, что число не входит в область решения; Это означает, что число входит в область решения.
Это означает, что число входит в область решения.





