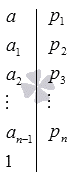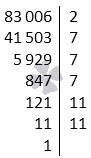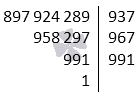Как найти целые множители числа

Была ли эта статья полезной?

Факториза́цией натурального числа называется его разложение в произведение простых множителей. Существование и единственность (с точностью до порядка следования множителей) такого разложения следует из основной теоремы арифметики.

В отличие от задачи распознавания простоты числа, факторизация предположительно является вычислительно сложной задачей. В настоящее время неизвестно, существует ли эффективный не квантовый алгоритм факторизации целых чисел. Однако доказательства того, что не существует решения этой задачи за полиномиальное время, также нет.

Предположение о том, что для больших чисел задача факторизации является вычислительно сложной, лежит в основе широко используемых алгоритмов (например, RSA). Многие области математики и информатики находят применение в решении этой задачи. Среди них: эллиптические кривые, алгебраическая теория чисел и квантовые вычисления.

История[править | править код]

Задача поиска эффективных способов разложения целых чисел на множители интересовала математиков с давних времён, особенно специалистов в области теории чисел. Существуют предположения о том, что Ферма был одним из первых, кто предложил метод разложения, заключающийся в том, чтобы представить число в виде разности квадратов , а затем, вычисляя , попытаться найти нетривиальный делитель . Данный способ позволяет находить два мало различающихся по величине делителя числа быстрее, чем простой перебор делителей^[1].

Далее Лежандр обнаружил, что при таком подходе достаточно получить сравнение , и использовал для этого цепные дроби. Также Эйлером и Гауссом были предложены некоторые способы нахождения чисел, связанных этим сравнением^[1].

Одним из ключевых моментов в развитии факторизации целых чисел было создание алгоритма RSA, что возобновило интерес учёных в данном направлении, так как имело практическое применение в области шифрования. Этот алгоритм был предложен в 1977 году тремя учёными Рональдом Ривестом, Ади Шамиром и Леонардом Адлеманом из Массачусетского технологического института и назван по первым буквам фамилий авторов методом RSA. Он основан на идее криптографии с открытым ключом и для взлома системы необходимо выполнить разложение числа на простые сомножители. На момент публикации алгоритма RSA были известны методы, которые позволяли факторизовать числа, состоящие не более чем из 25—30 цифр, а наиболее известным и применяемым все ещё оставался метод Ферма. Метод RSA позволяет факторизовать числа^{[уточнить]} из 100 и более десятичных знаков. Создатели, в свою очередь, пообещали за факторизацию числа из 129 десятичных знаков символические сто долларов США^[2].

На популярность задачи факторизации также повлияла публикация в 1977 году в журнале Scientific American Мартина Гарднера «Новый алгоритм шифрования, для взлома которого потребуются миллионы лет».^[3] Столь громкое название было воспринято в качестве вызова всему математическому сообществу. В результате этой гонки было предложено несколько новых и нестандартных идей факторизации^[2].

Эпопея с разложением 129-значного числа завершилась в 1994 году, когда коллектив под руководством А. Ленстры, используя 1600 компьютеров, подготовил за 220 дней систему линейных уравнений, содержавшую более полумиллиона неизвестных. Решение этой системы суперкомпьютером заняло два дня. Несмотря на то, что в то время уже были известны методы решета числового поля, данный результат был получен с помощью алгоритма квадратичного решета^[2].

Алгоритмы факторизации[править | править код]

Как правило, на вход таких алгоритмов подаётся число , которое необходимо факторизовать, состоящее из символов (если представлено в двоичном виде)^[4]. При этом алгоритм ищет первый простой делитель, после чего, при необходимости, можно запустить алгоритм заново для дальнейшей факторизации. Также, прежде чем начинать факторизацию большого числа, следует убедиться в том, что оно не простое. Для этого достаточно пройти тест числа на простоту. Эта задача детерминированно разрешима за полиномиальное время^[5].

В зависимости от сложности алгоритмы факторизации можно разбить на две группы. Первая группа — экспоненциальные алгоритмы, сложность которых экспоненциально зависит от длины входящих параметров (то есть от длины самого числа в бинарном представлении). Вторая группа — субэкспоненциальные алгоритмы.

Вопрос о существовании алгоритма факторизации с полиномиальной сложностью на классическом компьютере является одной из важных открытых проблем современной теории чисел. В то же время факторизация с полиномиальной сложностью возможна на квантовом компьютере с помощью алгоритма Шора (класс BQP)^[6].

Экспоненциальные алгоритмы[править | править код]

Перебор возможных делителей[править | править код]

Сложность или .

Один из самых простых и очевидных алгоритмов факторизации, заключающийся в том, чтобы последовательно делить факторизуемое число на натуральные числа от до . Формально достаточно делить только на простые числа в этом интервале, однако, для этого необходимо знать их множество. На практике составляется таблица простых чисел и производится проверка небольших чисел (например, до ). Для очень больших чисел алгоритм не используется в силу низкой скорости работы^[7].

Метод факторизации Ферма[править | править код]

Сложность или .

Идея алгоритма заключается в поиске таких чисел и , что факторизуемое число n представимо в виде: . Как и метод пробного деления, обычно не применяется на практике для факторизации больших чисел, так как имеет экспоненциальную сложность. Метод реализуем без операции деления, а только лишь с операциями сложения и вычитания^[9]. Если , при условии того, что и  — простые числа, не сильно различающиеся по величине, то метод Ферма факторизует n достаточно быстро^[10].

ρ-алгоритм Полларда[править | править код]

Сложность .

Алгоритм Полларда является вероятностным алгоритмом, позволяющим находить делитель составного числа , работающим со сложностью, зависящей лишь от величины делителя, но не величины факторизуемого числа . Это обуславливает удобство применимости данного алгоритма в тех случаях, когда другие алгоритмы, сложность которых зависит от , становятся неэффективны^[12]. Примечателен также тем, что существует вариант реализации такого алгоритма, при котором достаточно в памяти хранить всего 3 целых числа^[13].

Алгоритм Ленстры[править | править код]

Сложность .

Несмотря на относительно неплохую эффективность среди экспоненциальных алгоритмов, в алгоритме Ленстры есть необходимость неоднократно вычислять квадратный корень в одном из шагов алгоритма, что является более трудоёмким, чем сложение или вычитание^[15].

Алгоритм Полларда — Штрассена[править | править код]

Сложность .

Данный алгоритм имеет оценку сложности схожую с методом квадратичных форм Шенкса (что является наилучшей среди детерминированных алгоритмов факторизации), однако требует выделение памяти. Он может использоваться непосредственно для факторизации не очень больших целых чисел, а также в качестве вспомогательного алгоритма в субэкспоненциальном методе Диксона^[17] и для ускорения вычислений второго этапа метода факторизации с помощью эллиптических кривых.^[18]

Метод квадратичных форм Шенкса[править | править код]

Гарантированная сложность и при верности гипотезы Римана .

В отличие от алгоритма Полларда – Штрассена не требует выделения больших объёмов памяти, к тому же имеет достаточно простые расчётные формулы^[19].

P-1 алгоритм Полларда[править | править код]

Сложность ^[20].

Несмотря на экспоненциальную оценку сложности, алгоритм во всех случаях быстро находит небольшие простые делители , потому что они являются степенно-гладкими для небольшой границы гладкости . В практических задачах данный алгоритм обычно используется до применения субэкспоненциальных алгоритмов факторизации, чтобы отделить небольшие простые делители числа ^[20].

Метод Лемана[править | править код]

Сложность .

В настоящее время алгоритм представляет скорее исторический, чем практический интерес, так как этот алгоритм был первым детерминированным алгоритмом со сложностью выполнения быстрее, чем .

Субэкспоненциальные алгоритмы[править | править код]

Для обозначения сложности принята L-нотация^[4]:

где  — число подлежащее факторизации, и  — некоторые константы.

Алгоритм Диксона[править | править код]

Сложность .

Факторизация методом непрерывных дробей[править | править код]

Сложность ^[26].

Метод квадратичного решета[править | править код]

Сложность ^[26].

Данный метод с использованием нескольких многочленов эффективен и достаточно легко реализуем на компьютере. Есть основания полагать, что он является наилучшим из известных алгоритмов факторизации для (не считая метод факторизации с помощью эллиптических кривых, который в некоторых случаях может работать быстрее. Для чисел алгоритмы решета числового поля сработают быстрее, чем метод квадратичного решета^[27].

Факторизация Ленстры с помощью эллиптических кривых[править | править код]

Сложность , где  — наименьшее простое, которое делит ^[28].

Параметры выбираются случайно. Значения следует выбирать эмпирически, рассмотрев некоторую серию возрастающих значений^[28]. На практике при заданных алгоритм заключается в том, чтобы выполнить алгоритм с одной кривой. Это повторяется до тех пор, пока не разложится на множители или пока время, отведённое для алгоритма, не закончится.

Существуют модификации алгоритма, позволяющие работать с несколькими кривыми одновременно^[28].

Решето числового поля[править | править код]

В настоящее время самыми эффективными алгоритмами факторизации являются вариации решета числового поля^[29]:

Применение в криптографии[править | править код]

Предполагаемая большая вычислительная сложность задачи факторизации лежит в основе криптостойкости некоторых алгоритмов шифрования с открытым ключом, таких как RSA. Более того, если известен хотя бы один из параметров ключей RSA, то система взламывается однозначно, кроме того, существует множество алгоритмов восстановления всех ключей в системе, обладая какими-то данными^[31].

Текущее состояние[править | править код]

В марте 1994 года с помощью двойной вариации множественного полиномиального QS командой математиков под руководством Ленстры было разложено на множители 129-разрядное (428-битовое) число. Вычисления выполнялись добровольцами в Интернете — в течение восьми месяцев трудились 600 человек и 1600 компьютеров. Компьютеры соединялись по электронной почте, передавая свои результаты в центральное хранилище, где выполнялся окончательный анализ. В этих вычислениях использовались QS и теория пятилетней давности, NFS мог бы ускорить выполнение расчётов. Группа учёных сделала вывод о том, что широко используемые 512-битовые модули RSA могут быть вскрыты организацией, готовой потратить несколько миллионов долларов и подождать несколько месяцев^[32].

С целью развития искусства разложения на множители RSA Data Security, Inc. в марте 1991 года объявило о программе RSA Factoring Challenge (состязание RSA по разложению на множители). Состязание состоит в разложении на множители ряда трудных чисел, каждое из которых является произведением двух простых чисел примерно одинакового размера. Каждое простое число было выбрано конгруэнтным 2 по модулю 3. Всего было предложено 42 числа, по одному в диапазоне от 100 до 500 разрядов с шагом в 10 разрядов (плюс одно дополнительное, 129-разрядное число. Подробнее: RSA Factoring Challenge^[en][32].

Примечания[править | править код]

Литература[править | править код]

на русском языке

• Коблиц Н. Курс теории чисел и криптографии — 2-е издание — М.: Научное издательство ТВП, 2001. — 254 с. — ISBN 978-5-85484-014-9, 978-5-85484-012-5
• Черемушкин А. В. Лекции по арифметическим алгоритмам в криптографии — М.: МЦНМО, 2002. — 104 с. — ISBN 978-5-94057-060-8
• Василенко О. Н. Теоретико-числовые алгоритмы в криптографии — М.: МЦНМО, 2003. — 328 с. — ISBN 978-5-94057-103-2
• Ишмухаметов Ш. Т. Методы факторизации натуральных чисел: учебное пособие — Казань: Казанский университет, 2011. — 190 с.
• Нестеренко А. Ю. Теоретико-числовые методы в криптографии — М.: Московский государственный институт электроники и математики, 2012. — 224 с. — ISBN 978-5-94506-320-4
• Кнут, Д. Искусство программирования = The Art of Computer Programming. — Москва: Вильямс, 2007. — Т. 2. — 832 с. — ISBN 978-5-8459-0081-4.
• Введение в криптографию / Ященко, В. В.. — Москва: МЦНМО, 1999. — 272 с. — ISBN 5-900916-40-5.
• Шнайер, Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — Москва: Триумф, 2002. — 816 с. — 3000 экз. — ISBN 5-89392-055-4.

на английском языке

• Bressoud, D. M. Factorization and Primality Testing. — N. Y.: Springer-Verlag, 1989. — 260 p. — ISBN 0-387-97040-1.
• Mahoney, M. S. The Mathematical Career of Pierre de Fermat. — 2. — Princeton: Princeton Univercity Press, 1994. — P. 324—332. — 438 p. — ISBN 0-691-03666-7.

Данная статья дает ответы на вопрос о разложении числа на простыне множители. Рассмотрим общее представление о разложении с примерами. Разберем каноническую форму разложения и его алгоритм. Будут рассмотрены все альтернативные способы при помощи использования признаков делимости и таблицы умножения.

Что значит разложить число на простые множители?

Разберем понятие простые множители. Известно, что каждый простой множитель – это простое число. В произведении вида 2·7·7·23 имеем, что у нас 4 простых множителя в виде 2,7,7,23.

Разложение на множители предполагает его представление в виде произведений простых. Если нужно произвести разложение числа 30, тогда получим 2,3,5. Запись примет вид 30=2·3·5. Не исключено, что множители могут повторяться. Такое число как 144 имеет 144=2·2·2·2·3·3.

Не все числа предрасположены к разложению. Числа, которые больше 1 и являются целыми можно разложить на множители. Простые числа при разложении делятся только на 1 и на самого себя, поэтому невозможно представить эти числа в виде произведения.

При z, относящемуся к целым числам, представляется  в виде произведения а и b, где z делится на а и на b. Составные числа раскладывают на простые множители при помощи основной теоремы арифметики. Если число больше 1, то его разложение на множители p1, p2, …, pn принимает вид a=p1, p2, …, pn_. Разложение предполагается в единственном варианте.

Каноническое разложение числа на простые множители

При разложении множители могут повторяться. Их запись выполняется компактно при помощи степени. Если при разложении числа а имеем множитель p1, который встречается s1 раз и так далее pn – sn раз. Таким образом разложение примет вид a=p₁^s₁·a=p1s1·p2s2·…·pnsn. Эта запись имеет название канонического разложения числа на простые множители.

При разложении числа 609840 получим, что 609 840=2·2·2·2·3·3·5·7·11·11,его канонический вид будет 609 840=24·32·5·7·112. При помощи канонического разложения можно найти все делители числа и их количество.

Алгоритм разложения числа на простые множители

Чтобы правильно разложить на множители необходимо иметь представление о простых и составных числах. Смысл заключается в том, чтобы получить последовательное количество делителей вида p1, p2, …,pn чисел a, a1, a2, …, an-1, это дает возможность получить a=p1·a1, где a1=a:p1, a=p1·a1=p1·p2·a2, где a2=a1:p2, …, a=p1·p2·…·pn·an, где an=an-1:pn. При получении an=1, то равенство a=p1·p2·…·pn  получим искомое разложение числа а на простые множители. Заметим, что p1≤p2≤p3≤…≤pn.

Для нахождения наименьших общих делителей необходимо использовать таблицу простых чисел. Это выполняется на примере нахождения наименьшего простого делителя числа z. При взятии простых чисел 2,3,5,11 и так далее, причем на них делим число z. Так как z не является простым числом, следует учитывать, что наименьшим простым делителем не будет больше z.  Видно, что не существуют делителей z, тогда понятно, что z является простым числом.

Рассмотрим на примере числа 87.  При его делении на 2 имеем, что 87:2=43  с остатком равным 1. Отсюда следует, что 2 делителем не может являться, деление должно производиться нацело. При делении на 3 получим, что 87:3=29. Отсюда вывод – 3 является наименьшим простым делителем числа 87.

При разложении на простые множители необходимо пользоваться таблицей простых чисел, где a.  При разложении 95 следует использовать около 10 простых чисел, а при 846653 около 1000.

Рассмотрим алгоритм разложения на простые множители:

• нахождение наименьшего множителя при делителе p1 числа a по формуле a1=a:p1, когда a1=1, тогда а является простым числом и включено в разложение на множители, когда не равняется 1, тогда a=p1·a1 и следуем к пункту, находящемуся ниже;
• нахождение простого делителя p2 числа a1 при помощи последовательного перебора простых чисел, используя a2=a1:p2_, когда a2=1, тогда разложение примет вид a=p1·p2_, когда a2=1, тогда a=p1·p2·a2_, причем производим переход к следующему шагу;
• перебор простых чисел и нахождение простого делителя p3 числа a2 по формуле a3=a2:p3, когда a3=1, тогда получим, что a=p1·p2·p3_, когда не равняется 1, тогда a=p1·p2·p3·a3 и производим переход к следующему шагу;
• производится нахождение простого делителя pn числа an-1 при помощи перебора простых чисел с pn-1, а также an=an-1:pn, где an=1, шаг является завершающим, в итоге получаем, что a=p1·p2·…·pn_.

Результат алгоритма записывается в виде таблицы с разложенными множителями с вертикальной чертой последовательно в столбик. Рассмотрим рисунок, приведенный ниже.

Полученный алгоритм можно применять при помощи разложения чисел на простые множители.

Примеры разложения на простые множители

Во время разложения на простые множители следует придерживаться основного алгоритма.

Использование признаков делимости для разложения на простые множители

Чтобы разложить число на простые множители, нужно придерживаться алгоритма. Когда имеются небольшие числа, то допускается использование таблицы умножения и признаков делимости. Это рассмотрим на примерах.

Если необходимо произвести разложение на множители 10, то по таблице видно: 2·5=10. Получившиеся числа 2 и 5 являются простыми, поэтому они являются простыми множителями для числа 10.

Если необходимо произвести разложение числа 48, то  по таблице видно: 48=6·8. Но 6 и 8 – это не простые множители, так как их можно еще разложить как 6=2·3 и 8=2·4. Тогда полное разложение отсюда получается как 48=6·8=2·3·2·4. Каноническая запись примет вид 48=24·3.

При разложении числа 3400 можно пользоваться признаками делимости. В данном случае актуальны признаки делимости на 10 и на 100. Отсюда получаем, что 3 400=34·100, где 100 можно разделить на 10, то есть записать в виде 100=10·10, а значит, что 3 400=34·10·10. Основываясь на признаке делимости получаем, что 3 400=34·10·10=2·17·2·5·2·5. Все множители простые. Каноническое разложение принимает вид 3 400=23·52·17.

Когда мы находим простые множители, необходимо использовать признаки делимости и таблицу умножения. Если представить число 75 в виде произведения множителей, то необходимо учитывать правило делимости на 5. Получим, что 75=5·15, причем 15=3·5. То есть искомое разложение пример вид произведения 75=5·3·5.

Формат:
Кратко
Подробно
В столбик

Онлайн калькулятор раскладывает число в произведение простых множителей.
Для вычислений используется длинная арифметика, поэтому можно легко
разложить на множители даже большие числа.

Что такое разложение числа на множители?

Любое натуральное число можно представить в виде
произведения простых чисел. Это представление называется разложением
числа на простые множители.

Натуральное число называется делителем целого числа если для подходящего целого числа верно
равенство . В этом случае говорят, что делится на или что число кратно
числу .

Простым числом называют натуральное число , делящееся только на себя и на единицу. Составным
числом называют число, имеющее больше двух различных делителей (любое натуральное число не равное
имеет как минимум два делителя: и ). Например, числа – простые, а числа – составные.

Основная теорема арифметики. Любое натуральное число большее единицы, можно
разложить в произведение простых чисел, причём это разложение единственно с точностью до порядка следования
сомножителей.

Как разложить число на множители?

В школе на уроках математики разложение числа на множители обычно записывают столбиком в две колонки. Делается это
так: в левую колонку выписываем исходное число, затем

• Берём самое маленькое простое число — 2 и по признакам
  делимости или обычным делением проверяем, делится ли исходное число на 2.
• Если делится, то в правую колонку выписываем 2. Далее делим исходное число на 2 и записываем результат в левую
  колонку под исходным числом.
• Если не делится, то берём следующее простое число — 3.

Повторяем эти шаги, при этом работаем уже с последним числом в левой колонке и с текущим простым числом. Разложение
заканчивается, когда в левой колонке будет записано число 1.

Чтобы лучше понять алгоритм, разберём несколько примеров.

Пример. Разложить на множители число 84.

Решение. Записываем число 84 в левую колонку:

Берём первое простое число — два и проверяем, делится ли 84 на 2. Так как 84 оканчивается на 4, а 4 делится на 2,
то и 84 делится на 2 по признаку делимости. Записываем 2 в
правую колонку. 84:2 = 42, число 42 записываем в левую колонку. Получили вот что:

Теперь работаем уже с числом 42. Число 42 делится на 2, поэтому записываем 2 в правую колонку, 42:2 = 21, число
21 записываем в левую колонку.

Число 21 на 2 не делится, поэтому проверяем его делимость на следующее простое число — 3. Число 21 делится на 3,
21:3 = 7. Записали 3 в правую колонку, 7 — в левую. Получили

Число 7 — простое число, поэтому в правой колонке записываем 7, в левую пишем 1. В итоге получили:

Всё, число разложено!

В результате в правой колонке оказались записаны все простые множители числа 84. То есть 84=2∙2∙3∙7.

Онлайн калькулятор для разложения числа на множители

Программа раскладывает числа на множители методом
перебора делителей. Для вычислений используется длинная арифметика, поэтому раскладывать можно даже большие
числа. Однако если число простое или имеет большие простые делители, разложение его на множители занимает
продолжительное время.

Алгоритм поиска множителей числа, то есть представление какого либо числа в виде двух других чисел, при умножении которых мы получил непосредственно то число, которое нам нужно. Эта статья не рассказывает о каких либо идеальных/лучших алгоритмов, это своего рода оптимизация перебора чисел, и далеко не стоит по сравнению с тем же методом факторизации Ферма ну или Ро-алгоритмом Полларда.

В чем заключается данный алгоритм?

В первую очередь, берем интервал чисел, который представляем в виде двух целых чисел, это конец интервала и его начало. Так же нам нужно число, с которого мы хотим получить множители на интервале.

Теперь перейдем к самому алгоритму. Чтобы не идти вглубь математики, мы будем рассматривать этот метод исключительно на человеческом языке.
Для начала, нам нужны сами пределы интервала, их мы пусть присвоим ‘x‘ и ‘y‘, начало и конец соответственно.

x = start,
y = end;

Теперь мы, умножаем эти два числа: z = x*y, и если число, которое мы получили, будет меньше, чем число которое мы планируем факторизовать, то прибавляем к ‘x‘ — единицу(1), и снова умножаем: z = (x+1)*y, и так до тех пор, пока мы не получим (z > N), где ‘N‘ — число которое нужно факторизовать.

Если же, число которое мы получили больше N, то:

1. Мы ищем разницу между ‘z‘ и ‘N‘, то есть между числом которое мы получили и число которое мы хотим факторизовать.

z - N = q;

2.1. Число, которое мы получили после вычитания(q), делим на число которое символизирует начало интервала(x). После чего, проверяем условие: Если получается число, не целого типа, то множителей не будет, а следовательно мы увеличиваем начальное значение(x) на единицу и продолжаем поиск.

q/x = if(int) => Пункт 2.2
else if(double) => x += 1.

2.2. Если же, число которое мы получили при делении — целого типа, тогда мы: От конца интервала отнимаем число которое мы получили(пусть будет ‘l‘), в следствии чего мы получаем один из множителей, второй же множитель — это ‘x‘.

y - l = a,
a * x = N;

Пример:

Есть интервал чисел от 14 к 28, и число которое мы хотим разложить на множители, пусть будет 450.

Для начала нам нужно два числа, это начало и конец интервала, в данном случаи это 14 и 28. Дальше мы согласно алгоритму, эти два числа умножаем и получаем результат:

14*28 = 392 

Число, которое мы получили, меньше чем число, которое нам нужно разложить на множители, то есть 450, тогда мы увеличиваем 14 на единицу, и начинаем все с начала.

15*28 = 420

Опять же, 420 < 450, тогда мы к 15 прибавляем единицу и продолжаем поиск.

16*28 = 448

По тому же принципу, 448 < 450, значит мы к 16 прибавляем единицу и двигаемся дальше.

17*28 = 476

Уже здесь мы видим, что число, которое мы получили при умножении больше чем 450, тогда мы, согласно пункту «1» ищем разницу между 476 и 450.

476-450 = 26

Теперь главная проверка вечера, согласно пункту 2.1 мы делим это число на начало интервала в надежде на то, что мы получим целое число.

26/17 = ~ 1.53

К сожалению мы получили число НЕ целого типа, это значит что множителей тут нет, прибавляем к 17 единицу и продолжаем поиск.

18*28 = 504

Согласно пункту 1 ищем разницу: 504-450 = 54
Теперь главная проверка, делим полученное число на 18, получаем результат:

54/18 = 3

А вот и число целого типа, то есть уже на этом этапе понятно что множители мы нашли, теперь согласно пункту 2.2 нам нужно их точно высчитать:

28-3 = 25

Один множитель мы получили, отняв от конца интервала число которое мы посчитали.
Ну а второй множитель это конечно же сам ‘x‘ ну или же в нашем случаи это 18.
Проверяем: 25 * 18 = 450, Отлично! И самое главное что эти числа входят в наш интервал.

По такому принципу работает этот алгоритм, на самом деле он далеко не хороший, так как во первых при очень большом интервале поиск множителей может идти довольно долго, и вообще я без документации, без сторонней помощи вышел на него, возможно он уже и был где-то описан, но этот алгоритм можно назвать «ради идеи», ну и чтобы не деградировать.

Of course, winning is one of the main goals, but we must remember that there is no ideal, and if you think that you have achieved this ideal — you have lost.