Версия для печати и копирования в MS Word
1
На рисунке изображен график функции определенной на интервале
Определите количество целых точек, в которых производная функции отрицательна.
2
На рисунке изображен график функции y=f(x), определенной на интервале (−1; 12). Определите количество целых точек, в которых производная функции отрицательна.
3
Задания Д2 № 6423
На рисунке изображен график функции определенной на интервале
Определите количество целых точек, в которых производная функции
отрицательна.
4
Задания Д2 № 6871
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
5
Задания Д2 № 6873
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
6
Задания Д2 № 6875
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
7
Задания Д2 № 6881
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
8
Задания Д2 № 6897
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
9
Задания Д2 № 6899
На рисунке изображен график функции определенной на интервале
Определите количество целых точек, в которых производная функции отрицательна.
10
Задания Д2 № 6903
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
11
Задания Д2 № 6907
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
12
Задания Д2 № 6909
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
13
Задания Д2 № 6919
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
14
Задания Д2 № 6927
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
15
Задания Д2 № 6931
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
16
Задания Д2 № 6933
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
17
Задания Д2 № 6937
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
18
Задания Д2 № 6939
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
19
Задания Д2 № 6943
На рисунке изображен график функции определенной на интервале
Определите количество целых точек, в которых производная функции отрицательна.
20
Задания Д2 № 6949
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
21
Задания Д2 № 6955
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
22
Задания Д2 № 6957
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
23
Задания Д2 № 6959
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
24
Задания Д2 № 6963
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
25
Задания Д2 № 6967
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
26
Задания Д2 № 6969
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
27
Задания Д2 № 6973
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
28
Задания Д2 № 6977
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
29
Задания Д2 № 6983
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
30
Задания Д2 № 6989
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
31
Задания Д2 № 6991
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
32
Задания Д2 № 6993
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
33
Задания Д2 № 6995
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
34
Задания Д2 № 7003
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
35
Задания Д2 № 7005
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
36
Задания Д2 № 7011
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
37
Задания Д2 № 7017
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
38
Задания Д2 № 7019
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
39
Задания Д2 № 7021
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
40
Задания Д2 № 7025
На рисунке изображен график функции определенной на интервале
Определите количество целых точек, в которых производная функции отрицательна.
41
Задания Д2 № 7029
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
42
Задания Д2 № 7031
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
43
Задания Д2 № 7037
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
44
Задания Д2 № 7039
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
45
Задания Д2 № 7041
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
46
Задания Д2 № 7043
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
47
Задания Д2 № 7047
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
48
Задания Д2 № 7049
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
49
Задания Д2 № 7059
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
50
Задания Д2 № 7061
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
51
Задания Д2 № 7063
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
52
Задания Д2 № 7067
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
53
Задания Д2 № 7073
На рисунке изображен график функции
определенной на интервале
Определите количество целых точек,
в которых производная функции
отрицательна.
Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).
Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.
Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.
Ответ: (11.)
Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.
09
Авг 2013
Категория: 07 Производная, ПО
07. Применение производной к исследованию функции
2013-08-09
2023-04-30
Cледующая таблица будет весьма полезна при работе с данной темой.

или ее производной
Если дан график производной, то интересовать нас будут только знаки функции и нули. Никакие «холмики» и «впадины», как в случае
не интересуют нас в принципе!
Задача 1. На рисунке изображен график функции , определенной на интервале
. Определите количество целых точек, в которых производная функции
отрицательна.
Решение: + показать
Задача 2. На рисунке изображен график функции , определенной на интервале
. Найдите количество точек, в которых касательная к графику функции параллельна прямой
или совпадает с ней.
Решение:+ показать
Задача 3. На рисунке изображен график производной функции , определенной на интервале
. Найдите количество точек, в которых касательная к графику функции
параллельна прямой
или совпадает с ней.
Решение: + показать
Задача 4. На рисунке изображен график функции , определенной на интервале
. Найдите количество точек, в которых производная функции
равна 0.
Решение: + показать
Задача 5. На рисунке изображён график функции и одиннадцать точек на оси абсцисс:
. В скольких из этих точек производная функции
отрицательна?
Решение: + показать
Задача 6. На рисунке изображен график функции , определенной на интервале
. Найдите сумму точек экстремума функции
.
Решение: + показать
Задача 7. На рисунке изображен график производной функции , определенной на интервале
. Найдите промежутки возрастания функции
. В ответе укажите сумму целых точек, входящих в эти промежутки.
Решение: + показать
Задача 8. На рисунке изображен график производной функции , определенной на интервале
. Найдите промежутки возрастания функции
. В ответе укажите длину наибольшего из них.
Решение: + показать
Задача 9. На рисунке изображен график производной функции , определенной на интервале
. В какой точке отрезка
принимает наибольшее значение.

Задача 10. На рисунке изображен график — производной функции
, определенной на интервале
. Найдите количество точек максимума функции
, принадлежащих отрезку
.
Решение: + показать
Задача 11. На рисунке изображен график функции и отмечены точки -3, 1, 6, 8. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Решение: + показать
Задача 12. Функция определена на промежутке
На рисунке изображен график её производной. Найдите точку
в которой функция
принимает наименьшее значение, если
Решение: + показать
Задача 13. Функция определена и непрерывна на полуинтервале
На рисунке изображен график её производной. Найдите промежутки убывания функции
В ответе укажите сумму целых точек, входящих в эти промежутки.
Решение: + показать
Вы можете пройти тест «Применение производной к исследованию функции»
Автор: egeMax |
комментариев 29
Печать страницы
Исследование функции с помощью производной. В этой статье мы с вами разберём некоторые задачи связанные с исследованием графика функции. В таких задачах, даётся график функции y = f (x) и ставятся вопросы, связанные с определением количества точек, в которых производная функции положительна (либо отрицательна), а также другие. Их относят к заданиям на применение производной к исследованию функций.
Решение таких задач, и вообще задач связанных с исследованием, возможно только при полном понимании свойств производной для исследования графиков функций и геометрического смысла производной. Поэтому настоятельно рекомендую вам изучить соответствующую теорию. Можете изучить статью на блоге, а также посмотреть справочник (но в нём краткое изложение).
Задачи, где дан график производной мы будем также рассматривать в будущих статьях, не пропустите! Итак, задачи:
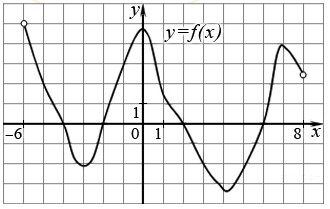
На рисунке изображен график функции у = f (х), определенной на интервале (−6; 8). Определите:
1. Количество целых точек, в которых производная функции отрицательна;
2. Количество точек, в которых касательная к графику функции параллельна прямой у = 2;
3. Количество точек, в которых производная равна нулю;
1. Производная функции отрицательна на интервалах, на которых функция убывает, то есть на интервалах (−6; –3), (0; 4,2), (6,9; 8). В них содержатся целые точки −5, −4, 1, 2, 3, 4, и 7. Получили 7 точек.
2. Прямая y = 2 параллельная оси ох. Касательная будет параллельна прямой y = 2 только в точках экстремума (в точках, где график меняет своё поведение с возрастания на убывание или наоборот). Таких точек четыре: –3; 0; 4,2; 6,9
3. Производная равна нулю в четырёх точках (в точках экстремума), их мы уже указали.
Решите самостоятельно:
Определите количество целых точек, в которых производная функции положительна.
Посмотреть решение.
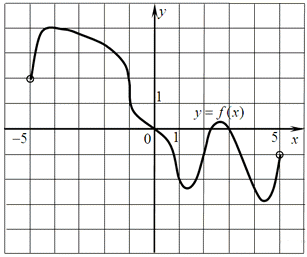
На рисунке изображен график функции у = f (х), определенной на интервале (−5; 5). Определите:
1. Количество целых точек, в которых производная функции положительна;
2. Количество целых точек, в которых касательная к графику функции параллельна прямой у = 3;
3. Количество точек, в которых производная равна нулю;
1. Из свойств производной функции известно, что она положительна на интервалах, на которых функция возрастает, т. е. на интервалах (1,4; 2,5) и (4,4;5). В них содержится только одна целая точка х = 2.
2. Прямая y = 3 параллельная оси ох. Касательная будет параллельна прямой y = 3 только в точках экстремума (в точках, где график меняет своё поведение с возрастания на убывание или наоборот).
Таких точек четыре: –4,3; 1,4; 2,5; 4,4
3. Производная равна нулю в четырёх точках (в точках экстремума), их мы уже указали.
Решите самостоятельно:
Определите количество целых точек, в которых производная функции f (x) отрицательна.
Посмотреть решение.
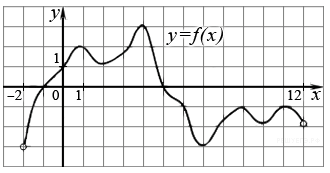
На рисунке изображен график функции у = f (х), определенной на интервале (−2; 12). Найдите:
1. Количество целых точек, в которых производная функции положительна;
2. Количество целых точек, в которых производная функции отрицательна;
3. Количество целых точек, в которых касательная к графику функции параллельна прямой у = 2;
4. Количество точек, в которых производная равна нулю.
1. Из свойств производной функции известно, что она положительна на интервалах, на которых функция возрастает, т. е. на интервалах (–2; 1), (2;4), (7; 9) и (10;11). В них содержатся целые точки: –1, 0, 3, 8. Всего их четыре.
2. Производная функции отрицательна на интервалах, на которых функция убывает, то есть на интервалах (1; 2), (4; 7), (9; 10), (11;12). В них содержатся целые точки 5 и 6. Получили 2 точки.
3. Прямая y = 2 параллельная оси ох. Касательная будет параллельна прямой y = 2 только в точках экстремума (в точках, где график меняет своё поведение с возрастания на убывание или наоборот). Таких точек семь: 1; 2; 4; 7; 9; 10; 11.
4. Производная равна нулю в семи точках (в точках экстремума), их мы уже указали.
Решите самостоятельно:
Найдите сумму точек экстремумов функции f (x). Посмотреть решение.
Как видите, ничего сложного нет. Желаю вам успехов!
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Взаимосвязи графика функции и графика ее производной
Приближенное и точное определение производной функции
Приближенным значением производной функции в точке $x_{0}$ со сдвигом 0,01 называется значение
$f’left(x_0right)approx frac{fleft(x_0+0,01right)-fleft(x_0right)}{left(x_0+0,01right)-left(x_0right)}$ $f’left(aright)approx frac{fleft(a+hright)-fleft(aright)}{left(a+hright)-left(aright)}$ Точное: $f’left(aright)=lim frac{fleft(a+hright)-fleft(aright)}{left(a+hright)-left(aright)}$ при $lim h=0$
- Производная в точке – это отношение: (приращение самой функции) / (малое приращение аргумента в этой точке).
- Физический смысл – производная функции показывает скорость изменения функции: роста или убывания функции.
- Геометрический смысл – производная в каждой точке равна тангенсу угла наклона касательной, проведенной к ее графику.
Пример 1: Дана функция $fleft(xright)=x^3-3x+2$ . Вычислить приближенное производную $f’left(x_0right)$
- в точке $x_0=1,2$ со сдвигом $h=0,2$ ? $Rightarrow$ $f’left(1,2right)approx frac{bigtriangleup fleft(xright)}{bigtriangleup x}approx frac{fleft(1,2+0,2right)-fleft(1,2right)}{1,4-1,2}=frac{1,4^3-3cdot 1,4+2-left(1,2^3-3cdot 1,2+2right)}{0,2}=1,555$
- В реальности мы получили тангенс угла наклона секущей, проходящей в точках графика $left(1,2;fleft(1,2right)right)$ и $left(1,4;fleft(1,4right)right)$
- в точке $x_0=0,5$ со сдвигом $h=0,0001$ ? $Rightarrow$ $f’left(0,4right)approx frac{fleft(0,4+hright)-fleft(0,4right)}{left(0,4+hright)-0,4}=frac{left(0,4+hright)^3-3cdot left(0,4+hright)+2-left(0,4^3-3cdot 0,4+2right)}{h}=frac{left(0,4+hright)^3-0,4^3}{h}-frac{3cdot left(0,4+hright)-3cdot 0,4}{h}=frac{0,4^3+3cdot 0,4^2cdot h+3cdot 0,4h^2+h^3-0,4^3}{h}-3=left(3cdot 0,4^2-3right)+hcdot left(3cdot 0,4+hright)approx 2,5201$
- точное производное $f’left(0,4right)=3cdot 0,4^2-3=2,52$ при $hsim 0$ !
- в точке $x_0=0,5$ со сдвигом $h=0,0001$ ? $Rightarrow$ $f’left(0,4right)approx frac{fleft(0,4+hright)-fleft(0,4right)}{left(0,4+hright)-0,4}=frac{left(0,4+hright)^3-3cdot left(0,4+hright)+2-left(0,4^3-3cdot 0,4+2right)}{h}=frac{left(0,4+hright)^3-0,4^3}{h}-frac{3cdot left(0,4+hright)-3cdot 0,4}{h}=frac{0,4^3+3cdot 0,4^2cdot h+3cdot 0,4h^2+h^3-0,4^3}{h}-3=left(3cdot 0,4^2-3right)+hcdot left(3cdot 0,4+hright)approx 2,5201$
- точное производное $f’left(0,4right)=3cdot 0,4^2-3=2,52$ при $hsim 0$ !
- $f’left(-0,6right)$ “На глаз по графику” ? $Rightarrow$ значения $fleft(-0,6right)approx 3,6$ и в сдвинутой $fleft(-0,4right)approx 3,1$. скорость изменения, наклон $f’left(-0,6right)approx frac{fleft(-0,4right)-fleft(-0,6right)}{-0,4-left(-0,6right)}approx frac{3,1-3,6}{0,2}=-2,5$
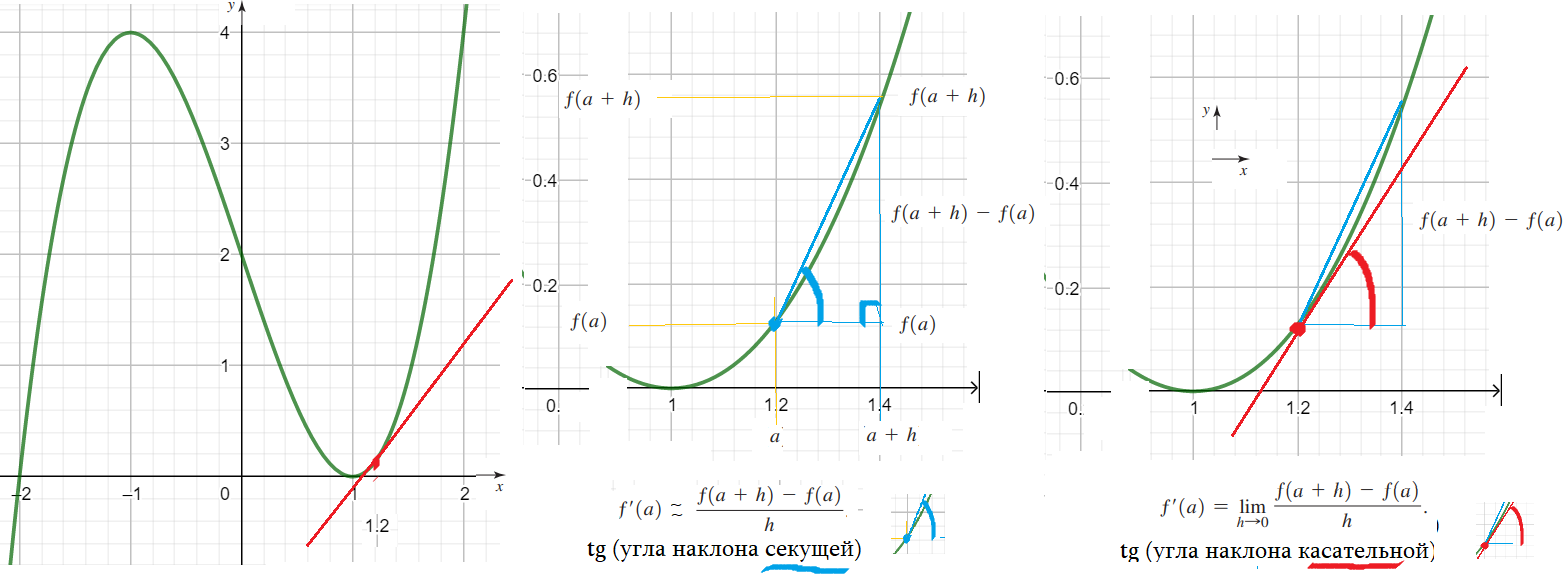
- Секущая графика функции – прямая, проходящая в точках графика $left(x_1;fleft(x_1right)right) и left(x_2;fleft(x_2right)right)$.
- Наклон секущей – тангенс угла наклона секущей к х – оси, равен $tg s=frac{fleft(x_2right)-fleft(x_1right)}{x_2-x_1}$.
- Касательной к графику в точке х = а – предел секущих в точках $left(a;fleft(aright)right) и left(a+h;fleft(a+hright)right)$ при h стремящемся к нулю.
- Наклон касательной – тангенс угла $k=frac{fleft(x+0,000001right)-fleft(xright)}{x+0,000001-x}$ . Точнее, “примерно равен”. Точнее: при малом h !.
- ….еще точнее “в пределе равен”. lim $frac{fleft(a+hright)-fleft(aright)}{h}$. Точка (a+h; f(a+h)) сближается с точкой (a; f(a)) при малом h !.
- Производная f'(a) равен тангенсу угла наклона касательной к графику функции f в точке (a, f(a)).
Пример 2: По графику функции найти производную – наклон касательной в указанной точке.
- Смотрим на касательную в точке х = 3. Для нахождения тангенса наклона надо “увидеть” прямоугольный треугольник с катетами вдоль х- и у- осей и с гипотенузой вдоль касательной.
- Считаем по клеткам: f'(3) = – 1 : 3 1 клетка по у – оси вниз (-), 3 клетки по х – оси вправо (+) .
- На 2-м рисунке: g'(5) = 2 : 2 2 клетки по у – оси вверх (+), 2 клетки по х – оси вправо (+) .
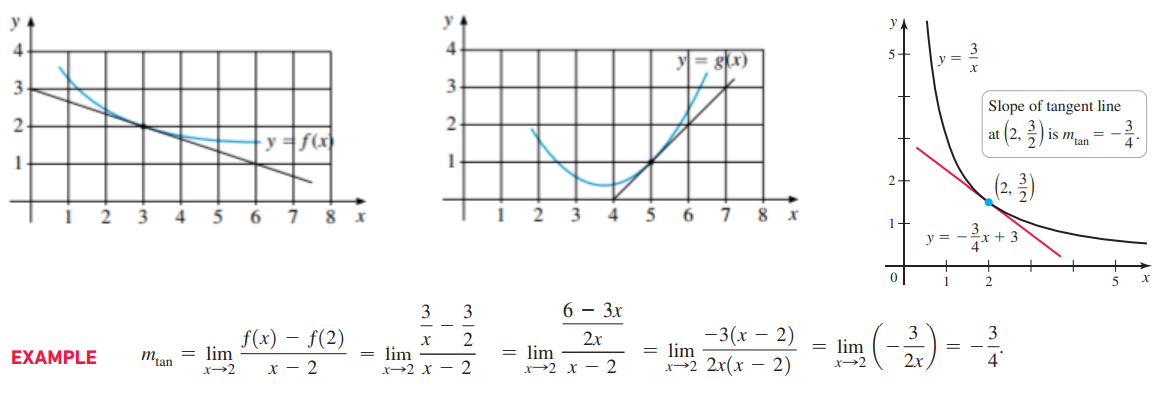
Уравнение касательной к графику функции $y=fleft(xright)$ в точке $x=x_0$ : $y=fleft(x_0right)+f’left(x_0right)cdotleft(x-x_0right)$ – касательная, прямая
- Функция $y=fleft(xright)$ и её касательная $y=ax+b$ в точке касания $x=x_0$ имеют одинаковые значения, наклон, производные.
- Наклон касательной = производное функции $a=f’left(x_0right)$ определяет как “течет” график: растет, убывает?
- Наклон положительный – касательная справа-налево – производная положительна – функция растет – график функции “течет” вверх.
- Наклон отрицательный – касательная слево-направо – производная отрицательна – функция убывает – график функции “течет” вниз, по склону.
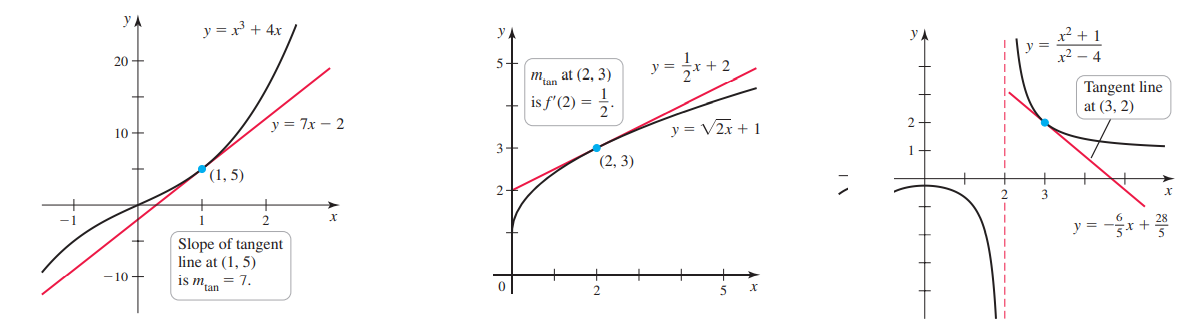
Производная – как детектор поведения функции
Вопрос: Как влияет на поведение функции $fleft(x_0right)$ около точки $x=x_0$ значение производной $f’left(x_0right)$ ?
- Из определения производной в точке $x=x_0$ $Rightarrow$ $f’left(x_0right)approxfrac{fleft(x_0+0,01right)-fleft(x_0right)}{x_0+0,01-x_0}$
- выразим значение функции чуть правее точки $x_0$ : $fleft(x_0+0,01right)approx fleft(x_0right)+0,01f’left(x_0right)$. Значит, функция будет иметь большее значение правее от $x_0$ , если только $f’left(x_0right) > 0$.
- Аналогичные рассуждения для значения функции чуть левее. Из $f’left(x_0right)approxfrac{fleft(x_0-0,01right)-fleft(x_0right)}{x_0-0,01-x_0}$ $Rightarrow$ $fleft(x_0-0,01right)approx fleft(x_0right)-0,01cdot f’left(x_0right)$ $Leftrightarrow$ понятно почему поведение функции левее $x_0$ зависит от знака производной в точке $x_0$.
- Сформулирует ответы на вопрос о влиянии знака производной в данной точке:
- если $f’left(x_0right) > 0$ то $fleft(x_0-0,01right) < fleft(x_0right) < fleft(x_0+0,01right)$ $Rightarrow $ функция растет (см. слева направо).
- если $f’left(x_0right) < 0$ то $fleft(x_0-0,01right) > fleft(x_0right) > fleft(x_0+0,01right)$ $Rightarrow $ функция убывает, график идет вниз.
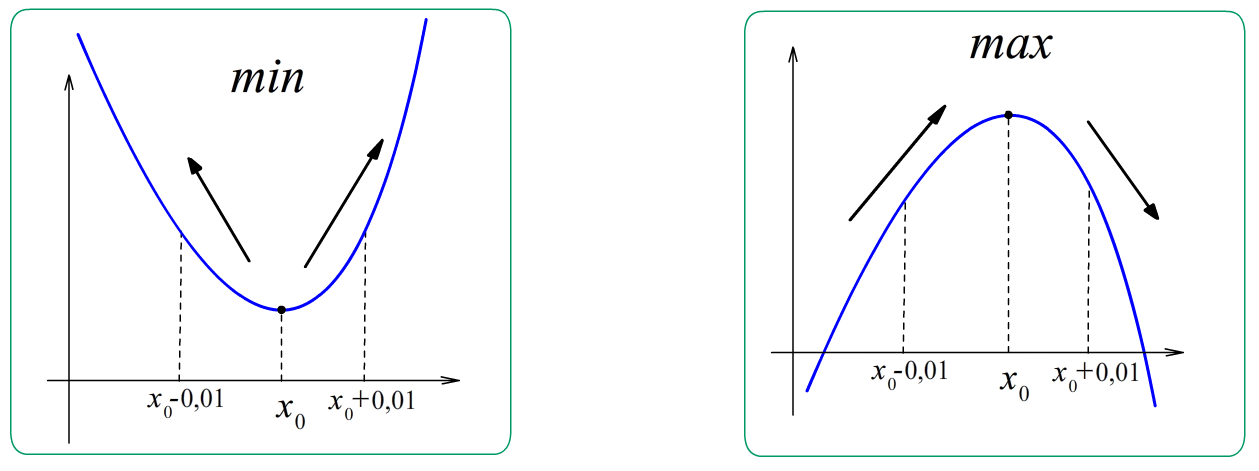
- если $f’left(x_0right)=0$ то ситуации более запутанные: при $fleft(x_0-0,01right) < fleft(x_0right) > fleft(x_0+0,01right)$ точка $x=x_0$ называется точкой максимума. В нем функция “выше”, чем по-соседству хоть слева, хоть справа.
В случае $fleft(x_0-0,01right) > fleft(x_0right) < fleft(x_0+0,01right)$, $x=x_0$ – точка минимума. Если ни то, ни другое, то точка перегиба.
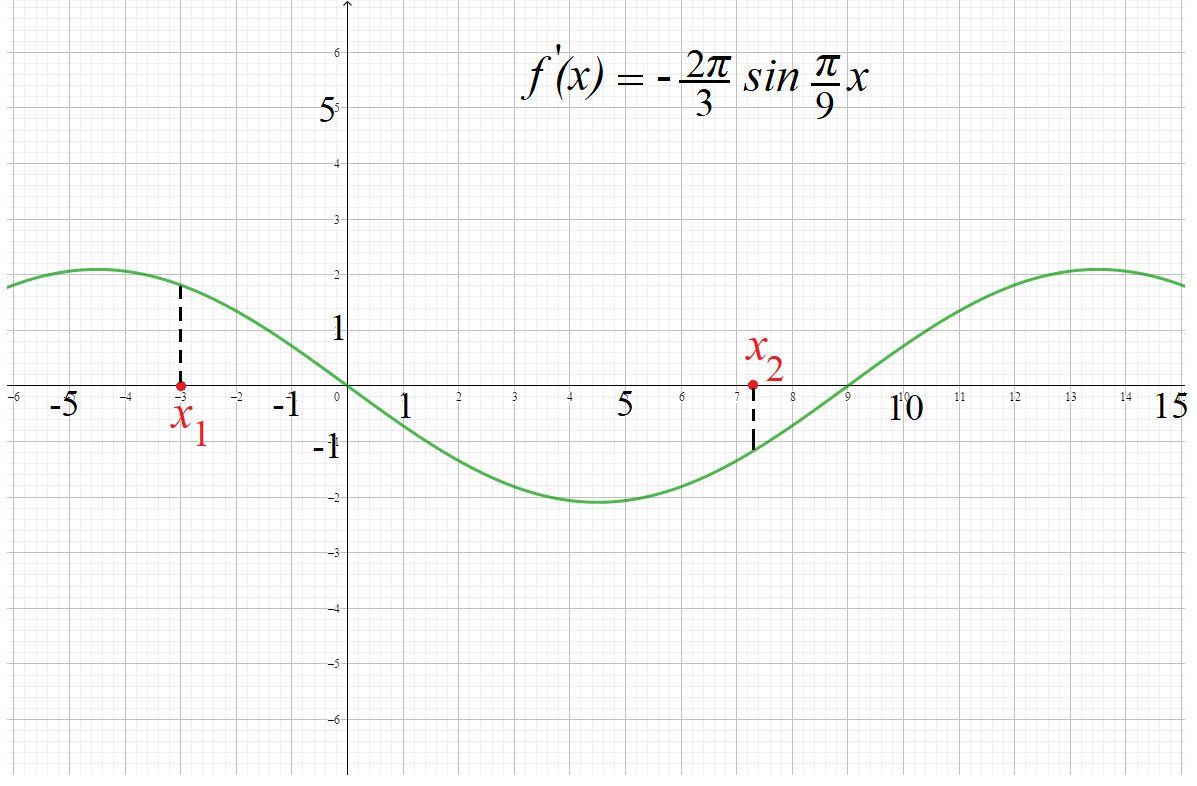
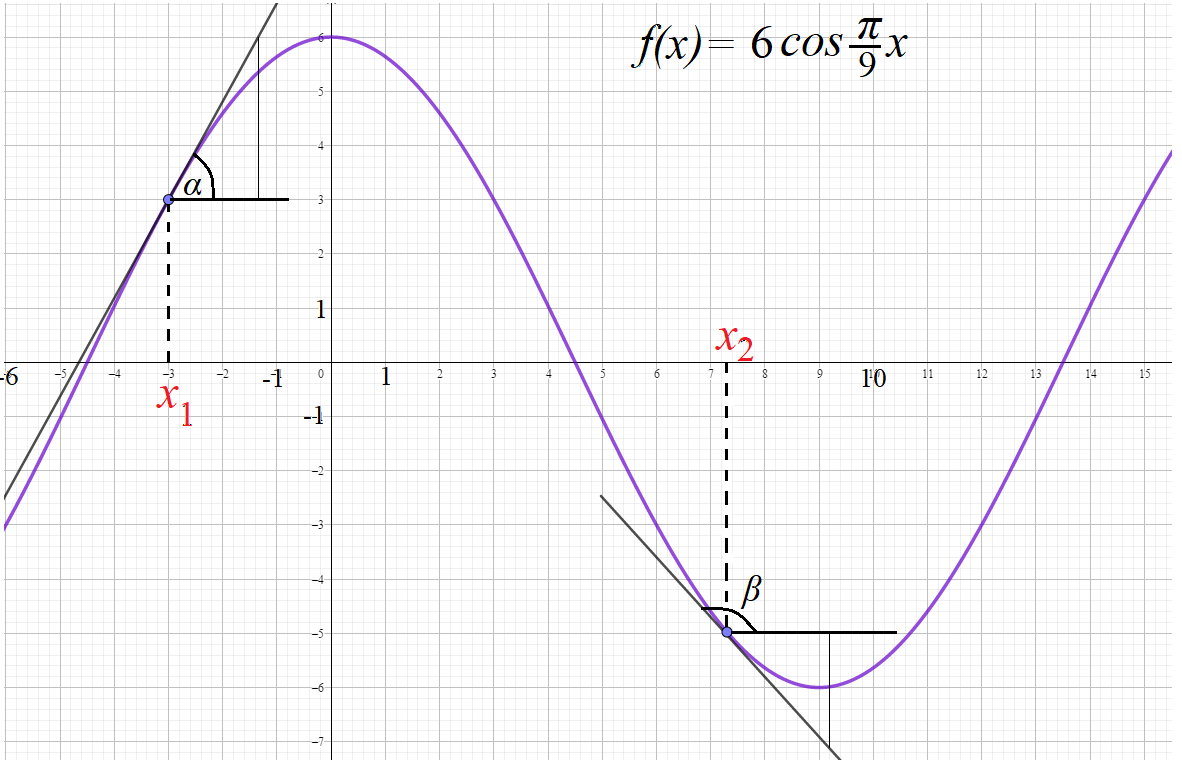
Пример 2: Каково взаимовлияние графика $fleft(xright)=6cosfrac{pi}{9}x$ и графике ее производной $f’left(xright)=-frac{2pi}{3}sinfrac{pi}{9}x$
- Производная от какой-то функции – это некая, связанная с ней функция, характеризующая поведение самой функции
- Рассмотрим точку $x_1=-3$ . В нем сама функция равна $fleft(-3right)=6cosfrac{pi}{9}(-3)=3$ , а ее производная – $f’left(-3right)=-frac{2pi}{3}sinfrac{pi}{9}(-3)approx1,77$,
- График график проходит в точке $(-3;3)$. Каково поведение графика около этой точки? Растет или убывает?
- Насколько быстро растет или убывает? На все эти вопросы ответы дает производная. Производная здесь $(-3;3)$ положительна, поэтому растет!
- Около точки $x_1=-3$ функция приближенно $fleft(xright)approx 3+1,77cdot(x+7)$
- Т.к. производная равна $1$, то тангенс угла наклона касательной, проведенной к графику нашей функции в данной точке ($-3; 3$) равен $1$.
- Значит, касательная направлена под углом $45$ градусов, ведь $tg45=1$.
- Значит, функция около этой точки растет “умеренно”, примерно под углом 45 градусов.
Значение производной $f’left(x_0right)$ в какой-либо точке указывает на рост или убывание исходной функции $fleft(xright)$ около этой точки $x_0$. Зная числовое значение производной, можно определить как ведет себя функция: стоит ли на месте, растет или убывает и как быстро изменяется. Производная от функции помогает узнать в каждой точке характер скорости изменений, поведения графика самой функции.
-
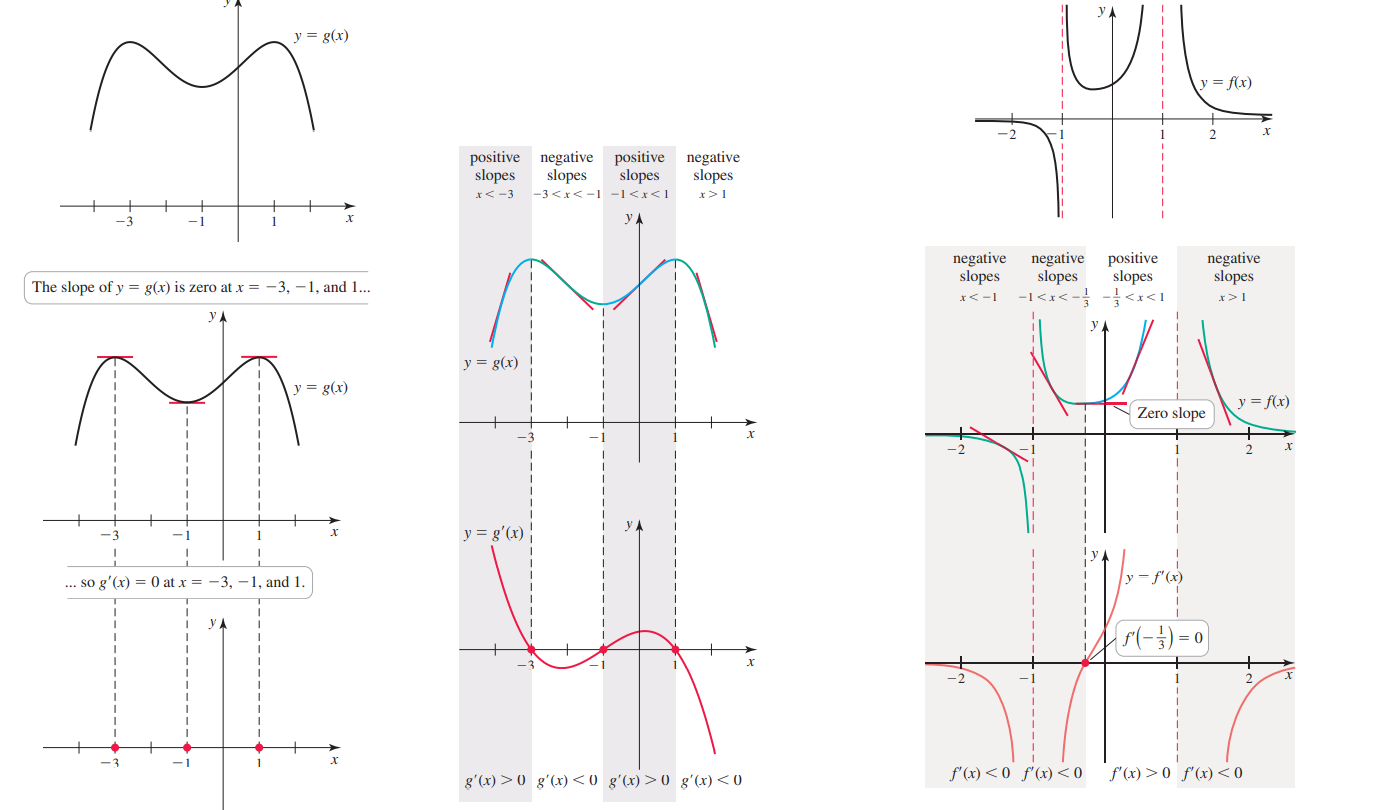
В тех точках, где функция растет – график поднимается вверх (если смотреть слева направо) – касательная к графику в этой точке наклонена вправо – – тангенс наклона положительный – производная в этой точке имеет положительное значение.
-
В тех точках, где функция убывает – график опускается вниз (если смотреть слева направо) – касательная к графику в этой точке наклонена влево – – тангенс наклона отрицательный, тупой угол – производная в этой точке имеет отрицательное значение.
-
Производная = 0 функция “остановилась”, “касательная горизонтальна” точка экстремума: минимум, максимум или перегиб.
-
Вторая производная в точке x показывает скорость изменения скорости, т.е. ускорение в этой точке. Вторая производная = 0 означает “ускорение обнулилось”. больше нуля – выпоукло вниз (min), меньше нуля – вверх (max).
Пример 3: Указать интервалы монотонности функции $fleft(xright)=x^3-3x+2$ . ;
- $f’left(xright)=left(x^3-3x+2right)’=3x^2-3$ находим производную от нашей функции
- $f’left(xright)>0$ $3x^2-3>0$ $left(-infty ;-1right) left(1;infty right)$ интервалы возрастания, неравенство больше
- $f’left(xright)<0$ $3x^2-3<0$ $left(-1;1right)$ интервалы убывания, производное минус
- $M_f$ области монотонности $ left(-infty ;-1right)+left(-1;1right)+left(1;infty right)$
Точки экстремумов функции. min-max
Из $f’left(x_0right)approxfrac{fleft(x_0+0,01right)-fleft(x_0right)}{x_0+0,01-x_0}$ выразим значение функции чуть правее точки $x_0$ : $fleft(x_0+0,01right)approx fleft(x_0right)+0,01f’left(x_0right)$.
Значит, функция будет иметь большее значение правее от $x_0$ , если только $f’left(x_0right) > 0$.
Аналогичные рассуждения для значения функции чуть левее. Из $f’left(x_0right)approxfrac{fleft(x_0-0,01right)-fleft(x_0right)}{x_0-0,01-x_0}$ $Rightarrow$ $fleft(x_0-0,01right)approx fleft(x_0right)-0,01cdot f’left(x_0right)$ $Leftrightarrow$ понятно почему поведение функции левее $x_0$ зависит от знака производной в точке $x_0$.
Итак:
-
если $f’left(x_0right) > 0$ то $fleft(x_0-0,01right) < fleft(x_0right) < fleft(x_0+0,01right)$ $Rightarrow $ функция растет (см. слева направо).
-
если $f’left(x_0right) < 0$ то $fleft(x_0-0,01right) > fleft(x_0right) > fleft(x_0+0,01right)$ $Rightarrow $ функция убывает, график идет вниз.
-
если $f’left(x_0right)=0$ то ситуации более запутанные: при $fleft(x_0-0,01right) < fleft(x_0right) > fleft(x_0+0,01right)$ точка $x=x_0$ называется точкой максимума. В нем функция “выше”, чем по-соседству хоть слева, хоть справа.
В случае $fleft(x_0-0,01right) > fleft(x_0right) < fleft(x_0+0,01right)$, $x=x_0$ – точка минимума. Если ни то, ни другое, то точка перегиба.
Определение: Точка, в которой производная обнуляется, называется экстремумом (минимум, максимум, перегиб).
В этой точке наклон графика равен нулю, т.е. касательная к графику горизонтальна.
Точка максимума – если функция растет, “застывает” в $x_0$” , затем убывает.
Производная функции больше нуля, в $x_0$ обнуляется, затем отрицательна.
Точка минимума наоборот – если функция убывает, “застывает” в $x_0$” , затем растет.
Производная меньше нуля, равна нулю в $x_0$”, затем положительна.
Нахождение точки минимума (максимума) функции $y=fleft(xright)$:
Точка минимума – это $x$ – число, в котором производная равна нулю, а сама исходная функция от убывания переходит к возрастанию. Надо “взять” производную исходной функции и составить уравнение экстремума “производная равна нулю”. Среди точек экстремума найти точку минимума.
Есть три способа:
- по поведению “рост / убывание” исходной функции ;
- либо поведение “отрицательности / положительности” производной;
- либо знак второй производной в этой точке; если 2-ая производная (“производная от производной”) в точке $x_0$ положительна, то это минимум.
min: $f’left(x_0right)=0$ , $fleft(x_0-0,01right) > fleft(x_0right) < fleft(x_0+0,01right)$ , $f’left(x_0-0.01right) < 0$ , $f’left(x_0+0.01right) > 0$ ; $f”left(x_0right) > 0$.
max: $f’left(x_0right)=0$ , $fleft(x_0-0,01right) < fleft(x_0right) > fleft(x_0+0,01right)$ , $f’left(x_0-0.01right) > 0$ , $f’left(x_0+0.01right) < 0$ ; $f”left(x_0right) < 0$.
Обозначения множеств, областей
$D_f$ область определения функции
$Z_f$ область знакопостоянства, интервалы положительности, отрицательности
$M_f$ области монотонности функции, интервалы возрастания, убывания
$X_f$ экстремумы функции, перечисление х – точек
$T_f$ уравнение касательной к функции в указанной х – точке
$E_f$ области значений функции, все у – значений