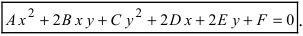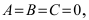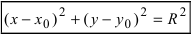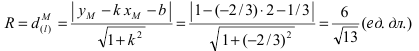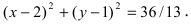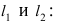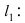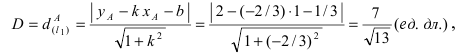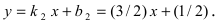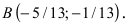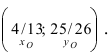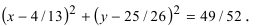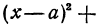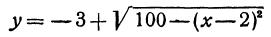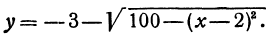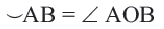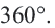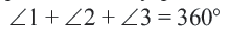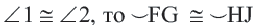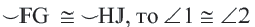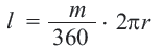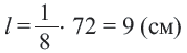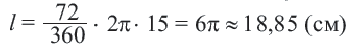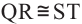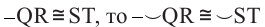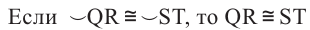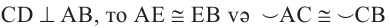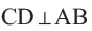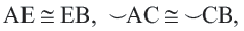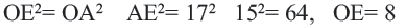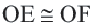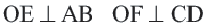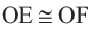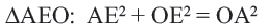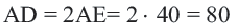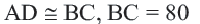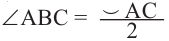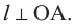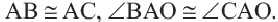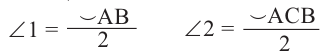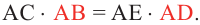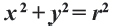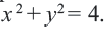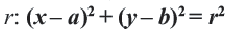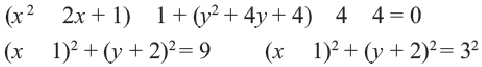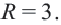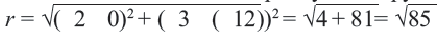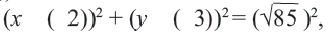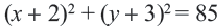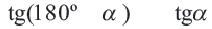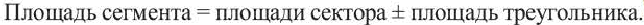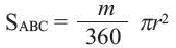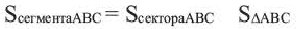Как определить радиус дуги или сегмента круга и найти центр
Иногда, при выполнении особо заковыристых работ по отделке приходится решать не совсем простые задачи. Например, имеется часть окружности, говоря по научному – дуга и для этой дуги нужно определить радиус и найти центр окружности.
Сделать это можно двумя методами. Первый метод основан на расчетах, а второй – прикладной. Сначала рассмотрим первый метод, его достоинства и недостатки, а затем второй.
Первый метод определения радиуса дуги или сегмента круга
Изначально это выглядит так:
Рисунок 463.1. а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.
Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.
Решение подобной задачи достаточно подробно рассматривалось в статье “Расчет арочной перемычки”, поэтому здесь лишь приведу основные формулы:
Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.
А теперь поговорим о недостатках.
Проблема данного метода даже не в том, что требуется помнить формулы из школьного курса геометрии, успешно забытые много лет назад – для того, чтобы напомнить формулы – есть интернет. А вот калькулятор с функцией arctg, arcsin и проч. есть далеко не у каждого пользователя. И хотя эту проблему также успешно позволяет решить интернет, но при этом не следует забывать, что мы решаем достаточно прикладную задачу. Т.е. далеко не всегда нужно определить радиус окружности с точностью до 0.0001 мм, точность 1 мм может быть вполне приемлема.
Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу. Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.
Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.
В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.
Второй метод определения радиуса дуги (метод последовательных приближений)
Итак продолжим рассмотрение имеющейся ситуации.
Так как нам все равно необходимо найти центр окружности, то для начала мы из точек, соответствующих началу и концу дуги, проведем как минимум две дуги произвольного радиуса. Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.
Теперь нужно соединить пересечение дуг с серединой хорды. Впрочем, если мы из указанных точек проведем не по одной дуге, а по две, то данная прямая будет проходить через пересечение этих дуг и тогда искать середину хорды вовсе не обязательно.
Ну а дальше все просто: измеряем расстояние от пересечения дуг до начала (или конца) рассматриваемой дуги, а затем расстояние от пересечения дуг до точки, соответствующей высоте сегмента.
Если расстояние от пересечения дуг до начала или конца рассматриваемой дуги больше, чем расстояние от пересечения дуг до точки, соответствующей высоте сегмента, то значит центр рассматриваемой дуги находится ниже на прямой, проведенной через пересечение дуг и середину хорды. Если меньше – то искомый центр дуги выше на прямой.
Исходя из этого на прямой принимается следующая точка, предположительно соответствующая центру дуги, и от нее производятся те же измерения. Затем принимается следующая точка и измерения повторяются. С каждой новой точкой разница измерений будет все меньше.
Вот собственно и все. Не смотря на столь пространное и мудреное описание, для определения радиуса дуги таким способом с точностью до 1 мм достаточно 1-2 минут.
Теоретически это выглядит примерно так:
Рисунок 463.2. Определение центра дуги методом последовательных приближений.
А на практике примерно так:
Фотография 463.1. Разметка заготовки сложной формы с разными радиусами.
Тут только добавлю, что иногда приходится находить и чертить несколько радиусов, потому на фотографии так много всего и намешано.
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье “Записаться на прием к доктору”
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины – номер гривневой карты (Приватбанк) 5168 7422 4128 9630
Категории:
- Расчет конструкций . Основы прикладной геометрии
Оценка пользователей:
8.5 (голосов: 2)
Переходов на сайт:
31889
Комментарии:
R = H/(1 – cos(a/2))
Радиус прямо пропорционален H.
Как так?
Я достаточно подробно ответил на ваш вопрос в статье “Расчет арочной перемычки”, где вы задали подобный вопрос.
Если угол не нужен для дальнейших расчетов, радиус находится проще – без тригонометрических функций и даже можно без калькулятора – на бумажке. R = L^2/(8*H) + H/2
Сначала термины:
Отрезок, соединяющий концы дуги называется хордой (a), а высота сегмента (перпендикуляр из середины хорды) — стрелкой (h).
Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов. То есть R^2=(R-h)^2+(a/2)^2.
А что касается нахождения центра, то перпендикуляры к серединам хорд пересекаются в центре!
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье “Записаться на прием к доктору” (ссылка в шапке сайта).
Определение центра окружности и центра дуги
Определение центра окружности (рис. 28).
- 1) Провести в окружности две непараллельные хорды АВ и CD.
- 2) К середине хорды А В восстановить перпендикуляр (см. деление отрезка на две равные части при помощи циркуля).
- 3) Выполнить аналогичное построение для хорды ВС.
Пересечение перпендикуляров является центром окружности.
Определение центра дуги окружности (рис. 29).
- 1) Назначить на дуге три произвольных точки А, В и С.
- 2) Соединить точки прямыми.
- 3) Через середины полученных хорд АВ и ВС провести перпендикуляры.
Точка О пересечения перпендикуляров является центром дуги.
Сопряжения
Сопряжением называется плавный переход от одной линии к другой.
Из всего многообразия сопряжений различных линий выделяют основные виды сопряжений:
- • сопряжение прямой линии с дугой окружности;
- • сопряжение двух различно расположенных прямых линий с помощью дуги окружности;
- • сопряжение дуг двух окружностей с помощью прямой линии;
- • сопряжение дуг двух окружностей с помощью третьей.
Дуги окружностей, с помощью которых выполняется сопряжение, называют дугами сопряжения. Для построения дуги сопряжения необходимо на чертеже выявить:
- • центр дуги сопряжения;
- • радиус этой дуги;
- • точки сопряжения, в которых дуга сопряжения переходит в сопрягаемые линии.
Задаваясь одним из этих параметров, остальные можно определить графически.
При сопряжении прямой линии с дугой окружности прямая линия является касательной к окружности. В этом случае центр дуги окружности О и точка сопряжения К лежат на перпендикуляре к сопрягаемой прямой (рис. 30).
При сопряжении дуг двух окружностей точка сопряжения К должна лежать на линии, соединяющей центры сопрягаемых дуг (рис. 31).
Сопряжение пересекающихся прямых линий с помощью дуги заданного радиуса.
Сопряжение двух взаимно перпендикулярных прямых а и b дугой окружности заданного радиуса R (рис. 32, а).
- 1) Из точки пересечения прямых как из центра провести дугу окружности радиусом R до пересечения с прямыми в точках А и В (рис. 32, б).
- 2) Из полученных точек/1 и В как из центров тем же радиусом провести дуги окружностей до взаимного пересечения в точке О (рис. 32, в).
3) Из точки О радиусом R провести дугу сопряжения (рис. 32, г). Точки А и В являются точками сопряжения.
Сопряжение двух пересекающихся прямых а и b под произвольным углом дугой заданного радиуса R (рис. 33, 34).
Центр сопряжения О должен лежать на расстоянии R от заданных прямых. Для его определения необходимо:
- 1) Из произвольных точек на заданных прямых провести дуги радиусом R.
- 2) Построить линии, касательные к дугам. Точка О пересечения этих линий является центром сопряжения (рис. 33, а).
- 3) Из точки О опустить перпендикуляры на заданные прямые.
Точки И и i? являются точками сопряжения (рис. 33,6).
4) Из точки О как из центра провести дугу радиуса R. Эта дуга является дугой сопряжения.
На рисунке 34 сопряжение прямых линий выполнено аналогично.
Сопряжение параллельных прямых дугой окружности. Если на одной из прямых а и b задана точка сопряжения А (рис. 35, а), сопряжение выполняют следующим образом.
- 1) Из точки А опустить перпендикуляр на прямую b (рис. 35, б).
- 2) Разделить отрезок АВ пополам (рис. 35, в).
- 3) Из точки О как из центра провести дугу сопряжения радиусом ОА (рис. 35, г).
Сопряжение дуги окружности радиуса R и прямой а дугой заданного радиуса Rj (рис. 36).
Для выполнения этого сопряжения сначала необходимо определить множество центров дуг радиуса Rx.
1) На расстоянии Rx от прямой а провести параллельную ей прямую т. Прямая т является множеством центров дуг радиуса Rx.
2) Из центра О провести дугу концентрической окружности радиусом (R + R). Точка Ох пересечения дуги с прямой т будет центром дуги сопряжения.
Точка сопряжения С получена на перпендикуляре, опущенном из точки 0 на прямую а, а точка В является точкой пересечения окружности с прямой, соединяющей точки О и Ох.
Сопряжение дуг двух окружностей с помощью прямой линии. Это сопряжение сводится к построению внешней (рис. 37) или внутренней (рис. 38) касательной к данным окружностям.
Построение внешней касательной, сопрягающей две окружности радиусов R и R (рис. 37, а).
- 1) Соединить центры окружностей.
- 2) Отрезок 00 разделить точкой О2 пополам.
- 3) Из точки О провести окружность радиусом (R — Rx), равным разности радиусов заданных окружностей (рис. 31,6).
- 4) На построенной окружности сделать засечки радиусом R2 = 020. Точки обозначены Е и D (рис. 37, в).
- 5) Продлить отрезки ОЕ и OD до пересечения с окружностью радиуса R. Полученные точки С и В являются точками сопряжения (рис. 37, г).
- 6) Соединить точки Ей D с центром Ох.
- 1) Из точек С и В параллельно отрезкам ОхЕ и OxD провести отрезки, сопрягающие две окружности.
Точки сопряжения на окружности радиуса R можно получить, опустив перпендикуляры из точки Ох к отрезкам ОхЕ и OxD.
Построение внутренних касательных, сопрягающих две окружности радиусов R и R (рис. 38, а).
- 1) Из середины отрезка ООх — точки 02 — проводят дугу радиусом R2 = 020 (рис. 38, б).
- 2) Из центра О проводят дугу радиусом (R + R), равным сумме радиусов заданных окружностей. В пересечении этих окружностей отмечают точки Е и D.
- 3) Точки Е п D соединить с точкой О (рис. 38, в). Точки С и В пересечения прямых ОЕ и OD с окружностью являются точками сопряжения.
- 4) Точки Е и D соединить с точкой О у.
- 5) Через точки С и В провести прямые линии параллельно отрезкам ЕО и DO у.
Прямые ССХ и ВВх являются касательными, сопрягающими заданные окружности. Точки сопряжения Су и В у лежат на пересечении перпендикуляров, проведенных из центра О, к прямым ССу и В By.
Построение сопряжения двух дуг окружностей. Сопряжение двух дуг окружностей может быть внешнее (рис. 39, а) и внутреннее (рис. 39, б). Точка сопряжения А лежит на прямой, соединяющей центры окружностей.
Расстояние между центрами при внешнем сопряжении равно сумме радиусов окружностей (R + Ry), а при внутреннем сопряжении — разности этих радиусов (R — Ry). В точке сопряжения А окружности имеют общую касательную t.
Построение сопряжения двух дуг окружностей дугой заданного радиуса.
Такой вид сопряжения может быть внешним, внутренним и смешанным.
Построение внешнего сопряжения двух дуг окружностей радиусов R и Ry с помощью дуги радиуса R2 (рис. 40, а). При внешнем сопряжении дуги находятся с внешней стороны дуги сопряжения, т.е. точки сопряжения представляют собой точки перегиба.
- 1) Из центра О радиусом (R + R2), а из центра Ох радиусом (Rx + R2) проводят дуги до пересечения в точке 02 (рис. 40, б). Точка 02 является центром дуги сопряжения.
- 2) Соединить точку 02 с центрами дуг О и Ох. Точки В и С, лежащие на линиях 020 и 020х, являются точками сопряжения (рис. 40, в).
- 3) Из точки 02 как из центра провести дугу сопряжения радиусом R2 (рис. 40, в).
Построение внутреннего сопряжения двух дуг окружностей радиусов R и Rx при помощи дуги радиуса R2 (рис. 41, а). При внутреннем сопряжении сопрягаемые дуги находятся внутри дуги сопряжения, т.е. дуга сопряжения и сопрягаемые дуги находятся по одну сторону касательных, проведенных через точки сопряжения. Точки сопряжения в этом случае представляют собой точки самоприкосновения.
Порядок построения следующий (рис. 41,5).
- 1) Из центра О провести дугу радиусом (Л2 – Л), а из центра Ох — дугу радиусом, равным (R2 — R<). В пересечении этих дуг получают точку 02 — центр дуги сопряжения.
- 2) Соединить точку 02 с центрами дуг О и О^. Точки В иВ, лежащие на прямых 020 и 020х, являются точками сопряжения.
- 3) Из точки 02 как из центра провести дугу сопряжения радиусом R2.
Построение смешанного сопряжения двух дуг окружностей радиусов Ru RC помощью дуги радиуса R2 (рис. 42, а). При смешанном сопряжении двух данных дуг окружностей третьей дугой одна сопрягаемая дуга находится внутри дуги сопряжения, а другая — вне ее, т.е. одна точка сопряжения является точкой самоприкосновения, а вторая — точкой перегиба.
Построение смешанного сопряжения аналогично построению внешнего и внутреннего сопряжений. При этом возможны два варианта.
1) Дуга сопряжения с дугой радиуса R имеет внутреннее сопряжение, а с дугой радиуса — внешнее (рис. 42, б).
При таком сопряжении из центра О необходимо провести дугу радиусом (R2 — R), а из центра Ох — радиусом (R2 + Ri). Пересечение проведенных дуг определяет центр дуги сопряжения — точку О2–
В этом случае точка В — точка самоприкосновения, а точка Вх — точка перегиба.
2) Дуга сопряжения с дугой радиуса R имеет внешнее сопряжение, а с дугой радиуса Ru внутреннее (рис. 42, в).
В этом случае из центра О необходимо провести дугу радиусом (/?2 + R), а из центра 0 — радиусом (R2 — R). Точка В стала точкой перегиба, а точка Вь точкой самоприкосновения.
На рисунке 43 показан случай смешанного сопряжения двух дуг окружностей третьей дугой заданного радиуса R2, когда расстояние а между центрами дуг меньше суммы их радиусов (R + R <).Построения ясны из чертежа.
Геометрия. Урок 5. Окружность
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение окружности
- Отрезки в окружности
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности .
Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
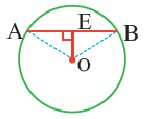
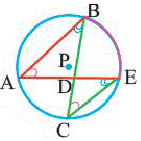
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
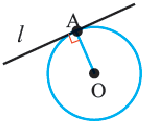
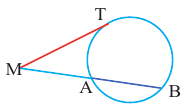
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
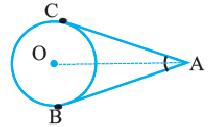
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Часть окружности, заключенная между двумя точками, называется дугой окружности .
Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .
Теорема 4:
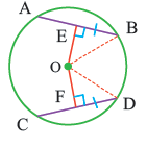
Равные хорды стягивают равные дуги.
Если A B = C D , то ∪ A B = ∪ C D
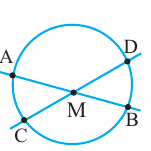
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
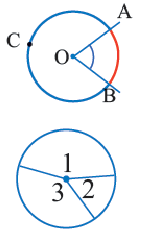
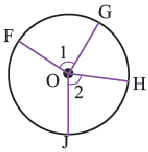
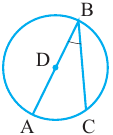
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
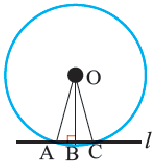
Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360 ° .
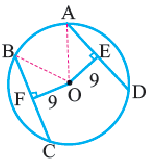
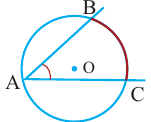
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.
Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:
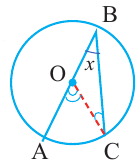
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .
Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Длина дуги окружности , на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
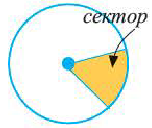
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
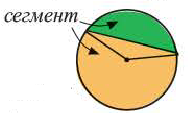
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
[spoiler title=”источники:”]
http://bstudy.net/787728/tehnika/opredelenie_tsentra_okruzhnosti_tsentra_dugi
[/spoiler]
Содержание:
Окружность:
Определение: Кривой второго порядка называется линия, описываемая уравнением 
Замечание: Если коэффициенты 
При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.
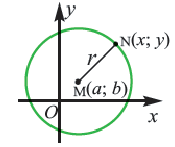
Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки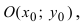 
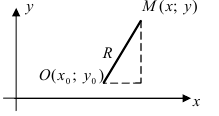
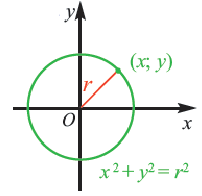
называемой центром окружности, на расстояние R, которое называется радиусом окружности.
Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:
Рис. 27. Вывод уравнения окружности.
Из рисунка видно, что по теореме Пифагора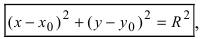 
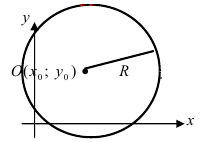
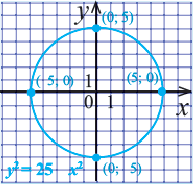
которое определяет уравнение окружности (Рис. 28): 
Рис. 28. Окружность. 
Если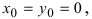 
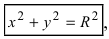
то уравнение принимает вид 
который называется каноническим уравнением окружности.
Пример:
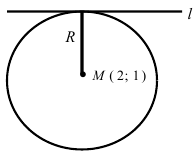
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия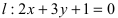 
является касательной к окружности.
Решение:
Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.
В уравнении окружности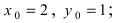 
таким образом оно имеет вид: 
Пример:
Составить уравнение окружности, касающейся двух параллельных прямых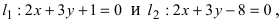 
причем одной из них в т. А (1; 2).
Решение:
Прежде всего определим, на какой из прямых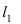 
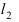
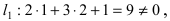
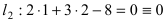
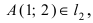
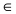
или 
лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых 
следовательно, точка A(1; 2) принадлежит линии 
(в сокращенной форме это предложение пишут так: 
где значок 
означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой 
а радиус окружности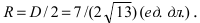 
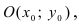
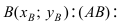
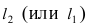
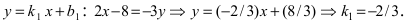
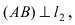
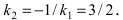
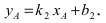
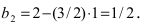
Найдём координаты центра окружности точки 
которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки 
перейдем от общего уравнения прямой 
к уравнению прямой с угловым коэффициентом 
Так как прямая
то её угловой коэффициент 
Прямая (АВ) проходит через известную точку A(1;2), следовательно, 
Отсюда находим 
Таким образом,уравнение прямой (АВ):
Найдем координаты точки B, которая является пересечением прямых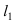 
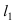
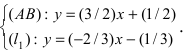
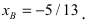
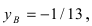
и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых 
и (АВ): (В): 
Подставим выражение для переменной у из второго у равнения в первое, получим 
Подставив это значение во второе уравнение системы, найдем 
т.е. 
Для вычисления координат точки О применим формулы деления отрезка пополам (О):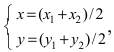 
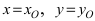
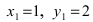
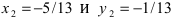
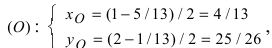
в этой формуле 
(координаты точки О), 
(координаты точки А), 
(координаты точки В), следовательно, 
т.е. координаты точки О 
Таким образом, уравнение искомой окружности имеет вид: 
Окружность в высшей математике
Рассмотрим уравнение
которое получается из уравнения (I), если положить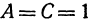 
, 
.
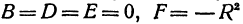
Если в формулу, выражающую расстояние между двумя точками, подставить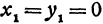 
, 
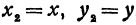
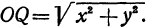
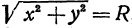
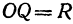
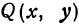
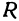
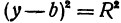
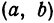
, то получим 
Из уравнения (1) находим, что 
, т. е. 
. Это значит, что все точки 
, координаты которых удовлетворяют уравнению (1), находятся на расстоянии 
от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса 
с центром в начале координат. Аналогично получаем, что уравнение 
определяет окружность радиуса с центром в точке 
.
Пример:
Найдем уравнение окружности с центром в точке 
и радиусом, равным 10.
Решение:
Полагая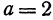
, 
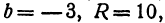
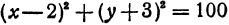
получим 
.
Разрешим это уравнение относительно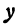 
, будем иметь
и
Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.
Центральный угол. Градусная мера дуги
Дуга окружности. Если отметить на окружности точки 
и 
, то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка 
является какой-либо точкой дуги 
, то 
. Если точки и являются концами диаметра, го каждая дуга является полуокружностью.
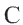
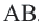
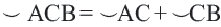
Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла: 
Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна 
Дуги окружности и их величины
Пример: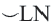 
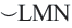
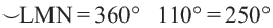
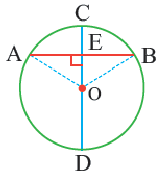
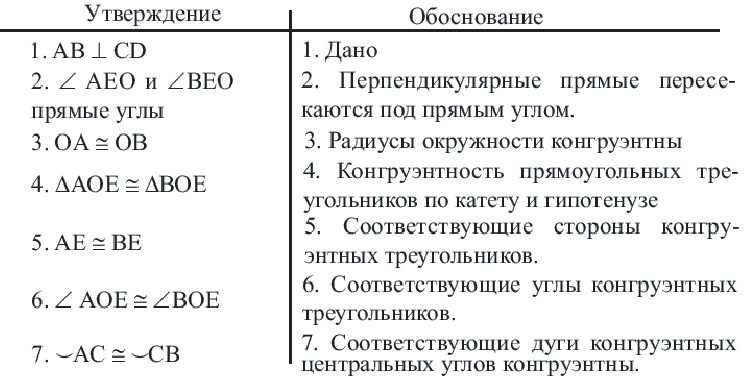
минорная дуга: 
мажорная дуга: 
Конгруэнтные дуги
В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.
Если 
Если 
Длина дуги
Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.
Длина дуги в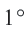 
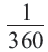
равна 
части длины окружности.
Длина дуги, соответствующей центральному углу с градусной мерой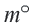 
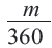
, составляет 
части длины окружности: 
Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)
Пример №1
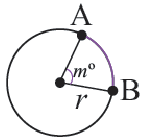
Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу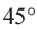 
.
Решение:
Так как центральный угол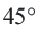 
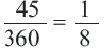
составляет 
часть полного угла, то длина искомой дуги: 
Пример №2
Найдите длину дуги, соответствующей центральному углу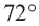 
в окружности радиусом 15 см.
Решение: подставляя значения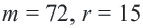 
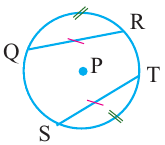
в формулу длины дуги находим: 
Окружность и хорда
Теорема о конгруэнтных хордах
Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.
Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.
1)Если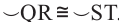 
, то 
2)Если 
Доказательство теоремы 1:
Теорема о серединном перпендикуляре хорд
Теорема 2.
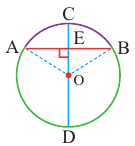
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.
Если 
Доказательство теоремы 2.
Дано: 
– центральный угол, 
Докажите: 
Начертите радиусы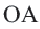 
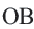
и 
окружности.
Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.
Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если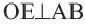 
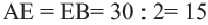
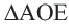
, то 
. Из 
по теореме Пифагора имеем: 
Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности
Теорема 3.
Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.
Если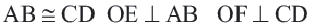 
, то 
Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.
Доказательство теоремы 3
Дано: Окружность с центром 
Докажите: 
Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам. 
и 
– серединные перпендикуляры конгруэнтных хорд 
и 
. 
, так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности 
и 
: 
. Прямоугольные треугольники, 
и 
конгруэнтны (по катету и гипотенузе). Так как и являются соответствующими сторонами данных треугольников, то они конгруэнтны: 
. Теорема доказана.
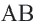
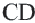
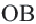
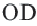
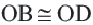
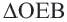
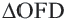
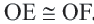
Задача. Хорды 
и 
находятся на одинаковом расстоянии от центра окружности. 
. Если радиус окружности равен 41 единице, то найдите 
.
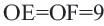
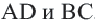
Решение: Так как хорды и находятся на одинаковом расстоянии от центра, то они конгруэнтны: 
Соединим точки 
и 
с точкой 
В прямоугольном треугольнике 
; 
; 
; 
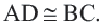
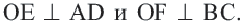
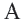
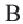
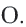
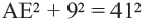
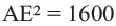
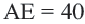
Так как 
Угол, вписанный в окружность
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.
является углом вписанным в окружность с центром 
, а 
дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.
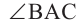
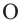
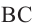
Угол, вписанный в окружность:
Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается. 
Доказательство (текстовое):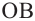 
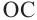
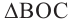
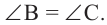
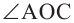
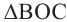
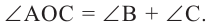
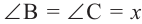
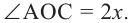
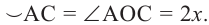
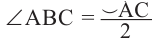
и 
радиусы окружности и 
равнобедренный треугольник. Значит, 
Так как 
является внешним углом 
, 
Если примем, что 
, то 
Так как градусные меры центрального угла и опирающейся на него дуги равны, то 
Следовательно, 
.
Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.
Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.
Конгруэнтные углы, вписанные в окружность
Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны.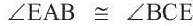 
, 
.
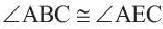
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если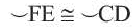 
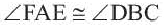
, то 
.
Касательная к окружности
Касательная. Признак касательной
Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Прямая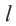 
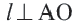
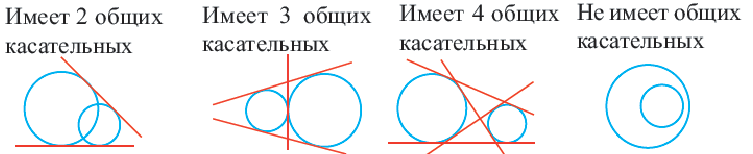
является касательной к окружности. Значит, 
Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.
Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.
Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.
Доказательство теоремы 1. Если прямая 
– касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая 
не перпендикулярна радиусу 
Проведем 
и на прямой выделим отрезок 
Тогда 
так как 
Значит, точка 
также находится на окружности. То есть прямая имеет с окружностью две общие точки, что противоречит условию. Значит, 
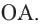
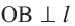
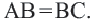
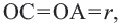
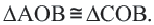
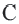
Свойства касательных, проведенных к окружности из одной точки
Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.
и 
касательные, проведенные из точки 
к окружности с центром 
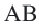
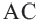
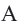
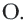
Углы, образованные секущими и касательными
Прямая, имеющая две общие точки с окружностью, называется секущей окружности.
Углы между двумя секущими
Вершина угла находится внутри окружности
Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному. 
Углы между касательной и секущей
Вершина угла находится на окружности
Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.
Углы, образованные касательной и секущей
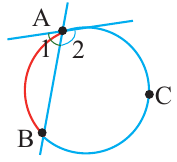
Вершина угла находится вне окружности
Теорема 1.
Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.
Отрезки секущих и касательных
Длина отрезков, секущих окружность
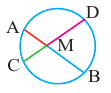
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.
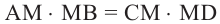
Теорема 2. Если из точки 
провести две прямые, пересекающие окружность соответственно в точках 
и 
, 
и 
то верно равенство 
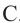
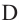
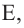
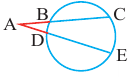
Теорема 3. Если из точки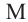 
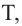
проведены прямая, которая пересекает окружность в точках и и касательная к окружности в точке 
то верно равенство: 
Уравнение окружности
Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом 
и с центром в начале координат. Расстояние между центром окружности 
и ее любой точкой 
равно радиусу окружности.
Расстояние между двумя точками
Упрощение
Возведение обеих частей в квадрат
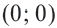
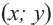
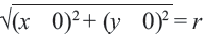
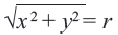
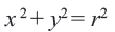
Уравнение окружности с центром в начале координат и радиусом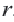 
: 
Например, уравнение окружности с центром в начале координат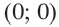 
и радиусом 2 имеет вид: 
По формуле расстояния между центром окружности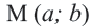 
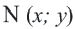
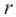
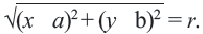
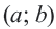
и точки 
на окружности радиуса 
имеем 
Возведя в квадрат обе части, получаем уравнение окружности с центром в точке 
и радиусом 
Например, уравнение окружности с центром в точке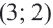 
и радиусом 4 имеет вид: 
Пример №3
Постройте на координатной плоскости окружность, заданную уравнением 
Решение: Напишем уравнение в виде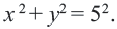 
Как видно, 
Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например,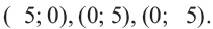 
Проведем окружность через эти точки.
Пример №4
Точка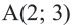 
находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.
Решение: Записав координаты точки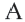 
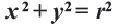
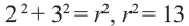
в уравнении 
, получим: 
Уравнение этой окружности: 
Пример №5
Найдем центр и радиус окружности, заданной уравнением 
Решение: 
Центр окружности точка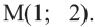 
Радиус 
Пример №6
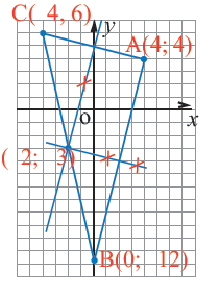
Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках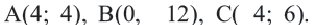 
На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.
Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка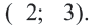 
Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности, 
Уравнение окружности: 
Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.
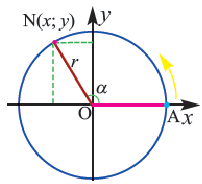
Координаты точек, находящихся на окружности, и тригонометрические отношения
Если точка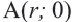 
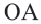
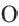
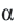
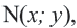
при повороте радиуса 
вокруг точки 
против движения часовой стрелки на угол 
преобразуется в точку 
то 
Для координат точки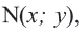 
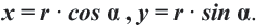
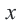
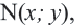
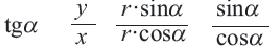
соответствующей углу поворота 
на окружности, верны формулы 
В этих формулах – угол, отсчитываемый от положительной оси 
против движения часовой стрелки. Если точка 
не находится на оси ординат, то 
.
Синусы смежных углов равны, а косинусы взаимно противоположны.
Из этих формул при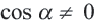 
почленным делением получаем:
С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.
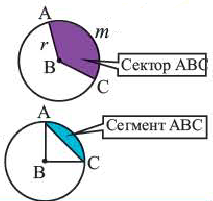
Сектор и сегмент
Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.
Например, часть круга, соответствующая центральному углу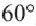 
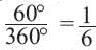
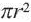
, составляет 
часть всего круга. Так как площадь круга 
, то площадь этого сектора будет 
Сегмент часть круга, ограниченная хордой и соответствующей дугой.
Площадь сектора
Площадь сектора: 
Площадь сегмента: 
Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь 
- Эллипс
- Гипербола
- Парабола
- Многогранник
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
Особенности построения
- Подробности
- Категория: Инженерная графика
НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
ДЕЛЕНИЕ ОТРЕЗКОВ ПРЯМЫХ НА РАВНЫЕ ЧАСТИ
Из многочисленных построений здесь рассматриваются только те, которые часто встречаются при выполнении чертежей.
Деление отрезка прямой на две и четыре равные части выполняется в следующей последовательности.
Из концов отрезка А В циркулем проводят две дуги окружности радиусом R, несколько большим половины данного отрезка, до взаимного пересечения в точках n и m (рис. 43, а). Точки тип соединяют прямой, которая пересекает отрезок АВ в точке С. Точка С делит отрезок А В на две равные части. Проделав подобное построение для отрезка АС, находим его середину — точку D. Повторив построение для отрезка СВ, разделим отрезок на четыре равные части.
При вычерчивании детали, показанной на рис. 43, б, применяется способ деления отрезка на четыре части.
Деление отрезка прямой на любое число равных частей. Пусть отрезок А В требуется разделить на И равных частей. Для этого из любого конца данного отрезка, например из точки В (рис. 44, проводят под произвольным острым углом вспомогательную прямую линию ВС, на которой от точки В измерительным циркулем откладывают 11 равных отрезков произвольной величины. Крайнюю точку 11 последней отложенной части соединяют с точкой А прямой Затем с помощью линейки и угольника проводят ряд прямых, параллельных прямой которые и разделяют отрезок А В на 11 равных частей.
На рис. 44, б показана деталь, при изготовлении которой необходимо разместить 10 центров отверстий; отверстия равномерно расположены на длине L. В этом случае применяется описанный выше способ деления отрезка прямой на равные части.
ПОСТРОЕНИЕ И ИЗМЕРЕНИЕ УГЛОВ ТРАНСПОРТИРОМ
Транспортир — это прибор для измерения и построения углов. Это полукруг с разбивкой на градусы, соединенный с опорной планкой.
Для измерения угла транспортир прикладывают опорной планкой к одной из сторон данного угла (рис. 45, а) так, чтобы вершина угла (точка А) совпадала с точкой О на транспортире. Величину угла САВ в градусах определяют по шкале транспортира.
Для построения угла заданной величины (в градусах) со стороной А В и вершиной в точке к прикладывают транспортир так, чтобы его центр (точка О) совпал с точкой А прямой АВ, затем у деления шкалы транспортира, соответствующего заданному числу градусов (например, 55°), наносят точку n. Транспортир убирают и проводят через точку n отрезок АС — получают заданный угол САВ (рис. 45, б).
Углы можно строить при помощи угольников с углами 45, 30 и 60° и линейки или рейсшины. На рис. 46 показано, как при различных положениях угольников на рейсшине можно строить углы 60 (120), 30 (150), 45° (135°) и другие при использовании одновременно двух угольников..
ПОСТРОЕНИЕ И ДЕЛЕНИЕ УГЛОВ
Деление угла на две и четыре равные части. Из вершины угла провести произвольным радиусом дугу до пересечения со сторонами угла в точках (рис. 47, а). Из полученных точек проводят две дуги радиусом R, несколько большим половины длины дуги n и к, до взаимного пересечения в точке m. Вершину угла соединяют с точкой т прямой, которая делит угол ВАС пополам. Эта прямая называется биссектрисой угла ВАС. Повторяя это построение с полученными углами В Ат и nАС угол ВАС можно разделить на четыре равные части и т. д.
Деление прямого угла на три равные части. Из вершины А прямого угла (рис. 47, б) произвольным радиусом R описывают дугу окружности до пересечения ее со сторонами прямого угла в точках a и b из которых проводят дуги окружности того же радиуса R до пересечения с дугой ab в точках m и n. Точки m и n соединяют с вершиной угла А прямыми и получают стороны Аm и Аn углов В Аm и nА С,равных 1/3 прямого угла, т. е. 30°. Если каждый из этих углов разделить пополам, то прямой угол будет разделен на шесть равных частей, каждый из углов будет равняться 15°. Прямой угол АВС можно разделить на три равные части угольником с углами 30 и 60° (рис. 48, а). При выполнении чертежей нередко требуется разделить прямой угол на две равные части. Это можно выполнять угольником с углом 45° (рис. 48, б).
Построение угла, равного данному. Пусть задан угол ВАС. Требуется построить такой же угол. Через произвольную точку А1 проводим прямую А1С1. Из точки А описываем дугу произвольным радиусом R, которая пересечет угол ВАС в точках (рис. 49,а). Из точки A 1 проводим дугу тем же радиусом и получаем точку m1. Из точки A1 проводим дугу радиусом R1 равным отрезку mn, до пересечения с ранее проведенной дугой радиуса R в точке n1 (рис. 49, б). Точку n1 соединяем с точкой А1 и получаем угол B1A1C1 величина которого равна заданному углу ВАС.
Применение вышеизложенного построения угла по заданному показано на рис. 49, в и г. На рис. 49, в изображена деталь, чертеж которой надо вычертить, а на рис. 49, г показан этот чертеж, при выполнении которого использован способ построения угла по заданному.
СПОСОБЫ ПОСТРОЕНИЯ МНОГОУГОЛЬНИКОВ
Способ триангуляции. Построение многоугольников этим способом основано на последовательном построении ряда треугольников, примыкающих сторонами друг к другу. Этот способ будет применяться в дальнейшем при построении разверток поверхностей геометрических тел.
Рассмотрим пример такого построения. На рис. 50, а показана пластина с пятиугольным отверстием. Измеряя длины сторон пятиугольника, можно построить на чертеже контурное очертание многоугольного отверстия.
Треугольники в рассматриваемом многоугольнике можно получить, проведя диагонали 14 (рис. 50, а). Последовательность построения многоугольника на чертеже в данном примере следующая.
На детали произвольно выбираем базовую линию (например, А В), на которую из точек 7 и 2 опускаем перпендикуляр, и получаем точки E и G. На чертеже наносим базовую линию A1B1 на которой откладываем отрезок E1G1 равный отрезку EG. Из точек и G, восставляем перпендикуляры, на которых откладываем взятые с детали отрезки и G1 (рис. 50, б). Получим точки 11и21. Из точек как из центров, циркулем описываем две дуги радиусами, равными отрезками 13 и 23, взятых с детали. Точка пересечения дуг является вершиной 31 искомого треугольника 112131. Таким же способом из точек 71 и 31 описываем две дуги радиусами, равными отрезкам 34 и 14, находим вершину 41. Затем из точек 41 и 11, как из центров, описываем две дуги радиусами, равными отрезкам 45 и 15, определяем последнюю вершину пятиугольника 51(рис. 50, б).
Построение многоугольника методом прямоугольных координат показано на рис. 50, в. В этом случае из вершин многоугольника 12345 (рис. 50, а) опускаем перпендикуляры на линию АВ, получаем точки GDEFG. Расстояние между этими точками откладываем на прямой A1B1(pиc. 50, в). Из полученных точек C1D1E1F1G1восставляем перпендикуляры, на которых откладываем отрезки С5 D4, E1, F3, G2. Искомые точки 71, 21, 31, 41, 51на чертеже соединяют и получают чертеж многоугольника.
ОПРЕДЕЛЕНИЕ ЦЕНТРА ДУГИ ОКРУЖНОСТИ
Многие детали машин и приборов имеют контур очертания, состоящий из прямых линий, лекальных кривых и дуг окружностей. При вычерчивании деталей часто приходится определять величину радиусов дуг окружностей контурных очертаний детали и находить положение центров этих дуг. На рис. 51, а показана деталь (кронштейн), левая часть ребра которой выполнена по дуге окружности.
Чтобы найти положение центра и величину радиуса данной дуги, предварительно делают отпечаток дуги на бумаге. При помощи циркуля и линейки можно определить центр и размер радиуса дуги окружности, для этого на отпечатке дуги намечают три произвольно расположенные на ней точки А, В и С (рис. 51, б) и проводят хорды АВ и ВС. При помощи циркуля и линейки проводят перпендикуляры через середины хорд А В и ВС. Точка пересечения перпендикуляров
(точка О) является искомым центром дуги детали, а расстояние от точки О до любой точки дуги будет размером радиуса.
ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ
Некоторые детали машин и приборов имеют элементы, равномерно расположенные по окружности, например, детали на рис. 52—59. При выполнении чертежей подобных деталей необходимо знать правила деления окружности на равное количество частей.
Деление окружности на четыре и восемь равных частей. На рис. 52, а показана крышка, в которой имеется восемь отверстий, равномерно расположенных по окружности. При построении чертежа контура крышки (рис. 52 г) необходимо разделить окружность на восемь равных частей. Это можно сделать с помощью угольника с углами 45° (рис. 52, в), гипотенуза угольника должна проходить через центр окружности, или построением.
Два взаимно перпендикулярных диаметра окружности делят ее на четыре равные части (точки 7, 3, 5, 7 на рис. 52, б). Чтобы разделить окружность на восемь равных частей, применяют известный прием деления прямого угла с помощью циркуля на две равные части. Получают точки 2, 4, 6, 8.
Деление окружности на три, шесть и двенадцать равных частей. Во фланце (рис. 53, а) имеется три отверстия, равномерно расположенных по окружности. При выполнении чертежа контура фланца (рис. 53, г) нужно разделить окружность на три равные части.
Для нахождения точек, делящих окружность радиуса R на три равные части, достаточно из любой точки окружности, например точки А, провести дугу радиусом R. Пересечения дуги с окружностью дают две искомые точки 2 и 3; третья точка деления будет находиться на пересечении оси окружности, проведенной из точки Л, с окружностью (рис. 53, б).
Разделить окружность на три равные части можно также угольником с углами 30 и 60° (рис. 53, в), гипотенуза угольника должна проходить через центр окружности.
На рис. 54, б показано деление окружности циркулем на шесть равных частей. В этом случае выполняется то же построение, что на рис. 53, б но дугу описывают не один, а два раза, из точек и радиусом R , равным радиусу окружности.
Разделить окружность на шесть равных частей можно и угольником с углами 30 и 60° (рис. 54, в). На рис. 54, а показана крышка, при выполнении чертежа которой необходимо выполнить деление окружности на шесть частей.
Чтобы выполнить чертеж детали (рис. 55, а), которая имеет 12 отверстий, равномерно расположенных по окружностям, нужно разделить осевую окружность на 12 равных частей (рис. 55, г).
При делении окружности на 12 равных частей с помощью циркуля можно использовать тот же прием, что и при делении окружности на шесть равных частей (рис. 54, б),но дуги радиусом R описывать четыре раза из точек 1, 7, 4и 10 (рис. 55, б).
Используя угольник с углами 30 и 60° с последующим поворотом его на 180°, делят окружность на 12 равных частей (рис. 55, в).
Деление окружности на пять, десять и семь равных частей. В плашке (рис. 56, а) имеется пять отверстий, равномерно расположенных по окружности. Выполняя чертеж плашки (рис. 56, в), необходимо разделить окружность на пять равных частей. Через намеченный центр О (рис. 56, б)
при помощи рейсшины и угольника проводят осевые линии и из точки О циркулем описывают окружность заданного диаметра. Из точки А радиусом R, равным радиусу данной окружности, проводят дугу, которая пересечет окружность в точке n. Из точки n опускают перпендикуляр на горизонтальную осевую линию, получают точку С. Из точки С радиусом R1 равным расстоянию от точки С до точки 1, проводят дугу, которая пересечет горизонтальную осевую линию в точке т. Из точки 1 радиусом R , равным расстоянию от точки 1 до точки m, проводят дугу, пересекающую окружность в точке 2. Дуга 12 является 1/5 длины окружности. Точки 3,4 и 5 находят, откладывая циркулем отрезки, равные m1.
Деталь «звездочка» (рис. 57, а) имеет 10 одинаковых элементов, равномерно расположенных по окружности. Чтобы выполнить чертеж звездочки (рис. 57, я), следует окружность разделить на 10 равных частей. В этом случае следует применить то же построение, что и при делении окружности на пять частей (см. рис. 56, б). Отрезок п1 будет равняться хорде, которая делит окружность на 10 равных частей.
На рис. 58, а изображен шкив, а на рис. 58, в — чертеж шкива, где окружность разделена на семь равных частей.
Деление окружности на семь равных частей показано на рис. 58, б. Из точки А проводится вспомогательная дуга радиусом R, равным радиусу данной окружности, которая пересечет окружность в точке . Из точки n опускают перпендикуляр на горизонтальную осевую линию. Из точки 1 радиусом, равным отрезку nс, делают по окружности семь засечек и получают семь искомых точек.
Деление окружности на любое число равных частей. С достаточной точностью можно делить окружность на любое число равных частей, пользуясь таблицей коэффициентов для подсчета длины хорды (табл. 9).
Зная, на какое число (n) следует разделить окружность, находят по таблице коэффициент . При умножении коэффициента k на диаметр окружности D получают длину хорды l, которую циркулем откладывают на окружности n раз.
При построении чертежа кольца (рис. 59, а) необходимо окружность диаметра D=142 мм разделить на 32 равные части. Количеству частей окружности n=32 соответствует коэффициент k=0,098. Подсчитав длину хорды l=Dk=142×0,098= 13,9 мм, ее циркулем откладывают на окружности 32 раза (рис. 59, б и в).
СОПРЯЖЕНИЕ ЛИНИЙ
При вычерчивании деталей машин и приборов, контуры очертаний которых состоят из прямых линий и дуг окружностей с плавными переходами от одной линии в другую, часто применяют сопряжения. Сопряжением называется плавный переход одной линии в другую. На рис. 60 показаны примеры применения сопряжений.
Контур рычага (рис. 60а) состоит из отдельных линий, плавно переходящих одна в другую, например, в точках А, А1 виден плавный переход от дуги окружности к прямой линии, а в точках В, В1 — от дуги одной окружности к дуге другой окружности (рис. 60, б). На рис. 60, в изображен двурогий крюк. На чертеже контура крюка (рис. 60, г) в точке А виден плавный переход от дуги окружности D=200 к прямой линии, а в точке В — от дуги окружности радиуса R460 к дуге радиуса R260.
Для точного и правильного выполнения чертежей необходимо уметь выполнять построения сопряжений, которые основаны на двух положениях.
- Для сопряжения прямой линии и дуги необходимо, чтобы центр окружности, которой принадлежит дуга, лежал на перпендикуляре к прямой, восставленном из точки сопряжения (рис. 61, а).
- Для сопряжения двух дуг необходимо, чтобы центры окружностей, которым принадлежат дуги, лежали на прямой, проходящей через точку сопряжения (рис. 61, 6).
СОПРЯЖЕНИЕ ДВУХ СТОРОН УГЛА ДУГОЙ ОКРУЖНОСТИ ЗАДАННОГО РАДИУСА
При выполнении чертежей деталей, показанных на рис. 62, б, г, е, выполняют построение сопряжения двух сторон угла дугой окружности заданного радиуса. На рис. 62, а выполнено построение сопряжения сторон острого угла дугой, на рис. 62, в — тупого угла, на рис. 62, д — прямого.
Сопряжение двух сторон угла (острого или тупого) дугой заданного радиуса R выполняют следующим образом (рис. 62, а и в).
Параллельно сторонам угла на расстоянии, равном радиусу дуги R, проводят две вспомогательные прямые линии. Точка пересечения этих прямых (точка О) будет центром дуги радиуса Я, т. е. центром сопряжения. Из центра О описывают дугу, плавно переходящую в прямые — стороны угла. Дугу заканчивают в точках сопряжения n и n1 которые являются Основаниями перпендикуляров, опущенных из центра О на стороны угла.
При построении сопряжения сторон прямого угла центр дуги сопряжения проще находить с помощью циркуля (рис. 62, д). Из вершины угла А проводят дугу радиусом R, равным радиусу сопряжения. На сторонах угла получают точки сопряжения n и n1 . Из этих точек, как из центров, проводят дуги радиусом R до взаимного пересечения в точке О, являющейся центром сопряжения. Из центра О описывают дугу сопряжения.
СОПРЯЖЕНИЕ ПРЯМОЙ С ДУГОЙ ОКРУЖНОСТИ
Сопряжение прямой с дугой окружности может быть выполнено при помощи дуги с внутренним касанием (рис. 63, в) и дуги с внешним касанием (рис. 63, а).
На рис. 63, а показано сопряжение дуги окружности радиусом R и прямой линии А В дугой окружности радиуса r с внешним касанием. Для построения такого сопряжения проводят окружность радиуса R и прямую АВ. Параллельно заданной прямой на расстоянии, равном радиусу r (радиус сопрягающей дуги), проводят прямую ab. Из центра О проводят дугу окружности
радиусом, равным сумме радиусов и r, до пересечения ее с прямой ab в точке О1 Точка О1 является центром дуги сопряжения.
Точку сопряжения с находят на пересечении прямой 00 1 с дугой окружности радиуса R. Точка сопряжения C1 является основанием перпендикуляра, опущенного из центра О1 на данную прямую При помощи аналогичных построений могут быть найдены точки 02,
c2, c3.
На рис. 63, б показан кронштейн, при вычерчивании контура которого необходимо выполнить построения, описанные выше.
На рис. 63, в выполнено сопряжение дуги радиуса R с прямой А В дугой радиуса r с внутренним касанием. Центр дуги сопряжения О1 находится на пересечении вспомогательной прямой, проведенной параллельно данной прямой на расстоянии r, с дугой вспомогательной окружности, описанной из центра О радиусом, равным разности R—r. Точка сопряжения является основанием перпендикуляра, опущенного из точки О1 на данную прямую. Точку сопряжения с находят на пересечении прямой ОО1 с сопрягаемой дугой. Такое сопряжение выполняют, например, при вычерчивании контура маховика, показанного на рис. 63, г.
СОПРЯЖЕНИЕ ДУГИ С ДУГОЙ
Сопряжение двух дуг окружностей может быть внутренним, внешним и смешанным.
При внутреннем сопряжении центры O и O1 сопрягаемых дуг находятся внутри сопрягающей дуги радиуса R (рис. 64, б).
При внешнем сопряжении центры и сопрягаемых дуг радиусов R1 и R2 находятся вне сопрягающей дуги радиуса R (рис. 64, в).
При смешанном сопряжении центр О, одной из сопрягаемых дуг лежит внутри сопрягающей дуги
радиуса R, а центр О другой сопрягаемой дуги вне ее (рис. 65, а).
На рис. 64, а показана деталь (серьга), при вычерчивании которой необходимо построение внутреннего и внешнего сопряжения.
Построение внутреннего сопряжения.
Задано:
а) радиусы сопрягаемых окружностей R1 и R2
б) расстояния l1 и l2 между центрами этих дуг;
в) радиус R сопрягающей дуги.
Требуется:
а) определить положение центра 02 сопрягающей дуги;
б) найти точки сопряжения s1 и s
в) провести дугу сопряжения.
Построение сопряжения показано на рис. 64, б. По заданным расстояниям между центрами 11 и l2 на чертеже намечают центры О и O1 из которых описывают сопрягаемые дуги радиусов R1 и R2. Из центра О1 проводят вспомогательную дугу окружности радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R2, а из центра О — радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R1 Вспомогательные дуги пересекутся в точке 02 которая и будет искомым центром сопрягающей дуги.
Для нахождения точек сопряжения точку 02 соединяют с точками О и О1 прямыми линиями. Точки пересечения продолжения прямых 020 и 020 с сопрягаемыми дугами являются искомыми точками сопряжения (точки S и s1).
Радиусом R из центра Ог проводят сопрягающую дугу между точками сопряжения s и s1
Построение внешнего сопряжения.
Задано:
а) радиусы R1и R2 сопрягаемых дуг окружностей;
б) расстояния и l2 между центрами этих дуг;
в) радиус R сопрягающей дуги.
Требуется:
а) определить положение центра 02 сопрягающей дуги;
б) найти точки сопряжения и s1;
в) провести дугу сопряжения.
Построение внешнего сопряжения показано на рис. 64, в. По заданным расстояниям между центрами l1 и l2 на чертеже находят точки О и О1 из которых описывают сопрягаемые дуги радиусов R1 и R2. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R1, и сопрягающей R, а из центра О1 — радиусом, равным сумме
радиусов сопрягаемой дуги R2 и сопрягающей R. Вспомогательные дуги пересекутся в точке O2, которая будет искомым центром сопрягающей дуги Для нахождения точек сопряжения центры дуг сое-
диняют прямыми линиями 002 и 0102. Эти две прямые пересекают сопрягаемые дуги в точках сопряжения S и s1
Из центра 02 радиусом R проводят сопрягающую дугу, ограничивая ее точками сопряжения и
Построение смешанного сопряжения. Пример смешанного сопряжения приведен на рис. 65, и где изображены кронштейн и его чертеж.
Задано:
а) радиусы Rx и R2 сопрягаемых дуг окружностей;
б) расстояния l1 и l2 между центрами этих дуг;
в) радиус R сопрягающей дуги.
Требуется:
а) определить положение центра 02 сопрягающей дуги;
б) найти точки сопряжения s и s1
в) провести дугу сопряжения.
По заданным расстояниям между центрами l1 и l2 на чертеже намечают центры 0 и 01, из которых описывают сопрягаемые дуги радиусов R1 и R2. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R1 и сопрягающей R, а из центра 01 — радиусом, равным разности радиусов R и R2. Вспомогательные дуги пересекутся в точке 02, которая будет искомым центром сопрягающей дуги.
Соединив точки О и 02 прямой, получают точку сопряжения соединив точки О1 и 02, находят точку сопряжения s. Из центра 02 проводят дугу сопряжения от s до s1
При вычерчивании контура детали необходимо разобраться, где имеются плавные переходы, и представить себе, где надо выполнить те или иные виды сопряжения.
Для приобретения навыков построения сопряжения выполняют упражнения по вычерчиванию контуров сложных деталей. Перед упражнением необходимо просмотреть задание, наметить порядок построения сопряжений и только после этого приступить к выполнению построений.
На рис. 66, а изображена деталь (кронштейн), а на рис. 66, б, в, г показана последовательность выполнения контурного очертания этой детали с построением различных видов сопряжений.
КОРОБОВЫЕ КРИВЫЕ ЛИНИИ
Контуры таких деталей, как фланец и кулачок, могут ограничиваться коробовыми кривыми. Коробовые кривые состоят из сопрягающихся дуг окружностей различных диаметров. К таким кривым относятся овалы, овоиды, завитки.
ПОСТРОЕНИЕ ОВАЛА И ОВОИДА
Последовательность построения овала по заданному размеру большой оси овала производят следующим образом (рис. 67, а). Ось А В делят на три равные части (A1O, 0102, 02В). Радиусом, равным 0202, из точек деления О1 и 02 проводят окружности, пересекающиеся в точках m и n.
Соединив точки п и т с точками и 02, получают прямые nO1 n02, m01 и m02, которые продолжают до пересечения с окружностями. Полученные точки 1, 2, 3 и 4 являются точками сопряжения дуг. Из точек m и n, как из центров, радиусом равным n2 и m3 , проводят верхнюю дугу 12 и нижнюю дугу 34.
Контур фланца, изображенный на рис. 67, б, имеет форму овала. Построение овала по двум заданным осям АВ и CD приведено на рис. 67, в.
Проводят оси АВ и CD. Из точки их пересечения радиусом ОС (половина малой оси овала) проводят Контуры таких деталей, как фланец и кулачок, могут ограничиваться коробовыми кривыми. Коробовые кривые состоят из сопрягающихся дуг окружностей различных диаметров. К таким кривым относятся овалы, овоиды, завитки.
дугу до пересечения с большой осью овала в точке N. Точку А соединяют прямой с точкой С и на ней от точки С откладывают отрезок , получают точку N1.
В середине отрезка AN1 восставляют перпендикуляр и продолжают его до пересечения с большой и малой осями овала в точках 01 и n. Расстояние 001 откладывают по большой оси овала вправо от точки О, а расстояние on от точки О откладывают по малой оси овала вверх, получают точки Точки n и n1, являются центрами верхней дуги 12 и нижней дуги 34 овала, а точки 01 и 02 — центрами дуг 13 и 24. Получают искомый овал.
Овоид в отличие от овала имеет только одну ось симметрии. Радиусы R и R1 дуг окружностей, центры которых лежат на оси симметрии овоида, не равны друг другу (рис. 67, д).
Построение овоида по заданной оси АВ выполняется в следующей последовательности (рис. 67, д).
Проводят окружность диаметром, равным оси овоида. Из точек А и В через точку (точка пересечения окружности радиуса R с осью симметрии)
проводят прямые. Из точек А и В, как из центров, радиусом R2, равным оси АВ, проводят дуги Аn и Bm, а из центра
О1радиусом R1 проводят малую дугу овоида nm.
На рис. 67, е показана часть распределительного вала двигателя; профиль кулачков вала имеет форму овоида.
ПОСТРОЕНИЕ ЗАВИТКОВ
Завиток — плоская спиральная кривая, вычерчиваемая циркулем путем сопряжения дуг окружностей.
Построение завитков выполняют при вычерчивании таких деталей, как пружины и спиральные направляющие (рис. 68,а).
Построение завитков выполняется из двух, трех и более центров и зависит от формы и размеров «глазка», который может быть окружностью, правильным треугольником, шестиугольником и т. п. Последовательность построения завитка следующая.
Вычерчивается в тонких линиях контур «глазка», например окружность с диаметром 0102 (рис. 68, б). Из точек O1 и 02 как из центров, проводят две сопряженные между собой полуокружности. Верхняя полуокружность 021 из центра 01, нижняя полуокружность 12 из центра О2 Получается искомый завиток.
На рис. 68, в «глазок» имеет форму правильного треугольника 00102. Стороны треугольника продолжают. Приняв за центры сопряжения вершины треугольника «глазка», проводят в направлении движения часовой стрелки ряд сопряженных между собой дуг. Центром первой дуги является точка , центром второй — точка О1.
ПОСТРОЕНИЕ УКЛОНА И КОНУСНОСТИ
ПОСТРОЕНИЕ И ОБОЗНАЧЕНИЕ УКЛОНА
Уклоном называют величину, характеризующую наклон одной прямой линии к другой прямой. Уклон выражают дробью или в процентах.
Уклон i отрезка ВС относительно отрезка ВА определяют отношением катетов прямоугольного треугольника АВС (рис. 69, а), т. е.
Для построения прямой ВС (рис. 69, а) с заданной величиной уклона к горизонтальной прямой, например 1:4, необходимо от точки А влево отложить отрезок А В, равный четырем единицам длины, а вверх отрезок АС, равный одной единице длины. Точки С и В соединяют прямой, которая дает направление искомого уклона.
Уклоны применяются при вычерчивании деталей, например, стальных балок и рельсов, изготовляемых на прокатных станах, и некоторых деталей, изготовленных литьем (рис. 69, д).
При вычерчивании контура детали с уклоном сначала строится линия уклона (рис. 69, в и г), а затем контур.
Если уклон задается в процентах, например, 20% (рис. 69, б), то линия уклона строится так же, как гипотенуза прямоугольного треугольника. Длину одного из катетов принимают равной 100%, а другого — 20%. Очевидно, что уклон 20% есть иначе уклон 1:5.
По ГОСТ 2.307—68 перед размерным числом, определяющим уклон, наносят условный знак, острый угол которого должен быть направлен в сторону уклона (рис. 69, в и г).
ПОСТРОЕНИЕ И ОБОЗНАЧЕНИЕ КОНУСНОСТИ
На рис. 70, а даны для примера детали: оправка, конус и сверло, которые имеют конусность.
Конусностью называется отношение диаметра основания конуса к его высоте (рис. 70, б), обозначается конусность буквой С. Если конус усеченный (рис. 70, в) с диаметрами оснований D и d и длиной L, то конусность определяется по формуле:
Например (рис. 70, в), если известны размеры D=30 мм, d= 20 мм и L=70 мм, то
Если известны конусность С, диаметр одного из оснований конуса d и длина конуса L, можно определить второй диаметр конуса. Например, С=1:7,d=20
мм и L=70 мм; D находят по формуле D=CL+d= 1/7x70+20=30 мм (рис. 70, г).
По ГОСТ 2.307—68 перед размерным числом, характеризующим конусность, необходимо наносить условный знак конусности, который имеет вид равнобедренного треугольника с вершиной, направленной в сторону вершины конуса (рис. 70, в и г).
Обычно на чертеже конуса дается диаметр большего основания конуса, так как при изготовлении конической детали этот диаметр можно измерить значительно легче и точнее.
Нормальные конусности и углы конусов устанавливает ГОСТ 8593—81 (СТ СЭВ 512—77). ГОСТ 25548— 82 (СТ СЭВ 1779—79) устанавливает термины и определения.
ЛЕКАЛЬНЫЕ КРИВЫЕ
ВЫЧЕРЧИВАНИЕ КРИВЫХ ПО ЛЕКАЛУ
При выполнении чертежей часто приходится прибегать к вычерчиванию кривых, состоящих из ряда сопряженных частей, которые невозможно провести циркулем. Такие кривые строят обычно по ряду принадлежащих им точек, которые затем соединяют плавной линией сначала от руки карандашом, а затем обводят при помощи лекал (рис. 71).
Рассматриваемые лекальные кривые располагаются в одной плоскости и называются поэтому плоскими.
Пространственные кривые здесь не рассматриваются.
Чтобы начертить плавную лекальную кривую, необходимо иметь набор из нескольких лекал. Выбрав подходящее лекало, надо подогнать кромку части лекала к возможно большему количеству заданных точек кривой. На рис. 71 участок кривой между точками 1—6 уже обведен. Чтобы обвести следующий участок кривой, нужно приложить кромку лекала, например, к точкам 5—10, при этом лекало должно касаться части уже обведенной кривой (между точками 5 и 6). Затем обводят кривую между точками и 9, оставляя участок между точками 9 и 10 необведенным, что позволит получить кривую между точками 9 и 72 более плавной.
Ниже рассмотрены способы построения кривых, наиболее часто встречающихся в технике.
КРИВЫЕ КОНИЧЕСКИХ СЕЧЕНИЙ
При сечении прямого кругового конуса плоскостями, различно расположенными по отношению к осям конуса, получаются контуры сечения, образующие эллипс, параболу и гиперболу.
При пересечении плоскостью Pv всех образующих конуса получается эллипс (рис. 72, а и б).
При пересечении конуса плоскостью Pv параллельной одной из образующих конуса (рис. 72, в), получается парабола (рис. 72, г).
При пересечении конуса плоскостью Pv параллельной оси конуса, получается гипербола (рис. 72, и Если плоскость Pv параллельна оси конуса и проходит через вершину конуса, в сечении получается треугольник.
Эллипс — замкнутая плоская кривая, сумма расстояний каждой точки которой до двух данных точек (фокусов), лежащих на большой оси, есть величина постоянная и равная длине большой оси.
Широко применяемый в технике способ построения эллипса по большой (АВ)и малой (CD) осям представлен на рис. 72, б.
Проводят две перпендикулярные осевые линии. Затем от центра О откладывают вверх и вниз по вертикальной оси отрезки, равные длине малой полуоси, а влево и вправо по горизонтальной оси — отрезки, равные длине большой полуоси.
Из центра О радиусами О А и ОС проводят две концентрические окружности и ряд лучей-диаметров. Из точек пересечения лучей с окружностями проводят линии, параллельные осям эллипса, до взаимного пересечения в точках, принадлежащих эллипсу. Полученные точки соединяют от руки и обводят по лекалу.
На рис. 73, а показан резервуар, контурное очертание днища которого имеет форму части эллипса.
Построение очертания днища (половины эллипса) приведено на рис. 73, б. Большой осью эллипса является диаметр D цилиндрической части резервуара, а малой полуосью эллипса — наибольшее расстояние по вертикали от большой оси до днища.
Парабола — плоская кривая, каждая точка которой равноудалена от директрисы DD1 прямой, перпендикулярной к оси симметрии параболы, и от фокуса F — точки, расположенной на оси симметрии параболы (см. рис. 72, г).
Расстояние KF между директрисой и фокусом называется параметром р параболы. Точка О, лежащая на оси симметрии, называется вершиной параболы и делит параметр р пополам.
Для построения параболы по заданной величине параметра р проводят ось симметрии параболы (на рисунке вертикально) и откладывают отрезок KF=p. Через точку К перпендикулярно оси симметрии проводят директрису DD1 Отрезок делят пополам и получают вершину О параболы. От вершины О вниз на оси симметрии намечают ряд произвольных точек l— VI с постепенно увеличивающимся расстоянием между ними. Через эти точки проводят вспомогательные прямые, перпендикулярные оси симметрии. На вспомогательных прямых из фокуса F делают засечки радиусом, равным расстоянию от прямой до директрисы. Например, из точки F на вспомогательной прямой.
проходящей через точки делают засечку дугой R1=KV; полученная точка 5 принадлежит параболе.
Если требуется построить параболу по заданной вершине О, оси ОС и точке В (рис. 74, а), то строят вспомогательный прямоугольник ABCO. Стороны прямоугольника А В и АО делят на равные части и точки делений нумеруют. Горизонтальный ряд делений соединяют лучами с вершиной О, а через точки делений, расположенные на АО, проводят прямые линии, параллельные оси параболы. Точки пересечения горизонтальных прямых 11, 2 1,31, с лучами 01, 02, 03, … принадлежат параболе.
В станкостроении и других отраслях машиностроения часто применяются детали, контурные очертания которых выполнены по параболе, например, стойка и рукав радиально-сверлильного станка (рис. 74, б).
Построение параболы для контурного очертания рукава радиально-сверлильного станка приведено на рис. 74, в. Данными для построения являются две точки параболы А и В и направление касательных, проходящих через эти точки и пересекающихся в точке С.
Гипербола — плоская кривая, состоящая из двух разомкнутых, симметрично расположенных ветвей (см. рис. 72, е). Разность расстояний от каждой точки гиперболы до двух данных точек (фокусов F и F1) есть величина постоянная и равная расстоянию между вершинами гиперболы А и В.
Рассмотрим прием построения гиперболы по заданным вершинам А и В и фокусному расстоянию FF1 (рис. 72, е).
Разделив фокусное расстояние пополам, получают точку О, от которой в обе стороны откладывают по половине заданного расстояния между вершинами А и В. Вниз от фокуса F намечают ряд произвольных точек 1, 2, 3, 4 … с постепенно увеличивающимся расстоянием между ними. Из фокуса F описывают дугу вспомогательной окружности радиусом R , равным, например, расстоянию от вершины гиперболы В до точки 3. Из фокуса F1 проводят вторую дугу вспомогательной окружности радиусом r, равным расстоянию от вершины А до точки 3. На пересечении этих дуг находят точки С и C1, принадлежащие гиперболе. Таким же способом находят остальные точки гиперболы.
Вторую ветвь гиперболы строят аналогичным образом.
На рис. 75 показана проушина с конической поверхностью, срезанной двумя плоскостями, параллельными оси конуса, контур среза ограничен гиперболой.
СИНУСОИДА
Синусоида — плоская кривая, изображающая изменение синуса в зависимости от изменения угла (рис. 76, a).
Величина L называется длиной волны синусоиды, L=πD.
Для построения синусоиды проводят горизонтальную ось и на ней откладывают заданную длину волны А В (рис. 76, а). Отрезок А В делят на несколько равных частей, например, на 12. Слева вычерчивают окружность, радиус которой равен величине амплитуды, и делят ее также на 12 равных частей; точки деления нумеруют и через них проводят горизонтальные прямые. Из точек деления отрезка AВ восставляют перпендикуляры к оси синусоиды и на их пересечении с горизонтальными прямыми находят точки синусоиды.
Полученные точки синусоиды a1 , a2,a3,… соединяют по лекалу кривой.
При выполнении чертежей деталей или инструментов, поверхности которых очерчены по синусоиде (рис. 76, б и в), величину длины волны обычно выбирают независимо от размера амплитуды г. Например, при вычерчивании шнека (рис. 76. б) длина волны L меньше размера 2πr. Такая синусоида называется сжатой. Если длина волны больше размера 2πr то синусоида называется вытянутой.
СПИРАЛЬ АРХИМЕДА
Спираль Архимеда — плоская кривая, которую описывает точка, движущаяся равномерно от центра О по равномерно вращающемуся радиусу (рис. 77).
Для построения спирали Архимеда задают ее шаг Р, из центра О проводят окружность радиусом, равным шагу Р спирали, и делят шаг и окружность на несколько равных частей (рис. 77, Точки деления нумеруют.
Из центра О проводят радиальные прямые, проходящие через точки деления окружности.
Из центра О радиусами 01, 02 и т. д. проводят дуги до пересечения с соответствующими радиальными прямыми. Например, дуга радиуса 03 пересекается с прямой 031 в точке III. Полученные точки II,…, VIII, принадлежащие спирали Архимеда, соединяют плавной кривой по лекалу.
В машиностроении спираль Архимеда применяется, например, для сообщения движения в радиальном направлении кулачкам зажимного патрона токарного станка (рис. 77, а).На тыльной стороне большой конической шестерни нарезаны канавки по спирали Архимеда. В канавки входят выступы кулачков, которые также выполнены по спирали. При вращении шестерни кулачки будут перемещаться в радиальном направлении.
ЭВОЛЬВЕНТА
Эвольвента окружности — траектория любой точки прямой линии, перекатываемой без скольжения по окружности.
Пусть неподвижный диск диаметром D огибает шнур длиной πВ (рис. 78, а). Один конец шнура закреплен в точке А, а другой при развертывании по направлению стрелок (в натянутом положении) опишет траекторию в виде плоской кривой линии — эвольвенты.
В машиностроении профили зубьев колес и зуборезный инструмент — пальцевую фрезу — выполняют по эвольвенте (рис. 78, b).
Для построения эвольвенты заданную окружность диаметра D делят на несколько равных частей (на рис. 78, в — на 12 частей), которые нумеруют. Из конечной точки (72) проводят касательную к окружности и на ней откладывают отрезок, равный длине окружности πD. Длину окружности делят также на равные части.
Из точек делений окружности 1, 2,3….., 12 проводят
касательные к окружности и на них откладывают отрезки; на первой касательной — отрезок 12 на второй — 12 2′ на третьей — 12 3 и т. д. Соединив точки I—XII по лекалу, получают эвольвенту окружности.
ПD. Длину окружности делят также на равные части. Из точек делений окружности 1, 2, 3, проводят касательные к окружности и на них откладывают отрезки; на первой касательной — отрезок 12 1′ , на второй — 12 2′ ,на третьей — и т. д. Соединив точки I—X11 по лекалу, получают эвольвенту окружности.
ЦИКЛОИДАЛЬНЫЕ КРИВЫЕ
Циклоида — плоская кривая, которую описывает точка А, лежащая на окружности, которая катится без скольжения по прямой CD (рис. 79, а).
Эпициклоида — плоская кривая, которую описывает точка А, лежащая на окружности, которая катится без скольжения, снаружи по направляющей окружности (рис. 79, б).
Гипоциклоида — плоская кривая, которую описывает точка А, лежащая на окружности, которая катится без скольжения внутри по направляющей окружности (рис. 79, в).
Построение циклоиды. На направляющей прямой ВС (рис. 79, а) откладывают длину производящей окружности диаметра D, равную nD. Окружность диаметра D и отрезок АA 12 ВС делят на равные части, например, на 12. Из точек делений прямой ВС (1′,2′,3′,…,12′) восставляют перпендикуляры до пересечения с продолжением горизонтальной оси окружности в точках 01 ,02 …, 012, а из точек делений окружности (1, 2, 3, …,12) проводят горизонтальные прямые. Из точек Ov 02, …, Ol2, как из центров, проводят окружности диаметра D, которые пересекаясь с горизонтальными линиями, образуют точки А1 ,A2,A3….,A12 , принадлежащие циклоиде.
Построение эпициклоиды. Производящую окружность диаметра D и направляющую окружность радиуса R проводят так, чтобы они касались (рис. 79, ). Производящую окружность диаметра D делят на 12 равных частей. Из центра 0О радиусом, равным R+0,5D, проводят вспомогательную дугу.
Центральный угол а определяют по формуле
Задачу можно решать многими способами. Например. Рассмотрим векторы образованные центром O(ox,oy) и точками A(ax,ay), B(bx,by). Их сумма по правилу паралеллограмма даст нам направление для биссеткрисы угла
которая образована AOB. Уравнение биссектрисы будет известно.
Решаем пересечение этой прямой с окружностью и получаем искомый центр дуги.
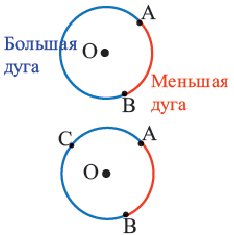
Что в этой задаче плохо. В этой задаче – “ленивый” автор который не удосужился придумать названия для точек и заставил всех придумывать свои нелепые названия или писать словами.
Что еще плохо. В этой задаче на самом деле не одна а две дуги. Но мы каким-то образом должны догадаться что речь идет о малой дуге. Об этом – тоже надо сообщать. Это раздражает.
На будущее – оформляй задачи как в задачнике.
(x – a) ** 2 + (y – b) ** 2 = R ** 2
a, b координаты середины
вычислить можно. но сложная формула. наброски: находим уравнение окружности (как система двух уравнений, радиус знаем). далее соединяем красные точки – хорда, середина хорды – среднее арифметическое координат. далее проводим диаметр перпендикулярно хорде. уравнение этой прямой находим по точке и коэффициенту k. находим точку пересечения этой прямой и окружности.
угол вычислить проще. длина хорды и два радиуса – это равнобедренный треугольник. теорема косинусов
Знаете 2 точки дуги – знаете длину хорды. Дальше надо на листке нарисовать окружность, хорду и серидинный перпендикуляр. Нарисовать несколько прямоугольных треугольников и найти длину куска от центра хорды до искомой середины. Пусть центр O, исходные точки A,B а искомая точка – M. Середина хорды С. OM = R. OС^2+CB^2=R^2, CM = OM-OC.
Итого – длина искомого куска CM = R - sqrt(R^2-|AB|^2/4)
Для нахождения координат M надо взять середину отрезка AB и отложить от нее перпендикулярный AB вектор длины по формуле выше.
A – начало дуги, B – конец дуги, C – искомый центр.
длина AC = длина BC = R (известно);
длину AB вычисляем по теореме Пифагора;
таким образом, имеем длины всех сторон треугольника ABC;
по теореме синусов (и по сумме углов) вычисляем все углы треугольника;
зная угол A, как угол пересечения прямых AB и AC, зная координаты точки A, а также зная уравнение прямой AB, легко построить уравнение прямой AC; остаётся отмерить вектор длиной R вдоль этой прямой, чтобы получить координаты точки C.
Ещё один вариант – после вычисления всех углов перейти в полярную систему координат с центром A, сложить (с учётом знаков) угол A с коэффициентом наклона прямой AB и сразу получить полярные координаты точки C (ведь R известен); затем обратно перейти в декартову систему координат.
Уверен, у каждого домашнего мастера был случай, когда ему нужно было сделать разметку какой-нибудь круглой заготовки и найти центр ее основания. Казалось бы, это очень просто сделать, но некоторые мастера долго не могут найти выход в данной ситуации. Сегодня я покажу вам два простых решения, с помощью которых можно быстро и точной найти центр любой окружности.
1. Первый способ подойдет для разметки небольших заготовок. В качестве примера я возьму заглушку от пластиковой трубы диаметром 50 мм.
Для того, чтобы найти центр окружности заглушки, не нужны будут какие-то математические вычисления и сложные манипуляции. Нам понадобятся всего лишь строительный угольник и обычная линейка (или второй угольник), которые есть в любой мастерской.
Складываем вместе угольник и линейку, так чтобы образовался угол в 45 градусов.
Затем, придерживая одной рукой угольник и линейку, прикладываем их к круглой заготовке (заглушке) так, чтобы она вплотную соприкасалась с двумя сторонами угольника.
Теперь берем карандаш и чертим на заглушке первую линию, потом немного ее поворачиваем и делаем вторую метку (достаточно провести две линии, но для уверенности можно поставить три метки).
Все задача решена! Точка пересечения этих двух линий и будет центром данной окружности. Данный способ один из самых быстрых и простых.
2. Второй способ подойдет, если окружность имеет большой диаметр или она расположена на плоскости. Для примера я обвел карандашом крышку от кастрюли. В этом случае тоже все очень просто. Для начала выбираем любую точку на окружности.
Потом от этой точки чертим две линии до пересечения с окружностью так, чтобы у нас получился прямой угол (90 градусов). Для построения данных линий проще всего воспользоваться угольником (если окружность очень большая, линии можно продлить с помощью линейки).
А теперь все очень просто, соединяем точки, в которых пересекаются линии с окружностью и измеряем длину получившегося отрезка. Его середина и будет центром окружности. Уверен, многие помнят это из уроков по геометрии. Середина гипотенузы прямого треугольника вписанного в окружность, является центром этой окружности.
