Эллипс – определение и вычисление с примерами решения
Эллипс:
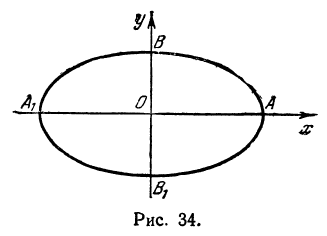
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 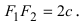
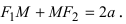
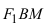
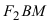
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 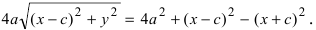
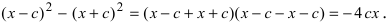
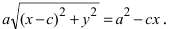
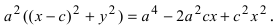
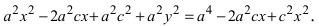
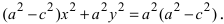
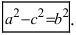
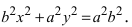
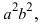
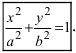
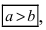
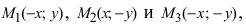
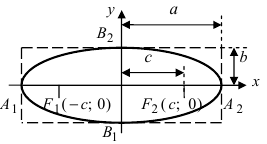
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 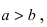
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 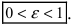
Если 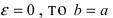
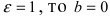
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 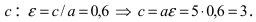
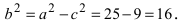
Пример:
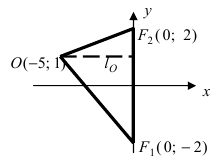
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 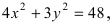
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
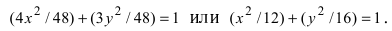
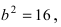
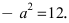
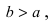
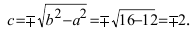
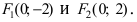
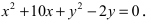
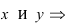
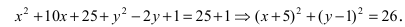
Построим в декартовой системе координат треугольник 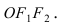
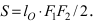
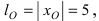
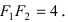
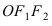
Эллипс в высшей математике
где 
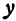
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 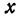
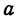
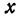
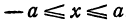
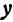
При 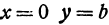
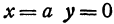

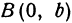
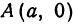
Полученная линия называется эллипсом. Число 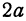
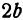
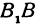
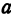
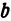
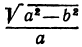
Пример:
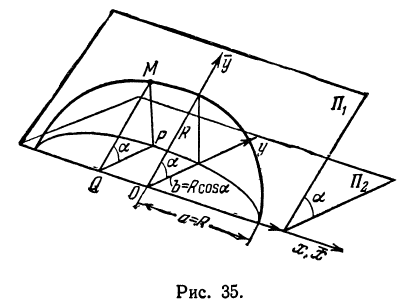
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 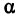
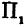
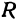
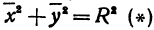
Пусть точка 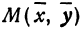
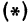
Обозначим проекцию точки 
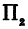
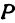
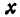
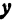
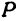

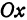
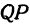
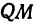
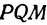
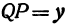
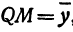
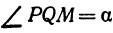
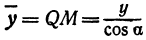

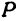
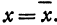
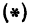
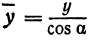
а это есть уравнение эллипса с полуосями 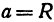
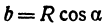
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 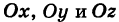
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 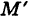
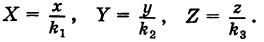
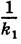
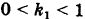
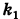
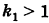
Подставляя эти формулы в уравнение (1), будем иметь
где 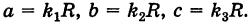
Величины 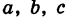
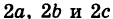
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Эллипсоиды
Определение эллипсоида
Эллипсоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением
где — положительные параметры, удовлетворяющие неравенствам .
Если точка принадлежит эллипсоиду (4.46), то координаты точек при любом выборе знаков также удовлетворяют уравнению (4.46). Поэтому эллипсоид (4.46) симметричен относительно координатных плоскостей, координатных осей и начала координат. Начало координат называют центром эллипсоида (4.46). Шесть точек пересечения эллипсоида с координатными осями называются его вершинами, а три отрезка координатных осей, соединяющих вершины, — осями эллипсоида. Оси эллипсоида, принадлежащие координатным осям , имеют длины соответственно. Если b>c” png;base64,iVBORw0KGgoAAAANSUhEUgAAAFEAAAAQBAMAAACcpY7MAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADXRSTlMAEacB0WkhgcA75ZFRKK9ZmAAAARhJREFUKM9jYKAEJHUQq1L0igGRKhlv45dXg7N47oAppgRcruuE2cl9EUyxaUxGs2vHtgCI0h6oUhPXpgkQpYdhiiKaBBgYZgWfvQw11RWiVPaq6UKIqSrBEBkRNakNDIyLGLicoTrFIUrPBnBehdpXAlbK6GJQW8DAfodBdgPMEvHlIHKvgOV1mNOqCkAOv8MgycBgtZjh7AF4SLqDSBcG9qswlSEglVZg58k2A82A2w5iMV9i4LgGsz0QRNk2gMkCBi8msFcZ0l2ZQe5kvs6QqwDxUUmAMVgNkJvAwKLAekkExevM2gwqAiheN3JgEApg4FytuksHNeRn7VJEDXnGjiJNkIABGyjaGDURkTERTApNQMQOUAQACxo8dxA2UAQAAAAASUVORK5CYII=” />, то число называется большой полуосью, число — средней полуосью, число — малой полуосью эллипсоида. Если полуоси не удовлетворяют условиям , то уравнение (4.46) не является каноническим. Однако при помощи переименования неизвестных можно всегда добиться выполнения неравенств .
Плоские сечения эллипсоида
Подставляя в уравнение (4.46), получаем уравнение линии пересечения эллипсоида с координатной плоскостью . Это уравнение в плоскости определяет эллипс Линии пересечения эллипсоида с другими координатными плоскостями также являются эллипсами. Они называются главными сечениями (главными эллипсами) эллипсоида.
Рассмотрим теперь сечение эллипсоида плоскостью, параллельной какой-нибудь координатной плоскости, например . Подставляя , где — произвольная постоянная (параметр), в уравнение (4.46), получаем
При c” png;base64,iVBORw0KGgoAAAANSUhEUgAAADoAAAAVBAMAAADlb+D4AAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADnRSTlMAg0KoBP0QXdEhwHEx4v6hyb4AAADaSURBVCjPY2DAD/ZAae4D2GSFGBiqlgNpRgUcsofD8ckyh+GT5W2Ay1piyk4VgMtOXoQhW1q9WAFm8uTlMAn2VWZgWdMm5gtweye3Q2i25mkXwbJXJzDGIFyVCJHOaGAMBMlyBjIwByC5OfEiiBQtYFMAybKHM7AaIMmmN4LIUKirgN49ugHJ5O4EEBUFleVtYBHNMYDJToS6KpiBgRMkmyrAsIL5AMxHUEkGCwY2c5CsqgLDXnOM0MhaaAx2FQ/QjASILJsRIpiSEiBhBQY4Y4Fs2U2wlINFFgCrpSqpbSiUhgAAAABJRU5ErkJggg==” style=”vertical-align: middle;” /> уравнение не имеет действительных решений (правая часть уравнения отрицательная, а левая неотрицательная), т.е. плоскость не пересекает эллипсоид. При уравнение (4.47) имеет нулевое решение . Следовательно, плоскости касаются эллипсоида в его вершинах . При , разделив обе части уравнения (4.47) на 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAGMAAAAwBAMAAAD3D9n/AAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADnRSTlMAmv2BWBABQTDA2LEhcNbL+n8AAAGvSURBVEjHY2CgJughWUeg9VRStQgyrCZVixCDFAmqWcvB1G4StDhpgUgODVJsUQSRUQ0kaGFRAenbwUKCFkYdIMHtXkiClqxlxwMYhJQUSdASNFtag6G9vIaUEFvKpkhqLDawKpOmg21VAjjMSIsWRlXStACtSNrgSpIWYLQ4uS0jSQvnAganQgd8KngC0AQSHRiYp2BXGw5OdxlGBeghlobLdObFO4Hms2lOKiA69J0CGEF+TDAioIXlKpy5moEdHGGEtKR5mUJZHMrQrERIC1ualwzUPmWgP4jRwsDGVgnRwwzSkkCMFiCo3A7TooSwxdkYBEDBHigIB8JwPYUzoFq0EojVcnAGzC9EO2w6SGWGMgOPNlHeZ4B5n00bGi9CDoS0wAKZwSiAcSlQp5KS0gRs6i7CI93LBp4tlgg1gGMqAZuOxFYpaApPMUWINuPLeUwXgqAOZksgMtUmNjBdILkaczpAqg7WJaSpb29g4G4gSUfn5I0MEhyk+IVDmU0pcbNlAQlaghaw7T05cyYp3r9EevBOaiBdSwLJWoQSGKJJ1BIl2ruCRC2p1iJ4ZAESoVYyhvDZkwAAAABJRU5ErkJggg==” style=”vertical-align: middle;” />, получаем уравнение эллипса полуосями . Следовательно, сечение эллипсоида плоскостью при представляет собой эллипс.
Плоские сечения дают возможность составить полное представление о виде эллипсоида (рис.4.40,а).
Эллипсоиды вращения
Эллипсоид, у которого две полуоси равны, называется эллипсоидом вращения (или сфероидом ). Такой эллипсоид является поверхностью вращения. Например, если , то линии (4.47) при являются окружностями. Следовательно, сечения эллипсоида плоскостями представляют собой окружности с центрами на оси аппликат. Такую поверхность можно получить, вращая вокруг оси эллипс заданный в плоскости (рис.4.41,а).
Если , то все сечения эллипсоида (4.46) плоскостями при эллипс (рис.4.41,б).
Если все полуоси эллипсоида равны , то он представляет собой сферу радиуса , которую можно получить, например, вращая окружность такого же радиуса вокруг любого диаметра.
Эллипсоид, у которого полуоси попарно различны b>c)” png;base64,iVBORw0KGgoAAAANSUhEUgAAAGAAAAAWBAMAAADNzYTXAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAXynYREhwNFB6DGRUQyCkmkAAAGUSURBVDjLY2AgHbBcIFYlkwOYcsYm51yCTRQsyLYUm9T2t9hEoxKABLsCNimep9hEmQ2AxL4AhG8c4EyJRjDlIoCige0ZkDiBJOahCmPFHYAY0RSArIFxEZCoAWJO49sJYAG4jnvKRWBaBK6D29ySgcEYqOYRkGO1tQ7iE0YPM4j0ubYoiIhIcwJEROuilgADEDE+AVr8ksEPFhnTwToYuwLYF0IEJIvBOljeMr5iYNQTYGB9CQytBoZzCTBnTrcGkqxvGNgfMsB0bACSeY0M2xgY/CAa/BQYuuAem1wNJHjfMsgtgApwmoM06IFd6Adx0rkJrI9h6qdbghPBM4Z5BlD1xRNAlB2YBDoJ5Gm9AN4nyRAHXYd4WughzJGyEC+AlLIxMGpBgvVeQsRLFUhEQAOJ+yn3E0hEwAJp3gVGjQAGcyBLQ4CBp8dycQFqxJ2wuIAacSxrjitAIi4PKBTKIAl2OVw9A+tGMKWEiGhpoAjbayBDWIH4rMMDcgfnUuI1gJM39gyEFTCaQDIe0VkUKfkTDwAVFViuYeRgnwAAAABJRU5ErkJggg==” style=”vertical-align: middle;” />, называется трехосным (или общим).
1. Плоскости определяют в пространстве основной прямоугольный параллелепипед , внутри которого находится эллипсоид (см. рис.4.40,б). Грани параллелепипеда касаются эллипсоида в его вершинах.
2. Эллипсоид можно определить, как геометрическое место точек, получаемое в результате трех сжатий (растяжений) сферы единичного радиуса к трем взаимно перпендикулярным плоскостям.
3. Начало канонической системы координат является центром симметрии эллипсоида, координатные оси — осями симметрии эллипсоида, координатные плоскости — плоскостями симметрии эллипсоида.
В самом деле, если точка принадлежит эллипсоиду, то точки с координатами при любом выборе знаков также принадлежат эллипсоиду, поскольку их координаты удовлетворяют уравнению (4.46).
Как найти центр эллипсоида по уравнению
Глава 46. Поверхности второго порядка
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
(1).
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c – сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
, (2)
. (3)
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), – двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
, (4)
, (5)
где p и q – положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), – гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).
Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).
Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М – произвольная точка пространства, не лежащая на плоскости , – основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.
Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).
ПРИМЕР. Доказать, что произвольный трехосный эллипсоид
может быть получен из сферы
в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть – точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .
Таким образом, мы получаем искомые выражения:
, , (6)
, , (7)
Предположим, что M(x; y; z ) – произвольная точка сферы
.
Заменим здесь x, y, z их выражениями (7); получим
,
.
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам
, , ;
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.
Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.
имеет две системы прямолинейных образующих, которые определяются уравнениями:
, ;
, ,
где и – некоторые числа, не равные одновременно нулю. Гиперболический параболоид
также имеет две системы прямолинейных образующих, которые определяются уравнениями
, ;
, .
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L – направляющей.
Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).
[spoiler title=”источники:”]
http://mathhelpplanet.com/static.php?p=ellipsoid
http://a-geometry.narod.ru/problems/problems_46.htm
[/spoiler]
Тема: Найти координаты точки центра Эллипсоида. Каноническое уравнение есть. (Прочитано 4585 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Уравнение:
(3x+3)2 + (4y+8)2 + (6z+18)2 =1
a=b=c=12, то есть знаменатель каждой дроби = 144
А какой центр то?
(-3; -8; -18) или (-1;-2;-3)?
или другой вообще?
Вы до конца не доделали.
За скобки вынесите для начала коэффициенты при x,y,z
( frac{{{3^2}{{left( {x + 1} right)}^2}}}{{{{12}^2}}} + frac{{{4^2}{{left( {y + 2} right)}^2}}}{{{{12}^2}}} + frac{{{6^2}{{left( {z + 3} right)}^2}}}{{{{12}^2}}} = 1 )
Затем сами доведите уравнение до канонического вида
« Последнее редактирование: 02 Декабря 2012, 15:35:06 от Dimka1 »
Решение задач – практическое искусство; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь….
Тогда после всех преобразований точка центра получается (-1;-2;-3)
а=4
b=3
с=2
Огромное спасибо за помощь))
Решение задач – практическое искусство; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь….
( frac{{{3^2}{{left( {x + 1} right)}^2}}}{{{{12}^2}}} + frac{{{4^2}{{left( {y + 2} right)}^2}}}{{{{12}^2}}} + frac{{{6^2}{{left( {z + 3} right)}^2}}}{{{{12}^2}}} = 1 )
а где 144 в знаменателе взялось?
В самом первом сообщении написано.
Она дроби не может набрать, вот словами и сказала.
Решение задач – практическое искусство; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь….
Она дроби не может набрать, вот словами и сказала.
а… поняла
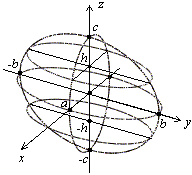
Эллипсоид
(рис.7) (от «эллипс»
и греч. «eidos» — вид) – замкнутая
центральная поверхность
второго порядка. Эллипсоид имеет
центр симметрии –

осями. Точки пересечения координатных
осей с эллипсоидом называются его
вершинами. Сечения эллипсоида плоскостями
являются эллипсами (в частности, всегда
можно указать круговые сечения эллипсоида).
Каноническое уравнение эллипсоида имеет
вид:
–
сфера.
В
сечении эллипсоида плоскостью,
перпендикулярной любой из координатных
осей, получается эллипс.
Форма эллипсоида.
Исследуем
форму эллипсоида. Из уравнения 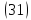
ограничены:
Эллипсоид
обладает тремя плоскостями симметрии,
тремя осями симметрии и центром симметрии.
Ими служат соответственно координатные
плоскости, координатные оси и начало
координат.
Для
выяснения формы эллипсоида рассмотрим
его сечения плоскостями. Найдем линию
пересечения эллипсоида с плоскостью

Так как любая точка плоскости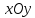
нулевую третью координату,
то координаты точек эллипсоида на
плоскости
уравнению:
Получаем,
что линия пересечения является эллипсом
с полуосями 
Рис.
8.
Сечение
плоскостью
Аналогично,
сечение в плоскости 
дает эллипс:
с
полуосями 

а сечение плоскостью
с
полуосями
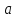
Рис.9.
Сечения эллипсоида координатными
плоскостями
Нарисованный
“каркас” из сечений уже дает
представление об эллипсоиде. Но чтобы
выяснить, как ведет себя поверхность
между нарисованными кривыми, рассмотрим
сечение эллипсоида плоскостью

Эта плоскость параллельна плоскости
пересекает ось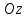
точке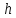
Уравнения этой линии:
Очевидно,
что если

то ни одна точка пространства не может
удовлетворять этой системе: в левой
части первого уравнения стоит
неотрицательное число, а в правой –
отрицательное.
Если

то в сечении получим лишь одну точку

зависимости от знака
Пусть
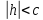
Тогда первое уравнение преобразуем к
виду:
то
есть к виду:
где
Уравнение

эллипсу, задаваемому уравнением
с коэффициентом подобия
полуосями

Ясно, что сечение плоскостью
таким же эллипсом, расположенным
симметрично первому относительно
плоскости
Нарисуем эти сечения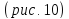
Рис.10.
Дополнительные сечения эллипсоида
Таким
образом, весь эллипсоид составлен из
эллипсов, лежащих в плоскостях,
параллельных плоскости
подобных эллипсу в плоскости

эллипсоида:
Рис.11.
Эллипсоид
Так
же, как для эллипса, точки пересечения
эллипсоида с координатными осями
называются вершинами эллипсоида, центр
симметрии – центром эллипсоида. Числа

полуосями. Если полуоси попарно различны,
то эллипсоид называется трехосным.
Если
две полуоси равны друг другу, то эллипсоид
называется эллипсоидом вращения.
Эллипсоид вращения может быть получен
вращением эллипса вокруг одной из осей.
Например, если

то все сечения эллипсоида плоскостями
будут окружностями. Сам эллипсоид может
быть получен из эллипса:
лежащего
в плоскости

при вращении его вокруг оси
Рис.12.
Эллипсоид
вращения
Эллипсоиды
Определение эллипсоида
Эллипсоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением
(4.46)
где — положительные параметры, удовлетворяющие неравенствам
.
Если точка принадлежит эллипсоиду (4.46), то координаты точек
при любом выборе знаков также удовлетворяют уравнению (4.46). Поэтому эллипсоид (4.46) симметричен относительно координатных плоскостей, координатных осей и начала координат. Начало координат называют центром эллипсоида (4.46). Шесть точек
пересечения эллипсоида с координатными осями называются его вершинами, а три отрезка координатных осей, соединяющих вершины, — осями эллипсоида. Оси эллипсоида, принадлежащие координатным осям
, имеют длины
соответственно. Если
, то число
называется большой полуосью, число
— средней полуосью, число
— малой полуосью эллипсоида. Если полуоси не удовлетворяют условиям
, то уравнение (4.46) не является каноническим. Однако при помощи переименования неизвестных можно всегда добиться выполнения неравенств
.
Плоские сечения эллипсоида
Подставляя в уравнение (4.46), получаем уравнение
линии пересечения эллипсоида с координатной плоскостью
. Это уравнение в плоскости
определяет эллипс Линии пересечения эллипсоида с другими координатными плоскостями также являются эллипсами. Они называются главными сечениями (главными эллипсами) эллипсоида.
Рассмотрим теперь сечение эллипсоида плоскостью, параллельной какой-нибудь координатной плоскости, например . Подставляя
, где
— произвольная постоянная (параметр), в уравнение (4.46), получаем
(4.47)
При уравнение не имеет действительных решений (правая часть уравнения отрицательная, а левая неотрицательная), т.е. плоскость
не пересекает эллипсоид. При
уравнение (4.47) имеет нулевое решение
. Следовательно, плоскости
касаются эллипсоида в его вершинах
. При
, разделив обе части уравнения (4.47) на
, получаем уравнение эллипса
полуосями
. Следовательно, сечение эллипсоида плоскостью
при
представляет собой эллипс.
Плоские сечения дают возможность составить полное представление о виде эллипсоида (рис.4.40,а).
Эллипсоиды вращения
Эллипсоид, у которого две полуоси равны, называется эллипсоидом вращения (или сфероидом). Такой эллипсоид является поверхностью вращения. Например, если , то линии (4.47) при
являются окружностями. Следовательно, сечения эллипсоида плоскостями
представляют собой окружности с центрами на оси аппликат. Такую поверхность можно получить, вращая вокруг оси
эллипс
заданный в плоскости
(рис.4.41,а).
Если , то все сечения эллипсоида (4.46) плоскостями
при
будут окружностями с центрами на оси абсцисс. Такой эллипсоид можно получить, вращая вокруг оси
эллипс
(рис.4.41,б).
Если все полуоси эллипсоида равны , то он представляет собой сферу
радиуса
, которую можно получить, например, вращая окружность такого же радиуса вокруг любого диаметра.
Эллипсоид, у которого полуоси попарно различны , называется трехосным (или общим).
Замечания 4.8.
1. Плоскости определяют в пространстве основной прямоугольный параллелепипед, внутри которого находится эллипсоид (см. рис.4.40,б). Грани параллелепипеда касаются эллипсоида в его вершинах.
2. Эллипсоид можно определить, как геометрическое место точек, получаемое в результате трех сжатий (растяжений) сферы единичного радиуса к трем взаимно перпендикулярным плоскостям.
3. Начало канонической системы координат является центром симметрии эллипсоида, координатные оси — осями симметрии эллипсоида, координатные плоскости — плоскостями симметрии эллипсоида.
В самом деле, если точка принадлежит эллипсоиду, то точки с координатами
при любом выборе знаков также принадлежат эллипсоиду, поскольку их координаты удовлетворяют уравнению (4.46).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
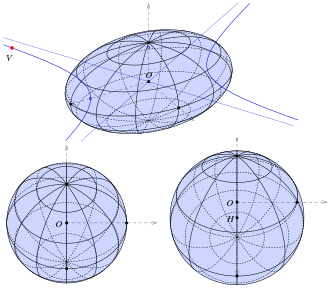
Examples of ellipsoids with equation x2/a2 + y2/b2 + z2/c2 = 1:
- Sphere, a = b = c = 4, top;
- Spheroid, a = b = 5, c = 3, bottom left;
- Tri-axial ellipsoid, a = 4.5, b = 6; c = 3, bottom right
An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.
An ellipsoid is a quadric surface; that is, a surface that may be defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, an ellipsoid is characterized by either of the two following properties. Every planar cross section is either an ellipse, or is empty, or is reduced to a single point (this explains the name, meaning “ellipse-like”). It is bounded, which means that it may be enclosed in a sufficiently large sphere.
An ellipsoid has three pairwise perpendicular axes of symmetry which intersect at a center of symmetry, called the center of the ellipsoid. The line segments that are delimited on the axes of symmetry by the ellipsoid are called the principal axes, or simply axes of the ellipsoid. If the three axes have different lengths, the figure is a triaxial ellipsoid (rarely scalene ellipsoid), and the axes are uniquely defined.
If two of the axes have the same length, then the ellipsoid is an ellipsoid of revolution, also called a spheroid. In this case, the ellipsoid is invariant under a rotation around the third axis, and there are thus infinitely many ways of choosing the two perpendicular axes of the same length. If the third axis is shorter, the ellipsoid is an oblate spheroid; if it is longer, it is a prolate spheroid. If the three axes have the same length, the ellipsoid is a sphere.
Standard equation[edit]
The general ellipsoid, also known as triaxial ellipsoid, is a quadratic surface which is defined in Cartesian coordinates as:
where 


The points 


In spherical coordinate system for which 
where 

When 
When 


Parameterization[edit]
The ellipsoid may be parameterized in several ways, which are simpler to express when the ellipsoid axes coincide with coordinate axes. A common choice is
where
These parameters may be interpreted as spherical coordinates, where θ is the polar angle and φ is the azimuth angle of the point (x, y, z) of the ellipsoid.[1]
Measuring from the equator rather than a pole,
where
θ is the reduced latitude, parametric latitude, or eccentric anomaly and λ is azimuth or longitude.
Measuring angles directly to the surface of the ellipsoid, not to the circumscribed sphere,
where
γ would be geocentric latitude on the Earth, and λ is longitude. These are true spherical coordinates with the origin at the center of the ellipsoid.[citation needed]
In geodesy, the geodetic latitude is most commonly used, as the angle between the vertical and the equatorial plane, defined for a biaxial ellipsoid. For a more general triaxial ellipsoid, see ellipsoidal latitude.
Volume[edit]
The volume bounded by the ellipsoid is
In terms of the principal diameters A, B, C (where A = 2a, B = 2b, C = 2c), the volume is
.
This equation reduces to that of the volume of a sphere when all three elliptic radii are equal, and to that of an oblate or prolate spheroid when two of them are equal.
The volume of an ellipsoid is 2/3 the volume of a circumscribed elliptic cylinder, and π/6 the volume of the circumscribed box. The volumes of the inscribed and circumscribed boxes are respectively:
Surface area[edit]
The surface area of a general (triaxial) ellipsoid is[2][3]
where
and where F(φ, k) and E(φ, k) are incomplete elliptic integrals of the first and second kind respectively.[4] The surface area of this general ellipsoid can also be expressed using the RF and RD Carlson symmetric forms of the elliptic integrals by simply substituting the above formula to the respective definitions:
Unlike the expression with F(φ, k) and E(φ, k), the variant based on the Carlson symmetric integrals yields valid results for a sphere and only the axis c must be the smallest, the order between the two larger axes, a and b can be arbitrary.
The surface area of an ellipsoid of revolution (or spheroid) may be expressed in terms of elementary functions:
or
or
and
which, as follows from basic trigonometric identities, are equivalent expressions (i.e. the formula for Soblate can be used to calculate the surface area of a prolate ellipsoid and vice versa). In both cases e may again be identified as the eccentricity of the ellipse formed by the cross section through the symmetry axis. (See ellipse). Derivations of these results may be found in standard sources, for example Mathworld.[5]
Approximate formula[edit]
Here p ≈ 1.6075 yields a relative error of at most 1.061%;[6] a value of p = 8/5 = 1.6 is optimal for nearly spherical ellipsoids, with a relative error of at most 1.178%.
In the “flat” limit of c much smaller than a and b, the area is approximately 2πab, equivalent to p = log23 ≈ 1.5849625007.
Plane sections[edit]
Plane section of an ellipsoid
The intersection of a plane and a sphere is a circle (or is reduced to a single point, or is empty). Any ellipsoid is the image of the unit sphere under some affine transformation, and any plane is the image of some other plane under the same transformation. So, because affine transformations map circles to ellipses, the intersection of a plane with an ellipsoid is an ellipse or a single point, or is empty.[7] Obviously, spheroids contain circles. This is also true, but less obvious, for triaxial ellipsoids (see Circular section).
Determining the ellipse of a plane section[edit]
Plane section of an ellipsoid (see example)
Given: Ellipsoid x2/a2 + y2/b2 + z2/c2 = 1 and the plane with equation nxx + nyy + nzz = d, which have an ellipse in common.
Wanted: Three vectors f0 (center) and f1, f2 (conjugate vectors), such that the ellipse can be represented by the parametric equation
(see ellipse).
Plane section of the unit sphere (see example)
Solution: The scaling u = x/a, v = y/b, w = z/c transforms the ellipsoid onto the unit sphere u2 + v2 + w2 = 1 and the given plane onto the plane with equation
Let muu + mvv + mww = δ be the Hesse normal form of the new plane and
its unit normal vector. Hence
is the center of the intersection circle and
its radius (see diagram).
Where mw = ±1 (i.e. the plane is horizontal), let
Where mw ≠ ±1, let
In any case, the vectors e1, e2 are orthogonal, parallel to the intersection plane and have length ρ (radius of the circle). Hence the intersection circle can be described by the parametric equation
The reverse scaling (see above) transforms the unit sphere back to the ellipsoid and the vectors e0, e1, e2 are mapped onto vectors f0, f1, f2, which were wanted for the parametric representation of the intersection ellipse.
How to find the vertices and semi-axes of the ellipse is described in ellipse.
Example: The diagrams show an ellipsoid with the semi-axes a = 4, b = 5, c = 3 which is cut by the plane x + y + z = 5.
Pins-and-string construction[edit]
Pins-and-string construction of an ellipse:
|S1 S2|, length of the string (red)
Pins-and-string construction of an ellipsoid, blue: focal conics
Determination of the semi axis of the ellipsoid
The pins-and-string construction of an ellipsoid is a transfer of the idea constructing an ellipse using two pins and a string (see diagram).
A pins-and-string construction of an ellipsoid of revolution is given by the pins-and-string construction of the rotated ellipse.
The construction of points of a triaxial ellipsoid is more complicated. First ideas are due to the Scottish physicist J. C. Maxwell (1868).[8] Main investigations and the extension to quadrics was done by the German mathematician O. Staude in 1882, 1886 and 1898.[9][10][11] The description of the pins-and-string construction of ellipsoids and hyperboloids is contained in the book Geometry and the imagination written by D. Hilbert & S. Vossen,[12] too.
Steps of the construction[edit]
- Choose an ellipse E and a hyperbola H, which are a pair of focal conics:
with the vertices and foci of the ellipse
and a string (in diagram red) of length l.
- Pin one end of the string to vertex S1 and the other to focus F2. The string is kept tight at a point P with positive y– and z-coordinates, such that the string runs from S1 to P behind the upper part of the hyperbola (see diagram) and is free to slide on the hyperbola. The part of the string from P to F2 runs and slides in front of the ellipse. The string runs through that point of the hyperbola, for which the distance |S1 P| over any hyperbola point is at a minimum. The analogous statement on the second part of the string and the ellipse has to be true, too.
- Then: P is a point of the ellipsoid with equation
- The remaining points of the ellipsoid can be constructed by suitable changes of the string at the focal conics.
Semi-axes[edit]
Equations for the semi-axes of the generated ellipsoid can be derived by special choices for point P:
The lower part of the diagram shows that F1 and F2 are the foci of the ellipse in the xy-plane, too. Hence, it is confocal to the given ellipse and the length of the string is l = 2rx + (a − c). Solving for rx yields rx = 1/2(l − a + c); furthermore r2
y = r2
x − c2.
From the upper diagram we see that S1 and S2 are the foci of the ellipse section of the ellipsoid in the xz-plane and that r2
z = r2
x − a2.
Converse[edit]
If, conversely, a triaxial ellipsoid is given by its equation, then from the equations in step 3 one can derive the parameters a, b, l for a pins-and-string construction.
Confocal ellipsoids[edit]
If E is an ellipsoid confocal to E with the squares of its semi-axes
then from the equations of E
one finds, that the corresponding focal conics used for the pins-and-string construction have the same semi-axes a, b, c as ellipsoid E. Therefore (analogously to the foci of an ellipse) one considers the focal conics of a triaxial ellipsoid as the (infinite many) foci and calls them the focal curves of the ellipsoid.[13]
The converse statement is true, too: if one chooses a second string of length l and defines
then the equations
are valid, which means the two ellipsoids are confocal.
Limit case, ellipsoid of revolution[edit]
In case of a = c (a spheroid) one gets S1 = F1 and S2 = F2, which means that the focal ellipse degenerates to a line segment and the focal hyperbola collapses to two infinite line segments on the x-axis. The ellipsoid is rotationally symmetric around the x-axis and
.
Properties of the focal hyperbola[edit]
Top: 3-axial Ellipsoid with its focal hyperbola.
Bottom: parallel and central projection of the ellipsoid such that it looks like a sphere, i.e. its apparent shape is a circle
- True curve
- If one views an ellipsoid from an external point V of its focal hyperbola, than it seems to be a sphere, that is its apparent shape is a circle. Equivalently, the tangents of the ellipsoid containing point V are the lines of a circular cone, whose axis of rotation is the tangent line of the hyperbola at V.[14][15] If one allows the center V to disappear into infinity, one gets an orthogonal parallel projection with the corresponding asymptote of the focal hyperbola as its direction. The true curve of shape (tangent points) on the ellipsoid is not a circle. The lower part of the diagram shows on the left a parallel projection of an ellipsoid (with semi-axes 60, 40, 30) along an asymptote and on the right a central projection with center V and main point H on the tangent of the hyperbola at point V. (H is the foot of the perpendicular from V onto the image plane.) For both projections the apparent shape is a circle. In the parallel case the image of the origin O is the circle’s center; in the central case main point H is the center.
- Umbilical points
- The focal hyperbola intersects the ellipsoid at its four umbilical points.[16]
Property of the focal ellipse[edit]
The focal ellipse together with its inner part can be considered as the limit surface (an infinitely thin ellipsoid) of the pencil of confocal ellipsoids determined by a, b for rz → 0. For the limit case one gets
In general position[edit]
As a quadric[edit]
If v is a point and A is a real, symmetric, positive-definite matrix, then the set of points x that satisfy the equation
is an ellipsoid centered at v. The eigenvectors of A are the principal axes of the ellipsoid, and the eigenvalues of A are the reciprocals of the squares of the semi-axes: a−2, b−2 and c−2.[17]
An invertible linear transformation applied to a sphere produces an ellipsoid, which can be brought into the above standard form by a suitable rotation, a consequence of the polar decomposition (also, see spectral theorem). If the linear transformation is represented by a symmetric 3 × 3 matrix, then the eigenvectors of the matrix are orthogonal (due to the spectral theorem) and represent the directions of the axes of the ellipsoid; the lengths of the semi-axes are computed from the eigenvalues. The singular value decomposition and polar decomposition are matrix decompositions closely related to these geometric observations.
Parametric representation[edit]
ellipsoid as an affine image of the unit sphere
The key to a parametric representation of an ellipsoid in general position is the alternative definition:
- An ellipsoid is an affine image of the unit sphere.
An affine transformation can be represented by a translation with a vector f0 and a regular 3 × 3 matrix A:
where f1, f2, f3 are the column vectors of matrix A.
A parametric representation of an ellipsoid in general position can be obtained by the parametric representation of a unit sphere (see above) and an affine transformation:
.
If the vectors f1, f2, f3 form an orthogonal system, the six points with vectors f0 ± f1,2,3 are the vertices of the ellipsoid and |f1|, |f2|, |f3| are the semi-principal axes.
A surface normal vector at point x(θ, φ) is
For any ellipsoid there exists an implicit representation F(x, y, z) = 0. If for simplicity the center of the ellipsoid is the origin, f0 = 0, the following equation describes the ellipsoid above:[18]
Applications[edit]
The ellipsoidal shape finds many practical applications:
- Geodesy
- Earth ellipsoid, a mathematical figure approximating the shape of the Earth.
- Reference ellipsoid, a mathematical figure approximating the shape of planetary bodies in general.
- Mechanics
- Poinsot’s ellipsoid, a geometrical method for visualizing the torque-free motion of a rotating rigid body.
- Lamé’s stress ellipsoid, an alternative to Mohr’s circle for the graphical representation of the stress state at a point.
- Manipulability ellipsoid, used to describe a robot’s freedom of motion.
- Jacobi ellipsoid, a triaxial ellipsoid formed by a rotating fluid
- Crystallography
- Index ellipsoid, a diagram of an ellipsoid that depicts the orientation and relative magnitude of refractive indices in a crystal.
- Thermal ellipsoid, ellipsoids used in crystallography to indicate the magnitudes and directions of the thermal vibration of atoms in crystal structures.
- Lighting
- Ellipsoidal reflector floodlight
- Ellipsoidal reflector spotlight
- Medicine
- Measurements obtained from MRI imaging of the prostate can be used to determine the volume of the gland using the approximation L × W × H × 0.52 (where 0.52 is an approximation for π/6)[19]
Dynamical properties[edit]
The mass of an ellipsoid of uniform density ρ is
The moments of inertia of an ellipsoid of uniform density are
For a = b = c these moments of inertia reduce to those for a sphere of uniform density.
Ellipsoids and cuboids rotate stably along their major or minor axes, but not along their median axis. This can be seen experimentally by throwing an eraser with some spin. In addition, moment of inertia considerations mean that rotation along the major axis is more easily perturbed than rotation along the minor axis.[20]
One practical effect of this is that scalene astronomical bodies such as Haumea generally rotate along their minor axes (as does Earth, which is merely oblate); in addition, because of tidal locking, moons in synchronous orbit such as Mimas orbit with their major axis aligned radially to their planet.
A spinning body of homogeneous self-gravitating fluid will assume the form of either a Maclaurin spheroid (oblate spheroid) or Jacobi ellipsoid (scalene ellipsoid) when in hydrostatic equilibrium, and for moderate rates of rotation. At faster rotations, non-ellipsoidal piriform or oviform shapes can be expected, but these are not stable.
Fluid dynamics[edit]
The ellipsoid is the most general shape for which it has been possible to calculate the creeping flow of fluid around the solid shape. The calculations include the force required to translate through a fluid and to rotate within it. Applications include determining the size and shape of large molecules, the sinking rate of small particles, and the swimming abilities of microorganisms.[21]
In probability and statistics[edit]
The elliptical distributions, which generalize the multivariate normal distribution and are used in finance, can be defined in terms of their density functions. When they exist, the density functions f have the structure:
where k is a scale factor, x is an n-dimensional random row vector with median vector μ (which is also the mean vector if the latter exists), Σ is a positive definite matrix which is proportional to the covariance matrix if the latter exists, and g is a function mapping from the non-negative reals to the non-negative reals giving a finite area under the curve.[22] The multivariate normal distribution is the special case in which g(z) = exp(−z/2) for quadratic form z.
Thus the density function is a scalar-to-scalar transformation of a quadric expression. Moreover, the equation for any iso-density surface states that the quadric expression equals some constant specific to that value of the density, and the iso-density surface is an ellipsoid.
In higher dimensions[edit]
A hyperellipsoid, or ellipsoid of dimension 

One can also define a hyperellipsoid as the image of a sphere under an invertible affine transformation. The spectral theorem can again be used to obtain a standard equation of the form
The volume of an n-dimensional hyperellipsoid can be obtained by replacing Rn by the product of the semi-axes a1a2…an in the formula for the volume of a hypersphere:
(where Γ is the gamma function).
See also[edit]
- Ellipsoidal dome
- Ellipsoid method
- Ellipsoidal coordinates
- Elliptical distribution, in statistics
- Flattening, also called ellipticity and oblateness, is a measure of the compression of a circle or sphere along a diameter to form an ellipse or an ellipsoid of revolution (spheroid), respectively.
- Focaloid, a shell bounded by two concentric, confocal ellipsoids
- Geodesics on an ellipsoid
- Geodetic datum, the gravitational Earth modeled by a best-fitted ellipsoid
- Homoeoid, a shell bounded by two concentric similar ellipsoids
- List of surfaces
- Superellipsoid
Notes[edit]
- ^ Kreyszig (1972, pp. 455–456)
- ^ F.W.J. Olver, D.W. Lozier, R.F. Boisvert, and C.W. Clark, editors, 2010, NIST Handbook of Mathematical Functions (Cambridge University Press), available online at “DLMF: 19.33 Triaxial Ellipsoids”. Archived from the original on 2012-12-02. Retrieved 2012-01-08. (see next reference).
- ^ NIST (National Institute of Standards and Technology) at http://www.nist.gov Archived 2015-06-17 at the Wayback Machine
- ^ “DLMF: 19.2 Definitions”.
- ^ W., Weisstein, Eric. “Prolate Spheroid”. mathworld.wolfram.com. Archived from the original on 3 August 2017. Retrieved 25 March 2018.
- ^ Final answers Archived 2011-09-30 at the Wayback Machine by Gerard P. Michon (2004-05-13). See Thomsen’s formulas and Cantrell’s comments.
- ^ Albert, Abraham Adrian (2016) [1949], Solid Analytic Geometry, Dover, p. 117, ISBN 978-0-486-81026-3
- ^ W. Böhm: Die FadenKonstruktion der Flächen zweiter Ordnung, Mathemat. Nachrichten 13, 1955, S. 151
- ^ Staude, O.: Ueber Fadenconstructionen des Ellipsoides. Math. Ann. 20, 147–184 (1882)
- ^ Staude, O.: Ueber neue Focaleigenschaften der Flächen 2. Grades. Math. Ann. 27, 253–271 (1886).
- ^ Staude, O.: Die algebraischen Grundlagen der Focaleigenschaften der Flächen 2. Ordnung Math. Ann. 50, 398 – 428 (1898).
- ^ D. Hilbert & S Cohn-Vossen: Geometry and the imagination, Chelsea New York, 1952, ISBN 0-8284-1087-9, p. 20 .
- ^ O. Hesse: Analytische Geometrie des Raumes, Teubner, Leipzig 1861, p. 287
- ^ D. Hilbert & S Cohn-Vossen: Geometry and the Imagination, p. 24
- ^ O. Hesse: Analytische Geometrie des Raumes, p. 301
- ^ W. Blaschke: Analytische Geometrie, p. 125
- ^ “Archived copy” (PDF). Archived (PDF) from the original on 2013-06-26. Retrieved 2013-10-12.
{{cite web}}: CS1 maint: archived copy as title (link) pp. 17–18. - ^ Computerunterstützte Darstellende und Konstruktive Geometrie. Archived 2013-11-10 at the Wayback Machine Uni Darmstadt (PDF; 3,4 MB), S. 88.
- ^ Bezinque, Adam; et al. (2018). “Determination of Prostate Volume: A Comparison of Contemporary Methods”. Academic Radiology. 25 (12): 1582–1587. doi:10.1016/j.acra.2018.03.014. PMID 29609953. S2CID 4621745.
- ^ Goldstein, H G (1980). Classical Mechanics, (2nd edition) Chapter 5.
- ^ Dusenbery, David B. (2009).Living at Micro Scale, Harvard University Press, Cambridge, Massachusetts ISBN 978-0-674-03116-6.
- ^ Frahm, G., Junker, M., & Szimayer, A. (2003). Elliptical copulas: applicability and limitations. Statistics & Probability Letters, 63(3), 275–286.
References[edit]
- Kreyszig, Erwin (1972), Advanced Engineering Mathematics (3rd ed.), New York: Wiley, ISBN 0-471-50728-8
External links[edit]
Wikimedia Commons has media related to Ellipsoids.
- “Ellipsoid” by Jeff Bryant, Wolfram Demonstrations Project, 2007.
- Ellipsoid and Quadratic Surface, MathWorld.
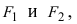
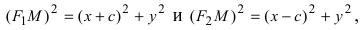
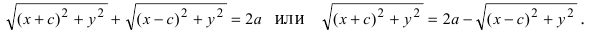
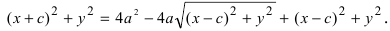
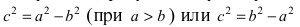
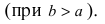
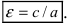
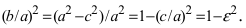
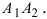
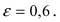
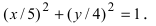
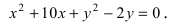
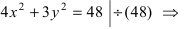
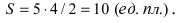

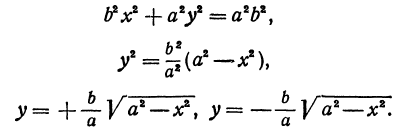
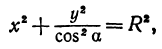
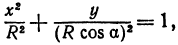

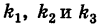
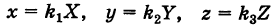
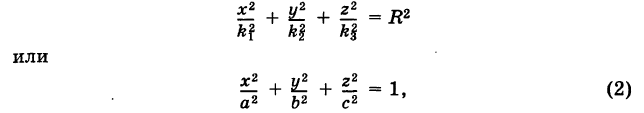




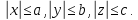














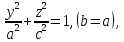










![{displaystyle {begin{aligned}R={}&{frac {abc}{sqrt {c^{2}left(b^{2}cos ^{2}lambda +a^{2}sin ^{2}lambda right)cos ^{2}gamma +a^{2}b^{2}sin ^{2}gamma }}},\[3pt]&-{tfrac {pi }{2}}leq gamma leq {tfrac {pi }{2}},qquad 0leq lambda <2pi .end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e87a3593c5b92d0d0a7a0f78bf98a9c69fb9f9b4)





![{displaystyle S=2pi c^{2}+2pi ableft[R_{F}left({frac {c^{2}}{a^{2}}},{frac {c^{2}}{b^{2}}},1right)-{frac {1}{3}}left(1-{frac {c^{2}}{a^{2}}}right)left(1-{frac {c^{2}}{b^{2}}}right)R_{D}left({frac {c^{2}}{a^{2}}},{frac {c^{2}}{b^{2}}},1right)right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15207ed0e8a0d927d3318a80bc689e550181feeb)




![{displaystyle Sapprox 4pi {sqrt[{p}]{frac {a^{p}b^{p}+a^{p}c^{p}+b^{p}c^{p}}{3}}}.,!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3ba7c5165e42013df15a6129b6c703ac3a57416)































![{displaystyle {begin{aligned}I_{mathrm {xx} }&={tfrac {1}{5}}mleft(b^{2}+c^{2}right),&I_{mathrm {yy} }&={tfrac {1}{5}}mleft(c^{2}+a^{2}right),&I_{mathrm {zz} }&={tfrac {1}{5}}mleft(a^{2}+b^{2}right),\[3pt]I_{mathrm {xy} }&=I_{mathrm {yz} }=I_{mathrm {zx} }=0.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abb475e7f50c8328a61ba8c81e5ee9ed5c77a321)




