I have drawn a rectangle. I know its (x1,y1) Top Left and (x2,y2) Bottom Right coordinates.. I also have the height h and width w of drawn rectangle.. How can I find the center coordinates (x,y) ?
I am currently using the following formula.
(x,y) = (x2 + x1)/2, (y2+y1)/2
It gives the correct y coordinate but no luck in x.
Lucifer
29.3k24 gold badges90 silver badges142 bronze badges
asked Mar 16, 2012 at 9:36
4
The center of rectangle is the midpoint of the diagonal end points of rectangle.
Here the midpoint is ( (x1 + x2) / 2, (y1 + y2) / 2 ).
That means:
xCenter = (x1 + x2) / 2
yCenter = (y1 + y2) / 2
Let me know your code.
answered Mar 16, 2012 at 10:12
Prasad GPrasad G
6,6927 gold badges42 silver badges65 bronze badges
3
Center x = x + 1/2 of width
Center y = y + 1/2 of height
If you know the width and height already then you only need one set of coordinates.
dota2pro
7,0687 gold badges43 silver badges78 bronze badges
answered Sep 21, 2013 at 11:29
frogfrog
3113 silver badges2 bronze badges
1
We can calculate using mid point of line formula,
centre (x,y) = new Point((boundRect.tl().x+boundRect.br().x)/2,(boundRect.tl().y+boundRect.br().y)/2)
answered Nov 21, 2013 at 6:58
VinayakVinayak
6,0261 gold badge32 silver badges30 bronze badges
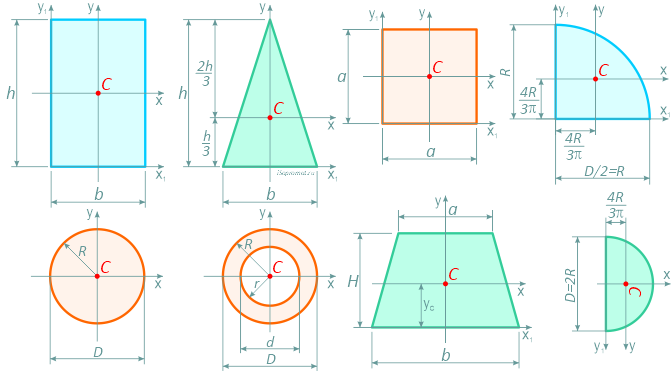
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.
Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
Ix , Iy — осевые моменты инерции сечения относительно главных осей;
Ix1 , Iy1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
Iρ — полярный момент инерции сечения;
Wx , Wy — осевые моменты сопротивления;
Wρ — полярный момент сопротивления
Прямоугольник
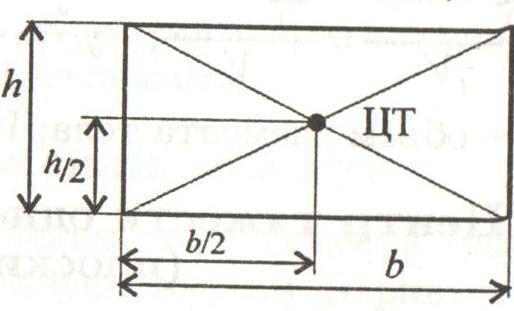
Прямоугольник высотой h и шириной b.
Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.
Площадь
Центральные осевые моменты инерции прямоугольника
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевые моменты сопротивления прямоугольного сечения
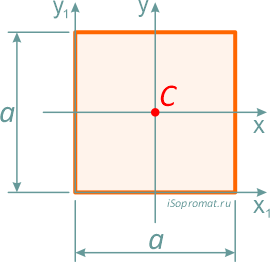
Квадрат
Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.
Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.
Площадь
Центральные осевые моменты инерции квадрата
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевой момент сопротивления квадратного сечения
Треугольник равнобедренный
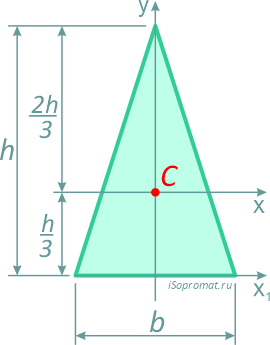
Равнобедренный треугольник высотой h и шириной основания b.
Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.
Площадь
Центральные осевые моменты инерции треугольника
Момент инерции относительно смещенной оси x1, проходящей через его основание
Прямоугольный треугольник
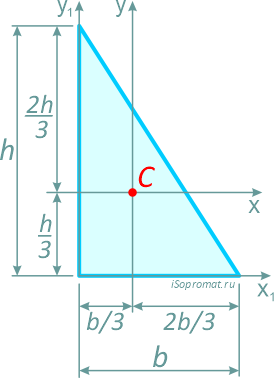
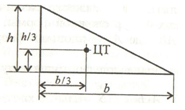
Прямоугольный треугольник высотой h и шириной основания b.
Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.
Площадь
Центральные осевые моменты инерции прямоугольного треугольника
Моменты инерции относительно смещенных осей x1 и y1, проходящих через точку, соединяющую его катеты
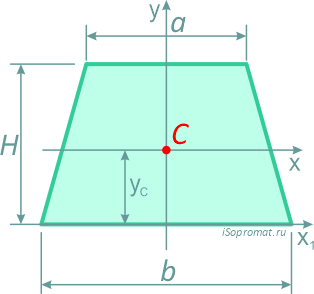
Трапеция
Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.
Площадь трапеции
Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:
Круг
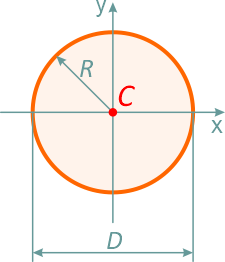
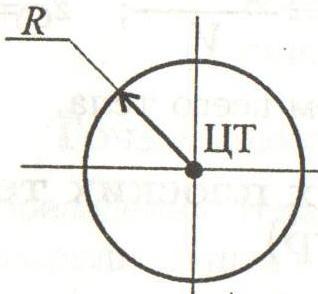
Круг диаметром D (d) или радиусом R (r)
Площадь круга через его диаметр и радиус
Центральные осевые и полярный моменты инерции круга
Осевые и полярный моменты сопротивления
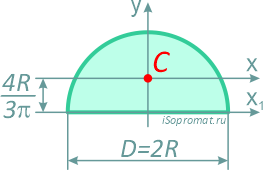
Полукруг
Половина круга диаметром D (d) или радиусом R (r)
Площадь
Осевые моменты инерции полукруга
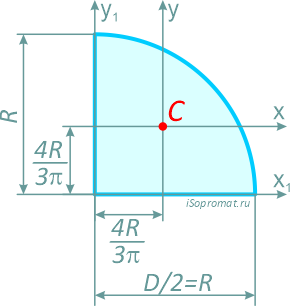
Четверть круга
Четверть круга диаметром D (d) или радиусом R (r)
Площадь
Центральные осевые моменты инерции четверти круга
Моменты инерции относительно смещенных осей x1 и y1
Кольцо
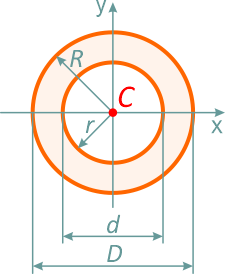
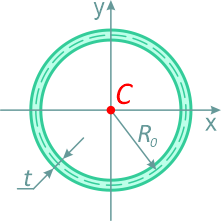
Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)
Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.
Площадь
Центральные осевые и полярный моменты инерции кольца
Осевые и полярный моменты сопротивления
Тонкостенное сечение (труба)
Тонкостенный профиль (сечение трубы) средним радиусом R0 и толщиной стенки трубы t при R0>>t
Площадь
Центральные осевые и полярный моменты инерции трубного сечения
Осевые и полярный моменты сопротивления
Пример определения координат центра тяжести сложной фигуры:
Другие видео
Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Положения центра тяжести некоторых фигур
Прямоугольник.
Так
как прямоугольник имеет две оси симметрии
, то его центр тяжести находится на
пересечении осей симметрии, т.е. в точке
пересечения диагоналей прямоугольника.
Треугольник.
Центр
тяжести лежит в точке пересечения его
медиан. Из геометрии известно, что
медианы треугольника пересекаются в
одной точке и делятся в отношении 1:2 от
основания.
Круг.
Так
как круг имеет две оси симметрии, то его
центр тяжести находится на пересечении
осей симметрии.
Полукруг.
Полукруг
имеет одну ось симметрии, то центр
тяжести лежит на этой оси. Другая
координата центра тяжести вычисляется
по формуле:
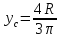
Многие
конструктивные элементы изготавливают
из стандартного проката – уголков,
двутавров, швеллеров и других. Все
размеры, а так же геометрические
характеристики прокатных профилей это
табличные данные, которые можно найти
в справочной литературе в таблицах
нормального сортамента (ГОСТ 8239-89, ГОСТ
8240-89).
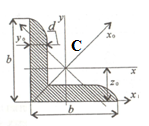
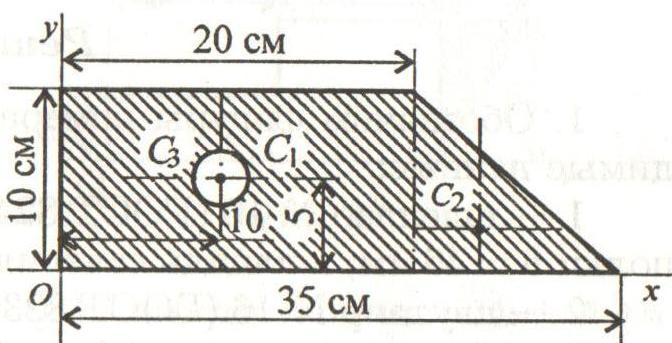
Пример
1. Определить
положение центра тяжести фигуры,
представленной на рисунке.
Решение:
-
Выбираем
оси координат, так чтобы ось Ох прошла
по крайнему нижнему габаритному размеру,
а ось Оу – по крайнему левому габаритному
размеру. -
Разбиваем
сложную фигуру на минимальное количество
простых фигур:
-
прямоугольник
20х10; -
треугольник
15х10; -
круг
R=3
см.
-
Вычисляем
площадь каждой простой фигуры, её
координаты центра тяжести. Результаты
вычислений заносим в таблицу
|
№ фигуры |
Площадь |
Координаты |
|
|
Х, |
У, |
||
|
1 |
|
20:2=10 |
10:2=5 |
|
2 |
|
|
|
|
3 |
|
10 |
5 |
-
Вычисляем
координаты центра тяжести фигуры по
формулам:
Ответ:
С(14,5; 4,5)
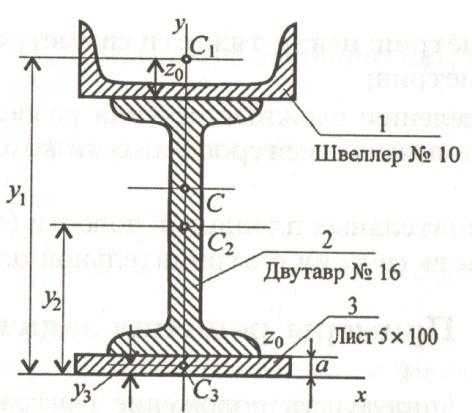
Пример
2.
Определить координаты центра тяжести
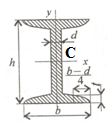
составного сечения, состоящего из листа
и прокатных профилей.
Решение.
-
Выбираем
оси координат, так как показано на
рисунке. -
Обозначим
фигуры номерами и выпишем из таблицы
необходимые данные:
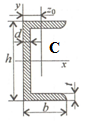
-
– швеллер
№10; высота h=100
мм; ширина b=46
мм; площадь сечения
;
-
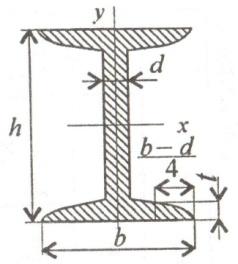
–
двутавр №16; высота
h=160
мм; ширина b=81
мм; площадь сечения
;
-
– лист
5х100; толщина 5 мм; ширина 100 мм.
-
Вычисляем
координаты центра тяжести каждой
фигуры. Составное сечение симметрично,
поэтому центр тяжести находится на оси
симметрии и координата
.
Результаты
вычислений заносим в таблицу
|
№ фигуры |
Площадь |
Координаты |
|
|
Х, |
У, |
||
|
1 |
|
0 |
|
|
2 |
|
0 |
|
|
3 |
|
0 |
|
-
Вычисляем
координаты центра тяжести фигуры по
формулам:
Ответ:
С(0; 10)
Лабораторная работа №1 «Определение центра тяжести составных плоских фигур»
Цель:
Определить центр тяжести заданной
плоской сложной фигуры опытным и
аналитическим способами и сравнить их
результаты.
Порядок выполнения работы
-
Начертить
в тетрадях свою плоскую фигуру по
размерам, с указанием осей координат. -
Определить
центр тяжести аналитическим способом.-
Разбить
фигуру на минимальное количество
фигур, центры тяжести которых, мы знаем,
как определить. -
Указать
номера площадей и координаты центра
тяжести каждой фигуры. -
Вычислить
координаты центра тяжести каждой
фигуры. -
Вычислить
площадь каждой фигуры. -
Вычислить
координаты центра тяжести всей фигуры
по формулам (положение центра тяжести
нанести на чертеж фигуры):
-
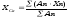
-
Записать
координаты центра тяжести.
-
Определить
центр тяжести опытным путем на установке
для определения координат центра
тяжести.-
Вырезать
данную фигуру из тонкого картона. -
Определить
центр тяжести своей фигуры на установке.
-
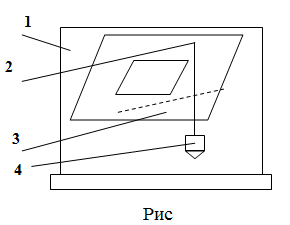
Установка
для опытного определения координат
центра тяжести способом подвешивания
состоит из вертикальной стойки 1
(см. рис.), к которой прикреплена игла 2.
Плоская фигура 3
изготовлена из картона, в котором легко
проколоть отверстие. Отверстия А
и В
прокалываются в произвольно расположенных
точках (лучше на наиболее удаленном
расстоянии друг от друга). Плоская фигура
подвешивается на иглу сначала в точке
А,
а потом в точке В.
При помощи отвеса 4,
закрепленного на той же игле, на фигуре
прочерчивают карандашом вертикальную
линию, соответствующую нити отвеса.
Центр тяжести С
фигуры будет находиться в точке
пересечения вертикальных линий,
нанесенных при подвешивании фигуры в
точках А
и В.
-
Приклеить
фигуру с определенным центром тяжести
в тетрадь. -
Записать
значения координат центра тяжести,
найденных при подвешивании фигур:
-
Сравнить
результаты:
;
-
Сделать
вывод:
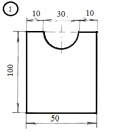
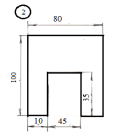
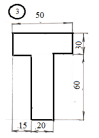
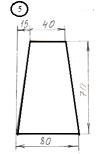
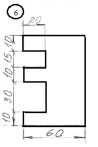
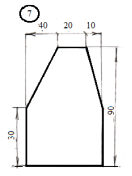
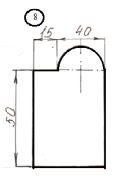
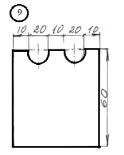
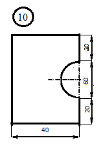
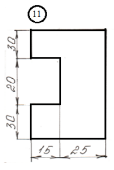
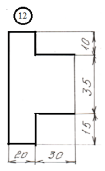
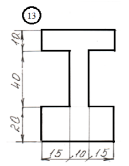
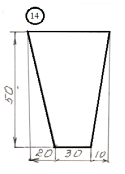
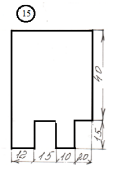
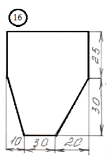
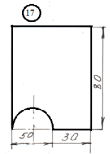
Задание
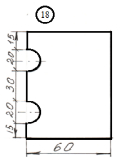
для лабораторной работы.
Номер схемы соответствует Вашему
порядковому номеру в журнале.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти центральную координату прямоугольника? [закрытый]
Я нарисовал прямоугольник. Я знаю его (x1,y1) верхние левые и (x2,y2) нижние правые координаты.. У меня тоже есть высота h и ширина W нарисованного прямоугольника.. Как найти координаты центра (x, y) ?
в настоящее время я использую следующую формулу.
Он дает правильную координату y, но не повезло в x.
3 ответов
Дайте мне знать ваш код.
центр x =
x + 1/2 ширины
Центр y =
y + 1/2 высоты
Если вы уже знаете ширину и высоту, вам нужен только один набор координат.
Определить центр прямоугольника
Не знаю, как точно называется. Допустим, есть прямоугольник такого вида:
Как определить его центр? Система координат декартова, координаты каждой вершины известны(x, y). Или подскажите, в какую сторону курить.
Должно работать для любого параллелепипеда:
Достаточно даже 2 противоположных вершин:
Всё ещё ищете ответ? Посмотрите другие вопросы с метками математика или задайте свой вопрос.
Site design / logo © 2022 Stack Exchange Inc; user contributions licensed under cc by-sa. rev 2022.6.10.42345
Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Как найти центр прямоугольника
Я нарисовал прямоугольник. Я знаю его (x1, y1) верхний левый и (x2, y2) нижний правый координаты. У меня также есть высота h и ширина w рисованного прямоугольника. Как найти координаты центра (x, y)?
В настоящее время я использую следующую формулу.
Он дает правильную координату y, но не везет в x.
- Выберите вкладку “Главная” панель “Рисование” раскрывающийся список “Прямоугольник” Угол .
найти
- Продолжайте нажимать клавишу пробела до тех пор, пока не появится курсор
Свойства
Зная стороны прямоугольника, можно вычислить все остальные его параметры, используя следующий ход действий. Периметр прямоугольника представляет собой удвоенную сумму его сторон, поэтому его можно сразу вычислить. P=2(a+b)
Площадь прямоугольника равна произведению его сторон, поэтому ее также можно найти сразу. S=ab
Диагонали в прямоугольнике являются конгруэнтными, каждая из них образует прямоугольный треугольник со сторонами прямоугольника. Из теоремы Пифагора каждая диагональ будет равна квадратному корню из суммы квадратов сторон прямоугольника. (рис. 56.1) d_1=d_2=√(a^2+b^2 )
Из этого же прямоугольного треугольника можно найти углы α и β при диагоналях, зная только стороны прямоугольника. Отношения катетов друг к другу дают тангенс или котангенс углов треугольника, поэтому α и β будут равны арктангенсу отношений сторон, а дальше значение в градусах можно найти, используя таблицы тангенсов. α=arc tan〖b/a〗 β=arc tan〖a/b〗
Углы γ и δ, образованные пересечением диагоналей, как видно из чертежа, через прямоугольный треугольник с полуосью, равны удвоенным значениям α и β соответственно. (рис.56.2) γ=2α δ=2β
Так как углы у прямоугольника все равны друг другу, вокруг него можно описать окружность. Центр окружности будет находиться в точке пересечения диагоналей, и следовательно, радиус описанной окружности будет равен половине диагонали. (рис.56.3) R=d/2=√(a^2+b^2 )/2
Не знаю, как точно называется. Допустим, есть прямоугольник такого вида:
Как определить его центр? Система координат декартова, координаты каждой вершины известны(x, y). Или подскажите, в какую сторону курить.
задан 10 авг 2017 в 23:23
4
Должно работать для любого параллелепипеда:
xc = average(x0, x1, x2, x3)
yc = average(y0, y1, y2, y3)
Достаточно даже 2 противоположных вершин:
xc = average(x0, x1)
yc = average(y0, y1)
ответ дан 10 авг 2017 в 23:38
ZergatulZergatul
11.3k1 золотой знак19 серебряных знаков32 бронзовых знака
1

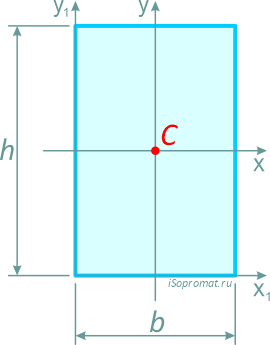
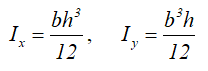
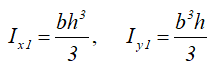
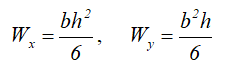
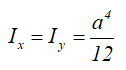
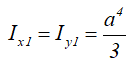
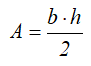
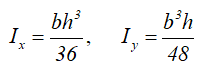
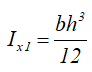
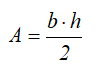
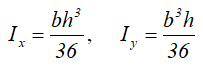
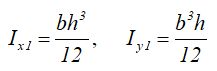
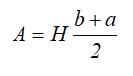
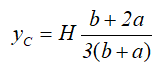
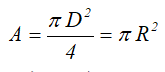
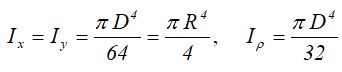
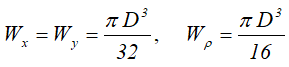
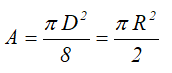
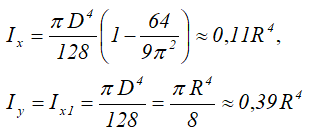
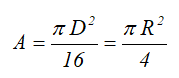
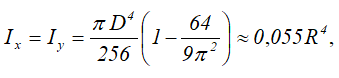
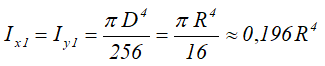
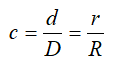
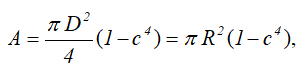
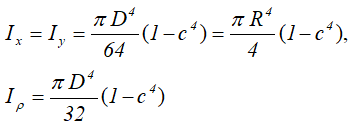
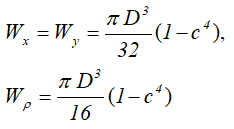
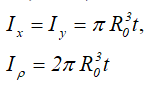
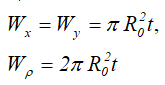
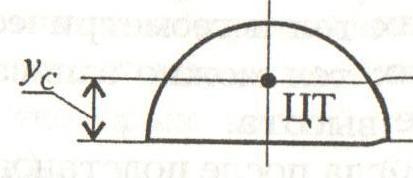
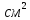
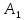 =20·10=200
=20·10=200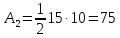
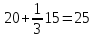
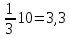
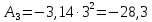
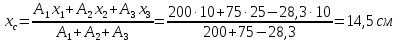
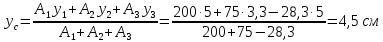
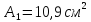 ;
;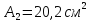 ;
;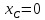 .
.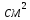
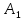 =10,9
=10,9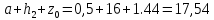
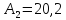
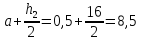
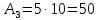
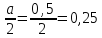
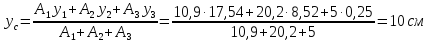
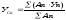
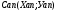
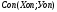
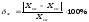 ;
;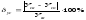



 найти
найти
