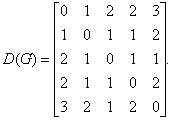Как найти центр графа по матрице

Утверждение. Если для двух вершин существует маршрут, связывающий их, то обязательно найдется минимальный маршрут, соединяющий эти вершины. Обозначим длину этого маршрута через d(v, w).

Определение. Величину d(v, w) (конечную или бесконечную) будем называть расстоянием между вершинами v, w. Это расстояние удовлетворяет аксиомам метрики:

1) d(v, w)  0, причем d(v, w) = 0 тогда и только тогда, когда v=w;

2) d(v, w) = d(w, v);

3) d(v, w)  d(v, u) + d(u, w).

Определение. Диаметром связного графа называется максимально возможное расстояние между двумя его вершинами.

Определение. Центром графа называется такая вершина, что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа.

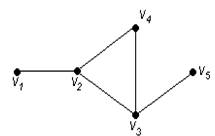
Пример 82.

Для графа G, изображенного на рис. 3.16, найти радиус, диаметр и центры.

Рис. 3.16. Граф для примера 82

Решение.

Чтобы определить центры, радиус, диаметр графа G, найдем матрицу D(G) расстояний между вершинами графа, элементами d_ij которой будут расстояния между вершинами v_i и v_j. Для этого воспользуемся графическим представлением графа. Заметим, что матрица D(G) симметрична относительно главной диагонали.

С помощью полученной матрицы для каждой вершины графа G определим наибольшее удаление из выражения:  для i, j = 1, 2, …, 5. В результате получаем: r(v₁) = 3, r(v₂) = 2, r(v₃) = 2, r(v₄) = 2, r(v₅) = 3. Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 2 и D(G) = 3, центрами являются вершины v₂, v₃, v₄.

1. Диаметр, радиус и центр графа

Для связного графа
определим
расстояние
между двумя его вершинами

и

как длину самой короткой цепи, соединяющей
эти вершины, и обозначим через
.
Длина цепи – это количество ребер,
составляющих цепь. Нетрудно проверить,
что введенное расстояние удовлетворяет
аксиомам метрики:

1)

2)
;

3)
.

Определим расстояние
от каждой вершины

графа

до самой далекой от нее вершины

,

которое называется
эксцентриситетом.
Очевидно, что эксцентриситет для всех
вершин в полного графа равен единице,
а для вершин простого цикла
–
.

Максимальный
эксцентриситет

носит название диаметра
графа, а
минимальный

– радиуса
графа
.
В полном графе имеем
,
а в простом цикле

–
.

Вершина

называется центральной, если
.
Граф может иметь несколько таких вершин,
а в некоторых графах все вершины являются
центральными. В простой цепи при нечетном
числе вершин только одна является
центральной, а при четном их числе таких
вершин две. В полном графе и для простого
цикла центральными являются все вершины.
Множество центральных вершин называется
центром
графа.

Пример 1.
Найти диаметр,
радиус и центр графа, приведенного на
рис. 4.

°

°

°
°
°

°
°

°

°

Рис.
4.

Для решения этой
задачи удобно предварительно вычислить
матрицу
расстояний
между вершинами графа. В данном случае
это будет матрица размером
,
в которой на месте

стоит расстояние от вершины

до вершины
:

Для каждой строки
матрицы находим наибольший элемент и
записываем его справа от черточки.
Наибольшее из этих чисел равно диаметру
графа
,
наименьшее – радиусу графа
.
Центр графа составляют центральные
вершины

и
.

Понятия центральной
вершины и центра графа появились в связи
с задачами оптимального размещения
пунктов массового обслуживания, таких
как больницы, пожарные части, пункты
охраны общественного порядка и т. п.,
когда важно минимизировать наибольшее
расстояние от любой точки некоторой
сети до ближайшего пункта обслуживания.

1. Матрицы достижимостей и контрадостижимостей

Матрица достижимостей

определяется следующим образом:

Множество вершин

графа
,
достижимых из заданной вершины
,
состоит из таких элементов
,
для которых
-й
элемент в матрице

равен 1. Это множество можно представить
в виде

.

Матрица
контрадостижимостей
(обратных
достижимостей)

определяется следующим образом:

Аналогично построению
достижимого множества

можно сформировать множество
,
используя следующее выражение:

.

Из определений
следует, что
-й
столбец матрицы

совпадает с
-й
строкой матрицы
,
т. е.
,
где

– матрица, транспонированная к матрице
.

Пример 2.
Найти матрицы достижимостей и
контрадостижимостей для графа,
приведенного на рис. 5.

°

°

°

°

°

°

°

Рис.
5.

Определим множества
достижимостей для вершин графа:

,

,

,

,

,

,

.

Следовательно,
матрицы достижимостей и контрадостижимостей
имеют вид:

,
.

Так как

– множество таких вершин, каждая из
которых принадлежит по крайней мере
одному пути, идущему от

к
,
то вершины этого множества называются
существенными
или неотъемлемыми
относительно концевых вершин

и
.
Все остальные вершины

называются несущественными
или избыточными,
поскольку их удаление не влияет на пути
от

к
.

Можно определить
также матрицы ограниченных
достижимостей и контрдостижимостей,
если потребовать, чтобы длины путей не
превышали некоторого заданного числа.
Тогда

будет верхней границей длины допустимых
путей.

Граф называют
транзитивным,
если из существования дуг

и

следует существование дуги
.
Транзитивным
замыканием
графа

является граф
,
где

– минимально возможное множество дуг,
необходимых для того, чтобы граф

был транзитивным. Очевидно, что матрица
достижимостей

графа

совпадает с матрицей смежности

графа
,
если в матрице

на главной диагонали поставить единицы.

6

Соседние файлы в папке LK

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Графы дорожных сетей и алгоритмы работы с ними

В математике сети дорог (автомобильных и не только) представляются взвешенным графом. Населенные пункты (или перекрестки) — это вершины графа, ребра — дороги, веса ребер — расстояния по этим дорогам.

Для взвешенных графов предлагается множество алгоритмов. Например, популярный алгоритм Дейкстры для поиска кратчайшего пути от одной вершины до другой. У всех этих алгоритмов есть общая принципиальная (для математики) особенность — они универсальны, т.е. могут успешно применяться для графов любой конструкции. В частности, для каждого алгоритма известна его сложность – она примерно соответствует увеличению времени выполнения алгоритма в зависимости от числа вершин графа. Все это подробно можно прочитать, например, в википедии.

Вернемся к практическим задачам. Дороги представляются взвешенным графом, но дороги — это не любой граф. Другими словами, нельзя из любого графа построить дорожную сеть. В отличие от виртуального графа как математической абстракции, дороги строятся людьми из реальных материалов и стоят довольно больших денег. Поэтому они прокладываются не как попало, а по определенным экономическим и практическим правилам.

Мы не знаем эти правила, однако, работая с дорожными сетями, вполне можно использовать алгоритмы, которые эффективны для графов дорог, хотя и не подходят для графов в универсальном или математическом смысле. Рассмотрим здесь два таких алгоритма.

Несколько важных понятий и условностей

1. Мы будем использовать взвешенные неориентированные графы с неотрицательными весами ребер. В частности, дороги в рамках региона (страны) представляют собой именно такой граф.

2. Матрица кратчайших расстояний (МКР) – ее маленький и простой пример можно найти во многих дорожных атласах. Эта табличка обычно называется примерно так: «расстояния между наиболее важными городами». Она выглядит как часть матрицы ниже или выше главной диагонали (из верхнего левого в нижний правый угол), потому что с другой стороны главной диагонали точно такие же цифры, другими словами элемент М(i,j)= М(j,i). Это происходит, потому что граф, как говорят математики, неориентированный. Строки и столбцы соответствуют городам (вершинам графа). В реальности такая таблица намного больше, так как в вершины графа, кроме городов, входят все деревни и перекрестки, но напечатать такую большую таблицу в атласе, естественно, невозможно.

Первым делом продолжим (мысленно) нашу таблицу на верхнюю часть, получим МКР, симметричную относительно главной диагонали и далее будем иметь в виду именно такую таблицу. В этом случае, столбец с некоторым номером равен строке с таким же номером и все равно, какое из понятий использовать. Мы используем и то, и другое, чтобы их пересекать между собой.

Наша МКР может быть: а) известна заранее, потому что мы ее подсчитали одним из методов поиска МКР; б) мы можем не знать МКР, а определять ее построчно по мере необходимости. Построчно – это значит, что для требуемой строки рассчитываются расстояния только от соответствующей ей вершины до остальных вершин, например, методом Дейкстры.

3. Еще пара понятий. Эксцентриситет данной вершины – это расстояние от этой вершины до самой удаленной от нее. Радиус графа – это наименьший из эксцентриситетов всех вершин. Центр графа – вершина, эксцентриситет которой равен радиусу.

Как это выглядит на практике. Центр дорожной сети – это город или перекресток, наименее удаленный от всех остальных пунктов этой сети. Радиус – максимальное расстояние от этого центрального узла до самого удаленного.

4. Степень вершины – количество ребер, которое присоединено к вершине.
У графов дорожных сетей, средняя степень всех вершин находится в районе от 2 до 4. Это вполне естественно – сложно и дорого строить перекрестки с большим количеством примыкающих дорог, не менее сложно потом пользоваться такой дорожной сетью. Графы, с невысокой средней степенью вершин называются разреженными, как видим, графы дорожных сетей именно такие.

Задача 1. Поиск радиус и центра графа по матрице кратчайших расстояний

Заметим, что у графа может быть несколько центров, но мы хотим найти любой из них.

Как задача решается в общем случае? Полным просмотром МКР. Ищется максимальный элемент в строке (эксцентриситет каждой вершины), а потом из этих максимальных элементов находится минимальный.

Это далеко не самый быстрый способ. Для чего нужно быстрее, если, казалось бы, радиус и центр графа можно найти один раз? Например, существуют задачи и алгоритмы на них, где в ходе перебора вершины постоянно «переобъединяются» в группы, а критерием для каждой группы является ее радиус. В этом случае радиус пересчитывается многократно, и скорость его поиска становится важным параметром. Как найти радиус быстрее?

Секрет в том, что для графов дорожных сетей все элементы просматривать не обязательно. На практике, достаточно просмотреть весьма малую часть всех строк.

Посмотрим, за счет чего это получается. Рассмотрим значения в одной строке матрицы МКР, другими словами, рассмотрим расстояния от одной вершины до всех остальных. Несложно доказать, что радиус графа не может быть больше чем максимальное значение в этой строке, и не может быть меньше чем минимальное значение в этой строке. Говоря математически, мы нашли верхнюю и нижнюю границу числа и если они совпадут – мы найдем число.

Допустим, мы нашли значения всего лишь в двух строках А и В. При этом, максимальное значение в строке А равно минимальному значению в строке В (эта величина будет стоять на пересечении столбца А и строки В). Несложно доказать, что А – центр графа, а найденное значение – его радиус. Задача решена.

Здорово, но такая ситуация на графах дорожных сетей маловероятна и решать задачу таким образом не получится. Поступим хитрее.
Возьмем пару строк В1 и В2. Из них сформируем вектор М таким образом: М(i)=max[B1(i),B2(i)]. Несложно доказать, что если для всех строк i значение min(M(i)) равно максимальному значению в столбце А, то, опять таки, А – центр, а найденное min(M(i)) – радиус.
Если пары строк окажется недостаточно, можно взять несколько строк, например три: B1, B2 и B3, тогда М(i)=max[B1(i),B2(i),B3(i)]. Особенность графов дорожных сетей состоит в том, что много строк не понадобится (удастся уложиться в десяток). Это легко проверить, поэкспериментировав на существующих графах сетей, скачав их из интернета: ссылка.

В общем случае и с точки зрения математики это, конечно, не так. Вполне можно построить теоретический граф в котором придется использовать очень много строк В (почти все, кроме, А). Вот только невозможно построить реальную дорожную сеть такого вида — денег не хватит.

Осталась последняя задача. Как быстро найти эти удачные строки B1, B2 и т.д. Для графов реальных дорожных сетей это сделать очень просто и быстро. Это будут максимально удаленные друг от друга вершины, но не обязательно самые удаленные (говоря математически, находить диаметр графа нам не требуется). Берем любую вершину, находим для нее самую дальнюю, для новой опять самую дальнюю и так, пока пара вершин не окажется самой дальней друг для друга.

Мы получили пару вершин В1 и В2. Находим для пары вектор М, как описано выше. Строка, в которой мы нашли min(M(i)) — претендент на центр, обозначим его А. Если в столбце А значение min(M(i)) – максимальное, то уже найдены центр и радиус. Если же нет, значит максимальное значение в столбце А соответствует расстоянию до другой вершины (не B1 и не B2). Значит, мы получили новую вершину B3 в список на поиск вектора М. Как вариант, можно и для B3 поискать самую удаленную вершину и если она не В1 и не B2, добавить ее как В4. Таким образом, увеличиваем список вершин B, пока центр и радиус не будут найдены.

Более строго, с алгоритмом и нужными доказательствами этот алгоритм описан в , там же приведены результаты его использования на некоторых графах дорожных сетей США, а в ссылка и ссылка он описан менее академически, но более понятно.

Задача 2. Поиск матрицы кратчайших расстояний

Наиболее популярные алгоритмы поиска МКР (Флойда-Уоршелла, например) описаны здесь . Все они универсальные, причем один из них – алгоритм Дейкстры с двоичной кучей – учитывает такое понятие как разреженный граф. Однако он тоже не использует особенности дорожных сетей.

Мы будем их использовать и на совершенно другом алгоритме и на существующих графах получим ускорение в десятки раз по сравнению с алгоритмом Дейкстры. Заметим сразу, что особенность этого алгоритма в том, что ищет именно МКР, причем сразу всю и точно (т.е. не приближенно, не эвристически).

Рассмотрим основную идею алгоритма. Суть ее в том, чтобы удалять вершины графа без изменения кратчайших расстояний для оставшихся точек. Если мы будем так делать, запоминая к каким точкам и на каких расстояниях была присоединена удаленная вершина, то сможем удалить все точки, кроме одной, а потом собрать их обратно в граф, но с уже подсчитанными расстояниями.

Начнем с простого, с вершины со степенью 1. Ее можно удалить в любом случае. Через нее не проходит никаких кратчайших путей, кроме путей к самой вершине, причем идут они именно через ту вершину, к которой была присоединена удаляемая вершина.

Пусть А – вершина со степенью 2 и присоединена она в вершинам В1 и В2. Если маршрут В1-А-В2 длиннее или равен ребру В1-В2, через точку А не проходит никаких маршрутов, кроме маршрутов к самой точке А (все остальные проходят через В1-В2). Значит, точку А можно удалить. В ином случае, т.е. если В1-А-В2 короче В1-В2 или ребра В1-В2 вообще нет, вершину А можно удалить, установив вес ребра В1-В2 равным сумме весов: |В1-А|+|А-В2|. Маршрут от А до других точек проходит либо через В1, либо через В2, если будут известны расстояния для В1 и В2, расстояния от А так же легко вычислить.

По такому же принципу можно удалить вершину с любой степенью, заменяя, по мере необходимости, Вi-А-Вj на Bi-Bj. Правда, нужно понимать, что чем больше степень вершины, тем больше возможных ребер надо проверить. Для вершины степени n это число равно n(n-1)/2.

Теоретически, таким способом можно удалить все вершины в любом графе, однако, в общем случае, нас ждет неприятность, связанная с ростом числа ребер. При удалении вершины со степенью n, степень вершин, смежной с удаляемой, может: уменьшится на -1, не измениться, увеличится до n-2. Отсюда следует, что при удалении вершин со степенью 3 и выше, степень остальных вершин, в общем случае, растет, граф становится все менее разреженным и, в конце концов, удаление вершин превратится в довольно трудоемкую задачу. Алгоритм, в общем случае, является крайне трудоемким и практически бесполезным, но это именно в общем случае.

Графы дорожных сетей имеют уникальную особенность такого рода: многие вершины могут быть удалены не только без роста, но и с уменьшением степени смежных вершин. Причем, если некоторая вершина не может быть «успешно» удалена сейчас, она может быть «успешно» удалена позже, после удаления некоторых, смежных с ней вершин.

Соответственно, нам просто требуется на каждом шаге правильно выбирать вершины на удаление, начиная с тех, которые удаляются более «удачно».

Сам алгоритм более подробно можно посмотреть здесь. Там описано, как удалить вершину, сохраняя расстояния и пути между оставшимися. Этот процесс называется разборкой. Там описано, как восстановить потом граф обратно, добавляя вершины в обратном порядке по одной, как пересчитывать при этом МКР. Этот процесс называется сборкой.

Там же приведены результаты использования алгоритма на графах дорожных сетей США по ссылке.

Вывод

Если рассматривать дорожные сети не как графы вообще, а как графы с некоторыми особенными свойствами, можно создавать и успешно применять более эффективные алгоритмы для многих практических задач.

МАТЕМАТИЧЕСКОЕ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ВЫЧИСЛИТЕЛЬНЫХ МАШИН…

УДК 519.173.5

А. Р. Ураков, А. А. Михтанюк, Т. В. Тимеряев

БЫСТРЫЙ ПОИСК ХАРАКТЕРИСТИК ВЗВЕШЕННОГО ГРАФА ПО МАТРИЦЕ КРАТЧАЙШИХ РАССТОЯНИЙ

Предлагаются алгоритмы быстрого поиска центра, радиуса и диаметра взвешенного графа по матрице кратчайших расстояний, использующие структурированность графов реальных дорожных сетей и приводятся результаты сравнительной оценки алгоритмов с поиском характеристик простым проходом по матрице. Центр графа; радиус графа; диаметр графа; матрица кратчайших расстояний; взвешенный граф; структурированность графа

ВВЕДЕНИЕ

Одними из важных характеристик графов являются центр, радиус и диаметр. Их нахождение часто является существенным этапом при решении задач на графах, а иногда и полностью решает поставленные задачи. Во многих случаях граф изначально представлен в виде списка ребер, в случае со взвешенным графом каждому ребру дополнительно приписан вес. При таких начальных условиях для графа находят матрицу кратчайших расстояний и одновременно с этим центр, радиус и диаметр. Соответственно, нахождение указанных величин будет быстрее при ускорении поиска кратчайших расстояний. В данном случае совершенствование методов решения более общей задачи дает и более быстрое нахождение указанных параметров графа. Методы ускорения поиска кратчайших расстояний между вершинами графа рассматриваются

в [1-3].

Другой вариант задачи, когда граф уже имеет вычисленную матрицу кратчайших расстояний, но его центр, радиус и диаметр неизвестны. Такие ситуации возникают в нескольких случаях:

• изначально вычислять какую-то из характеристик не требовалось;

• матрица кратчайших расстояний графа каким-то образом изменяется, корректируется без пересчета кратчайших расстояний между всеми парами вершин;

• требуется вычислять центр, радиус и диаметр не для всего графа, а для некоторой группы вершин. При этом таких групп может быть несколько и они могут изменять свой состав.

1. ПОИСК ЦЕНТРА, РАДИУСА И ДИАМЕТРА ВЗВЕШЕННОГО ГРАФА

Задан связный неориентированный взвешенный граф О = (V, Е, м>) с неотрицательной весовой функцией V и мощность множества вершин IV = п. Для данного графа дана матрица кратчайших расстояний М = (ті}). Необходимо найти центр, радиус и диаметр данного графа.

Интересующие нас характеристики графа определяются следующим образом. Эксцентриситет вершины – максимальное из расстояний от данной вершины до других вершин. Радиус графа – минимальный из эксцентриситетов вершин связного графа; вершина, на которой достигается этот минимум, называется центральной вершиной (центром графа). Диаметр графа – это максимум расстояния между вершинами для всех пар вершин.

При вычисленной матрице кратчайших расстояний поиск центра, соответствующего ему радиуса и диаметра графа сводится к просмотру всех элементов этой матрицы и определению, соответственно, столбца, максимум значений которого минимален, и максимального элемента. Для простоты будет рассматриваться взвешенный неориентированный простой граф. Для такого вида графов сложность нахождения центра с радиусом и диаметра составляет порядка 0(п2). Здесь п – количество вершин в графе.

При постройке дорожных сетей реального мира с себестоимостью прокладывания пути от одного узла до другого, человек структурирует сеть с целью минимизации затрат. Далее предлагаются алгоритмы, использующие эту структурированность для уменьшения времени поиска характеристик графов этих сетей.

Контактная информация: 8-917-751-30-10

А. Р. Ураков, А. А. Михтанюк, Т. В. Тимеряев • Быстрый поиск характеристик взвешенного графа.

165

1.1. Алгоритм быстрого поиска центра и радиуса

Алгоритм быстрого поиска центра и радиуса состоит из двух частей: ускорение поиска и непосредственно сам поиск центра и радиуса.

Ускорение поиска

На этапе ускорения ищется пара вершин (х,у), каждая из которых является самой удаленной для другой

х, у: т„, = тах ту = тах тХх.

7 ^ ху . -— гу . :— гх г =1,п г =1,п

Для этого выбирается любая вершина графа и обозначается р1, далее ищется вершина

Р,: тр, р, = тах тр1г.

i =1,’

Поиск вершин p;+1 продолжается до тех пор, пока не будет выполнено равенство p;-1 = p;+1. В случае если равенство выполнено, полагаем

x = Pj y = p+1.

Поиск центра и радиуса

Шаг 1. Поиск центра состоит в последовательном рассмотрении претендентов на центр. Первый претендент на центр c ищется как вершина, максимум удаления которой от пары (x, y) минимален

c: max(mcx,mcy) = min(max(miX, my)).

i=1,n

После нахождения c величина r = = max(mcx, mcy) является первым приближением радиуса графа.

Шаг 2. Для проверки c на центр ищется периферийная вершина

z: mZc = max mw.

i =1, n

Утверждение. Если mzc = r, то r – радиус, а c – один из центров графа.

Доказательство. Дано

max mic = r = min(max( mix, miy)),

i=1,n i=1,n

То есть r – максимальное расстояние от c до любой другой вершины, но в то же время r -минимальное расстояние до одной (а возможно, и обоих) из вершин (x, y). Поэтому для любой другой вершины d максимум расстояния до одной вершины из пары (x, y) будет не меньше r < < max(mdx, mdy). Следовательно, c – центр, хотя в общем случае и не единственный.

Если mzc > r, радиус графа R лежит в пределах r < R < mzc и необходимо выбрать другого претендента на центр. Перед тем как искать

следующего претендента, производится попытка ускорения поиска. Ищется вершина t: mzt > > mxy. Если вершина, удовлетворяющая этим условиям, найдена, то x = z, y = t и переходим к шагу 1 поиска центра и радиуса. Если же такая вершина не была найдена, ищем нового претендента на центр. Среди нерассмотренных на центр вершин находится вершина

d : max(m«x, mdy, mdz) = min(max(miX, mv, mlz)).

i =1, n

Если максимальное расстояние от этой вершины до других меньше, чем текущая верхняя граница радиуса max mdi < mzc, то d – новый

i =1, n

претендент на центр (c = d), переходим к шагу 2 поиска центра и радиуса. Если max mdi = mzc, то

i =1,n

c – центр, а r – радиус. Если maxmdi > mzc, то

i =1,n

заново ищем вершину d, помечая текущую как рассмотренную на центр.

1.2. Алгоритм быстрого поиска диаметра

Алгоритм быстрого поиска диаметра устроен подобно алгоритму поиска центра и радиуса. Так же, как и при поиске центра, ищем пару вершин (x, y), каждая из которых является самой удаленной для другой. Величина d = mxy при этом является текущим претендентом на диаметр. Далее, таким же образом, как и в алгоритме поиска центра и радиуса, ищется вершина c, максимум удаления которой от пары вершин (x, y) минимален среди всех остальных вершин. После этого диаметр ищется в столбцах матрицы только тех вершин i, для которых выполнено неравенство mci > d/2.

Утверждение. Диаметр графа D = d или находится в столбцах матрицы кратчайших расстояний тех вершин i, для которых выполнено неравенство mci > d/2.

Доказательство. Если d = mxy не является диаметром графа, то существует пара вершин z, t: mzt > mxy. Для матрицы кратчайших расстояний справедливо mzt < mzc + mct. Следовательно, m^ =2*d/2 < mzc + mct, то есть необходимо либо mzc>d/2, либо mct > d/2.

2. РЕЗУЛЬТАТЫ

Сравнение предложенных алгоритмов быстрого поиска (БП) с простым проходом по матрице кратчайших расстояний (ПМ) было проведено на 20 графах реальных дорожных сетей, характеристики которых приведены в таблице

ниже. Производилось вычисление отдельно центра с радиусом и диаметра, а также их совместное нахождение. Для уточнения результатов вычисления производились несколько раз, в таблицах представлены средние значения времени поиска. Так как тестовые графы обладают небольшим количеством вершин, при сравнении каждый метод выполнялся 1000 раз и замерялось общее время выполнения. Тестирование производилось на ПК с процессором Intel Core 2 Duo E8400.

Результаты испытаний и характеристики тестовых графов

Вершин Центр, радиус Диаметр Центр, радиус и диаметр

ПМ, с БП, с ПМ, с БП, с ПМ, с БП, с

528 1,4 G,G15 G,64 G,G15 1,5 G,G16

8i4 3,5 G,G47 1,5 G,G31 3,6 G,G31

1291 8,2 G,G47 4,1 G,G47 8,4 G,G62

Ш2 8,5 G,G47 4,1 G,G31 8,7 G,G62

Ш1 13 G,G63 6,2 G,G47 13 G,G63

1б41 13 G,23 6,5 G,G78 13 G,26

1б45 13 G,13 6,6 G,G93 14 G,2G3

187G 18 G,11 8,7 G,G78 18 G,13

2G59 21 4,2 Ш G,2G3 22 4,3

215G 23 G,G94 11 G,G62 23 G,G94

2194 24 G,G93 12 G,G78 25 G,G93

228G 24 G,16 13 G,1G9 25 G,2G3

2424 29 G,14 14 G,1G9 3G G,19

2484 3G G,81 15 G,1G9 32 G,83

2542 31 G,19 16 G,G94 32 G,22

289б 42 G,45 2G G,14 44 G,5

2921 42 G,1G9 21 G,G94 43 G,16

29б4 42 1,7 21 G,13 43 1,8

3G6G 44 G,25 22 G,11 45 G,23

33б4 55 G,23 27 G,2G4 56 G,28

Алгоритм быстрого поиска центра и радиуса справляется с задачей в среднем в 150 раз быстрее, чем простой проход по матрице кратчайших расстояний, ускорение времени вычисления варьируется от 5 до 380 раз. Для поиска диаметра эти цифры – в 125 раз, от 40 до 220 раз; для совместного поиска центра, радиуса и диаметра – в 135 раз, от 5 до 270 раз.

По таблице можно заметить значительную (0,75) корреляцию между временем поиска диаметра предложенным алгоритмом и количеством вершин в графе.

ЗАКЛЮЧЕНИЕ

В статье предложены точные, не эвристические алгоритмы быстрого поиска центра, радиуса и диаметра взвешенного графа по матрице кратчайших расстояний. Представленные алгоритмы на тестовых графах нашли центр и радиус в среднем в i5G раз, диаметр в i25 раз, а совместно центр, радиус и диаметр в i35 раз быстрее в сравнении с нахождением этих величин простым проходом по матрице кратчайших расстояний.

Предложенные алгоритмы не гарантируют ускорения вычисления указанных характеристик для произвольных графов, можно построить граф, на котором ускорения не будет. Но в реальности дорожная сеть, представленная таким графом, будет экономически невыгодной или даже не реализуемой.

СПИСОК ЛИТЕРАТУРЫ

1. Johnson D.B. Efficient algorithms for shortest paths in sparse graph // Journal of the ACM. 1977. № 24. P. i-i3.

2. Galil Z., Margalit O. All pairs shortest distances for graphs with small integer length edges // Information and Computation. 1997. № i34. P. Ш3-139.

3. Zwick U., Shoshan A. All pairs shortest paths in undirected graphs with integer weights // Proceedings of the 4Gth IEEE Symposium on Foundations of Computer Science, IEEE Computer Society, 1999. P. 6G5-614.

ОБ АВТОРАХ

Ураков Айрат Ренатович, доц. каф. компьютеры. математики УГАТУ. Дипл. инженер-системотехник (МГТУ, i993). Канд. физ.-мат. наук по применению вычислительн. техники, математическ. моделирования и математическ. методов в научных исследованиях (БашГУ, i997). Иссл. в обл. применения численных методов и верификации данных.

Михтанюк Алэна Александровна, доц. той же каф. Дипл. инженер-системоаналитик (УГАТУ, i995). Канд. техн. наук по САПР (УГАТУ, 2GG3). Иссл. в обл. методов оптимизации.

Тимеряев Тимофей Валерьевич, асп. той же каф. Дипл. магистр прикл. матем. и инф. (УГАТУ, 2Gii). Иссл. в обл. теории графов.

Определение

Эксцентриситетом вершины называется расстояние до самой дальней вершины графа.

Радиусом графа называется минимальный эксцентриситет среди всех вершин графа

Диаметром графа – это наибольшее расстояние между всеми парами вершин графа

Центральной вершиной графа является вершина чей эксцентриситет равен радиусу графа.

Периферийной вершиной графа является вершина чей эксцентриситет равен диаметру графа.

Поиск радиуса и диаметра

Сервис граф онлайн позволит вам найти радиус и диаметр, а также укажет центральные и периферийные вершины. Для этого выберете пункт меню Алгоритмы -> Поиск радиуса и диаметра графа.

Реализацию алгоритма на JavaScript можно найти по ссылке: http://graphonline.ru/script/plugins/RadiusAndDiameter.js