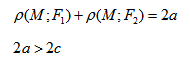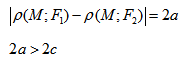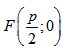Как найти центр канонической системы координат - Сайт, где вы сможете решить свои вопросы

Макеты страниц

Пусть в произвольной аффинной системе координат дана кривая

и прямая

неасимптотического направления; обозначим через точки пересечения кривой (1) с прямой (2).

Решим следующую задачу: когда хорда, имеющая направление делится в точке пополам? Другими слонами, когда точка является серединой отрезка

Для этого, очевидно, необходимо и достаточно, чтобы было

Но

Подставляя эти значения в (3), получаем

т. е.

Так как (как координаты направляющего вектора прямой ) не могут быть равны нулю одновременно, то условие (3) равносильно условию

Но и суть корни квадратного уравнения

значит, и условие (4) означает или

Это и есть условие для того, чтобы точка была отрезка т. е. хорды, высекаемой кривой (1) из прямой (2).

Определение центра. Напомним прежде всего, что точкой, имметричной точке относительно точки называется точка , обладающая тем свойством, что точка С есть середина отрезка ММ.

Координаты точки М однозначно определяются из условий . Точка С называется центром симметрии (или просто центром) данной линии, если, какова бы ни была точка , лежащая на этой линии, точка М, симметричная точке М относительно точки С, также лежит на данной линии (рис. 172).

Рис. 172.

Эти определения сохраняют силу и для комплексной плоскости.

Докажем следующее предложение.

Теорема 7. Для того чтобы точка была центром, кривой (1), необходимо и достаточно, чтобы координаты этой точки удовлетворяли следующим уравнениям (называемым ниями ):

Доказательство. А. Условие необходимо. Пусть есть центр кривой (1), и пусть хотя бы одно из двух чисел отлично от нуля. Приведем это предположение к противоречию. Рассмотрим равенство (5) как уравнение относительно . Переписывая его как пропорцию

видим, что оно удовлетворяется векторами лишь одного направления, а именно направления

Между тем для любого неасимптотического направления (а таковыми являются все направления, кроме двух) условие (5) должно быть выполнено (так как прямая (2) этого направления пересекает кривую (1) в двух точках и точка есть середина отрезка ).

Противоречие получено, необходимость нашего условия доказана.

Б. Условие достаточно. Пусть точка удовлетворяет условию (6). Перенесем начало координат в точку выполним преобразование координат

Оно переводит уравнение в уравнение , где

Но ввиду равенств (6) последнее уравнение имеет вид

В этом уравнении отсутствуют члены первой степени, откуда следует, что новое начало, т. е. точка есть центр симметрии нашей кривой. Теорема доказана.

Из доказанного вытекает, что в центральном случае, т. е. когда

кривая (1) имеет единственный центр симметрии координаты которого и находятся из уравнений (6).

Если центральная кривая задана своим уравнением в канонической системе координат, то начало координат и есть, как мы теперь знаем, единственный центр кривой.

Заметим вообще, что уравнения (6) имеют силу для любой аффинной системы координат. Поэтому для определения центра какой-либо кривой мы можем ограничиться рассмотрением ее уравнения в канонической для нее координатной системе.

Единственным центром пары пересекающихся прямых является их точка пересечения: это сразу следует из канонического уравнения

В параболическом случае мы имеем или параболу, ее каноническое уравнение есть

Или пару параллельных (в широком смысле) прямых

Для параболы, заданной уравнением (8), уравнения центра приобретают вид

Уже первое из этих уравнений противоречиво (так как поэтому система (10) несовместна — у параболы центра нет.

Для пары параллельных прямых, заданных уравнением (9), уравнения (6) имеют вид

Они определяют прямую все точки которой и являются центрами симметрии пары прямых (9), что очевидно и геометрически: пара параллельных прямых имеет прямую центров (это — средняя прямая между двумя данными).

Источник

Определение
9.1. Центром
линии второго порядка называется центр
симметрии этой линии.

ТЕОРЕМА
9.1. Пусть
относительно аффинной системы координат
задана линия второго порядка общим
уравнением

Для
того чтобы начало координат являлось
ее центром, необходимо и достаточно,
чтобы в уравнении

отсутствовали
члены с

в
первой степени, т.е. чтобы

,
иначе, чтобы уравнение линии имело
вид

Доказательство
достаточности. Если

,
то уравнение линии имеет вид

,
и если ему удовлетворяют
координаты

точки

,
то ему удовлетворяют и координаты

точки

,
симметричной точке

относительно
начала координат.

Доказательство
необходимости. Пусть
начало координат является центром
линии

.
Возьмем на линии произвольную точку

.
Ее координаты удовлетворяют уравнению

,
а так как начало координат

является
центром симметрии линии, то этому
уравнению удовлетворят и координаты
точки

,
симметричной точке

относительно
начала координат, т.е.

Вычитая
из

соотношение

,
находим, что координаты всех точек линии
удовлетворяют уравнению

.
Следовательно, уравнение линии приводится
к виду

,
то есть не

содержит членов с

в
первой степени.

ТЕОРЕМА
9.2. Если
относительно аффинной системы координат
задана линия второго порядка общим
уравнением

то
координаты

ее
центра определяются из системы
уравнений

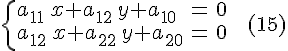
причем
в случае несовместности этой системы
линия не имеет центра (т.е. является
параболой).

Доказательство. Произведем
перенос данной системы координат так,
чтобы новым началом стала точка

.
В новой системе координат уравнение
линии

будет
иметь вид (согласно формулам

По
предыдущей теореме точка

является
центром данной линии тогда и только
тогда, когда

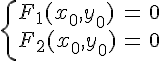
или
подробнее

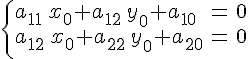
Определение
9.2. Любая
кривая второго порядка, имеющая
единственный центр называется
центральной.

Следовательно, кривая
является центральной, если

Замечание
9.1. При
приведении центральных кривых к
каноническому виду целесообразно
пользоваться следующим планом:

1. Найти
центр кривой.

2. Выполнить
параллельный перенос в центр и записать
уравнение кривой в перенесенной системе
координат

3. Повернуть
перенесенную систему координат на
угол

и
получить каноническую систему координат.

10 Пересечение кривой второго порядка с прямой. Асимптотические направления относительно кривой второго порядка

Пусть
задана кривая второго порядка общим
уравнением

и
прямая

параметрическими
уравнениями

Найдем
точки пересечения этой прямой с кривой
второго порядка.

Для этого подставим
значения переменных

из
уравнений

в
уравнение

.
Получаем уравнение с одним неизвестным

Преобразуем
его к виду

Введем
обозначения:

В
этих обозначениях, полученное уравнение,
запишется более просто, а именно

Находя
корни уравнения

,
и подставляя их в уравнения

,
мы получим координаты точек пересечения
кривой второго порядка и прямой

.
При этом возможны следующие случаи:

.
Следовательно,

–
квадратное уравнение, а поэтому оно
имеет два корня (вещественных или
комплексных),значит, прямая пересекает
КВП в двух точках(вещественных или
комплексно-сопряженных).

.
Тогда уравнение

примет
вид

a). Если

,
то прямая пересекает кривую в единственной
действительной точке.

b). Если

,
то прямая не имеет с кривой ни одной
общей точки(ни действительной, ни
мнимой).

c). Если

,
тогда любое значение

является
решением уравнения

,
а потому

лежит
на кривой второго порядка.

Определение
10.1. Множество
всех прямых, из которых любые две
параллельны, называется направлением.

Отметим,
что направление можно определить любым
направляющим вектором каждой из этих
прямых. Заметим, что коэффициент в
уравнении

зависит
только от направления прямой

и
не зависит от координат точки

,
лежащей на прямой.

Определение
10.2. Направление,
определяемое ненулевым вектором

,
называется асимптотическим направлением
относительно кривой второго порядка,
если любая прямая, параллельная
вектору

,
либо имеет с кривой не более одной общей
точки, либо содержится в кривой.

Из
предыдущего следует: направление,
определяемое ненулевым вектором

,
является асимптотическим направлением
относительно кривой второго порядка

,
тогда и только тогда, когда

Пользуясь
этой формулой, легко найти асимптотические
направления относительно кривой второго
порядка.

Если

,
то из

следует,
что

(
так как

—
ненулевой вектор), поэтому из

,
обозначая через

получаем

Отсюда
находим

Если
же

,
то уравнение

примет
вид

.
Этому уравнению удовлетворяют координаты
векторов

Выясним
теперь, сколько существует различных
асимптотических направлений относительно
кривой второго порядка.

Рассмотрим
три случая.

и,
значит,

.
Из формулы

мы
заключаем, что относительно кривой
второго порядка не существует
асимптотических направлений.

.
В этом случае существует два различных
асимптотических направления.

В самом
деле, если

,
то этот вывод следует из формулы

,
а если

,
то из

.
(Заметим, что в последнем случае

,
поэтому векторы из

не
коллинеарны.)

.
Очевидно, что в этом случае имеем
единственное асимптотическое направление,
определяемое вектором

.
Действительно, если

,
то это вытекает из

,
а если

,
то из

.
(Заметим, что в последнем случае

,
поэтому векторы из

коллинеарны.)

Ранее
было показано, что

не
зависит от выбора системы координат. В
соответствии с таблицей значений
инвариантов и количеством асимптотических
направлений принято разделять кривые
второго порядка на три
класса:

эллиптические

, гиперболические

и параболические

Определение
10.3. Асимптотой
кривой второго порядка называется
прямая асимптотического направления,
которая либо лежит на кривой, либо не
имеет с ней общих точек.

ТЕОРЕМА
10.1. Асимптота
к кривой гиперболического типа задается
уравнением

где

удовлетворяют

Доказательство. Запишем
уравнение

в
виде

или
в эквивалентной форме

Отметим
сначала, что это уравнение является
уравнением первой степени. Действительно,
предположим, что

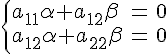
Откуда
следует, что

,
так как

.
А это противоречит тому, что вектор,
удовлетворяющий

,
ненулевой. Теперь необходимо проверить,
что прямая

имеет
асимптотическое направление, т.е. надо
убедится

в том, что вектор

имеет
асимптотическое направление. Действительно,
так как

—
вектор асимптотического направления,
то он удовлетворяют равенству

которое
равносильно

Таким
образом, вектор

коллинеарен
вектору асимптотического направления,
а значит, имеет асимптотическое
направление. Итак, прямая, заданная
уравнением

имеет
асимптотическое направление.

Кроме
того, если точка лежит на этой прямой,
то ее координаты

удовлетворяют
уравнению

Рассмотрим
выражение

Что
и требовалось доказать.

Замечание
10.1. Если
в общем уравнении кривой второго порядка
гиперболического типа

,
то уравнения

асимптот можно искать
в виде

где

определяются
по формуле

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

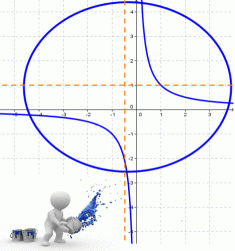
Кривая второго порядка – это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:

Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах – при вторых степенях одновременно не нули.

или можно встретить следующую форму записи:

К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.

Покажем на примере определение значений коэффициентов.

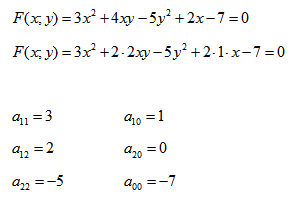
Рассмотрим кривую второго порядка:

Вычислим определитель из коэффициентов:

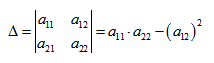
Если Δ = 0, кривая второго порядка параболического типа,

если Δ > 0, кривая второго порядка эллиптического типа,

если Δ < 0, кривая второго порядка гиперболического типа.

Эллипс – множество точек на плоскости, сумма расстояний от каждой из которых до двух данных точек F₁ и F₂ есть величина постоянная, большая расстояния между этими точками.

F₁ и F₂ – фокусы.

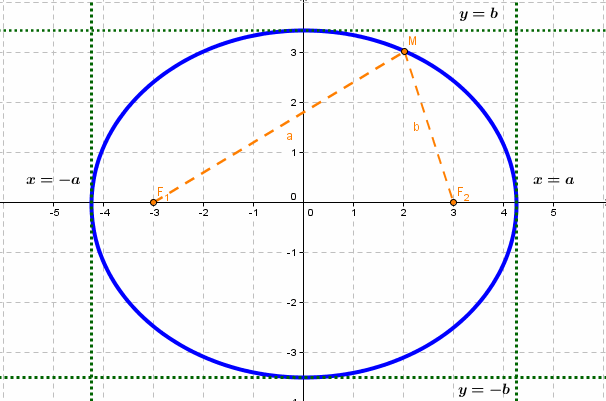с – фокальное расстояние,

F₁(-c;0) – левый фокус,

F₂(c;0) – правый фокус.

Каноническое уравнение эллипса с центром симметрии в начале координат:

2а – большая ось эллипса, 2b – малая ось эллипса.

а – большая полуось эллипса, b – малая полуось эллипса.

Если a = b, то имеем окружность с радиусов R = a = b:

Если центр эллипса находится не в начале координат, а в некоторой точке C(x₀;y₀), оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид:

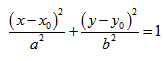
Эксцентриситет – число, равное отношению фокального расстояния к большей полуоси:

Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.

Гипербола – множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F₁ и F₂ есть величина постоянная, меньшая расстояния между этими точками.

F₁ и F₂ – фокусы.

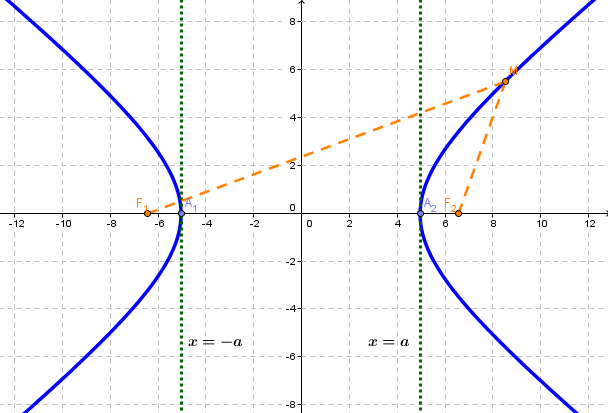с – фокальное расстояние,

F₁(-c;0) – левый фокус,

F₂(c;0) – правый фокус.

А₁(-а;0), А₂(а;0) – вершины.

Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.

Каноническое уравнение гиперболы с центром симметрии в начале координат:

x – действительная ось, y – мнимая ось.

а – действительная полуось, b – мнимая полуось.

Если центр гиперболы находится в некоторой точке C(x₀;y₀), оси симметрии параллельны осям координат, то каноническое уравнение имеет вид:

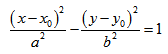
Эксцентриситет гиперболы – число, равное отношению фокусного расстояния к действительной полуоси.

Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.

Директриса гиперболы – прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.

f₁ – правая директриса, f₂ – левая директриса.

Уравнения директрис:

Порядок построения гиперболы:

1. Строим прямоугольник со сторонами 2a и 2b.

2. Провести асимптоты гиперболы – диагонали построенного прямоугольника.

3. Строим гиперболу с вершинами в точках А₁(-а;0), А₂(а;0).

Парабола – множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.

F – фокус параболы, f – директриса параболы.

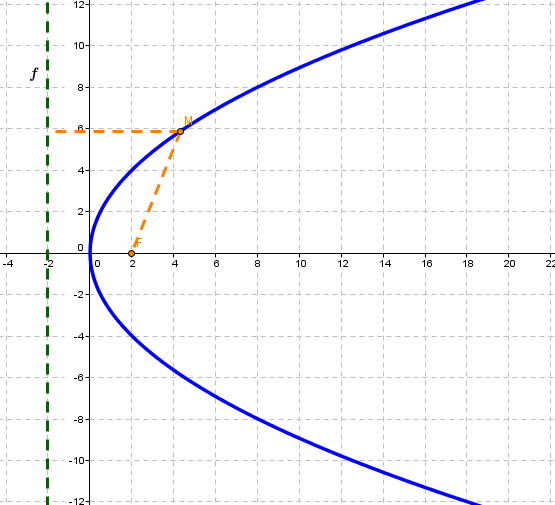р – фокальное расстояние

Фокус параболы:

Директриса параболы:

Пример по теме кривые второго порядка №1

Привести к каноническому виду и построить график кривой второго порядка.

Пример по теме кривые второго порядка №2

По виду уравнения определить тип кривой и нарисовать ее в декартовой системе координат:

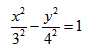
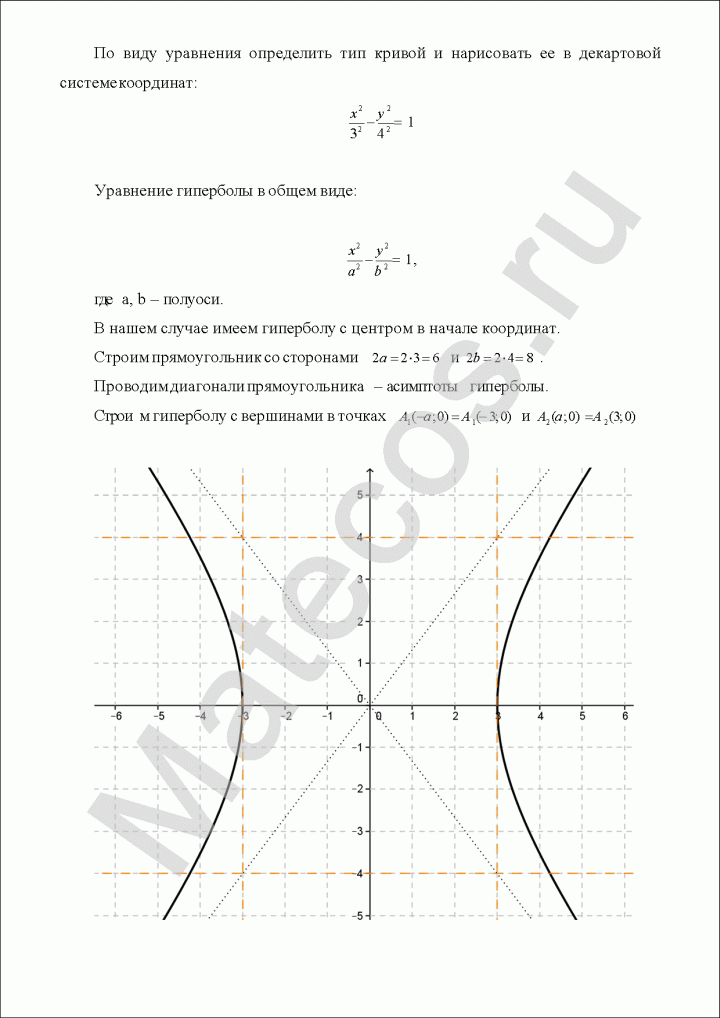
Пример по теме кривые второго порядка №3

Построить кривую второго порядка:

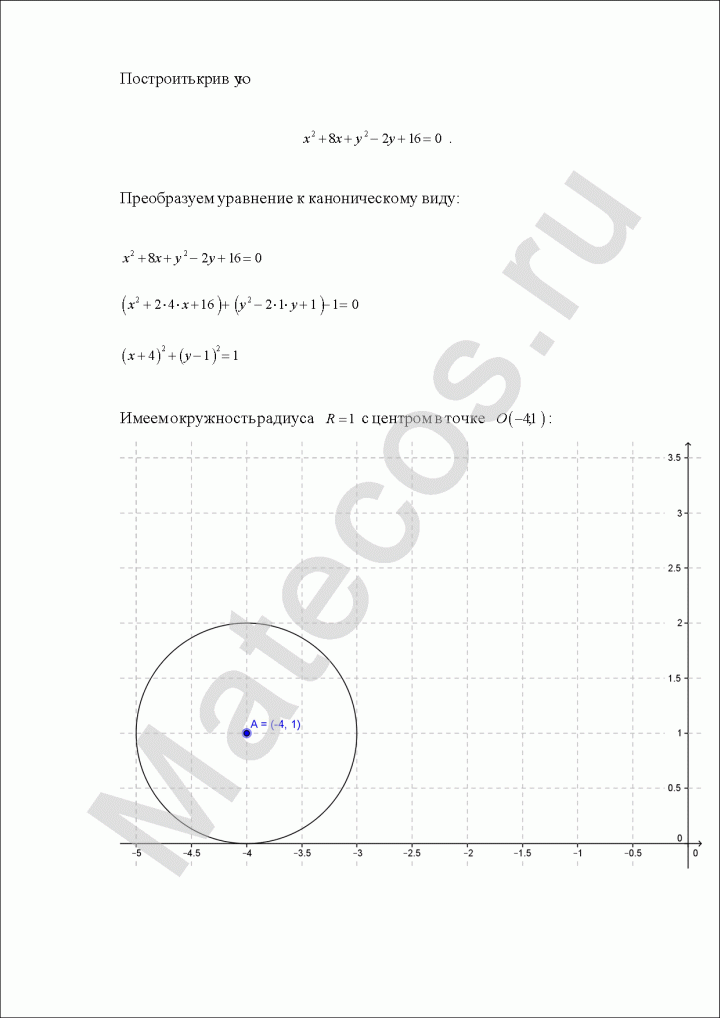
Пример по теме кривые второго порядка №4

Построить кривую второго порядка:

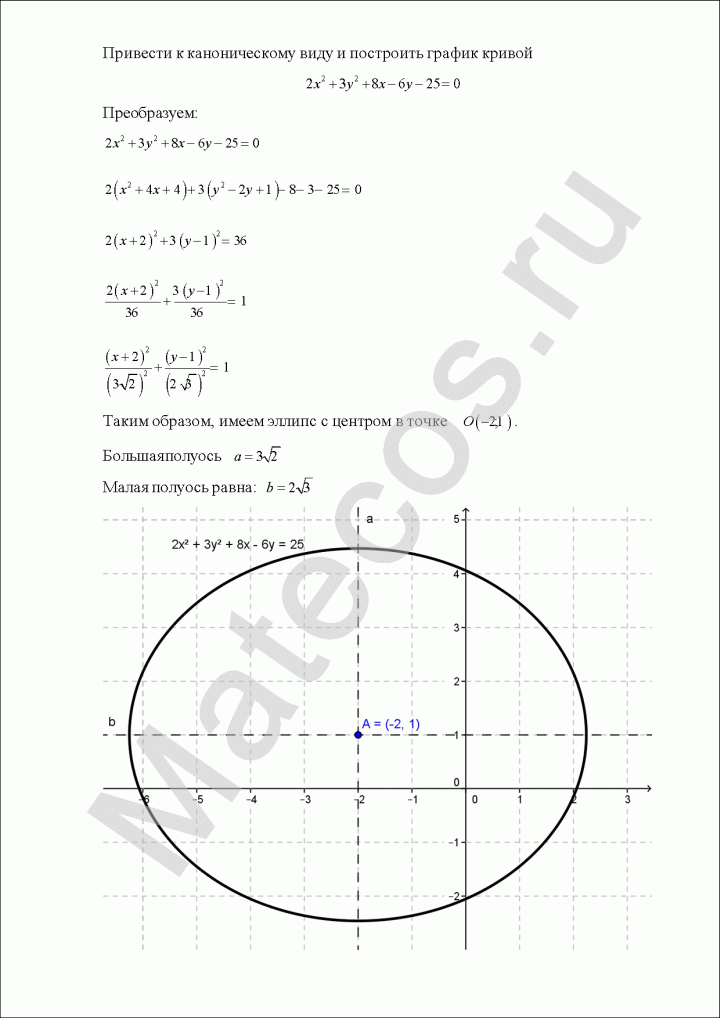
Пример по теме кривые второго порядка №5

Провести заданное уравнение линии второго порядка к каноническому виду и построить ее:

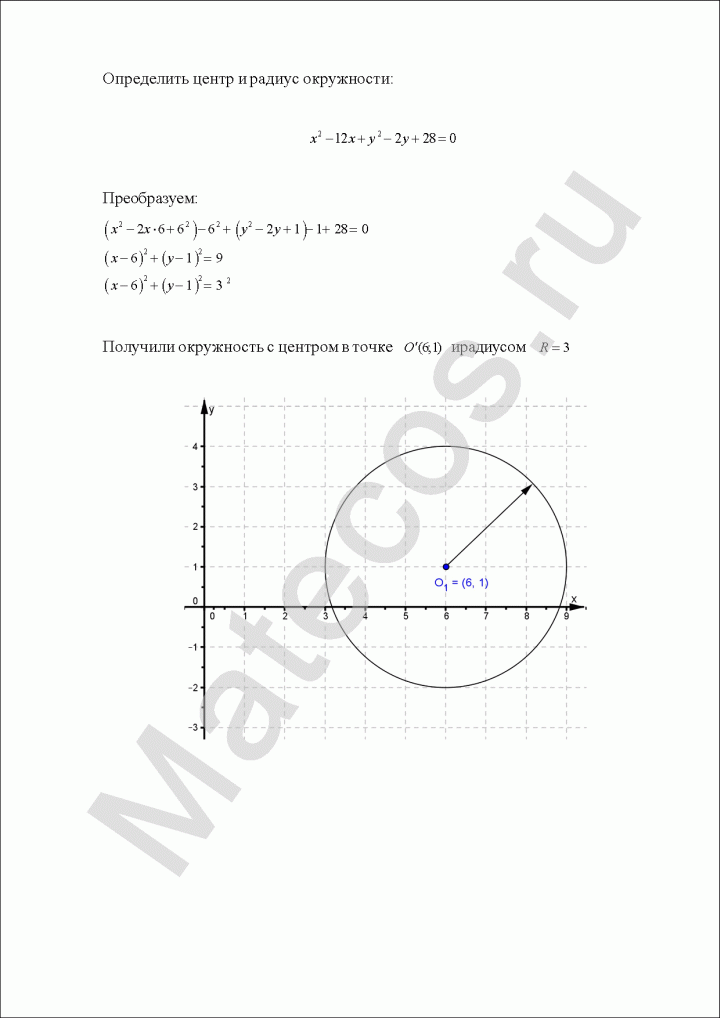
Пример по теме кривые второго порядка №6

Определить центр и радиус окружности:

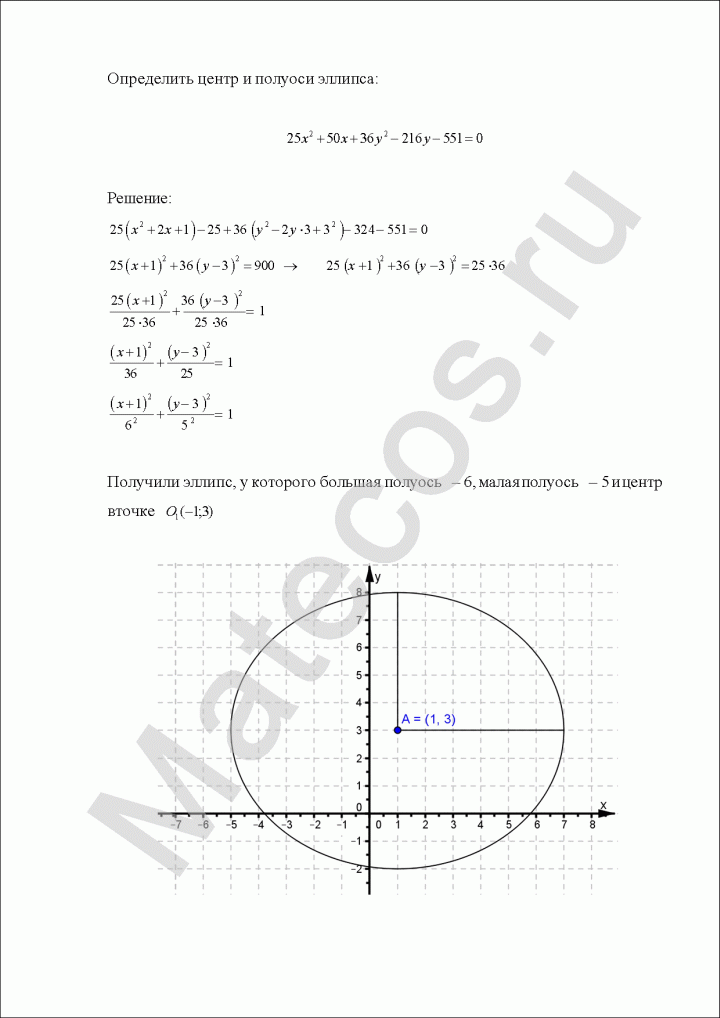
Пример по теме кривые второго порядка №7

Определить центр и полуоси эллипса:

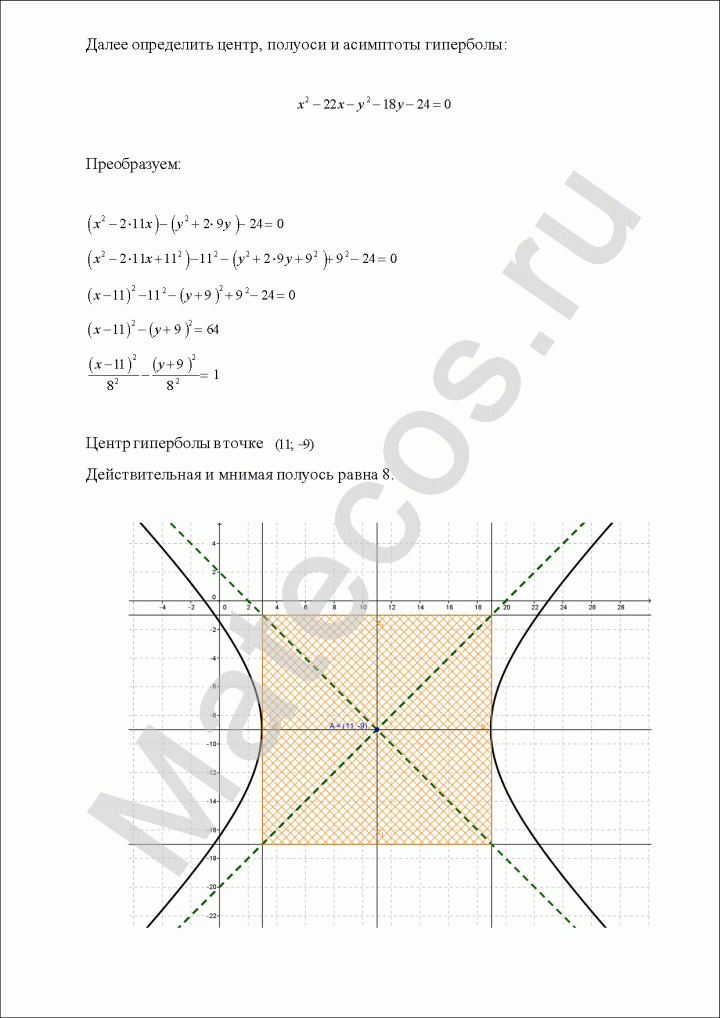
Пример по теме кривые второго порядка №8

Определить центр, полуоси и асимптоты гиперболы:

Пример по теме кривые второго порядка №9

Составить уравнение и построить линию, расстояние каждой точки которой от точки A(-1;0) вдвое меньше расстояния ее от прямой x=-4

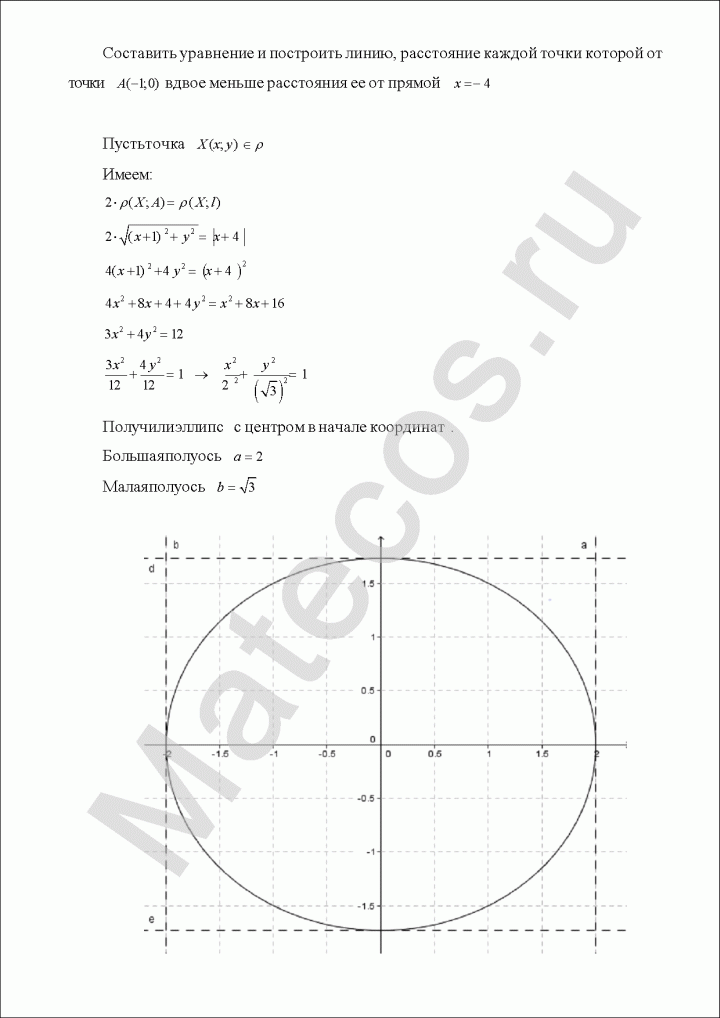
Пример по теме кривые второго порядка №10

Определить тип кривой второго порядка:

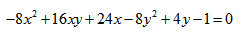
Пример по теме кривые второго порядка №11

Дана кривая:

Докажите, что эта кривая – эллипс.

Найдите координаты центра симметрии.

Найдите его большую и малую полуоси.

Запишите уравнение фокальной оси.

Постройте данную кривую.

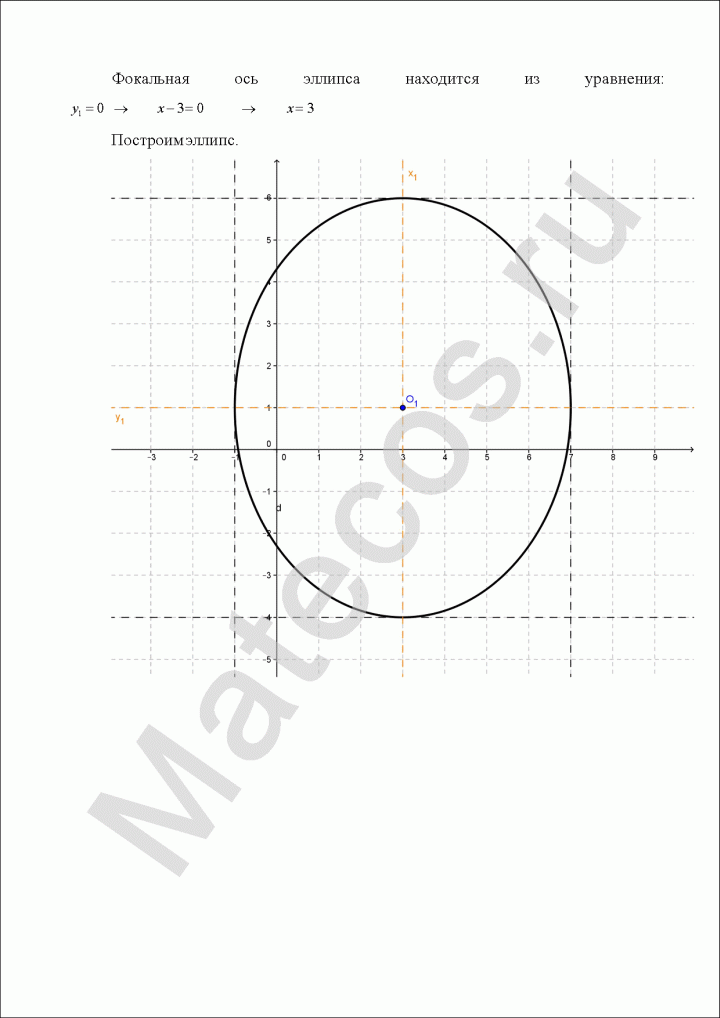
Пример по теме кривые второго порядка №12

Дана кривая:

Доказать, что данная кривая – парабола.

Найти координаты вершины параболы.

Найдите значение ее параметра.

Запишите уравнение оси симметрии параболы.

Постройте данную параболу.

Пример по теме кривые второго порядка №13

Дана кривая:

Докажите, что кривая – гипербола.

Найдите координаты центра симметрии гиперболы.

Найдите действительную и мнимую полуоси гиперболы.

Запишите уравнение фокальной оси гиперболы.

Найдите данную гиперболу.

Пример по теме кривые второго порядка №14

Все графике в этой статье были построены в Geogebra.Подробно о построении графиков функции быстрым и удобным способом читать тут:

Источник

Приведение уравнения поверхности 2-го порядка
к каноническому виду по инвариантам

Рассмотрим задачу приведения к каноническому виду уравнения поверхности второго порядка, заданной в прямоугольной системе координат Oxyz уравнением (4.67):

$a_{11}x^2+a_{22}y^2+a_{33}z^2+2a_{12}xy+2a_{13}xz+2a_{23}yz+2a_1x+2a_2y+2a_3z=0.$

(4.73)

Требуется определить один из семнадцати возможных канонических видов поверхности (см. теорему 4.3), найти каноническую систему координат O'x'y'z' , в которой уравнение поверхности имеет канонический вид, а затем построить поверхность в канонической и исходной системах координат. Построение, разумеется, производится только для вещественных поверхностей.

Алгоритм приведения уравнения поверхности 2-го порядка к каноническому виду

Для приведения поверхности второго порядка, заданной в прямоугольной системе координат Oxyz уравнением (4.73), к каноническому виду нужно выполнить следующие действия.

1. По уравнению (4.73) поверхности второго порядка составить матрицу квадратичной функции, матрицу квадратичной формы и столбец коэффициентов линейной формы:

$P= begin{pmatrix}a_{11}&a_{12}&a_{13}&a_1\a_{12}&a_{22}&a_{23}&a_2\a_{13}&a_{23}&a_{33}&a_3\a_1&a_2&a_3&a_0end{pmatrix}!, quad A=begin{pmatrix}a_{11}&a_{12}&a_{13}\a_{12}&a_{22}&a_{23}\a_{13}&a_{23}&a_{33}end{pmatrix}!, quad a=begin{pmatrix} a_1\a_2\a_3end{pmatrix}!.$

2. Составить характеристическое уравнение -lambda^3+tau_1lambda^2-tau_2lambda+delta=0 , либо вычисляя его коэффициенты по формулам: $tau_1=a_{11}+a_{22}+a_{33}$ ,

Продолжение

$tau_2= ,,vline,begin{matrix}a_{11}&a_{12}\a_{12}&a_{22}end{matrix},vline,,+ ,,vline,begin{matrix}a_{11}&a_{13}\a_{13}&a_{33}end{matrix},vline,,+,,vline,begin{matrix}a_{22}&a_{23}\a_{23}&a_{33}end{matrix},vline,,,quad delta=det A=,,vline,begin{matrix}a_{11}&a_{12}&a_{13}\a_{12}&a_{22}&a_{23}\a_{13}&a_{23}&a_{33}end{matrix},,vline,,$

либо разлагая определитель

$det(A-lambdacdot E)= ,,vline,begin{matrix}a_{11}-lambda&a_{12}&a_{13}\a_{12}&a_{22}-lambda&a_{23}\a_{13}&a_{23}&a_{33}-lambdaend{matrix},,vline,= -lambda^3+tau_1cdotlambda^2-tau_2cdotlambda+delta.$

Найти корни lambda_1,,lambda_2,,lambda_3 (с учетом кратности) характеристического уравнения.

Вычислить инвариант

$Delta=det{P}= ,,vline,begin{matrix} a_{11}&a_{12}&a_{13}&a_1\ a_{12}&a_{22}& a_{23}&a_2\ a_{13}&a_{23}&a_{33}&a_3\a_1&a_2&a_3&a_0end{matrix},,vline,.$

Если delta=Delta=0 , то вычислить семиинвариант

$kappa_2= ,,vline,begin{matrix} a_{11}&a_{12}&a_1\ a_{12}&a_{22}&a_2\ a_1&a_2&a_0end{matrix},,vline,+ ,,vline,begin{matrix} a_{11}&a_{13}&a_1\ a_{13}&a_{33}&a_3\ a_1&a_3&a_0end{matrix},,vline,+ ,,vline,begin{matrix} a_{22}&a_{23}&a_2\ a_{23}&a_{33}&a_3\a_2&a_3&a_0end{matrix},,vline,.$

Если delta=Delta=0 и tau_1=tau_2=0 , то вычислить семиинвариант

$kappa_1= ,,vline,begin{matrix}a_{11}&a_1\a_1&a_0end{matrix},,vline,+ ,,vline,begin{matrix}a_{22}&a_2\a_2&a_0end{matrix},,vline,+ ,,vline,begin{matrix}a_{33}&a_3\a_3&a_0end{matrix},,vline,.$

3. По таблице 4.3 определить вид поверхности.

4. Занумеровать корни lambda_1,,lambda_2,,lambda_3 характеристического уравнения в соответствии с правилами:

Продолжение

б) если поверхность гиперболического типа, то обозначить через lambda_1 и lambda_2 корни одного знака так, чтобы |lambda_1|leqslant|lambda_2| , а через lambda_3 — корень противоположного знака;

в) если поверхность параболического типа, то

– если нулевой корень двойной, то lambda_1=lambda_3=0 и lambda_2ne0 ;

– если нулевой корень простой, а ненулевые корни одного знака, то lambda_3=0 и |lambda_1|leqslant|lambda_2| ;

– если нулевой корень простой, а ненулевые корни разных знаков, то lambda_3=0 и

либо lambda_1>0 , если Deltane0 или Delta=kappa_2=0 ; либо lambda_1cdotkappa_2>0 , если Delta=0 и kappa_2ne0 .

5. Найти взаимно ортогональные собственные направления l_1,,l_2,,l_3 , соответствующие корням lambda_1,,lambda_2,,lambda_3 характеристического уравнения:

Продолжение

а) если lambda_1=lambda_2=lambda_3 , то базисные векторы исходной системы имеют искомые направления

$l_1=begin{pmatrix}1&0&0end{pmatrix}^T, quad l_2=begin{pmatrix}0&1&0end{pmatrix}^T, quad l_3=begin{pmatrix}0&0&1end{pmatrix}^T;$

б) если все корни lambda_1,,lambda_2,,lambda_3 простые, то для каждого корня найти ненулевое решение однородной системы уравнений (A-lambda_icdot E)cdot l_i=o, i=1,2,3 . Например, собственное направление $l_3=begin{pmatrix}x_3&y_3&z_3end{pmatrix}^T$ для простого корня lambda_3 находится как любое ненулевое решение системы

$begin{cases}(a_{11}-lambda_3)cdot x+a_{12}cdot y+a_{13}cdot z=0,\[3pt] a_{12}cdot x+(a_{22}-lambda_3)cdot y+a_{23}cdot z=0,\[3pt] a_{13}cdot x+a_{23}cdot y+(a_{33}-lambda_3)cdot z=0;end{cases}$ или (A-lambda_3cdot E)cdot l_3=o.

Если lambda_3=0 и корни lambda_1 и lambda_2 имеют разные знаки (lambda_1cdotlambda_2<0) , то направление l_3 должно удовлетворять дополнительному условию a^Tcdot l_3leqslant0 , в противном случае следует заменить столбец l_3 на противоположный (-l_3) .

Если lambda_3=0 и корни lambda_1 и lambda_2 одного знака (lambda_1cdotlambda_2>0) , то направление l_3 должно удовлетворять дополнительному условию tau_1cdot a^Tcdot l_3<0 , в противном случае следует заменить столбец l_3 на противоположный (-l_3) ;

в) если имеется двойной ненулевой корень lambda_1=lambda_2nelambda_3 , то для простого корня найти соответствующий собственный вектор l_3 — любое не нулевое решение системы (A-lambda_3cdot E)cdot l_3=o , а для кратного корня в качестве l_2 взять любой ненулевой столбец матрицы , а вектор l_1 найти, используя векторное произведение: $vec{l}_1=[,vec{l}_2,vec{l}_3,]$ ;

г) если имеется двойной нулевой корень lambda_1=lambda_3=0 , то направление l_2 , соответствующее простому корню lambda_2 , найти как ненулевое решение системы (A-lambda_2cdot E)cdot l_2=o . Вычислить проекцию а $a_{text{pr}}= a-frac{a^Tcdot l_2}{|l_2|^2}cdot l_2$ . Если $a_{text{pr}}=o$ , то направление l_1 найти как ненулевое решение системы Acdot l_1=o . Если $a_{text{pr}}ne o$ , то направление $l_1=-tau_1cdot a_{text{pr}}$ . Направление l_3 найти, используя векторное произведение: $vec{l}_3=[,vec{l}_1,vec{l}_2,]$ .

Нормируя полученные векторы l_1,,l_2,,l_3 , определить координатные $s_1=frac{1}{|l_1|}cdot l_1,$ $s_2=frac{1}{|l_2|}cdot l_2,$ $s_3=frac{1}{|l_3|}cdot l_3$ столбцы векторов $vec{s}_1,,vec{s}_2,,vec{s}_3$ канонического базиса.

6. Найти координаты x_0,y_0,z_0 начала канонической системы координат:

Продолжение

а) для поверхностей, имеющих хотя бы один центр (эллипсоидов, гиперболоидов, конусов, цилиндров, пар плоскостей), найти любое решение $s=begin{pmatrix}x_0&y_0&z_0end{pmatrix}^T$ системы уравнений

Acdot s+a=o или $begin{cases}a_{11}cdot x+a_{12}cdot y+a_{13}cdot z+a_1=0,\[3pt] a_{12}cdot x+a_{22}cdot y+a_{23}cdot z+a_2=0,\[3pt] a_{13}cdot x+a_{23}cdot y+a_{33}cdot z+a_3=0.end{cases}$

б) для поверхностей, не имеющих ни одного центра, найти:

– в случаях эллиптического или гиперболического параболоидов решение $s=begin{pmatrix}x_0&y_0&z_0end{pmatrix}^T$ системы

$begin{cases}lambda_1cdot s_1^Tcdot s+s_1^Tcdot a=0,\[3pt] lambda_2cdot s_2^Tcdot s+s_2^Tcdot a=0,\[3pt] (a+a_{text{pr}})^Tcdot s+a_0=0.end{cases}$ где $a_{text{pr}}=(a^Tcdot s_3)cdot s_3;$

– в случае параболического цилиндра — любое решение $s=begin{pmatrix}x_0&y_0&z_0end{pmatrix}^T$ системы

$begin{cases}lambda_2cdot s_2^Tcdot s+s_2^Tcdot a=0,\[3pt] (a+a_{text{pr}})^Tcdot z+a_0=0,end{cases}$ где $a_{text{pr}}= a-a_{perp}=,~a_{perp}=(a^Tcdot s_2)cdot s_2.$

7. Вычислить коэффициенты канонического уравнения:

а) для поверхностей эллиптического типа:

(1) — при Delta<0 — уравнение эллипсоида $frac{(x')^2}{a^2}+frac{(y')^2}{b^2}+frac{(z')^2}{c^2}=1$ с коэффициентами

$a^2=-frac{Delta}{lambda_1cdotdelta}, quad b^2=-frac{Delta}{lambda_2cdotdelta}, quad c^2=-frac{Delta}{lambda_3cdotdelta},;$

(2) при Delta>0 — уравнение мнимого эллипсоида $frac{(x')^2}{a^2}+frac{(y')^2}{b^2}+frac{(z')^2}{c^2}=-1$ с коэффициентами

$a^2=frac{Delta}{lambda_1cdotdelta}, quad b^2=frac{Delta}{lambda_2cdotdelta}, quad c^2=frac{Delta}{lambda_3cdotdelta},;$

(3) при Delta=0 — уравнение мнимого конуса $frac{(x')^2}{a^2}+frac{(y')^2}{b^2}+frac{(z')^2}{c^2}=0$ с коэффициентами

$a^2=frac{1}{|lambda_1|}, quad b^2=frac{1}{|lambda_2|}, quad c^2=frac{1}{|lambda_3|},;$

б) для поверхностей гиперболического типа:

(4) при Delta>0 — уравнение однополостного гиперболоида $frac{(x')^2}{a^2}+frac{(y')^2}{b^2}-frac{(z')^2}{c^2}=1$ с коэффициентами

$a^2=-frac{Delta}{lambda_1cdotdelta}, quad b^2=-frac{Delta}{lambda_2cdotdelta}, quad c^2=frac{Delta}{lambda_3cdotdelta},;$

(5) при Delta<0 — уравнение двуполостного гиперболоида $frac{(x')^2}{a^2}+frac{(y')^2}{b^2}-frac{(z')^2}{c^2}=-1$ с коэффициентами

$a^2=frac{Delta}{lambda_1cdotdelta}, quad b^2=frac{Delta}{lambda_2cdotdelta}, quad c^2=-frac{Delta}{lambda_3cdotdelta},;$

(6) при Delta=0 — уравнение конуса $frac{(x')^2}{a^2}+frac{(y')^2}{b^2}-frac{(z')^2}{c^2}=0$ с коэффициентами

$a^2=frac{1}{|lambda_1|}, quad b^2=frac{1}{|lambda_2|}, quad c^2=frac{1}{|lambda_3|},;$

в) для поверхностей параболического типа:

(7) при Delta<0 — уравнение эллиптического параболоида $frac{(x')^2}{a^2}+frac{(y')^2}{b^2}=2z$ с коэффициентами

$a^2=sqrt{-frac{Delta}{lambda_1^2cdottau_2}},quad b^2=sqrt{-frac{Delta}{lambda_2^2cdottau_2}},;$

(8) при Delta>0 — уравнение гиперболического параболоида $frac{(x')^2}{a^2}-frac{(y')^2}{b^2}=2z$ с коэффициентами

$a^2=sqrt{-frac{Delta}{lambda_1^2cdottau_2}},quad b^2=sqrt{-frac{Delta}{lambda_2^2cdottau_2}},;$

(9) при Delta=0,~tau_2>0,~tau_1cdotkappa_2<0 — уравнение эллиптического цилиндра $frac{(x')^2}{a^2}+frac{(y')^2}{b^2}=1$ с коэффициентами

$a^2=-frac{kappa_2}{lambda_1cdottau_2}, quad b^2=-frac{kappa_2}{lambda_2cdottau_2},;$

(10) при Delta=0,~tau_2>0,~tau_1cdotkappa_2>0 — уравнение мнимого эллиптического цилиндра $frac{(x')^2}{a^2}+frac{(y')^2}{b^2}=-1$ с коэффициентами

$a^2=frac{kappa_2}{lambda_1cdottau_2}, quad b^2=frac{kappa_2}{lambda_2cdottau_2},;$

(11) при Delta=0,~tau_2>0,~kappa_2=0 — уравнение пары мнимых пересекающихся плоскостей $frac{(x')^2}{a^2}+frac{(y')^2}{b^2}=0$ с коэффициентами

$a^2=frac{1}{|lambda_1|}, quad a^2=frac{1}{|lambda_2|},;$

(12) при Delta=0,~tau_2<0,~kappa_2ne0 — уравнение гиперболического цилиндра $frac{(x')^2}{a^2}-frac{(y')^2}{b^2}=1$ с коэффициентами

$a^2=-frac{kappa_2}{lambda_1cdottau_2}, quad b^2=frac{kappa_2}{lambda_2cdottau_2},;$

(13) при Delta=0,~tau_2<0,~kappa_2=0 — уравнение пары пересекающихся плоскостей

$frac{(x')^2}{a^2}-frac{(y')^2}{b^2}=0$ с коэффициентами $a^2=frac{1}{lambda_1},quad b^2=-frac{1}{lambda_2},;$

(14) при Delta=0,~tau_2=0,~kappa_2ne0 — уравнение параболического цилиндра

(y')^2=2px' с коэффициентом $p=sqrt{-frac{kappa_2}{tau_1^3}}$ ;

(15) при Delta=0,~tau_2=0,~kappa_2=0,~kappa_1<0 — уравнение пары параллельных плоскостей

(y')^2-b^2=0 с коэффициентом $b^2=-frac{kappa_1}{tau_1^2}$ ;

(16) при Delta=0,~tau_2=0,~kappa_2=0,~kappa_1>0 — уравнение пары мнимых параллельных плоскостей

(y')^2+b^2=0 с коэффициентом $b^2=frac{kappa_1}{tau_1^2}$ ;

(17) при Delta=0,~tau_2=0,~kappa_2=0,~kappa_1=0 — уравнение пары совпадающих плоскостей (y')^2=0 .

8. В координатном пространстве Oxyz изобразить каноническую систему координат O'x'y'z' , координаты x_0,y_0,z_0 начала которой найдены в пункте 6, а координаты базисных векторов — в пункте 5.

9. Построить поверхность второго порядка в канонической системе координат O'x'y'z' по каноническому уравнению, найденному в п.7. Построение центральных поверхностей (эллипсоида, гиперболоидов, конуса) удобно начинать с изображения основного параллелепипеда (см. разд.4.4.2-4.4.4). При построении параболоидов, цилиндров и пар плоскостей использовать разд.4.4.5; 3.3.2-3.3.4, 4.2.1-4.2.5). Мнимые поверхности не изображаются, за исключением уравнения мнимого конуса или пары мнимых пересекающихся плоскостей, действительными решениями которых являются точка или ось O'z' соответственно.

Таблица 4.3. Классификация поверхностей второго порядка по инвариантам

Замечания 4.16

1. Согласно пункту 3 замечаний 4.14 для нахождения начала координат параболоидов или параболического цилиндра (см. п.6,”б” алгоритма) можно использовать систему

$begin{cases}Acdot s+a_{perp}=o,\[3pt](a+a_{text{pr}})^Tcdot s+a_0=0,end{cases}$

где $a_{text{pr}}=(a^Tcdot s_3)cdot s_3,~a_{perp}=a-a_{text{pr}}$ в случае эллиптического или гиперболического параболоидов; $a_{perp}=(a^Tcdot s_2)cdot s_2,$ $a_{text{pr}}=a-a_{perp}$ в случае параболического цилиндра.

2. Системы уравнений в п.6,”б” алгоритма можно записать в эквивалентном виде:

– в случаях эллиптического или гиперболического параболоидов:

$begin{cases}lambda_1cdot l_1^Tcdot s+l_1^Tcdot a_{perp}=0,\[3pt] lambda_2cdot l_2^Tcdot s+l_2^Tcdot a_{perp}=0,\[3pt] (a+a_{text{pr}})^Tcdot s+a_0=0,end{cases}$ где $a_{text{pr}}=(a^Tcdot s_3)cdot s_3,~a_{perp}=a-a_{text{pr}};$

– в случае параболического цилиндра:

$begin{cases}lambda_2cdot l_1^Tcdot s+l_1^Tcdot a_{perp}=0,\[3pt] (a+a_{text{pr}})^Tcdot s+a_{perp}=0,end{cases}$ где $a_{text{pr}}=a-a_{perp},~a_{perp}=(a^Tcdot s_2)cdot s_2.$

3. Если требуется получить правую каноническую систему координат, а в результате применения алгоритма каноническая система координат оказалась левой, то достаточно изменить направление оси ординат на противоположное, т.е. заменить базисный вектор $vec{s}_2$ на противоположный вектор $(-vec{s}_2)$ .

4. Согласно пункту 6 замечаний 4.12, если известны корни lambda_1,,lambda_2,,lambda_3 (с учетом кратности) характеристического уравнения, то инварианты можно вы числить по формулам (см. п.2 алгоритма):

tau_1=lambda_1+lambda_2+lambda_3; quad tau_2=lambda_1cdotlambda_2+lambda_2cdotlambda_3+lambda_1cdotlambda_3; quad delta=lambda_1cdotlambda_2cdotlambda_3.

Примеры приведения уравнений поверхностей к каноническому виду по инвариантам

Пример 4.21. Поверхность второго порядка задана в прямоугольной системе координат Oxyz уравнением

2cdot x^2+5cdot y^2+5cdot z^2+6cdot ycdot z+4cdot x+16cdot y+16cdot z+10=0.

Найти канонический вид уравнения поверхности и каноническую систему координат.

Решение

Составляем матрицу квадратичной функции, матрицу квадратичной формы и столбец коэффициентов линейной формы:

$P=begin{pmatrix}2&0&0&2\0&5&3&8\0&3&5&8\2&8&8&10end{pmatrix}!, quad A=begin{pmatrix}2&0&0\0&5&3\0&3&5end{pmatrix}!, quad a=begin{pmatrix}2\8\8end{pmatrix}!.$

2. Составляем характеристическое уравнение

$vline,,begin{matrix}2-lambda&0&0\0&5-lambda&3\0&3&5-lambdaend{matrix},,vline,=0quad Leftrightarrow quad (2-lambda)[(5-lambda)^2-9]=0quad Leftrightarrow quad (2-lambda)^2(8-lambda)=0.$

Находим его корни lambda=2 (двойной корень) и lambda=8 (простой корень). Учитывая п.4 замечаний 4.16, вычисляем инварианты:

$Delta= ,,vline,begin{matrix} 2&0&0&2\0&5&3&8\ 0&3&5&8\2&8&8&10 end{matrix},,vline,= ,,vline,begin{matrix} 2&0&0&2\0&5&3&8\ 0&3&5&8\ 2&8&8&10 end{matrix},,vline,= 2cdot8cdot,,vline,begin{matrix} 5&3&8\3&5&8\ 1&1&1 end{matrix},,vline,= 16cdot(-16)=-256.$

3. По таблице 4.3 определяем, что поверхность эллиптического типа (все корни характеристического уравнения одного знака, что также подтверждается условиями tau_2=36>0 и tau_1cdotdelta=12cdot32>0 ). Поскольку Delta=-256<0 , заданная поверхность — эллипсоид.

5. Находим взаимно ортогональные собственные направления l_1,,l_2,,l_3 , соответствующие корням lambda_1,,lambda_2,,lambda_3 характеристического уравнения. Поскольку имеется двойной ненулевой корень lambda_1=lambda_2=2 (см. п.5,”в” алгоритма), то для простого корня lambda_3=8 находим ненулевое решение l_3 однородной системы уравнений (A-8cdot E)cdot l_3=o:

$begin{cases}(2-8)cdot x+0cdot y+0cdot z=0,\0cdot x+(5-8)cdot y+3cdot z=0,\0cdot x+3cdot y+(5-8)cdot z=0,end{cases}$ или $begin{pmatrix}-6&0&0\0&-3&3\0&3&-3end{pmatrix}!cdot! begin{pmatrix}x\y\zend{pmatrix}= begin{pmatrix}0\0\0end{pmatrix}!.$

Возьмем, например, решение x=0,~y=1,~z=1 , т.е. $l_3=begin{pmatrix}0&1&1end{pmatrix}^T$ . В качестве направления l_2 принимаем первый (ненулевой) столбец матрицы A-8cdot E: $l_2=begin{pmatrix}-6&0&0end{pmatrix}^T$ . Направление l_1 определяем, используя векторное произведение:

$vec{l}_1= [,vec{l}_2,vec{l}_3,]= ,,vline,begin{matrix}vec{i}&vec{j}&vec{k}\-6&0&0\0&1&1end{matrix},,vline,= 0cdotvec{i}+6cdotvec{j}-6cdotvec{k},$ следовательно, $l_1=begin{pmatrix}0&6&-6end{pmatrix}^T,$

Нормируя полученные векторы l_1,,l_2,,l_3 , определяем координатные столбцы векторов канонического базиса:

$begin{gathered}|l_1|=sqrt{l_1^Tcdot l_1}=sqrt{0^2+6^2+(-6)^2}=6sqrt{2}, quad |l_2|=sqrt{l_2^Tcdot l_2}=sqrt{6^2+0^2+0^2}=6,\ |l_3|=sqrt{l_3^Tcdot l_3}=sqrt{0^2+1^2+1^2}=sqrt{2},\[5pt] s_1=frac{l_1}{|l_1|}=begin{pmatrix}0\dfrac{1}{sqrt{2}}\[8pt] -dfrac{1}{sqrt{2}}end{pmatrix}!, quad s_2=frac{l_2}{|l_2|}=begin{pmatrix}-1\0\0end{pmatrix}!, quad s_3=frac{l_3}{|l_3|}=begin{pmatrix}0\dfrac{1}{sqrt{2}}\[8pt] dfrac{1}{sqrt{2}}end{pmatrix}!. end{gathered}$

6. Находим координаты x_0,,y_0,,z_0 начала канонической системы координат, решая систему уравнений (см. п.6,”а” алгоритма):

Acdot s+a=o или $begin{cases}2cdot x+0cdot y+0cdot z+2=0,\ 0cdot x+5cdot y+3cdot z+8=0,\ 0cdot x+3cdot y+5cdot z+8=0.end{cases}$

Получаем x_0=-1,~y_0=-1,~z_0=-1 . Следовательно, вектор vec{s}=overrightarrow{OO'} переноса начала координат имеет координаты $s=begin{pmatrix}-1&-1&-1end{pmatrix}^T$ , или, что то же самое, начало канонической системы координат имеет координаты O'(-1,-1,-1) в исходной системе координат.

7. Вычисляем коэффициенты канонического уравнения (1) эллипсоида (см. п.7,”а!’ алгоритма):

$a^2=b^2= -frac{Delta}{lambda_1cdotdelta}=-frac{-256}{2cdot32}=4, quad c^2=-frac{Delta}{lambda_3cdotdelta}=-frac{-256}{8cdot32}=1.$

Следовательно, каноническое уравнение заданной поверхности имеет вид

$frac{(x')^2}{2^2}+frac{(y')^2}{2^2}+frac{(z')^2}{1^2}=1.$

8. В координатном пространстве Oxyz изображаем каноническую систему координат O'x'y'y' с началом в точке O'(-1,-1,-1) и базисными векторами $vec{s}_1,,vec{s}_2,,vec{s}_3$ , координатные столбцы которых найдены в п.5 (рис.4.53).

9. Строим эллипсоид вращения в канонической системе координат O'x'y'y' по каноническому уравнению, найденному в п.7 (рис.4.53).

Эллипсоид вращения в канонической системе координат

Пример 4.22. Поверхность второго порядка задана в прямоугольной системе координат Oxyz уравнением

3x^2-7y^2+3z^2+8xy-8xz-8yz+10x-14y-6z+a_0=0,

где а) a_0=-8 ; б) a_0=-9 ; в) a_0=-10 .

Найти канонический вид уравнения поверхности и каноническую систему координат.

Решение

Составляем матрицу квадратичной функции, матрицу квадратичной формы и столбец а коэффициентов линейной формы:

$P=left(!!!begin{array}{*{20}{rrrr}}3&4&-4&5\4&-7&-4&-7\-4&-4&3&-3\5&-7&-3&a_0end{array}!right)!,quad A=left(!!begin{array}{*{20}{rrr}}3&4&-4\4&-7&-4\-4&-4&3end{array}!right)!,quad a=begin{pmatrix}5\-7\-3end{pmatrix}!.$

2. Характеристическое уравнение имеет корни lambda=-1,~lambda=9,~lambda=-9 (см. решение примера 4.18,”в”). Поэтому, учитывая п.4 замечаний 4.14, вычисляем инварианты:

$begin{aligned}tau_1&=lambda_1+lambda_2+lambda_3=-1+9-9=-1;\[8pt] tau_2&= lambda_1cdotlambda_2+lambda_2cdotlambda_3+lambda_1cdotlambda_3= (-1)cdot9+9cdot(-9)+(-1)cdot(-9)=-81;\[8pt] delta&= lambda_1cdotlambda_2cdotlambda_3= (-1)cdot9cdot(-9)=81;\[8pt] Delta&= begin{vmatrix}3&4&-4&5\4&-7&-4&-7\-4&-4&3&-3\5&-7&-3&a_0end{vmatrix}= begin{vmatrix}-1&0&-1&2\0&-11&-1&-10\-4&-4&3&-3\1&-11&0&a_0-3end{vmatrix}= begin{vmatrix}-1&0&-1&2\0&-11&-1&-10\0&-4&7&-11\0&-11&-1&a_0-1end{vmatrix}=\ &=(-1)cdot begin{vmatrix}-11&-1&-10\-4&7&-11\-11&-1&a_0-1end{vmatrix}= begin{vmatrix}11&1&10\-4&7&-11\-11&-1&a_0-1end{vmatrix}= begin{vmatrix}11&1&10\-81&0&-81\0&0&a_0+9end{vmatrix}= 81(a_0+9).end{aligned}$

3. По таблице 4.3 определяем, что поверхность гиперболического типа (корни характеристического уравнения имеют разные знаки). При a_0=-8 заданная поверхность — однополостный гиперболоид, так как Delta=81>0 ; при a_0=-9 заданная поверхность — конус, так как Delta=0 ; при a_0=-10 заданная поверхность — двуполостный гиперболоид, так как Delta=-81<0 .

4. Поскольку поверхность гиперболического типа, корни характеристического уравнения обозначим следующим образом (см. п.4,”б” алгоритма): lambda_1=-1, lambda_2=-9 , т.е. и корни одного знака, причем |lambda_1|leqslant|lambda_2| , а корень противоположного знака lambda_3=9 .

5. Находим взаимно ортогональные собственные направления l_1,,l_2,,l_3 , соответствующие корням lambda_1,,lambda_2,,lambda_3 характеристического уравнения. Поскольку все корни простые, то для каждого из них находим ненулевое решение однородной системы (A-lambda_icdot E)cdot l_i=o , i=1,2,3 . Учитывая решение примера 4.18,”в”, получаем

$l_1=begin{pmatrix}1\0\1end{pmatrix}!,quad l_2=begin{pmatrix}-1\4\1end{pmatrix}!,quad l_3=begin{pmatrix}2\1\-2end{pmatrix}!.$

Нормируя полученные векторы l_1,,l_2,,l_3 , определяем координатные столбцы векторов канонического базиса:

$begin{gathered}|l_1|=sqrt{1^2+0^2+1^2}=sqrt{2},quad |l_2|=sqrt{(-1)^2+4^2+1^2}=3sqrt{2},quad |l_3|=sqrt{2^2+1^2+(-2)^2}=3,\[5pt] s_1=frac{l_1}{|l_1|}=begin{pmatrix}dfrac{1}{sqrt{2}}\[8pt]0\[4pt]dfrac{1}{sqrt{2}}end{pmatrix}!,quad s_2=frac{l_2}{|l_2|}=begin{pmatrix}-dfrac{1}{3sqrt{2}}\[10pt]dfrac{4}{3sqrt{2}}\[9pt]dfrac{1}{3sqrt{2}}end{pmatrix}!,quad s_3=frac{l_3}{|l_3|}=begin{pmatrix}dfrac{2}{3}\[9pt]dfrac{1}{3}\[10pt]-dfrac{2}{3}end{pmatrix}!.end{gathered}$

6. Находим координаты x_0,,y_0,,z_0 начала канонической системы координат; решая систему уравнений (см. п.б,”а” алгоритма):

Acdot s+a=o или $begin{cases}phantom{-}3cdot x+4cdot y-4cdot z+5=0,\ phantom{-}4cdot x-7cdot y-4cdot z-7=0,\ -4cdot x-4cdot y+3cdot z-3=0.end{cases}$

Получаем x_0=1,~y_0=-1,~z_0=1 . Следовательно, вектор vec{s}=overrightarrow{OO'} переноса начала координат имеет координаты $s=begin{pmatrix}1&-1&1end{pmatrix}^T$ или, что то же самое, начало канонической системы координат имеет координаты O'(1,-1,1) относительно исходной системы координат.

7. Вычисляем коэффициенты канонического уравнения (см. п.7,”б” алгоритма):

– при a_0=-8 находим коэффициенты и каноническое уравнение (4) однополостного гиперболоида:

$begin{gathered}a^2=-frac{Delta}{lambda_1cdotdelta}=-frac{81}{(-1)cdot81}=1, quad b^2=-frac{Delta}{lambda_2cdotdelta}=-frac{81}{(-9)cdot81}=frac{1}{9},\[3pt] c^2=frac{Delta}{lambda_3cdotdelta}=frac{81}{9cdot81}=frac{1}{9},qquad boxed{frac{(x')^2}{1^2}+frac{(y')^2}{(1/3)^2}-frac{(z')^2}{(1/3)^2}=1}end{gathered}$

– при a_0=-9 находим коэффициенты и каноническое уравнение (6) конуса:

$begin{gathered}a_2=frac{1}{|lambda_1|}=frac{1}{|-1|}=1,quad b_2=frac{1}{|lambda_2|}=frac{1}{|-9|}=frac{1}{9},quad c_2=frac{1}{|lambda_3|}=frac{1}{|9|}=frac{1}{9},\[3pt] boxed{frac{(x')^2}{1^2}+frac{(y')^2}{(1/3)^2}-frac{(z')^2}{(1/3)^2}=0}end{gathered}$

– при a_0=-10 находим коэффициенты и каноническое уравнение (S) двуполостного гиперболоида:

$begin{gathered}a^2=frac{Delta}{lambda_1cdotdelta}=frac{-81}{(-1)cdot81}=1, quad b^2=frac{Delta}{lambda_2cdotdelta}=frac{-81}{(-9)cdot81}=frac{1}{9},\[3pt] c^2=-frac{Delta}{lambda_3cdotdelta}=-frac{-81}{9cdot81}=frac{1}{9},qquad boxed{frac{(x')^2}{1^2}+frac{(y')^2}{(1/3)^2}-frac{(z')^2}{(1/3)^2}=-1}end{gathered}$

8. В координатном пространстве Oxyz изображаем каноническую систему координат O'x'y'z' с началом в точке O'(1,-1,1) и базисными векторами $vec{s}_1,,vec{s}_2,,vec{s}_3$ , координатные столбцы которых найдены в п.5 (рис.4.54).

9. Строим однополостный гиперболоид (рис.4.54,а), конус (рис.4.54,б), двуполостный гиперболоид (рис.4.54,в) в канонической системе координат O'x'y'z' по каноническому уравнению, найденному в пункте 7.

Однополостный гиперболоид, конус, двуполостный гиперболоид в канонической системе координат

Пример 4.23. Поверхность второго порядка задана в прямоугольной системе координат Oxyz уравнением

-2x^2-2y^2+4z^2-20xy-8xz+8yz-26x-22y-4z-12=0

Найти канонический вид уравнения поверхности и каноническую систему координат.

Решение

$P=begin{pmatrix}-2&-10&-4&-13\-10&-2&4&-11\-4&4&4&-2\-13&-11&-2&-12end{pmatrix}!,quad A=begin{pmatrix}-2&-10&-4\-10&-2&4\-4&4&4end{pmatrix}!,quad a=begin{pmatrix}-13\-11\-2end{pmatrix}!.$

2. Вычисляем инварианты:

$begin{gathered}tau_1=a_{11}+a_{22}+a_{33}=-2-2+4=0, quad tau_2= begin{vmatrix},a_{11}&a_{12}\a_{12}&a_{22},end{vmatrix}+ begin{vmatrix},a_{11}&a_{13}\a_{13}&a_{33},end{vmatrix}+ begin{vmatrix},a_{22}&a_{23}\a_{23}&a_{33},end{vmatrix}=\[3pt] =begin{vmatrix},-2&-10\-10&-2,end{vmatrix}+ begin{vmatrix},-2&-4\-4&4,end{vmatrix}+ begin{vmatrix},-2&4\4&4,end{vmatrix}=-96-24-24=-144,\[3pt] delta=begin{vmatrix},a_{11}&a_{12}&a_{13}\a_{12}&a_{22}&a_{23}\a_{13}&a_{23}&a_{33},end{vmatrix}= begin{vmatrix},-2&-10&-4\-10&-2&4\-4&4&4,end{vmatrix}=0,\[3pt] Delta=begin{vmatrix},-2&-10&-4&-13\-10&-2&4&-11\-4&4&4&-2\-13&-11&-2&-12,end{vmatrix}= begin{vmatrix},24&-36&-30&-13\12&-24&-18&-11\0&0&0&-2\11&-35&-26&-12,end{vmatrix}= (-1)^{4+3}(-2)begin{vmatrix},24&-36&-30\12&-24&-18\11&-35&-26,end{vmatrix}=864.end{gathered}$

Составляем характеристическое уравнение: -lambda^3+144lambda=0 . Его корни: lambda=0,~lambda=pm12 .

3. По таблице 4.3 определяем, что поверхность параболического типа ( Delta=0 , т.е. характеристическое уравнение имеет нулевой корень). Поскольку Delta>0 , заданная поверхность — гиперболический параболоид (8).

4. Поскольку поверхность параболического типа, корни характеристического уравнения обозначим следующим образом (см. п.4,”в” алгоритма): lambda_3=0 — единственный нулевой корень; так как ненулевые корни разных знаков и Deltane0 , то lambda_1=12 , тогда lambda_2=-12 .

5. Находим взаимно ортогональные собственные направления l_1,,l_2,,l_3 , соответствующие корням lambda_1,,lambda_2,,lambda_3 характеристического уравнения. Поскольку все корни простые, то для каждого из них находим ненулевое решение однородной системы (A-lambda_icdot E)cdot l_i=o, i=1,2,3:

для lambda_1=12

$begin{pmatrix}-2-12&-10&-4\-10&-2-12&4\-4&4&4-12end{pmatrix}!cdot! begin{pmatrix}x\y\zend{pmatrix}!=! begin{pmatrix}0\0\0end{pmatrix}!quad Leftrightarrowquad begin{cases}x=1,\y=-1,\z=-1,end{cases} Leftrightarrowquad l_1=begin{pmatrix}1\-1\-1end{pmatrix}!;$

для lambda_2=-12

$begin{pmatrix}-2+12&-10&-4\-10&-2+12&4\-4&4&4+12end{pmatrix}!cdot! begin{pmatrix}x\y\zend{pmatrix}!=! begin{pmatrix}0\0\0end{pmatrix}!quad Leftrightarrowquad begin{cases}x=1,\y=1,\z=0,end{cases} Leftrightarrowquad l_2=begin{pmatrix}1\1\0end{pmatrix}!;$

для lambda_3=0

$begin{pmatrix}-2&-10&-4\-10&-2&4\-4&4&4end{pmatrix}!cdot! begin{pmatrix}x\y\zend{pmatrix}!=! begin{pmatrix}0\0\0end{pmatrix}!quad Leftrightarrowquad begin{cases}x=-1,\y=1,\z=-2,end{cases} Leftrightarrowquad l_3=begin{pmatrix}-1\1\-2end{pmatrix}!.$

Так как lambda_3=0 и корни lambda_1 и lambda_2 имеют разные знаки, то направление l_3 должно удовлетворять дополнительному условию a^Tcdot l_3leqslant0 . Найденное направление l_3 этому условию не удовлетворяет:

$a^Tcdot l_3=begin{pmatrix}-13&-11&-2end{pmatrix}!cdot! begin{pmatrix}-1\1\-2end{pmatrix}!=6>0.$

Поэтому его нужно заменить на противоположное, положив $l_3=begin{pmatrix}1&-1&2end{pmatrix}^T$ .

Нормируя полученные векторы l_1,,l_2,,l_3 , определяем координатные столбцы векторов канонического базиса:

$begin{gathered}|l_1|=sqrt{3},quad|l_2|=sqrt{2},quad|l_3|=sqrt{6},\[3pt] s_1=frac{l_1}{|l_1|}=begin{pmatrix}dfrac{1}{sqrt{3}}\[9pt]-dfrac{1}{sqrt{3}}\[9pt]-dfrac{1}{sqrt{3}}end{pmatrix}!,quad s_2=frac{l_2}{|l_2|}=begin{pmatrix}dfrac{1}{sqrt{2}}\[9pt]dfrac{1}{sqrt{2}}\[9pt]0end{pmatrix}!,quad s_3=frac{l_3}{|l_3|}=begin{pmatrix}dfrac{1}{sqrt{6}}\[9pt]-dfrac{1}{sqrt{6}}\[9pt]dfrac{2}{sqrt{6}}end{pmatrix}!.end{gathered}$

6. Так как заданная поверхность (параболоид) не имеет центра, то составляем систему уравнений для нахождения координат x_0,,y_0,,z_0 начала канонической системы координат (см. п.6,”б” алгоритма). Вычисляем

$begin{gathered}a^Tcdot s_3= begin{pmatrix}-13&-11&-2end{pmatrix}!cdot! begin{pmatrix}dfrac{1}{sqrt{6}}\[9pt]-dfrac{1}{sqrt{6}}\[9pt]dfrac{2}{sqrt{6}}end{pmatrix}!=-sqrt{6};quad a_{text{pr}}= (a^Tcdot s_3)cdot s_3= -sqrt{6}cdot! begin{pmatrix}dfrac{1}{sqrt{6}}\[9pt]-dfrac{1}{sqrt{6}}\[9pt]dfrac{2}{sqrt{6}}end{pmatrix}!=! begin{pmatrix}-1\[5pt]1\[5pt]-2end{pmatrix}!;\[3pt] s_1^Tcdot a= begin{pmatrix}dfrac{1}{sqrt{3}}&-dfrac{1}{sqrt{3}}&-dfrac{1}{sqrt{3}}end{pmatrix}!cdot! begin{pmatrix}-13\[2pt]-11\[2pt]-2end{pmatrix}!=0;quad s_2^Tcdot a= begin{pmatrix}dfrac{1}{sqrt{2}}&dfrac{1}{sqrt{2}}&0end{pmatrix}!cdot! begin{pmatrix}-13\[2pt]-11\[2pt]-2end{pmatrix}!=-frac{24}{sqrt{2}};\[3pt] a+a_{text{pr}}= begin{pmatrix}-13\[2pt]-11\[2pt]-2end{pmatrix}!+! begin{pmatrix}-1\[2pt]1\[2pt]-2end{pmatrix}!=! begin{pmatrix}-14\[2pt]-10\[2pt]-4end{pmatrix}!.end{gathered}$

Решаем систему уравнений

$begin{cases}lambda_1cdot s_1^Tcdot s+s_1^Tcdot a=0,\lambda_2cdot s_2^Tcdot s+s_2^Tcdot a=0,\[3pt] (a+a_{text{pr}})^Tcdot s+a_0=0,end{cases}Leftrightarrow! begin{cases}12cdot(x_0-y_0-z_0)=0,\[3pt] -12cdot(x_0+y_0)-24=0,\[3pt] -14cdot x_0-10cdot y_0-4cdot z_0-12=0.end{cases}$

Эта система имеет единственное решение x_0=0,~y_0=-2,~z_0=2 . Следовательно, вектор vec{s}=overrightarrow{OO'} переноса начала координат имеет координаты $s=begin{pmatrix}0&-2&2end{pmatrix}^T$ или, что то же самое, начало канонической системы координат имеет координаты O'(0,-2,2) в исходной системе координат.

Согласно п.1 замечаний 4.16, начало канонической системы координат можно найти, решая систему

$begin{cases}Acdot s+a_{perp}=o,\[3pt] (a+a_{perp})^Tcdot s+a_0=0,end{cases} Leftrightarrowquad! begin{cases}-2x_0-10y_0-4z_0-12=0,\ -10x_0-2y_0+4z_0-12=0,\ -4x_0+4y_0+4z_0+0=0,\ -14x_0-10y_0-4z_0-12=0,end{cases}$

где

$a_{perp}=a-a_{text{pr}}= begin{pmatrix}-13\-11\-2end{pmatrix}- begin{pmatrix}-1\1\-2end{pmatrix}= begin{pmatrix}-12\-12\0end{pmatrix}!.$

7. Вычисляем коэффициенты канонического уравнения (8) гиперболического параболоида (см. п.7,”в” алгоритма):

$a^2=sqrt{-frac{Delta}{lambda_1^2cdottau_2}}= sqrt{-frac{864}{12^2cdot(-144)}}= frac{sqrt{6}}{12}, quad b^2=sqrt{-frac{Delta}{lambda_2^2cdottau_2}}= sqrt{-frac{864}{(-12)^2cdot(-144)}}= frac{sqrt{6}}{12}.$

Следовательно, каноническое уравнение заданной поверхности имеет вид

$frac{(x')^2}{sqrt{6}/12}-frac{(y')^2}{sqrt{6}/12}=2cdot z'.$

8. В координатном пространстве Oxyz изображаем каноническую систему координат O'x'y'z' с началом в точке O'(0,-2,2) и ба зисными векторами $vec{s}_1,,vec{s}_2,,vec{s}_3$ , координатные столбцы которых найдены в п.5 (рис.4.55).

9. Строим гиперболический параболоид в канонической системе координат O'x'y'z' по каноническому уравнению, найденному в пункте 7 (рис.4.55).

Гиперболические параболоид и цилиндр, параболический цилиндр в канонической системе координат

Пример 4.24. Поверхность второго порядка задана в прямоугольной системе координат Oxyz уравнением

8cdot y^2+4cdot xcdot y+2cdot xcdot z+4cdot ycdot z+4cdot x+8cdot y-9=0.

Найти канонический вид уравнения поверхности и каноническую систему координат.

Решение

$P=begin{pmatrix}0&2&1&2\2&8&2&4\1&2&0&0\2&4&0&-9end{pmatrix}!,quad A=begin{pmatrix}0&2&1\2&8&2\1&2&0end{pmatrix}!,quad a=begin{pmatrix}2\4\0end{pmatrix}!.$

2. Вычисляем инварианты: $tau_1=a_{11}+a_{22}+a_{33}=0+8+0=8,$

$begin{gathered}tau_2= begin{vmatrix}a_{11}&a_{12}\a_{12}&a_{22}end{vmatrix}+ begin{vmatrix}a_{11}&a_{13}\a_{13}&a_{33}end{vmatrix}+ begin{vmatrix}a_{11}&a_{12}\a_{12}&a_{22}end{vmatrix}= begin{vmatrix}0&2\2&8end{vmatrix}+ begin{vmatrix}0&1\1&0end{vmatrix}+ begin{vmatrix}8&2\2&0end{vmatrix}=-9;\[3pt] delta= begin{vmatrix},a_{11}&a_{12}&a_{13}\a_{12}&a_{22}&a_{23}\a_{13}&a_{23}&a_{33},end{vmatrix}= begin{vmatrix},0&2&1\2&8&2\1&2&0,end{vmatrix}=0;\[3pt] Delta= begin{vmatrix},0&2&1&2\2&8&2&4\1&2&0&0\2&4&0&-9,end{vmatrix}= begin{vmatrix},0&2&1&2\2&8&2&4\1&2&0&0\0&0&0&-9,end{vmatrix}= (-1)^{4+4}(-9)delta=0. end{gathered}$

Так как Delta=delta=0 , то вычисляем

$begin{aligned}kappa_2&= begin{vmatrix},a_{11}&a_{12}&a_1\a_{12}&a_{22}&a_2\a_1&a_2&a_0,end{vmatrix}+ begin{vmatrix},a_{11}&a_{13}&a_1\a_{13}&a_{33}&a_3\a_1&a_3&a_0,end{vmatrix}+ begin{vmatrix},a_{22}&a_{23}&a_2\a_{23}&a_{33}&a_3\a_2&a_3&a_0,end{vmatrix}=\[3pt] &=begin{vmatrix},0&2&2\2&8&4\2&4&-9,end{vmatrix}+ begin{vmatrix},0&1&2\1&0&0\2&0&-9,end{vmatrix}+ begin{vmatrix},8&2&4\2&0&0\4&0&-9,end{vmatrix}=81. end{aligned}$

Составляем характеристическое уравнение: -lambda^3+ 8lambda^2+ 9lambda=0 . Его корни: lambda=-1,~lambda=0,~lambda=9 .

3. По таблице 4.3 определяем, что поверхность параболического типа ( Delta=0 , т.е. характеристическое уравнение имеет нулевой корень). Поскольку Delta=0 , то поверхность цилиндрическая. Так как tau_2<0 и kappa_2ne0 , то заданная поверхность — гиперболический цилиндр.

5. Находим взаимно ортогональные собственные направления l_1,,l_2,,l_3 , соответствующие корням lambda_1,,lambda_2,,lambda_3 характеристического уравнения. Поскольку все корни простые, то для каждого из них находим ненулевое решение однородной системы (A-lambda_icdot E)cdot l_i=o, i=1,2,3:

для lambda_1=9

$begin{pmatrix}0-9&2&1\2&8-9&2\1&2&0-9end{pmatrix}!cdot! begin{pmatrix}x\y\zend{pmatrix}!=! begin{pmatrix}0\0\0end{pmatrix}! Leftrightarrowquad! begin{cases}x=1,\y=4,\z=1,end{cases} Leftrightarrowquad l_1= begin{pmatrix} 1\4\1end{pmatrix}!;$

для lambda_2=-1

$begin{pmatrix}0+1&2&1\2&8+1&2\1&2&0+1 end{pmatrix}!cdot! begin{pmatrix}x\y\zend{pmatrix}!=! begin{pmatrix}0\0\0end{pmatrix}! Leftrightarrowquad! begin{cases}x=-1,\y=0,\z=1,end{cases} Leftrightarrowquad l_2=begin{pmatrix}-1\0\1end{pmatrix}!;$

для lambda_3=0

$begin{pmatrix} 0&2&1\2&8&2\1&2&0 end{pmatrix}!cdot! begin{pmatrix}x\y\zend{pmatrix}!=! begin{pmatrix}0\0\0end{pmatrix}! Leftrightarrowquad! begin{cases}x=2,\y=-1,\z=2,end{cases} Leftrightarrowquad l_3=begin{pmatrix}2\-1\2end{pmatrix}!.$

$a^Tcdot l_3= begin{pmatrix}2&4&0end{pmatrix}^Tcdot! begin{pmatrix}2\-1\2end{pmatrix}=0.$

Нормируя полученные векторы l_1,,l_2,,l_3 , определяем координатные столбцы векторов канонического базиса:

$begin{gathered}|l_1|=3sqrt{2},quad |l_2|=sqrt{2},quad |l_3|=3,\[3pt] s_1=frac{1}{|l_1|}cdot l_1cdot! begin{pmatrix}dfrac{1}{3sqrt{2}}\[9pt] dfrac{4}{3sqrt{2}}\[9pt] dfrac{1}{3sqrt{2}}end{pmatrix}!,quad s_2=frac{1}{|l_2|}cdot l_2cdot! begin{pmatrix}-dfrac{1}{sqrt{2}}\[9pt] 0\[9pt] dfrac{1}{sqrt{2}}end{pmatrix}!,quad s_3=frac{1}{|l_3|}cdot l_3cdot! begin{pmatrix}dfrac{2}{3}\[9pt] -dfrac{1}{3}\[9pt] dfrac{2}{3}end{pmatrix}!.end{gathered}$

6. Так как заданная поверхность (гиперболический цилиндр) не являет ся центральной (она имеет прямую центров), то достаточно найти любое решение $s=begin{pmatrix}x_0&y_0&z_0end{pmatrix}^T$ системы уравнений (см. п.6,”а” алгоритма):

Acdot s+a=o, или $begin{cases}0cdot x+2cdot y+1cdot z+2=0,\ 2cdot x+8cdot y+2cdot z+4=0,\ 1cdot x+2cdot y+0cdot z+0=0.end{cases}$

Возьмем, например, решение x_0=0,~y_0=0,~z_0=-2 . Следовательно, вектор vec{s}=overrightarrow{OO'} переноса начала координат имеет координаты $s=begin{pmatrix}0&0&-2end{pmatrix}^T$ или, что то же самое, начало канонической системы координат имеет координаты O'(0,0,-2) относительно исходной системы координат.

7. Вычисляем коэффициенты канонического уравнения (12) гиперболического цилиндра (см. п.7,”в” алгоритма):

$a^2=-frac{kappa_2}{lambda_1cdottau_2}=-frac{81}{9cdot(-9)}=1,quad b^2=frac{kappa_2}{lambda_2cdottau_2}=frac{81}{(-1)cdot(-9)}=9.quad$

Следовательно, каноническое уравнение заданной поверхности имеет вид

$frac{(x')^2}{1^2}-frac{(y')^2}{3^2}=1.$

8. В координатном пространстве Oxyz изображаем каноническую систему координат O'x'y'z' с началом в точке O'(0,0,-2) и базисными векторами $vec{s}_1,,vec{s}_2,,vec{s}_3$ , координатные столбцы которых найдены в п.5 (рис.4.56).

9. Строим гиперболический цилиндр в канонической системе координат O'x'y'z' по каноническому уравнению, найденному в п.7 (рис.4.56 см. выше).

Пример 4.25. Поверхность второго порядка задана в прямоугольной системе координат Oxyz уравнением

4cdot x^2+y^2+9cdot z^2+4cdot xcdot y-12cdot xcdot z-6cdot ycdot z+6cdot x-2cdot y-6cdot z+11=0.

Найти канонический вид уравнения поверхности и каноническую систему координат.

Решение

Найти канонический вид уравнения поверхности и каноническую систему координат.

$P=begin{pmatrix}4&2&-6&3\ 2&1&-3&-1\-6&-3&9&-3\ 3&-1&-3&11 end{pmatrix}!,qquad A=begin{pmatrix}4&2&-6\ 2&1&-3\-6&-3&9 end{pmatrix}!,qquad a=begin{pmatrix}3&-1&-3 end{pmatrix}!.$

2. Вычисляем инварианты:

$begin{aligned}&tau_1= a_{11}+a_{22}+a_{33}= 4+1+9=14,\[4pt] &tau_2= begin{vmatrix}a_{11}&a_{12}\ a_{12}&a_{22} end{vmatrix}+begin{vmatrix}a_{11}&a_{13}\ a_{13}&a_{33} end{vmatrix}+ begin{vmatrix}a_{22}&a_{23}\ a_{23}&a_{33} end{vmatrix}= begin{vmatrix} 4&2\2&1 end{vmatrix}+ begin{vmatrix}4&-6\-6&9 end{vmatrix}+ begin{vmatrix}1&-3\-3&9end{vmatrix}=0+0+0=0,\[4pt] &delta= begin{vmatrix}a_{11}&a_{12}&a_{13}\ a_{12}&a_{22}&a_{23}\ a_{13}&a_{23}&a_{33} end{vmatrix}= begin{vmatrix}4&2&-6\ 2&1&-3\-6&-3&9end{vmatrix}=0,\[4pt] &Delta= begin{vmatrix}4&2&-6&3\ 2&1&-3&-1\-6&-3&9&-3\ 3&-1&-3&11end{vmatrix}= begin{vmatrix}0&0&0&5\ 2&1&-3&-1\0&0&0&-6\ 3&-1&-3&11end{vmatrix}= (-1)^{1+4}cdot5cdot begin{vmatrix}2&1&-3\ 0&0&0\ 3&-1&-3end{vmatrix}=0. end{aligned}$

Так как Delta= delta=0 , то вычисляем семиинвариант:

$begin{aligned}kappa_2&= begin{vmatrix}a_{11}&a_{12}&a_{1}\ a_{12}&a_{22}&a_{2}\ a_{1}& a_{2}&a_{0}end{vmatrix}+ begin{vmatrix}a_{11}&a_{13}&a_{1}\ a_{13}&a_{33}&a_{3}\ a_{1}& a_{3}&a_{0} end{vmatrix}+ begin{vmatrix} a_{22}&a_{23}&a_{2}\ a_{23}&a_{33}&a_{3}\ a_{2}& a_{3}&a_{0} end{vmatrix}=\ &=begin{vmatrix}4&2&3\2&1&-1\ 3&-1&11end{vmatrix}+ begin{vmatrix}4&-6&3\-6&9&-3\ 3&-3&11 end{vmatrix}+ begin{vmatrix}1&-3&-1\-3&9&-3\-1&-3&11end{vmatrix}=-25-9-36=-70. end{aligned}$

Составляем характеристическое уравнение -lambda^3+14 lambda^2=0 .Его корни lambda=0 (двойной корень) и lambda=14 (простой корень).

3. По таблице 4.3 определяем, что поверхность параболического типа ( delta=0 , то есть характеристическое уравнение имеет нулевой корень). Поскольку Delta=0 , то поверхность цилиндрическая. Так как tau_2=0 и kappa_2ne0 , то заданная поверхность – параболический цилидр.

4. Поскольку поверхность параболического типа, корни характеристического уравнения обозначим следующим образом (см. п.4,”в” алгоритма): lambda_1= lambda_3=0 – двойной нулевой корень; тогда lambda_2=14 .

5. Находим взаимно ортогональные собственные направления l_1,,l_2,,l_3 , соответствующие корням lambda_1,,lambda_2,,lambda_3 характеристического уравнения. Поскольку lambda_1=lambda_3=0 – двойной нулевой корень (см. п.5,”г” алгоритма), то находим направление l_2 , соответствующее простому корню lambda_2=14 , как ненулевое решение системы (A-lambda_2cdot E)cdot l_2=ocolon

$begin{pmatrix}4-14&2&-6\ 2&1-14&-3\-6&-3&9-14 end{pmatrix}!cdot! begin{pmatrix}x\y\zend{pmatrix}= begin{pmatrix}0\0\0 end{pmatrix}quad Rightarrowquad begin{cases}x=-2,\ y=-1,\ z=3,end{cases} Rightarrowquad l_2=begin{pmatrix}-2\-1\3end{pmatrix}!.$

Вычисляем $a^Tcdot l_2= begin{pmatrix}3&-1&-3end{pmatrix}!cdot! begin{pmatrix}-2\-1\3 end{pmatrix}=-14;~ |l_2|^2=14;$

$a_{text{pr}}= a-frac{a^Tcdot l_2}{|l_2|^2}cdot l_2= begin{pmatrix}3\-1\-3 end{pmatrix}-frac{-14}{14}cdot! begin{pmatrix}-2\-1\3end{pmatrix}= begin{pmatrix}1\-2\0 end{pmatrix}!.$

Так как $a_{text{pr}}ne o$ , то направление $l_1=-tau_1cdot a_{text{pr}}=-14cdot a_{text{pr}}= begin{pmatrix}-14&28&0 end{pmatrix}^T$ . Направление l_3 находим, вычисляя векторное произведение

$vec{l}_3=vec{l}_1times vec{l}_2= begin{vmatrix}vec{i}& vec{j}& vec{k}\-14&28&0\-2&-1&3end{vmatrix}= 84,vec{i}+ 42,vec{j}+ 70,vec{k}$ . Следовательно, $l_3= begin{pmatrix}84&42&70 end{pmatrix}^T$ .

Нормируя полученные векторы l_1,,l_2,,l_3 , определяем координатные столбцы векторов канонического базиса:

$begin{gathered}|l_1|=14 sqrt{5},,qquad |l_2|=sqrt{14},,qquad |l_3|=14 sqrt{70},,\ s_1= frac{l_1}{|l_1|}= begin{pmatrix}-dfrac{1}{sqrt{5}}\[9pt] dfrac{2}{sqrt{5}}\[9pt]0 end{pmatrix}!,qquad s_2= frac{l_2}{|l_2|}= begin{pmatrix}-dfrac{2}{sqrt{14}}\[9pt]-dfrac{1}{sqrt{14}}\[9pt] dfrac{3}{sqrt{14}} end{pmatrix}!,qquad s_3= frac{l_3}{|l_3|}= begin{pmatrix}dfrac{6}{sqrt{70}}\[9pt]dfrac{3}{sqrt{70}}\[9pt] dfrac{5}{sqrt{70}} end{pmatrix}!. end{gathered}$

6. Так как заданная поверхность (параболический цилиндр) не имеет центров, то составляем систему уравнений для нахождения координат x_0,y_0,z_0 начала канонической системы координат (см. п.6,”б” алгоритма). Учитывая п.5, вычисляем

$a_{text{pr}}= begin{pmatrix}1\-2\0 end{pmatrix}!,quad a+a_{text{pr}}= begin{pmatrix}3\-1\-3end{pmatrix}+ begin{pmatrix}1\-2\0 end{pmatrix}= begin{pmatrix}4\-3\-3 end{pmatrix}!,quad s_2^Tcdot a= begin{pmatrix}-dfrac{2}{sqrt{14}}&-dfrac{1}{sqrt{14}}& dfrac{3}{sqrt{14}}end{pmatrix}^Tcdot! begin{pmatrix}3\-1\-3 end{pmatrix}=-sqrt{14},.$

Решаем систему уравнений

$left{! begin{aligned}& lambda_2cdot s_2^Tcdot s+ s_2^Tcdot a=0,\ &(a+ a_{text{pr}})^Tcdot s+a_0=0, end{aligned}right.quad Leftrightarrowquad left{! begin{aligned}&-2cdot x_0-y_0+3cdot z_0-1=0,\ &4cdot x_0-3cdot y_0-3cdot z_0+11=0. end{aligned}right.$

Эта система имеет бесконечно много решений. Возьмем, например, решение x_0=-5,~ y_0=0,~ z_0=-3 . Следовательно, вектор vec{s}= overrightarrow{OO'} переноса начала координат имеет координаты $s=begin{pmatrix}-5&0&-3end{pmatrix}^T$ или, что то же самое, начало канонической системы координат имеет координаты O'(-5,0,-3) в исходной системе координат.

Согласно п.1 замечаний 4.16, начало канонической системы координат
можно найти, решая систему уравнений

$left{! begin{aligned}&Acdot s+a_{perp}=o,\ &(a+a_{text{pr}})^Tcdot s+a_0=0, end{aligned}right.~Leftrightarrow~ left{! begin{aligned}&4,x_0+ 2,y_0-6,z_0+2=0,\ &2,x_0+ 1,y_0-3,z_0+1=0,\ &-6,x_0-3,y_0+9,z_0-3=0,\ &4,x_0-3,y_0-3,z_0+11=0, end{aligned}right.$ , где $a_{perp}-a_{text{pr}}= begin{pmatrix}3\-1\-3end{pmatrix}-begin{pmatrix}1\-2\0 end{pmatrix}= begin{pmatrix}2\1\-3 end{pmatrix}$ .

7. Вычисляем параметр канонического уравнения (14) параболического цилиндра (см. п.7,”в” алгоритма):

$p= sqrt{-frac{kappa_2}{tau_1^3}}=sqrt{-frac{-70}{14^3}}= sqrt{frac{5}{14^2}}= frac{sqrt{5}}{14},.$

Следовательно, каноническое уравнение заданной поверхности имеет вид

$(y')^2=2cdot frac{sqrt{5}}{14}cdot x'$ (рис.4.57).

8. В координатном пространстве Oxyz изображаем каноническую систему координат O'x'y'z' с началом в точке O'(-5,0,-3) и базисными векторами $vec{s}_1,, vec{s}_2,, vec{s}_3$ , координатные столбцы которых найдены в п.5 (рис.4.57).

9. Строим параболический цилиндр в канонической системе координат O'x'y'z' по каноническому уравнению, найденному в п.7 (рис.4.57).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

10 Пересечение кривой второго порядка с прямой. Асимптотические направления относительно кривой второго порядка

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://matecos.ru/images/Matematica/Kr2poryadka/Krv2poryadka.gif" alt="Krv2poryadka" width="256" height="273" />

Кривая второго порядка – это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:

Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах – при вторых степенях одновременно не нули.

Парабола – множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.

Пример по теме кривые второго порядка №1

Привести к каноническому виду и построить график кривой второго порядка.

Пример по теме кривые второго порядка №2

По виду уравнения определить тип кривой и нарисовать ее в декартовой системе координат:

Пример по теме кривые второго порядка №3

Построить кривую второго порядка:

Пример по теме кривые второго порядка №4

Построить кривую второго порядка:

Пример по теме кривые второго порядка №5

Провести заданное уравнение линии второго порядка к каноническому виду и построить ее:

Пример по теме кривые второго порядка №6

Определить центр и радиус окружности:

Пример по теме кривые второго порядка №7

Определить центр и полуоси эллипса:

Пример по теме кривые второго порядка №8

Определить центр, полуоси и асимптоты гиперболы:

Пример по теме кривые второго порядка №9

Составить уравнение и построить линию, расстояние каждой точки которой от точки A(-1;0) вдвое меньше расстояния ее от прямой x=-4

Пример по теме кривые второго порядка №10

Определить тип кривой второго порядка:

Пример по теме кривые второго порядка №11

Докажите, что эта кривая – эллипс.

Найдите его большую и малую полуоси.

Запишите уравнение фокальной оси.

Пример по теме кривые второго порядка №12

Доказать, что данная кривая – парабола.

Найти координаты вершины параболы.

Запишите уравнение оси симметрии параболы.

Пример по теме кривые второго порядка №13

Докажите, что кривая – гипербола.

Найдите координаты центра симметрии гиперболы.

Найдите действительную и мнимую полуоси гиперболы.

Запишите уравнение фокальной оси гиперболы.

Пример по теме кривые второго порядка №14

Все графике в этой статье были построены в Geogebra.Подробно о построении графиков функции быстрым и удобным способом читать тут:

Приведение уравнения поверхности 2-го порядкак каноническому виду по инвариантам

Алгоритм приведения уравнения поверхности 2-го порядка к каноническому виду

Примеры приведения уравнений поверхностей к каноническому виду по инвариантам

Вам также может понравиться

Как составить буклет в паблишер

Как найти регистрационный номер записи в реестре

Как найти кубометр доски

Добавить комментарий Отменить ответ

Приведение уравнения поверхности 2-го порядка
к каноническому виду по инвариантам