Как найти центр кривизны дуги

Макеты страниц

Мы видели, что кривизна к окружности есть величина, обратная ее радиусу

Чем больше радиус окружности, тем меньше ее кривизна. По аналогии вводится понятие радиуса кривизны кривой в данной точке.

Определение. Радиусом кривизны R в данной точке кривой называется величина, обратная кривизне

Так как кривизна кривой, вообще говоря, изменяется при переходе от данной ее точки к другой, то и радиус кривизны является переменной величиной.

Если кривая задана уравнением то ее радиус кривизны как величина, обратная кривизне, определяется следующей формулой:

Если же кривая задана параметрически, то ее радиус кривизны выражается формулой

Пример. Найти радиус кривизны кривой в точке М (1; 0).

Решение. Находим . По формуле (78) получим

Построим теперь в данной точке М кривой отрезок МР, направленный по нормали к кривой в сторону ее вогнутости и равный по величине радиусу кривизны кривой в точке М:

(рис. 201). Окружность с центром в точке Р и радиусом, равным радиусу кривизны кривой в данной точке , называется кругом кривизны. Центр Р этого круга называется центром кривизны. Очевидно, данная кривая и ее круг кривизны в точке М имеют общую касательную (рис. 201).

Рис. 201

Рис. 202

Покажем, как найти координаты центра кривизны кривой, заданной уравнением .

Пусть – точка данной кривой и – соответствующий ее центр кривизны (рис. 202). Уравнение нормали к кривой в точке имеет вид

Так как точка лежит на нормали, то ее координаты удовлетворяют этому уравнению:

Кроме того, расстояние между точками равно радиусу кривизны R кривой:

откуда

Решая совместно систему уравнений

и заменяя R его выражением по формуле (78), найдем

Предположим для определенности, что . Тогда кривая вогнута и (см. рис. 202), т. е. в правой части формулы (80) для следует взять знак «плюс», и, следовательно, в правой части формулы для – знак «минус». При этом, поскольку для координат центра кривизны мы получим следующие формулы:

Можно показать, что в случае формулы (81) сохраняют свой вид.

Источник

Радиус, центр и круг кривизны. Эволюта и эвольвента

Радиусом
кривизны называется величина, обратная
кривизне, т. е.

.

Если
плоская кривая отнесена к прямоугольной
системе координат и задана уравнением

,
то радиус кривизны

выражается формулой

Eсли
плоская кривая отнесена к прямоугольной
системе координат и задана параметрически
системой уравнений

, то радиус кривизны

выражается формулой

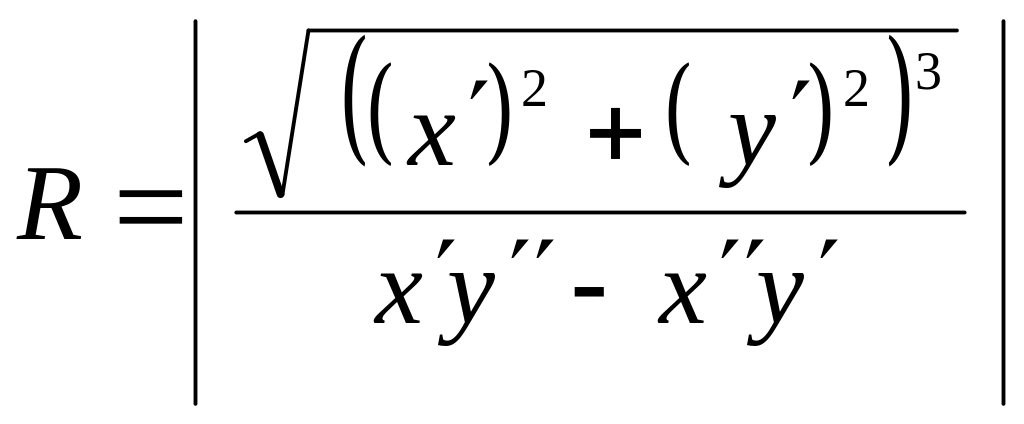
где

,

,

Если
плоская кривая отнесена к полярной
системе координат и задана уравнением

,
то радиус кривизны

выражается формулой

где

Окружностью
кривизны данной линии её точке А
называется
предельное положение окружности,
проходящей через три точки A,
B,
C
кривой, когда

и

.

Радиус
окружности кривизны равен радиусу
кривизны. Центр окружности кривизны
называется центром кривизны и находится
на нормали к линии, проведенной в точке
А
в сторону вогнутости этой линии.

Координаты

и

центра кривизны линии

вычисляются по формулам:

Эволютой
линии называется множество её центров
кривизны, а сама линия относительно
своей эволюты называется эвольвентой.

Формулы
для координат центра кривизны можно
рассматривать как параметрические
уравнения эволюты, где параметром
является абсцисса х
исходной линии.

Данная
линия может иметь лишь одну эволюту, но
у данной эволюты существует бесконечное
множество эвольвент.

Пример.
Найти
радиус кривизны линии

в
точке с абсциссой

Решение.
Найдем значения производных первого и
второго порядков функции

в точке с абсциссой

Подставим
найденные значения

в
формулу

Следовательно,
радиус кривизны
линии

в
точке с абсциссой

Пример.
Найти
радиус кривизны линии

в
точке

.

Решение.
Дифференцируя по t,
получим

Вычислим
значения производных в
точке

Подставляя
найденные значения

в
формулу

имеем

Следовательно,
радиус кривизны
линии

в
точке с абсциссой

Пример.
Найти
радиус кривизны кардиоиды

в
любой её точке.

Решение.
Найдем

Подставим
найденные выражения в формулу

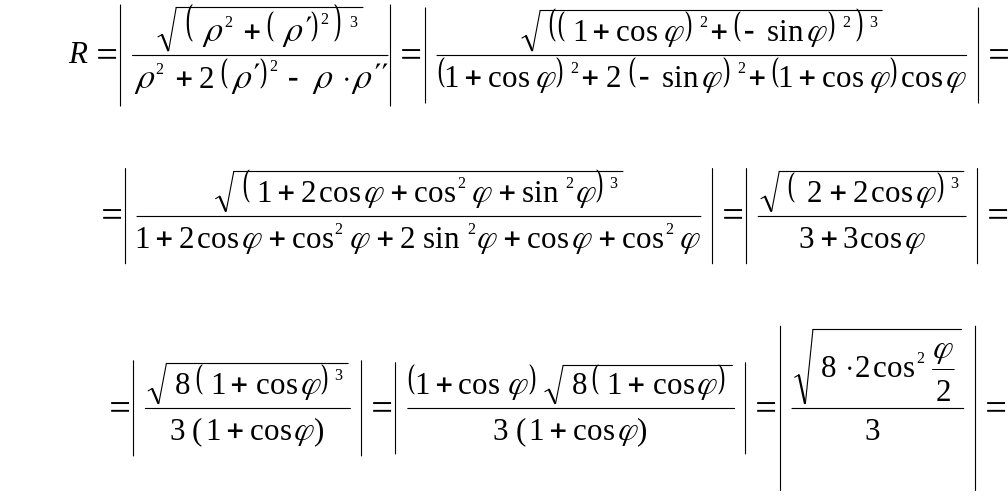
Следовательно,
радиус кривизны
кардиоиды

в
любой её точке

Пример.
Найти
координаты

центра кривизны линии

в
точке

.

Решение.
Найдем значения производных первого
и второго порядков функции

в точке с абсциссой

Подставим
значения

и найденные
значения

в
формулы

Следовательно,
координаты
центра кривизны линии

в
точке

Пример.
Составить
уравнение эволюты кривой

.

Решение.
Продифференцируем дважды уравнение
параболы:

;

Так
как

,
то

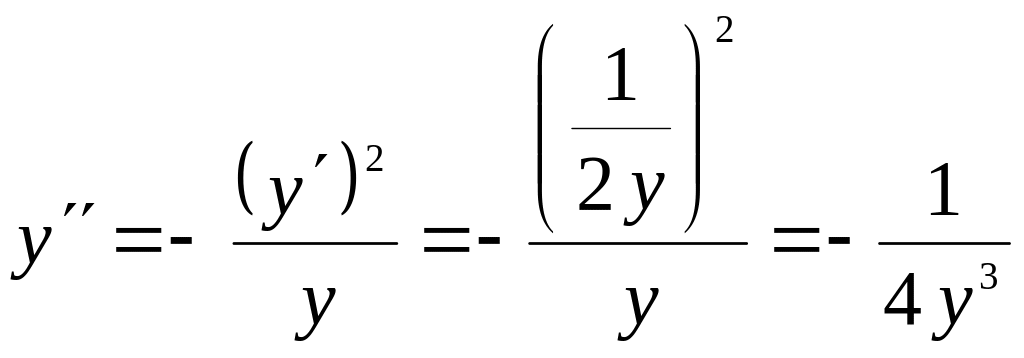
Найдем
координаты

центра кривизны линии ,
предварительно выразив х
из уравнения

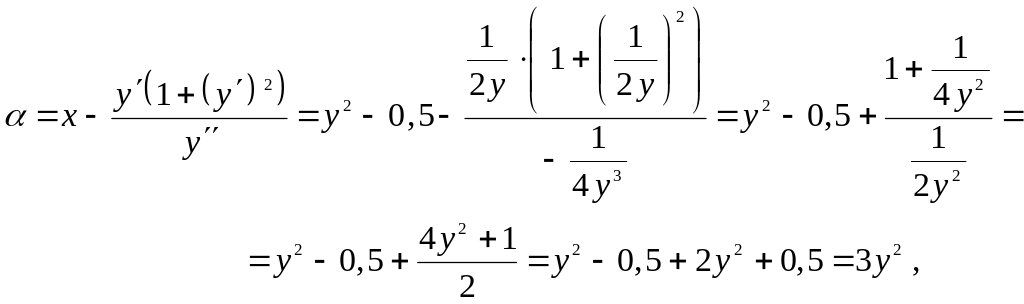
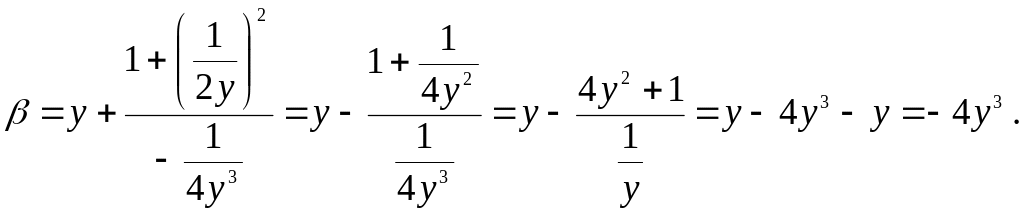
Имеем

–
уравнение эволюты в параметрической
форме. Выразим параметр у
из

и

;

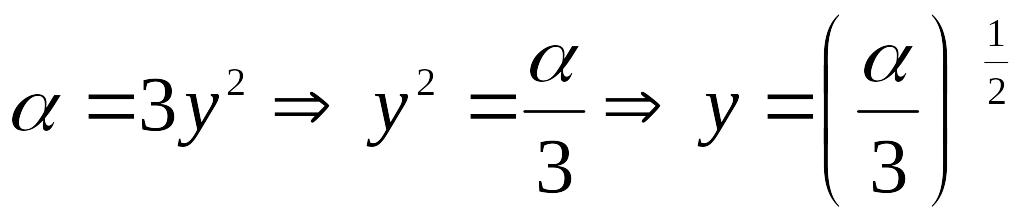
Окончательно
получаем,

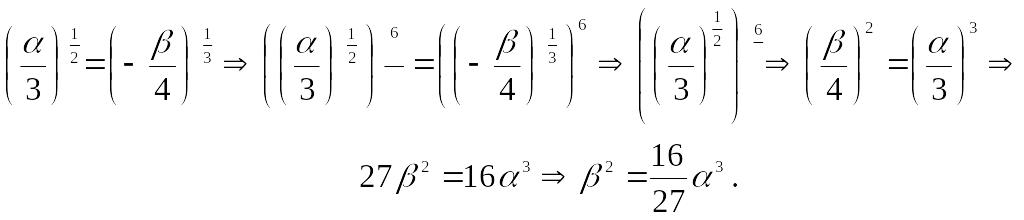
Следовательно,
уравнение
эволюты кривой

имеет вид

(уравнение
полукубической параболы).

Упражнения

1.
Найти радиус кривизны линии

в
точке A:

а)

,
A
(
2; 2 ), б)

,
A
(
0; 1 ) .

2.
Найти радиус кривизны трехлепестковой
розы

, при

.

3.
Найти координаты

центра кривизны линии

в
точке A:

а)

,
A
(
1; 1 ), б)

,
A
(
1; 0 ) .

4.
Составить уравнение эволюты кривой

а)

,
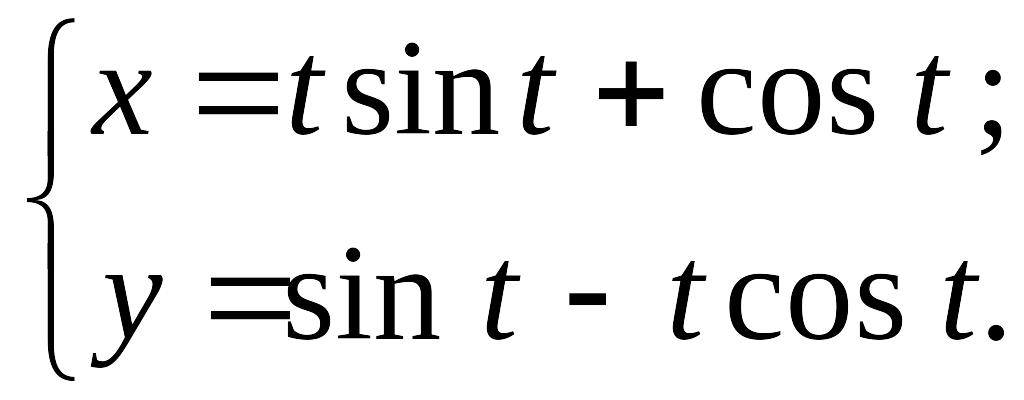
б)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Смысл понятий радиуса, круга и центра кривизны

В технических приложениях часто оказывается удобным использовать окружности для приближенной замены кривой в окрестностях рассматриваемых точек. Это существенно упрощает решение целого ряда задач за счет применения более удобных выражений.

Наиболее употребительными характеристиками любой кривой являются касательная и нормаль. Касательная — предельное положение секущей $MN$ при неограниченном приближении точки $N$ к точке $M$ вдоль кривой. Нормаль — прямая, проходящая через точку касания перпендикулярно касательной.

Уравнение касательной в точке $Mleft(x_{0} ,y_{0} right)$ к кривой $y=fleft(xright)$ имет вид $y-y_{0} =y’left(x_{0} right)cdot left(x-x_{0} right)$, уравнение нормали $y-y_{0} =-frac{1}{y’left(x_{0} right)} cdot left(x-x_{0} right)$.

Задача 1

Записать уравнения касательной и нормали к кривой $y=3cdot x^{2} -x+2$ в заданной точке $x_{0} =1$.

Значение функции в заданной точке: $y_{0} =yleft(x_{0} right)=yleft(1right)=3cdot 1^{2} -1+2=4$.

Значение производной в заданной точке:

[y’=left(3cdot x^{2} -x+2right)^{{‘} } =6cdot x-1; y’left(x_{0} right)=y’left(1right)=6cdot 1-1=5.]

Уравнение касательной: $y-4=5cdot left(x-1right)$ или $5cdot x-y-1=0$.

Уравнение нормали: $y-4=-frac{1}{5} cdot left(x-1right)$ или $x+5cdot y-21=0$.

Определение

Радиус кривизны — это параметр кривой, значение которого обратно значению кривизны $R=frac{1}{K} $. Следовательно, это такая же переменная величина, как и кривизна.

Если в данной точке $M$ построить нормаль к кривой и отложить на ней в сторону вогнутости кривой отрезок, равный по длине радиусу кривизны кривой в этой точке, то получим точку — центр кривизны. Окружность с центром в полученной точке и радиусом, равным радиусу кривизны — это круг кривизны. Так как данная кривая и её круг кривизны касаются в данной точке, то они имеют в данной точке общую касательную. Кроме того, значения кривизны кривой и круга кривизны в данной точке совпадают.

Важным свойством круга кривизны является то, что он является соприкасающимся кругом, то есть предельным положением круга, проходящего через три точки кривой, стремящимся к совпадению в данной.

Если некоторая точка перемещается вдоль кривой, то и соответствующий ей центр кривизны также описывает некоторую кривую. Геометрическое место центров кривизны данной кривой называется её эволютой. При этом данная кривая по отношению к своей эволюте называется её эвольвентой.

Вычисление радиуса и определение центра круга кривизны

Формулы для радиуса кривизны получить легко, если известны формулы для вычисления кривизны кривой.

При произвольном параметрическом задании кривой $x=xleft(tright)$ и $y=yleft(tright)$ имеем $R=frac{sqrt{left(left(x’_{t} right)^{2} +left(y’_{t} right)^{2} right)^{3} } }{y”_{tt} cdot x’_{t} -x”_{tt} cdot y’_{t} } $.

Если кривая задана в явном виде $y=fleft(xright)$, то $R=frac{sqrt{left(1+left(y’right)^{2} right)^{3} } }{y”} $.

Если кривая задана в полярных координатах $rho =rho left(phi right)$, то $R=frac{sqrt{left(rho ^{2} +left(rho ‘_{phi } right)^{2} right)^{3} } }{rho ^{2} +2cdot left(rho ‘_{phi } right)^{2} -rho cdot rho ”_{phi phi } } $.

«Радиус, круг и центр кривизны» 👇

Задача 2

Найти радиус кривизны экспоненты $y=e^{x} $ при $x=0$.

Находим производные: $y’=e^{x} $; $y”=e^{x} $.

По формуле для радиуса кривизны получаем:

[R=frac{sqrt{left(1+left(y’right)^{2} right)^{3} } }{y”} =frac{sqrt{left(1+left(e^{x} right)^{2} right)^{3} } }{e^{x} } =frac{sqrt{left(1+e^{2cdot x} right)^{3} } }{e^{x} } .]

Вычисляем радиус кривизны экспоненты при $x=0$:

[Rleft(0right)=frac{sqrt{left(1+e^{2cdot 0} right)^{3} } }{e^{0} } =2cdot sqrt{2} . ]

Задача 3

Найти радиус кривизны кардиоиды $rho =1+cos phi $.

Находим производные: $rho ‘=-sin phi $; $rho ”=-cos phi $.

Вычисляем:

[rho ^{2} +rho ‘^{2} =left(1+cos phi right)^{2} +left(-sin phi right)^{2} =2cdot left(1+cos phi right);]

[rho ^{2} +2cdot rho ‘^{2} -rho cdot rho ”=left(1+cos phi right)^{2} +2cdot left(-sin phi right)^{2} -left(1+cos phi right)cdot left(-cos phi right)=]

[=3cdot left(1+cos phi right).]

По формуле для радиуса кривизны получаем:

[R=frac{sqrt{left(rho ^{2} +left(rho ‘_{phi } right)^{2} right)^{3} } }{rho ^{2} +2cdot left(rho ‘_{phi } right)^{2} -rho cdot rho ”_{phi phi } } =frac{sqrt{left(2cdot left(1+cos phi right)right)^{3} } }{3cdot left(1+cos phi right)} =frac{2}{3} cdot sqrt{2cdot left(1+cos phi right)} =frac{4}{3} cdot cos frac{phi }{2} .]

Найдем координаты центра кривизны $Pleft(x_{C} ;y_{C} right)$ кривой $y=fleft(xright)$.

Координаты центра кривизны для точки $Mleft(x;yright)$ удовлетворяют уравнению нормали $y_{C} -y=-frac{1}{y’left(xright)} cdot left(x_{C} -xright)$.

Уравнение круга кривизны: $left(x-x_{C} right)^{2} +left(y-y_{C} right)^{2} =R^{2} $.

Решив систему $left{begin{array}{c} {y_{C} -y=-frac{1}{y’left(xright)} cdot left(x_{C} -xright)} \ {left(x-x_{C} right)^{2} +left(y-y_{C} right)^{2} =R^{2} } end{array}right. $, получим искомые координаты центра кривизны: $left{begin{array}{c} {x_{C} =x-frac{y’cdot left(1+y’^{2} right)}{y”} } \ {y_{C} =y+frac{1+y’^{2} }{y”} } end{array}right. $.

Координаты центра кривизны по существу являются параметрическими уравнения эволюты.

Задача 4

Найти эволюту параболы $y=x^{2} $. Результаты представить графически.

Находим производные: $y’=2cdot x$; $y”=2$.

По формулам $left{begin{array}{c} {x_{C} =x-frac{y’cdot left(1+y’^{2} right)}{y”} } \ {y_{C} =y+frac{1+y’^{2} }{y”} } end{array}right. $ находим координаты центра кривизны для произвольной точки $Mleft(x;yright)$.

Получаем:

[x_{C} =x-frac{2cdot xcdot left(1+left(2cdot xright)^{2} right)}{2} =-4cdot x^{3} ;]

[y_{C} =y+frac{1+left(2cdot xright)^{2} }{2} =3cdot x^{2} +frac{1}{2} .]

Полученные выражения фактически представляют собой параметрические уравнения эволюты, в которых $x$ является параметром. Если исключить параметр $x$ из этих уравнений, то может быть получено уравнение вида $Fleft(x_{C} ;y_{C} right)=0$, которое непосредственно связывает координаты эволюты.

Совмещенный график эвольвенты $y=x^{2} $ и её эволюты:

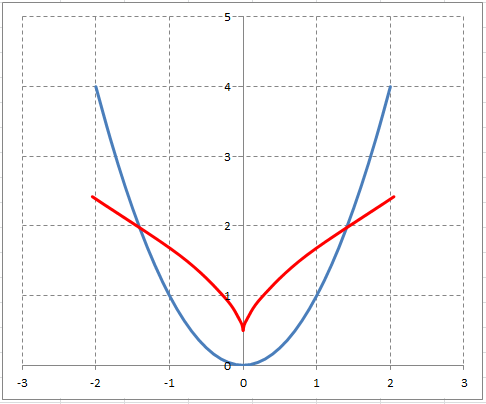
На графике синей линией изображена парабола $y=x^{2} $, а красной линией — её эволюта. Эволюта представляет собой полукубическую параболу.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Радиус кривизны и центр кривизны

В дифференциальной геометрии, радиус кривизны, R, является обратной величиной кривизны. Для кривой он равен радиусу дуги окружности , которая наилучшим образом приближает кривую в этой точке. Для поверхностей радиус кривизны – это радиус круга, который наилучшим образом соответствует нормальному сечению или их комбинациям.

Содержание

1 Определение
2 Формула
- 2.1 Вывод
3 Примеры
- 3.1 Полукруги и окружности
- 3.2 Эллипсы
4 Применения
- 4.1 Напряжение в полупроводниковых структурах
5 См. Также
6 Ссылки
7 Дополнительная литература
8 Внешние ссылки

Определение

В случае пространственной кривой радиус кривизны – это длина кривизны вектор.

В случае плоской кривой , тогда R является абсолютным значением of

R ≡ | d s d φ | = 1 κ, { displaystyle R Equiv left | { frac {ds} {d varphi}} right | = { frac {1} { kappa}},} ${ displaystyle R Equiv left | { frac {ds} {d varphi}} right | = { frac {1} { kappa}},}$

где s – длина дуги от фиксированной точки на кривой, φ – это тангенциальный угол, а κ – кривизна.

Если кривая задана в декартовых координатах как y (x), то радиус кривизны равен (при условии, что кривая дифференцируема до порядка 2):

R = | (1 + y ′ 2) 3 2 y ″ |, где y ′ = dydx, y ″ = d 2 ydx 2, { displaystyle R = left | { frac { left (1 + y ‘^ {, 2} right) ^ { frac {3} {2}}} {y ”}} right |, qquad { t_dv {where}} quad y ‘= { frac {dy} {dx}}, quad y’ ‘= { frac { d ^ {2} y} {dx ^ {2}}},} ${displaystyle R=left|{frac {left(1+y'^{,2}right)^{frac {3}{2}}}{y''}}right|,qquad {t_dv{where}}quad y'={frac {dy}{dx}},quad y''={frac {d^{2}y}{dx^{2}}},}$

и | z | обозначает абсолютное значение z.

Если кривая задана параметрически функциями x (t) и y (t), то радиус кривизны равен

R = | d s d φ | = | (x ˙ 2 + y ˙ 2) 3 2 x ˙ y ¨ – y ˙ x ¨ |, где x ˙ = d x d t, x ¨ = d 2 x d t 2, y ˙ = d y d t, y ¨ = d 2 y d t 2. { Displaystyle R = left | { frac {ds} {d varphi}} right | = left | { frac { left ({{ dot {x}} ^ {2} + { dot {y}} ^ {2}} right) ^ { frac {3} {2}}} {{ dot {x}} { ddot {y}} – { dot {y}} { ddot {x}}}} right |, qquad { t_dv {где}} quad { dot {x}} = { frac {dx} {dt}}, quad { ddot {x}} = { frac {d ^ {2} x} {dt ^ {2}}}, quad { dot {y}} = { frac {dy} {dt}}, quad { ddot {y}} = { frac {d ^ {2} y} {dt ^ {2}}}.} ${ displaystyle R = left | { frac {ds} {d varphi}} right | = left | { frac { left ({{ dot {x}} ^ {2} + { dot {y}} ^ {2}} right) ^ { frac {3} {2}}} {{ dot {x}} { ddot {y}} - { dot {y}} { ddot {x}}}} right |, qquad { t_dv {where}} quad { dot {x}} = { frac {dx} {dt}}, quad { ddot {x}} = { frac {d ^ {2} x} {dt ^ {2}}}, quad { dot {y} } = { frac {dy} {dt}}, quad { ddot {y}} = { frac {d ^ {2} y} {dt ^ {2}}}.}$

Эвристически этот результат можно интерпретировать как

R = | v | 3 | v × v ˙ |, где | v | = | (x ˙, y ˙) | = R d φ d t. { displaystyle R = { frac { left | mathbf {v} right | ^ {3}} { left | mathbf {v} times mathbf { dot {v}} right |}}, qquad { t_dv {where}} quad left | mathbf {v} right | = { big |} ({ dot {x}}, { dot {y}}) { big | } = R { frac {d varphi} {dt}}.} ${ displaystyle R = { frac { left | mathbf {v} right | ^ {3}} { left | mathbf {v} times mathbf { точка {v}} right |}}, qquad { t_dv {where}} quad left | mathbf {v} right | = { big |} ({ dot {x}}, { точка {y}}) { big |} = R { frac {d varphi} {dt}}.}$

Формула

Если γ : ℝ → ℝ – параметризованная кривая в ℝ, то радиус кривизны в каждой точке кривой ρ: ℝ → ℝ определяется как

ρ = | γ ′ | 3 | γ ′ | 2 | γ ″ | 2 – (γ ′ ⋅ γ ″) 2 { displaystyle rho = { frac { left | { boldsymbol { gamma}} ‘ right | ^ {3}} { sqrt { left | { boldsymbol { gamma}} ‘ right | ^ {2} , left | { boldsymbol { gamma}}’ ‘ right | ^ {2} – left ({ boldsymbol { gamma}}’ cdot { boldsymbol { gamma}} ” right) ^ {2}}}}} ${displaystyle rho ={frac {left|{boldsymbol {gamma }}'right|^{3}}{sqrt {left|{boldsymbol {gamma }}'right|^{2},left|{boldsymbol {gamma }}''right|^{2}-left({boldsymbol {gamma }}'cdot {boldsymbol {gamma }}''right)^{2}}}}}$

Как частный случай, если f (t) является функцией от ℝ до, то радиус кривизны ее график, γ(t) = (t, f (t)), равно

ρ (t) = | 1 + f ′ 2 (t) | 3 2 | f ″ (t) |. { displaystyle rho (t) = { frac { left | 1 + f ‘^ {, 2} (t) right | ^ { frac {3} {2}}} { left | f’ ‘(t) right |}}.} ${displaystyle rho (t)={frac {left|1+f'^{,2}(t)right|^{frac {3}{2}}}{left|f''(t)right|}}.}$

Вывод

Пусть γ как указано выше, и зафиксируйте t. Мы хотим найти радиус ρ параметризованного круга, который соответствует γ в его нулевой, первой и второй производных в точке t. Ясно, что радиус не будет зависеть от положения γ (t), только от скорости γ ′ (t) и ускорения γ ″ (t). Есть только три независимых скаляра, которые могут быть получены из двух векторов v и w, а именно v· v, v· wи w· w. Таким образом, радиус кривизны должен быть функцией трех скаляров | γ ′ (t) |, | γ ″ (t) | и γ ′ (t) · γ″(t).

Общее уравнение для параметризованной окружности в:

g (u) = a соз ⁡ час (U) + б грех ⁡ час (U) + с { displaystyle mathbf {g} (u) = mathbf {a} cos h (u) + mathbf {b} sin h (u)) + mathbf {c}}

{ displaystyle mathbf {g} (u) = mathbf {a} соз час (и) + mathbf {b} грех час (и) + mathbf {c}}

где c ∈ ℝ – центр окружности (не имеет значения, поскольку он исчезает в производных), a,b∈ ℝ – перпендикулярные векторы длины ρ (что есть, a· a= b· b= ρ и a· b= 0), а h: ℝ → ℝ – произвольная функция, дважды дифференцируемая в точке t.

Соответствующие производные от g оказываются

| g ′ | 2 = ρ 2 (h ′) 2 g ′ ⋅ g ″ = ρ 2 h ′ h ″ | г ″ | 2 знак равно ρ 2 ((h ‘) 4 + (h ″) 2) { displaystyle { begin {align} | mathbf {g}’ | ^ {2} = rho ^ {2} (h ‘) ^ {2} \ mathbf {g} ‘ cdot mathbf {g}’ ‘= rho ^ {2} h’h’ ‘\ | mathbf {g}’ ‘| ^ {2} = rho ^ {2} left ((h ‘) ^ {4} + (h’ ‘) ^ {2} right) end {align}}} ${displaystyle {begin{aligned}|mathbf {g} '|^{2}=rho ^{2}(h')^{2}\mathbf {g} 'cdot mathbf {g} ''=rho ^{2}h'h''\|mathbf {g} ''|^{2}=rho ^{2}left((h')^{4}+(h'')^{2}right)end{aligned}}}$

Если теперь мы приравняем эти производные g к соответствующим производным от γ при t, получаем

| γ ′ (t) | 2 = ρ 2 h ′ 2 (t) γ ′ (t) ⋅ γ ″ (t) = ρ 2 h ′ (t) h ″ (t) | γ ″ (t) | 2 знак равно ρ 2 (час ‘4 (t) + час ″ 2 (t)) { displaystyle { begin {align} | { boldsymbol { gamma}}’ (t) | ^ {2} = rho ^ {2} h ‘^ {, 2} (t) \ { boldsymbol { gamma}}’ (t) cdot { boldsymbol { gamma}} ” (t) = rho ^ { 2} h ‘(t) h’ ‘(t) \ | { boldsymbol { gamma}}’ ‘(t) | ^ {2} = rho ^ {2} left (h’ ^ {, 4} (t) + h ” ^ {, 2} (t) right) end {align}}} ${displaystyle {begin{aligned}|{boldsymbol {gamma }}'(t)|^{2}=rho ^{2}h'^{,2}(t)\{boldsymbol {gamma }}'(t)cdot {boldsymbol {gamma }}''(t)=rho ^{2}h'(t)h''(t)\|{boldsymbol {gamma }}''(t)|^{2}=rho ^{2}left(h'^{,4}(t)+h''^{,2}(t)right)end{aligned}}}$

Эти три уравнения с тремя неизвестными (ρ, h ′ (t) и h ″ ( t)) можно решить относительно ρ, дав формулу для радиуса кривизны:

ρ (t) = | γ ′ (t) | 3 | γ ′ (t) | 2 | γ ″ (t) | 2 – (γ ′ (t) ⋅ γ ″ (t)) 2 { displaystyle rho (t) = { frac { left | { boldsymbol { gamma}} ‘(t) right | ^ {3 }} { sqrt { left | { boldsymbol { gamma}} ‘(t) right | ^ {2} , left | { boldsymbol { gamma}}’ ‘(t) right | ^ {2} – { big (} { boldsymbol { gamma}} ‘(t) cdot { boldsymbol { gamma}}’ ‘(t) { big)} ^ {2}}}}} ${displaystyle rho (t)={frac {left|{boldsymbol {gamma }}'(t)right|^{3}}{sqrt {left|{boldsymbol {gamma }}'(t)right|^{2},left|{boldsymbol {gamma }}''(t)right|^{2}-{big (}{boldsymbol {gamma }}'(t)cdot {boldsymbol {gamma }}''(t){big)}^{2}}}}}$

или, опуская параметр t для удобства чтения,

ρ = | γ ′ | 3 | γ ′ | 2 | γ ″ | 2 – (γ ′ ⋅ γ ″) 2. { displaystyle rho = { frac { left | { boldsymbol { gamma}} ‘ right | ^ {3}} { sqrt { left | { boldsymbol { gamma}}’ right | ^ {2} ; left | { boldsymbol { gamma}} ” right | ^ {2} – left ({ boldsymbol { gamma}} ‘ cdot { boldsymbol { gamma}}’ ‘ right) ^ {2}}}}.} ${displaystyle rho ={frac {left|{boldsymbol {gamma }}'right|^{3}}{sqrt {left|{boldsymbol {gamma }}'right|^{2};left|{boldsymbol {gamma }}''right|^{2}-left({boldsymbol {gamma }}'cdot {boldsymbol {gamma }}''right)^{2}}}}.}$

Примеры

Полукруги и окружности

Для полукруга радиуса a в верхней половине- плоскость

y = a 2 – x 2, y ′ = – xa 2 – x 2, y ″ = – a 2 (a 2 – x 2) 3 2, R = | – а | = а. { displaystyle y = { sqrt {a ^ {2} -x ^ {2}}}, quad y ‘= { frac {-x} { sqrt {a ^ {2} -x ^ {2} }}}, quad y ” = { frac {-a ^ {2}} { left (a ^ {2} -x ^ {2} right) ^ { frac {3} {2}} }}, quad R = | -a | = a.} ${displaystyle y={sqrt {a^{2}-x^{2}}},quad y'={frac {-x}{sqrt {a^{2}-x^{2}}}},quad y''={frac {-a^{2}}{left(a^{2}-x^{2}right)^{frac {3}{2}}}},quad R=|-a|=a.}$

Эллипс (красный) и его evolute (синий). Точки – это вершины эллипса в точках наибольшей и наименьшей кривизны.

Для полукруга радиуса a в нижней полуплоскости

y = – a 2 – x 2, R = | а | = а. { displaystyle y = – { sqrt {a ^ {2} -x ^ {2}}}, quad R = | a | = a.} ${ displaystyle y = - { sqrt {a ^ {2} -x ^ { 2}}}, quad R = | a | = a.}$

окружность радиуса a имеет радиус кривизны равен a.

Эллипсы

В эллипсе с большой осью 2a и малой осью 2b вершины на большой оси имеют наименьший радиус кривизны любые точки, R = b / a; а вершины на малой оси имеют наибольший радиус кривизны из всех точек, R = a / b.

Приложения

Для использования в дифференциальной геометрии см. Уравнение Чезаро.
Для радиуса кривизны земли (аппроксимированного сплющенным эллипсоидом) см. Радиус кривизны Земли.
Радиус кривизны также используется в уравнении из трех частей для изгиба лучей.
Радиус кривизны (оптика)
Тонкопленочные технологии
Печатная электроника

Напряжение в полупроводниковых структурах

Напряжение в полупроводниковой структуре, включающей напыленные тонкие пленки, обычно возникает в результате теплового расширения (теплового напряжения) во время производственный процесс. Термическое напряжение возникает из-за того, что осаждение пленки обычно производится при температуре выше комнатной. При охлаждении от температуры осаждения до комнатной температуры разница в коэффициентах теплового расширения подложки и пленки вызывает тепловое напряжение.

возникает из-за микроструктуры, созданной в пленке, поскольку атомы нанесен на подложку. Напряжение растяжения возникает из-за микропор (небольших отверстий, которые считаются дефектами) в тонкой пленке из-за притягивающего взаимодействия атомов через пустоты.

Напряжение в тонкопленочных полупроводниковых структурах приводит к короблению пластин. Радиус кривизны напряженной конструкции связан с тензором напряжений в конструкции и может быть описан как модифицированный. Топография напряженной конструкции, включая радиусы кривизны, может быть измерена с помощью методов оптического сканирования. Современные инструменты сканера позволяют измерять полную топографию подложки и измерять оба главных радиуса кривизны, обеспечивая при этом точность порядка 0,1% для радиусов кривизны 90 метров и более.

См. Также

Ссылки

Дополнительная литература

do Carmo, Manfredo (1976). Дифференциальная геометрия кривых и поверхностей. ISBN 0-13-212589-7.

Внешние ссылки

Источник

From Wikipedia, the free encyclopedia

This article is about the general mathematical concept. For its optical applications, see Radius of curvature (optics).

In differential geometry, the radius of curvature (Rc), R, is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof.^[1]^[2]^[3]

Definition[edit]

In the case of a space curve, the radius of curvature is the length of the curvature vector.

In the case of a plane curve, then R is the absolute value of^[3]

${displaystyle Requiv left|{frac {ds}{dvarphi }}right|={frac {1}{kappa }},}$

where s is the arc length from a fixed point on the curve, φ is the tangential angle and κ is the curvature.

Formula[edit]

In 2D[edit]

If the curve is given in Cartesian coordinates as y(x), i.e., as the graph of a function, then the radius of curvature is (assuming the curve is differentiable up to order 2):

${displaystyle R=left|{frac {left(1+y'^{,2}right)^{frac {3}{2}}}{y''}}right|,qquad {mbox{where}}quad y'={frac {dy}{dx}},quad y''={frac {d^{2}y}{dx^{2}}},}$

and |z| denotes the absolute value of z.
Also in Classical mechanics branch of Physics Radius of curvature is given by (Net Velocity)²/Acceleration Perpendicular

If the curve is given parametrically by functions x(t) and y(t), then the radius of curvature is

${displaystyle R=left|{frac {ds}{dvarphi }}right|=left|{frac {left({{dot {x}}^{2}+{dot {y}}^{2}}right)^{frac {3}{2}}}{{dot {x}}{ddot {y}}-{dot {y}}{ddot {x}}}}right|,qquad {mbox{where}}quad {dot {x}}={frac {dx}{dt}},quad {ddot {x}}={frac {d^{2}x}{dt^{2}}},quad {dot {y}}={frac {dy}{dt}},quad {ddot {y}}={frac {d^{2}y}{dt^{2}}}.}$

Heuristically, this result can be interpreted as^[2]

${displaystyle R={frac {left|mathbf {v} right|^{3}}{left|mathbf {v} times mathbf {dot {v}} right|}},qquad {mbox{where}}quad left|mathbf {v} right|={big |}({dot {x}},{dot {y}}){big |}=R{frac {dvarphi }{dt}}.}$

In n dimensions[edit]

If γ : ℝ → ℝⁿ is a parametrized curve in ℝⁿ then the radius of curvature at each point of the curve, ρ : ℝ → ℝ, is given by^[3]

${displaystyle rho ={frac {left|{boldsymbol {gamma }}'right|^{3}}{sqrt {left|{boldsymbol {gamma }}'right|^{2},left|{boldsymbol {gamma }}''right|^{2}-left({boldsymbol {gamma }}'cdot {boldsymbol {gamma }}''right)^{2}}}}}$

As a special case, if f(t) is a function from ℝ to ℝ, then the radius of curvature of its graph, γ(t) = (t, f(t)), is

${displaystyle rho (t)={frac {left|1+f'^{,2}(t)right|^{frac {3}{2}}}{left|f''(t)right|}}.}$

Derivation[edit]

Let γ be as above, and fix t. We want to find the radius ρ of a parametrized circle which matches γ in its zeroth, first, and second derivatives at t. Clearly the radius will not depend on the position γ(t), only on the velocity γ′(t) and acceleration γ″(t). There are only three independent scalars that can be obtained from two vectors v and w, namely v · v, v · w, and w · w. Thus the radius of curvature must be a function of the three scalars |γ′(t)|², |γ″(t)|² and γ′(t) · γ″(t).^[3]

The general equation for a parametrized circle in ℝⁿ is

{displaystyle mathbf {g} (u)=mathbf {a} cos(h(u))+mathbf {b} sin(h(u))+mathbf {c} }

where c ∈ ℝⁿ is the center of the circle (irrelevant since it disappears in the derivatives), a,b ∈ ℝⁿ are perpendicular vectors of length ρ (that is, a · a = b · b = ρ² and a · b = 0), and h : ℝ → ℝ is an arbitrary function which is twice differentiable at t.

The relevant derivatives of g work out to be

${displaystyle {begin{aligned}|mathbf {g} '|^{2}&=rho ^{2}(h')^{2}\mathbf {g} 'cdot mathbf {g} ''&=rho ^{2}h'h''\|mathbf {g} ''|^{2}&=rho ^{2}left((h')^{4}+(h'')^{2}right)end{aligned}}}$

If we now equate these derivatives of g to the corresponding derivatives of γ at t we obtain

${displaystyle {begin{aligned}|{boldsymbol {gamma }}'(t)|^{2}&=rho ^{2}h'^{,2}(t)\{boldsymbol {gamma }}'(t)cdot {boldsymbol {gamma }}''(t)&=rho ^{2}h'(t)h''(t)\|{boldsymbol {gamma }}''(t)|^{2}&=rho ^{2}left(h'^{,4}(t)+h''^{,2}(t)right)end{aligned}}}$

These three equations in three unknowns (ρ, h′(t) and h″(t)) can be solved for ρ, giving the formula for the radius of curvature:

${displaystyle rho (t)={frac {left|{boldsymbol {gamma }}'(t)right|^{3}}{sqrt {left|{boldsymbol {gamma }}'(t)right|^{2},left|{boldsymbol {gamma }}''(t)right|^{2}-{big (}{boldsymbol {gamma }}'(t)cdot {boldsymbol {gamma }}''(t){big )}^{2}}}}}$

or, omitting the parameter t for readability,

${displaystyle rho ={frac {left|{boldsymbol {gamma }}'right|^{3}}{sqrt {left|{boldsymbol {gamma }}'right|^{2};left|{boldsymbol {gamma }}''right|^{2}-left({boldsymbol {gamma }}'cdot {boldsymbol {gamma }}''right)^{2}}}}.}$

Examples[edit]

Semicircles and circles[edit]

For a semi-circle of radius a in the upper half-plane

${displaystyle y={sqrt {a^{2}-x^{2}}},quad y'={frac {-x}{sqrt {a^{2}-x^{2}}}},quad y''={frac {-a^{2}}{left(a^{2}-x^{2}right)^{frac {3}{2}}}},quad R=|-a|=a.}$

An ellipse (red) and its evolute (blue). The dots are the vertices of the ellipse, at the points of greatest and least curvature.

For a semi-circle of radius a in the lower half-plane

${displaystyle y=-{sqrt {a^{2}-x^{2}}},quad R=|a|=a.}$

The circle of radius a has a radius of curvature equal to a.

Ellipses[edit]

In an ellipse with major axis 2a and minor axis 2b, the vertices on the major axis have the smallest radius of curvature of any points, R = b²/a; and the vertices on the minor axis have the largest radius of curvature of any points, R = a²/b.

The ellipse’s radius of curvature, as a function of parameter t

${displaystyle R(t)={frac {(b^{2}cos ^{2}t+a^{2}sin ^{2}t)^{3/2}}{ab}};,;;{text{where}};;theta =tan ^{-1}{Big (}{frac {y}{x}}{Big )}=tan ^{-1}{Big (}{frac {b}{a}};tan ;t{Big )}}$

^[4]

And as a function of θ

${displaystyle R(theta )={frac {a^{2}}{b}}{biggl (}{frac {1-e^{2}(2-e^{2})(cos theta )^{2})}{1-e^{2}(cos theta )^{2}}}{biggr )}^{3/2}}$

Where e is the eccentricity of the ellipse and is given by:

${displaystyle e^{2}=1-{frac {b^{2}}{a^{2}}}}$

Applications[edit]

For the use in differential geometry, see Cesàro equation.
For the radius of curvature of the earth (approximated by an oblate ellipsoid); see also: arc measurement
Radius of curvature is also used in a three part equation for bending of beams.
Radius of curvature (optics)
Thin films technologies
Printed electronics
Minimum railway curve radius
AFM probe

Stress in semiconductor structures[edit]

Stress in the semiconductor structure involving evaporated thin films usually results from the thermal expansion (thermal stress) during the manufacturing process. Thermal stress occurs because film depositions are usually made above room temperature. Upon cooling from the deposition temperature to room temperature, the difference in the thermal expansion coefficients of the substrate and the film cause thermal stress.^[5]

Intrinsic stress results from the microstructure created in the film as atoms are deposited on the substrate. Tensile stress results from microvoids (small holes, considered to be defects) in the thin film, because of the attractive interaction of atoms across the voids.

The stress in thin film semiconductor structures results in the buckling of the wafers. The radius of the curvature of the stressed structure is related to stress tensor in the structure, and can be described by modified Stoney formula.^[6] The topography of the stressed structure including radii of curvature can be measured using optical scanner methods. The modern scanner tools have capability to measure full topography of the substrate and to measure both principal radii of curvature, while providing the accuracy of the order of 0.1% for radii of curvature of 90 meters and more.^[7]

References[edit]

^ Weisstien, Eric. “Radius of Curvature”. Wolfram Mathworld. Retrieved 15 August 2016.
^ ^a ^b Kishan, Hari (2007). Differential Calculus. Atlantic Publishers & Dist. ISBN 9788126908202.
^ ^a ^b ^c ^d Love, Clyde E.; Rainville, Earl D. (1962). Differential and Integral Calculus (Sixth ed.). New York: MacMillan.
^ Weisstein, Eric W. “Ellipse”. mathworld.wolfram.com. Retrieved 2022-02-23.
^ “Controlling Stress in Thin Films”. Flipchips.com. Retrieved 2016-04-22.
^ “On the determination of film stress from substrate bending : Stoney’s formula and its limits” (PDF). Qucosa.de. Retrieved 2016-04-22.
^ Peter Walecki. “Model X”. Zebraoptical.com. Retrieved 2016-04-22.

External links[edit]

The Geometry Center: Principal Curvatures
15.3 Curvature and Radius of Curvature
Weisstein, Eric W. “Principal Curvatures”. MathWorld.
Weisstein, Eric W. “Principal Radius of Curvature”. MathWorld.

Источник

Радиус, центр и круг кривизны. Эволюта и эвольвента

Смысл понятий радиуса, круга и центра кривизны

Вычисление радиуса и определение центра круга кривизны

Содержание

Определение