Как найти центр масс окружности с вырезом
2016-11-20
Определить центр масс плоского однородного диска с вырезанным отверстием (см. рис.). Величины $R, r$ и $d$ известны.
При решении задач данного типа удобно применять следующий прием. Мысленно вырежем еще одно отверстие в диске, симметричное имеющемуся относительно точки О. Получившаяся фигура (диск без двух отверстий) обладает центром симметрии О и, следовательно, ее центр масс также расположен в точке О.
Центр масс мысленно вырезанного круга находится в его центре.
Будем отыскивать центр масс искомой фигуры, полагая, что она состоит из двух тел: круга и диска с двумя отверстиями. Согласно полученным во введении к разделу результатам, эта задача эквивалентна нахождению центра масс двух точечных масс, сосредоточенных в точках О и $O^< prime>$.
Выберем систему координат с началом в точке О.
Согласно определению центра масс:
Обозначим через $rho$ массу диска, приходящуюся на единицу его площади. Тогда масса круга равна:
а масса диска с двумя отверстиями:
Подставляя (2, 3) в (1) и сокращая на $rho pi$, окончательно получаем:
Таким образом, центр масс искомой фигуры расположен на отрезке $OO^< prime>$ на расстоянии $x_<цм>$ от точки О.
Тема 1.5. Центр тяжести тела
§1. Центр тяжести однородного тела.
Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.
Если разбить тело на элементарные части объемом ∆Vi , то на каждую его часть будет действовать сила притяжения ∆Pi, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.
Рис.1. Параллельная система сил
Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
§2. Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Рис.2. Центр тяжести тел, имеющих ось симметрии
2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.
Рис.3. Центр тяжести сплошной
сложной геометрической фигуры
– центр тяжести и площадь первой фигуры;
– центр тяжести и площадь второй фигуры;
– координата центра тяжести сплошной сложной геометрической фигуры по оси x;
– координата центра тяжести сплошной сложной геометрической фигуры по оси y;
3. Метод отрицательных площадей. Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
Рис.4. Центр тяжести сложной геометрической фигуры,
– центр тяжести и площадь первой фигуры;
– центр тяжести и площадь второй фигуры;
– координата центра тяжести сложной геометрической фигуры по оси x;
– координата центра тяжести сложной геометрической фигуры по оси y;
§3. Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =1/3(x1+x2+x3) ; yc =1/3(y1+y2+y3).
Рис.5. Центр тяжести треугольника
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2 ; yc =h/2.
Рис. 6. Центр тяжести треугольника
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2 ; yc =4R/3π.
Рис. 7. Центр тяжести полукруга
4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: xc =R ; yc =R.
Рис. 8. Центр тяжести круга
Вопросы для самопроверки:
– Что называется центром параллельных сил?
– Что называется центром тяжести тела?
– Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?
– Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?
– Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?
– Как используются свойства симметрии при определении центров тяжести тел?
– В чем состоит сущность способа отрицательных площадей?
– Каким графическим построением можно найти центр тяжести треугольника?
– Запишите формулу, определяющую центр тяжести треугольника.
Найти центр масс окружности
iSopromat.ru

Формулы для расчета координат положения центра тяжести треугольника, дуги окружности и кругового сегмента.

Центр тяжести треугольника
Центр тяжести площади треугольника совпадает с точкой пересечения его медиан (рисунок 1.10, а).
Центр тяжести дуги окружности
Дуга имеет ось симметрии (рисунок 1.10, б). Центр тяжести лежит на этой оси, т.е. yC = 0.
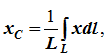
dl – элемент дуги, dl = Rdφ, R – радиус окружности, x = Rcosφ, L = 2αR,
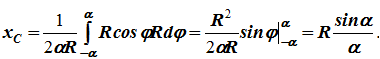
Центр тяжести кругового сектора
Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox, на которой находится центр тяжести (рисунок 1.10, в).
Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса (2/3)R.
Центр тяжести сектора совпадает с центром тяжести дуги AB:
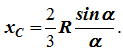
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Тема 1.5. Центр тяжести тела
§1. Центр тяжести однородного тела.
Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.
Если разбить тело на элементарные части объемом ∆Vi , то на каждую его часть будет действовать сила притяжения ∆Pi, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.
Рис.1. Параллельная система сил
Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
§2. Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Рис.2. Центр тяжести тел, имеющих ось симметрии
2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.
Рис.3. Центр тяжести сплошной
сложной геометрической фигуры
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сплошной сложной геометрической фигуры по оси x;
— координата центра тяжести сплошной сложной геометрической фигуры по оси y;
3. Метод отрицательных площадей. Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
Рис.4. Центр тяжести сложной геометрической фигуры,
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сложной геометрической фигуры по оси x;
— координата центра тяжести сложной геометрической фигуры по оси y;
§3. Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =1/3(x1+x2+x3) ; yc =1/3(y1+y2+y3).
Рис.5. Центр тяжести треугольника
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2 ; yc =h/2.
Рис. 6. Центр тяжести треугольника
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2 ; yc =4R/3π.
Рис. 7. Центр тяжести полукруга
4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: xc =R ; yc =R.
Рис. 8. Центр тяжести круга
Вопросы для самопроверки:
— Что называется центром параллельных сил?
— Что называется центром тяжести тела?
— Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?
— Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?
— Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?
— Как используются свойства симметрии при определении центров тяжести тел?
— В чем состоит сущность способа отрицательных площадей?
— Каким графическим построением можно найти центр тяжести треугольника?
— Запишите формулу, определяющую центр тяжести треугольника.
Центр тяжести тела — формулы и примеры нахождения

Общие сведения
Пусть имеется физическое тело, на которое не оказывается влияние, то есть другие объекты не действуют или их силы воздействия скомпенсированы. Рассматриваемое тело будет находиться в состоянии прямолинейного движения или покоя. Для удобства можно принять, что объект неподвижен, например, пусть это будет лодка на поверхности воды.
Если к плавательному средству приложить силу, смещённую к началу лодки F1, судно начнёт поворачиваться в сторону направления воздействия. Если ее переместить в горизонтальной плоскости в другой конец судна, лодка начнёт также поворачиваться, но направление вращения изменится. Отсюда можно сделать вывод, что существует такая точка приложения силы, точнее, линия, при воздействии на которую лодка не изменит своего положения, то есть плавательное средство начнёт двигаться ускоренно поступательно. Допустим, это будет сила F3.
Логично, что можно подобрать и другую силу, вызывающую поступательное прямолинейное перемещение, например, F4.
При этом точку воздействия можно перемещать по линии её направления, так как, согласно правилу, величина действия при этом не изменяется. В итоге получится точка, где пересекутся приложенные силы F3 и F4. Таких моментов можно приложить сколько угодно, при этом они все соединятся в одном месте. Точку пересечения линий действия сил, которые вызывают ускоренное поступательное движение тела, называют центром масс.
На лодку действует ещё одна сила — притяжения. На самом деле она воздействует на каждую частичку объекта, поэтому на тело одновременно оказывает влияние огромное количество моментов. Это множество и принято заменять их равнодействующей — то есть силой, приложенной к центру тяжести. В физике параметр обозначают как mg. Другими словами, это точка приложения равнодействующих сил тяжести.
Существует взаимосвязь между массой и тяжестью. Если тело разбить на кусочки и бросить их, скорость падения будет для всех тел одинаковой, так как ускорение не зависит от массы. При этом падающий объект движется поступательно.
А значит, приложенная сила проходит через центр масс, то есть через центр тяжести, поэтому несмотря на разный принцип определения этих точек, их положение совпадает.
Поиск центра тяжести
Чтобы определить центр тяжести для тела сложной формы, его нужно разделить на простые фигуры и определить точки равновесия для каждой из них. Для простых геометрических объектов используют симметрию. Например, в шаре параметр располагается в центре, в однородном цилиндре — в точке на середине оси. Частным случаем разбиения фигуры при определении является метод отрицательных площадей. Его применяют к телам, которые имеют вырезы, и при этом площадь удалённой части известна.
Вот формулы для вычисления центра в некоторых фигурах:
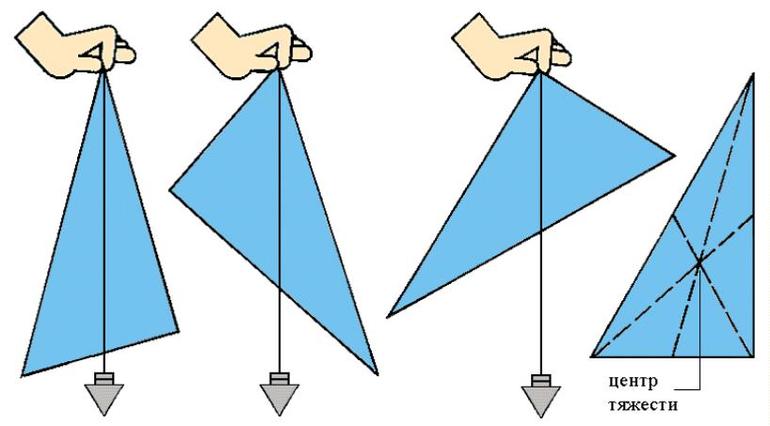
- В треугольнике: x = (1/3) * (x1 + x2 + x3); y = (1/3) * (y1 + y2 + y3). Физически центр находится в точке пересечения медиан и представляет собой среднее арифметическое из координат вершин.
- В прямоугольнике: x = b/2; y = h/2. Центр равновесия располагается в точке пересечения диагональных прямых.
- В полукруге: x =D/2; y = 4R/3π. Искомая точка лежит на оси симметрии.
- В круге: x = R; y = R. Точка тяжести находится в центре фигуры.
Стоит отметить, что центр тяжести объёмных тел может находиться и вне фигуры, например, как у кольца. Вообще же для трёхмерного пространства, как учат на уроках физики в 7 классе, центр тяжести тела вычисляют по формулам: x = (ΣΔ m * x) / m; y = (ΣΔ m * y) / m; z = (ΣΔ m * z) / m, где: m — масса тела, x, y, z — координаты искомой точки в пространстве. Уравнение можно переписать и в векторной форме: r = (1 / m) Σm * r, где r — радиус вектор.
Существует и ряд теорем, благодаря которым можно определить точку массы в теле:
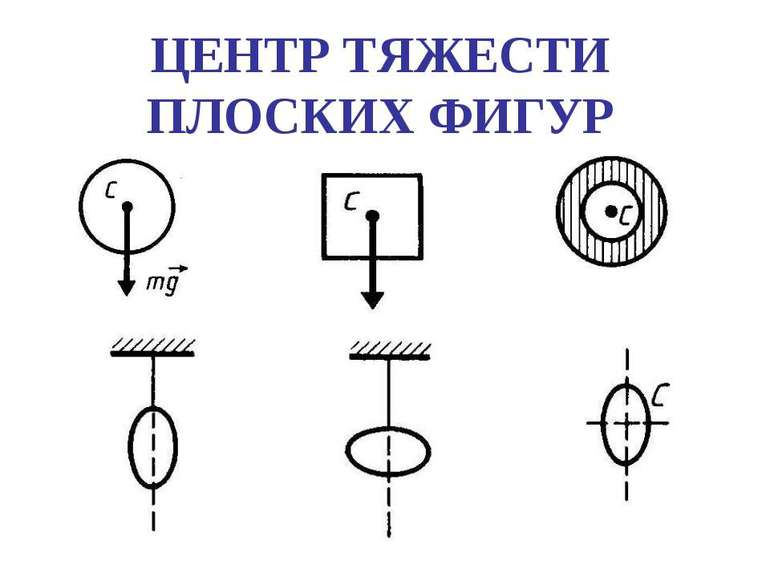
- При рассмотрении однородного тела, имеющего плоскость симметрии, центр массы будет находиться в этой плоскости.
- Если однородное тело обладает осью симметрии, центр располагается на ней.
- Центр симметрии однородной фигуры совпадает с центром массы.
- Центр масс симметричных фигур находится в их геометрическом центре.
Точку равновесия фигуры можно находить и через объём: R = (1 / V) * ∫ ∫ ∫rdV. Для плоских объектов используется формула R = (1 / S) * ∫ ∫ ∫rdS, а однородной линии R = (1 / L) * ∫ ∫ ∫rdL. Стоит отметить, что понятие точки тяжести применимо только к твёрдым объектам. Если это не так, использование понятия не имеет смысла.
Пример задания
Теоретический материал лучше всего усваивается на практических заданиях. Не исключение и понятие о центре тяжести. Тема несложная, но при нахождении параметра желательно фигуру изобразить на рисунке.
Наиболее часто ученикам преподаватель предлагает решить задачу о нахождении центра масс сложного тела, но при этом достаточно симметричного. Например, пусть имеется диск из однородной пластины, в котором вырезан кусок треугольной формы. Необходимо найти центр равновесия оставшегося объекта.
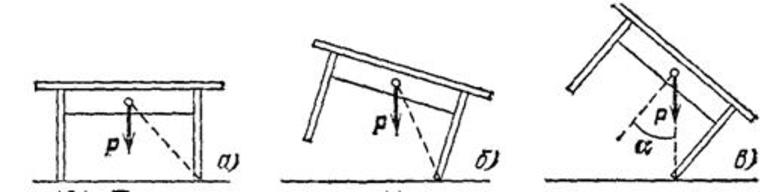
Если нарисовать условие задачи, станет понятно, что треугольник прямоугольный, а центр масс находится на горизонтальной прямой, проходящей через середину диска. Пусть это будет ось x. Чтобы решить задачу, нужно разбить сложную фигуру на несколько частей, в каждой из которых можно найти искомую точку.
Симметрично удалённому треугольнику можно выделить аналогичную часть. В итоге останется круг с вырезанным внутри квадратом. Точка масс диска находится в центре. Для удобства её можно обозначить как x1. Вторая фигура — это треугольник. Точка равновесия у него находится на пересечении медиан. То есть на 1/3 высоты. Обозначить точку можно как x2.
Если масса треугольника равна М2, а круга М1, искомую координату можно определить по формуле: x = (m1x1 + m2x2) / m1 + m2. Далее, нужно найти, чему равняется сторона вырезанного треугольника. Из рисунка можно понять, что это расстояние будет r * √2, где r — радиус диска.
Теперь можно найти, чему будут равны x1 и x2. x1 будет равняться нулю, так как эту точку можно принять за начало координат. x2 же будет равняться 1/3 длины медианы. Высота фигуры совпадает с радиусом диска, значит: x2 = R/3.
В таких задачах самое сложное — это найти массы. Первую можно определить исходя из того, что она будет равняться массе диска минус значение квадрата. Так как фигура однородная, масса прямо пропорциональна площади. Тогда для первого участка m1 = σ * S = σ * (Sкруга — Sквадрата) = σ * (pR2 — 2R2) = σR2 * (p — 2), где: σ — поверхностная площадь. Соответственно, m2 = σ * Sтреугольника = σ * R2. Все найденные величины нужно подставить в формулу и найти ответ: x = ((r * σ * R 2 /3)) / (σ * R2 * (p — 2) + σ * R2) = (r / 3 (p — 1)). Это и будет искомая координата.
Простая задачка
Пусть имеются 2 шара. Они расположены так, что соприкасаются друг с другом. Сделаны тела из одного материала, но при этом радиусы у них отличаются вдвое. Значение первого равняется r = 20 см, а второго 40, то есть 2r. Найти, где находится точка равновесия такого объекта. Такого рода задачи обычно любят демонстрировать на презентациях, касающихся темы. Задача простая, но между тем помогает понять принцип нахождения центра равновесия.

Итак, при решении нужно будет воспользоваться формулой: x = (m1x1 + m2x2) / m1 + m2. Так как по условию радиусы шаров отличаются вдвое, их массы будут отличаться в 8 раз. Объём всегда пропорционален кубу линейных размеров.
Массу первого шара можно обозначить как m, а второго — 8m. Начало координат для удобства лучше поместить в центр меньшей фигуры. В результате середина большого шара будет иметь координату 3r. Значит, искомая координата равняется: x = ((m* 0 + 8m * 3r)) / (m + 8m) = (8 * 3r) / 9 = 8r/3.
То есть нужная точка находится на расстоянии 1/3 радиуса ближе к маленькому шару (если отсчитывать от середины большого).
[spoiler title=”источники:”]
http://www.sites.google.com/site/tehmehprimizt/lekcii/teoreticeskaa-mehanika/statika/centr-tazesti
http://b4.cooksy.ru/articles/nayti-tsentr-mass-okruzhnosti
[/spoiler]

Рис. 1.8
Пример 2.
Внутри диска радиусом R = 105,6 см, изготовленного из плоскопараллельной однородной пластинки, вырезан квадрат таким образом, как показано на рис. 1.8. Найти положение центра тяжести диска с вырезом.
Решение. Нахождение положения центра тяжести однородных тел, имеющих вырез, в рамках школьной программы возможно лишь при условии, что известны положения центров тяжести целого тела и вырезанной части. При этом на чертеже тело с вырезом нужно расположить так, чтобы центры тяжести целого тела и вырезанной части находились в плоскости рисунка на горизонтальной прямой. Тогда силу тяжести целого тела можно представить как сумму двух параллельных сил – силы тяжести вырезанной части и силы тяжести оставшейся фигуры, т.е. тела с вырезом.
Рассмотрим конкретную задачу.
Если бы диск массой m был без выреза, то на него действовала бы сила тяжести mg = m1g + m2 g , где m1, m2 – масса вырезанного квадрата и
масса диска с вырезом соответственно. При этом сила тяжести mg приложена к центру тяжести диска без выреза (к геометрическому центру диска), m1g – к центру тяжести квадрата (к геометрическому центру квадрата), m2 g – в некоторой точке О/, соответствующей центру тяжести диска с выре-
зом. При этом диск находился бы в равновесии.
Запишем уравнение моментов целого диска относительно оси OZ, проходящей через точку О (геометрический центр диска) перпендикулярно плоскости чертежа, считая диск состоящим из двух частей – квадрата и диска с вырезом:
|
∑M Z = m1g |
R |
− m2 gxc = 0 , |
(1) |
|
2 |
где хс – расстояние от оси OZ до центра тяжести пластинки с вырезом. Выразив массы вырезанного квадрата и диска через плотность и объем
|
m = 1 |
ρhR2 |
, |
m =ρhπR2 |
(2) |
|
|
1 |
2 |
||||
(где h – толщина пластинки; ρ – плотность материала, из которого она изготовлена), из (1) – (2) находим
101

|
1 m R |
1 m R |
R |
|||||||
|
xc = |
2 |
1 |
= |
2 |
1 |
= |
≈ 0,1 м . |
||
|
m2 |
m − m1 |
2(2π −1) |
|||||||
|
Ответ: xc = |
R |
≈ 0,1 м. |
|||||||
|
2(2π−1) |
|||||||||
Пример 3.
Лестница массой m = 30 кг прислонена к гладкой вертикальной стене под некоторым углом к полу. Коэффициент трения между лестницей и полом µ = 0,3. Определить наименьший угол наклона лестницы к полу, при котором она может оставаться в равновесии, и силу, с которой лестница давит на стену, когда скользит.
Решение. На лестницу кроме силы тяжести mg , приложенной к ее центру масс (сере-
дине), действуют силы: со стороны пола – сила
|
реакции N1 – и сила трения покоя Fтр. пок. ; со |
|
|
стороны стены – сила реакции N2 (рис. 1.9). |
|
|
При этом сила трения направлена таким обра- |
|
|
зом, чтобы препятствовать скольжению лест- |
|
|
ницы по полу. |
|
|
Введем систему координат XYZ. Относи- |
|
|
Рис. 1.9 |
тельно оси OZ, проходящей через точку О пер- |
|
пендикулярно плоскости чертежа, момент силы |
|
|
трения покоя Fтр. |
пок. равен нулю, сила тяжести mg и сила реакции стены |
|
N2 «вращают» лестницу по часовой стрелке, а сила реакции пола N1 – |
|
против. С учетом этого запишем уравнения равновесия лестницы в виде |
|||
|
∑M Z = mg 1 cosα + N2 |
sin α − N1 |
cosα = 0 , |
(1) |
|
2 |
|||
|
∑Fx = N2 − Fтр. пок. = 0 , |
(2) |
||
|
∑Fy = N1 − mg = 0 . |
(3) |
||
|
Поскольку сила трения покоя |
|||
|
Fтр. пок. ≤ Fтр. max = µN1, |
|||
|
то уравнения (2) – (3) можно записать в виде |
|||
|
N2 = Fтр. пок. ≤ µN1 ; |
N1 = mg ; |
N2 ≤ µmg . |
(4) |
102

Преобразуем уравнение (1) с учетом выражений (4):
|
mg |
+µmgtgα ≥ mg . |
|||||
|
Отсюда находим |
2 |
|||||
|
tgα ≥ |
1 |
; |
αmin = arctg |
1 |
≈ 59 . |
|
|
2µ |
2µ |
|||||
Обратимся теперь ко второму вопросу задачи.
При скольжении лестницы сила трения будет равна Fтр = µN1 . Следо-
вательно, сила N2/ (по третьему закону Ньютона N2/ = N2 , с которой лестница будет давить на стену
N2/ = Fтр = µN1 = µmg =88,2 H .
Ответ: αmin = arctg 21µ ≈ 59 ; N2/ = µmg =88,2 H .
Пример 4.
На цилиндр намотана нить, конец которой закреплен на стойке в верхней точке наклонной плоскости так, как показано на рис. 1.10. Коэффициент трения цилиндра о плоскость – µ. При каком максимальном значении угла α цилиндр не будет скатываться с наклонной плоскости?
Решение. На цилиндр действуют четыре силы: сила тяжести mg , сила натяжения нити Т , сила реакции N и
сила трения Fтр. пок. , препятствующая скольжению цилиндра по плоскости.
|
Так как цилиндр покоится, алгебраи- |
|
|
ческая сумма моментов сил, действующих |
|
|
на цилиндр, относительно произвольно вы- |
|
|
бранной оси равна нулю. Запишем уравне- |
|
|
ние моментов, например, относительно оси, |
|
|
перпендикулярной плоскости чертежа и |
Рис. 1.10 |
|
совпадающей с осью цилиндра, а также |
|
уравнения равновесия для сил в проекциях на оси ОХ и ОY: |
|
|
∑M Z =TR − Fтр. пок.R = 0 , |
(1) |
|
∑FX =T + Fтр. пок. − mg sin α = 0 , |
(2) |
|
∑FY = N − mg cosα = 0 . |
(3) |
103
Выразив из уравнения (1) силу натяжения нити Т и подставив в (2), получим
|
2Fтр. пок. − mg sin α = 0 . |
(4) |
Поскольку сила трения покоя Fтр. пок. ≤ Fтр. max =µN , то уравнение (4) с учетом (3) можно записать в виде
|
F |
пок. |
= mg sin α |
≤ µN = µmg cos α . |
|
|
тр. |
2 |
|||
|
Следовательно |
||||
|
tgα ≤ 2µ; |
α ≤ arctg2µ; |
αmax = arctg2µ. |
||
|
Ответ: αmax = arctg2µ. |
104
2. УЧЕБНЫЙ БЛОК «ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА»
Введение
Раздел динамики вращательного движения является одним из основных разделов физики, изучаемой в университете. Это обусловлено, вопервых, достаточно новым материалом, который в школьном курсе физики не изучается. Во-вторых, этот раздел имеет большое значение при изучении других дисциплин: теоретической механики, сопротивления материалов, строительной механики, теории машин и т.д. Поэтому материал этого блока, по сравнению с другими блоками, предлагается на лекции, и не выносится на самостоятельное изучение. Вместе с тем для изучения этого блока необходимо наличие у студентов определенных знаний и умений.
При изучении данного блока студенты
должны знать:
–законы динамики поступательного движения материальной точки;
–понятие момента сил и центра масс;
–законы сохранения механики поступательного движения материальной точки;
иметь представление:
–о правилах векторного и скалярного произведений;
–о методах интегрирования;
–о способах определения центра масс;
–о кинематических характеристиках движения по окружности.
Учебная программа блока
|
Содержание блока |
Форма |
Литература |
||
|
подготовки |
||||
|
Динамика твердого тела |
||||
|
1. |
Основные понятия: момент импульса, момент |
лекция |
[3] |
|
|
инерции, момент импульса силы |
||||
|
2. |
II закон Ньютона для вращательного движения |
лекция |
[3], [4] |
|
|
3. |
Закон сохранения момента импульса |
лекция |
[2], [4] |
|
|
4. |
Кинетическая энергия вращательного движения. |
лекция |
[3] |
|
|
Работа |
||||
|
Свободное вращение твердого тела |
||||
|
5. |
Понятие о степени свободы твердых тел |
лекция |
[4] |
|
|
6. |
Момент инерции сложных тел |
лекция |
[2], [3], [4] |
105

|
Окончание табл. |
||||
|
7. |
Вращение тела относительно свободной оси |
лекция |
[4] |
|
|
8. |
Вращение тела относительно заданной точки |
лекция |
– |
|
|
9. Гироскопический эффект |
самост. |
[2], [4] |
Цели обучения
|
студент должен знать |
студент должен уметь |
|
– законы динамики вращательного движе- |
– определять моменты сил и плечо сил; |
|
ния (законы сохранения и II закон Ньютона |
– определятьмоментинерциитвердыхтел; |
|
для вращательной динамики); |
– определять динамические характеристики |
|
– понятие и методику определения момента |
вращательного движения на основе зако- |
|
инерции твердых тел; |
новдинамикивращательногодвижения; |
|
– способы определения направления век- |
– решать комплексные задачи механики |
|
торов момента силы, момента импульса; |
сучетомкаченияивращениятвердыхтел |
|
– понятие степени свободы твердого тела; |
|
|
– понятие свободной оси и особенности |
|
|
движения твердого тела со свободной осью |
2.1. Краткое содержание теоретического материала
Закон сохранения момента импульса
В динамике систем материальных точек твердого тела известны две величины, которые в замкнутой системе сохраняются: импульс и энергия. Определим еще одну такую величину.
Рассмотрим систему, состоящую из двух взаимодействующих точек, на которые действуют также внешние силы (рис. 2.1). Уравнения движения точек имеют вид
|
m1υ1 = f12 + F1 и |
m2υ2 = f21 + F2 , |
где υ – производная скорости точек по времени (ускорение).
Умножим первое уравнение на r1 , а второе – на радиус-вектор второй частицы r2 , которые для мгновения времени, можно считать радиусами окружностей, по которым движутся материальные точки m1 и m2 и получим:
|
m |
r , υ |
= r f |
+ r F |
; |
m |
r ,υ |
= r f |
+ r F |
. |
|||||
|
1 |
1 1 |
1 12 |
1 1 |
2 |
2 |
2 |
2 |
21 |
2 2 |
Поскольку векторное произведение rυ эквивалентно dtd [rυ], то получаем уравнение движения в виде
106

|
m |
d |
[r υ ]= |
r |
, f |
+ r F |
; |
m |
d |
[r υ |
2 |
]= r |
, f |
21 |
+ |
r F |
(1) |
|||||||||||
|
1 |
dt |
1 1 |
1 12 |
1 1 |
2 |
dt |
2 |
2 |
2 2 |
||||||||||||||||||
|
Сложив уравнения вместе с учетом p = mυ и − f12 = f21 |
|||||||||||||||||||||||||||
|
d |
([r1 p1]+ |
[r2 p2 ]) |
|||||||||||||||||||||||||
|
dt |
= (r1 − r2 )F12 |
+ r1F1 + |
r2F2 , |
||||||||||||||||||||||||
|
векторное произведение |
(r |
− r |
), f |
= 0 , так как вектора r |
− r |
и |
f |
парал- |
|||||||||||||||||||
|
1 |
2 |
12 |
1 |
2 |
12 |
||||||||||||||||||||||
|
лельны. |
|||||||||||||||||||||||||||
|
Если внешние силы отсутствуют, так как система замкнута, то |
|||||||||||||||||||||||||||
|
d |
([r1 p1]+[r2 p2 ])= 0 или [r1 p1]+[r2 p2 ]= const . |
(2) |
|||||||||||||||||||||||||
|
dt |
Величина L =[rp] носит название момента импульса относительно
точки О.
Закон сохранения момента импульса: в замкнутой системе момент импульса системы тел всегда сохраняется постоянным.
Величина M = rF , как известно, носит название момента силы F
относительно точки О.
Определение модуля момента импульса показано на примерах (рис. 2.2), где а – момент импульса точки массой m относительно оси ( L = mυl = mυr sin α = pl (3)), а б – момент импульса точки, движущейся по
окружности радиуса R ( L = mυR = pR (4)).
|
а |
Рис. 2.2 |
б |
|||
|
Направление вектора L |
определяют по правилу левой руки: если |
четыре пальца ладони направить по направлению плеча импульса, а ладонь расположить так, чтобы импульс входил в ладонь, то момент импульса силы
107
будет направлен по направлению большого пальца ладони, отогнутого на угол 90˚.
Обобщая уравнения (1) и (2), связь момента импульса системы материальных точек с моментами сил, действующих на точки, получаем в виде
|
d |
m |
||||||||||
|
L = ∑ ri Fi , |
(5) |
||||||||||
|
dt |
|||||||||||
|
i |
|||||||||||
|
m |
ri Fi – суммарный момент внешних сил. |
||||||||||
|
где M = ∑ |
|||||||||||
|
i |
|||||||||||
|
Если |
суммарный |
момент |
сил на некоторую ось равен |
нулю |
|||||||
|
∑M z = 0 , то |
|||||||||||
|
d |
Lz = |
∑M z , |
d |
Lz = 0 , |
Lz = const |
||||||
|
dt |
dt |
и момент импульса системы также сохраняется.
Второй закон Ньютона для вращательного движения. Момент инерции тел
На основе уравнений (4) и (5) для материальной точки, движущейся по окружности, можно записать
где левая часть – изменение момента импульса материальной точки под действием импульса момента силы, представленного правой частью уравнения. Так как υ = ωR , то уравнение (6) можно переписать в виде
|
mR |
2 |
dω |
= F R = M , |
|
|
dt |
||||
|
или, вводя угловое ускорение ε, в виде |
||||
|
mR2ε = M , |
(7) |
где величина J = mR2 является мерой инертности при вращательном движении и получила название момента инерции. Таким образом, для вращательного движения твердого тела уравнение (7), выражающее Второй закон Ньютона, можно записать в виде
где JT – момент инерции тела, εT – мгновенное угловое ускорение тела под действием результирующего момента сил, действующих на тело.
108

Так как масса твердого тела распределена по его объему, то для определения момента инерции тела можно поступать следующим образом:
–разбить тело на микрообъемы dVi;
–определить кратчайшее расстояние ri от dVi до оси вращения тела;
–определить массу микрообъема mi = ρi dVi ;
–определить момент инерции такой массы Ji = miri2 ;
–осуществить операцию суммирования Ji
|
N |
N |
N |
|
JT = ∑Ji =∑miri2 |
= ∑ρidVi ri2 . |
|
|
i=1 |
i=1 |
i=1 |
Операцией, эквивалентной суммированию, является интегрирование функции J по объему тела. Поэтому в общем случае
V
где ρ – плотность вещества тела.
Уравнение (9) позволяет определить J для любого тела (формы и распределения массы) и любой оси вращения этого тела. Однако определение J может быть упрощено в ряде случаев, например, если известен момент инерции тела относительно некоторой оси вращения его, проходящей через центр массы – Jo, а реальная ось вращения параллельно смещена (рис. 2.2).
Рис. 2.2.
АА– ось вращения, для которой известно J0;
ВВ– ось вращения тела, для которой определяется J
Вращение тела относительно оси ВВ с угловой скоростью ω можно представить в виде двух движений:
–движение центра массы mT (точка О) по окружности с радиусом d вокруг оси ВВ;
–вращение тела относительно оси АА.
109
При этом оба движения осуществляются с угловой скоростью ω. Поэтому можно записать
Выражение (10) называется теоремой Штейнера.
Энергия и работа при вращательном движении
Пусть на элементы тела массой mi действуют внутренние fi и внешние Fi силы. Эти силы совершают работу, которая для i-го элемента будет записана в виде формулы
dAi = fiυidt + Fiυidt = fi [ωri ]dt + Fi [ωiri ]dt ,
и которая приводит к движению i-го элемента по окружности относительно некоторой оси с угловой скоростью ω, вектор которой совпадает с осью вращения z.
Тогда для всех элементов тела элементарная работа равна dA = ∑dAi = ω(∑Miвнутр )dt + ω(∑Miвнеш )dt .
Сумма моментов внутренних сил равна 0. Поэтому
dA = ωMdt = ωM ωdt = ωM t dt ,
так как проекция Mω = M z , поскольку ось z совпадает с вектором угловой скорости. Учитывая, что dϕ = ωdt , получаем выражение для работы по повороту твердого тела вокруг оси z на бесконечно малый угол dϕ:
dA = M zdϕ
Для поворота тела на конечный угол ϕ, требуемая работа равна
ϕ
A = ∫dA =M zϕ.
0
Определить энергию вращающегося тела с угловой скоростью ω можно суммированием энергий движения по окружностям всех бесконечно малых элементов (точек) твердого тела, которая является кинетической энергией.
Для одной i-ой точки твердого тела
|
W |
= |
miυi2 |
= |
miω2Ri2 |
= |
J |
m R 2ω2 |
= 1 ω2 J |
zi |
. |
|
кi |
2 |
2 |
2 |
i i |
2 |
|||||
110
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
1 (Определить центр тяжести однородного диска с вырезанным квадратом)
2019-05-122019-05-12СтудИзба
Описание файла
Документ из архива “Определить центр тяжести однородного диска с вырезанным квадратом”,
который расположен в категории “”.
Всё это находится в предмете “педагогика” из 6 семестр, которые можно найти в файловом архиве МГУ им. Ломоносова.
Не смотря на прямую связь этого архива с МГУ им. Ломоносова, его также можно найти и в других разделах. .
Онлайн просмотр документа “1”
Текст из документа “1”
Принцип дополнительности
Задача. Определить центр тяжести однородного диска с вырезанным квадратом, как показано на рис. 1. Радиус диска R, сторона квадрата а.
Дано: R, а; хЦТ – ?
Решение: В силу симметрии центр тяжести диска будет находиться на оси х (рис. 2). У диска без выреза центр тяжести находится в точке О. Очевидно, что после выреза центр тяжести сместится влево от точки О, так как правая часть диска будет легче благодаря сделанному вырезу. В точке О’ приложена сила тяжести оставшейся части (рис. 2).
, (1)
где ρ – плотность материала, h – толщина диска, FT1 – сила тяжести вырезанной части. Если вырезанную часть вернуть на прежнее место, то в точке О (по определению центра тяжести) приложена равнодействующая сил тяжести и
. Тогда относительно оси, проходящей через точку О, сумма моментов сил
и
должна быть равна 0:
. (2)
Воспользовавшись формулами (1) и (2), получим для хЦТ:
.
Свежие статьи
Популярно сейчас
Ответы на популярные вопросы
То есть уже всё готово?
Да! Наши авторы собирают и выкладывают те работы, которые сдаются в Вашем учебном заведении ежегодно и уже проверены преподавателями.
А я могу что-то выложить?
Да! У нас любой человек может выложить любую учебную работу и зарабатывать на её продажах! Но каждый учебный материал публикуется только после тщательной проверки администрацией.
А если в купленном файле ошибка?
Вернём деньги! А если быть более точными, то автору даётся немного времени на исправление, а если не исправит или выйдет время, то вернём деньги в полном объёме!
Отзывы студентов
Добавляйте материалы
и зарабатывайте!
Продажи идут автоматически
575
Средний доход
с одного платного файла
Обучение Подробнее
