2019-05-11
Две одинаковые гантели движутся друг к другу без вращения по горизонтальному столу на воздушной подушке (рис.). Каждую гантель можно рассматривать как две точечные массы $m$, скрепленные невесомым стержнем длиной $2l$. Опишите движение гантелей после их упругого столкновения. Изобразите зависимости скоростей центров масс гантелей от времени.
Решение:
Так как гантели приближаются друг к другу с одинаковыми скоростями, то в системе координат, связанной со столом, сумма их импульсов нулевая (как и у центра масс системы). Таким образом, закон сохранения импульса подразумевает, что центры масс этих гантелей всегда движутся с одинаковыми скоростями, но в противоположных направлениях.
Когда гантели сталкиваются, энергия и суммарный момент импульса сохраняются, так как система изолирована от внешних воздействий, а столкновения абсолютно упругие. Состояния системы до и после столкновения показаны на рисунке. Перед столкновением гантели обладают только поступательной кинетической энергией, в то время как после столкновения появляется вращательная энергия. Вычислив момент импульса для гантелей относительно их точки контакта Р, запишем уравнения законов сохранения энергии и момента импульса системы:
$2 left ( frac{2mv^{2} }{2} right ) = 2 left ( frac{2mV^{2} }{2} + frac{2 ml^{2} omega^{2} }{2} right )$,
$4mvl = 2mVl + 2ml^{2} omega$.
Нетривиальное решение ( $V neq v, omega neq 0$ ) этой системы уравнений таково: $V = 0, omega = frac{v}{l}$. Это означает, что центры масс гантелей прекращают перемещаться после столкновения, сталкивающиеся точечные массы изменяют свои скорости, в то время как несталкивающиеся сохраняют свои первоначальные скорости. Ситуацию можно интерпретировать следующим образом: точечные массы, соединенные твердым, но невесомым стержнем, не ощущают присутствия друг друга в ходе мгновенного столкновения; стержень передает момент силы, возникающей из-за деформации ударяющихся шаров, когда гантель вращается относительно своего неподвижного центра масс.
Понятно, что гантели, совершив каждая пол-оборота, т.е. через время $t = frac{ pi}{ omega}$, снова сталкиваются. Используя предыдущие результаты, дальнейшее движение гантелей можно предсказать без решения уравнений: вращение гантелей прекращается, и они снова движутся поступательно с теми же самыми скоростями, как перед первым столкновением. Их путь – та же самая прямая, только шары у гантелей поменялись местами.
Скорость гантелей как функция времени показана на рисунке.
Copy
Если
в задаче рассматривается не одна
материальная точка, а система точек, то
момент импульса системы равен векторной
сумме моментов импульсов всех материальных
точек системы
,
где
все векторы
определены относительно одной и той же
точки заданной системы отсчета.
Сумма
моментов всех внутренних сил будет
равна нулю, так как силы, с которыми
взаимодействуют любые две материальные
точки системы, удовлетворяют третьему
закону Ньютона и действуют вдоль одной
прямой, поэтому их плечи одинаковые, а
направления противоположные.
Закон изменения
момента импульса для системы тел имеет
вид
,
то
есть изменение момента импульса системы
равно сумме моментов всех внешних сил
относительно той же точки.
Если сумма моментов
всех внешних сил равна нулю, то момент
импульса системы сохраняется
.
Как
и в случае закона сохранения импульса,
момент импульса незамкнутой системы
сохраняется при условии что:
1) суммарный момент
внешних сил равен нулю,
2)
если момент внешних сил относительно
точки отличен от нуля, но относительно
некоторой оси равен нулю, то момент
импульса относительно этой оси
сохраняется,
3)
если действие внешних сил ограничено
во времени
(удар, взрыв), то изменением момента
импульса
за время удара можно пренебречь.
Ранее
было показано, что в некоторых случаях
решение задач, связанных с импульсом
системы, упрощается, если их решать в
системе центра масс (раздел IV).
Решение задач на момент импульса также
упрощается в этой системе отсчета. Это
связано с тем, что полный импульс системы
частиц в системе центра масс равен нулю,
и поэтому момент импульса системы не
зависит от выбора точки, относительно
которой его определяют. Поэтому этот
момент называют собственным моментом
импульса и обозначают
.
Момент импульса
системы частиц в произвольной системе
складывается из ее собственного момента
импульса
и момента
,
обусловленного движением системы частиц
как целого
.
Решение задач
6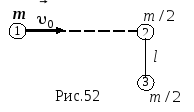
Шарик массы
m,
двигавшийся со скоростью
испытал упругое лобовое столкновение
с одним из шариков покоившейся жесткой
гантели (рис.52). Масса каждого шарика
гантели равна m/2,
длина легкого соединительного стержня
гантели – l.
Считая шарики материальными точками,
найдите:
а)
скорость каждого шарика сразу после
соударения,
б)*
скорость центра масс системы после
соударения,
в)*
собственный момент импульса
гантели (в системе центра масс).
Решение.
а) Рассмотрим момент импульса системы
относительно точки соударения (шарик
2 рис.52). Относительно этой точки момент
импульса системы до столкновения равен
нулю. Рассматриваемая система является
замкнутой, поэтому момент импульса
сохраняется и остается равным нулю.
Следовательно, после столкновения
скорость нижнего шарика гантели равна
нулю
(т.к. плечо импульса 3 шарика не равно
нулю, а плечи импульсов 1 и 2 шариков
равны нулю).
Поскольку
удар абсолютно упругий, импульс и
кинетическая энергия системы также
сохраняются:
,
(1)
,
(2)
где
и
– скорости отлетевшего шарика (шарик 1
рис.52) и верхнего шарика гантели (шарик
2 рис.52) сразу после удара. Решая совместно
уравнения (1) и (2), найдем скорость верхнего
шарика гантели и скорость отлетевшего
шарика сразу после удара
и
.
б)
Момент импульса системы частиц
складывается из ее собственного момента
импульса
и момента, обусловленного движением
системы частиц как целого
:
,
(3)
где
и
– радиус-вектор центра масс и суммарный
импульс системы частиц соответственно.
Так как момент импульса системы после
столкновения равен нулю, из уравнения
(3) следует, что собственный момент
импульса гантели после столкновения
равен:
.
Центр
масс гантели после столкновения (также
как и до столкновения) находится
посередине соединительного стержня,
т.е.
,
скорость ее центра масс
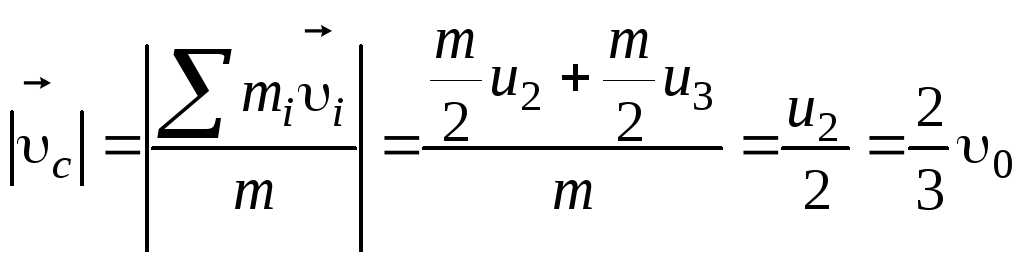
в)
Учитывая, что
получим искомую величину:
.
6.5.
Гладкий
горизонтальный диск вращают относительно
Земли, вращение которой не учитывается,
с угловой скоростью
вокруг вертикальной оси, проходящей
через его центр – точку 0. Из этой точки
в момент
пустили небольшую шайбу массой m
со скоростью
.
Найдите момент импульса шайбы
относительно точки 0 в системе отсчета
связанной с диском.
Решение.
Система отсчета, связанная с вращающимся
диском, является неинерциальной системой
отсчета. В этой системе момент импульса
шайбы относительно точки 0 равен
,
где
–
скорость шайбы относительно диска.
Раскрыв векторное произведение, получим
,
где
– угол между векторами
и
.
Из условия задачи известна скорость
шайбы относительно Земли, которая
является инерциальной системой отсчета
–
.
Запишем связь между скоростями шайбы
в этих системах отсчета
.
В
ыразим
из последнего выражения
и определим ее направление (рис.53). Из
рисунка видно, что вектор
является диагональю прямоугольника,
значит
.
Учитывая, что
,
найдем момент
импульса шайбы
относительно точки 0 в системе отсчета
связанной с диском, подставив найденные
величины в исходное выражение
.
А
направление вектора
покажем на рис.53.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вопрос: При выполнении каких условий твердое тело может находиться в состоянии покоя под действием трех сил, линии действия которых не параллельны?
Задача: «Гантель» из легкого жесткого стержня и двух массивных маленьких шариков одинакового радиуса положили в гладкую полусферическую «ямку». Длина стержня в раз больше радиуса ямки. Оказалось, что гантель находится в равновесии, если радиус, проведенный к первому шарику, составляет угол
с вертикалью. Найти отношение масс шариков.
Спрятать решение
Решение.
Ответ на вопрос. Условия равновесия твердого тела требуют равенства нулю векторной суммы всех приложенных к телу сил и суммы моментов этих сил: Для случая трех непараллельных сил, линии действия которых лежат в одной плоскости, последнее требование можно сделать более наглядным: если выбрать для подсчета моментов ось, проходящую через точку пересечения линий действия двух сил, то моменты этой пары сил равны нулю, и поэтому должен быть равен нулю и момент третьей силы, и поэтому ее линия действия должна проходить через ту же точку! Итак, в этом случае линии действия всех трех сил должны пересекаться в одной точке.
Решение задачи. На стержень с шариками действуют силы нормальной реакции поверхности «ямки». Ясно, что линии их действия — радиусы сферы, и они пересекаются в центре сферической поверхности (точка O). В роли третьей силы здесь выступает равнодействующая сил тяжести шариков. Ее точка приложения — центр масс, а линия ее действия вертикальна и (как следует из ответа на вопрос) проходит через точку O. Таким образом, центр масс гантели — точка С. Значит, Кроме того, соотношение между длиной стержня и радиусом позволяет определить угол при вершине O в треугольнике OAB: это равнобедренный треугольник с основанием в
раз больше боковой стороны, и он является прямоугольным, а углы при основании равны
Из теоремы синусов получим, что
и
поэтому
Ответ:
Спрятать критерии
Критерии проверки:
Для вопросов:
Есть отдельные правильные соображения — 1 балл.
Ответ в целом правилен, но содержит существенные неточности, или существенно неполон, или отсутствует обоснование (для вопросов, в которых необходимо обоснование) — 2 балла.
Ответ правилен, но присутствуют мелкие неточности, или ответ недостаточно полон, или отсутствует достаточное обоснование (для вопросов, в которых необходимо обоснование) — 3 балла.
Ответ полностью правильный, но недостаточно обоснованный (для вопросов, в которых необходимо обоснование) — 4 балла.
Правильный, полный и обоснованный ответ — 5 баллов (максимальная оценка).
Для задач:
Есть отдельные правильные соображения — 1−2 балла.
Есть часть необходимых для решения соображений, решение не закончено или содержит серьезные ошибки — 3−4 балла.
Присутствует большая часть необходимых для решения соображений, правильно записана часть необходимых соотношений, решение не закончено или содержит ошибки — 5−7 баллов.
Присутствуют все необходимые для решения соображения, правильно записаны почти все необходимые для решения исходные уравнения, но решение не закончено или содержит ошибки — 8−10 баллов.
Присутствуют все необходимые для решения соображения, правильно записаны все необходимые для решения исходные уравнения, решение выстроено правильно с физической и логической точки зрения, но содержит ошибки —11−14 баллов.
Присутствуют все необходимые для решения соображения, правильно записаны все необходимые для решения исходные уравнения, решение выстроено правильно с физической и логической точки зрения, но содержит одну-две мелкие неточности, не позволившие получить правильный ответ, или правильное решение с недостаточным обоснованием существенных использованных результатов — 15−17 баллов.
Правильное обоснованное решение с верным аналитическим ответом, но мелкой неточностью при получении численного ответа, либо правильное решение с правильными ответами с недостаточным обоснованием одного из использованных результатов (из числа не ключевых для решения, но необходимых) — 18−19 баллов.
Полное, правильное, обоснованное решение с правильными ответами — 20 баллов (максимальная оценка).
Классификатор: Механика. Статика. Равновесие вращ. и невращ. тел
Центр масс, теория и онлайн калькуляторы
Центр масс
Определение центра масс
Определение
При рассмотрении системы частиц, часто удобно найти такую точку, которая характеризует положение и движение
рассматриваемой системы как единого целого. Такой точкой является центр масс.
Если у нас две частицы одинаковой массы, то такая точка находится посередине между ними.
Координаты центра масс
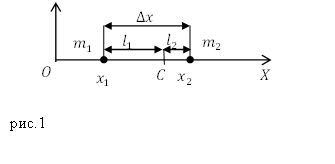
Допустим, что две материальные точки, имеющие массы $m_1$ и $m_2$ находятся на оси абсцисс и имеют координаты $x_1$ и $x_2$. Расстояние ($Delta x$) между этими частицами равно:
[Delta x=x_2-x_1left(1right).]
Определение
Точку С (рис.1), делящую расстояние между этими частицами на отрезки, обратно
пропорциональные массам частиц называют центром масс этой системы частиц.
В соответствии с определением для рис.1 имеем:
[frac{l_1}{l_2}=frac{m_2}{m_1}left(2right).]
Так как:
[l_1{=x}_c-x_1;; l_1{=x}_2-x_cleft(3right),]
где $x_c$ – координата центра масс, то получаем:
[m_1left(x_c-x_1right)=m_2{(x}_2-x_c)(4).]
Из формулы (4) получим:
[x_c=frac{m_1x_1+m_2x_2}{m_1+m_2}left(5right).]
Выражение (5) легко обобщается для множества материальных точек, которые расположены произвольным образом. При этом абсцисса центра масс равна:
[x_c=frac{sumlimits^N_{i=1}{m_ix_i}}{sumlimits^N_{i=1}{m_i}}left(6right).]
Аналогично получают выражения для ординаты ($y_c$) центра масс и его аппликаты ($z_c$):
[y_c=frac{sumlimits^N_{i=1}{m_iy_i}}{sumlimits^N_{i=1}{m_i}}left(7right).]
[z_c=frac{sumlimits^N_{i=1}{m_iz_i}}{sumlimits^N_{i=1}{m_i}}left(8right).]
Формулы (6-8) совпадают с выражениями, определяющими центр тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.
Если положение N материальных точек системы задано в векторной форме, то радиус – вектор, определяющий положение центра масс находим как:
[{overline{r}}_c=frac{sumlimits^N_{i=1}{m_i{overline{r}}_i}}{sumlimits^N_{i=1}{m_i}}left(9right).]
Движение центра масс
Выражение для скорости центра масс (${overline{v}}_c=frac{d{overline{r}}_c}{dt}$) имеет вид:
[{overline{v}}_c=frac{m_1{overline{v}}_1+m_2{overline{v}}_2+dots +m_n{overline{v}}_n}{m_1+m_2+dots +m_n}=frac{overline{P}}{M}left(10right),]
где $overline{P}$ – суммарный импульс системы частиц; $M$ масса системы. Выражение (10) справедливо при движениях со скоростями которые существенно меньше скорости света.
Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.
Примеры задач с решением
Пример 1
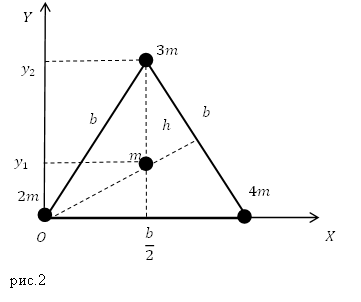
Задание. Запишите координаты центра масс системы из трех шариков, которые находятся в вершинах и центра равностороннего треугольника, сторона которого равна $b (м)$ (рис.2).
Решение. Для решения задачи используем выражения, определяющие координаты центра масс:
[x_c=frac{m_1x_1+m_2x_2+m_3x_3+m_4x_4}{m_1+m_2+m_3+m_4}(2.1);;]
[y_c=frac{m_1y_1+m_2y_2+m_3y_3+m_4y_4}{m_1+m_2+m_3+m_4}(2.2).]
Из рис.2 мы видим, что абсциссы точек:
[left{ begin{array}{c}
m_1=2m, x_1=0;; \
{rm }m_2=3m, x_2=frac{b}{2};; \
m_3=m, x_3=frac{b}{2};; \
m_4=4m, x_4=b. end{array}
right.left(2.3right).]
Тогда абсцисса центра масса равна:
[x_c=frac{2mcdot 0+3mcdot frac{b}{2}+mcdot frac{b}{2}+4mcdot b}{2m+3m+m+4m}=frac{6mb}{10m}=0,6b (м);;]
Найдем ординаты точек.
[ begin{array}{c}
m_1=2m, y_1=0;; \
{rm }m_2=3m, y_2=frac{bsqrt{3}}{2};; \
m_3=m, y_3=frac{bsqrt{3}}{6};; \
m_4=4m, y_4=0. end{array}
left(2.4right).]
Для нахождения ординаты $y_2$ вычислим, чему равна высота в равностороннем треугольнике:
[h=sqrt{b^2-frac{b^2}{4}}=frac{bsqrt{3}}{2}=y_2left(2.5right).]
Ординату $y_3$ найдем, помня, что медианы в равностороннем треугольнике точкой пересечения делятся в отношении 2:1 от вершины, получаем:
[y_3=hcdot frac{1}{3}=frac{bsqrt{3}}{6} left(2.6right).]
Вычислим ординату центра масс:
[y_c=frac{2mcdot 0+3mcdot frac{bsqrt{3}}{2}+mcdot frac{bsqrt{3}}{6}+4mcdot 0}{2m+3m+m+4m}=frac{10mfrac{bsqrt{3}}{6}}{10m}=frac{bsqrt{3} }{6}(м).]
Ответ. $x_c=0,6b {rm }{rm м}$; $y_c=frac{bsqrt{3} }{6}$ м
Пример 2
Задание. Запишите закон движения центра масс.
Решение. Закон изменения импульса системы частиц является законом движения центра масс. Из формулы:
[{overline{v}}_c=frac{overline{P}}{M}to overline{P}=M{overline{v}}_cleft(2.1right)]
при постоянной массе $M$ продифференцировав обе части выражения (2.1), получим:
[frac{doverline{P}}{dt}=Mfrac{d{overline{v}}_c}{dt}left(2.2right).]
Выражение (2.2) означает, что скорость изменения импульса системы равняется произведению массы системы на ускорение ее центра масс. Так как
[frac{doverline{P}}{dt}=sumlimits^N_{i=1}{{overline{F}}_ileft(2.3right),}]
имеем:
[Mfrac{d{overline{v}}_c}{dt}=sumlimits^N_{i=1}{{overline{F}}_ileft(2.4right).}]
В соответствии с выражением (2.4) получаем, что центр масс системы движется так, как двигалась бы одна материальная точка массы M, если на нее действует сила, равная сумме всех внешних сил, действующих на частицы, которые входят в рассматриваемую систему. Если $sumlimits^N_{i=1}{{overline{F}}_i=0,}$ то центр масс движется равномерно и прямолинейно.
Читать дальше: центр тяжести.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!