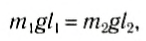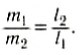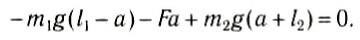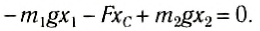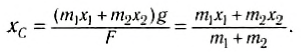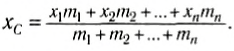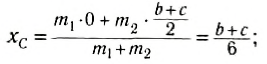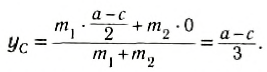Как найти центр масс груза

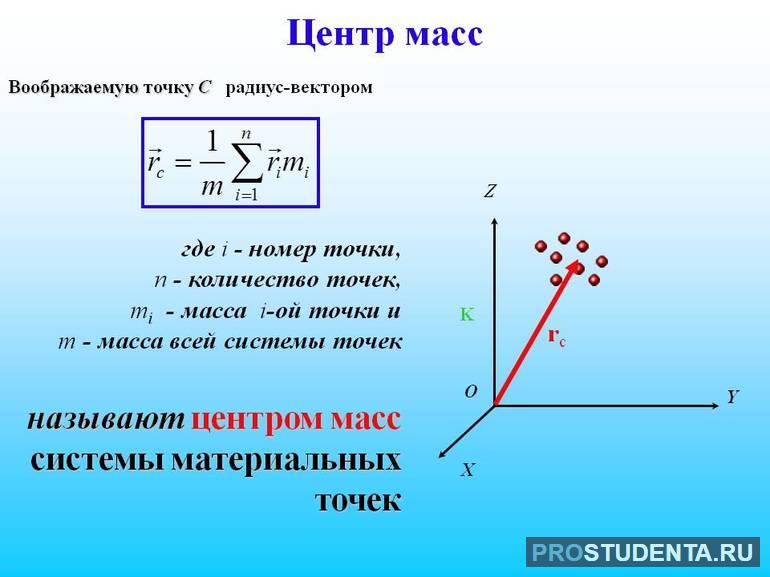
Сущность понятия «центр масс»

Понятие “центр масс” широко используется в физике для решения задач, связанных с движением тел. Например, математический маятник удобно представить себе как подвешенное на нити тело, вся масса которого сконцентрирована в единой точке. В законе всемирного тяготения тоже речь идет о расстоянии не между телами, а между центрами тел, под каковыми подразумеваются именно центры масс, а не геометрические центры.

Признаком центра масс является то, что если тело подвесить, закрепив за эту точку, оно останется в покое, т.е. не будет раскачиваться или вращаться относительно этого центра. В простейшем случае, если речь идет о симметричном теле с равномерной плотностью, центр масс находится на пересечении осей симметрии рассматриваемого тела. Например, если взять линейку длиной 30 см, то ее центр масс будет расположен на отметке “15 см”. Подложив карандаш под эту отметку, легко привести линейку в положение равновесия.

На практике далеко не все тела, центр масс которых нужно найти, являются симметричными и однородными по плотности. Более того, многие исследуемые объекты представляют собой системы из нескольких тел с различными геометрическими и химическими характеристиками. Для расчетов их разбивают на элементарные фрагменты и производят вычисления поэтапно.

Нахождение координат центра масс

Отсюда следует, что чем массивнее тело в такой элементарной системе, тем ближе оно к общему центру масс.

Расстояние между точечными телами равно:

$Delta x = x_2 – x_1$

Пропорция между массами и расстояниями, согласно определению:

$frac{l_1}{l_2} = frac{m_2}{m_1}$,

«Как найти координаты центра масс» 👇

где $l_1$, $l_2$ – расстояния от соответствующих тел до центра масс.

Выразив, длины через координаты

$l_1 = x_c – x_1; l_2 = x_2 – x_c$,

центр масс можно определить как

$x_c = frac{m_1 cdot x_1 + m_2 cdot x_2}{m_1 + m_2}$.

где $x_c$ – координата центра тяжести.

Разложив любую сложную систему на множество элементарных тел с точечными массами, можно обобщить изложенный принцип в виде формулы (для оси абсцисс):

$x_c = frac{sumlimits^N_{i=1}{m_i cdot x_i}}{sumlimits^N_{i=1}{m_i}}$

В большинстве случаев центр масс требуется найти не на координатной прямой, а в двух- или трехмерной системе координат. Для дополнительных осей координаты центра масс ($y_c$, $z_c$) находят по аналогичному принципу.

Определение массы и расположения центра тяжести груза

Стропальщик
должен уметь определять массу и центр
тяжести груза с целью обеспечения
безопасности погрузо-разгрузочных
работ.

Под
массой груза следует понимать (скалярную,
ненаправленную) физическую характеристику
тела, являющуюся
мерой его инерционных и гравитационных
свойств.
Значения массы тела не зависят от
ускорения свободного
падения в пункте определения. В состоянии
покоя
ее определяют взвешиванием на рычажных
весах. Результат
взвешивания показывает сравнительную
с массой гирь величину, выраженную в
единицах массы — граммах
(г), килограммах (кг), тоннах (т).

Под
силой
тяжести следует
понимать векторную (направленную)
величину, определяющую силу притяжения
тела к Земле или к другому небесному
телу. Значение
силы тяжести зависит от ускорения
свободного падения
в пункте измерения. Сила тяжести на
полюсе больше,
а на экваторе меньше. По мере удаления
тела от
поверхности Земли его сила тяжести
уменьшается. Эту
величину измеряют с помощью динамометра
в условиях
относительного покоя тела. Силу тяжести,
как и любую
другую силу, выражают в единицах силы
— ньютонах
(Н),
килоньютонах
(кН) и других дольных и кратных
значениях этой величины.

Вес
тела — сила, с которой тело действует
вследствие
силы тяжести к Земле на опору (или
подвес), удерживающую
его от падения. Вес тела равен его силе
тяжести,
если опора и тело неподвижны относительно
Земли.
Единица веса (и силы тяжести) в Международной
системе
единиц (СИ)—ньютон (Н).

Под
грузоподъемностью
крана,
автопогрузчика, электрокара
следует понимать максимальную массу
груза, которую
способно в один прием поднять, переместить
или
перевезти транспортное средство.

Грузоподъемность,
как и масса, — скалярная величина
и измеряется единицами массы — грамм
(г),
килограмм
(кг),
тонна
(т).

Грузоподъемная
(подъемная)
сила (по аналогии с силой
тяжести) — величина, характеризующая
способность
транспортного средства преодолевать
при подъеме
или перемещении массу груза. Единицами
грузоподъемной
силы служат ньютоны (Н),
килоньютоны
(кH)
и другие дольные и кратные значения
ньютона.

Перед
строповкой груза, предназначенного для
перемещения, стропальщик должен
определить его массу. Массу
изготовленной на заводе продукции
проставляют на
чертежах изделий. Массу оборудования,
приспособлений,
механизмов указывают в табличке,
прикрепленной
к раме или станине. Если груз упакован,
то массу его
указывают на обшивке. Однако массу
груза, подлежащего перемещению,
стропальщику часто приходится определять
визуально. Удельная масса часто
встречающихся
материалов приведена ниже, кг/м³

Алюмений	2550—2700		Олово	7300
Бетон	2200 1000		Парафин	900 11300
Вольфрам Древесина: береза, дуб сосна	19300 700 800 500		Сталь: твердая расплавленная	7300 7500 6900—7300
Земля, глина Песчаник Песок: сухой влажный	1300—2500 2200—2500 1400—1600 1900—2000		Чугун: белый ковкий серый Уголь Кокс	7650 7300 7550 900 450
Кирпичная кладка	1420—1700		Азот жидкий	790 700
латунь	8500
Лед	900		Воздух (жидкий)	860
Медь	8900		Керосин	800
Мел	2400		Кислород (жид)	1140
Никель	8900		Мазут	900

Для
определения массы груза используют
следующие формулы:

для простых грузов
Q=mV;

для
сложных грузов Q=mVi,

где
Q — масса груза; т — удельная масса,
численно равная плотности материала;
V
— объем
груза; Vt
—
объем
отдельных частей груза; 
— сумма всех частей груза.

Объем правильных
геометрических фигур приведен в табл.
1.

Пример.
Определим
массу слитка, размеры которого
приведены на рис. 6.

Разбиваем
условно слиток на три усеченных конуса
и
определяем объем каждого. Для этого в
табл. 1 находим
формулу объема усеченного конуса

V=
(3,14/3) h
(R²+
r²
+ Rr)

Находим объемы
каждого элемента слитка

V₁.
~
(3,14/3) 1,700 [0,55²
+ 0,45²
+ 0,55-0,45]
1,34 м³;

V₂
~
(3,14/3) 0,05 [0,55²
+ 0,42²
+ 0,55-0,42] ~ 0,04 м³;

Vз
~ (3,14/3) 0,4 [0,42²
+ 0,4²
+ 0,42-0,4]

0,21
м³.

Определяем суммарный
объем слитка

V=V₁+V₂+V₃
=
1,34+0,04+0,21
= 1,59 м³.

Принимаем
удельную массу слитка равной 7,8 т/м³,
тогда
масса слитка

Q
= mV
= 7,8-1,59~
12,4 т.

При
выборе мест строповки груза возникает
_необходимость
определить расположение центра тяжести
поднимаемого
груза. Если при строповке это не учитывать,
то
возможны аварийные ситуации, связанные
с перегрузкой отдельных ветвей стропов,
грузоподъемных средств;
потерей устойчивости и опрокидыванием
поднимаемого
объекта.

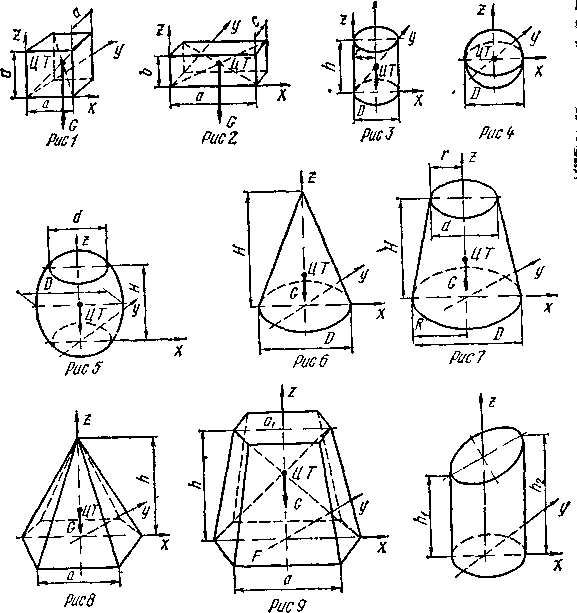
Положение
центра тяжести различных геометрических
тел находят по координатам х_ц._Т,
y_ц._т,
z_ц._т,
определяемым по формулам

х_цТ,=Q_ix_i
/Q
,
y_ц._т,
=Q_iy_i
/Q
z_ц._Т,=Q_iz_i
/Q

где
х_ц._т,
y_ц._т,
z_ц._т,
—
расстояние от центра тяжести тела до
плоскости, проходящей перпендикулярно
измеряемой оси
через центр координат, м; x_i,-,
y_i,
z_i—расстояние
от центра
тяжести отдельной рассматриваемой
части тела до
той же плоскости, м; Q
— общая
масса тела, т; Q_i:–
— масса
отдельной рассматриваемой части тела,
т.

Координаты центра
тяжести правильных геометрических
фигур приведены в табл.1

Пример.
Определим
расположение центра тяжести
стального слитка, изображенного на рис.
1.

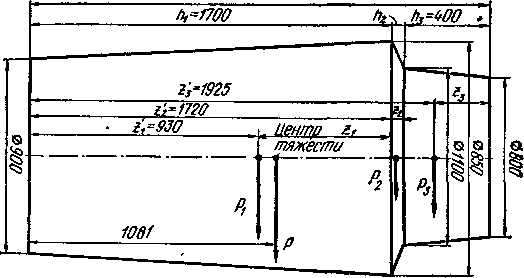
Условно
разбиваем слиток на три правильных
усеченных
конуса. По табл. 1 находим формулы,
определяющие
их координаты расположения центра
тяжести. Плоскость отсчета принимаем
проходящей через нижнее основание
слитка -перпендикулярно его оси. Из
предыдущего примера известно, что
отдельные части слитка
имеют массу q₁
= 10,45;
Q₂
=0,31; Q₃=1,64
т, общая масса
12,4 т. Учитывая, что слиток симметричен
относительно
своей оси, определяем расположение
только координаты
z_цт,
Координаты x_цт,
у_цт
будут
расположены
на оси. Формула для определения координаты
z_цт
усеченного
конуса имеет вид

z_цт
=h[(R²+2Rr+3r²)/(R²+Rr+r²)]/4

Рис. 1. Схема слитка

Зная,
что h₁=l,7
м; R₁=0,55
м; r₁=0,45
м, имеем z₁=0,77м

Величину
z₁^`
до
принятой плоскости отсчета определяют
как разность 1,7 — z₁
= l,7
— 0,77=0,930 м. Зная
h₂=0,05
м; R₂=0,55
м; г₂=0,425
м, имеем

Z₂=0,021

До
принятой плоскости отсчета z₂
определяют как сумму
1,7+z₂==1,7+0,02=1,72
м.

Зная
h_з=0,4
м; R₃=0,425
м; г₃=0,40
м, имеем

z₃=0,176м

До
принятой плоскости отсчета zз определяют
как сумму
1,7+0,05+0,176= 1,926м.

Определяем
расположение центра тяжести по формуле

z_цт
=(Q₁Z₁+Q₂z₂+Q₃z₃)/Q

подставляя
в формулу соответствующие значения,
находим
расстояние между центром тяжести и
началом координат

z_цт
= (10,45-0,93+ 0,31-1,72+ 1,64.1,926)/12,4 = 1,081 м.

Таблица
1. Объем и расположение центра тяжести
простых геометрических тел

Наименование	Изображение	Объем	Положение центра тяжести
Куб	Рис. 1	V = a3	x = а/2, у = а/2, z = а/2 х = у = z = а/2
Прямоугольный параллелепипед	Рис. 2	V = abc	x = а/2, у = c/2, z = b/2 х = r , y =0 , z = b/2
Цилиндр	Рис. 3	V = 3,14 xr2h	х = г, у= 0, г = h2/2
Шар	Рис. 4	V = 3,14/D3/6	Если оси координат про» ходят через центр шара, то x=у=z=0 (центр тяжести совпадает с цент« ром шара)
Боченок	Рис. 5	V=3,14/12Hx x(2D2 + d2)	х = у = 0, z=H/2
Конус	Рис. 6	V= 3,14/12D2H	x = у = 0, z=H/4
Усеченный конус	Рис. 7	V=(3,14H/3)x(R2+r2+Rr)	х = у= 0 z = H/4 [(R2 + 3r2 +2Rr)/(R2+r2+Rr)
Пирамида	Рис. 8	V=(Fh)/3, где F — площадь основания многоугольника	х = у = 0, z=h/4
Усеченная пирамида	Рис. 9	V=h[F + f + + Ff]/3	x = y = 0, z= h/4[F + + 2Ff + 3f/F] Ff+f
Усеченный цилиндр	Рис. 10	V = 3,14R2(h1+h2)/2	x=y=0, z=(h1+h2)/2

Определив
расстояние центра тяжести от принятого
начала координат, его переносят на
поднимаемый груз и делают пометку мелом
или другим способом.

Места
застроповки груза должны располагаться
симметрично центру тяжести таким
образом, чтобы отвесная прямая, проходящая
через центр тяжести, размещалась между
местами застроповки. Чем больше расстояние
между местами застроповки, тем устойчивее
положение груза при
прочих равных условиях.

На упакованных
грузах расположение центра тяжести
указывают на упаковке.

В тех
случаях, когда конфигурация груза
вызывает затруднения при расчете
положения центра тяжести, а его
необходимо определить, то можно
использовать практический
прием. После определения массы груза
подбирают соответствующий строп и им
приподнимают груз за один из краев. На
приподнятом грузе на двух плоскостях
проводят отвесные линии как продолжение
ветви стропа. Затем груз опускают и
приподнимают за другой конец. На тех же
плоскостях снова проводят отвесные
прямые.
Точки пересечения отвесов определяют
расположение
центра тяжести определяемого груза.

В тех
случаях, когда стропальщик затрудняется
определить массу перемещаемого груза
и расположения центра тяжести, он обязан
обратиться за уточнением к своему
бригадиру, мастеру или руководителю
работ.

При
монтаже несущих конструкций ОПЗ
из двух возможных схем перемещения
стрелового крана – вдоль пролетов или
поперек пролетов -обычно выбирают
первую, так как путь крана в этом случае
гораздо короче. При монтаже стеновых
панелей стреловой кран движется снаружи
по периметру здания. При строительстве
многоэтажных
жилых и гражданских зданий
башенный кран обычно передвигается
снаружи здания вдоль длинной его стороны.
Монтаж ведется в направлении “на
кран”, то есть в первую очередь
устанавливаются наиболее удаленные от
крана конструкции. В многоэтажных
промышленных зданиях
башенный или стреловой кран может
перемещаться внутри здания, монтируя
его на всю высоту “на себя” с
постепенным выездом за пределы здания.

При совместной
работе нескольких монтажных кранов
схема движения разрабатывается с учетом
требований техники безопасности. Здание
разбивают на монтажные зоны по числу
работающих кранов, в пределах каждой
зоны разрешается работа только одного
из них. Другой в это время должен работать
в своей монтажной зоне или простаивать.

4)
Рабочая
привязка монтажных
кранов и подъемников – это установление
точного взаимного расположения
возводимого здания и грузоподъемных
машин. Правильная привязка обеспечивает
требуемый “охват” всего объекта
монтажными машинами и безопасные условия
производства работ.

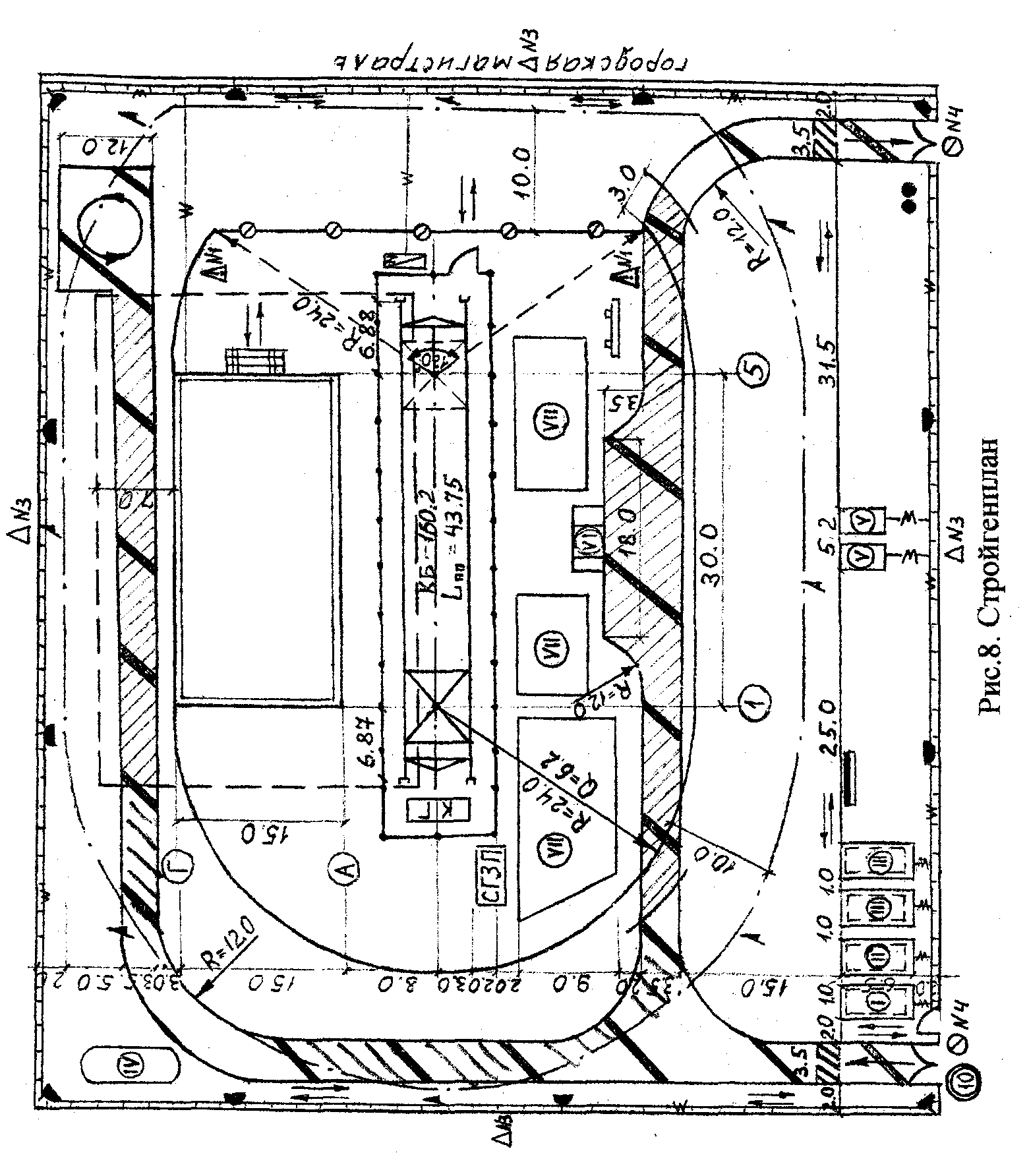
Рабочая
привязка башенных
кранов состоит в поперечной и продольной
привязке крана, подкрановых путей и их
ограждений.

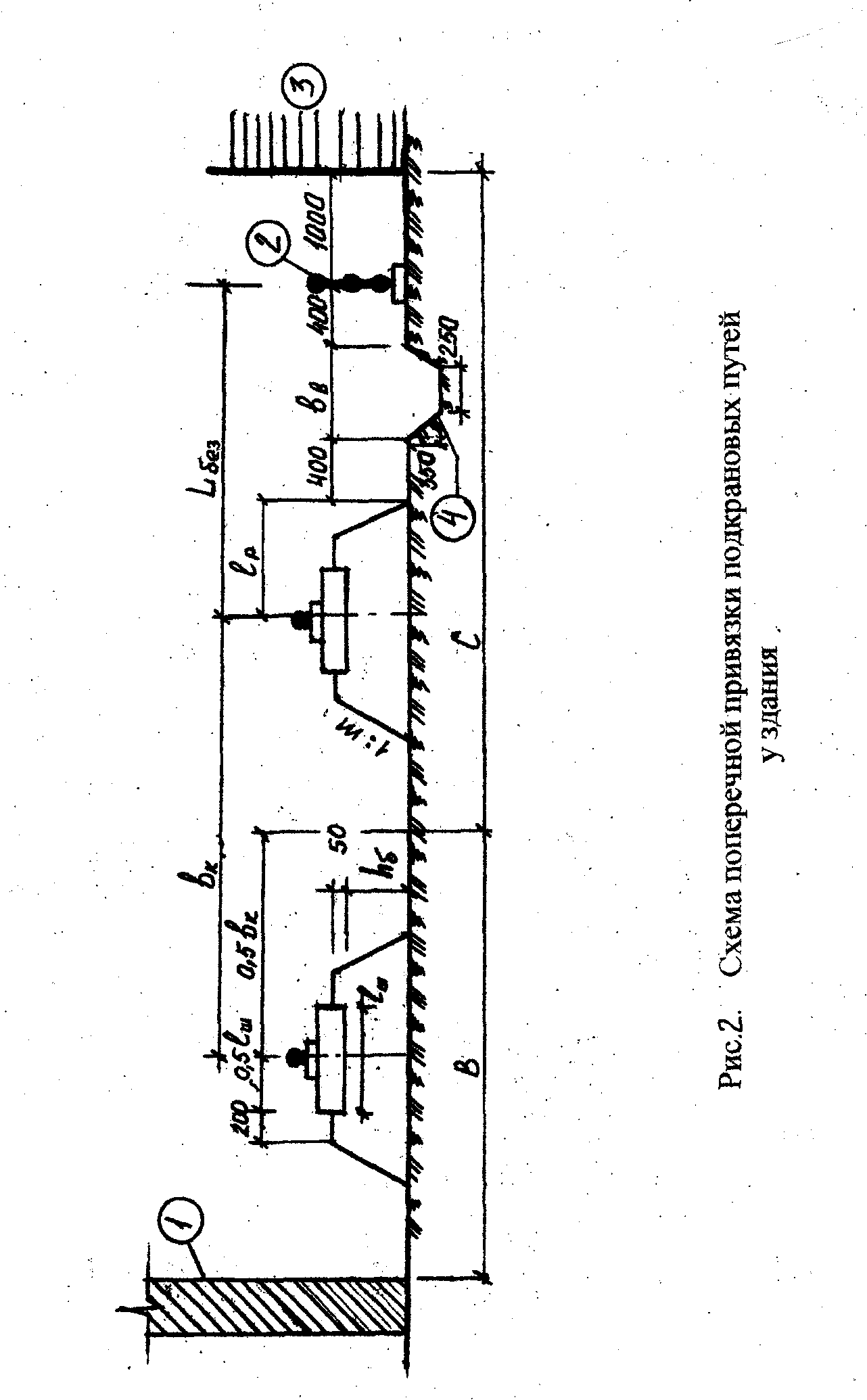
Поперечная
привязка при возведении надземной части
здания заключается в определении
расстояния от оси подкрановых путей до
ближайшей к крану грани строящегося
здания (рис.2: 1 – строящееся здание; 2 –
инвентарное ограждение путей; 3 – склад;
4 – водоотводная канава). Это расстояние
зависит от конструктивного исполнения
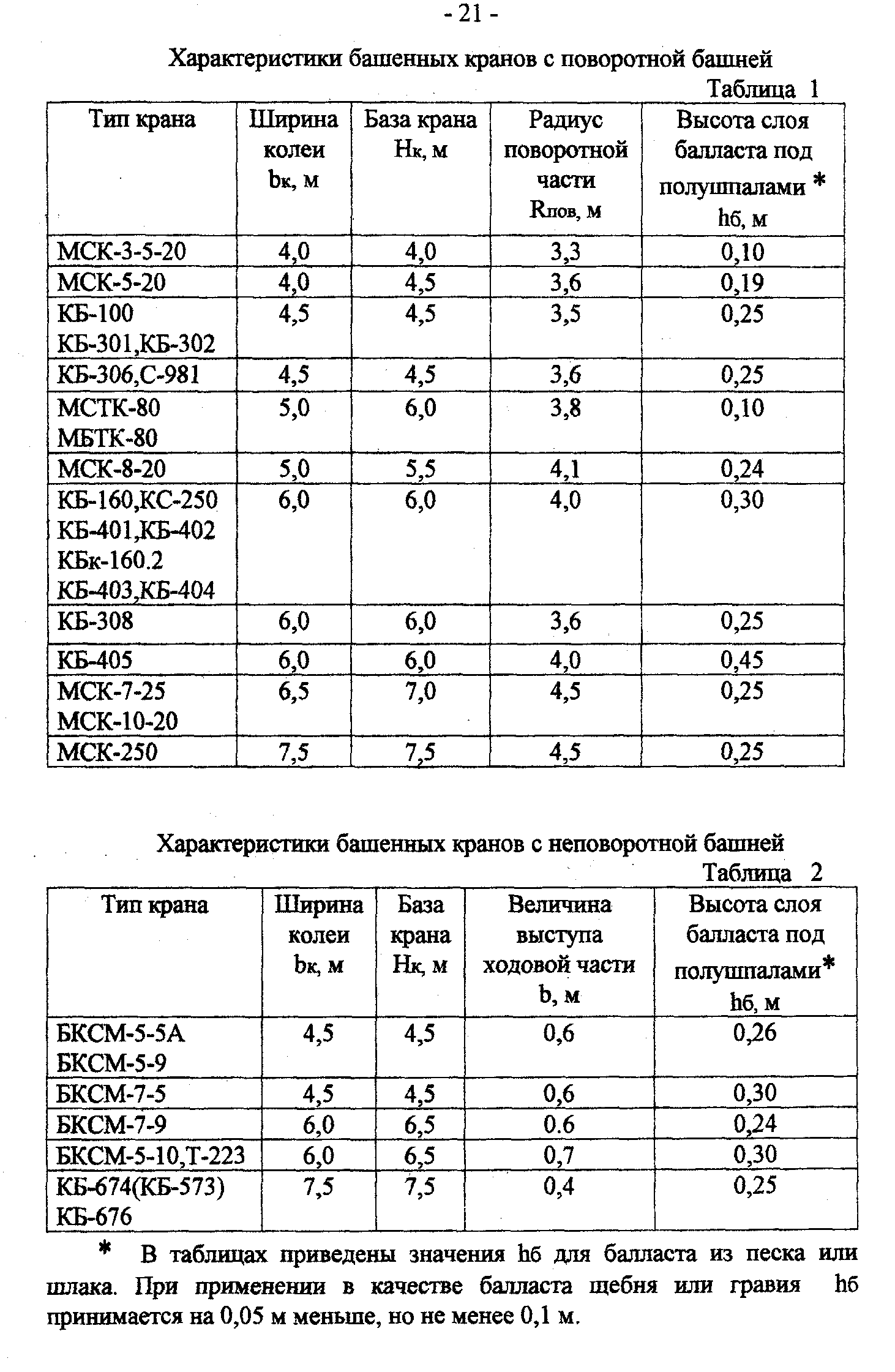
крана и ширины колеи. У кранов с
поворотной башней
наиболее приближены к зданию поворотная
платформа или нижний противовес. Привязка
таких кранов осуществляется по формуле:

B
= R_пов
+ 1_без
,

где В –
минимальное расстояние от оси подкрановых
путей до наружной грани здания (м );

R_пов
– радиус поворотной части или противовеса,
принимают по справочникам или
таблице 1 (м );

1_без
– минимально допустимое расстояние
по горизонтали между выступающей частью
крана и зданием, принимается на высоте
до 2 м от уровня земли не менее 0,7 м; на
высоте более 2 м – не менее 0,4 м.

Краны с неповоротной
башней могут располагаться ближе к
зданию, поскольку механизм поворота и
противовесная консоль располагаются
выше строящегося объекта. У этих кранов
наиболее приближенной к зданию является
ходовая часть, для них:

В =
0,5 Ьк + b
+ 1без ,

где Ьк – ширина
колеи крана ( м);

b
– величина выступающей за колею
ходовой части (м),

определяется по
паспорту крана или таблице 2 .

Привязку
башенных и рельсовых стреловых
кранов при возведении подземной части
здания у неукрепленных котлованов и
траншей производят исходя из глубины
выемки h
и вида грунта, что обеспечивает
расположение машин за пределами призмы
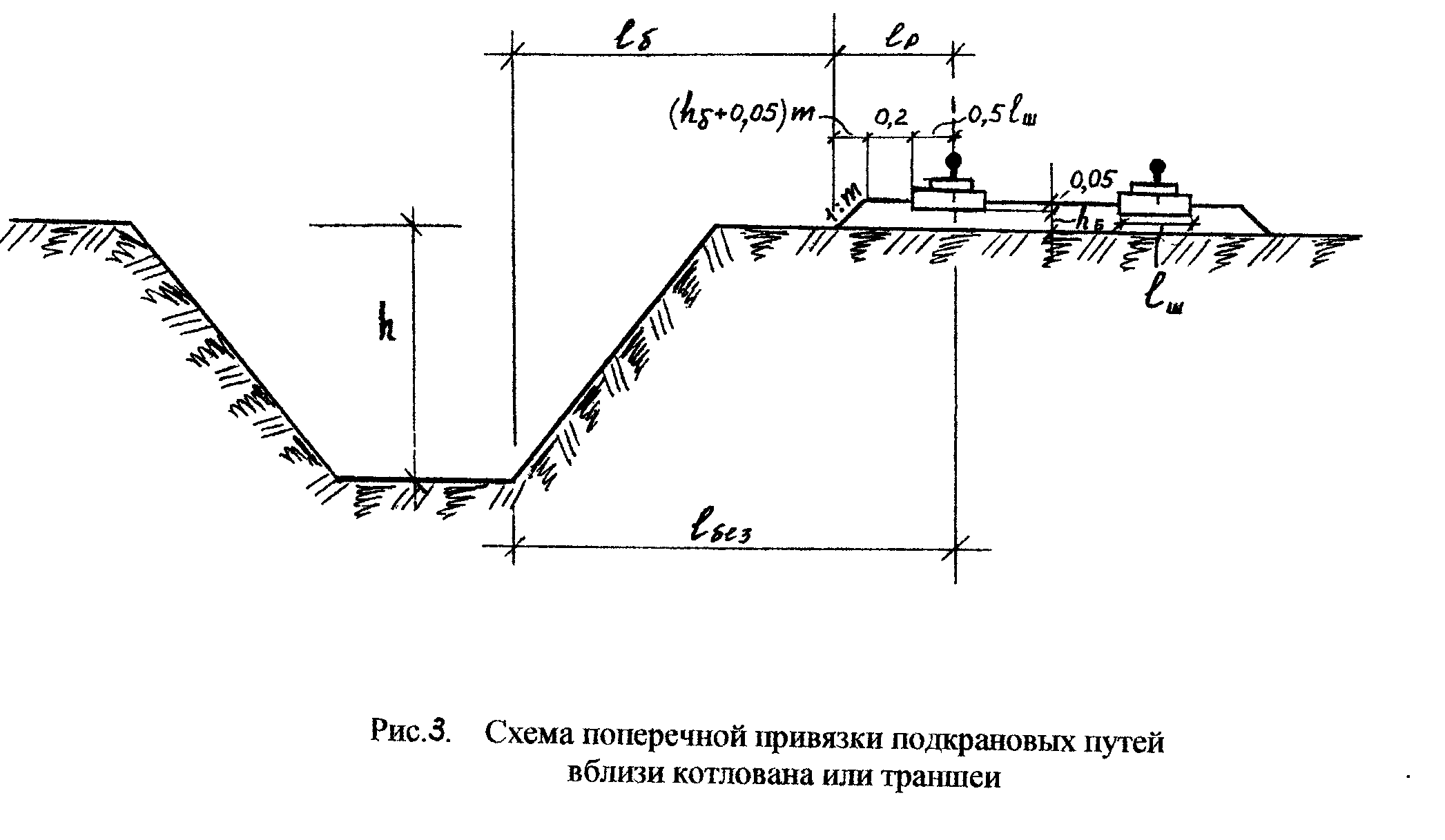
обрушения (рис.3). Безопасное расстояние
по горизонтали от основания откоса
выемки до оси ближайшего рельса
определяется по формуле:

l_без
= 1_б
+ 1_р
,

где
1б – минимальное расстояние от основания
откоса выемки до нижнего края балластной
призмы; для песчаных и супесчаных грунтов
1б > l,5h
+ 0,4; для глинистых и суглинистых грунтов
1б > h
+ 0,4(м); 1р – расстояние от нижнего края
балластной призмы до оси рельса (м),
определяется по формуле:

1р =
(h_б
+ 0,05)m
+ 0,2 + 0,51_ш
,

hб
– высота слоя балласта под полушпалами
(м), зависит от вида

балласта и типа
крана (таблицы 1,2);

0,05 – углубление
полушпалы в балласт (м);

m
– показатель крутизны откосов балластной
призмы, для щебня и гравия m
=1,5;

для
песка
и шлака т=2;

0,2 – минимально
допустимое расстояние от верхнего
края балластной призмы до конца
полушпалы (м);

1ш – длина деревянной
полушпалы, 1ш = 1,35 м.

Поперечную привязку
ограждений подкрановых путей к наружному
рельсу производят исходя из необходимости
соблюдения безопасного расстояния
между конструкциями крана и ограждением.

Для кранов с
поворотной башней расстояние от оси
ближнего к ограждению рельса до ограждения
определяют по формуле:

L_без
= (R_пов
–
0,5b_к)
+ 0,7

При
привязке ограждений башенных кранов с
неповоротной башней учитывается
выступающая за колею ходовая часть:

L без
= b
+ 0,7

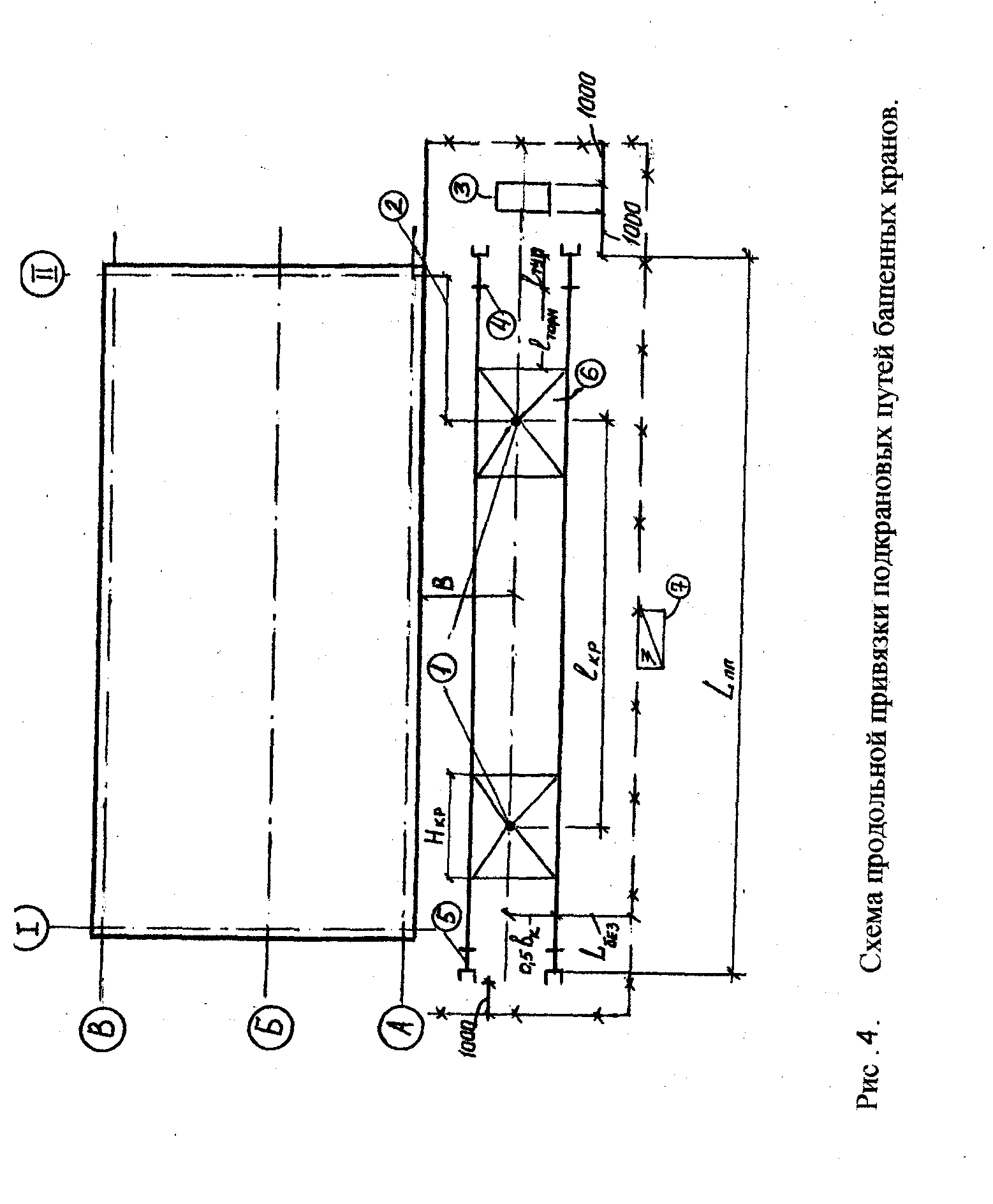
Крайние из этих засечек определяют
положение крайних стоянок, а измеренное
по чертежу в соответствии с принятым
масштабом расстояние и есть 1кр. На
стройгенплане крайние стоянки должны
быть обозначены и привязаны к осям
здания (рис.4: 1- крайние стоянки; 2 –
привязка крайних стоянок к оси; 3 –
контрольный груз; 4 – место установки
тупика; 5 – конец рельса; 6 – база крана; 7
– шкаф электропитания ).

Длину подкрановых путей
корректируют в сторону увеличения с
учетом кратности длине полузвена (6,25
м). Минимально допустимая длина путей
согласно правилам Госгортехнадзора
составляет два звена (25 м). Таким образом,
принятая длина путей должна удовлетворять
условию: Ln.n
= 6,25пзв > 25 м, где nзв
– число полузвеньев. Например,
если по расчету длина путей составляет
40 м, следует принять Ln.n=43,75
м (7 полузвеньев).

При необходимости кран может быть
установлен и на одном звене, то есть на
приколе. В этом случае для исключения
просадки подкрановых путей звено должно
быть уложено на жестком основании,
например, на специальных сборных
железобетонных конструкциях.

При продольной привязке
ограждений подкрановых путей на
стройгенплане должно быть показано
место нахождения контрольного груза
для проверки ограничителей грузоподъемности.
При этом выдерживается минимальное
расстояние 1 м :

– от конца рельса до ограждения;

от конца рельса до контрольного груза;

от контрольного груза до ограждения.

На стройгенплане показывается шкаф
электропитания крана, который
устанавливается за ограждением с
наружной от здания стороны кранового
пути.

Рабочая привязка самоходных
стреловых кранов заключается в нанесении
на стройгенплан осей их движения и
стоянок. Установка и работа гусеничных,
пневмоколесных и автомобильных кранов
вблизи котлованов и траншей с
неукрепленными откосами разрешается
только за пределами призмы обрушения
грунта. Безопасное расстояние от
основания откоса выемки до оси перемещения
крана 1_без
определяется по формуле:

1_без
= 1_оп
+ 0,5b_к
,

где 1оп – минимальное расстояние по
горизонтали от основания откоса до оси
ближайшей к выемке гусеницы, колеса или
выносной опоры ( м), принимается по
таблице 3;

b_к
– ширина колеи крана
(м), принимается по таблицам 4,5. При
монтаже подземной части объекта
самоходный стреловой кран обычно
передвигается вдоль бровки траншеи или
котлована. На выносных опорах пневмоколесные
и автомобильные краны устанавливаются
по направлению движения, при этом
продольная ось крана совпадает с осью
движения (рис.5).

Установка стрелового крана должна
производиться так, чтобы расстояние
между поворотной частью крана и
строениями, штабелями и другими предметами
было не менее 1 м [6]. Привязка крана при
монтаже надземной части здания
осуществляется по формуле:

В = R_пов
+ 1 ,

где В – минимальное расстояние от оси
движения крана до наружной

грани здания (м);

R_пов
– радиус поворотной части (м), принимается
по табл. 4,5.

Рабочая привязка строительных подъемников
производится так, чтобы основные
конструкции, материалы, изделия и
оборудование могли подаваться средствами
горизонтального транспорта в зоны их
действия без перегрузок. Стационарные
подъемники обычно располагаются на
границе или середине захваток, что
удобно с точки зрения обслуживания
грузоподъемных машин.

5) Зоны
влияния определяют
после привязки строительных машин с
целью обеспечения требований безопасности
труда. При организации строительной
площадки устанавливают опасные для
людей зоны, в пределах которых
постоянно действуют или потенциально
могут действовать опасные производственные
факторы.

К зонам постоянно
действующих опасных факторов относятся
зоны перемещения монтажных и грузоподъемных
машин, их частей и рабочих органов; зоны,
над которыми происходит перемещение
грузов кранами. Эти зоны во избежание
доступа посторонних лиц ограждаются
защитными ограждениями панельной или
панель-стоечной конструкции. К зонам
потенциально действующих
опасных факторов относятся
участки территории вблизи строящегося
здания. Эти зоны для предупреждения об
опасности ограждаются сигнальными
ограждениями из проволоки или каната
по стойкам. Защитные и сигнальные
ограждения должны соответствовать ГОСТ
Р 51 248 – 99. Следует устанавливать и
обозначать на стройгенплане следующие
опасные для людей зоны: -монтажную;

– зону обслуживания краном;

– опасную зону работы крана;

-опасную зону подкрановых путей или
опасную зону поворотной платформы;

– опасную зону работы подъемника.

Монтажной зоной
называют пространство, в котором возможно
падение элементов при их установке и
закреплении. Эта зона является потенциально
опасной. Согласно действующим нормативам,
границы этой зоны устанавливаются от
внешнего контура здания и зависят от
его высоты (табл.6; рис. 6а). В этой зоне
можно размещать только монтажный
механизм, складировать конструкции и
материалы здесь нельзя. Проход

людей через монтажную зону к строящемуся
зданию устанавливают со стороны, где
не работает кран; направление прохода
на стройгенплане показывают стрелками
в соответствии с принятыми условными
обозначениями. Места проходов через
эту зону защищают сплошными навесами
шириной не менее ширины входа с вылетом
не менее 2 м от стены здания. На стройгенплане
монтажную зону обозначают пунктирной
линией.

Все рассматриваемые ниже зоны влияния
относятся к зонам постоянно действующих
опасных производственных факторов.

Зона обслуживания краном
– это пространство, описываемое крюком
крана на максимальном необходимом для
работы вылете. Определяется для башенных
кранов путем нанесения на план из крайних
стоянок полуокружностей радиусом Rмакс
и соединения их прямыми линиями (рис. 6
). Для стреловых кранов зона обслуживания
тоже определяется максимальным рабочим
вылетом стрелы, но показывается по
отдельным стоянкам. На стройгенплане
обозначается утолщенной сплошной
линией.

Опасная зона работы крана
– это пространство, в
котором возможно падение груза при его
перемещении с учетом рассеивания при
падении. Рассеивание может быть вызвано
раскачиванием груза на крюке при движении
крана и под давлением ветра.

Для башенных кранов границу
опасной зоны Ron
определяют по формуле:

Rоп
= Rмакс
+ 0,51макс + 1без ,

где Rмакс
– максимальный рабочий вылет стрелы
крана ( м );

1макс – длина наибольшего перемещаемого
груза (м);

1без – дополнительное расстояние для
безопасной работы, зависит от высоты
подъема груза и устанавливается в
соответствии со СНИП [ 2 ] ( табл.6; рис.бв
).

Опасная зона подкрановых
путей башенных кранов
определяется при поперечной привязке
ограждений ( рис.7: 1 – знак безопасности
№3 на границе опасной зоны с обозначением
его номера 2.7 по ГОСТу; 2 – груз; 3 – ось
подкрановых путей; 4 – инвентарное
ограждение подкрановых путей и знак
безопасности №4 с обозначением его
номера 1.3 по ГОСТу ). На стройгенплане с
помощью условного обозначения показывают
инвентарное сетчатое ограждение
подкрановых путей с калиткой для прохода
машиниста.

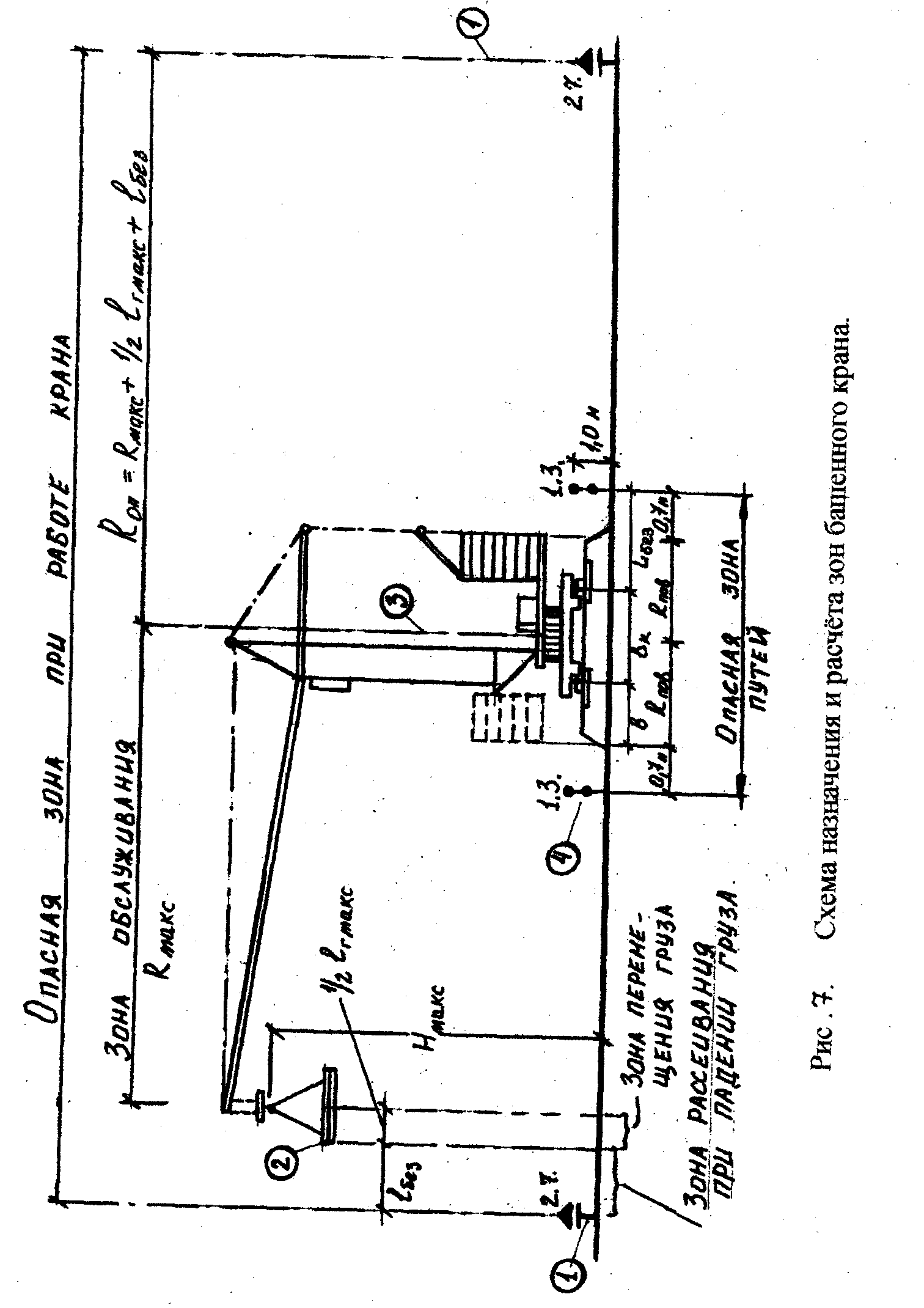
Зону обозначают на
стройгенплане штрихпунктирной линией
( рис.бг, табл.8).

Технические характеристики строительных
подъемников

Таблица 8

Модель	Назначение	Грузоподъ­емность, кг	Высота подъема, м	Габаритные размеры платформы (кабины), м
ТП-ЗА(С-598А)	грузовой	320	9	1,5×0,9
ТП-2(С-447)	грузовой	500	17	1,5 х 1,0
ТП-7(С-447М)	грузовой	500	27	1,5 х 1,0
ТП-9	грузовой	500	17	1,5×0,9
ТП-12	грузовой	500	27	1,5×0,9
ТП-14	грузовой	500	50	1,45 хО,68
ПР-1-172	грузопасса­жирский	580	70	2,4×1,2
ПГС-800-16	грузопасса­жирский	800	80	3,1×1,5
МГП-1000	грузопасса­жирский	1000	150	2,5 х 1,5

Опасная зона поворотной
части стреловых кранов
определяется по формуле:

Яоп.пов
= RnoB
+ 1 (м),

Расчет приводится в пояснительной
записке, зона на стройгенплане не
показывается. На местности эту опасную
зону обозначают инвентарной переставной
обноской из проволоки по стойкам.

Опасная зона работы
подъемника (А) – это
пространство, в котором возможно падение
поднимаемого груза. При высоте подъема
груза Н до 20 м зону следует принимать
не менее 5 м от габаритов подъемника в
плане, а при подъеме на большую высоту
величина зоны составляет:

А = 5 + 1/15(Н – 20)

Зону обозначают на стройгенплане
штрихпунктирной линией ( рис.бг, табл.8).

6) Ограничения
в работу вводят при
совместном использовании на объекте
нескольких кранов и при работе в
стесненных условиях.

Совместная работа нескольких механизмов
в одной монтажной зоне, как правило,
запрещена. В случае производственной
необходимости одновременная работа
допускается при условии осуществления
специальных мероприятий по технике
безопасности.

Если краны расположены с двух сторон
здания, совместная работа должна быть
организована так, чтобы траектории
движения их стрел не пересекались. Тогда
минимальное расстояние между осями
вращения кранов при их предельном
сближении определяется по формулам:

– для башенных кранов

С = L_l
+ L₂
+ 0,5 (l₁
+ 1₂)
+ Δ₁
+ Δ₂
+ 2Δ_б

– для стреловых кранов

С = L_l
+ L₂
+ 0,5 (l₁
+ 1₂)
+ Δ₁
+ Δ₂
,

где – L₁,
L₂
– вылеты стрел при совместной работе
(м);

l_l,
1₂ –
максимальный горизонтальный размер
монтируемых конструкций (м);

Δ_1,
Δ₂
– отклонение конструкций от вертикали
при вращении стрелы:

Δ = 900L
/ (900 – ω²H)
– L

ω – максимальная частота
вращения поворотной части (мин
^-1) [3]; ориентировочно
можно принять: для башенных кранов-
ω=0,7; для гусеничных- ω=0,3; для пневмоколесных-
ω=1,2; для кранов на спецшасси автомобильного
типа- ω=1,6; для автомобильных кранов- ω=
2,0;

Н – высота подъема конструкции (м);

Δ_б
– возможное отклонение от вертикали
башни крана в результате ее податливости
и уклона пути, Δ_б
=0,5 м.

Пример.
С двух сторон здания на монтаже плит
покрытия длиной 1 = 6 м работают два
башенных крана КБ-100. Вылет при совместной
работе L
= 20 м, высота подъема плит Н = 33 м.
Максимальная частота вращения башни
крана ω = 0,7 мин^-1.

Расчет: Δ = 900* 20/ (900 – О,7²х33)
– 20 = 0,37 м

С = 20 + 20 + 1/2(6 + 6) + 0,37 + 0,37 + 2*0,5
= 47,74 м.

Расстояние между крюками
должно быть не менее 47,74 – 20х2 = 7,74 м.

Если монтаж конструкций ведется двумя
кранами, расположенными с одной стороны,
то это та сторона здания, где нет входов
в него. При сближении башенных кранов,
установленных на общих рельсовых путях,
требованиями техники безопасности
предусматривается установка концевых
выключателей механизмов передвижения
для остановки кранов на расстоянии не
менее 5 м между перемещаемыми грузами
или выступающими конструкциями кранов.

При работе монтажного крана в стесненных
условиях приходится вводить ограничения
на определенные рабочие движения крана,
например, на поворот башни во избежание
проноса груза над действующей городской
магистралью. Ограничения могут быть
принудительными или условными, их
показывают на стройгенплане или
прилагаемых к нему схемах.

Принудительные ограничения
зоны обслуживания применяют при работе
кранов с электрическим приводом
(башенных, козловых). Эти ограничения
осуществляются установкой концевых
выключателей, при срабатывании которых
независимо от действий машиниста
происходит остановка определенного
механизма и исключается пронос груза
в зону ограничения. На башенных кранах
устанавливают концевые выключатели
механизмов передвижения крана и тележки,
поворота стрелы, изменения вылета. При
ограничении поворота стрелы после
срабатывания выключателей расстояние
до зоны ограничения должно быть не менее
тормозного пути стрелы крана с максимальным
грузом (указан в паспорте крана, можно
принять 2 м). В этом случае на стройгенплане
обозначают:

– угол
ограничения а, который
проставляется в запрещенном секторе;

– места
расположения предупреждающих знаков
Ml,
которые устанавливают
на расстоянии тормозного пути до места
срабатывания концевых выключателей;

– линию
запрещающих знаков №2, устанавливаемых
по контуру зоны ограничения (рис.8,9).

Условные (визуальные)
ограничения зоны обслуживания применяются
при работе башенных и стреловых самоходных
кранов; они рассчитаны на внимание
крановщика и стропальщиков. На местности
зону ограничения обозначают хорошо
видимыми с крана красными флажками, а
в темное время суток- гирляндами из
красных ламп. На стройгенплане показывают:

– места
расположения предупреждающих знаков
№1, которые
устанавливают на расстоянии тормозного
пути до линии ограничения;

– линия
запрещающих знаков М2, т.е.
линия ограничения, пронос груза за
которую запрещен;

– запись
об условиях работы крана, “крановщик
обязан остановить груз, не доходя 1 метра
до предупреждающего знака №1,далее до
места установки груза перемещать его
повторными короткими включениями “.

Была ли эта статья полезной?

Точку, в которой происходит равное распределение величины, определяющей инерционные и гравитационные свойства, называют центром масс. Формула для определения параметра зависит от радиус-вектора частиц системы и их полной энергии. Эту характеристику тела отличают от тяжести, при этом в трудах советских учёных Ландау, Лифшица для неё используется термин «центр инерции».

Оглавление:

• Общие сведения
• Связь с центром тяжести
• Вычисление положения
• Геометрический способ определения

Общие сведения

Допустим, имеется тело, на которое действуют скомпенсированные силы. В этом случае оно будет в состоянии покоя или прямолинейного равномерного движения. Пусть тело будет неподвижным. Например, лодка на воде. К ней можно приложить воздействие F1 в районе её кормы. Под действием силы она начнёт разворачиваться. Аналогично если воздействовать на её нос F2, то она тоже будет поворачиваться, но при этом разворот будет происходить в другую сторону.

Получается, что можно подобрать такую линию, на которой действие сил приведёт её к ускоренно поступательному движению. Пусть это будет F3. На самом деле таких сил может быть несколько. При этом их можно перемещать вдоль линии их воздействия. Если все такие силы изобразить в виде линий, то они пересекутся в одной точке. Такое место и называют центром масс тела (ЦМ). То есть точку, в которой пересекаются линии действия сил, вызывающие только ускоренное поступательное механическое движение.

Эта важная точка в теле и движется она довольно просто. Перемещение любого тела можно представить, как комбинацию двух видов движения:

• центра масс;
• вращения.

Существует теорема: ЦМ тела движется так, как перемещалась бы материальная точка, в которой сосредоточена вся масса и к которой приложены все воздействия, действующие на объект. Таким образом, различные виды изменения положения точек в пространстве можно описать с помощью законов Ньютона. Согласно же теореме их можно применять и к телу, если считать, что все силы приложены к центру масс.

Рассматривая объект, можно не учитывать его размер, форму, а брать во внимание только инерцию, ускорение и принцип парного взаимодействия. Фактически в механике перемещение сколь угодно сложного вида рассматривается по принципу суперпозиции и закона сохранении энергии. При этом довольно удобно изучать изменение положения в системе отсчёта связанной с этим центром. В ней полный импульс всегда будет равным нулю, что позволяет упростить уравнение движения.

Связь с центром тяжести

Пусть имеется объект, находящийся на Земле. Говорят, что на него действует сила тяжести. Но на самом деле она воздействует не на вещество, а на каждый его атом, частичку. Если предположить, что ускорение свободного падения буде одинаковым, то на объект действует очень множество сил тяжести. Рассматривать такую систему неудобно. Поэтому все воздействия заменяют равнодействующей. И считают, что действует одна сила, которая приложена к центру тяжести твёрдого тела.

Для того чтобы найти взаимосвязь между тяжестью и массой нужно представить, что объект вдруг распался на отдельные равные кусочки. Они держатся вместе, но не прикреплены друг к другу. Если тело отпустить, то они будут падать вместе, так как ускорение свободного падения не зависит от массы. При этом движение будет поступательным. Значит, сила, приложенная к телу в целом, будет приложена к центру масс.

Получается, что центральная точка является общей как для тяжести, так и для масс. Это две точки положение которых совпадает несмотря на разный их принцип определения в физике. Но существуют условия, когда это правило не выполняется. Например, если система материальных точек неоднородна по объёму плотности в гравитационном поле, то центры не совпадут.

Для примера можно привести список однородных фигур с указанием их центральной точки:

• отрезок — середина;
• параллелограмм — место пересечения диагоналей;
• треугольник — точка пересечения медиан (центроид);
• любой правильный многоугольник — центр поворотной симметрии;
• полукруг — точка, в которой перпендикулярный радиус делится в отношении 4:3p считая от центра круга.

Чтобы найти координату центра масс объекта, который можно представить, как совокупность связанных материальных точек используют два метода: аналитический и геометрический. Но второй способ не всегда можно применить. В однородном гравитационном поле центры тяжести и масс всегда совпадают. И это часто подтверждается на практике, из-за того, что внешнее гравитационное поле в задачах, связанных с действиями на Земле, считают постоянным в пределах объёма тела.

Поэтому эти термины объединяют в геометрии, статике и так далее. То есть в тех областях, где применение определения можно назвать метафорическим и предполагается ситуация их эквивалентности.

При таком понимании оба термина синонимичны, но при этом чаще предпочитают использовать термин, связанный с тяжестью. Это происходит в силу того, что исторически он появился раньше.

Вычисление положения

Пусть тело представляет собой совокупность материальных точек, лежащих на одной прямой при этом их массы разные. Задача состоит в нахождении его центра. Для этого следует вести систему координат с осью икс, которая будет совпадать с линией расположения точек. При этом тело пусть подвешено на невесомой опоре и находится под действием Земного тяготения. Это условие даёт возможность воспользоваться тем фактом, что положения центров масс и тяжести совпадают.

На каждую из материальных точек действует своя сила: m1g, m2g… mng. Если предоставить это тело самому себе, то оно будет в состоянии свободного падения. Остановить тело — подпереть, но при этом так, чтобы оно находилось в равновесии. Это значит, что сила реакции опоры должна проходить через центр тяжести, так как равнодействующая тоже её пересекает.

Получится, что сила реакции опоры будет лежать на одной прямой с силой тяжести действующей на тело в совокупности и их моменты тоже будут проходить через неё. С помощью координатной оси точкам можно присвоить положение, x1, x2… xn, а ЦМ xц. Чтобы тело находилось в равновесии необходимо выполнение двух условий:

• векторная сумма всех сил должна быть равной нулю: m1g + m2g +…+mng + F = 0;
• сумма моментов равняться нулю: Mm 1 g + Mm 2 g +…+ Mmng + MF = 0.

Из первого условия можно найти силу реакции опоры: F = (m1 + m2 +…+mn) * g. Если вращение выбрать против часовой стрелки, тогда относительно оси все моменты силы тяжести будут отрицательными, а опоры — положительные. Тогда справедливо записать: F * хц = (m1 x 1 + m2 x 2 +…+mn xn) * g.

Из последнего равенства можно выразить координату ЦМ: xц = ((m1 x 1 + m2 x 2 +…+mn xn) * g) / F. В эту формулу можно подставить выражение для F. В результате ускорение свободного падения сократится и получится: xц = (m1 x 1 + m2 x 2 +…+mn xn) / (m1 + m2 +…+mn). Это формула выглядит громоздко, но запомнить её легко. В числителе стоят произведения масс материальных точек на их координаты, а в знаменателе — вес всего тела.

Если точки не будут лежать на одной прямой, то координата ЦМ тоже не изменится. То есть приведённая формула справедлива для любого положения тела относительно координаты y.

При этом её можно применять и для рассмотрения предметов в пространстве, так как все направления в существующем мире равноправные.

Геометрический способ определения

Для простейших симметричных фигур ЦМ можно определить геометрическим методом. Для этого используются свойства диагоналей и медиан. Пусть имеется произвольной формы четырёхугольник. Изготовлен он из однородного материала.

Идея вычисления состоит в том, что эту фигуру необходимо разбить на два треугольника. Для этого нужно провести диагональ, которая разделит фигуру на два тела. Затем провести в каждом треугольном теле три медианы. Точка их пересечения и будет ЦМ. В результате вместо четырёхугольника можно рассматривать две материальные точки.

Несмотря на то что масса у них разная ЦМ будет находиться на соединяющем их отрезке. Теперь четырёхугольник можно разбить на два других треугольника и выполнить аналогичные действия уже для них. Получится два отрезка, на которых одновременно расположен ЦМ. Значит, его положение будет определяться точкой их пересечения.

Для более сложной фигуры, например, шести или восьмиугольника можно использовать такой же подход. Сначала нужно разделить тело на прямоугольники, а затем треугольники. Найти ЦМ для полученных фигур и определить точку пересечения. Следует понимать, что ЦМ может находиться и за пределами объекта.

Но в реальных ситуациях бывают фигуры, которые имеют неправильную форму. Для них нельзя применить расчёт или геометрический метод. Поэтому выясняют, где расположен ЦМ экспериментальным путём.

Например, пусть имеется тело сложной неправильной формы. Чтобы найти ЦМ необходимо фигуру подвесить в пространстве. На неё действует две силы: тяжести и реакции оси. Первая заставляет фигуру поворачиваться с определённой скоростью до тех пор, пока момент силы тяжести относительно оси крепления не станет равным нулю. То есть точка опоры, ось и центр тяжести окажутся на одной вертикале.

Чтобы узнать, где же находится ЦМ, тело нужно подвесить, используя другую точку. При этом на самой фигуре следует отметить, как проходит вертикаль.

Повторяя такой опыт минимум три раза, можно увидеть точку пересечения осей, которая и будет искомым ЦМ. Причём чем будет больше экспериментов, тем точнее он будет определён.

Центр тяжести (центр масс):

Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.

Центр тяжести – геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.

На каждую точку тела в поле сил тяжести действует сила, а на все тело – равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.

Центр масс (центр инерции) – точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе  внешние силы.

При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.

Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.

При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, – параллельными.

Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.

 Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.

Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.

Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.

Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.

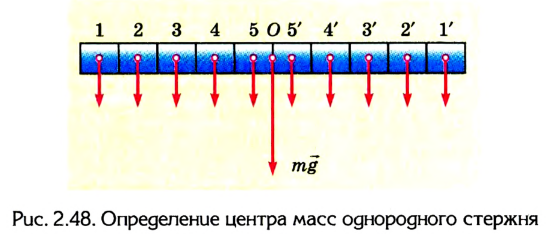
1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О – середине стержня.

Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.

Центр тяжести однородного стержня расположен в середине стержня.

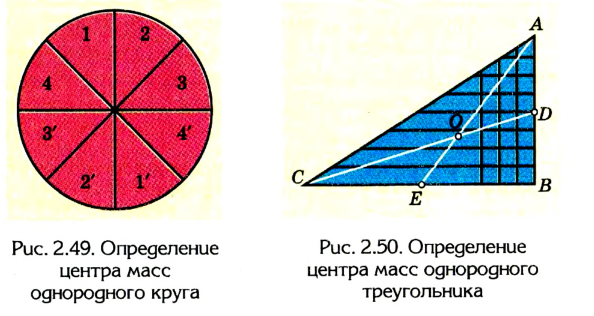
2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).

Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.

Центр тяжести однородного круга совпадает с его центром.

Центр тяжести однородного треугольника находится в точке пересечения его медиан.

3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.

Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.

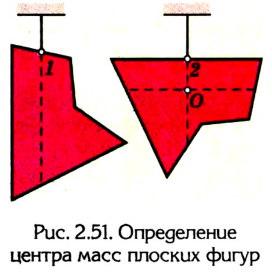
4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).

Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.

Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.

Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.

• Заказать решение задач по физике

Центр тяжести тела и центр масс тела

Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.

Рис. 151

Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.

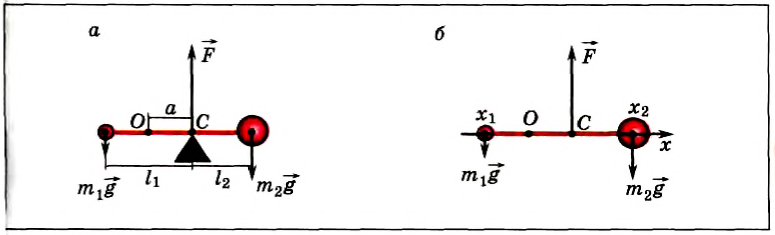
Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m₁ и m₂, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:

или

Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:

Рис. 152

Поскольку F=(m₁ + m₂)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.

Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х₁, х_с и х₂. Запишем условие моментов относительно точки О:

Отсюда

При выводе этой формулы было использовано значение силы F = (m₁ + m₂) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии х_с, определенном формулой (2).

Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.

Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.

Если произвольное тело можно разбить на n элементов, массы которых m₁, m₂…,    m_n, и если известны координаты центров масс этих элементов x₁, x₂…,   x_n относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:

Естественно, что такие же соотношения можно записать и для у_с и z_c. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m₁ = 2m₂). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C₁) и линейки (C₂).

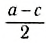
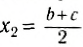
Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х₁ = 0, y₁ =, а координаты центра масс линейки: , y₂ = 0 .
По формуле (3):    .

Таким образом, центр масс угольника находится вне тела.

Главные выводы:

1. Центр тяжести — точка, в которой приложена сила тяжести.
2. Центр масс симметричных однородных тел находится в их геометрическом центре.
3. Координаты центра масс тела можно вычислить по формуле (3).