Координаты центров тяжести неоднородных тел.
Координаты центра
тяжести неоднородного
твердого тела
в выбранной системе отсчета определяются
следующим образом:
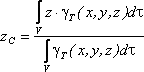
где
– вес единицы объема тела (удельный вес)
– вес всего тела.
Если твердое тело
представляет собой неоднородную
поверхность,
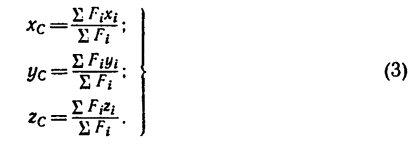
то координаты центра тяжести в выбранной
системе отсчета определяются следующим
образом:
где
– вес единицы площади тела,
– вес всего тела.
Если твердое тело
представляет собой неоднородную
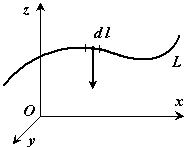
линию, то
координаты центра тяжести в выбранной
системе отсчета определяются следующим
образом:
где– вес единицы длины тела
,
–
вес всего тела.
Координаты центров тяжести однородных тел.
Для однородного
тела вес
любой его части пропорционален объему
этой части:
,
а весР
всего тела
пропорционален объему V
этого тела
,
где– вес единицы объема.
Подставив эти
значения Р
и
в предыдущие формулы, мы заметим, что в
числителекак общий множитель выносится за скобку
и сокращается с
в знаменателе.
В результате получим:
Как видно, центр
тяжести однородного тела зависит только
от его геометрической формы, а от величины
не зависит. По этой причине точку
С,
координаты которой определяются
формулами, называют центром тяжести
объема V.
Путем аналогичных
рассуждений легко найти, что если тело
представляет собой однородную плоскую
и тонкую пластину, то для нее
где S
– площадь всей пластины, a
–
площади ее частей.
Точку, координаты
которой определяются
формулами называют
центром тяжести площади S.
Точно так же получаются
формулы для координат центра тяжести
линии:
где L
— длина всей
линии, l
— длины ее частей.
Таким образом, центр
тяжести однородного тела определяется,
как центр тяжести соответствующего
объема, площади или линии.
Способы определения координат центра тяжести.
Исходя из полученных
выше общих формул, можно указать
конкретные способы определения
координат центров тяжести тел.
1. Симметрия.
Если однородное тело имеет плоскость,
ось или центр симметрии, то его центр
тяжести лежит соответственно в плоскости
симметрии, оси симметрии или в центре
симметрии.
2. Разбиение.
Тело разбивается на конечное число
частей, для каждой из которых положение
центра тяжести и площадь известны.
.
3. Дополнение.
Частный случай
способа разбиения. Он применяется к
телам, имеющим вырезы, если центры
тяжести тела без выреза и вырезанной
части известны.
.
Центры тяжести некоторых однородных тел.
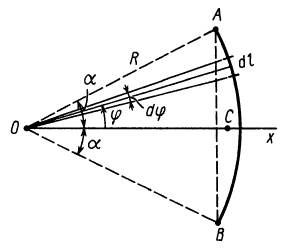
1) Центр
тяжести дуги окружности.
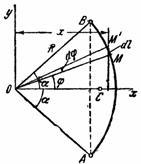
Рассмотрим дугу АВ
радиуса R
с центральным
углом
.
В силу симметрии центр тяжести этой
дуги лежит на осиOx
(рис. 37).
Рис.37
Найдем координату
по формуле
.
Для этого выделим на дугеАВ
элемент ММ’
длиною
,
положение которого определяется углом.
Координатах
элемента ММ’
будет
.
Подставляя эти значениях
и
и
имея в виду, что интеграл должен быть
распространен на всю длину дуги, получим:
где
L
– длина дуги АВ,
равная
.
Отсюда окончательно находим, что
центр тяжести дуги окружности лежит на
ее оси симметрии на расстоянии от центра
О,
равном
где
угол
измеряется в радианах.
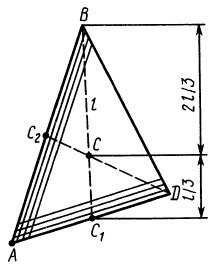
2) Центр
тяжести площади треугольника.
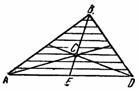
Разобьем площадь треугольника ABD
(рис. 38) прямыми, параллельными AD,
на узкие полоски; центры тяжести этих
полосок будут лежать на медиане BE
треугольника.
Рис.38
Следовательно, и
центр тяжести всего треугольника
лежит на этой медиане. Аналогичный
результат получается для двух других
медиан. Отсюда заключаем, что центр
тяжести площади треугольника лежит в
точке пересечения его медиан.
При этом, как
известно,
3) Центр
тяжести площади кругового сектора.
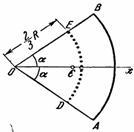
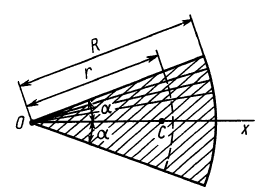
Рассмотрим круговой сектор ОАВ
радиуса R
с центральным углом
(рис. 39). Разобьем мысленно площадь
сектораОАВ
радиусами, проведенными из центра О,
на п
секторов. В пределе, при неограниченном
увеличении числа
,
эти секторы можно рассматривать как
плоские треугольники, центры тяжести
которых лежат на дугеDE
радиуса
.
Следовательно, центр тяжести сектораОAB
будет совпадать с центром тяжести
дуги DE.
Окончательно получим, что центр тяжести
площади кругового сектора лежит на его
центральной оси симметрии на расстоянии
от начального центра
О,
равном
Рис.39
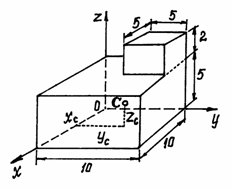
Пример
1.
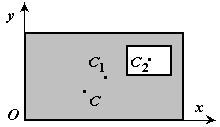
Определим центр тяжести однородного
тела, изображённого на рис. 40.
Рис.40
Тело однородное,
состоящее из двух частей, имеющих
симметричную форму. Координаты центров
тяжести их:
Объёмы их:
.
Поэтому координаты
центра тяжести тела
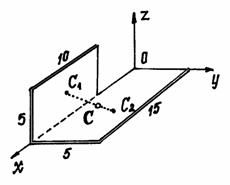
Пример
2. Найдем
центр тяжести пластины, согнутой под
прямым углом. Размеры – на чертеже
(рис.41).
Рис.41
Координаты центров
тяжести:
Площади:
Поэтому:
Рис.
6.5.
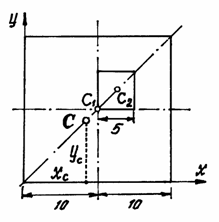
Пример
3. У
квадратного листа
см
вырезано квадратное отверстие
см (рис.42). Найдем центр тяжести листа.
Рис.42
В этой задаче удобнее
разделить тело на две части: большой
квадрат и квадратное отверстие. Только
площадь отверстия надо считать
отрицательной. Тогда координаты центра
тяжести листа с отверстием:
координата
так как тело имеет ось симметрии
(диагональ).
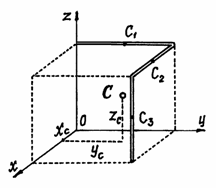
Пример
4.
Проволочная скобка (рис.43) состоит из
трёх участков одинаковой длины l.
Рис.43
Координаты центров
тяжести участков:
,
;
,
Поэтому координаты центра тяжести всей
скобки:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Центр тяжести:
При рассмотрении движения тел, особенно таких, как самолеты, ракеты, космические корабли, важное значение имеет понятие центра тяжести.
Определения и формулы для вычисления центров тяжести
Для введения понятия центра тяжести разобьем мысленно рассматриваемое тело на достаточно большое число малых по сравнению с телом или элементарных его частей произвольной формы. Силу тяжести элементарной частицы тела с индексом
Радиус-вектор центра тяжести тела 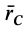
где 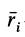

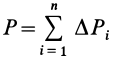

Рис. 88
Если в (1) перейти к пределу, увеличивая число элементарных частей 

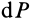
где 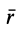
где 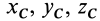
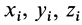
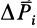
Используя понятие центра тяжести тела, введем понятие его центра масс. Силы тяжести элементарных частей тела и всего тела можно выразить через их массы 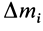
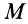

Подставляя эти значения сил тяжести в (1) и (1′) после сокращения на 
и соответственно
По формулам (2) и (2′) определяют радиус-вектор центра масс тела. Центр масс обычно определяют независимо от центра тяжести как геометрическую точку, радиус-вектор, которой вычисляется по формулам (2) или (2′). В проекциях на оси координат из (2) и (2′) получаем:
и
где 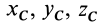
Для однородного тела силу тяжести элементарной частицы тела и ее массу можно вычислить по формулам
где 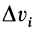


где 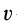


по которым определяют центр тяжести объема тела.
Если тело имеет форму поверхности, т. е. один из размеров мал по сравнению с двумя другими, как, например, у тонкого листа железа, то имеем
где 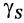
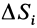
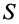
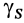
Для однородных тел типа проволоки, у которых два размера малы по сравнению с третьим, можно определить радиус-вектор центра тяжести длины линии по формулам
где 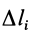
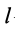
Методы определения центров тяжести (Центров масс)
Метод симметрии
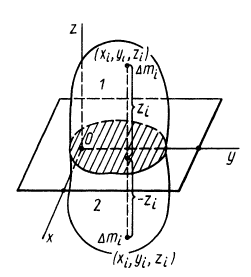
При определении центров тяжести широко используется симметрия тел. Докажем, что для однородного тела, имеющего плоскость симметрии, центр тяжести находится в плоскости симметрии. Для доказательства выберем начало координат в плоскости симметрии тела и одну из осей координат, ось 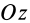
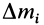
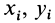
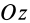
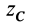
Разбивая сумму в числителе на две по симметричным частям тела, получаем, что
так как симметричные части тела 1 и 2 одинаковы.
Таким образом, центр масс расположен в плоскости симметрии и для его определения достаточно вычислить только две его координаты 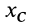
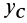
Аналогично доказывается, что для однородного тела, имеющего ось или центр симметрии, центр масс находится соответственно на оси симметрии или в центре симметрии.
Рис. 89
Метод разбиения на части (метод группировки)
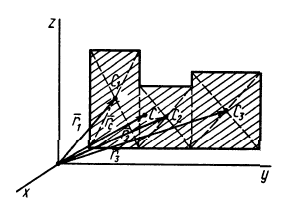
Некоторые тела сложной формы можно разбить на части, центры тяжести которых известны или предварительно могут быть определены. В таких случаях центры тяжести сложных тел вычисляются по общим формулам, определяющим центр тяжести, только вместо элементарных частиц тела берутся его конечные части, на которые оно разбито. Покажем это на частном примере плоской фигуры, изображенной на рис. 90. Плоскую фигуру можно разбить на три части, центры тяжести которых 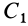
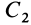
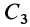
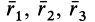
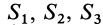
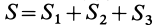
Используя определение центра тяжести и производя группировку слагаемых под знаком суммы по частям фигуры, на которые она разбита, получим
Радиусы-векторы центров тяжести частей тела выразятся в такой форме:
или
Используя эти формулы для радиуса-вектора всей фигуры, имеем
Полученная формула имеет ту же структуру, что и формула, определяющая радиус-вектор центра тяжести тела при разбиении его на элементарные частицы, только в нее входят величины для конечных частей тела.
Рис. 90
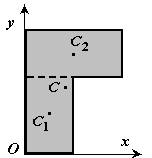
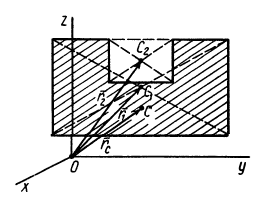
Метод отрицательных масс
Видоизменением метода разбиения на части является метод отрицательных масс. Проиллюстрируем его тоже на примере плоской фигуры (рис. 91). Для определения центра тяжести этой фигуры ее можно разбить на три части. Можно поступить по-другому. Для этого дополним нашу фигуру до прямоугольника и примем, что этот прямоугольник с площадью 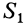
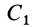
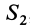
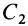
В отличие от обычного метода разбиения на части в формуле (4) массы и, следовательно, площади входят со знаком минус.
Метод отрицательных масс особенно удобен при вычислении положения центров тяжести тел, имеющих отверстия.
Рис. 91
Центры тяжести простейших тел
Для определения центров тяжести тел сложной формы методом разбиения на части или методом отрицательных масс необходимо уметь вычислять центры тяжести простейших тел, на которые разбивается тело сложной формы. Рассмотрим некоторые из тел, для определения центров тяжести которых известны простые способы их нахождения или вычисления по формулам.
Прямолинейный отрезок
Центр тяжести прямолинейного однородного отрезка располагается на его середине, а неоднородного— на самом отрезке и не может находиться вне отрезка.
Площадь треугольника
Для определения центра тяжести площади треугольника разобьем его прямыми линиями, параллельными одной из его сторон 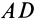

Затем разобьем треугольник на полоски прямыми линиями, параллельными другой стороне 
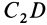

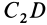
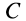

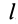
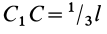
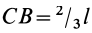
Рис. 92
Дуга окружности
Дуга окружности 
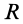
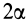
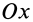

Рис. 93
В рассматриваемом случае
Подставляя эти значения в формулу для 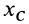
Таким образом,
Для полуокружности 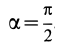
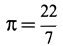
Площадь кругового сектора
Центр тяжести площади кругового сектора с радиусом 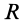
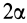
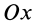
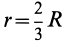
Рис. 94
Используя формулу для центра тяжести дуги окружности, получим
или
Для площади полукруга 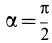
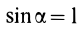
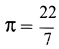
Объем пирамиды и конуса
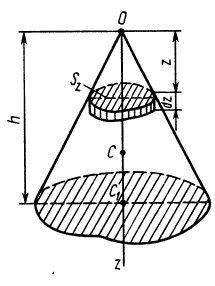
Определим положение центра тяжести объема конуса (рис. 95). Для простоты рассмотрим прямой конус, у которого высота является осью симметрии. Высотой конуса является отрезок, соединяющий его вершину 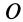
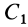
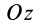
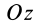
Разобьем конус плоскостями, перпендикулярными оси 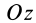
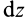
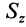
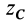
Отношения линейных размеров сечений к соответствующим размерам основания конуса пропорциональны их расстояниям до вершины конуса. Отношения площадей пропорциональны квадратам расстояний. Приняв 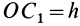
Учитывая, что
имеем
или
Таким образом, центр тяжести прямого конуса находится на расстоянии 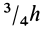
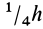
Рис. 95
Это справедливо для объема любого конуса и любой пирамиды, как прямых, так и наклонных, т. е. центр тяжести объема пирамиды или конуса находится на расстоянии 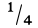
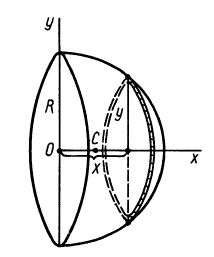
Объем полушара
Полушар имеет ось симметрии, которую примем за координатную ось 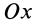
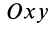
где 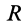
где 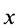
Объем элементарного диска
так как радиус диска 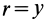
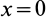
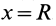
Таким образом, центр тяжести объема полушара находится от его центра на расстоянии
Это расстояние меньше половины радиуса полушара.
Рис. 96
Задача №1
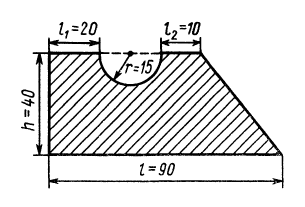
Определить координаты центра тяжести площади плоской фигуры, имеющей размеры, указанные на рис. 97.
Рис.97
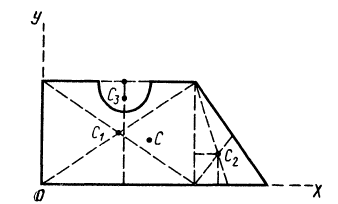
Рис. 98
Решение. Присоединим к заданной фигуре дополнительно полукруг 3 и разобьем полученную фигуру на прямоугольник 1 и треугольник 2. Получили три фигуры, две из которых имеют положительные площади (прямоугольник 1 и треугольник 2) и одна — отрицательную (полукруг 3). В выбранной системе координат для координат центра тяжести заданной фигуры имеем
где 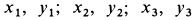
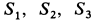
Вычислим площади и координаты центров тяжести отдельных фигур, учитывая рис. 98 Имеем:
так как 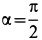
Подставляя полученные значения в (а), получим:
Центр тяжести плоской фигуры
постановка задачи. Найти площадь и координаты центра тяжести плоской фигуры.
План решения:
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
2. Выбираем систему координат. Вычисляем площади и координаты 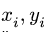
3. Находим общую площадь фигуры по формуле
4. Определяем координаты центра тяжести фигуры:
Задача №2
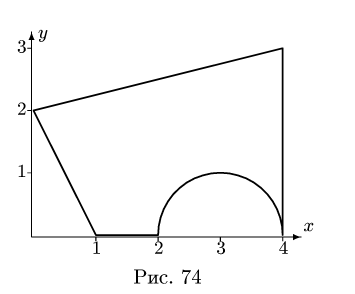
Найти площадь и координаты центра тяжести плоской фигуры. Криволинейный участок контура является половиной окружности с центром на оси Ох (рис. 74). Размеры на рисунке даны
Решение
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
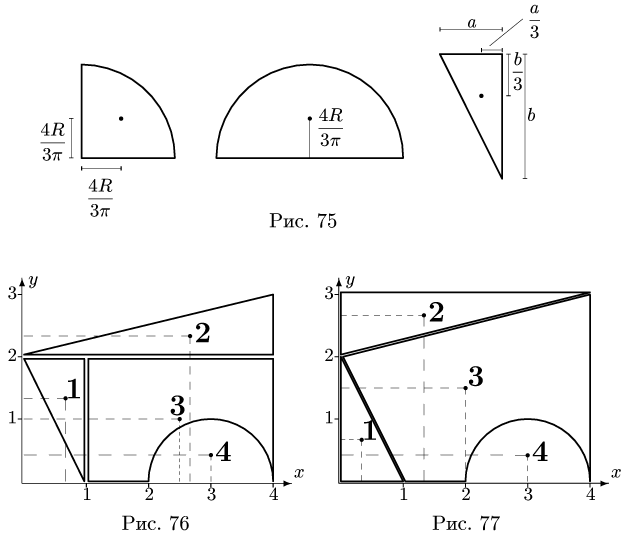
Центр тяжести прямоугольника находится в его геометрическом центре, положение центра тяжести других фигур, встречающихся в задачах, изображено на рис. 75
Представляем фигуру в виде двух треугольников 1,2, прямоугольника 3 и выреза 4 в виде полукруга (рис. 76).
2. Вычисляем площадь (в 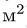
Площадь выреза берем со знаком минус.
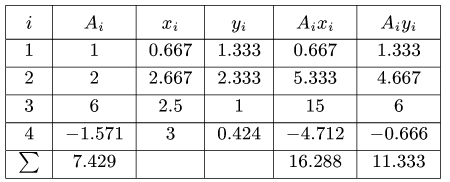
3.Площадь фигуры
4. Находим координаты центра тяжести всей фигуры:
Вычисления удобно свести в таблицу:
Сначала заполняем столбцы 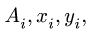
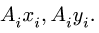
Замечание 1. Большинство задач на определение центра тяжести допускает несколько способов разбиения фигуры. Это можно использовать для проверки решения. Второй вариант разбиения фигуры в данном примере состоит из прямоугольника 3 с размерами 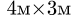
Замечание 2. Решение задачи в системе Maple V методом контурного интегрирования.
- Заказать решение задач по теоретической механике
Пространственная стержневая система
Постановка Задачи. Найти координаты центра тяжести пространственной фигуры, состоящей из N однородных стержней.
План решения:
1. Разбиваем фигуру на отдельные стержни.
2. Выбираем систему координат. Вычисляем длины и координаты 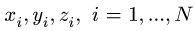
3. Находим суммарную длину стержней системы
4. Определяем координаты центра тяжести тела по формулам
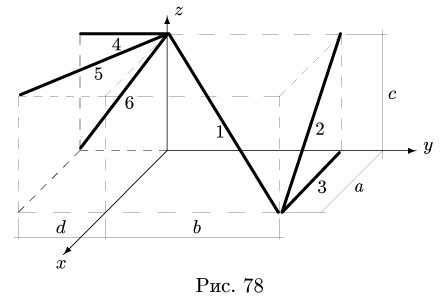
Задача №3
Найти координаты центра тяжести пространственной фигуры, состоящей из шести однородных стержней (рис. 78). Даны размеры:
Решение
1. Разбиваем фигуру на шесть стержней.
2. Выбираем систему координат (рис. 78). Вычисляем длины и координаты 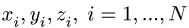
3. Находим суммарную длину стержней системы:
Промежуточные результаты удобно занести в таблицу:
4. Определяем координаты центра тяжести тела по формулам
Постановка задачи. Найти координаты центра тяжести однородного объемного тела.
План решения:
1. Разбиваем тело на простые части, положение центров тяжести которых известно.
2. Выбираем систему координат. Вычисляем объемы 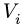
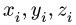
3. Находим общий объем тела по формуле
4. Определяем координаты центра тяжести тела:
Задача №4
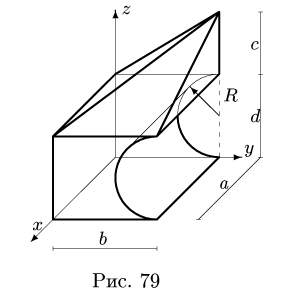
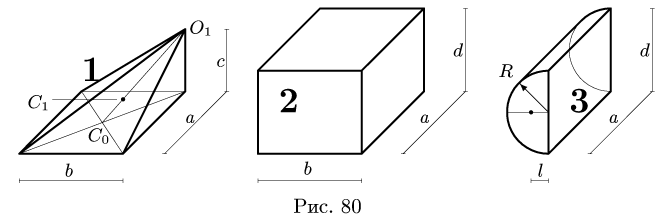
Найти координаты центра тяжести однородного объемного тела (рис.79);
Решение
1. Разбиваем тело на пирамиду 1, параллелепипед 2 и половину цилиндра 3 (рис. 80).
2. Выбираем систему координат. Вычисляем объемы 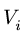
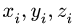
Центр тяжести параллелепипеда 2 совпадает с его геометрическим центром:
Объем половины цилиндра 3 берем со знаком минус:
где 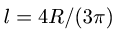
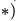
3. Находим общий объем тела:
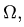
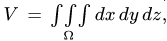
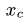
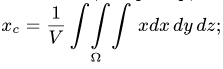
4. Определяем координаты центра тяжести тела:
Центр тяжести
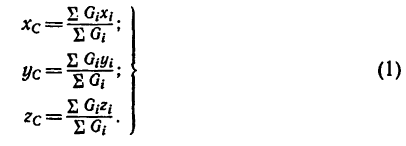
Центр тяжести — точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил. Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
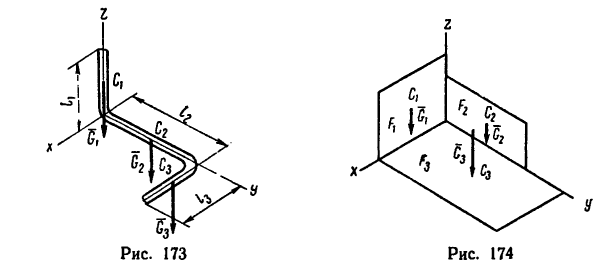
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес 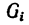
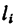
где d — постоянный для всей фигуры вес единицы длины материала.
После подстановки в формулы (1) вместо 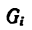
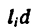
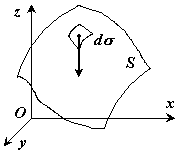
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174),
то вес каждой плоскости (поверхности) можно представить так:
где 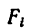
После подстановки этого значения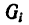
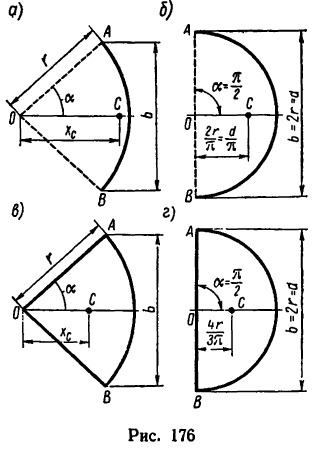
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части
где 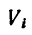
После подстановки значений 
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.
Если известен радиус дуги г и центральный угол 2а, стягиваемый дугой и выраженный в радианах, то положение центра тяжести С (рис. 176, а) относительно центра дуги О определится формулой
Если же задана хорда 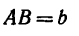
и тогда
В частном случае для полуокружности обе формулы примут вид (рис. 176, б)
Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы
Если же задана хорда сектора, то
В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.
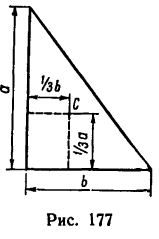
У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).
При решении задач на определение положения центра тяжести любого однородного тела, й составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:
- выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;
- разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;
- определить или длины, или площади, или объемы составных частей;
- выбрать расположение осей координат;
- определить координаты центров тяжести составных частей;
- найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
- по найденным координатам указать на рисунке положение центра тяжести тела.
- Кинематика точки
- Плоское движение твердого тела
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Условия равновесия системы сил
- Плоская система сил
- Трение
- Пространственная система сил
Центр масс (также фокус или иногда , чтобы отличить его от геометрического центра тяжести и центра тяжести называет) из тела является массой средневзвешенной позиций его материальных точек . Для непрерывных распределений масс , то локальное среднее по плотности определяется как центр масс. В случае однородного тела (т.е. с одинаковой плотностью всюду) центр масс совпадает с геометрическим центром тяжести . Стоячий человек является примером неоднородного тела.
Понятие центра масс используется в физике для сведения сложного протяженного твердого тела к одной материальной точке для упрощения расчета его траектории при приложении силы . Многие вычисления также упрощаются в системе центра тяжести , в которой центр масс используется как начало координат (см. Также систему нескольких тел ). Внешние силы, действующие в центре масс, не могут изменить вращательное состояние объекта, потому что они не создают крутящего момента из-за отсутствия плеча рычага в центре тяжести . Оси, проходящие через центр тяжести, также называют осями тяжести .
В небесной механике центр масс системы из нескольких небесных тел называется барицентром .
Центр масс тела не обязательно должен находиться внутри тела. Примеры этого – тор , бумеранг , чашка или центр тяжести прыгуна в высоту . Но если тело выпуклое , центр тяжести никогда не находится снаружи.
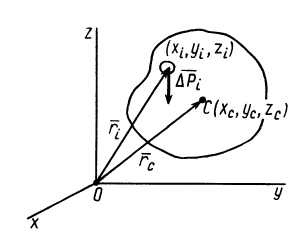
Центр масс двух точечных масс на стержне
Учитывая длину стержня . Две точечные массы и расположены на этом стержне в точках и .
Рис.1: Стержень с двумя точечными массами и центром масс (здесь отмечен значком )
Затем центр масс (центр масс) можно рассчитать следующим образом:
Соотношение масс – это тоже, так сказать, процентный коэффициент . Если масса становится бесконечно большой, центр тяжести смещается на место . Однако, если масса по отношению к ней бесконечно велика, центр тяжести смещается в это место .
Что-то более общее:
Изображение 2: Центр масс немного более общий
Из рисунка 1 видно, что это применимо. На рисунке 2 точечные массы больше не находятся в начальной и конечной точках стержня. Поскольку на изображениях шкала проходит слева направо, вам нужно добавить расстояние между начальной точкой стержня и точкой массы . Это приводит к следующей формуле:
Центр масс нескольких точечных масс на стержне
Чтобы продолжить предыдущий раздел, теперь мы разместим 3-х точечные гири на стержне.
Рис.3: Стержень с тремя точечными массами
Чтобы определить центр масс, мы разделили эту конструкцию на 2 части стержня. Для этого мы разрезаем стержень на месте и делим массу пополам на одну часть стержня, а другую половину – на другую часть стержня. Сначала мы вычисляем центры тяжести частичных стержней следующим образом, как известно из предыдущего раздела:
С учетом общей массы частичных стержней и центра масс частичные стержни теперь можно суммировать как новую точечную массу:
С этими новыми значениями теперь вычисляется другой центр масс, который в конечном итоге является центром масс трех точечных масс:
При использовании это выглядит так:
Если немного переформулировать это уравнение, получится следующий результат:
Если сравнить этот результат с результатом из предыдущего раздела, можно увидеть закономерность. Если теперь распределить n много точечных масс на стержне, центр масс можно определить следующим образом:
Это общая масса, т.е. сумма всех точечных масс:
Центр масс с непрерывным распределением массы вдоль стержня
Здесь мы используем формулу из предыдущего раздела и формируем предельное значение. Это дает интегральное представление.
Центр массы:
Функция плотности:
Общая масса:
Пример расчета
Учитывая длину стержня . Плотность увеличивается пропорционально длине стержня. Теперь вычислите центр масс стержня!
Функция плотности:
Коэффициент пропорциональности здесь выбран произвольно как .
Общая масса:
Центр массы:
Математическое определение
Центр масс – это средневзвешенное значение векторов положения всех массовых точек тела:

Это плотность на месте и в элементе объема . Знаменатель этих терминов – полная масса.
В случае однородного тела плотность может быть принята как множитель перед интегралом, тогда центр масс совпадает с центром объема (геометрическим центром тяжести). Во многих случаях можно упростить расчет; например, если центральная точка объема лежит на оси симметрии тела, например, в случае сферы в центре.
В дискретных системах объемный интеграл можно заменить суммой по векторам положения всех массовых точек:
где сумма всех индивидуальных масс равна:
Термин центр масс по сравнению с центром тяжести
Гравитационный эффект тела на все материальные точки. Только в однородном гравитационном поле возникает общий эффект, как если бы гравитационная сила действовала в центре масс. Поскольку гравитационное поле часто можно считать однородным, например B. Вблизи земной поверхности термины « центр тяжести» и « центр масс» часто недифференцированы и называются центром тяжести . В неоднородном поле эта эффективная точка отличается от центра масс и центров тяжести в упомянутых неоднородных полях . В таком случае возникают приливные силы .
Термин центр масс по сравнению с центром масс
Если тело однородно (т.е. если оно состоит из материала, имеющего всюду одинаковую плотность), его центр масс совпадает с его геометрическим центром тяжести. Если тело состоит из частей разной плотности, центр масс может отклоняться от центра тяжести объема. Если распределение массы внутри тела известно, центр масс можно вычислить интегрированием . Это был повод, который побудил Исаака Ньютона (в то же время, что и Лейбниц ) разработать исчисление .
Определение центра масс
Центр тяжести находится ниже точки подвеса на «центре тяжести».
Центр тяжести также находится под другой точкой подвеса. Таким образом, положение центра тяжести можно определить по пересечению двух линий.
Приведенные выше объяснения приводят к простому методу приближенного определения центра масс любого твердого тела. Приближение состоит в игнорировании отклонений от центра тяжести и центра масс и, следовательно, также изменений положения центра тяжести при вращении тела: если вы повесите тело в любой точке, (приблизительный) центр тяжести масса лежит (в состоянии покоя) на вертикальной линии (= «линия тяжести»), проходящей через точку подвеса (синяя линия на рисунке справа).
Если вы повторите это с другой точкой подвеса, вы найдете (приблизительно) центр масс как пересечение двух таких прямых линий («линии центра тяжести»). Однако тот факт, что такое пересечение действительно существует и не зависит от выбора точек подвеса, менее тривиален, чем предполагает первое впечатление.
Следующий метод определения центра масс узкого и вытянутого предмета (например, линейки или метлы) удивителен: поместите предмет поперек двух указательных пальцев, вытянутых вперед на одинаковой высоте, что легко возможно, если пальцы все еще далеко. обособленно. Теперь медленно сведите указательные пальцы вместе, пока они не соприкоснутся, всегда удерживая их на одной высоте, насколько это возможно. Если вы сделаете это достаточно медленно, объект будет медленно скользить по пальцам, не наклоняясь в сторону. Палец, который находится ближе к центру масс, подвергается большему давлению, что приводит к большему трению. Это означает, что объект в основном скользит по другому пальцу. Это регулирует систему таким образом, что оба пальца имеют примерно одинаковое трение, а центр масс находится в их центре. Наконец, указательные пальцы соприкасаются, объект по-прежнему находится в горизонтальном положении, а центр тяжести находится над двумя пальцами. Однако, если объект слишком сильно согнуть, возникает вышеупомянутый эффект и центр тяжести находится ниже точки опоры.
Смотри тоже
- Массовое распространение
- Массовая линия (метод)
литература
- Физика: словарь всей школьной физики . Schülerduden, Bibliographisches Institut, Mannheim 1974, ISBN 3-411-01122-X , стр. 367–368.
Индивидуальные доказательства
- ↑ Д. Гросс, В. Хаугер, Й. Шредер и В. А. Уолл: Technische Mechanik 1: Statik. Учебник Springer 2011, ISBN 9783642138058 , стр.114.
- ↑ Джон МакЛестер, Питер Сен-Пьер: Прикладная биомеханика: концепции и связи . Cengage Learning, 2008, ISBN 978-0-495-10586-2 , стр. 28.
- ↑ Джон Харрис, Вальтер Бененсон, Хорст Штёкер: Справочник по физике . Springer, 2002, ISBN 978-0-387-95269-7 , стр.94.
- ↑ Тео Купелис, Карл Ф. Кун: В поисках вселенной . Jones & Bartlett Learning, 13 апреля 2007 г., ISBN 978-0-7637-4387-1 , стр. 86.
- ↑ Филип Болл: Матрица жизни: биография воды . Калифорнийский университет Press, 2001, ISBN 978-0-520-23008-8 , стр. 37.
You should upgrade or use an alternative browser.
-
Forums
-
Homework Help
-
Introductory Physics Homework Help
Center of mass of a non-uniform rod
-
Thread starter
Linus Pauling -
Start date
Oct 24, 2009 -
-
Tags -
Center
Center of mass
Mass
Rod
-
- Oct 24, 2009
- #1
2. X_cm = (1/M)Integral(x dm)
3. To obtain M, I did a*Integral(x^2 dx) from 0 to L, obtaining M = (1/3)aL^3
I then did x_cm = (1/M)*a*Integral(x^3) from 0 to L, obtaining:
(3/4)(a^2/L)
Apparently the answer does not depend on a
Answers and Replies
- Oct 24, 2009
- #2
M = (1/3)aL^3
But what is the next integral I need to do? I know it’s (1/M)*Integral(x dm)
where dm = ax^2 dx. What is x? I’m going psycho.
- Oct 24, 2009
- #3
I know it’s (1/M)*Integral(x dm)where dm = ax^2 dx. What is x?
What do you mean, what is x? It’s the x-coordinate along the wire, just like before. Just write dm in terms of dx (like you just did) and you’ll have what you need to integrate.
- Oct 24, 2009
- #4
Dividing by M=(1/3)aL^3 I obtain L, which is incorrect.
?
- Oct 24, 2009
- #5
The length of the rod is L. So if I integrate L*ax^2 dx from 0 to L I obtain (1/3)aL^4.
Why are you integrating that?
x_cm = (1/M) ∫ x dm, just like you stated in your last post. Just write dm in terms of x, which you also stated in your last post.
Suggested for: Center of mass of a non-uniform rod
- Aug 20, 2022
- Mar 30, 2022
- Oct 30, 2022
- Apr 8, 2020
- Jul 4, 2021
- Nov 30, 2021
- Jun 1, 2022
- Jul 19, 2022
- Jul 31, 2020
- Dec 21, 2020
-
Forums
-
Homework Help
-
Introductory Physics Homework Help

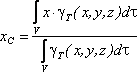
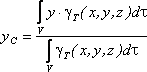
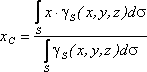
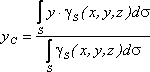
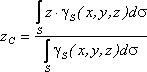
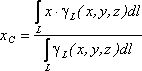

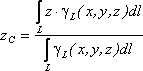

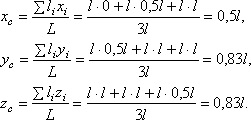
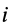
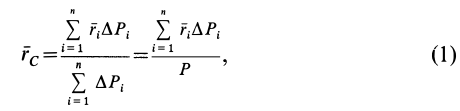


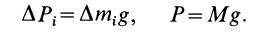


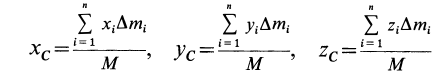
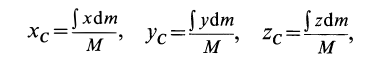


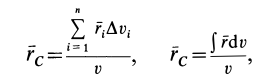
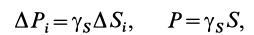
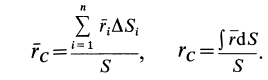
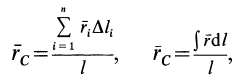
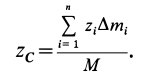
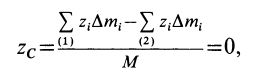
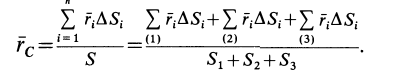
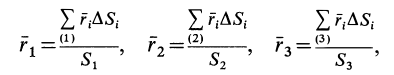
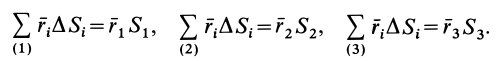
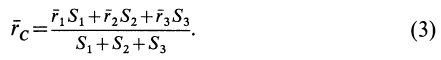

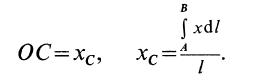
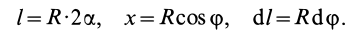
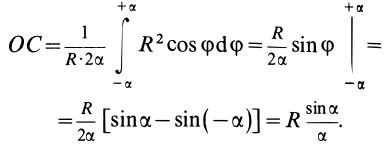

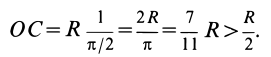
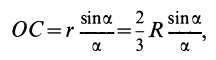

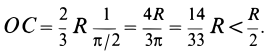
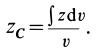
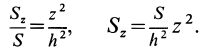
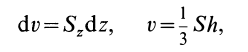
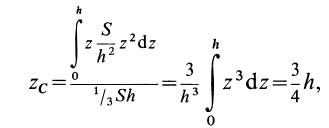

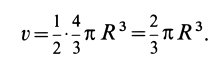
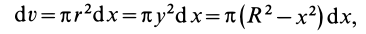
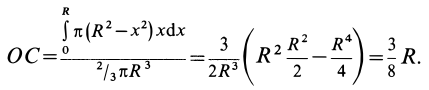

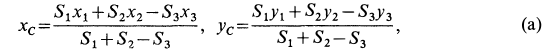
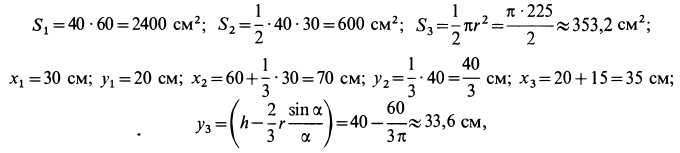

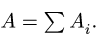
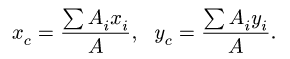
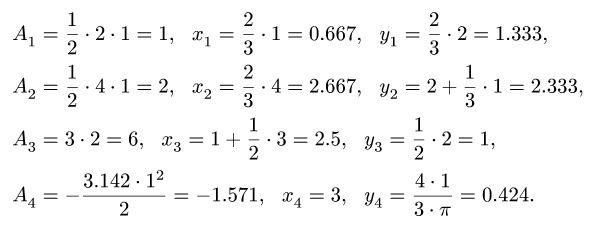
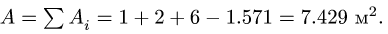

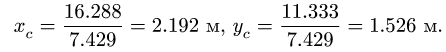
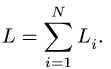
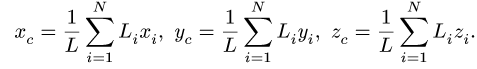
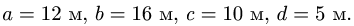
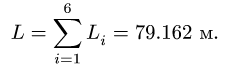
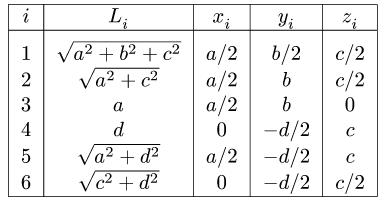
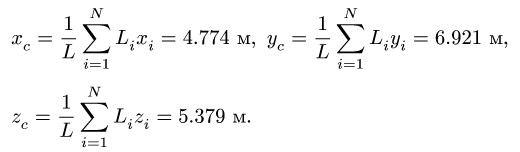
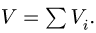
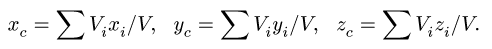
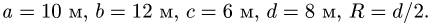
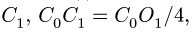
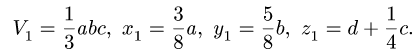
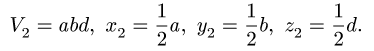
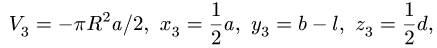
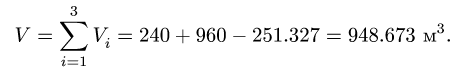

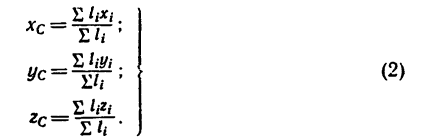
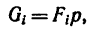
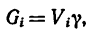
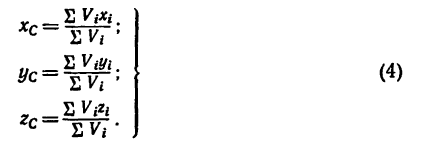
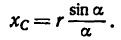
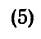
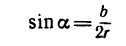




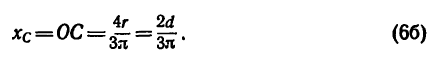





























![{ displaystyle M = int _ {0} ^ {l} cx ; mathrm {d} x = { frac {c} {2}} cdot left [x ^ {2} right] _ { 0} ^ {l} = 0 {,} 5 ; mathrm {кг}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e456fee771c1691011f43a31bc82d997886f7890)
![{ displaystyle x_ {s} = { frac {1} {M}} cdot int _ {0} ^ {l} {x cdot cx ; mathrm {d} x} = { frac {1 } {M}} cdot left [{ frac {1} {3}} x ^ {3} right] _ {0} ^ {l} приблизительно 0 {,} 667 ; mathrm {m} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7ac88ef3573fec621a88c145353e24ce43d35f1)












