Координаты центров тяжести неоднородных тел.
Координаты центра
тяжести неоднородного
твердого тела
в выбранной системе отсчета определяются
следующим образом:

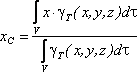
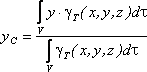
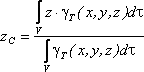
где
![]() – вес единицы объема тела (удельный вес)
– вес единицы объема тела (удельный вес)
![]() – вес всего тела.
– вес всего тела.
Если твердое тело
представляет собой неоднородную
поверхность,
то координаты центра тяжести в выбранной
системе отсчета определяются следующим
образом:
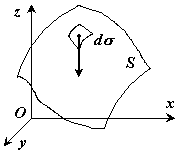
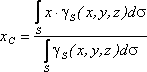
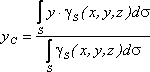
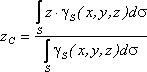
где
![]() – вес единицы площади тела,
– вес единицы площади тела,
![]() – вес всего тела.
– вес всего тела.
Если твердое тело
представляет собой неоднородную
линию, то
координаты центра тяжести в выбранной
системе отсчета определяются следующим
образом:
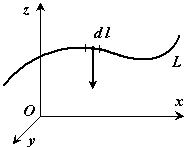
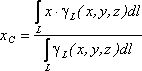

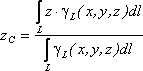
где![]() – вес единицы длины тела
– вес единицы длины тела
,
![]() –
–
вес всего тела.
Координаты центров тяжести однородных тел.
Для однородного
тела вес
![]() любой его части пропорционален объему
любой его части пропорционален объему![]() этой части:
этой части:![]() ,
,
а весР
всего тела
пропорционален объему V
этого тела
![]() ,
,
где![]() – вес единицы объема.
– вес единицы объема.
Подставив эти
значения Р
и
![]() в предыдущие формулы, мы заметим, что в
в предыдущие формулы, мы заметим, что в
числителе![]() как общий множитель выносится за скобку
как общий множитель выносится за скобку
и сокращается с![]()
в знаменателе.
В результате получим:
![]()
![]()
![]()
Как видно, центр
тяжести однородного тела зависит только
от его геометрической формы, а от величины
![]() не зависит. По этой причине точку
не зависит. По этой причине точку
С,
координаты которой определяются
формулами, называют центром тяжести
объема V.
Путем аналогичных
рассуждений легко найти, что если тело
представляет собой однородную плоскую
и тонкую пластину, то для нее
![]()
![]()
где S
– площадь всей пластины, a
![]() –
–
площади ее частей.
Точку, координаты
которой определяются
формулами называют
центром тяжести площади S.
Точно так же получаются
формулы для координат центра тяжести
линии:
![]()
![]()
![]()
где L
— длина всей
линии, l
— длины ее частей.
Таким образом, центр
тяжести однородного тела определяется,
как центр тяжести соответствующего
объема, площади или линии.
Способы определения координат центра тяжести.
Исходя из полученных
выше общих формул, можно указать
конкретные способы определения
координат центров тяжести тел.

1. Симметрия.
Если однородное тело имеет плоскость,
ось или центр симметрии, то его центр
тяжести лежит соответственно в плоскости
симметрии, оси симметрии или в центре
симметрии.
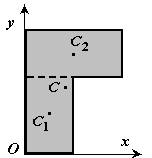
2. Разбиение.
Тело разбивается на конечное число
частей, для каждой из которых положение
центра тяжести и площадь известны.
![]()
![]()
![]()
![]()
![]() .
.
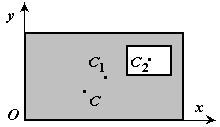
3. Дополнение.
Частный случай
способа разбиения. Он применяется к
телам, имеющим вырезы, если центры
тяжести тела без выреза и вырезанной
части известны.
![]()
![]()
![]()
![]()
![]() .
.
Центры тяжести некоторых однородных тел.
1) Центр
тяжести дуги окружности.
Рассмотрим дугу АВ
радиуса R
с центральным
углом
![]() .
.
В силу симметрии центр тяжести этой
дуги лежит на осиOx
(рис. 37).
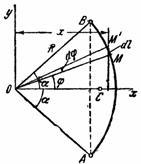
Рис.37
Найдем координату
![]() по формуле
по формуле![]() .
.
Для этого выделим на дугеАВ
элемент ММ’
длиною
![]() ,
,
положение которого определяется углом![]() .
.
Координатах
элемента ММ’
будет
![]() .
.
Подставляя эти значениях
и
![]() и
и
имея в виду, что интеграл должен быть
распространен на всю длину дуги, получим:
![]()
где
L
– длина дуги АВ,
равная
![]() .
.
Отсюда окончательно находим, что
центр тяжести дуги окружности лежит на
ее оси симметрии на расстоянии от центра
О,
равном
![]()
где
угол
![]() измеряется в радианах.
измеряется в радианах.
2) Центр
тяжести площади треугольника.
Разобьем площадь треугольника ABD
(рис. 38) прямыми, параллельными AD,
на узкие полоски; центры тяжести этих
полосок будут лежать на медиане BE
треугольника.
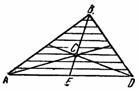
Рис.38
Следовательно, и
центр тяжести всего треугольника
лежит на этой медиане. Аналогичный
результат получается для двух других
медиан. Отсюда заключаем, что центр
тяжести площади треугольника лежит в
точке пересечения его медиан.
При этом, как
известно,
![]()
3) Центр
тяжести площади кругового сектора.
Рассмотрим круговой сектор ОАВ
радиуса R
с центральным углом
![]() (рис. 39). Разобьем мысленно площадь
(рис. 39). Разобьем мысленно площадь
сектораОАВ
радиусами, проведенными из центра О,
на п
секторов. В пределе, при неограниченном
увеличении числа
![]() ,
,
эти секторы можно рассматривать как
плоские треугольники, центры тяжести
которых лежат на дугеDE
радиуса
![]() .
.
Следовательно, центр тяжести сектораОAB
будет совпадать с центром тяжести
дуги DE.
Окончательно получим, что центр тяжести
площади кругового сектора лежит на его
центральной оси симметрии на расстоянии
от начального центра
О,
равном
![]()
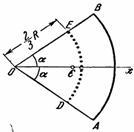
Рис.39
Пример
1.
Определим центр тяжести однородного
тела, изображённого на рис. 40.
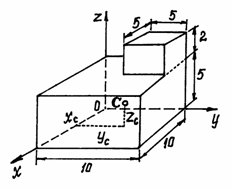
Рис.40
Тело однородное,
состоящее из двух частей, имеющих
симметричную форму. Координаты центров
тяжести их:
![]()
Объёмы их:
![]()
![]() .
.
Поэтому координаты
центра тяжести тела
![]()
![]()
![]()
Пример
2. Найдем
центр тяжести пластины, согнутой под
прямым углом. Размеры – на чертеже
(рис.41).
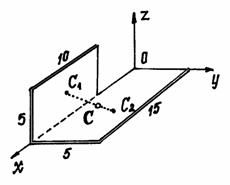
Рис.41
Координаты центров
тяжести:
![]()
![]()
![]()
![]()
![]()
![]()
Площади:
![]()
![]()
Поэтому:
![]()
Рис.
6.5.
![]()
![]()
Пример
3. У
квадратного листа
![]() см
см
вырезано квадратное отверстие
![]() см (рис.42). Найдем центр тяжести листа.
см (рис.42). Найдем центр тяжести листа.
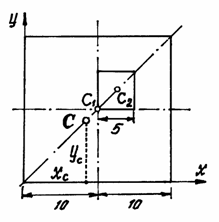
Рис.42
В этой задаче удобнее
разделить тело на две части: большой
квадрат и квадратное отверстие. Только
площадь отверстия надо считать
отрицательной. Тогда координаты центра
тяжести листа с отверстием:
![]()
координата
![]() так как тело имеет ось симметрии
так как тело имеет ось симметрии
(диагональ).
Пример
4.
Проволочная скобка (рис.43) состоит из
трёх участков одинаковой длины l.
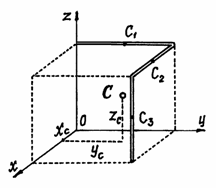
Рис.43
Координаты центров
тяжести участков:
![]()
![]() ,
,![]() ;
;![]() ,
,![]()
![]()
![]()
![]()
![]() Поэтому координаты центра тяжести всей
Поэтому координаты центра тяжести всей
скобки:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2.6.2. Центр тяжести тела
Подобно тому, как задача о вычислении центра тяжести плоской фигуры решалась с
помощью двойного интеграла, задача об отыскании центра тяжести тела
решается аналогичным способом – с помощью тройного интеграла.
Что такое центр тяжести тела, довольно удачно объяснил ещё Архимед. Если тело подвесить на нить за центр тяжести,
то оно будет сохранять равновесие в любом положении (как бы мы его предварительно ни повернули). В известной степени это не
реализуемо (таки центр тяжести внутри тела), но зато очень понятно. И вполне в стиле древнегреческого учёного, который просил
дать ему точку опоры, чтобы с помощью рычага перевернуть Землю.
Центр тяжести ![]() неоднородного тела
неоднородного тела ![]() рассчитывается по формулам:
рассчитывается по формулам:
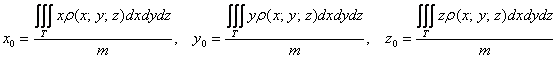 , где
, где ![]() – функция плотности тела, а
– функция плотности тела, а ![]() – масса тела.
– масса тела.
Если же тело однородно (стеклянное, оловянное, пластмассовое и т.д.), то формулы упрощаются. Так как плотность ![]() постоянна, и масса
постоянна, и масса ![]() – есть произведение плотности на объём, получаем:
– есть произведение плотности на объём, получаем:
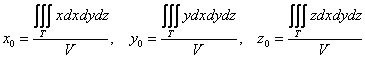 , а объём тела рассчитывается (ещё не забыли? =)) с помощью тройного интеграла
, а объём тела рассчитывается (ещё не забыли? =)) с помощью тройного интеграла ![]() .
.
Для центра тяжести однородного тела справедливы следующие утверждения:
– если у тела есть центр симметрии, то он является центром тяжести (простейший пример – центр шара);
– если у тела существует линия симметрии, то центр тяжести обязательно принадлежит данной линии;
– если у тела есть плоскость симметрии, то центр тяжести непременно лежит в этой плоскости.
Как видите, практически полная аналогия с центром тяжести плоской фигуры.
Ну и, само собой, не могу не порадовать вас тематической задачей:
Пример 42
Найти центр тяжести однородного тела, ограниченного поверхностями ![]() ,
, ![]() . Выполнить чертежи данного тела и его проекции на плоскость
. Выполнить чертежи данного тела и его проекции на плоскость ![]() .
.
Решение: искомое тело ограничено координатными плоскостями и плоскостью ![]() , которую в целях последующего построения удобно представить в
, которую в целях последующего построения удобно представить в
отрезках: ![]() . Выберем «а» за единицу
. Выберем «а» за единицу
масштаба и выполним трёхмерный чертёж:
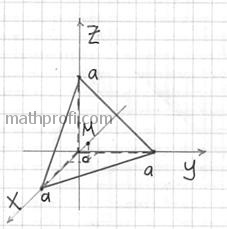
На чертеже уже поставлена готовая точка центра тяжести, однако, пока мы её не знаем.
Проекция тела на плоскость ![]() очевидна, но, тем не менее, напомню, как её найти аналитически – ведь такие
очевидна, но, тем не менее, напомню, как её найти аналитически – ведь такие
простые случаи встречаются далеко не всегда. Чтобы найти прямую, по которой пересекаются плоскости ![]() нужно решить систему, составленную из их уравнений:
нужно решить систему, составленную из их уравнений:
![]()
Подставляем значение ![]() в 1-е
в 1-е
уравнение системы: ![]() и получаем
и получаем
уравнение ![]() «плоской» прямой:
«плоской» прямой:
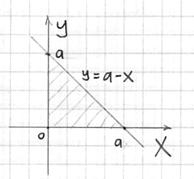
Для взятия грядущих интегралов выберем «классический» порядок обхода тела:
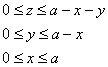
Координаты ![]() центра тяжести
центра тяжести ![]() тела
тела ![]() вычислим по формулам:
вычислим по формулам:
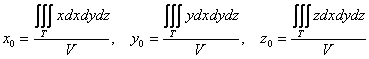 , где
, где ![]() – объём данного тела. И понеслась песня:
– объём данного тела. И понеслась песня:
1) Сначала вычислим объём тела. Его, кстати, можно узнать заранее, пользуясь известной задачей геометрии об объёме
тетраэдра. Объём тетраэдра равен 1/6-й объёма прямоугольного параллелепипеда, построенного на его трёх смежных рёбрах. В нашем
случае параллелепипед представляет собой куб с ребром «а», а посему: ![]() .
.
Осталось аккуратно провести штатные вычисления:
В примерах с громоздкими преобразованиями рекомендую записывать решение «столбиком» – меньше шансов запутаться: 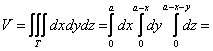
 (да, так можно – сразу снести
(да, так можно – сразу снести
![]() в средний интеграл)
в средний интеграл)

![]() , и дело за тремя тройными
, и дело за тремя тройными
интегралами:
2) Вычислим «иксовый» интеграл, …и местечка у меня тут не хватает, поэтому решение в столбик отменяется: 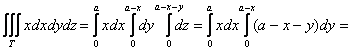
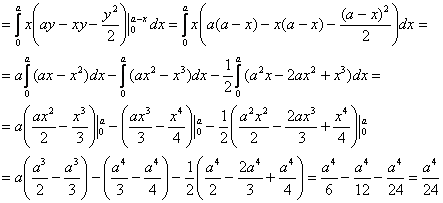
Таким образом, «иксовая» координата центра тяжести: 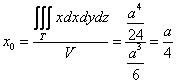 , ну что же, выглядит правдоподобно, по крайне мере, мы «попали внутрь» тела.
, ну что же, выглядит правдоподобно, по крайне мере, мы «попали внутрь» тела.
Учитывая симметрию тела, две другие координаты должны получиться такими же. Теперь ошибочный финал практически исключён! И
я вам предлагаю рассчитать ![]() самостоятельно, после чего можно записать красивый ответ.
самостоятельно, после чего можно записать красивый ответ.
…А вы, наверное, не так давно и представить себе не могли, что окажетесь в эпицентре такого кошмара =)
 3. Криволинейные интегралы
3. Криволинейные интегралы
 2.6. Физические приложения тройного интеграла
2.6. Физические приложения тройного интеграла
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Точку, в которой происходит равное распределение величины, определяющей инерционные и гравитационные свойства, называют центром масс. Формула для определения параметра зависит от радиус-вектора частиц системы и их полной энергии. Эту характеристику тела отличают от тяжести, при этом в трудах советских учёных Ландау, Лифшица для неё используется термин «центр инерции».
Оглавление:
- Общие сведения
- Связь с центром тяжести
- Вычисление положения
- Геометрический способ определения

Общие сведения
Допустим, имеется тело, на которое действуют скомпенсированные силы. В этом случае оно будет в состоянии покоя или прямолинейного равномерного движения. Пусть тело будет неподвижным. Например, лодка на воде. К ней можно приложить воздействие F1 в районе её кормы. Под действием силы она начнёт разворачиваться. Аналогично если воздействовать на её нос F2, то она тоже будет поворачиваться, но при этом разворот будет происходить в другую сторону.
Получается, что можно подобрать такую линию, на которой действие сил приведёт её к ускоренно поступательному движению. Пусть это будет F3. На самом деле таких сил может быть несколько. При этом их можно перемещать вдоль линии их воздействия. Если все такие силы изобразить в виде линий, то они пересекутся в одной точке. Такое место и называют центром масс тела (ЦМ). То есть точку, в которой пересекаются линии действия сил, вызывающие только ускоренное поступательное механическое движение.

Эта важная точка в теле и движется она довольно просто. Перемещение любого тела можно представить, как комбинацию двух видов движения:
- центра масс;
- вращения.
Существует теорема: ЦМ тела движется так, как перемещалась бы материальная точка, в которой сосредоточена вся масса и к которой приложены все воздействия, действующие на объект. Таким образом, различные виды изменения положения точек в пространстве можно описать с помощью законов Ньютона. Согласно же теореме их можно применять и к телу, если считать, что все силы приложены к центру масс.
Рассматривая объект, можно не учитывать его размер, форму, а брать во внимание только инерцию, ускорение и принцип парного взаимодействия. Фактически в механике перемещение сколь угодно сложного вида рассматривается по принципу суперпозиции и закона сохранении энергии. При этом довольно удобно изучать изменение положения в системе отсчёта связанной с этим центром. В ней полный импульс всегда будет равным нулю, что позволяет упростить уравнение движения.
Связь с центром тяжести
Пусть имеется объект, находящийся на Земле. Говорят, что на него действует сила тяжести. Но на самом деле она воздействует не на вещество, а на каждый его атом, частичку. Если предположить, что ускорение свободного падения буде одинаковым, то на объект действует очень множество сил тяжести. Рассматривать такую систему неудобно. Поэтому все воздействия заменяют равнодействующей. И считают, что действует одна сила, которая приложена к центру тяжести твёрдого тела.
Для того чтобы найти взаимосвязь между тяжестью и массой нужно представить, что объект вдруг распался на отдельные равные кусочки. Они держатся вместе, но не прикреплены друг к другу. Если тело отпустить, то они будут падать вместе, так как ускорение свободного падения не зависит от массы. При этом движение будет поступательным. Значит, сила, приложенная к телу в целом, будет приложена к центру масс.
Получается, что центральная точка является общей как для тяжести, так и для масс. Это две точки положение которых совпадает несмотря на разный их принцип определения в физике. Но существуют условия, когда это правило не выполняется. Например, если система материальных точек неоднородна по объёму плотности в гравитационном поле, то центры не совпадут.
Для примера можно привести список однородных фигур с указанием их центральной точки:
- отрезок — середина;
- параллелограмм — место пересечения диагоналей;
- треугольник — точка пересечения медиан (центроид);
- любой правильный многоугольник — центр поворотной симметрии;
- полукруг — точка, в которой перпендикулярный радиус делится в отношении 4:3p считая от центра круга.

Чтобы найти координату центра масс объекта, который можно представить, как совокупность связанных материальных точек используют два метода: аналитический и геометрический. Но второй способ не всегда можно применить. В однородном гравитационном поле центры тяжести и масс всегда совпадают. И это часто подтверждается на практике, из-за того, что внешнее гравитационное поле в задачах, связанных с действиями на Земле, считают постоянным в пределах объёма тела.
Поэтому эти термины объединяют в геометрии, статике и так далее. То есть в тех областях, где применение определения можно назвать метафорическим и предполагается ситуация их эквивалентности.
При таком понимании оба термина синонимичны, но при этом чаще предпочитают использовать термин, связанный с тяжестью. Это происходит в силу того, что исторически он появился раньше.
Вычисление положения
Пусть тело представляет собой совокупность материальных точек, лежащих на одной прямой при этом их массы разные. Задача состоит в нахождении его центра. Для этого следует вести систему координат с осью икс, которая будет совпадать с линией расположения точек. При этом тело пусть подвешено на невесомой опоре и находится под действием Земного тяготения. Это условие даёт возможность воспользоваться тем фактом, что положения центров масс и тяжести совпадают.

На каждую из материальных точек действует своя сила: m1g, m2g… mng. Если предоставить это тело самому себе, то оно будет в состоянии свободного падения. Остановить тело — подпереть, но при этом так, чтобы оно находилось в равновесии. Это значит, что сила реакции опоры должна проходить через центр тяжести, так как равнодействующая тоже её пересекает.
Получится, что сила реакции опоры будет лежать на одной прямой с силой тяжести действующей на тело в совокупности и их моменты тоже будут проходить через неё. С помощью координатной оси точкам можно присвоить положение, x1, x2… xn, а ЦМ xц. Чтобы тело находилось в равновесии необходимо выполнение двух условий:
- векторная сумма всех сил должна быть равной нулю: m1g + m2g +…+mng + F = 0;
- сумма моментов равняться нулю: Mm 1 g + Mm 2 g +…+ Mmng + MF = 0.
Из первого условия можно найти силу реакции опоры: F = (m1 + m2 +…+mn) * g. Если вращение выбрать против часовой стрелки, тогда относительно оси все моменты силы тяжести будут отрицательными, а опоры — положительные. Тогда справедливо записать: F * хц = (m1 x 1 + m2 x 2 +…+mn xn) * g.
Из последнего равенства можно выразить координату ЦМ: xц = ((m1 x 1 + m2 x 2 +…+mn xn) * g) / F. В эту формулу можно подставить выражение для F. В результате ускорение свободного падения сократится и получится: xц = (m1 x 1 + m2 x 2 +…+mn xn) / (m1 + m2 +…+mn). Это формула выглядит громоздко, но запомнить её легко. В числителе стоят произведения масс материальных точек на их координаты, а в знаменателе — вес всего тела.
Если точки не будут лежать на одной прямой, то координата ЦМ тоже не изменится. То есть приведённая формула справедлива для любого положения тела относительно координаты y.
При этом её можно применять и для рассмотрения предметов в пространстве, так как все направления в существующем мире равноправные.
Геометрический способ определения
Для простейших симметричных фигур ЦМ можно определить геометрическим методом. Для этого используются свойства диагоналей и медиан. Пусть имеется произвольной формы четырёхугольник. Изготовлен он из однородного материала.
Идея вычисления состоит в том, что эту фигуру необходимо разбить на два треугольника. Для этого нужно провести диагональ, которая разделит фигуру на два тела. Затем провести в каждом треугольном теле три медианы. Точка их пересечения и будет ЦМ. В результате вместо четырёхугольника можно рассматривать две материальные точки.
Несмотря на то что масса у них разная ЦМ будет находиться на соединяющем их отрезке. Теперь четырёхугольник можно разбить на два других треугольника и выполнить аналогичные действия уже для них. Получится два отрезка, на которых одновременно расположен ЦМ. Значит, его положение будет определяться точкой их пересечения.
Для более сложной фигуры, например, шести или восьмиугольника можно использовать такой же подход. Сначала нужно разделить тело на прямоугольники, а затем треугольники. Найти ЦМ для полученных фигур и определить точку пересечения. Следует понимать, что ЦМ может находиться и за пределами объекта.
Но в реальных ситуациях бывают фигуры, которые имеют неправильную форму. Для них нельзя применить расчёт или геометрический метод. Поэтому выясняют, где расположен ЦМ экспериментальным путём.
Например, пусть имеется тело сложной неправильной формы. Чтобы найти ЦМ необходимо фигуру подвесить в пространстве. На неё действует две силы: тяжести и реакции оси. Первая заставляет фигуру поворачиваться с определённой скоростью до тех пор, пока момент силы тяжести относительно оси крепления не станет равным нулю. То есть точка опоры, ось и центр тяжести окажутся на одной вертикале.
Чтобы узнать, где же находится ЦМ, тело нужно подвесить, используя другую точку. При этом на самой фигуре следует отметить, как проходит вертикаль.
Повторяя такой опыт минимум три раза, можно увидеть точку пересечения осей, которая и будет искомым ЦМ. Причём чем будет больше экспериментов, тем точнее он будет определён.
Центр тяжести материального тела
В физике, центр тяжести материального тела – это точка, которую можно использовать для краткого описания гравитационных взаимодействий. В однородном гравитационном поле центр масс служит центром тяжести. Это очень хорошее приближение для более мелких тел у поверхности Земли, поэтому нет практической необходимости различать «центр тяжести» от «центра масс» в большинстве приложений, таких как инженерия и медицина.
В неоднородном поле гравитационные эффекты, такие как потенциальная энергия, сила и крутящий момент, больше не могут быть рассчитаны с использованием центра одной массы. В частности, неоднородное гравитационное поле может создавать крутящий момент на объекте, даже вокруг оси, проходящей через центр масс. Центр тяжести пытается объяснить этот эффект. Формально центр тяжести – это точка приложения равнодействующей гравитационной силы на тело. Такой точки может не быть, и если она существует, то она не уникальна. Далее можно определить уникальный центр тяжести, аппроксимировав поле параллельным или сферически симметричным.
Концепция центра тяжести в отличие от центра масс редко используется в приложениях, даже в небесной механике, где важны неоднородные поля. Поскольку центр тяжести зависит от внешнего поля, его движение определить труднее, чем движение центра масс. Обычным методом работы с гравитационными моментами является теория поля.
Содержание
- 1 Центр масс
- 2 Центры тяжести в поле
- 2.1 Параллельные поля
- 2.2 Сферически-симметричные поля
- 2.3 Использование
- 3 Примечания
- 4 Ссылки
Центр масс
Один из способов определить центр тяжести тела – это уникальная точка в теле, если она существует, которая удовлетворяет следующему требованию: нет крутящего момента вокруг точки для любого позиционирования тела в силовом поле, в котором оно находится. Этот центр тяжести существует только тогда, когда сила однородна, и в этом случае он совпадает с центром масс. Этот подход восходит к Архимеду.
Центры тяжести в поле
Когда на тело воздействует неоднородное внешнее гравитационное поле, иногда можно определить центр тяжести относительно этого поля. это будет действовать как точка приложения силы тяжести. В таких учебниках, как Лекции Фейнмана по физике, центр тяжести описывается как точка, вокруг которой отсутствует крутящий момент. Другими словами, центр тяжести – это точка приложения результирующей силы. Согласно этой формулировке центр тяжести rcgопределяется как точка, которая удовлетворяет уравнению
- rcg × F = τ, { displaystyle mathbf {r} _ { mathrm {cg}} times mathbf { F} = { boldsymbol { tau}},}
где F и τ – общая сила и крутящий момент, действующие на тело под действием силы тяжести.
Одна из трудностей, связанных с rcg, заключается в том, что его определяющее уравнение в общем случае не разрешимо. Если F и τ не ортогональны, то решения нет; сила тяжести не имеет равнодействующей и не может быть заменена одной силой в любой точке. Есть несколько важных особых случаев, когда F и τ гарантированно ортогональны, например, если все силы лежат в одной плоскости или выровнены с одной точкой.
Если уравнение разрешимо, возникает еще одна сложность: его решения не единственны. Вместо этого существует бесконечно много решений; набор всех решений известен как линия действия силы. Эта линия параллельна весу F . В общем, нет возможности выбрать конкретную точку в качестве уникального центра тяжести. Единственная точка может быть выбрана в некоторых особых случаях, например, если гравитационное поле параллельно или сферически симметрично. Эти случаи рассматриваются ниже.
Параллельные поля
Некоторая неоднородность в гравитационном поле может быть смоделирована переменным, но параллельным полем: g(r) = g (r)n, где n – некоторый постоянный единичный вектор. Хотя неоднородное гравитационное поле не может быть точно параллельным, это приближение может быть справедливым, если тело достаточно маленькое. Центр тяжести может быть определен как определенное средневзвешенное значение положений частиц. составляя тело. В то время как центр масс усредняется по массе каждой частицы, центр тяжести в среднем по массе каждой частицы:
- rcg = 1 W ∑ iwiri, { displaystyle mathbf {r} _ { mathrm {cg}} = { frac {1} {W}} sum _ {i} w_ {i} mathbf {r} _ {i},}
где w i – (скалярный) вес i-й частицы, а W – (скалярный) общий вес всех частиц. Это уравнение всегда имеет единственное решение, а в приближении параллельного поля оно совместимо с требованием крутящего момента.
Общая концепция иллюстрации rns Луна в поле Земли. Используя определение средневзвешенного значения, Луна имеет центр тяжести, расположенный ниже (ближе к Земле), чем ее центр масс, потому что на ее нижнюю часть сильнее влияет гравитация Земли.
Сферически симметричный поля
Если внешнее гравитационное поле сферически симметрично, то оно эквивалентно полю точечной массы M в центре симметрии r . В этом случае центр тяжести можно определить как точку, в которой общая сила, действующая на тело, определяется законом Ньютона :
- G m M (r c g – r) | г с г – г | 3 = F, { displaystyle { frac {GmM ( mathbf {r} _ { mathrm {cg}} – mathbf {r})} {| mathbf {r} _ { mathrm {cg}} – mathbf {r} | ^ {3}}} = mathbf {F},}
где G – гравитационная постоянная, а m – масса тела. Пока общая сила отлична от нуля, это уравнение имеет единственное решение и удовлетворяет требованиям крутящего момента. Удобная особенность этого определения состоит в том, что если тело само сферически симметрично, то rcgлежит в его центре масс. В общем, по мере того, как расстояние между r и телом увеличивается, центр тяжести приближается к центру масс.
Другой способ увидеть это определение – рассмотреть гравитационное поле тела ; тогда rcgявляется очевидным источником гравитационного притяжения для наблюдателя, находящегося в r . По этой причине rcgиногда называют центром тяжести M относительно точки r.
Использование
Центры тяжести, определенные выше, не являются фиксированными точками на теле; скорее, они меняются по мере изменения положения и ориентации тела. Эта характеристика затрудняет работу с центром тяжести, поэтому эта концепция не имеет практического применения.
Когда необходимо учитывать гравитационный момент, легче представить гравитацию как силу, действующую в центре масса плюс зависимая от ориентации пара . К последнему лучше всего подойти, рассматривая гравитационный потенциал как поле.
Примечания
Ссылки
- Asimov, Isaac (1988) [1966], Понимание физики, Barnes Noble Books, ISBN 0-88029-251-2
- Битти, Миллард Ф. (2006), Принципы инженерной механики, Том 2: Динамика – анализ движения, математические концепции и методы в науке и технике, 33, Springer, ISBN 0-387-23704-6
- Фейнман, Ричард ; Лейтон, Роберт Б. ; Сэндс, Мэтью (1963), Лекции Фейнмана по физике, 1(шестое издание, февраль 1977 года изд.), Addison-Wesley, ISBN 0- 201-02010-6
- Фраучи, Стивен К. ; Оленик, Ричард П.; Апостол, Том М. ; Гудштейн, Дэвид Л. (1986), Механическая вселенная: механика и тепло, расширенное издание, Cambridge University Press, ISBN 0-521-30432-6
- Гольдштейн, Герберт ; Пул, Чарльз; Сафко, Джон (2002), Classical Mechanics (3-е изд.), Addison-Wesley, ISBN 0-201-65702-3
- Goodman, Lawrence E. ; Уорнер, Уильям Х. (2001) [1964], Statics, Dover, ISBN 0-486-42005-1
- Хэмилл, Патрик (2009), Intermediate Dynamics, Jones Bartlett Learning, ISBN 978-0-7637-5728-1
- Jong, IG; Роджерс, Б.Г. (1995), Engineering Mechanics: Statics, Saunders College Publishing, ISBN 0-03-026309-3
- Милликен, Роберт Эндрюс (1902), Механика, молекулярная физика и тепло: двенадцатинедельный курс в колледже, Чикаго: Скотт, Форесман и компания, получено 25 мая 2011 г.
- Поллард, Дэвид Д.; Флетчер, Раймонд К. (2005), Основы структурной геологии, Cambridge University Press, ISBN 978-0-521-83927-3
- Пител, Эндрю; Киусалаас, Яан (2010), Инженерная механика: Статика, 1 (3-е изд.), Cengage Learning, ISBN 978-0-495-29559-4
- Розен, Джо; Готард, Лиза Куинн (2009), Encyclopedia of Physical Science, Infobase Publishing, ISBN 978-0-8160-7011-4
- Serway, Raymond A.; Джуэтт, Джон В. (2006), Принципы физики: текст, основанный на исчислении, 1 (4-е изд.), Thomson Learning, ISBN 0-534-49143 -X
- Ширли, Джеймс Х.; Fairbridge, Rhodes Whitmore (1997), Энциклопедия планетных наук, Springer, ISBN 0-412-06951-2
- De Silva, Clarence W. (2002), Руководство по вибрации и ударам, CRC Press, ISBN 978-0-8493-1580-0
- Саймон, Кейт Р. (1971), Механика, Эддисон-Уэсли, ISBN 978-0-201-07392-8
- Tipler, Paul A.; Моска, Джин (2004), Физика для ученых и инженеров, 1A (5-е изд.), WH Freeman and Company, ISBN 0-7167-0900-7
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Сущность понятия «центр масс»
Понятие “центр масс” широко используется в физике для решения задач, связанных с движением тел. Например, математический маятник удобно представить себе как подвешенное на нити тело, вся масса которого сконцентрирована в единой точке. В законе всемирного тяготения тоже речь идет о расстоянии не между телами, а между центрами тел, под каковыми подразумеваются именно центры масс, а не геометрические центры.
Определение 1
Центр масс – точка, характеризующая размещение и движение исследуемой системы как единого целого.
Признаком центра масс является то, что если тело подвесить, закрепив за эту точку, оно останется в покое, т.е. не будет раскачиваться или вращаться относительно этого центра. В простейшем случае, если речь идет о симметричном теле с равномерной плотностью, центр масс находится на пересечении осей симметрии рассматриваемого тела. Например, если взять линейку длиной 30 см, то ее центр масс будет расположен на отметке “15 см”. Подложив карандаш под эту отметку, легко привести линейку в положение равновесия.
На практике далеко не все тела, центр масс которых нужно найти, являются симметричными и однородными по плотности. Более того, многие исследуемые объекты представляют собой системы из нескольких тел с различными геометрическими и химическими характеристиками. Для расчетов их разбивают на элементарные фрагменты и производят вычисления поэтапно.
Нахождение координат центра масс
Определение 2
Центр масс двух тел с точечными массами $m_1$ и $m_2$ и координатами на координатной прямой $x_1$ и $x_2$ находится в точке, делящей расстояние между этими телами на отрезки с длинами обратно пропорциональными массам рассматриваемых тел.
Отсюда следует, что чем массивнее тело в такой элементарной системе, тем ближе оно к общему центру масс.
Расстояние между точечными телами равно:
$Delta x = x_2 – x_1$
Пропорция между массами и расстояниями, согласно определению:
$frac{l_1}{l_2} = frac{m_2}{m_1}$,
«Как найти координаты центра масс» 👇
где $l_1$, $l_2$ – расстояния от соответствующих тел до центра масс.
Выразив, длины через координаты
$l_1 = x_c – x_1; l_2 = x_2 – x_c$,
центр масс можно определить как
$x_c = frac{m_1 cdot x_1 + m_2 cdot x_2}{m_1 + m_2}$.
где $x_c$ – координата центра тяжести.
Разложив любую сложную систему на множество элементарных тел с точечными массами, можно обобщить изложенный принцип в виде формулы (для оси абсцисс):
$x_c = frac{sumlimits^N_{i=1}{m_i cdot x_i}}{sumlimits^N_{i=1}{m_i}}$
В большинстве случаев центр масс требуется найти не на координатной прямой, а в двух- или трехмерной системе координат. Для дополнительных осей координаты центра масс ($y_c$, $z_c$) находят по аналогичному принципу.
Замечание 1
Центр тяжести системы тел представляет собой точку, подобную центру масс, но рассчитывается не для масс, а для весов (обусловленных гравитацией сил), действующих на точечные тела, входящие в систему. Центр тяжести определяется так же, как и центр масс, если размеры системы малы в сравнении с радиусом планеты Земля. Он в большинстве случаев с достаточной для практики точностью совпадает с центром масс рассматриваемой системы.
Пример 1
Найти центр масс двух линеек, изготовленных из одинакового материала, одинаковой толщины и ширины, левые концы линеек совмещены. Длины линеек – 10 и 30 см. Толщиной линеек можно пренебречь.
Поскольку толщиной можно пренебречь, найти нужно лишь координату центра масс по оси $x$.
Разобьем мысленно систему на два отрезка. Первый – где толщина линеек складывается. Его координаты – $[0, 10]$. Второй отрезок – где длинная линейка продолжается одна. Его координаты – $[10, 30]$. Примем за единицу измерения массу одного погонного сантиметра линейки. Тогда масса второго фрагмента:
$m_2 = 30 – 10 = 20$
На каждый сантиметр первого фрагмента приходится вдвое больше массы, поскольку там сложены две линейки:
$m_1 = 10 cdot 2 = 20$
Центры масс отрезков находятся на их осях симметрии, т.е. на середине длины каждого:
$x_{c1} = frac{10}{2} = 5$;
$x_{c2} = 10 + frac{20}{2} = 20$
Подставим значения в формулу:
$x_c = frac{m_1 cdot x_1 + m_2 cdot x_2}{m_1 + m_2}$
$x_c = frac{20 cdot 5 + 20 cdot 20}{20 +20} = frac{100 + 400}{40} = 12, 5$
Ответ: центр масс находится на расстоянии 12,5 см от левого конца системы линеек.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме



