Как найти центр масс однородной пластинки

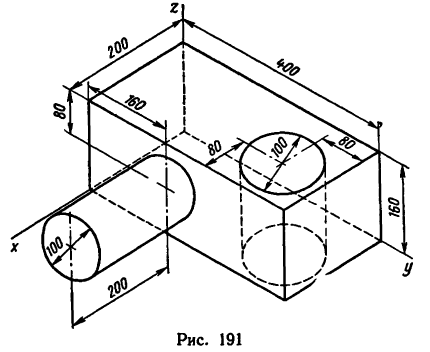
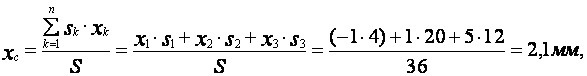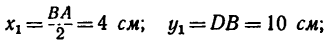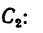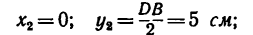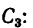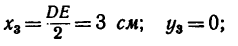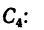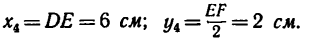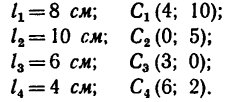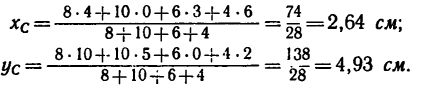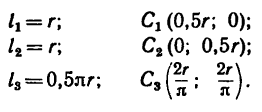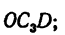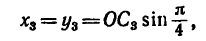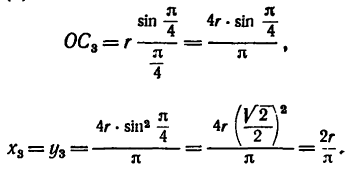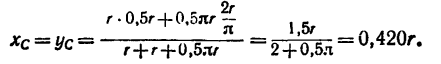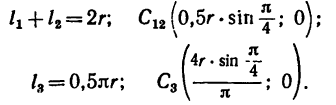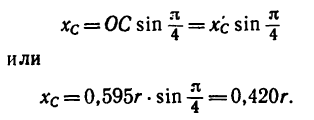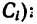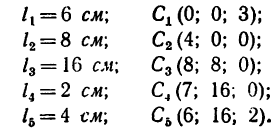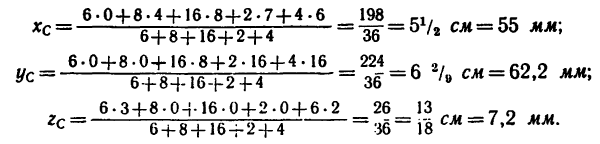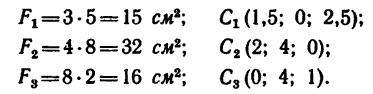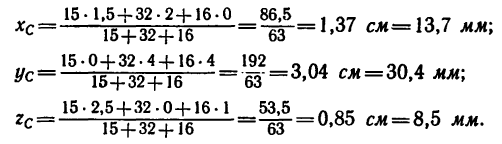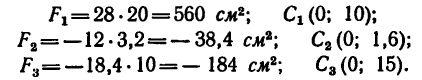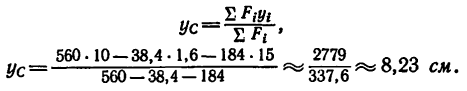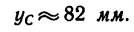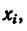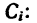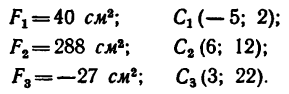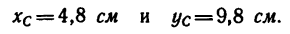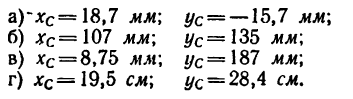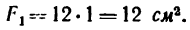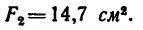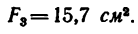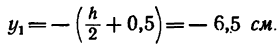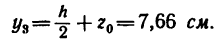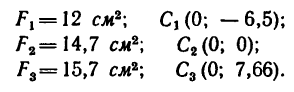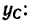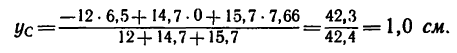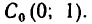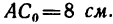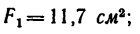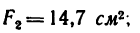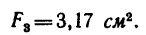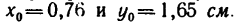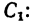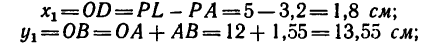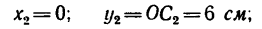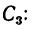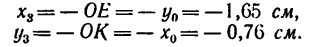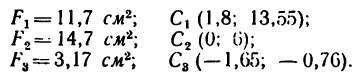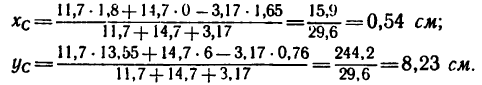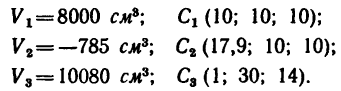         Приведем пример
определения центра массы тела методом разделения его на отдельные тела, центры
масс которых известны.

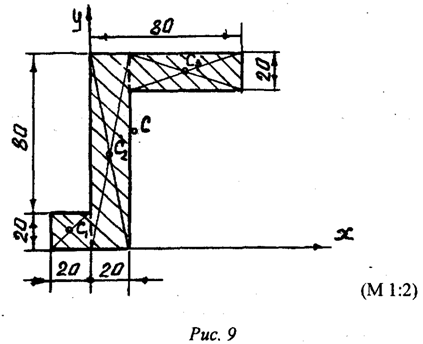
Пример 1. Определить координаты центра массы однородной
пластины (рис.9). Размеры заданы в миллиметрах  на рисунке 9.

Решение:  Показываем оси координат  и
. Разбиваем пластину на части,
которые образованы тремя прямоугольниками. Для каждого прямоугольника проводим
диагонали, точки пересечения которых  и определяют положения центров массы
каждого прямоугольника. В  принятой системе координат несложно найти значения
координат этих точек. А именно:

(-1;
1), (1;5),(5;9).
Площади каждого тела соответственно равны:

 ; ;
.

Площадь всей пластины равна:

.

         Для определения
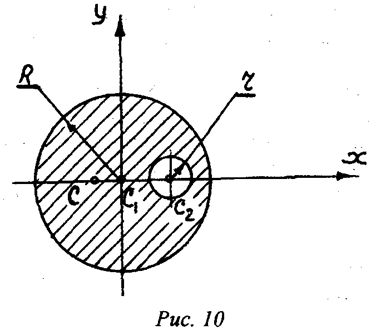
координат центра массы заданной пластины применяем выражения (21). Подставим
значения всех известных величин в  данном уравнении, получим

.

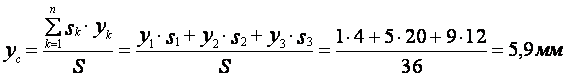
         Согласно полученных
значений координат центра массы пластины укажем точку С на рисунке. Как видно,
центр массы (геометрическая точка) пластины находится за ее пределами.

Способ дополнения. Этот способ есть частичным случаем способа
разделения. Он может применяться к телам, которые имеют вырезы (пустоты).
Причем, без  вырезанной части, положение центра массы тела известно. Рассмотрим
например применение такого  метода.

Пример 2. Определить положение центра массы веса круглой
пластины радиусом  R, в которой есть вырез радиусом  r (рис.10). Расстояние .

Решение: Как видим, из  рис.10 центр массы пластины лежит на
оси симметрии пластины, то есть на прямой ,
поскольку эта прямая есть осью симметрии. Таким образом, для определения
положения центра массы этой пластины необходимо определить только одну
координату , поскольку вторая координата  будет расположена на оси симметрии и
уравновешивает нулевые. Покажем оси координат , . Примем, что
пластина складывается из двух тел – из  полного круга (как будто без выреза) и
тела, которое как будто выполнено с вырезом. В принятой системе координат
координаты  для указанных тел будут равны: .Площади  тел равны: ; .
Общая  площадь всего тела будет равна разнице между площадями  первого и
второго тела, а именно

.

 Теперь,
 для определения неизвестной координаты центра массы заданной пластины
применяем первое уравнение выражения (21). Подставим значения всех известных
величин в это уравнение, получаем

.

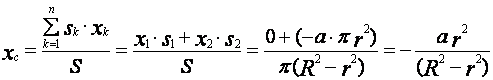
Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

Приложения кратных интегралов в механике

Краткая теория

---

Масса и статистические моменты пластики

Если

 – область плоскости

, занятая пластинкой, и

 – поверхностная плотность пластики в точке

, то масса

 пластинки и ее статистические моменты

 и

 относительно осей

 и

 выражаются двойными интегралами:

Если
пластика однородна, то

Координаты центра тяжести пластики

Если

 – центр тяжести пластики, то

где

 – масса пластинки и

 – ее статистические моменты относительно осей
координат.

Моменты инерции пластики

Моменты
инерции пластинки относительно осей

 и

 соответственно равны:

Момент инерции пластики относительно
начала координат:

Полагая

, получаем геометрические моменты инерции плоской
фигуры.

Масса тела, занимающего область
 и статистические моменты тела относительно
координатных плоскостей

где

 – плоскость тела в точке

Координаты центра тяжести

Если тело
однородно, то формулах для координат центра тяжести можно положить

.

Моменты инерции относительно
осей координат

Полагая в
этих формулах

, получаем геометрические
моменты инерции тела.

Примеры решения задач

---

Задача 1

Вычислить
массу материальной пластины, занимающей область

 плоскости

, если поверхностная
плотность

 и границы области

 заданы уравнениями.

Решение

Сделаем
чертеж области

:

Искомая
масса материальной пластины:

Ответ:

---

Задача 2

Найти
статистический момент фигуры, ограниченной линиями

 и

 относительно оси абсцисс.

Решение

Сделаем
чертеж:

Статистический
момент относительно оси

:

Ответ:

---

Задача 3

Вычислить
координаты центра масс однородной

 материальной пластины

, ограниченной данными
линиями:

Решение

Сделаем
чертеж:

Масса
пластинки:

Статистические
моменты:

Искомые
координаты центра масс:

Ответ:

.

---

Задача 4

Вычислить массу тела

, ограниченного заданными поверхностями

 -плотность в
точке

.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Изобразим
тело на рисунке:

С боков
тело будет ограничено цилиндром

 и плоскостями

. Сверху плоскостью

Проекция на плоскость

:

           

Ответ:

---

Задача 5

Найти
момент инерции однородного шара

 с массой

 относительно оси

.

Решение

Момент
инерции относительно оси

 можно найти по формуле:

Шар
однородный, поэтому плотность:

Перейдем
к сферическим координатам:

Получаем:

Ответ:

Центры тяжести многоугольников и многогранников

Центром тяжести (или центром масс) некоторого тела называется точка, обладающая тем свойством, что если подвесить тело за эту точку, то оно будет сохранять свое положение.

Ниже рассмотрены двумерные и трёхмерные задачи, связанные с поиском различных центров масс — в основном с точки зрения вычислительной геометрии.

В рассмотренных ниже решениях можно выделить два основных факта. Первый — что центр масс системы материальных точек равен среднему их координат, взятых с коэффициентами, пропорциональными их массам. Второй факт — что если мы знаем центры масс двух непересекающихся фигур, то центр масс их объединения будет лежать на отрезке, соединяющем эти два центра, причём он будет делить его в то же отношении, как масса второй фигуры относится к массе первой.

Двумерный случай: многоугольники

На самом деле, говоря о центре масс двумерной фигуры, можно иметь в виду одну из трёх следующих задач:

• Центр масс системы точек — т.е. вся масса сосредоточена только в вершинах многоугольника.
• Центр масс каркаса — т.е. масса многоугольника сосредоточена на его периметре.
• Центр масс сплошной фигуры — т.е. масса многоугольника распределена по всей его площади.

Каждая из этих задач имеет самостоятельное решение, и будет рассмотрена ниже отдельно.

Центр масс системы точек

Это самая простая из трёх задач, и её решение — известная физическая формула центра масс системы материальных точек:

где — массы точек, — их радиус-векторы (задающие их положение относительно начала координат), и — искомый радиус-вектор центра масс.

В частности, если все точки имеют одинаковую массу, то координаты центра масс есть среднее арифметическое координат точек. Для треугольника эта точка называется центроидом и совпадает с точкой пересечения медиан:

Для доказательства этих формул достаточно вспомнить, что равновесие достигается в такой точке , в которой сумма моментов всех сил равна нулю. В данном случае это превращается в условие того, чтобы сумма радиус-векторов всех точек относительно точки , домноженных на массы соответствующих точек, равнялась нулю:

и, выражая отсюда , мы и получаем требуемую формулу.

Центр масс каркаса

Будем считать для простоты, что каркас однороден, т.е. его плотность везде одна и та же.

Но тогда каждую сторону многоугольника можно заменить одной точкой — серединой этого отрезка (т.к. центр масс однородного отрезка есть середина этого отрезка), с массой, равной длине этого отрезка.

Теперь мы получили задачу о системе материальных точек, и применяя к ней решение из предыдущего пункта, мы находим:

где — точка-середина -ой стороны многоугольника, — длина -ой стороны, — периметр, т.е. сумма длин сторон.

Для треугольника можно показать следующее утверждение: эта точка является точкой пересечения биссектрис треугольника, образованного серединами сторон исходного треугольника. (чтобы показать это, надо воспользоваться приведённой выше формулой, и затем заметить, что биссектрисы делят стороны получившегося треугольника в тех же соотношениях, что и центры масс этих сторон).

Центр масс сплошной фигуры

Мы считаем, что масса распределена по фигуре однородно, т.е. плотность в каждой точке фигуры равна одному и тому же числу.

Случай треугольника

Утверждается, что для треугольника ответом будет всё тот же центроид, т.е. точка, образованная средним арифметическим координат вершин:

Случай треугольника: доказательство

Приведём здесь элементарное доказательство, не использующее теорию интегралов.

Первым подобное, чисто геометрическое, доказательство привёл Архимед, но оно было весьма сложным, с большим числом геометрических построений. Приведённое здесь доказательство взято из статьи Apostol, Mnatsakanian “Finding Centroids the Easy Way”.

Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид.

Разобьём данный треугольник на четыре, соединив середины сторон, как показано на рисунке:

Четыре получившихся треугольника подобны треугольнику с коэффициентом .

Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого лежит в точке пересечения его диагоналей (поскольку это фигура, симметричная относительно обеих диагоналей, а, значит, её центр масс обязан лежать на каждой из двух диагоналей). Точка находится посередине общей стороны треугольников №1 и №2, а также лежит на медиане треугольника :

Пусть теперь вектор — вектор, проведённый из вершины к центру масс треугольника №1, и пусть вектор — вектор, проведённый из к точке (которая, напомним, является серединой стороны, на которой она лежит):

Наша цель — показать, что вектора и коллинеарны.

Обозначим через и точки, являющиеся центрами масс треугольников №3 и №4. Тогда, очевидно, центром масс совокупности этих двух треугольников будет точка , являющаяся серединой отрезка . Более того, вектор от точки к точке совпадает с вектором .

Искомый центр масс треугольника лежит посередине отрезка, соединяющего точки и (поскольку мы разбили треугольник на две части равных площадей: №1-№2 и №3-№4):

Таким образом, вектор от вершины к центроиду равен . С другой стороны, т.к. треугольник №1 подобен треугольнику с коэффициентом , то этот же вектор равен . Отсюда получаем уравнение:

Таким образом, мы доказали, что вектора и коллинеарны, что и означает, что искомый центроид лежит на медиане, исходящей из вершины .

Более того, попутно мы доказали, что центроид делит каждую медиану в отношении , считая от вершины.

Случай многоугольника

Перейдём теперь к общему случаю — т.е. к случаю мноугоугольника. Для него такие рассуждения уже неприменимы, поэтому сведём задачу к треугольной: а именно, разобьём многоугольник на треугольники (т.е. триангулируем его), найдём центр масс каждого треугольника, а затем найдём центр масс получившихся центров масс треугольников.

Окончательная формула получается следующей:

где — центроид -го треугольника в триангуляции заданного многоугольника, — площадь -го треугольника триангуляции, — площадь всего многоугольника.

Триангуляция выпуклого многоугольника — тривиальная задача: для этого, например, можно взять треугольники , где .

Случай многоугольника: альтернативный способ

С другой стороны, применение приведённой формулы не очень удобно для невыпуклых многоугольников, поскольку произвести их триангуляцию — сама по себе непростая задача. Но для таких многоугольников можно придумать более простой подход. А именно, проведём аналогию с тем, как можно искать площадь произвольного многоугольника: выбирается произвольная точка , а затем суммируются знаковые площади треугольников, образованных этой точкой и точками многоугольника: . Аналогичный приём можно применить и для поиска центра масс: только теперь мы будем суммировать центры масс треугольников , взятых с коэффициентами, пропорциональными их площадям, т.е. итоговая формула для центра масс такова:

где — произвольная точка, — точки многоугольника, — центроид треугольника , — знаковая площадь этого треугольника, — знаковая площадь всего многоугольника (т.е. ).

Трёхмерный случай: многогранники

Аналогично двумерному случаю, в 3D можно говорить сразу о четырёх возможных постановках задачи:

• Центр масс системы точек — вершин многогранника.
• Центр масс каркаса — рёбер многогранника.
• Центр масс поверхности — т.е. масса распределена по площади поверхности многогранника.
• Центр масс сплошного многогранника — т.е. масса распределена по всему многограннику.

Центр масс системы точек

Как и в двумерном случае, мы можем применить физическую формулу и получить тот же самый результат:

который в случае равных масс превращается в среднее арифметическое координат всех точек.

Центр масс каркаса многогранника

Аналогично двумерному случаю, мы просто заменяем каждое ребро многогранника материальной точкой, расположенной посередине этого ребра, и с массой, равной длине этого ребра. Получив задачу о материальных точках, мы легко находим её решение как взвешенную сумму координат этих точек.

Центр масс поверхности многогранника

Каждая грань поверхности многогранника — двухмерная фигура, центр масс которой мы умеем искать. Найдя эти центры масс и заменив каждую грань её центром масс, мы получим задачу с материальными точками, которую уже легко решить.

Центр масс сплошного многогранника

Случай тетраэдра

Как и в двумерном случае, решим сначала простейшую задачу — задачу для тетраэдра.

Утверждается, что центр масс тетраэдра совпадает с точкой пересечения его медиан (медианой тетраэдра называется отрезок, проведённый из его вершины в центр масс противоположной грани; таким образом, медиана тетраэдра проходит через вершину и через точку пересечения медиан треугольной грани).

Почему это так? Здесь верны рассуждения, аналогичные двумерному случаю: если мы рассечём тетраэдр на два тетраэдра с помощью плоскости, проходящей через вершину тетраэдра и какую-нибудь медиану противоположной грани, то оба получившихся тетраэдра будут иметь одинаковый объём (т.к. треугольная грань разобьётся медианой на два треугольника равной площади, а высота двух тетраэдров не изменится). Повторяя эти рассуждения несколько раз, получаем, что центр масс лежит на точке пересечения медиан тетраэдра.

Эта точка — точка пересечения медиан тетраэдра — называется его центроидом. Можно показать, что она на самом деле имеет координаты, равные среднему арифметическому координат вершин тетраэдра:

(это можно вывести из того факта, что центроид делит медианы в отношении )

Таким образом, между случаями тетраэдра и треугольника принципиальной разницы нет: точка, равная среднему арифметическому вершин, является центром масс сразу в двух постановках задачи: и когда массы находится только в вершинах, и когда массы распределены по всей площади/объёму. На самом деле, этот результат обобщается на произвольную размерность: центр масс произвольного симплекса (simplex) есть среднее арифметическое координат его вершин.

Случай произвольного многогранника

Перейдём теперь к общему случаю — случаю произвольного многогранника.

Снова, как и в двумерном случае, мы производим сведение этой задачи к уже решённой: разбиваем многогранник на тетраэдры (т.е. производим его тетраэдризацию), находим центр масс каждого из них, и получаем окончательный ответ на задачу в виде взвешенной суммы найденных центров масс.

Центр тяжести треугольника

Этот онлайн калькулятор находит центроид, или барицентр (центр тяжести) треугольника по координатам его вершин

Центр тяжести (центр масс, барицентр) треугольника для треугольника с равномерно распределённой массой (или в вершинах которого находятся равные массы) находится в центроиде треугольника. Центроидом называется точка пересечения медиан треугольника. Центроид относится к так называемым замечательным точкам треугольника. Например, помимо того, что он является центром тяжести, он также делит каждую медиану в отношении 2:1, считая от вершины, а три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника.

Чтобы вычислить положение центра тяжести по координатам вершин треугольника, достаточно вычислить среднее арифметическое координат вершин по оси x и по оси y, что и делает калькулятор ниже.

Как найти центр масс треугольника?

Где находится центр масс равностороннего треугольника?

Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан. Центр равностороннего треугольника является также центром вписанной и описанной окружности. Центроид расположен на отрезке, соединяющем ортоцентр и центр описанной окружности. Центроид делит отрезок 2:1.

Где находится центр масс?

Центр масс – точка пересечения прямых, вдоль которых действуют внешние силы, вызывающие поступательное движение тела. Это более общее понятие, чем понятие центра тяжести. Центр тяжести и центр масс часто совпадают. Центр масс симметричных тел находится в их геометрическом центре.

Где находится центр тяжести однородной пластинки треугольной формы?

1258 Из физики известно, что центр тяжести однородной треугольной пластинки находится в точке пересечения медиан.

Как найти центр масс четырехугольника?

Центроид (барицентр или центр масс) вершин произвольного четырёхугольника лежит в точке пересечения средних линий четырёхугольника (двух отрезков, соединяющих середины противолежащих сторон) и (третьего) отрезка, соединяющего середины диагоналей, и делит все три отрезка пополам.

Где лежит центр тяжести в прямоугольном треугольнике?

Центроид треугольника (также барицентр треугольника и центр тяжести треугольника) — точка пересечения медиан в треугольнике. . Центроид треугольника относится к замечательным точкам треугольника и он перечислен в энциклопедии центров треугольника Кларка Кимберлинга, как точка X(2).

Где находится центр тяжести у кольца?

Так, центр тяжести однородных диска и шара расположен в их центре, однородного цилиндра в точке на середине его оси; однородного параллелепипеда на пересечении его диагоналей и т, д. У всех однородных тел центр тяжести совпадает с центром симметрии. Центр тяжести может находиться вне тела, например, у кольца.

Как экспериментально определить центр масс тела?

Объяснение: Для этого достаточно поочередно подвесить тело за две различные точки на его поверхности и провести через точки подвеса вертикали. Пересечение этих линий — линий действия сил тяжести — и определяет положение центра тяжести тела.

Где находится центр масс Солнечной системы?

Барицентром или центром масс Солнечной системы называется точка, где уравновешиваются массы самого Солнца, всех планет, лун и астероидов. Барицентр удалось определить с помощью пульсаров.

Что такое центр масс простыми словами?

Центр масс является точкой, характеризующей распределение масс в данном теле (или в механической системе). . Если тело движется поступательно под действием нескольких сил, значит, точка приложения равнодействующей этих сил находится в центре масс этого тела.

Где находится центр тяжести тонкой однородной пластинки имеющей форму прямоугольника?

Вероятно, вы знаете, что центр тяжести тонкой однородной пластинки, имеющей форму прямоугольника или форму ромба, находится в точке пересечения диагоналей, а если пластинка треугольная, то в точке пересечения медиан, если круглая, то в центре этого круга.

Как найти координаты центра тяжести в треугольнике?

Как найти координаты центра тяжести треугольника?

1. Рисуем треугольник ABC.
2. Ставим точку M – середина BC.
3. Ставим точку H – середина AC.
4. Пересечение BH и AM – и есть центр тяжести треугольника ABC.
5. Найдем его координаты (координаты точки O (xo, yo, zo) )

Как найти центр масс системы?

Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус – вектор, определяющий положение центра масс находим как: ¯rc=N∑i=1mi¯riN∑i=1mi(4). Выражение (4) считают определением центра масс системы.

Как найти центр сложной фигуры?

1. Если фигура не имеет округлостей, то разбивай на треугольники. Точка пересечения биссектрис является центром тяжести треугольника. Вычисляешь массу каждого треугольника (если тело однородно, то m/M=s/S, где m и M массы, а s и S площади каждого треугольника и всей фигуры).

Когда центр масс тела совпадает с центром тяжести?

В однородном гравитационном поле центр тяжести всегда совпадает с центром масс. В некосмических задачах гравитационное поле обычно может считаться постоянным в пределах объёма тела, поэтому на практике эти два центра почти совпадают.

[spoiler title=”источники:”]

http://planetcalc.ru/9363/

http://topobzor10.ru/kak-naiti-tsentr-mass-treugolnika

[/spoiler]

Содержание:

1. Центр масс
2. Центр параллельных сил
3. Центр тяжести
4. Центры тяжести некоторых плоских однородных фигур
5. Центр тяжести дуги окружности
6. Центр тяжести кругового сектора
7. Центр тяжести кругового сегмента
8. Центр тяжести треугольника
9. Центр тяжести трапеции
10. Примеры решения задач на тему: Центр масс
11. Способы определения координат центра тяжести тела
12. Метод симметрии
13. Метод разбиения
14. Метод дополнения
15. Экспериментальные способы
16. Центры тяжести некоторых однородных тел
17. Центр тяжести дуги окружности
18. Центр тяжести треугольника
19. Центр тяжести сектора

Центр масс – это геометрическая точка, положение которой определяется распределением массы в теле, а перемещение характеризует движение тела или механической системы как целого.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Центр масс

Центр масс – это некоторое положение, определяемое относительно объекта или системы объектов и это среднее положение всех частей системы, взвешенное в соответствии с их массами.

Центр параллельных сил

Если на тело действует система параллельных сил , ,…, , то точка , через которую проходит равнодействующая этой системы сил, называется центром параллельных сил (рис.9.1).

Координаты центра параллельных сил определяются по зависимостям:

где  – координаты точек приложения сил .

Центр параллельных сил имеет ту особенность, что через него обязательно будет проходить линия действия равнодействующей при вращении линий действия всех сил системы вокруг точек их приложения на один и тот же угол в одну и ту же сторону. Модули сил при вращении не должны меняться.

Центр тяжести

Если твердое тело находится возле поверхности Земли, то на каждую материальную часть этого тела действует сила тяжести­ , которая направлена к центру Земли. Поскольку размеры тела небольшие по сравнению с размерами Земли, то образованную систему сил можно рассматривать как параллельную. Равнодействующая этой параллельной системе сил , которая равна их сумме, называется тяжестью тела, а центр этой системы – точка называется центром тяжести тела (рис.9.2).

Координаты центра тяжести твердого тела можно определить как координаты центра параллельных сил:

где  – сила тяжести элементарной частицы тела;

 – тяжесть тела;

 – координаты центра тяжести;

 – координаты элементарной частицы тела.

Если тело однородное, то есть удельный вес не меняется по объему , то:

где  – объем тела;

 – объем элементарной частицы.

Тогда формулы для определения координат центра тяжести твердого тела приобретут вид:

Положение центра тяжести однородного тела зависит только от формы объема, что занимает тело, и называется центром тяжести этого объема.

Если однородное тело имеет форму тонкой пластины, то его можно рассматривать как материальную плоскую фигуру. В этом случае положение центра тяжести плоской фигуры определяется двумя координатами  и и зависит от формы площади фигуры:

где  – площадь элементарной части плоской фигуры;

 – площадь плоской фигуры.

Центр тяжести однородной пластины называется центром тяжести плоской фигуры.

Если выбранный элементарный объем  (площадь элементарной площадки в плоском случае) направить к нулю, то формулы для вычисления координат центра тяжести приобретут интегральный вид:

а) для однородного твердого тела:

где  – объем тела, интегрирование выполняется по всему объему тела;

б) для однородной поверхности:

где  – площадь поверхности, интегрирование выполняется по всей поверхности тела;

в) для однородной плоской фигуры, лежащей в плоскости xy:

г) для однородной линии:

где  – длина линии, интегрирование выполняется по всей длине линии.

Центры тяжести некоторых плоских однородных фигур

Для упрощения определения центра тяжести используются следующие вспомогательные правилами:

1. Если тело имеет плоскость симметрии, то центр тяжести лежит на этой плоскости.
2. Если тело симметрично относительно оси, то центр тяжести лежит на этой оси.
3. Если тело симметрично относительно точки, то центр тяжести лежит в центре симметрии.
4. Если тело состоит из нескольких частей, центры тяжести которых можно определить, то центр тяжести такого тела находят как центр тяжести нескольких материальных точек, а именно тех, в которых расположены весы каждой отдельной части тела.

Центр тяжести дуги окружности

Центр тяжести дуги окружности  (рис.9.3) лежит на ее оси симметрии и на расстоянии от центра окружности:

где  – радиус окружности;

 – половина центрального угла, опирающегося на дугу .

Центр тяжести кругового сектора

Центр тяжести кругового сектора лежит на оси симметрии и имеет координаты:

где  – радиус окружности;

 – половина центрального угла сектора.

Центр тяжести кругового сегмента

Центр тяжести кругового сегмента лежит на оси симметрии сегмента и имеет координаты:

где  – радиус окружности;

 – половина центрального угла сегмента.

Центр тяжести треугольника

Центр тяжести треугольника (рис. 9.6) лежит в точке пересечения его медиан – на расстоянии 1/3 каждой медианы от соответствующего основания треугольника.

Центр тяжести трапеции

Центр тяжести трапеции (рис.9.7) с основаниями  и  и высотой лежит на прямой , которая соединяет середины основ.

Расстояния  и центра тяжести площади трапеции от ее основ определяются по формулам:

Наиболее распространенный способ определения положения центра тяжести однородного тела сложной формы заключается в том, что его разбивают на такие части, положение центров тяжести которых известно, или может быть легко определено.

Например, однородную плоскую фигуру (рис.9.8) разбивают на три части 1,2 и 3, положения центров тяжести которых, можно определить.

Координаты центра тяжести фигуры определяются по формулам:

где  – координаты центра тяжести первой части плоской фигуры;

 – площадь первой части и т.п.

Этим способом удобно пользоваться и при определении положения центра тяжести плоской фигуры, из которой вырезана некоторая часть (рис.9.9).

В этом случае площадь плоской фигуры можно записать в виде разницы площадей сплошной фигуры 1 (площадь положительная) и вырезанной части 2 (площадь отрицательная), то есть .

Координаты центра тяжести фигуры равны:

где  – координаты центра тяжести сплошной фигуры 1, площадь которой равна ;

 – координаты центра тяжести вырезанной части 2, площадь которой равна – .

Первый из этих методов имеет название “метод разбиения”, второй – “метод дополнения”, или “метод отрицательных масс”. В общем случае формулы для определения центра тяжести плоской фигуры имеют вид:

где  – площадь всей фигуры.

Примеры решения задач на тему: Центр масс

Задача № 1

Найти центр тяжести двутаврового профиля, размеры которого в сантиметрах указаны на рис.9.10.

Решение. Поскольку форма сечения имеет ось симметрии, ось направим вдоль оси симметрии, а ось перпендикулярно ей.

В силу симметричности профиля относительно оси центр тяжести будет лежать на этой оси, то есть

Линиями и поделим профиль на три прямоугольника 1, 2 и 3.

Запишем уравнение для определения абсциссы центра тяжести площади:

где  – абсциссы центров тяжести прямоугольников 1, 2, 3;

 – площади этих прямоугольников.

Поскольку центры тяжести прямоугольников и лежат на пересечении их диагоналей, то (рис.9.10):

Площади этих прямоугольников соответственно равны:

Тогда: 

Таким образом, центр тяжести фигуры лежит в точке с координатами: 

Ответ: 

Задача № 2

Найти координаты центра тяжести поперечного пересечения разностороннего угольника (рис.9.11), полки которого имеют ширину  и толщину

Решение. Разделим пересечение линией на два прямоугольника и , центры тяжести которых лежат на пересечении соответствующих диагоналей.

Запишем формулы для координат  и  центра тяжести пересечения:

где  и  – координаты центров тяжести прямоугольников 1 и 2;

,  – площади прямоугольников 1 и 2.

С рис.9.11 видим, что

Тогда: 

Ответ: 

Задача № 3

Определить положение центра тяжести плоской фигуры (рис.9.12), ограниченной полуокружностью  радиуса и двумя прямыми равной длины и , причем

Решение. Данная площадь имеет ось симметрии, вдоль которой направим ось . Поскольку центр тяжести площади лежит на оси симметрии, то

Разделим площадь линией на две части: полуокружность и равнобедренный треугольник .

Абсцисса центра тяжести площади будет равняться:

где  – координата центра тяжести половины круга ;

 – координата центра тяжести треугольника ;

,  – площади половины круга и треугольника.

Для определения воспользуемся приведенными в разделе 9.3.2 координатами центра тяжести кругового сектора

В случае половины круга 

Площадь половины круга равна:

Центр тяжести треугольника лежит на пересечении его медиан (раздел 9.3.4). Поскольку треугольник равнобедрен, то линия  будет его медианой и расстояние будет равняться третьей части от :

Площадь треугольника равна:

Подставив найденные значения , ,  и  в уравнение для , получим:

Ответ: 

Задача № 4

Найти координаты центра тяжести квадратной пластины с вырезом в виде сегмента радиуса (рис.9.13), если

Решение. Осью симметрии рассматриваемой фигуры будет диагональ прямоугольника

Поэтому направим ось вдоль этой линии, а ось – перпендикулярно (рис.9.13).

Центр тяжести пластины будет лежать на оси , то есть

Площадь фигуры можно представить как разницу площадей квадрата (положительная площадь) и сектора (отрицательная площадь).

Абсцисса центра тяжести фигуры будет равняться:

где  – абсцисса центра тяжести квадрата ;

 – абсцисса центра тяжести сектора ;

 и  – площади квадрата и сектора.

Для квадрата получим:

Как следует из рис. 9.13, равняется

где  – расстояние от точки к центру тяжести кругового сектора .

Для кругового сектора (раздел 9.3.2) получим:

Поскольку  и , то 

Таким образом, абсцисса равняется:

Площадь кругового сектора :

Подставив значение , ,  и  в формулу для , получим:

Ответ:  

Задача № 5

Найти координаты центра тяжести площади, ограниченной (рис.9.14) правой веткой параболы , осью  и прямой

Решение. На расстоянии  от оси выделяем элементарную площадку шириной (заштрихованная область).

Площадь выделенной элементарной площадки будет равняться:

Площадь фигуры, что ограничена заданными линиями:

Поскольку точка представляет собой пересечение параболы и прямой , то 

Отсюда: 

Тогда:

Абсцисса центра тяжести

Для определения координаты выделим элементарную площадку шириной на расстоянии  от оси .

Площадь выделенной площадки:

Ордината центра тяжести:

Тогда: 

Ответ: 

Способы определения координат центра тяжести тела

Существует несколько способов определения координат центра тяжести тел. среди них различают: метод симметрии, метод разбиения и дополнения, экспериментальные способы.

Рассмотрим последовательно эти способы.

Метод симметрии

Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, или на оси симметрии, или в центре симметрии.

Таким образом, центр тяжести однородных симметричных тел, таких как кольца,
прямоугольные пластины, прямоугольные параллелепипеды, шары и другие тела, которые
имеют центр симметрии, расположенный в геометрических центрах (центры симметрии) этих тел.

Метод разбиения

Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести нетрудно определяется, то координаты центра тяжести всего тела можно определить непосредственно по формулам выше. Причем количество слагаемых в числителе каждого из указанных выражений будет равно количеству частей, на которое разбивается тело.

Приведем пример определения центра тяжести тела методом разбиения его на отдельные тела, центры тяжести которых известны.

Пример:

Определить координаты центра тяжести однородной пластины. Размеры в
мм заданные на рис. 1.64

Решение.

Выберем оси координат x и y. Разбиваем пластину на отдельные прямоугольные части. Для каждого прямоугольника проводим диагонали, точки пересечения которых c₁, c₂ и c₃ соответствуют центрам веса каждого прямоугольника. В принятой системе координат нетрудно получить значение координат этих точек. А именно: c₁ (–1,1), c₂ (1,5), c₃ (5,9). Площади каждого тела соответственно равны: I — s₁ = 4 см²; II — s₂ = 20 см²; III — s₃ = 12 см². Площадь всей пластины равна: S = s₁ + s₂ + s₃ = 36 см².

Для определения координат центра тяжести заданной пластины используем выражение выше. Подставив значения всех известных величин в уравнения, получим

По вычисленным значениям координат центра тяжести пластины можно обозначить точку C на рисунке. Как видим, центр тяжести (геометрическая точка) пластины расположен за ее пределами.

Метод дополнения

Способ, о котором говорится далее, является некоторым случаем способа разбиения. Он может применяться к телам, которые имеют вырезы, полости, причем без учета выреза, или вырезанной части тела положение центра тяжести тела известно. Рассмотрим пример применения такого метода.

Пример. Определить положение центра тяжести круглой пластины радиусом R, имеет круговое отверстие радиуса r (рис. 1.65). Расстояние C₁C₂ = a.

Решение.

Как видно из рисунка, центр тяжести пластины находится на оси симметрии пластины x, то есть на прямой, проходящей через точки C₁ и C₂. Таким образом, для определения положения центра тяжести этой пластины необходимо вычислить только одну координату x_C, поскольку вторая координата y_C равна нулю. Покажем оси координат x, y. Примем, что пластина состоит из двух тел — с полного круга (без учета выреза) и тела,
образовано вырезом. В принятой системе координаты x для указанных тел будут равны: x₁ = 0; x₂ = C₁C₂ = a. Площади тел равны: Общая площадь всего тела будет равна физической разницы между площадями первого и второго тел, а именно
Для определения неизвестной координаты центра тяжести
заданной пластины используем первое уравнение выражения.

Подставив значения всех известных величин в это уравнение, получим

Таким образом, значение координаты x_C отрицательное, а потому, поскольку вторая координата 0 y_C = 0, то центр тяжести пластины C размещен на оси x слева от точки C₁.

Экспериментальные способы

Эти способы нашли широкое применение при отыскании положения центра тяжести тел сложных форм и конфигураций, для которых другие способы почти непригодны вследствие громоздкости и сложности. К таким телам, в первую очередь, следует отнести комбайны, тракторы, сложные сельскохозяйственные машины и орудия. При применении экспериментальных способов отыскания положения
центра тяжести наиболее широко используют метод подвешивания и метод взвешивания тел.

При применении метода подвешивания тело на тросе подвешивают за различные его точки. Направление троса, будет давать каждый раз направление силы веса тела. Тогда точка пересечения этих направлений и дает положение центра тяжести тела.

Использование второго метода — взвешивание требует измерения веса всего тела, а также отдельных его частей. Рассмотрим пример применения этого метода.

Пример.

Определим продольную координату центра тяжести трактора, у которого продольная база составляет l (рис. 1.66).

Решение.

Сначала поставим на платформу весов задние колеса трактора, как это показано на рисунке. Итак, определяем силу давления задних колес на платформу, или реакцию . Аналогично определяем вес переднего моста, или реакцию . Вполне понятно, что сумма этих реакций равна общему весу трактора, а именно:

Q = R_A + R_B.

Теперь составим алгебраическую сумму моментов всех сил относительно точки A. Она равна

Откуда определяем продольную координату центра тяжести:

x_C = .

Для определения поперечной координаты центра тяжести трактора необходимо знать реакции левых колес (переднего и заднего) и правых, а также поперечную базу трактора. Дальше аналогичным выражением определяется эти координаты центра тяжести.

Центры тяжести некоторых однородных тел

Определим далее координаты центров тяжести некоторых простых однородных тел.

Центр тяжести дуги окружности

Рассмотрим дугу AB окружности радиусом R, в которой центральный угол OAB равен 2α (радиан) (рис. 1.67). Покажем оси координат x, y начало которых разместим в точке O. Вследствие того, что дуга имеет ось симметрии Ox, то центр ее тяжести будет расположен именно на этой оси (y_C = 0). Остается только вычислить координату x_C.

Используем для вычисления этой координаты первое уравнение выражения, а именно

Определим составляющие, которые необходимо подставить в это уравнение. Для этого выделим на дуге AB элемент M M₁ длиной dl, равной:

dl = R · dφ.

Если φ — угол, определяющий положение элемента M M₁ на дуге AB, то координата x элемента M M₁ будет равна:

x = Rcosφ.

Общая длина дуги AB равна:

L = 2α · R.

Подставим эти значения в первое уравнение выражения. При этом считается, что интеграл в числителе данного выражения должен быть определенным по всей длине дуги. Будем иметь:

Таким образом, координата x_C будет равняться

x_C = .

Центр тяжести треугольника

Есть произвольный треугольник, вершины которого в принятой системе координат Oxy соответствуют точкам с координатами A₁ (x₁, y₁), A₂ (x₂, y₂), A₃ (x₃, y₃) (рис. 1.68). Если провести прямые, которые будут параллельны основе A₁A₃ и провести их достаточное количество, то вся площадь треугольника будет состоять из полос бесконечно малой ширины, центры тяжести которых будут размещены посередине каждой полосы, а потому и центр тяжести треугольника будет расположенный на его медиане. А если провести линии, параллельные другой стороне треугольника, то и в этом случае центр тяжести будет размещен на соответствующей медиане. Таким образом, совершенно очевидно, что центр тяжести треугольника C будет расположен в точке пересечения его медиан.

Определим координаты этой точки. По курсу аналитической геометрии известно, что точка пересечения медиан треугольника в принятой системе координат определяется такими зависимостями

где x₁, x₂, …, y₃  — координаты вершин треугольника.

Полезно также знать, что

Центр тяжести сектора

Рассмотрим круговой сектор OAB радиуса R, центральный угол которого равен 2α (радиан) (рис. 1.69). Центр тяжести сектора, вполне очевидно, лежит на оси его симметрии, то есть на биссектрисе угла AOB. Эту биссектрису примем за ось x и найдем на этой оси положение центра C. Разобьем площадь сектора на бесконечно большое число элементарных секторов с центральными углами ∆φ.

Будем рассматривать каждый сектор как треугольник с основанием R · ∆φ и высотой R. Центр тяжести каждого треугольника расположен на расстоянии  от центра сектора. Таким образом, центры тяжести всех треугольников расположены на дуге A´B´. Итак, если 0 ∆φ → 0, то центры тяжести образуют дугу AB, тогда необходимо найти центр тяжести дуги A´B´. Используем формулу, по которой определяется центр тяжести дуги окружности радиусом r:

Тогда учитывая, что

Будем иметь

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Момент силы
4. Пара сил
5. Произвольная система сил
6. Плоская произвольная система сил
7. Трение
8. Расчет ферм
9. Расчет усилий в стержнях фермы
10. Пространственная система сил
11. Произвольная пространственная система сил
12. Плоская система сходящихся сил
13. Пространственная система сходящихся сил
14. Равновесие тела под действием пространственной системы сил
15. Естественный способ задания движения точки
16. Центр параллельных сил
17. Параллельные силы
18. Система произвольно расположенных сил
19. Сосредоточенные силы и распределенные нагрузки
20. Кинематика
21. Кинематика твердого тела
22. Движения твердого тела
23. Динамика материальной точки
24. Динамика механической системы
25. Динамика плоского движения твердого тела
26. Динамика относительного движения материальной точки
27. Динамика твердого тела
28. Кинематика простейших движений твердого тела
29. Общее уравнение динамики
30. Работа и мощность силы
31. Обратная задача динамики
32. Поступательное и вращательное движение твердого тела
33. Плоскопараллельное (плоское) движение твёрдого тела
34. Сферическое движение твёрдого тела
35. Движение свободного твердого тела
36. Сложное движение твердого тела
37. Сложное движение точки
38. Плоское движение тела
39. Статика твердого тела
40. Равновесие составной конструкции
41. Равновесие с учетом сил трения
42. Колебания материальной точки
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки

Определение положения центра тяжести тела, составленного из тонких однородных стержней

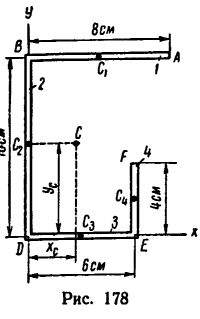
Задача 122-23. Определить положение центра тяжести плоской фигуры (рис. 178), изогнутой из тонкой проволоки.

Решение.

1.    Фигура состоит из четырех прямых отрезков:

2.    Оси координат расположим так, чтобы они совпали с отрезками DE (ось х) и DB (ось у). Так как фигура плоская, третья ось здесь не нужна.

3.    Для центров тяжести 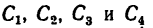каждого отрезка соответственно найдем, исходя из размеров фигуры, их координаты.

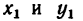
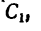
а    Обозначив координаты найдем, что

координаты

координаты

координаты

Для удобства, а также ввиду того, что координаты центров тяжести можно определить непосредственно по рисунку, данные для подстановки в формулы следует представлять в таком виде:

4. Подставим значения 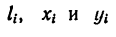в формулы (2) и сделаем вычисления:

5. Отложив вдоль осей х и у найденные координаты, отметим на рис. 178 положение центра тяжести С данной фигуры.

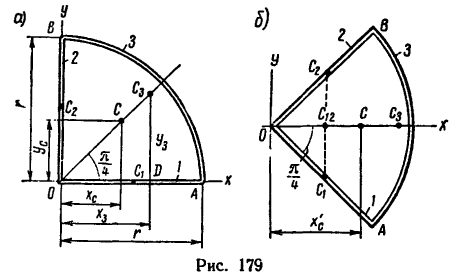
Задача 123-23. Определить положение центра тяжести плоской фигуры ОАВ, изогнутой из тонкой проволоки в виде квадранта (рис. 179).

Решение 1.

1.    Фигура состоит из трех частей: двух прямолинейных отрезков 1 и 2 длиной r и дуги 3, равной четверти окружности.

2.    Совместив оси координат с прямолинейными отрезками ОА и ОВ (рис. 179, а), приведем данные для подстановки в формулы:

Координаты 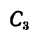находим из прямоугольного треугольника

но по формуле (5)
поэтому
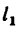
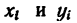
3.    Подставим значение и координат в формулы (2) и сделаем вычисления:

Решение 2.

1.    Так как фигура имеет одну ось симметрии, проходящую по биссектрисе прямого угла, одну из осей координат целесообразно совместить с осью симметрии (рис. 179, б)

В этом случае общий центр тяжести отрезков ОА и ОВ (точка 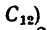находится на оси симметрии (оси х).

2.    Определим исходные данные для подстановки в формулы (2):

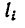
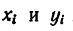
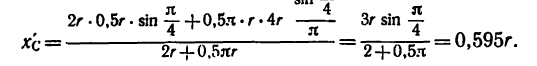
3. Найденные значенияи координат подставим в формулы (2):

.
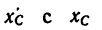
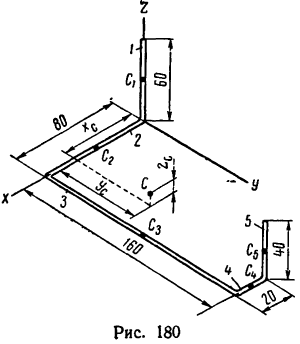
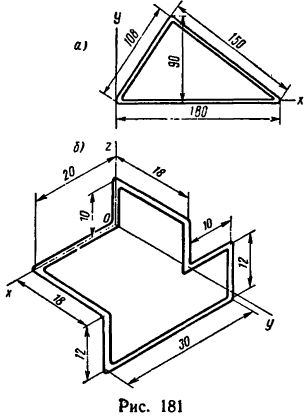
Сравнивая из первого решения, видим, что (см. 2

Задача 124-23. Определить положение центра тяжести пространственно изогнутой проволочной фигуры (рис. 180); размеры — в мм.

Решение.

1.    Расположив проволочную фигуру в осях координат как показано на рис. 180, разделим ее на пять прямолинейных участков 1, 2, 3, 4 и 5 и отметим точками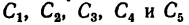центры тяжести каждого участка.

2.    Найдем исходные данные для подстановки в формулы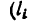 — длины участков и координаты

3.    Найденные исходные данные подставим в формулы (2) и вычислим координаты центра тяжести всей фигуры:

4.    Таким образом, центр тяжести фигуры расположен в точке С (55,0; 62,2; 7,2).

Следующую задачу рекомендуется решить самостоятельно.

Задача 125-23. Определить положение центров тяжести плоской и пространственной проволочных фигур, показанных на рис 181
(размеры в мм).

Ответ (в осях, показанных на рис. 181);

а)    С (85,5; 26,5);

б)    С (6; 9,95; -2,19).

Определение положения центра тяжести фигур, составленных из пластинок

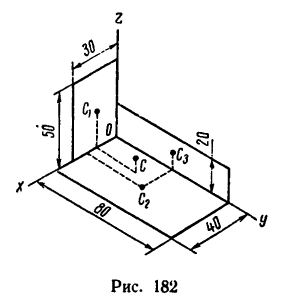
Задача 126-24. Определить положение центра тяжести фигуры, составленной из трех тонких плоских пластинок прямоугольной формы, пересекающихся друг с другом под прямыми углами (рис. 182); размеры —в мм.

Решение.

1.    Поместим начало координат в вершине трехгранного угла и расположим оси координат вдоль линий пересечения пластинок.

Фигура состоит из трех прямоугольников с центрами тяжести 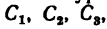расположенными на пересечении прямых, соединяющих середины противоположных сторон.

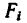
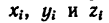
2. Исходя из размеров фигуры, определим необходимые данные для подстановки в формулы (3): — площади прямоугольников и координаты их центров тяжести:

3. Подставим эти данные в формулы (4) и вычислим искомые координаты центра тяжести фигуры:

Центр тяжести фигуры расположен в точке С (13,7; 30,4; 8,5).

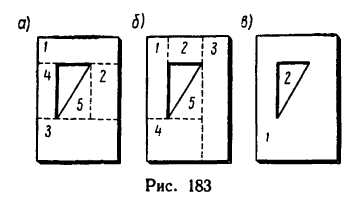
В последней задаче, а также в задачах, приведенных в предыдущем параграфе, расчленение фигур на составные части не вызывает особых затруднений. Но иногда фигура имеет такой вид, который позволяет разделить ее на составные части несколькими способами, например тонкую пластинку прямоугольной формы с треугольным вырезом (рис. 183). При определении положения центра тяжести такой пластинки ее площадь можно разделить на четыре прямоугольника (1, 2, 3 и 4) и один прямоугольный треугольник 5 — несколькими способами. Два варианта показаны на рис. 183, а к б.

Наиболее рациона.льным является тот способ деления фигуры на составные части, при котором образуется наименьшее их число. Если в фигуре есть вырезы, то их можно также включать в число составных частей фигуры, но площадь вырезанной части считать отрицательной. Поэтому такое деление получило название способа отрицательных площадей.

Пластинка на рис. 183,в делится при помощи этого способа всего на две части: прямоугольник 1 с площадью всей пластинки, как будто она целая, и треугольник 2 с площадью, которую считаем отрицательной.

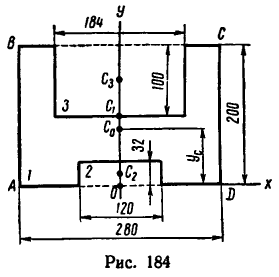
Задача 127-24. Определить положение центра тяжести тонкой однородной пластинки, имеющей ось симметрии. Формаш размеры пластинки показаны на рис. 184.

Решение.

1.    Пластинка имеет ось симметрии, на которой находится центр тяжести. Совместим с осью симметрии ось у, а ось х — с нижним краем пластинки.
2.    Дополнив пластинку до прямоугольника ABCD, разобьем ее тем самым на три части: 1, 2 и 3.

3.    Определим площади каждой части в 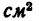и координаты их центров тяжести в см:

4.    Определим ординату центра тяжести пластинки, подставив найденные значения во вторую формулу системы (3):

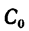
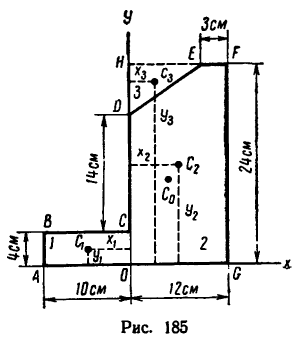
Таким образом, центр тяжести имеет ординату

Задача 128-24. Определить положение центра тяжести плоской однородной пластинки ABCDEFG, размеры которой в см указаны на рис. 185.

Решение.

1.    Разбиваем пластинку на два прямоугольника АВСО и OHFG и на треугольник DHE, площадь которого считаем отрицательной.

2.    Начало координат помещаем в точке О, ось х совмещаем с прямой AG, ось у — с прямой CD.

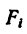
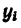
3.    Определяем площади составных частей и координаты их центров тяжести

4.    Подставляем найденные значения площадей и координат в две первые формулы (3) и производим .вычисление:

Таким образом, центр тяжести пластинки находится в точке 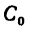(4,8; 9,8).

Следующую задачу рекомендуется решить самостоятельно.

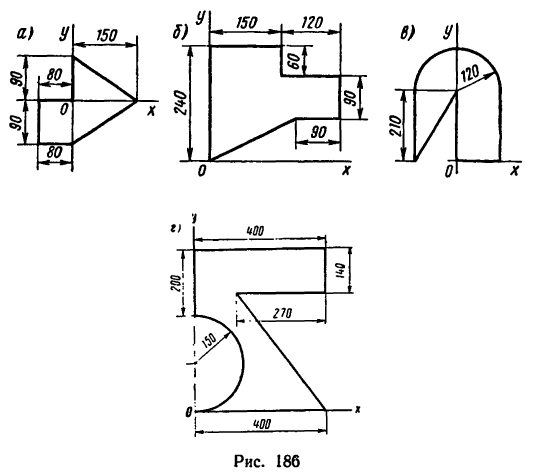
Задача 129-24. Определить положение центров тяжести тонких однородных пластинок, форма и размеры которых показаны на рис 186.

Ответ:

§ 28-8. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ЦЕНТРА ТЯЖЕСТИ СЕЧЕНИЙ, СОСТАВЛЕННЫХ ИЗ ПРОФИЛЕЙ СТАНДАРТНОГО ПРОКАТА
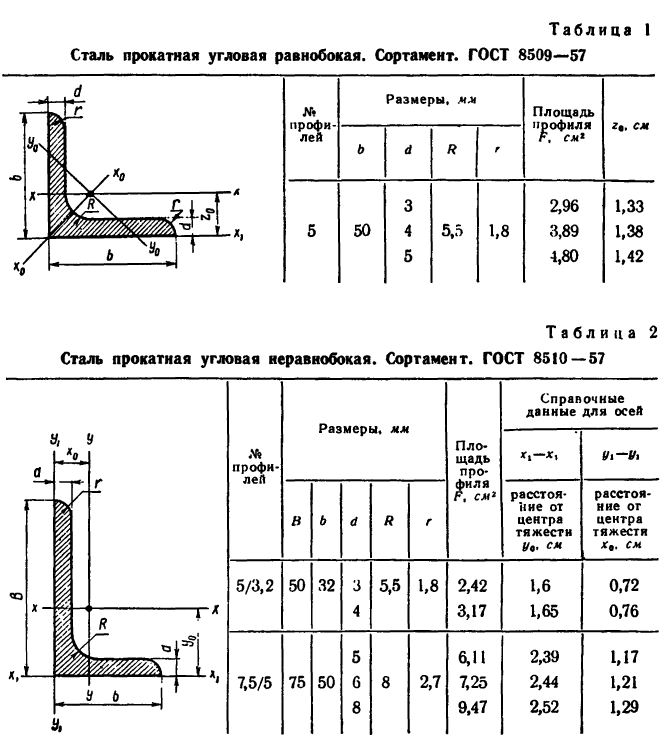
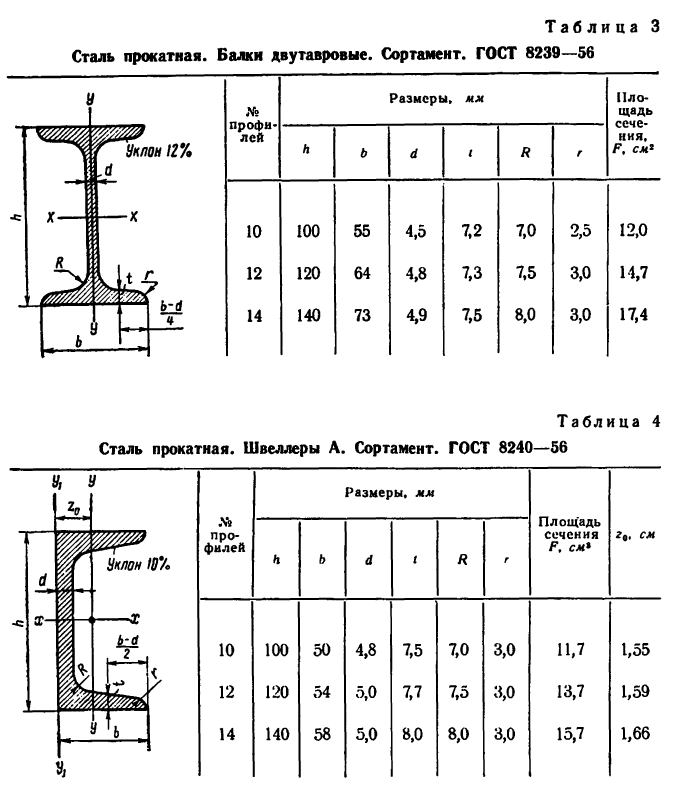
При решении задач, приведенных в этом параграфе, нужно пользоваться таблицами из ГОСТа на прокатную сталь (табл. 1—4).

Эти таблицы для каждого профиля содержат их размеры и площадь, а для уголков и швеллера, кроме того, — координаты центров тяжести.

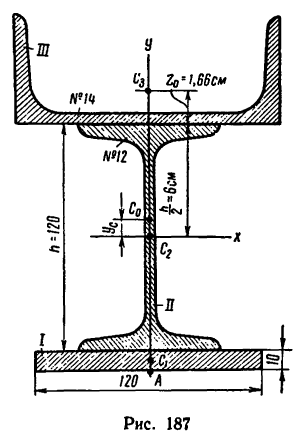
Задача 130-25. Определить положение центра тяжести симметричного сечения, составленного, как показано на рис. 187, из полосы размером 120×10 мм, двутавра № 12 (ГОСТ 8239—56) и швеллера 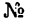14 (ГОСТ 8240—56).

Решение.

1.    Разбиваем сечение на три части: / — полоса, //—двутавр и /// — швеллер.

2.    Находим площади каждой части, выражая их в 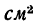. Площадь полосы определяем путем перемножения двух данных размеров, а площади двутавра и швеллера —по таблицам из ГОСТа.

Площадь сечения полосы

Площадь сечения двутавра № 12

Площадь сечения швеллера № 14

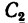
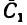
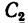
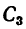
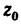
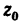
3.    Данное сечение имеет вертикальную ось симметрии. Совместим с этой осью ось у, а ось х проведем через середину двутавра через точку — центр тяжести его сечения. Центр тяжести сечения полосы расположен ниже точки , принятой в данном случае за начало координат, на расстоянии

Центр тяжести швеллера находим при помощи тех же таблиц из ГОСТа Положение центра тяжести швеллеров в таблицах обозначено одной координатой ; для швеллера № 14 = 1,66 см, следовательно,

Таким образом,

4.    Подставляем эти значения в расчетную формулу для ординаты

В выбранных осях положения центра тяжести сечения выражены координатами

Это значит, что центр тяжести сечения находится от его нижнего края (от точки А) на расстоянии

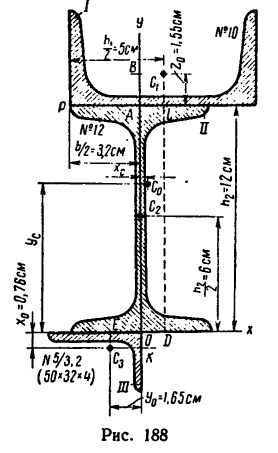
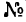
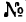
Задача 131-25. Определить положение центра тяжести сечения, составленного, как показано на рис 188, из трех профилен стандартного проката: швеллера 10 (ГОСТ 8240—56), двутавра 12 (ГОСТ 8239—56) и неравпобокого уголка № 5/3,2 (размеры 50x32x4 мм ГОСТ 8510—57).

Решение.

1.    Разбиваем сечение на три части: / — швеллер, //-двутавр и ///—неравнобокий уголок.

2.    Начало координат поместим в вершине прямого угла неравнобокого уголка; ось х совместим с нижней полкой двутавра,

а ось у — с его вертикальной осью симметрии.

3 При помощи таблиц из ГОСТа находим:

площадь сечения швеллера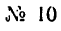  

площадь сечения двутавра № 12

площадь сечения уголка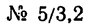  

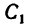
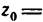
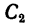
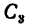
4.    В таблицах из ГОСТа положение центра тяжести швеллерапоказано одной координатой 1,55см, так’ как швеллер имеет одну ось симметрии. Положение центра тяжести двутавра в таблицах не показано, так как он имеет две оси симметрии и его центр тяжести расположен на их пересечении. Положение центра тяжести неравнобокого уголка № 5/3,2 показано двумя координатами:

Располагаем центры тяжести 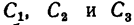на рисунке (см. рис. 188), а затем при помощи таблиц находим их координаты в выбранных осях, учитывая другие необходимые размеры профилей, которые также берутся из таблиц: координаты центра тяжести

координаты центра тяжести

координаты центра тяжести

5.    Таким образом,

6.    Подставляем эти значения в расчетные формулы:

7.    Центр тяжести данного составного сечения имеет координаты (в мм) 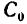(5,4; 82,3).

Следующую задачу рекомендуется решить самостоятельно.

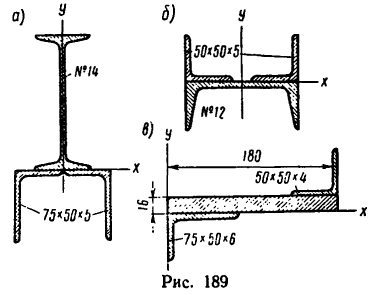
Задача 132-25. Определить положение центра тяжести трех сечений, составленных из профилей стандартного проката, как показано на рис. 189.

Ответ (в мм):

а)    С (0; 31,1);

Определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму

Чтобы решать задачи на определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму, необходимо иметь навыки определения координат

центра тяжести фигур, составленных из линий или площадей.

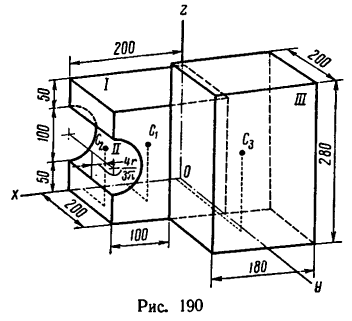
Задача 133-26. Определить положение центра тяжести тела, составленного из куба /, имеющего горизонтальную цилиндрическую канавку //, и прямоугольного параллелепипеда 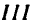(рис. 190); размеры —в мм.

Решение.

1. Тело состоит из куба /, полуцилиндра //, объем которого считаем отрицательным, так как он вырезан из объема куба /, и прямоугольного параллелепипеда

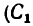
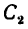
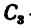
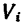
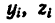
2. Отметив на рисунке положение центра тяжести составных частей —центр тяжести куба, — центр тяжести полуцилиндра и —центр тяжести параллелепипеда), найдем исходные величины для подстановки их в формулы (4) – объемы – и координатыих центров тяжести:

3.    После подстановки в расчетные формулы имеем:

Таким образом, центр тяжести данного тела находится в точке 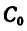(44; 216; 106).

Эту точку рекомендуется отметить на рис. 190 самостоятельно.

Задача 134-26 (для самостоятельного решения). Определить положение центра тяжести тела, форма и размеры (в мм) которого показаны на рис. 191.

Ответ. С (122; 184; 80).

РАЗДЕЛ ВТОРОЙ

КИНЕМАТИКА
В кинематике изучаются законы движения материальных точек и твердых тел с чисто геометрической стороны. Законом движения точки или тела можно назвать такую совокупность математических образов и уравнений, которая в любой момент времени позволяет установить, где находится точка или тело, куда и как они движутся. При этом в кинематике не рассматриваются вопросы, почему точка или тело двигается именно так, а не иначе. Эти вопросы изучаются в разделе «Динамика».

Прежде чем решить задачи но кинематике, необходимо выяснить следующее:

а)    можно ли данный в задаче движущийся предмет рассматривать как материальную точку или его нужно считать твердым телом;

б)    в какой форме закон движения задан в задаче.

Необходимость выяснения первого положения вызывается тем,

что законы движения материальных точек (предметов, формой и размерами которых можно пренебречь) и законы движения твердых тел (предметов, состоящих из множества материальных точек), как правило, отличаются друг от друга.

От способа задания закона движения зависит ход решения задачи.