Enter the x and y dimensions and masses of up to 5 individual points into the calculator. The calculator will determine the center of mass of the masses entered.
- All Mass Calculators
- Mass Momentum of Inertia
- Reduced Mass Calculator
- Mass Percent Calculator
- Mass Flow Rate Calculator
- Tipping Force Calculator
Center of Mass Formula
The following formula is used to calculate a center of mass of multiple point masses.
Center of mass = (m1x1y1 + m2x2y2 + … + mNrN) / (m1 + m2 + … + mN)
- Where m is the mass of each point
- x is the coordinate distance of each point along the x-axis
- y is the coordinate distance of each point along the y-axis
To calculate a center of mass, multiply the point masses by each coordinate, add these values together, then divide by the sum of the point masses.
Center of Mass Definition
The center of mass is defined as the point in which if all of the mass of an object was located at that single point, it would behave the same way as the true body of the mass.
Center of Mass Example
How to calculate a center of mass
- First, measure all of the individual point masses
In this case, it’s extremely important that the masses you are using can be modeled as point masses. If they were irregular objects, this formula would not hold.
- Next, measure the distance of each mass
Measure the distance of each mass from an origin of x=0 and y=0
- Calculate the center of mass
Calculate the center of mass using the formula above and the measured values from steps 1 & 2.
FAQ
What is a center of mass?
A center of mass is a term used in physics to describe a single point location that could be used in order to model where a mass of an object was located if all of that mass of the individual object was located at one discrete point.
What is a point mass?
A point mass is a single point in which mass is located.
An online center of mass calculator is intuitively designed to find center of mass of single or multiple objects in one, two or three dimensions, respectively. Here, you should have a proper understanding of some quantitative terms that are described below.
Keep scrolling down!
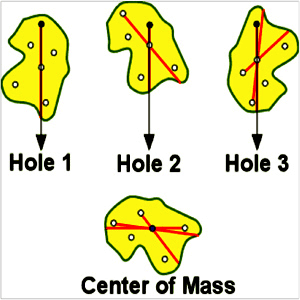
What Is Center Of Mass (COM)?
“A point where the whole mass of an object becomes concentrated is termed center of mass
Brief explanation:
Whenever we are interested in studying the dynamics regarding the system motion of particles as a whole, then we do not need to know about the dynamics of each and every particle separately. What we need to focus on is the pivot point that is the center of mass.
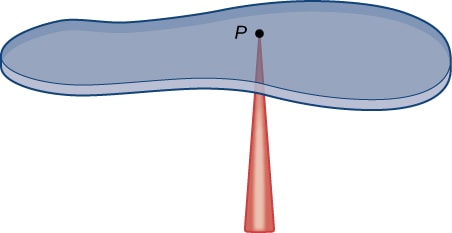
Basically it is a point where an object can be balanced perfectly if suspended horizontally.
As there exist some external forces exerted by surrounding bodies also, it must be kept in mind that the resultant of all these forces is directed to the center of mass.
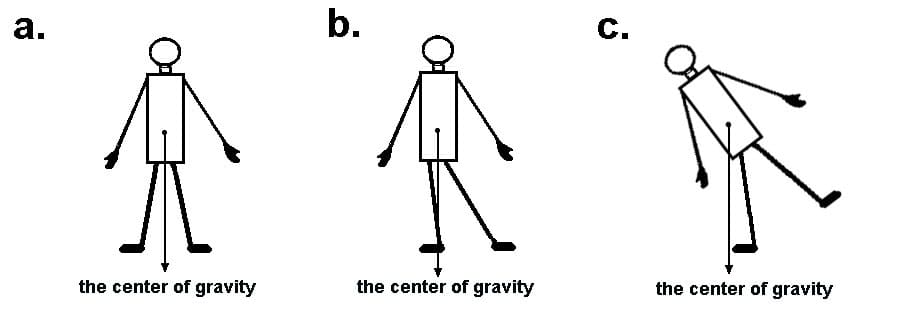
Center Of Gravity(COG):
“It is a point where the gravitational force acts to pull it towards the ground.”
The center of gravity changes with respect to the position of an object or human body and is not always fixed. In a uniform gravitational field, the center of gravity calculation is same as it is for the center of mass.
Relationship Between Center Of Mass And Center Of Gravity:
In a uniform gravitational field, both the center of mass and center of gravity are considered equal. But in case there is a non-uniform gravitational field, these terms get different from each other. The reason is that the center of mass is a fixed point but the center of gravity is not.
Center Of Mass Equation:
You can easily calculate center of mass with the help of the formula given below:
$$ center of mass = frac{left(m_{1}r_{1} + m_{2}r_{2} + … + m_{n}r_{n}right)}{left(m_{1} + m_{2} + … + m_{n}right)} $$
Where:
m = mass of the individual objects
n = number of the objects
r = distance of point from reference position
The above is a general form of center of mass equation. However, you can also perform a center of mass calculation in either one, two or three dimensional coordinate system, respectively.
COM For Two Dimensional System:
In case we have a 2D system, the center of mass calculations can be performed as follows:
$$ x_{com} = frac{1}{M} * Sum m_{n}x_{n} $$
$$ y_{com} = frac{1}{M} * Sum m_{n}y_{n} $$
Where:
n = 1, 2, 3, …
COM For Three Dimensional System:
You can calculate center of mass in a 3D system by following the equations below:
$$ x_{com} = frac{1}{M} * Sum m_{n}x_{n} $$
$$ y_{com} = frac{1}{M} * Sum m_{n}y_{n} $$
$$ z_{com} = frac{1}{M} * Sum m_{n}z_{n} $$
Where:
n = 1, 2, 3, …
Our free online center of mass calculator depicts the center of mass by using the same formulae.
How To Calculate Center Of Mass?
You can find center of mass easily using a center mass equation. Let us solve a couple of examples to clarify the concept in more depth.
Example # 01:
The mass of an object is 10kg and its reference distance is about 3.5m. Similarly we have a second object having a mass of 3kg and reference distance as 2m. How to calculate center of mass?
Solution:
Using the general center of mass equation:
$$ center of mass = frac{left(m_{1}r_{1} + m_{2}r_{2} + … + m_{n}r_{n}right)}{left(m_{1} + m_{2} + … + m_{n}right)} $$
Putting the values of both masses and their distances from the zero point as follows:
$$ center of mass = frac{(10)(3.5) + (3)(2)}{10 + 3} $$
$$ center of mass = frac{(10)(3.5) + (3)(2)}{10 + 3} $$
$$ center of mass = frac{41}{13} $$
$$ center of mass = 3.153m $$
Here, our free online center of mass calculator calculates the same results but instantly to save your precious time.
Example # 02:
How to find the center of mass of two objects having following values below:
Mass of one object = 2kg
X coordinate of first object = 1.5cm
Y coordinate of first object = 2cm
Mass of second object = 1kg
X coordinate of second object = 3cm
Y coordinate of second object = 4cm
Solution:
We know that for a 2D system:
$$ x_{com} = frac{1}{M} * Sum m_{n}x_{n} $$
$$ y_{com} = frac{1}{M} * Sum m_{n}y_{n} $$
Performing center of mass calculation:
$$ x_{com} = frac{1}{M} * Sum m_{n}x_{n} $$
$$ x_{com} = frac{1}{2 + 1} * (2)(1.5) + (1)(3) $$
$$ x_{com} = frac{1}{3} * 6 $$
$$ x_{com} = 2cm $$
Similarly:
$$ y_{com} = frac{1}{M} * Sum m_{n}y_{n} $$
$$ y_{com} = frac{1}{2 + 1} * (2)(2) + (1)(4) $$
$$ x_{com} = frac{1}{3} * 8 $$
$$ x_{com} = 2.66cm $$
So, the required center of mass is given as follows:
$$ COM = left(2, 2.66right) $$
Which is our answer.
For the center of mass calculation in a three dimensional coordinate system, you can use a free online center of mass calculator 3D.
How Center Of Mass Calculator Works?
You can depict accurate results by fetching values to our free center of mass calculus calculator. What you need to do is described below.
Input:
- First of all, select the system that could be either 1D, 2D or 3D.
If you select 1D system:
- Select the number of masses which is upto 10.
- Write down the mass of each object.
- Also write its general position from the zero reference.
- Hit the calculate button.
If you select 2D system:
- Select the number of masses which is upto 10.
- Write down the mass of each object.
- Enter the value of x coordinates of both masses
- Also, enter the y coordinates of both the masses
- Click ‘calculate’
If you select 3D system:
- Select the number of masses which is upto 10.
- Write down the mass of each object.
- Enter x coordinates of each object.
- Similarly enter the y coordinates
- Enter the z coordinates in the same way
- Click ‘calculate’
Output:
The center of mass integral calculator finds:
- Center of mass for the objects given in various units of length.
FAQ’s:
Is the center of mass a reality?
No, the center of mass of any system is just a hypothetical point where the system becomes at rest.
What is the speed of center of mass?
all the individual masses have their own accelerations in a particular direction. But the center of mass has a fixed acceleration in the direction of the x coordinate which is about (0.33 m/s^{2}).
What do you mean by momentum of a body?
The product of mass and velocity of a body is called its momentum. It is a vector quantity having a particular direction and magnitude.
What are the dimensions of the center of mass?
As the SI unit of center of mass is meter(m), the dimensions of center of mass are in the direction of length as well which are [L].
Conclusion:
Center of mass has vast applications in the field of mechanics, aeronautics and aerospace where they are used to keep the aircrafts and spacecrafts in state of equilibrium. Professional scholars make vast use of a free online center of mass calculator to find the point of reference where the overall mass is pivoted.
References:
From the source of wikipedia: Barycentric coordinates, Center of gravity, Linear and angular momentum.
From the source of khan academy: Force vs. time graphs, conservation of momentum.
From the source of lumen learning: Internal and External Forces, Force and Momentum, Center of Mass and Conservation of Momentum, Center of Mass of Continuous Objects
Расчёт геометрических характеристик сложного поперечного сечения
|
Операции Двутавр
Швеллер
Равнополочный уголок
Неравнопол. уголок
Неравнопол. уголок
Полоса (прямоугольник)
Круг
Полукруг
Четверть круга
Равнобедр. треугольник
Прямоуг. треугольник
Прямоуг. треугольник
Имена осей
Состав сечения В данном расчёте не задано ни одного профиля. Для задания профилей перейдите в панель “Операции” и выберите необходимый профиль. |
Центр масс, теория и онлайн калькуляторы
Центр масс
Определение центра масс
Определение
При рассмотрении системы частиц, часто удобно найти такую точку, которая характеризует положение и движение
рассматриваемой системы как единого целого. Такой точкой является центр масс.
Если у нас две частицы одинаковой массы, то такая точка находится посередине между ними.
Координаты центра масс
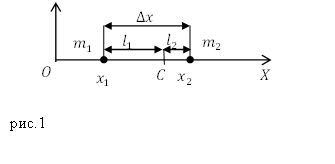
Допустим, что две материальные точки, имеющие массы $m_1$ и $m_2$ находятся на оси абсцисс и имеют координаты $x_1$ и $x_2$. Расстояние ($Delta x$) между этими частицами равно:
[Delta x=x_2-x_1left(1right).]
Определение
Точку С (рис.1), делящую расстояние между этими частицами на отрезки, обратно
пропорциональные массам частиц называют центром масс этой системы частиц.
В соответствии с определением для рис.1 имеем:
[frac{l_1}{l_2}=frac{m_2}{m_1}left(2right).]
Так как:
[l_1{=x}_c-x_1;; l_1{=x}_2-x_cleft(3right),]
где $x_c$ – координата центра масс, то получаем:
[m_1left(x_c-x_1right)=m_2{(x}_2-x_c)(4).]
Из формулы (4) получим:
[x_c=frac{m_1x_1+m_2x_2}{m_1+m_2}left(5right).]
Выражение (5) легко обобщается для множества материальных точек, которые расположены произвольным образом. При этом абсцисса центра масс равна:
[x_c=frac{sumlimits^N_{i=1}{m_ix_i}}{sumlimits^N_{i=1}{m_i}}left(6right).]
Аналогично получают выражения для ординаты ($y_c$) центра масс и его аппликаты ($z_c$):
[y_c=frac{sumlimits^N_{i=1}{m_iy_i}}{sumlimits^N_{i=1}{m_i}}left(7right).]
[z_c=frac{sumlimits^N_{i=1}{m_iz_i}}{sumlimits^N_{i=1}{m_i}}left(8right).]
Формулы (6-8) совпадают с выражениями, определяющими центр тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.
Если положение N материальных точек системы задано в векторной форме, то радиус – вектор, определяющий положение центра масс находим как:
[{overline{r}}_c=frac{sumlimits^N_{i=1}{m_i{overline{r}}_i}}{sumlimits^N_{i=1}{m_i}}left(9right).]
Движение центра масс
Выражение для скорости центра масс (${overline{v}}_c=frac{d{overline{r}}_c}{dt}$) имеет вид:
[{overline{v}}_c=frac{m_1{overline{v}}_1+m_2{overline{v}}_2+dots +m_n{overline{v}}_n}{m_1+m_2+dots +m_n}=frac{overline{P}}{M}left(10right),]
где $overline{P}$ – суммарный импульс системы частиц; $M$ масса системы. Выражение (10) справедливо при движениях со скоростями которые существенно меньше скорости света.
Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.
Примеры задач с решением
Пример 1
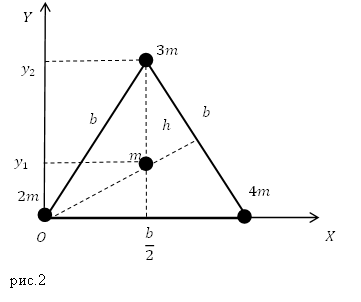
Задание. Запишите координаты центра масс системы из трех шариков, которые находятся в вершинах и центра равностороннего треугольника, сторона которого равна $b (м)$ (рис.2).
Решение. Для решения задачи используем выражения, определяющие координаты центра масс:
[x_c=frac{m_1x_1+m_2x_2+m_3x_3+m_4x_4}{m_1+m_2+m_3+m_4}(2.1);;]
[y_c=frac{m_1y_1+m_2y_2+m_3y_3+m_4y_4}{m_1+m_2+m_3+m_4}(2.2).]
Из рис.2 мы видим, что абсциссы точек:
[left{ begin{array}{c}
m_1=2m, x_1=0;; \
{rm }m_2=3m, x_2=frac{b}{2};; \
m_3=m, x_3=frac{b}{2};; \
m_4=4m, x_4=b. end{array}
right.left(2.3right).]
Тогда абсцисса центра масса равна:
[x_c=frac{2mcdot 0+3mcdot frac{b}{2}+mcdot frac{b}{2}+4mcdot b}{2m+3m+m+4m}=frac{6mb}{10m}=0,6b (м);;]
Найдем ординаты точек.
[ begin{array}{c}
m_1=2m, y_1=0;; \
{rm }m_2=3m, y_2=frac{bsqrt{3}}{2};; \
m_3=m, y_3=frac{bsqrt{3}}{6};; \
m_4=4m, y_4=0. end{array}
left(2.4right).]
Для нахождения ординаты $y_2$ вычислим, чему равна высота в равностороннем треугольнике:
[h=sqrt{b^2-frac{b^2}{4}}=frac{bsqrt{3}}{2}=y_2left(2.5right).]
Ординату $y_3$ найдем, помня, что медианы в равностороннем треугольнике точкой пересечения делятся в отношении 2:1 от вершины, получаем:
[y_3=hcdot frac{1}{3}=frac{bsqrt{3}}{6} left(2.6right).]
Вычислим ординату центра масс:
[y_c=frac{2mcdot 0+3mcdot frac{bsqrt{3}}{2}+mcdot frac{bsqrt{3}}{6}+4mcdot 0}{2m+3m+m+4m}=frac{10mfrac{bsqrt{3}}{6}}{10m}=frac{bsqrt{3} }{6}(м).]
Ответ. $x_c=0,6b {rm }{rm м}$; $y_c=frac{bsqrt{3} }{6}$ м
Пример 2
Задание. Запишите закон движения центра масс.
Решение. Закон изменения импульса системы частиц является законом движения центра масс. Из формулы:
[{overline{v}}_c=frac{overline{P}}{M}to overline{P}=M{overline{v}}_cleft(2.1right)]
при постоянной массе $M$ продифференцировав обе части выражения (2.1), получим:
[frac{doverline{P}}{dt}=Mfrac{d{overline{v}}_c}{dt}left(2.2right).]
Выражение (2.2) означает, что скорость изменения импульса системы равняется произведению массы системы на ускорение ее центра масс. Так как
[frac{doverline{P}}{dt}=sumlimits^N_{i=1}{{overline{F}}_ileft(2.3right),}]
имеем:
[Mfrac{d{overline{v}}_c}{dt}=sumlimits^N_{i=1}{{overline{F}}_ileft(2.4right).}]
В соответствии с выражением (2.4) получаем, что центр масс системы движется так, как двигалась бы одна материальная точка массы M, если на нее действует сила, равная сумме всех внешних сил, действующих на частицы, которые входят в рассматриваемую систему. Если $sumlimits^N_{i=1}{{overline{F}}_i=0,}$ то центр масс движется равномерно и прямолинейно.
Читать дальше: центр тяжести.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
This online Center of Mass Calculator calculates the coordinates of the center of mass for an arbitrary number of point masses in the case of one-dimensional, two-dimensional or three-dimensional space. To get the result, you first select the space dimension. Then enter the known values of masses and coordinates into the input fields of this calculator and click the ‘Calculate’ button. To add or delete a mass you may click the “+” symbol or the “–” symbol respectively.
Center of Mass Formula
In physics, the center of mass of a distribution of mass in space (a.k.a the balance point) is the unique point where the weighted relative position of the distributed mass sums to zero. This is the point, the application of forces to which, causes a linear acceleration without an angular acceleration.
Calculations in mechanics are often simplified if they are formulated with respect to the center of mass. The center of mass can be thought of as a hypothetical point at which it can be assumed that the entire mass of an object is concentrated. This makes it easier to visualize the motion of that object. In other words, the center of mass is a hypothetical particle equivalent to a given object to which Newton’s laws of motion can be applied.
The terms “center of mass” and “center of gravity” are used as synonyms in the case of a uniform gravitational field. Both terms refer to a unique point in an object or system that can be used to describe the system’s response to external forces and torques.
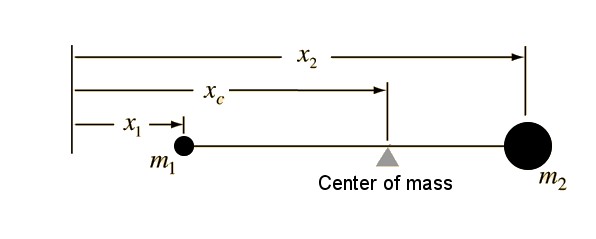
In the case of a plane and two masses, this is like balancing a seesaw around a pivot point with respect to the torques produced. For two masses we have the following center of mass formula:
$$x_{c}=frac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}},$$
where
(m_{i}) is the mass of particle (i),
(x_{i}) is the coordinate of particle (i),
(x_{c}) is the center of mass coordinate.
If you are making measurements from the center of mass point for such a two-mass system, then the center of mass condition can be expressed as:
$$m_1 | x_1 | = m_2 | x_2 |.$$
The center of mass lies on the line connecting the two masses.
In the case of an arbitrary number of particles, the formula for the center of mass is generalized as follows:
$$x_{c}=frac{m_{1}x_{1}+m_{2}x_{2}+m_{3}x_{3}+…}{m_{1}+m_{2}+m_{3}+…}.$$
In the case of multidimensional space, this formula also applies to the (y) and (z) coordinates.
With our Center of Mass Calculator you can easily compute the coordinates of the center of mass for an arbitrary number of point masses in one-dimensional, two-dimensional or three-dimensional space.
Related calculators
Check out our other physics calculators such as Torque Calculator or Work Calculator.