Как найти центр масс пирамиды

Сообщения без ответов | Активные темы | Избранное

	Центр масс вершин пирамиды 18.01.2011, 12:36
10/10/10 7	Здравствуйте! Подскажите, пожалуйста, как для треугольной пирамиды с вершинами А(6; 7;-1), В(6;11;1), С(8;9;2), D(10;7;-3) найти центр масс вершин пирамиды. Где можно посмотреть формулы для вычисления?

ewert	Re: Центр масс вершин пирамиды 18.01.2011, 12:39
Заслуженный участник 11/05/08 32162	Сложить и поделить на количество вершин.

IrinaP	Re: Центр масс вершин пирамиды 18.01.2011, 13:10
10/10/10 7	Если я правильно понимаю, в этом случае мы найдем ЦЕНТР МАСС пирамиды. А в задаче требуется найти ЦЕНТР МАСС ВЕРШИН пирамиды. Или это одно и то же?

TOTAL	Re: Центр масс вершин пирамиды 18.01.2011, 13:24
Заслуженный участник 23/08/07 5188 Нов-ск	Если я правильно понимаю, в этом случае мы найдем ЦЕНТР МАСС пирамиды. А в задаче требуется найти ЦЕНТР МАСС ВЕРШИН пирамиды. Или это одно и то же? Это не одно и то же, т.к. “ЦЕНТР МАСС ВЕРШИН пирамиды” – бессмыслица.

ИСН	Re: Центр масс вершин пирамиды 18.01.2011, 13:25
Заслуженный участник 18/05/06 13415 с Территории	Фигасе предъява Смысл есть. Совпадают ли они – очень может быть, но это отдельный вопрос.

ewert	Re: Центр масс вершин пирамиды 18.01.2011, 13:30
Заслуженный участник 11/05/08 32162	в этом случае мы найдем ЦЕНТР МАСС пирамиды. А в задаче требуется найти ЦЕНТР МАСС ВЕРШИН пирамиды. Нет, буквально так определяется центр масс именно вершин, а не самой пирамиды. Другое дело, что результат для самой пирамиды получается, как ни странно, тем же (если под пирамидой понимается, конечно, именно тетраэдр).

IrinaP	Re: Центр масс вершин пирамиды 18.01.2011, 13:35
10/10/10 7	в задаче сказано “треугольная пирамида”. тетраэдром ее в задаче не называют

TOTAL	Re: Центр масс вершин пирамиды 18.01.2011, 13:37
Заслуженный участник 23/08/07 5188 Нов-ск	Фигасе предъява Смысл есть. Совпадают ли они – очень может быть, но это отдельный вопрос. Смысл появится, когда в вершинах появятся какие-то массы. Если об этом не задумываться, то и будут возникать вопросы “а что это и это такое, и чем они друг от друга отличаются, и дайте мне формулу, а я механически подставлю и отдам училке”.

ewert	Re: Центр масс вершин пирамиды 18.01.2011, 13:38
Заслуженный участник 11/05/08 32162	в задаче сказано “треугольная пирамида” это и есть тетраэдр — Вт янв 18, 2011 14:39:52 — Смысл появится, когда в вершинах появятся какие-то массы. В таком случае ровно по тем же причинам нет никакого смысла и у центра масс самой пирамиды. Пока в ней не появились какие-то плотности.

TOTAL	Re: Центр масс вершин пирамиды 18.01.2011, 13:42
Заслуженный участник 23/08/07 5188 Нов-ск	В таком случае ровно по тем же причинам нет никакого смысла и у центра масс самой пирамиды. Пока в ней не появились какие-то плотности. Правильно.

IrinaP	Re: Центр масс вершин пирамиды 18.01.2011, 14:04
10/10/10 7	если я правильно поняла, то мне для того, чтобы найти центр масс вершин треугольной пирамиды, надо сложить соответствующие координать вершин и полученную сумму разделить на 4. верно?

ewert	Re: Центр масс вершин пирамиды 18.01.2011, 14:07
Заслуженный участник 11/05/08 32162	Ну что ж тут поделаешь, коли у треугольной пирамиды вершин именно четыре. Значит — действительно на четыре.

IrinaP	Re: Центр масс вершин пирамиды 18.01.2011, 14:18
10/10/10 7

Модераторы: Модераторы Математики, Супермодераторы

Содержание:

Центр тяжести:

При рассмотрении движения тел, особенно таких, как самолеты, ракеты, космические корабли, важное значение имеет понятие центра тяжести.

Определения и формулы для вычисления центров тяжести

Для введения понятия центра тяжести разобьем мысленно рассматриваемое тело на достаточно большое число малых по сравнению с телом или элементарных его частей произвольной формы. Силу тяжести элементарной частицы тела с индексом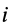

Радиус-вектор центра тяжести тела 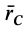вычисляем как радиус-вектор центра параллельных сил (рис. 88) по формуле

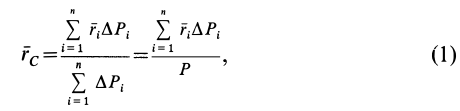
где 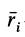— радиус-вектор точки приложения силы тяжести элементарной части тела, принятой за точку; — сила тяжести элементарной частицы; 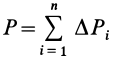— сила тяжести всего тела; — число частей, на которое мысленно разбито все тело. Центр тяжести является точкой приложения равнодействующей силы тяжести, если силы тяжести отдельных его частей считать системой параллельных сил.

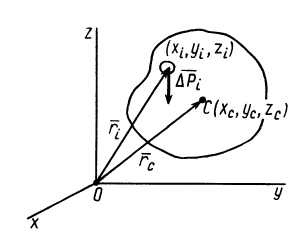
Рис. 88

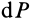Если в (1) перейти к пределу, увеличивая число элементарных частей до бесконечности, то после замены  дифференциалом , а суммы — интегралом получим

где 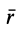— радиус-вектор элементарной части тела, принятой за точку. В проекциях на оси координат из (1) и (1′) получаем:

где 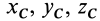— координаты центра тяжести;  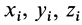— координаты точки приложения силы тяжести .

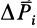Используя понятие центра тяжести тела, введем понятие его центра масс. Силы тяжести элементарных частей тела и всего тела можно выразить через их массы 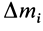и 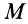и ускорение силы тяжести с помощью формул

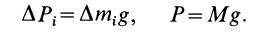
Подставляя эти значения сил тяжести в (1) и (1′) после сокращения на , которое принимаем одинаковым для всех частей тела, имеем

и соответственно

По формулам (2) и (2′) определяют радиус-вектор центра масс тела. Центр масс обычно определяют независимо от центра тяжести как геометрическую точку, радиус-вектор, которой вычисляется по формулам (2) или (2′). В проекциях на оси координат из (2) и (2′) получаем:

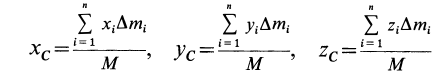
и

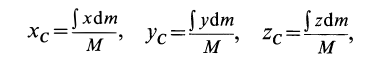
где 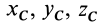— координаты центра масс тела.

Для однородного тела силу тяжести элементарной частицы тела и ее массу можно вычислить по формулам

где 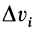 — объем элементарной частицы тела;  и  — соответственно удельный вес и плотность тела. Сила тяжести и масса всего тела

где 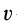— объем тела. Подставляя эти значения в (2) и (2′), после сокращения на  и  соответственно получим формулы

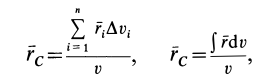
по которым определяют центр тяжести объема тела.

Если тело имеет форму поверхности, т. е. один из размеров мал по сравнению с двумя другими, как, например, у тонкого листа железа, то имеем

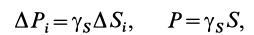
где 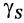— удельный вес; 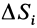— площадь элементарной частицы поверхности; 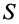— площадь всей поверхности. После сокращения на  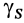для однородной поверхности получим следующие формулы для определения центра тяжести ее площади:

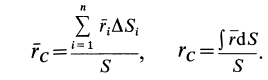
Для однородных тел типа проволоки, у которых два размера малы по сравнению с третьим, можно определить радиус-вектор центра тяжести длины линии по формулам

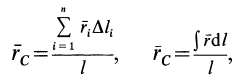
где 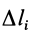— длина элемента линии; 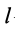—общая длина линии, центр тяжести которой определяется.

Методы определения центров тяжести (Центров масс)

Метод симметрии

При определении центров тяжести широко используется симметрия тел. Докажем, что для однородного тела, имеющего плоскость симметрии, центр тяжести находится в плоскости симметрии. Для доказательства выберем начало координат в плоскости симметрии тела и одну из осей координат, ось 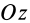направим перпендикулярно плоскости симметрии, а две других оси расположатся в плоскости симметрии (рис. 89). Каждая частица массой 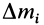, находясь по одну сторону плоскости симметрии, имеет симметричную частицу такой же массы по другую сторону этой плоскости. Координаты 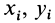у симметричных частиц одинаковы при сделанном выборе осей координат, а координаты по оси 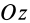отличаются только знаком. Для координаты центра масс 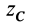имеем следующее выражение:

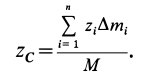
Разбивая сумму в числителе на две по симметричным частям тела, получаем, что

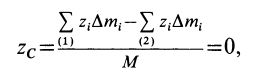
так как симметричные части тела 1 и 2 одинаковы.

Таким образом, центр масс расположен в плоскости симметрии и для его определения достаточно вычислить только две его координаты 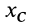и 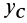в этой плоскости.

Аналогично доказывается, что для однородного тела, имеющего ось или центр симметрии, центр масс находится соответственно на оси симметрии или в центре симметрии.

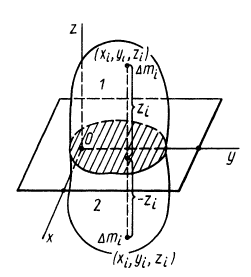
Рис. 89

Метод разбиения на части (метод группировки)

Некоторые тела сложной формы можно разбить на части, центры тяжести которых известны или предварительно могут быть определены. В таких случаях центры тяжести сложных тел вычисляются по общим формулам, определяющим центр тяжести, только вместо элементарных частиц тела берутся его конечные части, на которые оно разбито. Покажем это на частном примере плоской фигуры, изображенной на рис. 90. Плоскую фигуру можно разбить на три части, центры тяжести которых 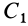, 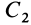и 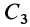известны. Они находятся на пересечении диагоналей прямоугольников. Их радиусы-векторы обозначим 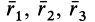и площади 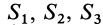. Общая площадь сложной фигуры будет .

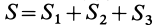Используя определение центра тяжести и производя группировку слагаемых под знаком суммы по частям фигуры, на которые она разбита, получим

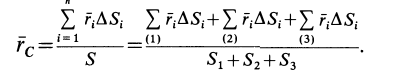
Радиусы-векторы центров тяжести частей тела выразятся в такой форме:

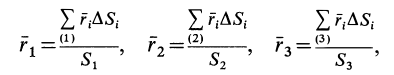
или

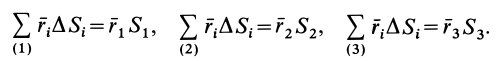
Используя эти формулы для радиуса-вектора всей фигуры, имеем

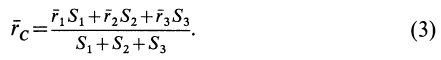
Полученная формула имеет ту же структуру, что и формула, определяющая радиус-вектор центра тяжести тела при разбиении его на элементарные частицы, только в нее входят величины для конечных частей тела.

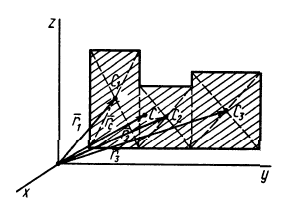
Рис. 90

Метод отрицательных масс

Видоизменением метода разбиения на части является метод отрицательных масс. Проиллюстрируем его тоже на примере плоской фигуры (рис. 91). Для определения центра тяжести этой фигуры ее можно разбить на три части. Можно поступить по-другому. Для этого дополним нашу фигуру до прямоугольника и примем, что этот прямоугольник с площадью 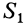 и центром масс 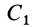полностью заполнен массой (имеет положительную площадь). На той части фигуры, которую добавили, следует распределить отрицательную массу (отрицательную площадь) той же плотности. Площадь этой фигуры с отрицательной массой обозначим 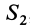, а ее центр масс — 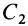. Применяя метод разбиения на части, радиус-вектор заданной фигуры определим по формуле

В отличие от обычного метода разбиения на части в формуле (4) массы и, следовательно, площади входят со знаком минус.

Метод отрицательных масс особенно удобен при вычислении положения центров тяжести тел, имеющих отверстия.
 

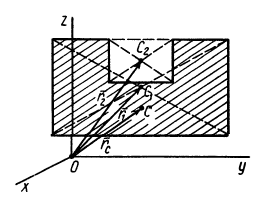
 Рис. 91

Центры тяжести простейших тел

Для определения центров тяжести тел сложной формы методом разбиения на части или методом отрицательных масс необходимо уметь вычислять центры тяжести простейших тел, на которые разбивается тело сложной формы. Рассмотрим некоторые из тел, для определения центров тяжести которых известны простые способы их нахождения или вычисления по формулам.

Прямолинейный отрезок

Центр тяжести прямолинейного однородного отрезка располагается на его середине, а неоднородного— на самом отрезке и не может находиться вне отрезка.

Площадь треугольника

Для определения центра тяжести площади треугольника разобьем его прямыми линиями, параллельными одной из его сторон 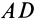, на полоски, которые в пределе можно принять за прямолинейные отрезки (рис. 92). Центры тяжести отрезков и, следовательно, полосок находятся посередине полоски. Все они расположатся на медиане . В пределе центры тяжести полосок непрерывно покроют медиану, но не равномерно, так как площади полосок разные. В каждом центре масс полоски следует считать сосредоточенной массу или площадь этой полоски, пропорциональную длине полоски, если ширину полосок выбирать одинаковой.

Затем разобьем треугольник на полоски прямыми линиями, параллельными другой стороне треугольника. Центры их тяжести в пределе покроют неравномерно медиану 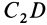. Центры тяжести неоднородных прямолинейных отрезков и 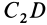должны располагаться на этих отрезках, а следовательно, в точке их пересечения 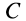, являющейся точкой пересечения медиан треугольника. Эта точка делит медианы в отношении 1 к 2, т. е. 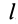если длина медианы равна , то , .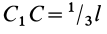

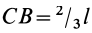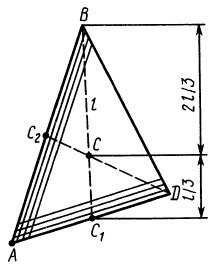
Рис. 92

Дуга окружности

Дуга окружности  определяется радиусом 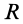и стягиваемым ею центральным углом 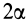(рис. 93). Она имеет ось симметрии, делящую угол пополам. Центр тяжести находится на оси симметрии дуги, которую примем за ось координат 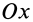. Координату центра тяжести дуги вычисляем по формуле

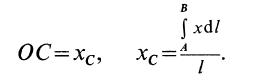
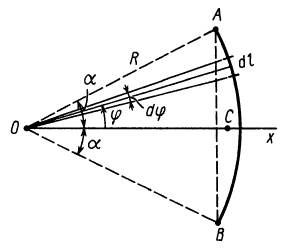
Рис. 93

В рассматриваемом случае

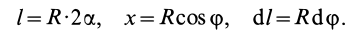
Подставляя эти значения в формулу для 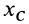, получим

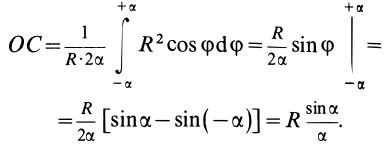
Таким образом,

Для полуокружности 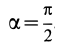. Приняв 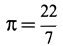,  получим:

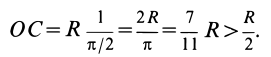
Площадь кругового сектора

Центр тяжести площади кругового сектора с радиусом 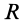и центральным углом 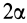находится на оси симметрии, принимаемой за ось 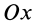(рис. 94). Разобьем сектор на элементарные треугольники одинаковой величины. Центры тяжести треугольников в пределе при увеличении их числа до бесконечности равномерно покроют дугу окружности радиусом .

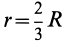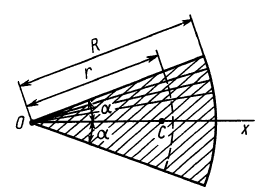
Рис. 94

Используя формулу для центра тяжести дуги окружности, получим

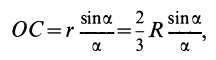
или

Для площади полукруга 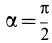, 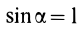. При 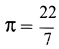 получим

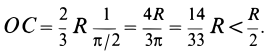
Объем пирамиды и конуса

Определим положение центра тяжести объема конуса (рис. 95). Для простоты рассмотрим прямой конус, у которого высота является осью симметрии. Высотой конуса является отрезок, соединяющий его вершину 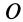с центром тяжести площади основания 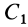. Выберем начало координат в вершине конуса, а ось 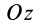направим по оси симметрии конуса. Тогда центр тяжести объема конуса расположится на оси .

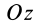Разобьем конус плоскостями, перпендикулярными оси 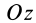, на элементарные тонкие диски толщиной 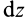и площадью 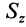. Все полученные сечения (диски) конуса подобны его основанию. Координату  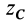центра тяжести объема конуса вычислим по формуле

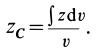
Отношения линейных размеров сечений к соответствующим размерам основания конуса пропорциональны их расстояниям до вершины конуса. Отношения площадей пропорциональны квадратам расстояний. Приняв 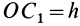, получим

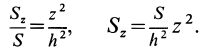
Учитывая, что

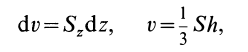
имеем

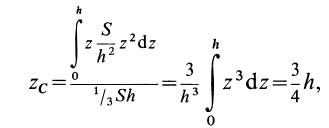
или

Таким образом, центр тяжести прямого конуса находится на расстоянии 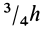 от вершины или 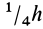от основания.

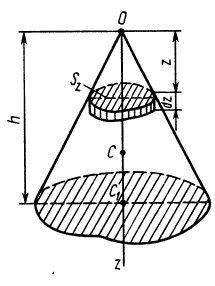
Рис. 95

Это справедливо для объема любого конуса и любой пирамиды, как прямых, так и наклонных, т. е. центр тяжести объема пирамиды или конуса находится на расстоянии 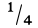 расстояния от центра тяжести площади основания до вершины.

Объем полушара

Полушар имеет ось симметрии, которую примем за координатную ось 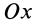(рис. 96). Разобьем объем полушара на элементарные диски толщиной dx и радиусом у, который является координатой точки окружности, которая получилась от пересечения полушара с координатной плоскостью 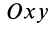. Уравнение этой окружности

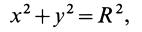
где 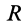— радиус полушара. Для координаты центра тяжести объема полушара имеем

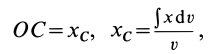
где 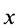 — координата центра тяжести элементарного диска. Объем полушара

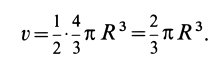
Объем элементарного диска

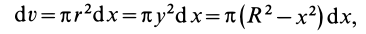
так как радиус диска 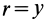. Выполняя интегрирование в пределах от 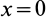до 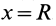, получим

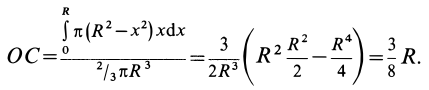
Таким образом, центр тяжести объема полушара находится от его центра на расстоянии

Это расстояние меньше половины радиуса полушара.

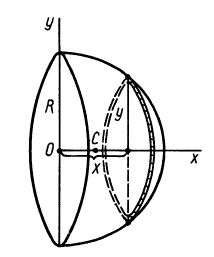
Рис. 96

Задача №1

Определить координаты центра тяжести площади плоской фигуры, имеющей размеры, указанные на рис. 97.

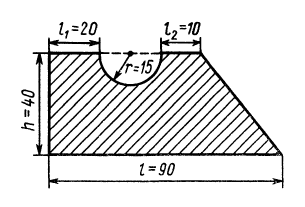
Рис.97

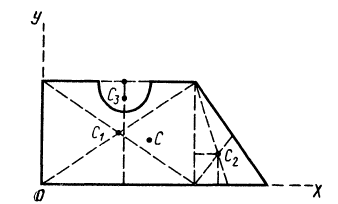
Рис. 98

Решение. Присоединим к заданной фигуре дополнительно полукруг 3 и разобьем полученную фигуру на прямоугольник 1 и треугольник 2. Получили три фигуры, две из которых имеют положительные площади (прямоугольник 1 и треугольник 2) и одна — отрицательную (полукруг 3). В выбранной системе координат для координат центра тяжести заданной фигуры имеем

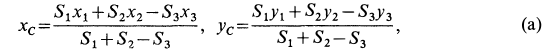
где 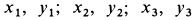 — координаты центров тяжести отдельных фигур; 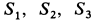— площади этих фигур.

Вычислим площади и координаты центров тяжести отдельных фигур, учитывая рис. 98 Имеем:

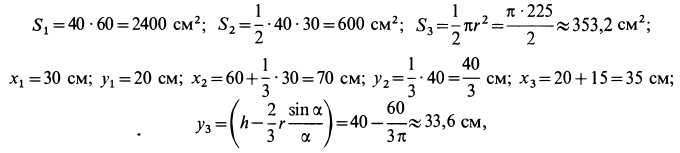
так как .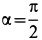

Подставляя полученные значения в (а), получим:

Центр тяжести плоской фигуры

постановка задачи. Найти площадь и координаты центра тяжести плоской фигуры.

План решения:

1.    Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.

2.    Выбираем систему координат. Вычисляем площади и координаты 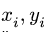центров тяжести отдельных частей. Площади вырезанных частей берем со знаком минус.

3.    Находим общую площадь фигуры по формуле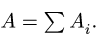

4.    Определяем координаты центра тяжести фигуры:

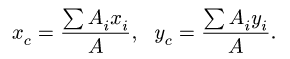
Задача №2

Найти площадь и координаты центра тяжести плоской фигуры. Криволинейный участок контура является половиной окружности с центром на оси Ох (рис. 74). Размеры на рисунке даны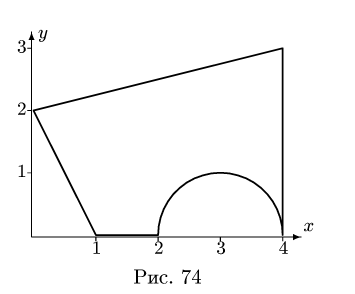 

Решение

1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.

Центр тяжести прямоугольника находится в его геометрическом центре, положение центра тяжести других фигур, встречающихся в задачах, изображено на рис. 75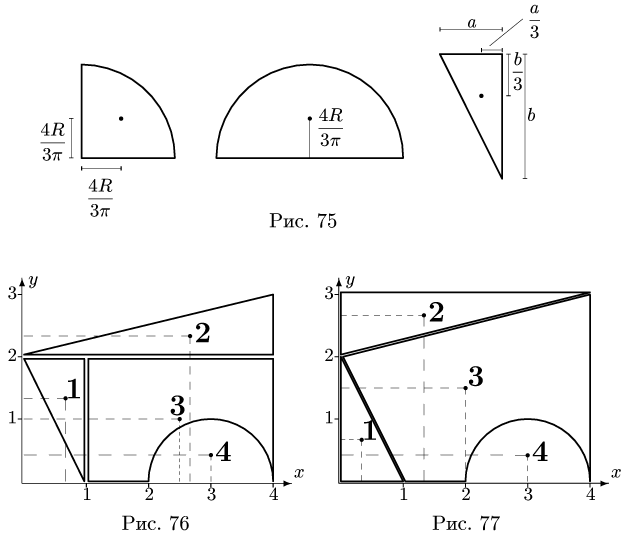

Представляем фигуру в виде двух треугольников 1,2, прямоугольника 3 и выреза 4 в виде полукруга (рис. 76).

2. Вычисляем площадь (в 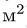) и координаты центра тяжести (в м) каждого элемента: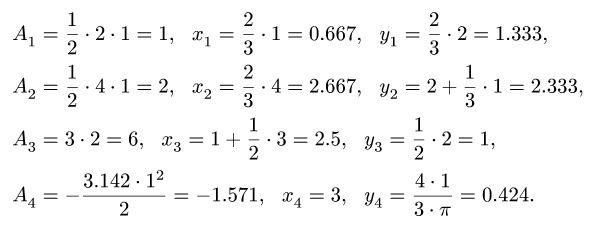

Площадь выреза берем со знаком минус.

3.Площадь фигуры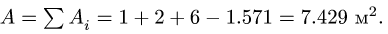

4. Находим координаты центра тяжести всей фигуры:

Вычисления удобно свести в таблицу: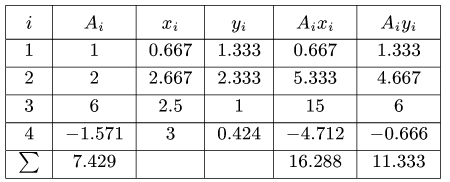

Сначала заполняем столбцы 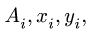затем вычисляем статические моменты 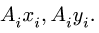Внизу записываем суммы столбцов, необходимые для вычисления координат центра тяжести. Таким образом

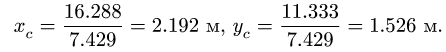
Замечание 1. Большинство задач на определение центра тяжести допускает несколько способов разбиения фигуры. Это можно использовать для проверки решения. Второй вариант разбиения фигуры в данном примере состоит из прямоугольника 3 с размерами 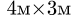и вырезанных из него полукруга 4 и двух треугольников 1 и 2 (рис. 77).

Замечание 2. Решение задачи в системе Maple V методом контурного интегрирования.

• Заказать решение задач по теоретической механике

Пространственная стержневая система

Постановка Задачи. Найти координаты центра тяжести пространственной фигуры, состоящей из N однородных стержней.

План решения:

1. Разбиваем фигуру на отдельные стержни.

2. Выбираем систему координат. Вычисляем длины и координаты 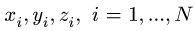 центров тяжести отдельных стержней. Координаты центра прямолинейного однородного стержня вычисляем как полусумму координат его концов.

3. Находим суммарную длину стержней системы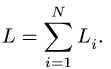

4. Определяем координаты центра тяжести тела по формулам

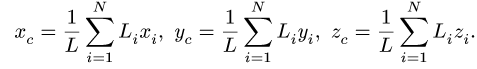
Задача №3

Найти координаты центра тяжести пространственной фигуры, состоящей из шести однородных стержней (рис. 78). Даны размеры: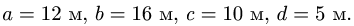

Решение

1. Разбиваем фигуру на шесть стержней.

2. Выбираем систему координат (рис. 78). Вычисляем длины и координаты 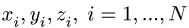центров тяжести отдельных стержней.

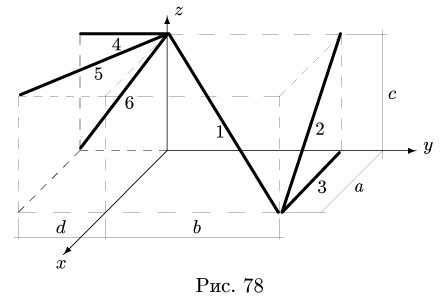
3. Находим суммарную длину стержней системы:

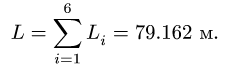
Промежуточные результаты удобно занести в таблицу:

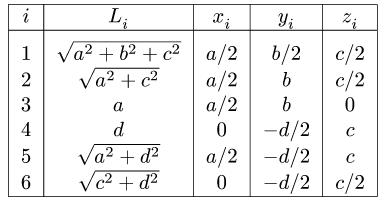
4. Определяем координаты центра тяжести тела по формулам

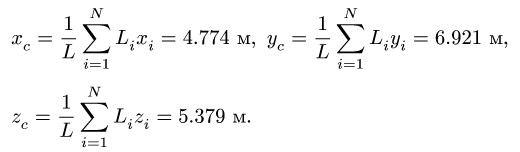
Постановка задачи. Найти координаты центра тяжести однородного объемного тела.

План решения:

1. Разбиваем тело на простые части, положение центров тяжести которых известно.

2. Выбираем систему координат. Вычисляем объемы 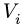и координаты 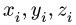центров тяжести отдельных частей. Объемы вырезанных частей берем со знаком минус.

3. Находим общий объем тела по формуле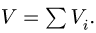

4. Определяем координаты центра тяжести тела:

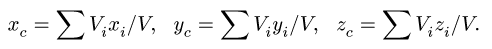
Задача №4

Найти координаты центра тяжести однородного объемного тела (рис.79);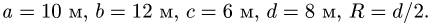

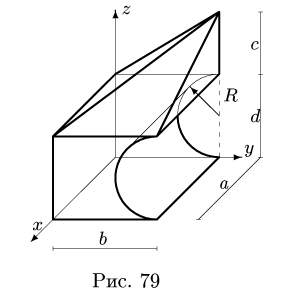
Решение

1. Разбиваем тело на пирамиду 1, параллелепипед 2 и половину цилиндра 3 (рис. 80).

2. Выбираем систему координат. Вычисляем объемы 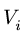и координаты 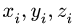центров тяжестей отдельных частей. Центр тяжести пирамиды 1 лежит в точке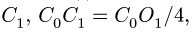

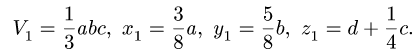
Центр тяжести параллелепипеда 2 совпадает с его геометрическим центром:

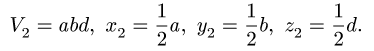
Объем половины цилиндра 3 берем со знаком минус:

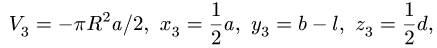
где 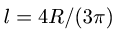— расстояние по оси у от оси цилиндра до его центра тяжести .

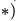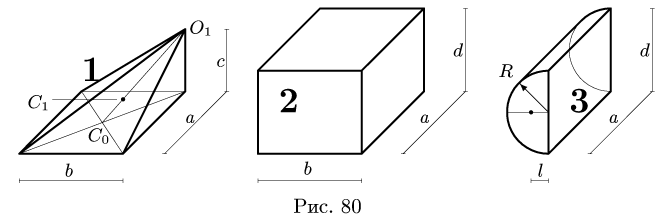
3. Находим общий объем тела: 

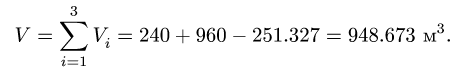
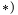В общем случае объем тела, лежащего в области 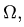можно найти, вычисляя тройной интеграл по области 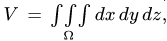а координаты центра тяжести, например, 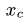однородного тела можно определить по формуле 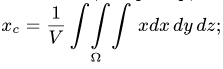см.

4. Определяем координаты центра тяжести тела:

Центр тяжести

Центр тяжести — точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил. Поэтому формулы для определения положения центра тяжести различных тел имеют вид:

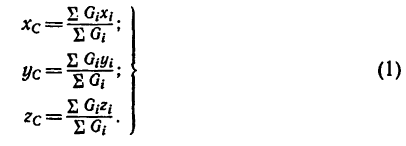
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес 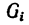каждого отрезка 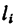можно представить в виде произведения

где d — постоянный для всей фигуры вес единицы длины материала.
После подстановки в формулы (1) вместо 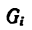их значений 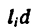постоянный множитель d в каждом слагаемом числителя и знаменателя можно вынести за скобки (за знак суммы) и сократить. Таким образом, формулы для определения координат центра тяжести фигуры, составленной из отрезков линий, примут вид:

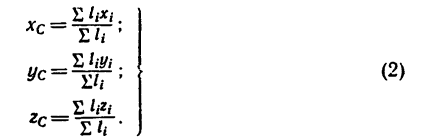
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174),

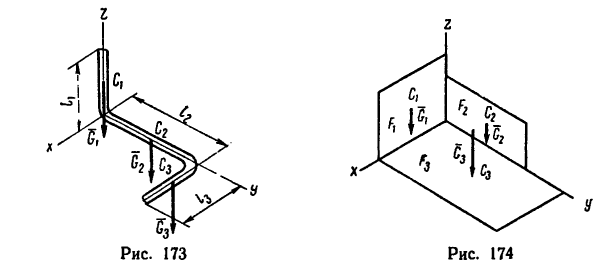
то вес каждой плоскости (поверхности) можно представить так:

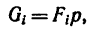
где 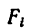— площади каждой поверхности, ар — вес единицы площади фигуры.

После подстановки этого значения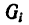 в формулы (1) получаем формулы координат центра тяжести фигуры, составленной из площадей:

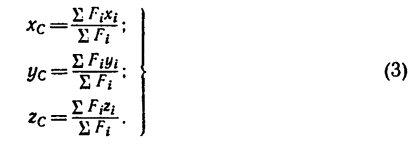
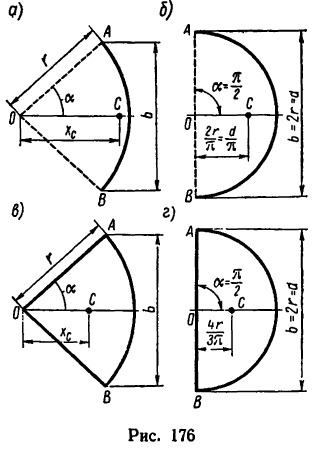
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части

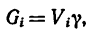
где 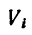— объем каждой части, а у — вес единицы объема тела.

После подстановки значений 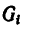в формулы (I) получаем формулы для определения координат центра тяжести тела, составленного из однородных объемов;

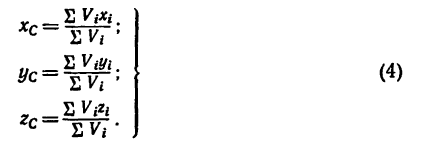
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.

Если известен радиус дуги г и центральный угол 2а, стягиваемый дугой и выраженный в радианах, то положение центра тяжести С (рис. 176, а) относительно центра дуги О определится формулой

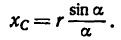
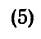
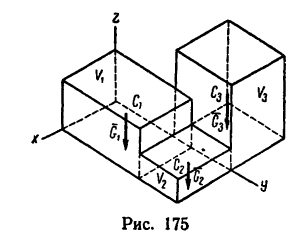
Если же задана хорда 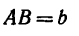дуги, то в формуле (5) можно произвести замену

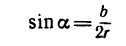
и тогда

В частном случае для полуокружности обе формулы примут вид (рис. 176, б)

Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы

Если же задана хорда сектора, то

В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)

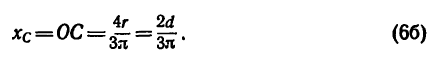
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.

У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).

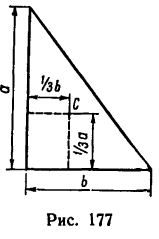
При решении задач на определение положения центра тяжести любого однородного тела, й составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:

1. выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;
2. разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;
3. определить или длины, или площади, или объемы составных частей;
4. выбрать расположение осей координат;
5. определить координаты центров тяжести составных частей;
6. найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
7. по найденным координатам указать на рисунке положение центра тяжести тела.