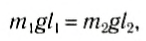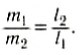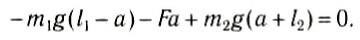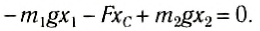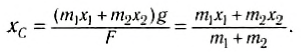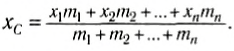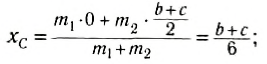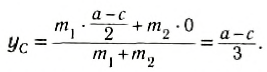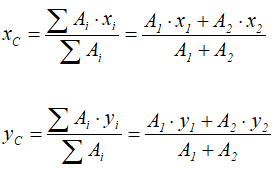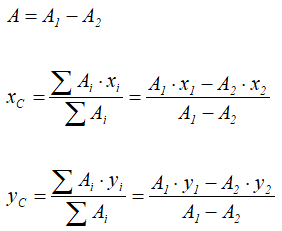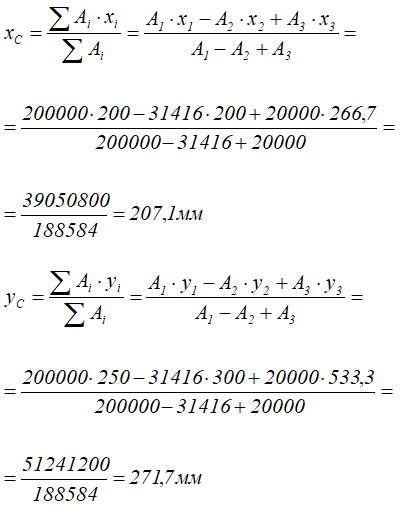Как найти центр масс плоской фигуры

Содержание:

1. Центр масс
2. Центр параллельных сил
3. Центр тяжести
4. Центры тяжести некоторых плоских однородных фигур
5. Центр тяжести дуги окружности
6. Центр тяжести кругового сектора
7. Центр тяжести кругового сегмента
8. Центр тяжести треугольника
9. Центр тяжести трапеции
10. Примеры решения задач на тему: Центр масс
11. Способы определения координат центра тяжести тела
12. Метод симметрии
13. Метод разбиения
14. Метод дополнения
15. Экспериментальные способы
16. Центры тяжести некоторых однородных тел
17. Центр тяжести дуги окружности
18. Центр тяжести треугольника
19. Центр тяжести сектора

Центр масс – это геометрическая точка, положение которой определяется распределением массы в теле, а перемещение характеризует движение тела или механической системы как целого.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Центр масс

Центр масс – это некоторое положение, определяемое относительно объекта или системы объектов и это среднее положение всех частей системы, взвешенное в соответствии с их массами.

Центр параллельных сил

Если на тело действует система параллельных сил , ,…, , то точка , через которую проходит равнодействующая этой системы сил, называется центром параллельных сил (рис.9.1).

Координаты центра параллельных сил определяются по зависимостям:

где  – координаты точек приложения сил .

Центр параллельных сил имеет ту особенность, что через него обязательно будет проходить линия действия равнодействующей при вращении линий действия всех сил системы вокруг точек их приложения на один и тот же угол в одну и ту же сторону. Модули сил при вращении не должны меняться.

Центр тяжести

Если твердое тело находится возле поверхности Земли, то на каждую материальную часть этого тела действует сила тяжести­ , которая направлена к центру Земли. Поскольку размеры тела небольшие по сравнению с размерами Земли, то образованную систему сил можно рассматривать как параллельную. Равнодействующая этой параллельной системе сил , которая равна их сумме, называется тяжестью тела, а центр этой системы – точка называется центром тяжести тела (рис.9.2).

Координаты центра тяжести твердого тела можно определить как координаты центра параллельных сил:

где  – сила тяжести элементарной частицы тела;

 – тяжесть тела;

 – координаты центра тяжести;

 – координаты элементарной частицы тела.

Если тело однородное, то есть удельный вес не меняется по объему , то:

где  – объем тела;

 – объем элементарной частицы.

Тогда формулы для определения координат центра тяжести твердого тела приобретут вид:

Положение центра тяжести однородного тела зависит только от формы объема, что занимает тело, и называется центром тяжести этого объема.

Если однородное тело имеет форму тонкой пластины, то его можно рассматривать как материальную плоскую фигуру. В этом случае положение центра тяжести плоской фигуры определяется двумя координатами  и и зависит от формы площади фигуры:

где  – площадь элементарной части плоской фигуры;

 – площадь плоской фигуры.

Центр тяжести однородной пластины называется центром тяжести плоской фигуры.

Если выбранный элементарный объем  (площадь элементарной площадки в плоском случае) направить к нулю, то формулы для вычисления координат центра тяжести приобретут интегральный вид:

а) для однородного твердого тела:

где  – объем тела, интегрирование выполняется по всему объему тела;

б) для однородной поверхности:

где  – площадь поверхности, интегрирование выполняется по всей поверхности тела;

в) для однородной плоской фигуры, лежащей в плоскости xy:

г) для однородной линии:

где  – длина линии, интегрирование выполняется по всей длине линии.

Центры тяжести некоторых плоских однородных фигур

Для упрощения определения центра тяжести используются следующие вспомогательные правилами:

1. Если тело имеет плоскость симметрии, то центр тяжести лежит на этой плоскости.
2. Если тело симметрично относительно оси, то центр тяжести лежит на этой оси.
3. Если тело симметрично относительно точки, то центр тяжести лежит в центре симметрии.
4. Если тело состоит из нескольких частей, центры тяжести которых можно определить, то центр тяжести такого тела находят как центр тяжести нескольких материальных точек, а именно тех, в которых расположены весы каждой отдельной части тела.

Центр тяжести дуги окружности

Центр тяжести дуги окружности  (рис.9.3) лежит на ее оси симметрии и на расстоянии от центра окружности:

где  – радиус окружности;

 – половина центрального угла, опирающегося на дугу .

Центр тяжести кругового сектора

Центр тяжести кругового сектора лежит на оси симметрии и имеет координаты:

где  – радиус окружности;

 – половина центрального угла сектора.

Центр тяжести кругового сегмента

Центр тяжести кругового сегмента лежит на оси симметрии сегмента и имеет координаты:

где  – радиус окружности;

 – половина центрального угла сегмента.

Центр тяжести треугольника

Центр тяжести треугольника (рис. 9.6) лежит в точке пересечения его медиан – на расстоянии 1/3 каждой медианы от соответствующего основания треугольника.

Центр тяжести трапеции

Центр тяжести трапеции (рис.9.7) с основаниями  и  и высотой лежит на прямой , которая соединяет середины основ.

Расстояния  и центра тяжести площади трапеции от ее основ определяются по формулам:

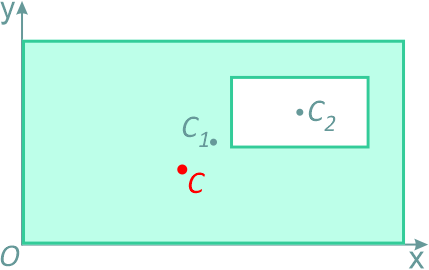
Наиболее распространенный способ определения положения центра тяжести однородного тела сложной формы заключается в том, что его разбивают на такие части, положение центров тяжести которых известно, или может быть легко определено.

Например, однородную плоскую фигуру (рис.9.8) разбивают на три части 1,2 и 3, положения центров тяжести которых, можно определить.

Координаты центра тяжести фигуры определяются по формулам:

где  – координаты центра тяжести первой части плоской фигуры;

 – площадь первой части и т.п.

Этим способом удобно пользоваться и при определении положения центра тяжести плоской фигуры, из которой вырезана некоторая часть (рис.9.9).

В этом случае площадь плоской фигуры можно записать в виде разницы площадей сплошной фигуры 1 (площадь положительная) и вырезанной части 2 (площадь отрицательная), то есть .

Координаты центра тяжести фигуры равны:

где  – координаты центра тяжести сплошной фигуры 1, площадь которой равна ;

 – координаты центра тяжести вырезанной части 2, площадь которой равна – .

Первый из этих методов имеет название “метод разбиения”, второй – “метод дополнения”, или “метод отрицательных масс”. В общем случае формулы для определения центра тяжести плоской фигуры имеют вид:

где  – площадь всей фигуры.

Примеры решения задач на тему: Центр масс

Задача № 1

Найти центр тяжести двутаврового профиля, размеры которого в сантиметрах указаны на рис.9.10.

Решение. Поскольку форма сечения имеет ось симметрии, ось направим вдоль оси симметрии, а ось перпендикулярно ей.

В силу симметричности профиля относительно оси центр тяжести будет лежать на этой оси, то есть

Линиями и поделим профиль на три прямоугольника 1, 2 и 3.

Запишем уравнение для определения абсциссы центра тяжести площади:

где  – абсциссы центров тяжести прямоугольников 1, 2, 3;

 – площади этих прямоугольников.

Поскольку центры тяжести прямоугольников и лежат на пересечении их диагоналей, то (рис.9.10):

Площади этих прямоугольников соответственно равны:

Тогда: 

Таким образом, центр тяжести фигуры лежит в точке с координатами: 

Ответ: 

Задача № 2

Найти координаты центра тяжести поперечного пересечения разностороннего угольника (рис.9.11), полки которого имеют ширину  и толщину

Решение. Разделим пересечение линией на два прямоугольника и , центры тяжести которых лежат на пересечении соответствующих диагоналей.

Запишем формулы для координат  и  центра тяжести пересечения:

где  и  – координаты центров тяжести прямоугольников 1 и 2;

,  – площади прямоугольников 1 и 2.

С рис.9.11 видим, что

Тогда: 

Ответ: 

Задача № 3

Определить положение центра тяжести плоской фигуры (рис.9.12), ограниченной полуокружностью  радиуса и двумя прямыми равной длины и , причем

Решение. Данная площадь имеет ось симметрии, вдоль которой направим ось . Поскольку центр тяжести площади лежит на оси симметрии, то

Разделим площадь линией на две части: полуокружность и равнобедренный треугольник .

Абсцисса центра тяжести площади будет равняться:

где  – координата центра тяжести половины круга ;

 – координата центра тяжести треугольника ;

,  – площади половины круга и треугольника.

Для определения воспользуемся приведенными в разделе 9.3.2 координатами центра тяжести кругового сектора

В случае половины круга 

Площадь половины круга равна:

Центр тяжести треугольника лежит на пересечении его медиан (раздел 9.3.4). Поскольку треугольник равнобедрен, то линия  будет его медианой и расстояние будет равняться третьей части от :

Площадь треугольника равна:

Подставив найденные значения , ,  и  в уравнение для , получим:

Ответ: 

Задача № 4

Найти координаты центра тяжести квадратной пластины с вырезом в виде сегмента радиуса (рис.9.13), если

Решение. Осью симметрии рассматриваемой фигуры будет диагональ прямоугольника

Поэтому направим ось вдоль этой линии, а ось – перпендикулярно (рис.9.13).

Центр тяжести пластины будет лежать на оси , то есть

Площадь фигуры можно представить как разницу площадей квадрата (положительная площадь) и сектора (отрицательная площадь).

Абсцисса центра тяжести фигуры будет равняться:

где  – абсцисса центра тяжести квадрата ;

 – абсцисса центра тяжести сектора ;

 и  – площади квадрата и сектора.

Для квадрата получим:

Как следует из рис. 9.13, равняется

где  – расстояние от точки к центру тяжести кругового сектора .

Для кругового сектора (раздел 9.3.2) получим:

Поскольку  и , то 

Таким образом, абсцисса равняется:

Площадь кругового сектора :

Подставив значение , ,  и  в формулу для , получим:

Ответ:  

Задача № 5

Найти координаты центра тяжести площади, ограниченной (рис.9.14) правой веткой параболы , осью  и прямой

Решение. На расстоянии  от оси выделяем элементарную площадку шириной (заштрихованная область).

Площадь выделенной элементарной площадки будет равняться:

Площадь фигуры, что ограничена заданными линиями:

Поскольку точка представляет собой пересечение параболы и прямой , то 

Отсюда: 

Тогда:

Абсцисса центра тяжести

Для определения координаты выделим элементарную площадку шириной на расстоянии  от оси .

Площадь выделенной площадки:

Ордината центра тяжести:

Тогда: 

Ответ: 

Способы определения координат центра тяжести тела

Существует несколько способов определения координат центра тяжести тел. среди них различают: метод симметрии, метод разбиения и дополнения, экспериментальные способы.

Рассмотрим последовательно эти способы.

Метод симметрии

Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, или на оси симметрии, или в центре симметрии.

Таким образом, центр тяжести однородных симметричных тел, таких как кольца,
прямоугольные пластины, прямоугольные параллелепипеды, шары и другие тела, которые
имеют центр симметрии, расположенный в геометрических центрах (центры симметрии) этих тел.

Метод разбиения

Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести нетрудно определяется, то координаты центра тяжести всего тела можно определить непосредственно по формулам выше. Причем количество слагаемых в числителе каждого из указанных выражений будет равно количеству частей, на которое разбивается тело.

Приведем пример определения центра тяжести тела методом разбиения его на отдельные тела, центры тяжести которых известны.

Пример:

Определить координаты центра тяжести однородной пластины. Размеры в
мм заданные на рис. 1.64

Решение.

Выберем оси координат x и y. Разбиваем пластину на отдельные прямоугольные части. Для каждого прямоугольника проводим диагонали, точки пересечения которых c₁, c₂ и c₃ соответствуют центрам веса каждого прямоугольника. В принятой системе координат нетрудно получить значение координат этих точек. А именно: c₁ (–1,1), c₂ (1,5), c₃ (5,9). Площади каждого тела соответственно равны: I — s₁ = 4 см²; II — s₂ = 20 см²; III — s₃ = 12 см². Площадь всей пластины равна: S = s₁ + s₂ + s₃ = 36 см².

Для определения координат центра тяжести заданной пластины используем выражение выше. Подставив значения всех известных величин в уравнения, получим

По вычисленным значениям координат центра тяжести пластины можно обозначить точку C на рисунке. Как видим, центр тяжести (геометрическая точка) пластины расположен за ее пределами.

Метод дополнения

Способ, о котором говорится далее, является некоторым случаем способа разбиения. Он может применяться к телам, которые имеют вырезы, полости, причем без учета выреза, или вырезанной части тела положение центра тяжести тела известно. Рассмотрим пример применения такого метода.

Пример. Определить положение центра тяжести круглой пластины радиусом R, имеет круговое отверстие радиуса r (рис. 1.65). Расстояние C₁C₂ = a.

Решение.

Как видно из рисунка, центр тяжести пластины находится на оси симметрии пластины x, то есть на прямой, проходящей через точки C₁ и C₂. Таким образом, для определения положения центра тяжести этой пластины необходимо вычислить только одну координату x_C, поскольку вторая координата y_C равна нулю. Покажем оси координат x, y. Примем, что пластина состоит из двух тел — с полного круга (без учета выреза) и тела,
образовано вырезом. В принятой системе координаты x для указанных тел будут равны: x₁ = 0; x₂ = C₁C₂ = a. Площади тел равны: Общая площадь всего тела будет равна физической разницы между площадями первого и второго тел, а именно
Для определения неизвестной координаты центра тяжести
заданной пластины используем первое уравнение выражения.

Подставив значения всех известных величин в это уравнение, получим

Таким образом, значение координаты x_C отрицательное, а потому, поскольку вторая координата 0 y_C = 0, то центр тяжести пластины C размещен на оси x слева от точки C₁.

Экспериментальные способы

Эти способы нашли широкое применение при отыскании положения центра тяжести тел сложных форм и конфигураций, для которых другие способы почти непригодны вследствие громоздкости и сложности. К таким телам, в первую очередь, следует отнести комбайны, тракторы, сложные сельскохозяйственные машины и орудия. При применении экспериментальных способов отыскания положения
центра тяжести наиболее широко используют метод подвешивания и метод взвешивания тел.

При применении метода подвешивания тело на тросе подвешивают за различные его точки. Направление троса, будет давать каждый раз направление силы веса тела. Тогда точка пересечения этих направлений и дает положение центра тяжести тела.

Использование второго метода — взвешивание требует измерения веса всего тела, а также отдельных его частей. Рассмотрим пример применения этого метода.

Пример.

Определим продольную координату центра тяжести трактора, у которого продольная база составляет l (рис. 1.66).

Решение.

Сначала поставим на платформу весов задние колеса трактора, как это показано на рисунке. Итак, определяем силу давления задних колес на платформу, или реакцию . Аналогично определяем вес переднего моста, или реакцию . Вполне понятно, что сумма этих реакций равна общему весу трактора, а именно:

Q = R_A + R_B.

Теперь составим алгебраическую сумму моментов всех сил относительно точки A. Она равна

Откуда определяем продольную координату центра тяжести:

x_C = .

Для определения поперечной координаты центра тяжести трактора необходимо знать реакции левых колес (переднего и заднего) и правых, а также поперечную базу трактора. Дальше аналогичным выражением определяется эти координаты центра тяжести.

Центры тяжести некоторых однородных тел

Определим далее координаты центров тяжести некоторых простых однородных тел.

Центр тяжести дуги окружности

Рассмотрим дугу AB окружности радиусом R, в которой центральный угол OAB равен 2α (радиан) (рис. 1.67). Покажем оси координат x, y начало которых разместим в точке O. Вследствие того, что дуга имеет ось симметрии Ox, то центр ее тяжести будет расположен именно на этой оси (y_C = 0). Остается только вычислить координату x_C.

Используем для вычисления этой координаты первое уравнение выражения, а именно

Определим составляющие, которые необходимо подставить в это уравнение. Для этого выделим на дуге AB элемент M M₁ длиной dl, равной:

dl = R · dφ.

Если φ — угол, определяющий положение элемента M M₁ на дуге AB, то координата x элемента M M₁ будет равна:

x = Rcosφ.

Общая длина дуги AB равна:

L = 2α · R.

Подставим эти значения в первое уравнение выражения. При этом считается, что интеграл в числителе данного выражения должен быть определенным по всей длине дуги. Будем иметь:

Таким образом, координата x_C будет равняться

x_C = .

Центр тяжести треугольника

Есть произвольный треугольник, вершины которого в принятой системе координат Oxy соответствуют точкам с координатами A₁ (x₁, y₁), A₂ (x₂, y₂), A₃ (x₃, y₃) (рис. 1.68). Если провести прямые, которые будут параллельны основе A₁A₃ и провести их достаточное количество, то вся площадь треугольника будет состоять из полос бесконечно малой ширины, центры тяжести которых будут размещены посередине каждой полосы, а потому и центр тяжести треугольника будет расположенный на его медиане. А если провести линии, параллельные другой стороне треугольника, то и в этом случае центр тяжести будет размещен на соответствующей медиане. Таким образом, совершенно очевидно, что центр тяжести треугольника C будет расположен в точке пересечения его медиан.

Определим координаты этой точки. По курсу аналитической геометрии известно, что точка пересечения медиан треугольника в принятой системе координат определяется такими зависимостями

где x₁, x₂, …, y₃  — координаты вершин треугольника.

Полезно также знать, что

Центр тяжести сектора

Рассмотрим круговой сектор OAB радиуса R, центральный угол которого равен 2α (радиан) (рис. 1.69). Центр тяжести сектора, вполне очевидно, лежит на оси его симметрии, то есть на биссектрисе угла AOB. Эту биссектрису примем за ось x и найдем на этой оси положение центра C. Разобьем площадь сектора на бесконечно большое число элементарных секторов с центральными углами ∆φ.

Будем рассматривать каждый сектор как треугольник с основанием R · ∆φ и высотой R. Центр тяжести каждого треугольника расположен на расстоянии  от центра сектора. Таким образом, центры тяжести всех треугольников расположены на дуге A´B´. Итак, если 0 ∆φ → 0, то центры тяжести образуют дугу AB, тогда необходимо найти центр тяжести дуги A´B´. Используем формулу, по которой определяется центр тяжести дуги окружности радиусом r:

Тогда учитывая, что

Будем иметь

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Момент силы
4. Пара сил
5. Произвольная система сил
6. Плоская произвольная система сил
7. Трение
8. Расчет ферм
9. Расчет усилий в стержнях фермы
10. Пространственная система сил
11. Произвольная пространственная система сил
12. Плоская система сходящихся сил
13. Пространственная система сходящихся сил
14. Равновесие тела под действием пространственной системы сил
15. Естественный способ задания движения точки
16. Центр параллельных сил
17. Параллельные силы
18. Система произвольно расположенных сил
19. Сосредоточенные силы и распределенные нагрузки
20. Кинематика
21. Кинематика твердого тела
22. Движения твердого тела
23. Динамика материальной точки
24. Динамика механической системы
25. Динамика плоского движения твердого тела
26. Динамика относительного движения материальной точки
27. Динамика твердого тела
28. Кинематика простейших движений твердого тела
29. Общее уравнение динамики
30. Работа и мощность силы
31. Обратная задача динамики
32. Поступательное и вращательное движение твердого тела
33. Плоскопараллельное (плоское) движение твёрдого тела
34. Сферическое движение твёрдого тела
35. Движение свободного твердого тела
36. Сложное движение твердого тела
37. Сложное движение точки
38. Плоское движение тела
39. Статика твердого тела
40. Равновесие составной конструкции
41. Равновесие с учетом сил трения
42. Колебания материальной точки
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июля 2022 года; проверки требуют 3 правки.

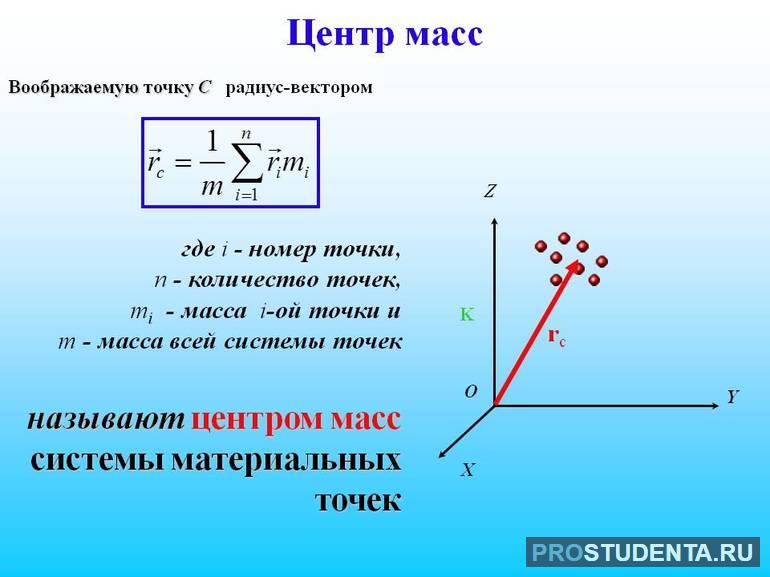
Центр масс (тж. центр ине́рции) — геометрическая точка, положение которой определяется распределением массы в теле, а перемещение характеризует движение тела или механической системы как целого^[1]. Радиус-вектор данной точки задаётся формулой

где — зависящая от координат плотность, а интегрирование осуществляется по объёму тела. Центр масс может оказаться как внутри, так и вне тела.

Использование понятия центра масс, а также системы координат, связанной с центром масс, удобно во многих приложениях механики и упрощает расчёты. Если на механическую систему не действуют внешние силы, то её центр масс движется с постоянной по величине и направлению скоростью.

Джованни Чева применял рассмотрение центров масс к решению геометрических задач, в результате были сформулированы теоремы Менелая и теоремы Чевы^[2].

В случае систем материальных точек и тел в однородном гравитационном поле центр масс совпадает с центром тяжести, хотя в общем случае это разные понятия.

Центр масс в классической механике[править | править код]

Определение[править | править код]

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом^[3]:

где  — радиус-вектор центра масс,  — радиус-вектор i-й точки системы,  — масса i-й точки.

Для случая непрерывного распределения масс:

где  — суммарная масса системы,  — объём,  — плотность.
Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.

Если система состоит не из материальных точек, а из протяжённых тел с массами , то радиус-вектор центра масс такой системы связан с радиус-векторами центров масс тел соотношением^[4]:

Действительно, пусть даны несколько систем материальных точек с массами Радиус-вектор -ной системы:

При переходе к протяженным телам с непрерывным распределением плотности в формулах будут интегралы вместо сумм, что даст тот же результат.

Иначе говоря, в случае протяжённых тел справедлива формула, по своей структуре совпадающая с той, что используется для материальных точек.

Примеры[править | править код]

Центры масс плоских однородных фигур

• У отрезка — середина.
• У многоугольников :
  • У параллелограмма — точка пересечения диагоналей.
  • У треугольника — точка пересечения медиан (центроид).
• У правильного многоугольника — центр поворотной симметрии.
• У полукруга — точка, делящая перпендикулярный радиус в отношении от центра круга.

Координаты центра масс однородной плоской фигуры можно вычислить по формулам (следствие из теорем Паппа — Гульдина):

и , где — объём тела, полученного вращением фигуры вокруг соответствующей оси, — площадь фигуры.

Центры масс периметров однородных фигур

• Центр масс сторон треугольника находится в центре вписанной окружности дополнительного треугольника (треугольника с вершинами, расположенными в серединах сторон данного треугольника). Эту точку называют центром Шпикера. Это означает то, что если стороны треугольника сделать из тонкой проволоки одинакового сечения, то центр масс (барицентр) полученной системы будет совпадать с центром вписанной окружности дополнительного треугольника или с центром Шпикера.

Использование[править | править код]

Понятие центра масс широко используется в физике, в частности, в механике.

Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс и вращательного движения тела вокруг его центра масс. Центр масс при этом движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами (материальная точка). Последнее означает, в частности, что для описания этого движения применимы все законы Ньютона. Во многих случаях можно вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс.

Часто бывает удобно рассматривать движение замкнутой системы в системе отсчёта, связанной с центром масс. Такая система отсчёта называется системой центра масс (Ц-система), или системой центра инерции. В ней полный импульс замкнутой системы всегда остаётся равным нулю, что позволяет упростить уравнения её движения.

Центр масс в релятивистской механике[править | править код]

В случае высоких скоростей (порядка скорости света) (например, в физике элементарных частиц) для описания динамики системы применяется аппарат СТО. В релятивистской механике (СТО) понятия центра масс и системы центра масс также являются важнейшими понятиями, однако, определение понятия меняется:

где  — радиус-вектор центра масс,  — радиус-вектор i-й частицы системы,  — полная энергия i-й частицы.

Данное определение относится только к системам невзаимодействующих частиц. В случае взаимодействующих частиц в определении должны в явном виде учитываться импульс и энергия поля, создаваемого частицами^[5].

Во избежание ошибок следует понимать, что в СТО центр масс характеризуется не распределением массы, а распределением энергии. В курсе теоретической физики Ландау и Лифшица предпочтение отдается термину «центр инерции». В западной литературе по элементарным частицам применяется термин «центр масс» (англ. center-of-mass): оба термина эквивалентны.

Скорость центра масс в релятивистской механике можно найти по формуле:

Смежные понятия[править | править код]

Центр масс vs. барицентр[править | править код]

Термин «центр масс» синонимичен одному из значений понятия барицентр (от др.-греч. βαρύς — тяжёлый + κέντρον — центр), однако последнее применяется преимущественно в задачах астрофизики и небесной механики. Под барицентром подразумевается общий для нескольких небесных тел центр масс, вокруг которого эти тела движутся. Примером может выступить совместное движение планеты и звезды (см. рис.) или компонент двойных звёзд. Центр масс (барицентр) в таком случае находится на отрезке длины , соединяющем тела массами и , на удалении от тела .

Другое значение слова барицентр относится, скорее, к геометрии, нежели к физике; в этом значении выражение для координаты барицентра отличается от формулы для центра масс отсутствием плотности (как если бы всегда было const).

Центр масс vs. центр тяжести[править | править код]

Центр масс тела не следует путать с центром тяжести.

Центром тяжести механической системы называется точка, относительно которой суммарный момент сил тяжести (действующих на систему) равен нулю. Например, в системе, состоящей из двух одинаковых масс, соединённых несгибаемым стержнем, и помещённой в неоднородное гравитационное поле (например, планеты), центр масс будет находиться в середине стержня, в то время как центр тяжести системы будет смещён к тому концу стержня, который находится ближе к планете (ибо вес P = m·g зависит от параметра гравитационного поля g), и, вообще говоря, даже расположен вне стержня.

В однородном гравитационном поле центр тяжести всегда совпадает с центром масс. В некосмических задачах гравитационное поле обычно может считаться постоянным в пределах объёма тела, поэтому на практике эти два центра почти совпадают.

По этой же причине понятия центр масс и центр тяжести совпадают при использовании этих терминов в геометрии, статике и тому подобных областях, где применение его по сравнению с физикой можно назвать метафорическим и где неявно предполагается ситуация их эквивалентности (поскольку реального гравитационного поля нет, то и учёт его неоднородности не имеет смысла). В этих применениях традиционно оба термина синонимичны, и нередко второй предпочитается просто в силу того, что он более старый.

См. также[править | править код]

• Классическая механика
• Теоретическая механика
• Теорема о движении центра масс системы
• Неваляшка
• Барицентр
• Центроид треугольника

Примечания[править | править код]

Литература[править | править код]

• Бобылёв Д. К. Центр, в физике // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• Журавлёв В. Ф.  Основы теоретической механики. 2-е изд. — М.: Физматлит, 2001. — 320 с. — ISBN 5-94052-041-3..

Центр тяжести (центр масс):

Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.

Центр тяжести – геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.

На каждую точку тела в поле сил тяжести действует сила, а на все тело – равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.

Центр масс (центр инерции) – точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе  внешние силы.

При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.

Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.

При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, – параллельными.

Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.

 Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.

Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.

Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.

Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.

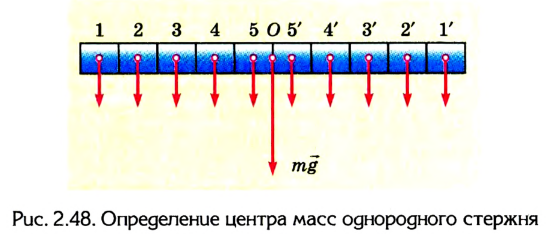
1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О – середине стержня.

Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.

Центр тяжести однородного стержня расположен в середине стержня.

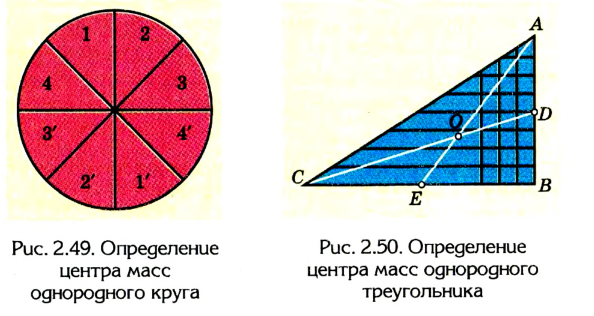
2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).

Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.

Центр тяжести однородного круга совпадает с его центром.

Центр тяжести однородного треугольника находится в точке пересечения его медиан.

3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.

Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.

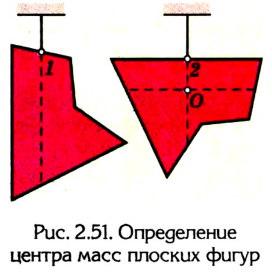
4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).

Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.

Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.

Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.

• Заказать решение задач по физике

Центр тяжести тела и центр масс тела

Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.

Рис. 151

Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.

Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m₁ и m₂, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:

или

Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:

Рис. 152

Поскольку F=(m₁ + m₂)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.

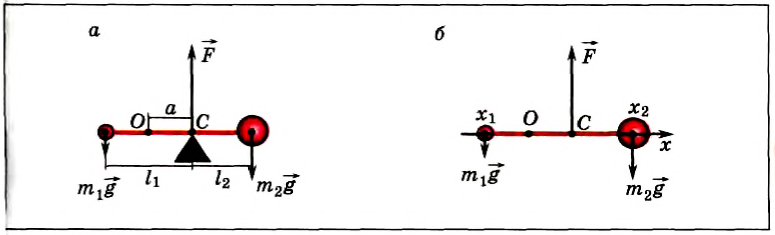
Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х₁, х_с и х₂. Запишем условие моментов относительно точки О:

Отсюда

При выводе этой формулы было использовано значение силы F = (m₁ + m₂) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии х_с, определенном формулой (2).

Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.

Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.

Если произвольное тело можно разбить на n элементов, массы которых m₁, m₂…,    m_n, и если известны координаты центров масс этих элементов x₁, x₂…,   x_n относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:

Естественно, что такие же соотношения можно записать и для у_с и z_c. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m₁ = 2m₂). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C₁) и линейки (C₂).

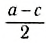
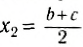
Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х₁ = 0, y₁ =, а координаты центра масс линейки: , y₂ = 0 .
По формуле (3):    .

Таким образом, центр масс угольника находится вне тела.

Главные выводы:

1. Центр тяжести — точка, в которой приложена сила тяжести.
2. Центр масс симметричных однородных тел находится в их геометрическом центре.
3. Координаты центра масс тела можно вычислить по формуле (3).

Определение координат центра тяжести x_C и y_C плоских фигур нестандартной формы выполняется при решении задач для последующих расчетов остальных геометрических характеристик, например, таких как радиусы и осевые моменты инерции поперечных сечений.

Рассмотрим способы и пример определения координат положения центра тяжести фигуры нестандартной формы.

Способы определения координат центра тяжести

Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.

Существует 5 способов расчета координат положения центра тяжести:

1. Аналитический (путем интегрирования).
2. Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
3. Экспериментальный. (метод подвешивания тела).
   Этот способ подходит в основном для плоских и линейных тел.
4. Разбиение. Тело или фигура разбивается на конечное число частей (простых тел или фигур), для каждой из которых положение центра тяжести C и площадь A известны.

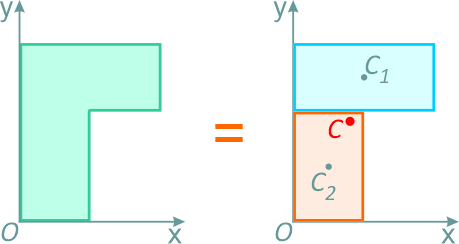
   Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями A₁ и A₂ (A = A₁+ A₂).
   

   Рисунок 1.8

   Центры тяжести этих фигур находятся в точках C₁(x₁, y₁) и C₂(x₂, y₂). Тогда координаты центра тяжести тела равны:
   

5. Дополнение (Метод отрицательных площадей или объемов).
   Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.

   Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
   

   Рисунок 1.9

   Тогда координаты центра тяжести фигуры с отверстием можно определить по формулам:
   

При решении задач по определению координат центра тяжести плоских фигур и объемных тел применяются последние два способа (разбиение и дополнение).

Пример определения координат центра тяжести сложной фигуры в нашем коротком видео:

Другие видео

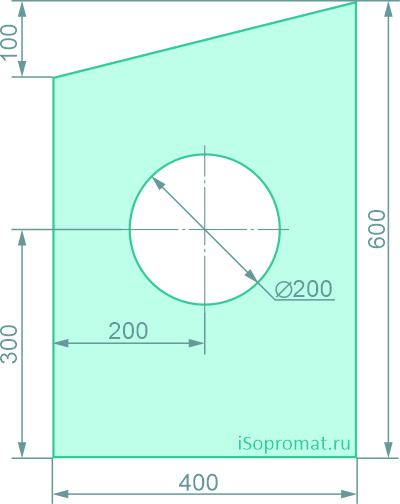
Пример определения координат центра тяжести плоской фигуры

Задача
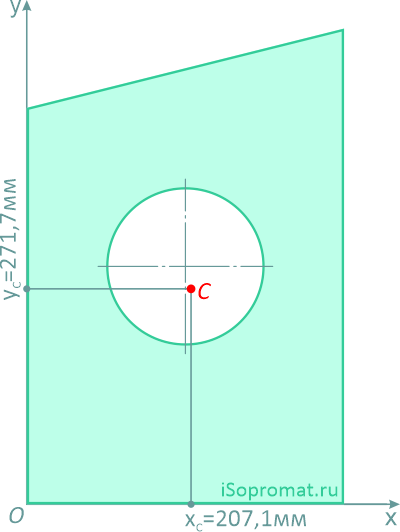
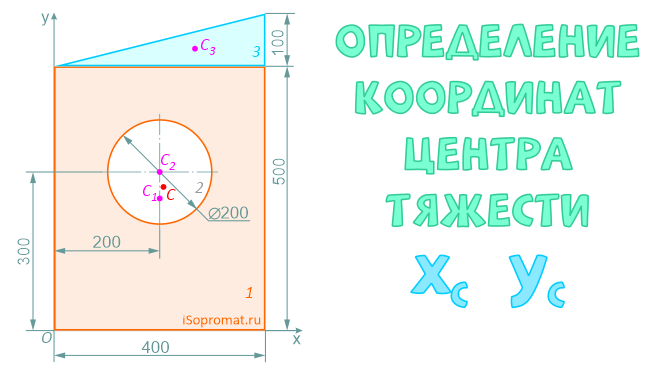
Определить координаты центра тяжести плоской фигуры с круглым отверстием

Решение
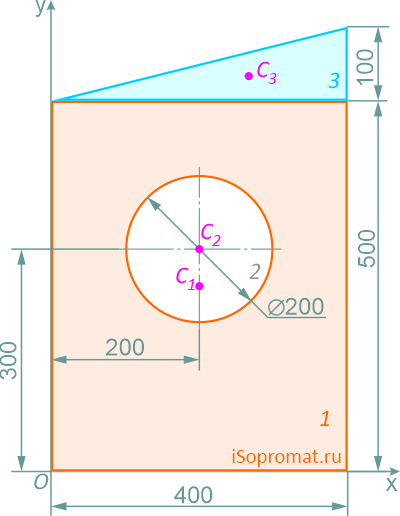
Разделим заданное сечение на простые фигуры – прямоугольник, круг и прямоугольный треугольник.
Через нижнюю левую точку фигуры проведем координатные оси x и y.

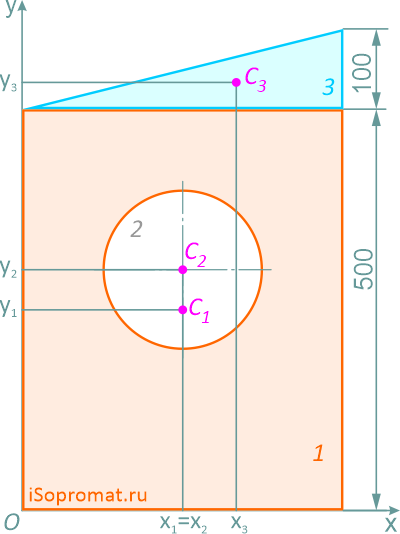
Рассчитаем необходимые для решения задачи площади A и координаты x,y центров тяжести C_i отдельных фигур:

Прямоугольник (фигура 1)
Площадь
A₁=400×500=200000 мм²
Положение центра тяжести
x₁=200мм
y₁=250мм

Круг (2) (вычитаемая фигура)
Площадь
A₂=π×200²/4=31416 мм²
Центр тяжести
x₂=200мм
y₂=300мм

Прямоугольный треугольник (3)
Площадь
A₃=400*100/2=20000 мм²
Положение центра тяжести треугольника находится на пересечении его медиан (на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин)
x₃=400×2/3=266,7мм
y₃=500+100×1/3=533,3мм

Координаты x и y центра тяжести C всей плоской фигуры определим по формулам:

Ответ: Таким образом, центр тяжести заданной фигуры находится в точке C с координатами x_C=207,1мм, y_C=271,7мм.

Другие примеры решения задач >
Центры тяжести простейших фигур >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Точку, в которой происходит равное распределение величины, определяющей инерционные и гравитационные свойства, называют центром масс. Формула для определения параметра зависит от радиус-вектора частиц системы и их полной энергии. Эту характеристику тела отличают от тяжести, при этом в трудах советских учёных Ландау, Лифшица для неё используется термин «центр инерции».

Оглавление:

• Общие сведения
• Связь с центром тяжести
• Вычисление положения
• Геометрический способ определения

Общие сведения

Допустим, имеется тело, на которое действуют скомпенсированные силы. В этом случае оно будет в состоянии покоя или прямолинейного равномерного движения. Пусть тело будет неподвижным. Например, лодка на воде. К ней можно приложить воздействие F1 в районе её кормы. Под действием силы она начнёт разворачиваться. Аналогично если воздействовать на её нос F2, то она тоже будет поворачиваться, но при этом разворот будет происходить в другую сторону.

Получается, что можно подобрать такую линию, на которой действие сил приведёт её к ускоренно поступательному движению. Пусть это будет F3. На самом деле таких сил может быть несколько. При этом их можно перемещать вдоль линии их воздействия. Если все такие силы изобразить в виде линий, то они пересекутся в одной точке. Такое место и называют центром масс тела (ЦМ). То есть точку, в которой пересекаются линии действия сил, вызывающие только ускоренное поступательное механическое движение.

Эта важная точка в теле и движется она довольно просто. Перемещение любого тела можно представить, как комбинацию двух видов движения:

• центра масс;
• вращения.

Существует теорема: ЦМ тела движется так, как перемещалась бы материальная точка, в которой сосредоточена вся масса и к которой приложены все воздействия, действующие на объект. Таким образом, различные виды изменения положения точек в пространстве можно описать с помощью законов Ньютона. Согласно же теореме их можно применять и к телу, если считать, что все силы приложены к центру масс.

Рассматривая объект, можно не учитывать его размер, форму, а брать во внимание только инерцию, ускорение и принцип парного взаимодействия. Фактически в механике перемещение сколь угодно сложного вида рассматривается по принципу суперпозиции и закона сохранении энергии. При этом довольно удобно изучать изменение положения в системе отсчёта связанной с этим центром. В ней полный импульс всегда будет равным нулю, что позволяет упростить уравнение движения.

Связь с центром тяжести

Пусть имеется объект, находящийся на Земле. Говорят, что на него действует сила тяжести. Но на самом деле она воздействует не на вещество, а на каждый его атом, частичку. Если предположить, что ускорение свободного падения буде одинаковым, то на объект действует очень множество сил тяжести. Рассматривать такую систему неудобно. Поэтому все воздействия заменяют равнодействующей. И считают, что действует одна сила, которая приложена к центру тяжести твёрдого тела.

Для того чтобы найти взаимосвязь между тяжестью и массой нужно представить, что объект вдруг распался на отдельные равные кусочки. Они держатся вместе, но не прикреплены друг к другу. Если тело отпустить, то они будут падать вместе, так как ускорение свободного падения не зависит от массы. При этом движение будет поступательным. Значит, сила, приложенная к телу в целом, будет приложена к центру масс.

Получается, что центральная точка является общей как для тяжести, так и для масс. Это две точки положение которых совпадает несмотря на разный их принцип определения в физике. Но существуют условия, когда это правило не выполняется. Например, если система материальных точек неоднородна по объёму плотности в гравитационном поле, то центры не совпадут.

Для примера можно привести список однородных фигур с указанием их центральной точки:

• отрезок — середина;
• параллелограмм — место пересечения диагоналей;
• треугольник — точка пересечения медиан (центроид);
• любой правильный многоугольник — центр поворотной симметрии;
• полукруг — точка, в которой перпендикулярный радиус делится в отношении 4:3p считая от центра круга.

Чтобы найти координату центра масс объекта, который можно представить, как совокупность связанных материальных точек используют два метода: аналитический и геометрический. Но второй способ не всегда можно применить. В однородном гравитационном поле центры тяжести и масс всегда совпадают. И это часто подтверждается на практике, из-за того, что внешнее гравитационное поле в задачах, связанных с действиями на Земле, считают постоянным в пределах объёма тела.

Поэтому эти термины объединяют в геометрии, статике и так далее. То есть в тех областях, где применение определения можно назвать метафорическим и предполагается ситуация их эквивалентности.

При таком понимании оба термина синонимичны, но при этом чаще предпочитают использовать термин, связанный с тяжестью. Это происходит в силу того, что исторически он появился раньше.

Вычисление положения

Пусть тело представляет собой совокупность материальных точек, лежащих на одной прямой при этом их массы разные. Задача состоит в нахождении его центра. Для этого следует вести систему координат с осью икс, которая будет совпадать с линией расположения точек. При этом тело пусть подвешено на невесомой опоре и находится под действием Земного тяготения. Это условие даёт возможность воспользоваться тем фактом, что положения центров масс и тяжести совпадают.

На каждую из материальных точек действует своя сила: m1g, m2g… mng. Если предоставить это тело самому себе, то оно будет в состоянии свободного падения. Остановить тело — подпереть, но при этом так, чтобы оно находилось в равновесии. Это значит, что сила реакции опоры должна проходить через центр тяжести, так как равнодействующая тоже её пересекает.

Получится, что сила реакции опоры будет лежать на одной прямой с силой тяжести действующей на тело в совокупности и их моменты тоже будут проходить через неё. С помощью координатной оси точкам можно присвоить положение, x1, x2… xn, а ЦМ xц. Чтобы тело находилось в равновесии необходимо выполнение двух условий:

• векторная сумма всех сил должна быть равной нулю: m1g + m2g +…+mng + F = 0;
• сумма моментов равняться нулю: Mm 1 g + Mm 2 g +…+ Mmng + MF = 0.

Из первого условия можно найти силу реакции опоры: F = (m1 + m2 +…+mn) * g. Если вращение выбрать против часовой стрелки, тогда относительно оси все моменты силы тяжести будут отрицательными, а опоры — положительные. Тогда справедливо записать: F * хц = (m1 x 1 + m2 x 2 +…+mn xn) * g.

Из последнего равенства можно выразить координату ЦМ: xц = ((m1 x 1 + m2 x 2 +…+mn xn) * g) / F. В эту формулу можно подставить выражение для F. В результате ускорение свободного падения сократится и получится: xц = (m1 x 1 + m2 x 2 +…+mn xn) / (m1 + m2 +…+mn). Это формула выглядит громоздко, но запомнить её легко. В числителе стоят произведения масс материальных точек на их координаты, а в знаменателе — вес всего тела.

Если точки не будут лежать на одной прямой, то координата ЦМ тоже не изменится. То есть приведённая формула справедлива для любого положения тела относительно координаты y.

При этом её можно применять и для рассмотрения предметов в пространстве, так как все направления в существующем мире равноправные.

Геометрический способ определения

Для простейших симметричных фигур ЦМ можно определить геометрическим методом. Для этого используются свойства диагоналей и медиан. Пусть имеется произвольной формы четырёхугольник. Изготовлен он из однородного материала.

Идея вычисления состоит в том, что эту фигуру необходимо разбить на два треугольника. Для этого нужно провести диагональ, которая разделит фигуру на два тела. Затем провести в каждом треугольном теле три медианы. Точка их пересечения и будет ЦМ. В результате вместо четырёхугольника можно рассматривать две материальные точки.

Несмотря на то что масса у них разная ЦМ будет находиться на соединяющем их отрезке. Теперь четырёхугольник можно разбить на два других треугольника и выполнить аналогичные действия уже для них. Получится два отрезка, на которых одновременно расположен ЦМ. Значит, его положение будет определяться точкой их пересечения.

Для более сложной фигуры, например, шести или восьмиугольника можно использовать такой же подход. Сначала нужно разделить тело на прямоугольники, а затем треугольники. Найти ЦМ для полученных фигур и определить точку пересечения. Следует понимать, что ЦМ может находиться и за пределами объекта.

Но в реальных ситуациях бывают фигуры, которые имеют неправильную форму. Для них нельзя применить расчёт или геометрический метод. Поэтому выясняют, где расположен ЦМ экспериментальным путём.

Например, пусть имеется тело сложной неправильной формы. Чтобы найти ЦМ необходимо фигуру подвесить в пространстве. На неё действует две силы: тяжести и реакции оси. Первая заставляет фигуру поворачиваться с определённой скоростью до тех пор, пока момент силы тяжести относительно оси крепления не станет равным нулю. То есть точка опоры, ось и центр тяжести окажутся на одной вертикале.

Чтобы узнать, где же находится ЦМ, тело нужно подвесить, используя другую точку. При этом на самой фигуре следует отметить, как проходит вертикаль.

Повторяя такой опыт минимум три раза, можно увидеть точку пересечения осей, которая и будет искомым ЦМ. Причём чем будет больше экспериментов, тем точнее он будет определён.