Прямоугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:

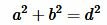 . . |
(1) |
Из равенства (1) найдем d:
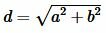 . . |
(2) |
Пример 1. Стороны прямоугольника равны  . Найти диагональ прямоугольника.
. Найти диагональ прямоугольника.
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя  в (2), получим:
в (2), получим:

Ответ: 
Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
| ( small R=frac<large d> <large 2>) | (3) |
Подставляя (3) в (2), получим:
| ( small R=frac<large sqrt> <large 2>) | (4) |
Пример 2. Стороны прямоугольника равны  . Найти радиус окружности, описанной вокруг прямоугольника.
. Найти радиус окружности, описанной вокруг прямоугольника.
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя  в (4), получим:
в (4), получим:


Ответ: 
Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
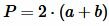 |
(5) |
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны  . Найти периметр прямоугольника.
. Найти периметр прямоугольника.
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя  в (5), получим:
в (5), получим:

Ответ: 
Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
 |
(6) |
 |
(7) |
Из формулы (7) найдем ( small b ) и подставим в (6):
 |
(8) |
 |
(9) |
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
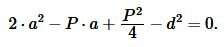 |
(10) |
Вычислим дискриминант квадратного уравнения (10):
Сторона прямоугольника вычисляется из следующих формул:
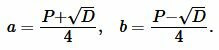 |
(12) |
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
( frac< P><2>>d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*).
Пример 4. Диагональ прямоугольника равна  , а периметр равен
, а периметр равен  . Найти стороны прямоугольника.
. Найти стороны прямоугольника.
Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим  ,
,  в (11):
в (11):

Подставляя значения  и
и  в первую формулу (12), получим:
в первую формулу (12), получим:

Найдем другую сторону ( small b ) из формулы (8). Подставляя значения  и
и  в формулу, получим:
в формулу, получим:

Ответ:  ,
, 
Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.
Описанная окружность
Окружность описанная около многоугольника – это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник – это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема
Около любого треугольника можно описать окружность.
Доказательство
Дано: произвольный  АВС.
АВС.
Доказать: около  АВС можно описать окружность.
АВС можно описать окружность.
Доказательство:
1. Проведем серединные перпендикуляры к сторонам  АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).
АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин  АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около
АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около  АВС. Теорема доказана.
АВС. Теорема доказана.
Замечание 1
Около треугольника можно описать только одну окружность.
Доказательство
Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.
Замечание 2
Около четырехугольника не всегда можно описать окружность.
Доказательство
Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно “поместить” в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя “поместить” ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:
В любом вписанном четырехугольнике сумма противоположных углов равна 180 0 .
Доказательство
Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D – вписанные, тогда по теореме о вписанном угле:  В =
В = 
 АDС,
АDС,  D =
D = 
 АВС, откуда следует
АВС, откуда следует  В +
В +  D =
D = 
 АDС +
АDС + 
 АВС =
АВС =  (
( АDС +
АDС +  АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е.
АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е.  АDС +
АDС +  АВС = 360 0 , тогда
АВС = 360 0 , тогда  В +
В +  D =
D = 
 360 0 = 180 0 . Что и требовалось доказать.
360 0 = 180 0 . Что и требовалось доказать.
Верно и обратное утверждение:
Если сумма противоположных углов четырехугольника равна 180 0 , то около него можно описать окружность.
Доказательство
Дано: четырехугольник АВСD,  BАD +
BАD +  BСD = 180 0 .
BСD = 180 0 .
Доказать: около АВСD можно описать окружность.
Доказательство:
Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), – и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.
Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

 ВСD – внешний угол
ВСD – внешний угол  СFD, следовательно,
СFD, следовательно,  BСD =
BСD =  ВFD +
ВFD +  FDE. (1)
FDE. (1)
Углы ВFD и FDE – вписанные. По теореме о вписанном угле  ВFD =
ВFD = 
 ВАD и
ВАD и  FDE =
FDE = 
 ЕF, тогда, подставляя данные равенства в (1), получим:
ЕF, тогда, подставляя данные равенства в (1), получим:  BСD =
BСD = 
 ВАD +
ВАD + 
 ЕF =
ЕF =  (
( ВАD +
ВАD +  ЕF), следовательно,
ЕF), следовательно,  ВСD
ВСD

 ВАD.
ВАD.
 BАD – вписанный, тогда по теореме о вписанном угле
BАD – вписанный, тогда по теореме о вписанном угле  BАD =
BАD = 
 ВЕD, тогда
ВЕD, тогда  BАD +
BАD +  BСD
BСD
 (
( ВЕD +
ВЕD +  ВАD).
ВАD).
Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е.  ВЕD +
ВЕD +  ВАD = 360 0 , тогда
ВАD = 360 0 , тогда  BАD +
BАD +  BСD
BСD

 360 0 = 180 0 .
360 0 = 180 0 .
Итак, мы получили, что  BАD +
BАD +  BСD
BСD 180 0 . Но это противоречит условию
180 0 . Но это противоречит условию  BАD +
BАD +  BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.
BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.
Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в  ВСF:
ВСF:  С +
С +  В +
В +  F = 180 0 , откуда
F = 180 0 , откуда  С = 180 0 – (
С = 180 0 – (  В +
В +  F). (2)
F). (2)
 В – вписанный, тогда по теореме о вписанном угле
В – вписанный, тогда по теореме о вписанном угле  В =
В = 
 ЕF. (3)
ЕF. (3)
 F и
F и  ВFD – смежные, поэтому
ВFD – смежные, поэтому  F +
F +  ВFD = 180 0 , откуда
ВFD = 180 0 , откуда  F = 180 0 –
F = 180 0 –  ВFD = 180 0 –
ВFD = 180 0 – 
 ВАD. (4)
ВАD. (4)
Подставим (3) и (4) в (2), получим:
 С = 180 0 – (
С = 180 0 – (
 ЕF + 180 0 –
ЕF + 180 0 – 
 ВАD) = 180 0 –
ВАD) = 180 0 – 
 ЕF – 180 0 +
ЕF – 180 0 + 
 ВАD =
ВАD =  (
( ВАD –
ВАD –  ЕF), следовательно,
ЕF), следовательно,  С
С

 ВАD.
ВАD.
 А – вписанный, тогда по теореме о вписанном угле
А – вписанный, тогда по теореме о вписанном угле  А =
А = 
 ВЕD, тогда
ВЕD, тогда  А +
А +  С
С
 (
( ВЕD +
ВЕD +  ВАD). Но это противоречит условию
ВАD). Но это противоречит условию  А +
А +  С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.
С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.
Примечание:
Окружность всегда можно описать:
Поделись с друзьями в социальных сетях:
Как найти центр окружности описанной около прямоугольника
Найдите абсциссу центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно
Это задание ещё не решено, приводим решение прототипа.
Найдите абсциссу центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).
Диагональ прямоугольника образует два прямоугольных треугольника. Диагональ равна диаметру окружности, описанной около треугольника, следовательно, центр окружности лежит на середине диагонали прямоугольника. Тогда можно легко найти координаты центра окружности.
[spoiler title=”источники:”]
http://budu5.com/manual/chapter/3523
http://math-ege.sdamgia.ru/problem?id=59643
[/spoiler]
Окружность вписана в n-угольник, если она касается всех сторон этого n-угольника (рис. 8.106).
Окружность описана около n-угольника, если все вершины n-угольника лежат на окружности (рис. 8.107).

Свойства вписанной окружности
1. Окружность можно вписать в любой треугольник.
2. Окружность можно вписать в четырехугольник, если суммы длин его противолежащих сторон равны.
Например, на рисунке 8.106  .
.
Так, окружность можно вписать в квадрат и в ромб, но нельзя вписать в параллелограмм и в прямоугольник.
Свойства описанной окружности
1. Окружность можно описать около любого треугольника.
2. Окружность можно описать около четырехугольника, если суммы его противолежащих углов равны.
Например, на рисунке 8.107  .
.
Так, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.
Расположение центров окружностей, описанных около треугольника:
1) центр окружности расположен на пересечении серединных перпендикуляров к сторонам треугольника;
2) если треугольник остроугольный, то центр окружности расположен в этом треугольнике:
а) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают (рис. 8.108);
б) в равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию (рис. 8.109);
3) если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы (рис. 8.110);
4) если треугольник тупоугольный, то центр окружности расположен вне треугольника (рис. 8.111).

Расположение центров окружностей, вписанных в треугольник:
1) центр окружности, вписанной в треугольник, расположен в этом треугольнике (рис. 8.112 – 8.115);
2) центром окружности является точка пересечения биссектрис треугольника;
3) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника.

Формулы для вычисления радиусов вписанной и описанной окружностей
Радиус окружности, описанной около многоугольника, как правило, обозначают  , а радиус окружности, вписанной в многоугольник, обозначают
, а радиус окружности, вписанной в многоугольник, обозначают  :
:
1) для равностороннего треугольника со стороной  :
:
 , (8.34)
, (8.34)
 ; (8.35)
; (8.35)
2) для произвольного треугольника со сторонами  и площадью
и площадью  :
:
 , (8.36)
, (8.36)
 ; (8.37)
; (8.37)
3) для прямоугольного треугольника с катетами  и гипотенузой
и гипотенузой  :
:
 , (8.38)
, (8.38)
 ; (8.39)
; (8.39)
4) для квадрата со стороной  и диагональю
и диагональю  :
:
 , (8.40)
, (8.40)
 ; (8.41)
; (8.41)
5) для прямоугольника с диагональю  :
:
 ; (8.42)
; (8.42)
6) для ромба с высотой  :
:
 ; (8.43)
; (8.43)
7) для трапеции с высотой  , при условии, что в трапецию можно вписать окружность:
, при условии, что в трапецию можно вписать окружность:
 . (8.44)
. (8.44)
Если около трапеции можно описать окружность, то, проведя диагональ трапеции и рассмотрев один из полученных треугольников со сторонами  и площадью
и площадью  , по формуле
, по формуле  найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);
найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);
8) для правильного шестиугольника со стороной  :
:
 , (8.45)
, (8.45)
 . (8.46)
. (8.46)
Правильный шестиугольник состоит из шести правильных треугольников (рис. 8.117) и точка  является центром вписанной в него и описанной около него окружностей.
является центром вписанной в него и описанной около него окружностей.

Пример 1. Найдите сторону квадрата, если известно, что разность между площадью квадрата и площадью вписанного в него круга равна  .
.
Решение. Так как площадь круга радиуса  находят по формуле 8.32, а площадь квадрата со стороной
находят по формуле 8.32, а площадь квадрата со стороной  находят по формуле
находят по формуле  , то согласно условию задачи запишем:
, то согласно условию задачи запишем:  ,
,  .
.
А так как  , то
, то  ,
,  ,
,  ,
,  ,
,  .
.
Ответ:  .
.
Пример 2. Площадь прямоугольника равна 4, а разность длин его смежных сторон рана 3. Найдите радиус окружности, описанной около этого прямоугольника.

Решение. Площадь прямоугольника со смежными сторонами  и
и  находят по формуле
находят по формуле  .
.
Пусть  , тогда
, тогда  (рис. 8.118).
(рис. 8.118).
Получим:  ,
,  , откуда
, откуда  , следовательно,
, следовательно,  ,
,  .
.
По теореме Пифагора найдем диагональ прямоугольника:  ,
,  . Согласно формуле 8.42
. Согласно формуле 8.42  .
.
Ответ:  .
.
Пример 3. Найдите радиус окружности, вписанной в ромб, если его диагонали равны 6 и 8.

Решение. По теореме Пифагора найдем сторону ромба (рис. 8.119):
 ,
,  ,
,  .
.
По формуле 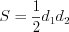 найдем площадь ромба:
найдем площадь ромба:  .
.
Но площадь ромба можно найти и по формуле  , а так как
, а так как  , то
, то  . Тогда
. Тогда  , а
, а  .
.
Ответ: 2,4.
Пример 4. Найдите длину окружности, вписанной в правильный треугольник, если его площадь равна  .
.
Решение. Площадь правильного треугольника со стороной  находят по формуле:
находят по формуле: 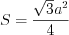 .
.
Зная площадь треугольника, найдем его сторону:  ,
,  ,
,  .
.
По формуле 8.35 найдем радиус окружности, вписанной в этот треугольник:  .
.
По формуле 8.30 найдем длину окружности:  .
.
Ответ:  .
.
Пример 5. Радиус окружности, описанной около равнобедренного прямоугольного треугольника равен 2. Найдите радиус окружности, вписанной в этот треугольник.
Решение. Радиус окружности, описанной около прямоугольного треугольника с гипотенузой  находят по формуле 8.38. Тогда
находят по формуле 8.38. Тогда  .
.
Так как треугольник равнобедренный, то его катеты  и
и  раны и по теореме Пифагора
раны и по теореме Пифагора  , откуда
, откуда  ,
,  .
.
Радиус окружности, вписанной в прямоугольный треугольник, находят по формуле 8.39. В нашем случае  ,
,  .
.
Ответ:  .
.
Пример 6. Один из катетов прямоугольного треугольника равен 8, а радиус окружности, вписанной в треугольник равен 3. Найдите площадь треугольника.

Решение. Рассмотрим прямоугольный треугольник  . Точка
. Точка  является центром вписанной в треугольник окружности (рис. 8.120).
является центром вписанной в треугольник окружности (рис. 8.120).
Так как радиусы вписанной в треугольник окружности перпендикулярны сторонам треугольника в точках касания, то имеем квадрат  со стороной 3. Если катет
со стороной 3. Если катет  , а сторона квадрата
, а сторона квадрата  , то
, то  .
.
Пусть отрезок  . По свойству касательных
. По свойству касательных  и
и  .
.
Тогда по теореме Пифагора  или
или  , откуда
, откуда  ,
,  .
.
Найдем катет  :
:  .
.
Найдем площадь треугольника:  ,
,  .
.
Ответ: 60.
Пример 7. Окружность, центр которой расположен на большей стороне треугольника, делит эту сторону на отрезки 4 и 8 и касается двух других его сторон, длина одной из которых равна 6. Найдите радиус окружности, вписанной в этот треугольник (рис.8.121).
Решение. Согласно свойству биссектрисы треугольника запишем:  , откуда
, откуда  .
.
Радиус окружности, вписанной в треугольник, найдем по формуле 8.37.
В свою очередь по формуле Герона  найдем площадь треугольника. Так как
найдем площадь треугольника. Так как  , то
, то  .
.
Тогда  .
.
Ответ:  .
.
Пример 8. В прямоугольную трапецию вписана окружность радиуса 3, которая в точке касания делит ее боковую сторону на отрезки 4 и 5. Найдите площадь трапеции.
Решение. Согласно условию задачи и рисунку 8.122, запишем:  ,
,  .
.
По свойству четырехугольника, описанного около окружности, получим:  ,
,  ,
,  .
.
Согласно формуле 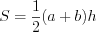 найдем площадь трапеции:
найдем площадь трапеции:  .
.
Ответ: 45.
Пример 9. Длины оснований равнобедренной трапеции относятся как  , а длина ее высоты равна 17. Вычислите площадь круга, описанного около трапеции, если известно, что средняя линия трапеции равна ее высоте.
, а длина ее высоты равна 17. Вычислите площадь круга, описанного около трапеции, если известно, что средняя линия трапеции равна ее высоте.
Решение. Рассмотрим равнобедренную трапецию  (рис. 8.123) и проведем диагональ трапеции
(рис. 8.123) и проведем диагональ трапеции 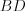 .
.
Радиус окружности, описанной около треугольника  , найдем по формуле 8.36:
, найдем по формуле 8.36:
 ,
,  .
.
Зная, что  и вводя коэффициент пропорциональности
и вводя коэффициент пропорциональности  , получим
, получим  ,
,  .
.
Так как длина средней линии трапеции равна высоте трапеции, то  , откуда
, откуда  . Тогда
. Тогда  ,
,  .
.
Поскольку четырехугольник  является прямоугольником, то
является прямоугольником, то  , тогда
, тогда  .
.
Согласно теореме Пифагора запишем:
 ,
,  ;
;
 ,
,  .
.
По формуле 8.36 найдем радиус окружности, описанной около треугольника  , а, следовательно, и около трапеции
, а, следовательно, и около трапеции  :
:
 .
.
Согласно формуле 8.32 найдем площадь круга:  .
.
Ответ:  .
.
Пример 10. В правильный шестиугольник вписана окружность и около него описана окружность. Найдите площадь образовавшегося кольца, если сторона шестиугольника равна  .
.
Решение. По формуле 8.45 найдем радиус окружности, описанной около правильного шестиугольника:  .
.
По формуле 8.46 найдем радиус окружности, вписанной в этот шестиугольник. Так как  , то
, то  .
.
Площадь круга находят по формуле 8.32. Тогда  , а
, а  .
.
Найдем площадь кольца:  ,
,  .
.
Ответ:  .
.
1. В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.
2. Не во всякий четырехугольник можно вписать окружность. Например, окружность можно вписать в ромб и квадрат, но нельзя вписать в параллелограмм и прямоугольник.
3. Не около всякого четырехугольника можно описать окружность. Например, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.
4. Не во всякую трапецию можно писать окружность и не около всякой трапеции можно описать окружность. Описать окружность можно только около равнобедренной трапеции.
5. Если многоугольник правильный (все его стороны и все его углы равны между собой), то в него всегда можно вписать окружность и около него всегда можно описать окружность. Причем, центры этих окружностей совпадают.
Длину окружности радиуса  находят по формуле:
находят по формуле:
 . (8.30)
. (8.30)
Площадь круга радиуса  находят по формуле:
находят по формуле:
 . (8.32)
. (8.32)
Описанная окружность — подробнее
Определение
Описанная окружность – такая окружность, что проходит через все три вершины треугольника, около которого она описана.
Свойства и центр описанной кружности
И вот, представь себе, имеет место удивительный факт:
Вокруг всякого треугольника можно описать окружность.
Почему этот факт удивительный?
Потому что треугольники ведь бывают разные!
И для всякого найдётся окружность, которая пройдёт через все три вершины, то есть описанная окружность.
Доказательство этого удивительного факта мы приведем чуть позже, а здесь заметим только, что если взять, к примеру, четырехугольник, то уже вовсе не для всякого найдётся окружность, проходящая через четыре вершины.
Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!
А есть только для прямоугольника:
Подробнее об этом смотри в статье о вписанных четырехугольниках!
Ну вот, а треугольник всякий и всегда имеет собственную описанную окружность! И даже всегда довольно просто найти центр этой окружности.
Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника.
Знаешь ли ты, что такое серединный перпендикуляр?
Серединный перпендикуляр — это прямая, проходящая через середину отрезка и перпендикулярная ему.
Прямая ( displaystyle a) – это серединный перпендикуляр к отрезку ( displaystyle AB).
А теперь посмотрим, что получится, если мы рассмотрим целых три серединных перпендикуляра к сторонам треугольника.
Вот оказывается (и это как раз и нужно доказывать, хотя мы и не будем), что все три перпендикуляра пересекутся в одной точке. Смотри на рисунок – все три серединных перпендикуляра пересекаются в одной точке ( displaystyle O).
Это и есть центр описанной около (вокруг) треугольника ( displaystyle ABC) окружности.
Как ты думаешь, всегда ли центр описанной окружности лежит внутри треугольника? Представь себе – вовсе не всегда!
Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи!
Вот так:
А вот если остроугольный, то внутри:
Что же делать с прямоугольным треугольником?
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.
Здорово, правда?
Если треугольник – прямоугольный, то не надо строить аж три перпендикуляра, а можно просто найти середину гипотенузы – и центр описанной окружности готов!
Да ещё с дополнительным бонусом:
В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.
Раз уж заговорили о радиусе описанной окружности: чему он равен для произвольного треугольника? И есть ответ на этот вопрос: так называемая теорема синусов.
А именно:
В произвольном треугольнике:
( Large displaystyle frac{a}{sin angle A}=2R)
Ну и, конечно,
( displaystyle begin{array}{l}frac{b}{sin angle B}=2R\frac{c}{sin angle C}=2Rend{array})
Так что ты теперь всегда сможешь найти и центр , и радиус окружности, описанной вокруг треугольника.
То есть чтобы найти радиус описанной окружности, нужно знать одну (!) сторону и один (!) противолежащий ей угол.
Хорошая формула? По-моему, просто отличная!
Доказательство теоремы
Теорема. Вокруг всякого треугольника можно описать окружность, при том единственным образом.
Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.
Смотри, вот так:
Давай наберёмся мужества и докажем эту теорему.
Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.
Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).
Геометрическое место точек, обладающих свойством «( displaystyle X)» — такое множество точек, что все они обладают свойством «( displaystyle X)» и никакие другие точки этим свойством не обладают.
Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы.
А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют.
В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:
Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудалённых от концов отрезка.
Тут множество – это серединный перпендикуляр, а свойство «( displaystyle X)» — это «быть равноудаленной (точкой) от концов отрезка».
Проверим? Итак, нужно удостовериться в двух вещах:
- Всякая точка на серединном перпендикуляре находится на одинаковом расстоянии от концов отрезка
- Всякая точка, которая равноудалена от концов отрезка – находится на серединном перпендикуляре к ему
Приступим:
Проверим 1. Пусть точка ( displaystyle M) лежит на серединном перпендикуляре к отрезку ( displaystyle AB).
Соединим ( displaystyle M) с ( displaystyle A) и с ( displaystyle B).Тогда линия ( displaystyle MK) является медианой и высотой в ( displaystyle Delta AMB).
Значит, ( displaystyle Delta AMB) – равнобедренный, ( displaystyle MA=MB) – убедились, что любая точка ( displaystyle M), лежащая на серединном перпендикуляре, одинаково удалена от точек ( displaystyle A) и ( displaystyle B).
Теперь 2. Почти точно так же, но в другую сторону. Пусть точка ( displaystyle M) равноудалена от точек ( displaystyle A) и ( displaystyle B), то есть ( displaystyle MA=MB).
Возьмём ( displaystyle K) – середину ( displaystyle AB) и соединим ( displaystyle M) и ( displaystyle K). Получилась медиана ( displaystyle MK). Но ( displaystyle Delta AMB) – равнобедренный по условию ( displaystyle (MA=MB)Rightarrow MK) не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка ( displaystyle M) — точно лежит на серединном перпендикуляре.
Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.
Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».
Рассмотрим треугольник ( displaystyle ABC). Проведём два серединных перпендикуляра ( displaystyle {{a}_{1}}) и ( displaystyle {{a}_{2}}), скажем, к отрезкам ( displaystyle AB) и ( displaystyle BC). Они пересекутся в какой-то точке, которую мы назовем ( displaystyle O).
А теперь, внимание!
Точка ( displaystyle O) лежит на серединном перпендикуляре ( displaystyle {{a}_{1}}Rightarrow OA=OB);
точка ( displaystyle O) лежит на серединном перпендикуляре ( displaystyle {{a}_{2}}Rightarrow OB=OC).
И значит, ( displaystyle OA=OB=OC) и ( displaystyle OA=OC).
Отсюда следует сразу несколько вещей:
Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 6. Описанная окружность. Многоугольники
Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства.
Около каких фигур можно, а вокруг каких нельзя описать окружность.
Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.
Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.
ЕГЭ 6. Вписанная окружность
В этом видео мы узнаем, что такое вписанная окружность, где находится её центр, и другие свойства.
В какие фигуры можно, а в какие нельзя вписать окружность. Научимся решать задачи на вписанную окружность.
Прямоугольник. Формулы и свойства прямоугольника
Определение.
Прямоугольник – это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.
Стороны прямоугольника одновременно является его высотами.
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
AB||CD, BC||AD
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
AC = BD
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d2 = 2a2 + 2b2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника – квадрат).
Стороны прямоугольника
Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.
Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
a = √d2 – b2
b = √d2 – a2
2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
3. Формула стороны прямоугольника (длины и ширины прямоугольника) через периметр и другую сторону:
4. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол α:
a = d sinα
b = d cosα
5. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол β:
Диагональ прямоугольника
Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.
Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d = √a2 + b2
2. Формула диагонали прямоугольника через площадь и любую сторону:
| d = | √S2 + a4 | = | √S2 + b4 |
| a | b |
3. Формула диагонали прямоугольника через периметр и любую сторону:
| d = | √P2 – 4Pa + 8a2 | = | √P2 – 4Pb + 8b2 |
| 2 | 2 |
4. Формула диагонали прямоугольника через радиус описанной окружности:
d = 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
d = Dо
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула диагонали прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d = √2S : sin β
Периметр прямоугольника
Определение.
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a + 2b
P = 2(a + b)
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a2 | = | 2S + 2b2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a + √d2 – a2) = 2(b + √d2 – b2)
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a + √4R2 – a2) = 2(b + √4R2 – b2)
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a + √Do2 – a2) = 2(b + √Do2 – b2)
Площадь прямоугольника
Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.
Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
S = a · b
2. Формула площади прямоугольника через периметр и любую сторону:
| S = | Pa – 2a2 | = | Pb – 2b2 |
| 2 | 2 |
3. Формула площади прямоугольника через диагональ и любую сторону:
S = a√d2 – a2 = b√d2 – b2
4. Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
S = a√4R2 – a2 = b√4R2 – b2
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
S = a√Do2 – a2 = b√Do2 – b2
Окружность описанная вокруг прямоугольника
Определение.
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
2. Формула радиуса окружности описанной вокруг прямоугольника через периметр квадрата и любую сторону:
| R = | √P2 – 4Pa + 8a2 | = | √P2 – 4Pb + 8b2 |
| 4 | 4 |
3. Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:
| R = | √S2 + a4 | = | √S2 + b4 |
| 2a | 2b |
4. Формула радиуса окружности описанной вокруг прямоугольника через диагональ квадрата:
5. Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:
6. Формула радиуса окружности описанной вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула радиуса окружности описанной вокруг прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
Угол между стороной и диагональю прямоугольника
Формулы определения угла между стороной и диагональю
1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:
Угол между диагоналями прямоугольника
Формулы определения угла между диагоналями прямоугольника
1. Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:
β = 2α
2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:
Содержание:
Окружность, которая касается стороны треугольника и продолжений двух других его сторон, называется вневписанной окружностью треугольника. На рисунке 146 изображен треугольник АВС и три его вневписанные окружности с центрами 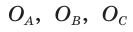
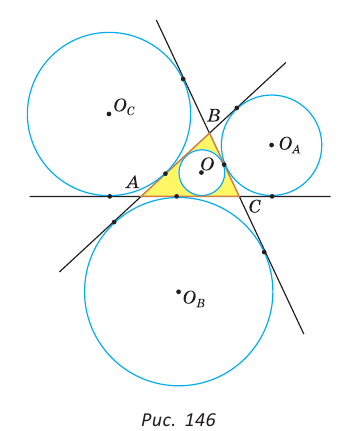
Вневписанные окружности обладают рядом интересных свойств:
1. Центры вписанной и вневписанной окружностей лежат на биссектрисе соответствующего внутреннего угла треугольника.
2. 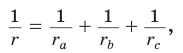 где
где 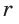 — радиус вписанной окружности треугольника,
— радиус вписанной окружности треугольника,
3. 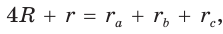 где R — радиус описанной окружности
где R — радиус описанной окружности 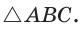
Попробуйте доказать некоторые из этих свойств.
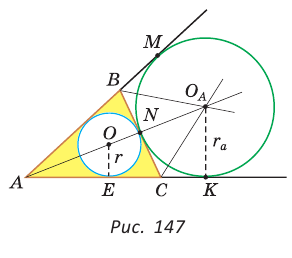
Найдем радиус 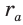 вневписанной окружности треугольника АВС со сторонами а, b и с (рис. 147). Для этого проведем радиусы
вневписанной окружности треугольника АВС со сторонами а, b и с (рис. 147). Для этого проведем радиусы  По свойству касательной
По свойству касательной 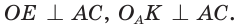 Из подобия прямоугольных треугольников АОЕ и
Из подобия прямоугольных треугольников АОЕ и 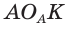 (по острому углу) следует
(по острому углу) следует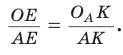 Так как
Так как 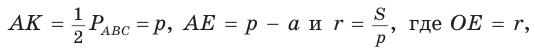 то
то 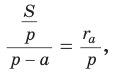 откуда
откуда 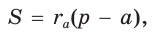
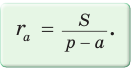
Пример:
Вычислим, используя данную формулу, радиус вневписанной окружности прямоугольного треугольника с катетами 3 и 4, которая касается гипотенузы: 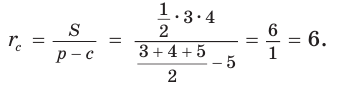
Описанная и вписанная окружности треугольника
Определение. Окружность называется описанной около треугольника, если она проходит через все его вершины.
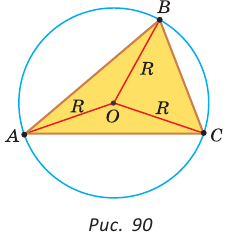
На рисунке 90 изображена окружность с радиусом R и центром  описанная около треугольни ка АВС.
описанная около треугольни ка АВС.
Так как ОА = ОВ = ОС = R, то центр описанной окружности равноудален от вершин треугольника.
Вместо слов «окружность, описанная около треугольника АВС», также говорят «окружность, описанная вокруг треугольника АВС», или «описанная окружность треугольника АВС».
Теорема (об окружности, описанной около треугольника).
Около любого треугольника можно описать окружность, причем только одну, ее центр находится в точке пересечения серединных перпендикуляров к сторонам треугольника.
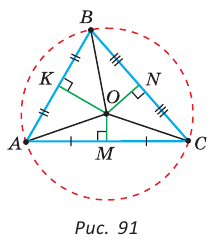
Доказательство:
Рассмотрим произвольный треугольник АВС (рис. 91). Пусть О — точка пересечения серединных перпендикуляров к его сторонам. Проведем отрезки ОА, ОВ и ОС. По свойству серединного перпендикуляра ОА = ОС, ОС = ОВ. Так как точка О равноудалена от всех вершин треугольника АВС, то окружность с центром в точке О и радиусом ОА проходит через все вершины треугольника АВС, т. е. является его описанной окружностью. Единственность описанной окружности докажите самостоятельно.
Замечание. Так как все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, то для нахождения центра описанной окружности достаточно построить точку пересечения любых двух из них.
Определение. Окружность называется вписанной в треугольник, если она касается всех его сторон.
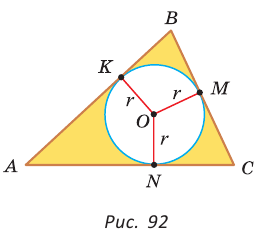
На рисунке 92 изображена окружность с центром О и радиусом  вписанная в треугольник АВС; К, М и N — точки ее касания со сторонами треугольника АВС.
вписанная в треугольник АВС; К, М и N — точки ее касания со сторонами треугольника АВС.
Так как  и по свойству касательной к окружности
и по свойству касательной к окружности 
 то центр вписанной окружности равноудален от сторон треугольника.
то центр вписанной окружности равноудален от сторон треугольника.
Вместо слов «окружность, вписанная в треугольник АВС», также говорят «вписанная окружность треугольника АВС».
Теорема (об окружности, вписанной в треугольник).
В любой треугольник можно вписать окружность, причем только одну, ее центр находится в точке пересечения биссектрис треугольника.
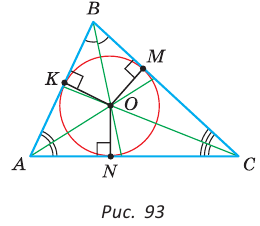
Доказательство:
Рассмотрим произвольный треугольник АВС (рис. 93). Пусть О — точка пересечения его биссектрис. Проведем из точки О перпендикуляры ОК, ОМ и ON соответственно к сторонам АВ, ВС и АС. По свойству биссектрисы угла ОК = ON, ON = ОМ. Окружность с центром в точке О и радиусом ОК будет проходить через точки К, М и N и касаться сторон АВ, ВС и АС в указанных точках по признаку касательной.
Следовательно, эта окружность является вписанной в треугольник АВС. Единственность вписанной окружности докажите самостоятельно.
Замечание. Так как все три биссектрисы треугольника пересекаются в одной точке, то для нахождения центра вписанной окружности достаточно построить точку пересечения любых двух из них.
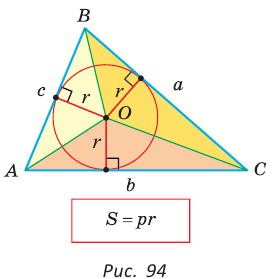
Теорема. Площадь треугольника можно найти по формуле 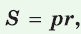 где
где 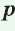 — полупериметр треугольника,
— полупериметр треугольника, 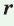 — радиус окружности, вписанной в этот треугольник.
— радиус окружности, вписанной в этот треугольник.
Доказательство:
Пусть дан треугольник АВС со сторонами  — центр его вписанной окружности (рис. 94). Соединим отрезками точку О с вершинами А, В и С. Треугольник АВС разобьется на три треугольника:
— центр его вписанной окружности (рис. 94). Соединим отрезками точку О с вершинами А, В и С. Треугольник АВС разобьется на три треугольника: 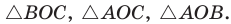 Радиусы
Радиусы 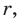 проведенные в точки касания, будут высотами этих треугольников. Площадь треугольника АВС равна сумме площадей указанных треугольников:
проведенные в точки касания, будут высотами этих треугольников. Площадь треугольника АВС равна сумме площадей указанных треугольников:
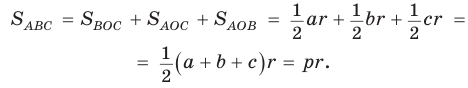
Теорема доказана.
Следствие:
Радиус окружности, вписанной в треугольник, можно найти по формуле
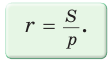
Одной из важнейших задач данной темы является задача нахождения радиуса описанной и радиуса вписанной окружностей данного треугольника.
Пример:
Найти радиус окружности, описанной около равнобедренного треугольника АВС, у которого АВ = ВС = 26 см, высота ВК = 24 см
(рис. 95).
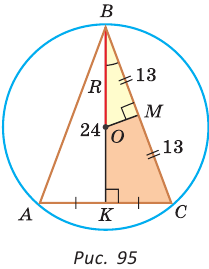
Решение:
Способ 1 (метод подобия). Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника. Проведем серединные перпендикуляры к сторонам АС и ВС, которые пересекутся в точке О — центре описанной окружности. Так как в равнобедренном треугольнике высота, проведенная к основанию, является медианой, то ВК — серединный перпендикуляр к стороне АС. Пусть МО — серединный перпендикуляр к стороне ВС. Тогда ВМ = 13 см, ВО = R -— искомый радиус. Поскольку  (как прямоугольные с общим острым углом СВК), то ,
(как прямоугольные с общим острым углом СВК), то , 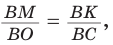
 откуда
откуда 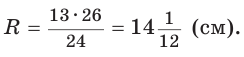
Способ 2 (тригонометрический метод). Из 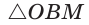 (см. рис. 95)
(см. рис. 95) 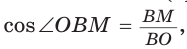 из
из 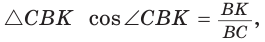 откуда
откуда 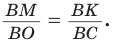 Дальнейшее решение совпадает с приведенным в способе 1.
Дальнейшее решение совпадает с приведенным в способе 1.
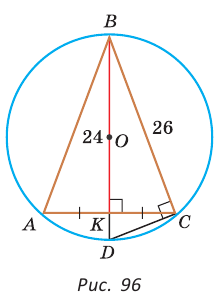
Способ 3* (среднее пропорциональное). Продлим высоту ВК до пересечения с описанной окружностью в точке D (рис. 96). Так как центр описанной окружности равнобедренного треугольника лежит на прямой ВК (см. способ 1), то BD = 2R — диаметр данной окружности. В прямоугольном треугольнике BCD 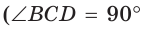 как вписанный, опирающийся на диаметр) катет ВС есть среднее пропорциональное между гипотенузой BD и проекцией ВК катета ВС на гипотенузу. Поэтому
как вписанный, опирающийся на диаметр) катет ВС есть среднее пропорциональное между гипотенузой BD и проекцией ВК катета ВС на гипотенузу. Поэтому 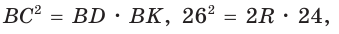 откуда
откуда 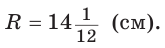
Ответ: 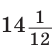 см.
см.
Замечание. Из решения ключевой задачи 1 следует свойство: «Центр окружности, описанной около равнобедренного треугольника, лежит на его высоте, проведенной к основанию, или на ее продолжении».
Верно и обратное утверждение: «Если центр окружности, описанной около треугольника, лежит на высоте треугольника или на ее продолжении, то этот треугольник равнобедренный».
Обратное утверждение докажите самостоятельно.
Полезно запомнить!
Если в ключевой задаче 1 боковую сторону обозначить 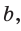 а высоту, проведенную к основанию, —
а высоту, проведенную к основанию, — 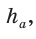 то получится пропорция
то получится пропорция 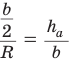 .
.
Отсюда следует удобная формула для нахождения радиуса окружности, описанной около равнобедренного треугольника:
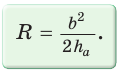
Пример:
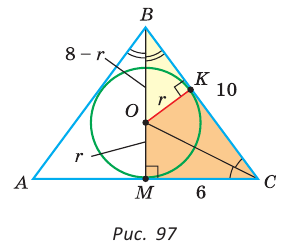
Найти радиус окружности, вписанной в равнобедренный треугольник АВС, у которого АВ = ВС = 10 см, АС = 12 см.
Решение:
Способ 1 (метод подобия). Центр вписанной окружности находится в точке пересечения биссектрис треугольника. Проведем в треугольнике АВС биссектрисы из вершин В и С, которые пересекутся в точке О — центре вписанной окружности (рис. 97). Биссектриса ВМ, проведенная к основанию равнобедренного треугольника АВС, будет его высотой и медианой, луч СО — биссектриса угла С,  — искомый радиус вписанной окружности. Так как AM = МС = 6 см, то из
— искомый радиус вписанной окружности. Так как AM = МС = 6 см, то из 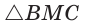 по теореме Пифагора
по теореме Пифагора 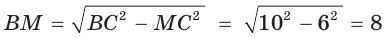 (см), откуда
(см), откуда 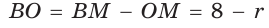 (см). Проведем радиус ОК в точку касания окружности со стороной
(см). Проведем радиус ОК в точку касания окружности со стороной 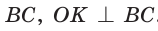 . Из подобия прямоугольных треугольников ВКО и ВМС (
. Из подобия прямоугольных треугольников ВКО и ВМС ( — общий) следует:
— общий) следует: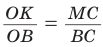 . Тогда
. Тогда 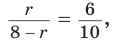
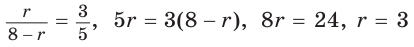 (см).
(см).
Способ 2 (тригонометрический метод). Из 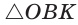 (см. рис. 97)
(см. рис. 97) 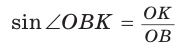 , из
, из 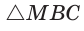
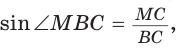 откуда
откуда 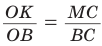 . Дальнейшее решение совпадает с приведенным в способе 1.
. Дальнейшее решение совпадает с приведенным в способе 1.
Способ 3 (свойство биссектрисы треугольника). СО — биссектриса 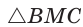 . Известно, что биссектриса треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Поэтому
. Известно, что биссектриса треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Поэтому 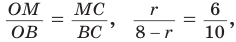 ‘ откуда
‘ откуда 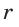 = 3 (см).
= 3 (см).
Способ 4 (формула 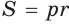 ).
). 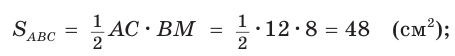
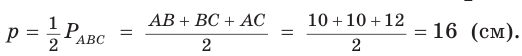 Из формулы площади треугольника
Из формулы площади треугольника 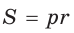 следует:
следует: 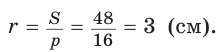
Ответ: 3 см.
Замечание. Из решения ключевой задачи 2 следует свойство: «Центр окружности, вписанной в равнобедренный треугольник, лежит на его высоте, проведенной к основанию».
Верно и обратное утверждение: «Если центр окружности, вписанной в треугольник, лежит на высоте треугольника, то этот треугольник равнобедренный».
Обратное утверждение докажите самостоятельно.
Пример:
Дан равносторонний треугольник со стороной а. Найти радиус R его описанной окружности и радиус  его вписанной окружности.
его вписанной окружности.
Решение:
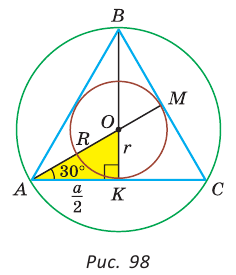
Способ 1 (тригонометрический метод).Так как в равностороннем треугольнике биссектрисы являются и высотами, и медианами, то его биссектрисы лежат на серединных перпендикулярах к сторонам треугольника. Поэтому в равностороннем треугольнике центры описанной и вписанной окружностей совпадают.
Рассмотрим равносторонний треугольник АВС со стороной а, у которого высоты AM и ВК пересекаются в точке О — центре описанной и вписанной окружностей (рис. 98). Тогда ОА = OB = R — радиусы описанной, 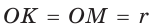 — радиусы вписанной окружности. Так как AM — биссектриса и
— радиусы вписанной окружности. Так как AM — биссектриса и 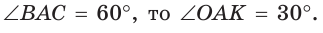 Поскольку ВК — высота и медиана, то
Поскольку ВК — высота и медиана, то 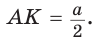 Из
Из 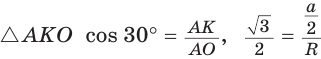 , откуда
, откуда 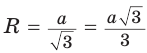 .
.
В 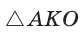 катет ОК лежит против угла в 30°, поэтому
катет ОК лежит против угла в 30°, поэтому 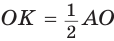 ,
, 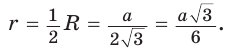
Способ 2 (свойство медиан). Поскольку AM и ВК — медианы треугольника АВС (см. рис. 98), то по свойству медиан 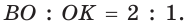 Высоту равностороннего треугольника можно найти по формуле
Высоту равностороннего треугольника можно найти по формуле 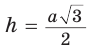 . Откуда
. Откуда
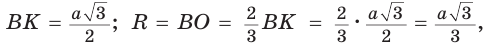
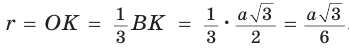
Ответ: 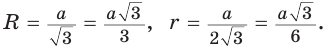
Полезно запомнить!
Поскольку радиус описанной окружности равностороннего треугольника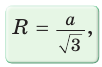 то
то 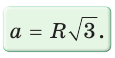 Значит, сторона равностороннего
Значит, сторона равностороннего
треугольника в 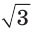 раз больше радиуса его описанной окружности.
раз больше радиуса его описанной окружности.
Чтобы найти радиус R описанной окружности равностороннего треугольника, нужно сторону 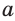 разделить на
разделить на 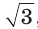 , а чтобы найти его сторону а, нужно радиус R умножить на
, а чтобы найти его сторону а, нужно радиус R умножить на 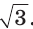 . Радиус вписанной окружности равностороннего треугольника
. Радиус вписанной окружности равностороннего треугольника 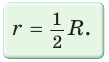
Прямоугольный треугольник и его описанная и вписанная окружности
Теорема. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а ее радиус равен половине гипотенузы, т. е. 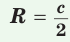 где с — гипотенуза.
где с — гипотенуза.
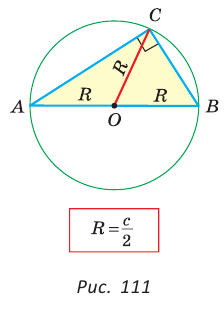
Доказательство:
Проведем в прямоугольном треугольнике АВС медиану СО к гипотенузе АВ (рис. 111). Так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы, то ОС = ОА = ОВ.
Тогда середина гипотенузы — точка О — равноудалена от точек А, В и С и поэтому является центром описанной окружности треугольника АВС. Радиус этой окружности 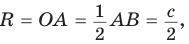 где с — гипотенуза.
где с — гипотенуза.
Теорема доказана.
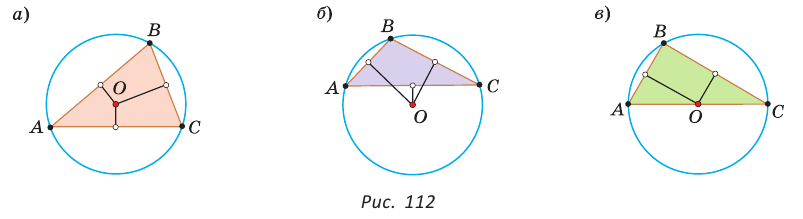
Замечание. Также можно доказать, что серединные перпендикуляры к катетам прямоугольного треугольника пересекаются на середине гипотенузы.
Отметим, что у остроугольного треугольника центр описанной окружности лежит внутри треугольника (рис. 112, а), у тупоугольного — вне треугольника (рис. 112, б), у прямоугольного — на середине гипотенузы (рис. 112, в). Обоснуйте первые два утверждения самостоятельно.
Теорема. Радиус окружности, вписанной в прямоугольный треугольник, можно найти по формуле 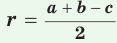 , где
, где 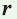 — искомый радиус,
— искомый радиус, 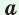 и
и 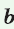 — катеты,
— катеты, 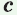 — гипотенуза треугольника.
— гипотенуза треугольника.
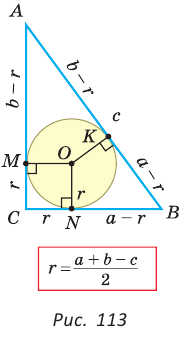
Доказательство:
Рассмотрим прямоугольный треугольник АВС с катетами 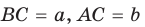 и гипотенузой
и гипотенузой 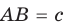 . Пусть вписанная в треугольник окружность с центром О и радиусом
. Пусть вписанная в треугольник окружность с центром О и радиусом 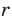 касается сторон треугольника в точках М, N и К (рис. 113).
касается сторон треугольника в точках М, N и К (рис. 113).
Проведем радиусы в точки касания и получим: 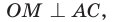
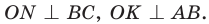 Четырехугольник CMON — квадрат, так как у него все углы прямые и
Четырехугольник CMON — квадрат, так как у него все углы прямые и 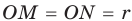 . Тогда
. Тогда 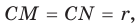
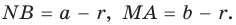 Так как отрезки касательных, проведенных из одной точки к окружности, равны между собой, то
Так как отрезки касательных, проведенных из одной точки к окружности, равны между собой, то 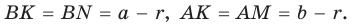 Но
Но 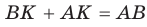 , т. е.
, т. е. 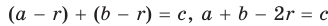 , откуда
, откуда 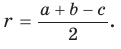
Теорема доказана.
Следствие: 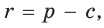 где р — полупериметр треугольника.
где р — полупериметр треугольника.
Доказательство:
Преобразуем формулу радиуса вписанной окружности:
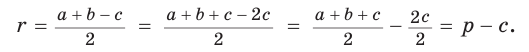
Формула 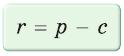 в сочетании с формулами
в сочетании с формулами 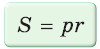 и
и 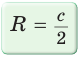 дает возможность решать многие задачи, связанные с прямоугольным треугольником, алгебраическим методом.
дает возможность решать многие задачи, связанные с прямоугольным треугольником, алгебраическим методом.
Пример. Дан прямоугольный треугольник, 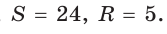 Найти
Найти 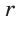 .
.
Решение:
Так как 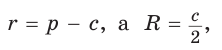 то
то 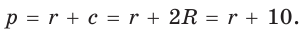
Из формулы 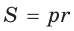 следует
следует 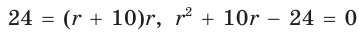 . По теореме Виета (обратной)
. По теореме Виета (обратной)  — посторонний корень.
— посторонний корень.
Ответ: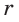 = 2.
= 2.
Пример:
Найти радиус окружности, описанной около прямоугольного треугольника, у которого один из катетов равен 6, а радиус вписанной окружности равен 2.
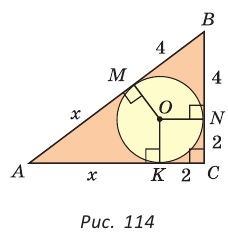
Решение:
Способ 1 (геометрический). Пусть в треугольнике АВС, где  — радиус вписанной окружности (рис. 114). Проведем из центра О вписанной окружности перпендикуляры ОК, ОМ и ON к сторонам треугольника, которые будут радиусами вписанной окружности. Так как
— радиус вписанной окружности (рис. 114). Проведем из центра О вписанной окружности перпендикуляры ОК, ОМ и ON к сторонам треугольника, которые будут радиусами вписанной окружности. Так как  — квадрат, то
— квадрат, то 
По свойству касательных 
Тогда  По теореме Пифагора
По теореме Пифагора
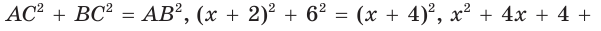
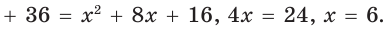
Следовательно, 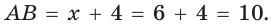
Радиус описанной окружности 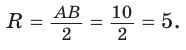
Способ 2 (алгебраический). Подставив в формулу 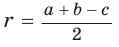 значения
значения 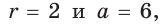 получим
получим 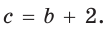 По теореме Пифагора
По теореме Пифагора 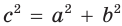 , т. е.
, т. е. 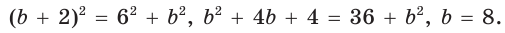 Тогда
Тогда 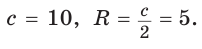
Ответ: 5.
Пример:
Гипотенуза прямоугольного треугольника 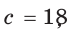 радиус вписанной в него окружности
радиус вписанной в него окружности 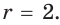 Найти площадь треугольника.
Найти площадь треугольника.
Решение:
Способ 1 (геометрический). Пусть в 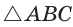 гипотенуза АВ – = с = 18,0 — центр вписанной окружности, ОК, ОМ, ON — ее радиусы, проведенные в точки касания (рис. 115). Так как
гипотенуза АВ – = с = 18,0 — центр вписанной окружности, ОК, ОМ, ON — ее радиусы, проведенные в точки касания (рис. 115). Так как 
 , то CMON — квадрат co стороной, равной радиусу
, то CMON — квадрат co стороной, равной радиусу 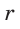 вписанной окружности,
вписанной окружности, 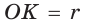 — высота
— высота  . Поскольку отрезки касательных, проведенных из одной точки к окружности, равны между собой, то АК = AM, ВК = BN.
. Поскольку отрезки касательных, проведенных из одной точки к окружности, равны между собой, то АК = AM, ВК = BN.
Отсюда 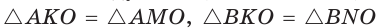 по катету и гипотенузе.
по катету и гипотенузе.
Площадь  равна сумме удвоенной площади
равна сумме удвоенной площади  и площади квадрата CMON, т. е.
и площади квадрата CMON, т. е.
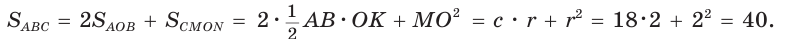
Способ 2 (алгебраический). Из формулы 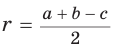 следует
следует 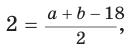
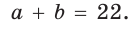 Возведем части равенства в квадрат:
Возведем части равенства в квадрат: 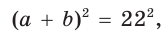
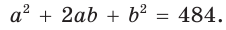 Так как
Так как 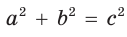 и
и 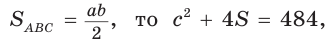
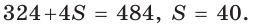
Способ 3 (алгебраический). Из формулы  следует, что
следует, что 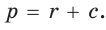 Из формулы
Из формулы 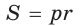 следует, что
следует, что 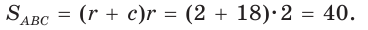
Ответ: 40.
Реальная геометрия:
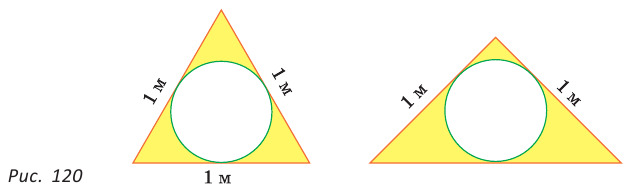
Есть два листа ДСП (древесно-стружечной плиты). Один из них имеет форму равностороннего треугольника со стороной 1 м, другой — форму прямоугольного равнобедренного треугольника с катетами, равными 1 м (рис. 120). Из каждого листа необходимо вырезать по одному кругу наибольшего диаметра. Определите, из какого листа будет вырезан круг большего диаметра и каким в этом случае будет процент отходов, если известно, что площадь круга можно найти по формуле 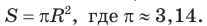

Вписанные и описанные четырехугольники
Определение. Окружность называется описанной около многоугольника, если она проходит через все его вершины. При этом многоугольник называется вписанным в окружность.
Окружность называется вписанной в многоугольник, если она касается всех его сторон. При этом много угольник называется описанным около окружности.
Пятиугольник ABCDE (рис. 121, а) является вписанным в окружность а четырехугольник MNPK (рис. 121, б) — описанным около окружности.
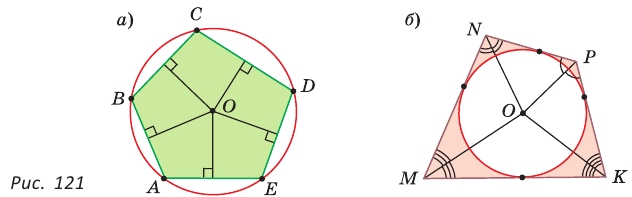
Центр описанной окружности многоугольника находится в точке пересечения серединных перпендикуляров к его сторонам, а центр вписанной — в точке пересечения биссектрис его углов.
Обоснуйте эти утверждения самостоятельно.
Теорема (свойство вписанного четырехугольника).
Сумма противоположных углов четырехугольника, вписанного в окружность, равна 180°.
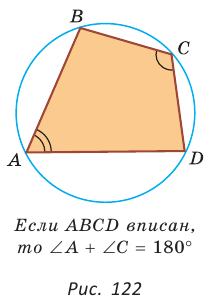
Доказательство:
Пусть ABCD — четырехугольник, вписанный в окружность (рис. 122). Его углы А, В, С и D являются вписанными в окружность. Так как вписанный угол равен половине дуги, на которую он опирается, то 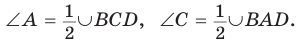 Дуги BCD и BAD дополняют друг друга до окружности, и поэтому сумма их градусных мер равна 360°. Отсюда
Дуги BCD и BAD дополняют друг друга до окружности, и поэтому сумма их градусных мер равна 360°. Отсюда 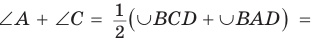
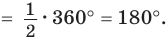 Аналогично доказывается, что
Аналогично доказывается, что  180°. Теорема доказана.
180°. Теорема доказана.
Теорема (признак вписанного четырехугольника).
Если сумма противоположных углов четырехугольника равна  то около него можно описать окружность.
то около него можно описать окружность.
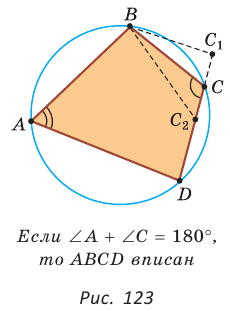
Доказательство:
Рассмотрим четырехугольник ABCD, у которого 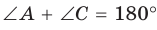 (рис. 123). Через вершины А, В и D проведем окружность (около любого треугольника можно описать окружность). Если бы вершина С не лежала на данной окружности, а находилась вне ее в положении
(рис. 123). Через вершины А, В и D проведем окружность (около любого треугольника можно описать окружность). Если бы вершина С не лежала на данной окружности, а находилась вне ее в положении 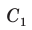 или внутри нее в положении
или внутри нее в положении 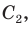 то в первом случае угол С был бы меньше, а во втором — больше половины градусной меры дуги BAD (по свойству угла между секущими и угла между пересекающимися хордами).
то в первом случае угол С был бы меньше, а во втором — больше половины градусной меры дуги BAD (по свойству угла между секущими и угла между пересекающимися хордами).
Тогда сумма 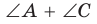 не была бы равна 180°. Следовательно, вершина С лежит на данной окружности. Теорема доказана.
не была бы равна 180°. Следовательно, вершина С лежит на данной окружности. Теорема доказана.
Замечание. Так как сумма углов четырехугольника равна 360°, то для того чтобы около четырехугольника можно было описать окружность, достаточно, чтобы сумма любой пары его противоположных углов была равна 180°.
Следствия.
1. Около параллелограмма можно описать окружность, только если этот параллелограмм — прямоугольник (рис. 124, а). Центр этой окружности лежит в точке пересечения диагоналей прямоугольника.
2. Около ромба можно описать окружность, только если этот ромб — квадрат (рис. 124, б).
3. Около трапеции можно описать окружность, только если она равнобедренная (рис. 124, в).
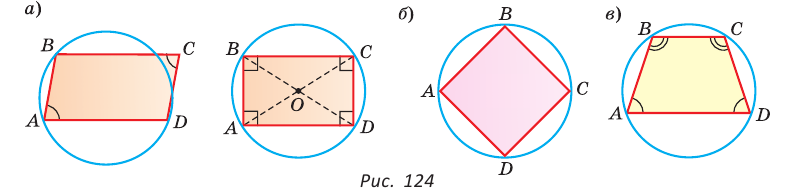
Докажите эти следствия самостоятельно.
Теорема (свойство описанного четырехугольника ).
Суммы противоположных сторон описанного четырехугольника равны между собой.
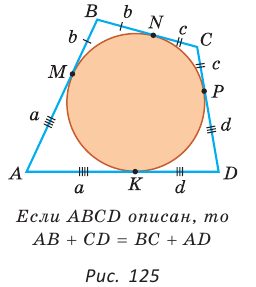
Доказательство:
Пусть ABCD — описанный четырехугольник, М, N, Р и К — точки касания его сторон с окружностью (рис. 125). Так как отрезки касательных, проведенных к окружности из одной точки, равны между собой, то AM = АК = а, ВМ = BN = b, СР = CN = с, DP = DK = d. Тогда
откуда AD + ВС = AB + CD.
Теорема доказана.
Следствие:
Периметр описанного четырехугольника равен удвоенной сумме длин любой пары его противоположных сторон:
Теорема (признак описанного четырехугольника).
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
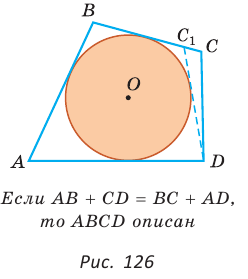
Доказательство:
Пусть для выпуклого четырехугольника ABCD справедливо, что
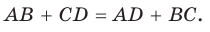 (1)
(1)
Проведем окружность, которая касается прямых AD, АВ и ВС (рис. 126). Такая окружность существует, ее центр находится в точке пересечения биссектрис углов А и В. Если окружность не касается стороны CD, то либо прямая CD не имеет с окружностью общих точек, либо является секущей. Рассмотрим первый случай. Проведем отрезок 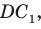 который касается окружности. По свойству описанного четырехугольника
который касается окружности. По свойству описанного четырехугольника
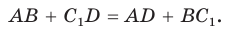 (2)
(2)
Отняв почленно от равенства (1) равенство (2), получим 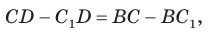
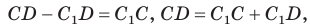 что противоречит неравенству треугольника.
что противоречит неравенству треугольника.
Рассмотрев случай, когда прямая DC — секущая, также придем к противоречию (сделайте это самостоятельно). Следовательно, данная окружность касается стороны CD и в четырехугольник ABCD можно вписать окружность. Теорема доказана.
Следствия.
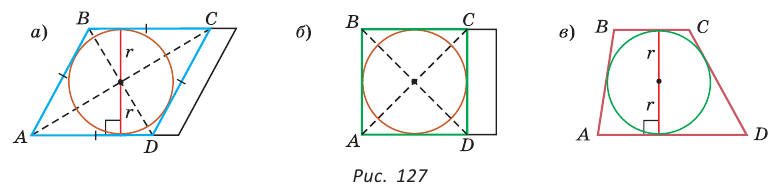
1. В параллелограмм можно вписать окружность, только если этот параллелограмм — ромб. Центр этой окружности лежит в точке пересечения диагоналей ромба, а ее диаметр равен высоте ромба (рис. 127, а).
2. В прямоугольник можно вписать окружность, только если этот прямоугольник — квадрат (рис. 127, б).
3. Диаметр окружности, вписанной в трапецию, равен ее высоте (рис. 127, в).
Докажите эти следствия самостоятельно.
Для описанного многоугольника справедлива формула 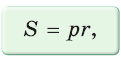 , где S — его площадь, р — полупериметр,
, где S — его площадь, р — полупериметр, 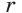 — радиус вписанной окружности.
— радиус вписанной окружности.
Доказательство аналогично приведенному в § 8 для треугольника. Выполните его самостоятельно, используя рисунок 128.
Пример:
Найти радиус окружности, вписанной в ромб с периметром 24 см и острым углом, равным 45°.
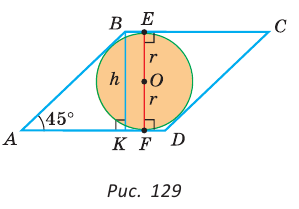
Решение:
Способ 1 (решение прямоугольного треугольника). Пусть ABCD — ромб (рис. 129), О — центр вписанной в ромб окружности. Известно, что высота ВК ромба равна диаметру EF вписанной окружности, т. е. 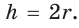 Так как у ромба все стороны равны , то
Так как у ромба все стороны равны , то 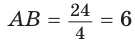 (см).
(см).
Из прямоугольного треугольника АВК находим. что 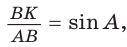 откуда
откуда 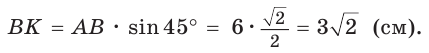 Искомый радиус вписанной окружности
Искомый радиус вписанной окружности 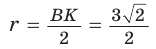 (см).
(см).
Способ 2 (метод площадей). Ромб — параллелограмм. По формуле площади параллелограмма 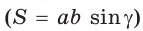 найдем площадь данного ромба:
найдем площадь данного ромба: 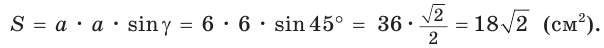 С другой стороны , площадь ромба можно найти по формуле площади описанного многоугольника
С другой стороны , площадь ромба можно найти по формуле площади описанного многоугольника 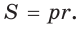 Поскольку
Поскольку 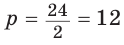 (см), то
(см), то 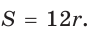 Отсюда
Отсюда 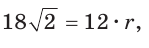
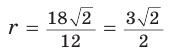 (см).
(см).
Ответ: 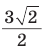 см.
см.
Пример:
Окружность, вписанная в прямоугольную трапецию ABCD, где 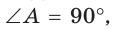 делит точкой касания большую боковую сторону CD на отрезки СК = 1, KD = 4. Найти площадь трапеции (рис. 130).
делит точкой касания большую боковую сторону CD на отрезки СК = 1, KD = 4. Найти площадь трапеции (рис. 130).
Решение:
Способ 1. Площадь трапеции находится по формуле 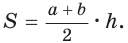 Необходимо найти сумму оснований и высоту трапеции. Проведем высоту
Необходимо найти сумму оснований и высоту трапеции. Проведем высоту 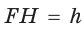 трапеции, проходящую через центр О вписанной окружности. По свойству касательных, проведенных из одной точки к окружности, CF = СК = 1, DH = DK = 4. Проведем высоту СМ. Так как HFCM — прямоугольник (все углы прямые), то НМ = FC = 1, MD = 3. В прямоугольном треугольнике CMD по теореме Пифагора
трапеции, проходящую через центр О вписанной окружности. По свойству касательных, проведенных из одной точки к окружности, CF = СК = 1, DH = DK = 4. Проведем высоту СМ. Так как HFCM — прямоугольник (все углы прямые), то НМ = FC = 1, MD = 3. В прямоугольном треугольнике CMD по теореме Пифагора 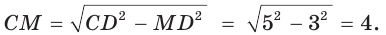 Тогда
Тогда 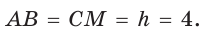 По свойству описанного четырехугольника
По свойству описанного четырехугольника 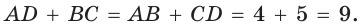 Отсюда
Отсюда 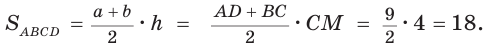
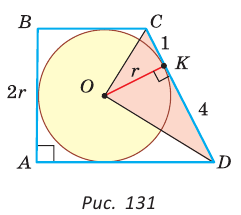
Способ 2*. Центр О вписанной окружности лежит на пересечении биссектрис углов  и
и  Так как
Так как  как внутренние односторонние углы при
как внутренние односторонние углы при 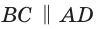 и секущей CD, то
и секущей CD, то 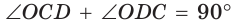 (рис. 131). Тогда
(рис. 131). Тогда 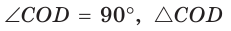 — прямоугольный, радиус
— прямоугольный, радиус 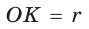 является его высотой, проведенной к гипотенузе CD. Высота прямоугольного треугольника, проведенная к гипотенузе, — есть среднее пропорциональное между проекциями катетов на гипотенузу. Поэтому
является его высотой, проведенной к гипотенузе CD. Высота прямоугольного треугольника, проведенная к гипотенузе, — есть среднее пропорциональное между проекциями катетов на гипотенузу. Поэтому 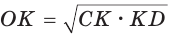 или
или 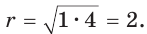 Высота
Высота 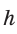 описанной трапеции равна диаметру вписанной окружности, откуда
описанной трапеции равна диаметру вписанной окружности, откуда 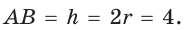 Так как по свойству описанного четырехугольника
Так как по свойству описанного четырехугольника 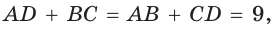 то
то 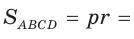
Ответ: 18.
Замечание. Полезно запомнить свойство: «Боковая сторона описанной трапеции видна из центра вписанной окружности под углом 90°».
Пример:
Внутри острого угла А взята точка М, из которой опущены перпендикуляры МВ и МС на стороны угла А, 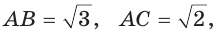
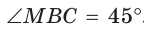 Найти величину угла ВАС (рис. 132, а).
Найти величину угла ВАС (рис. 132, а).
Решение:
Так как в четырехугольнике АВМС сумма углов В и С равна 180°, то около него можно описать окружность. Проведем в ней хорду AM (рис. 132, б). Поскольку  как вписанные углы, опирающиеся на одну и ту же дугу МС, то
как вписанные углы, опирающиеся на одну и ту же дугу МС, то  и прямоугольный треугольник АМС является равнобедренным,
и прямоугольный треугольник АМС является равнобедренным, 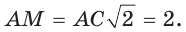 В прямоугольном треугольнике ABM
В прямоугольном треугольнике ABM 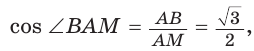 откуда
откуда 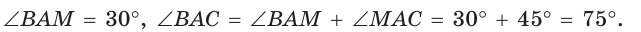
Ответ: 75°.
Окружность, вписанная в треугольник
Пример:
Окружность вписана в треугольник АВС со сторонами ВС = а, АС = Ь, АВ = с. Вывести формулу для нахождения длин отрезков, на которые точки касания окружности со сторонами делят каждую сторону треугольника.
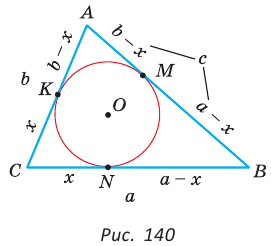
Решение:
Пусть К, М и N — точки касания вписанной окружности соответственно со сторонами АС, АВ и ВС треугольника АВС (рис. 140). Известно, что отрезки касательных, проведенных из одной точки к окружности, равны между собой.
Тогда, если 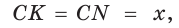 то
то 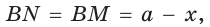
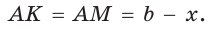 Так как АВ = AM + МВ, то
Так как АВ = AM + МВ, то 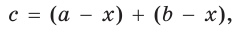 откуда
откуда 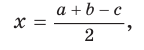 т. е.
т. е. 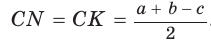 . После преобразований получим:
. После преобразований получим: 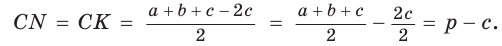 Аналогично:
Аналогично: 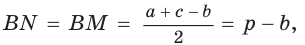
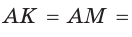
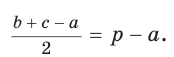
Ответ: 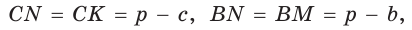
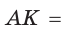
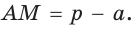
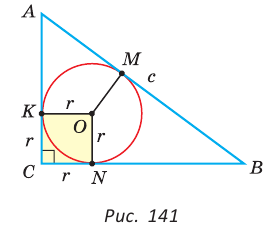
Замечание. Если 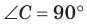 (рис. 141), то
(рис. 141), то 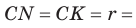
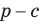 (см. c. 69). Формула радиуса окружности, вписанной в прямоугольный треугольник,
(см. c. 69). Формула радиуса окружности, вписанной в прямоугольный треугольник, 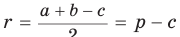 — частный случай результата задачи 1.
— частный случай результата задачи 1.
Описанная трапеция
Пример:
Найти площадь описанной равнобедренной трапеции с основаниями а и Ь.
Решение:
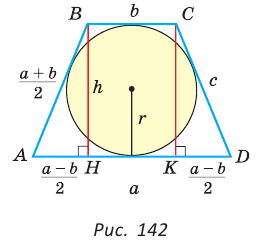
Площадь трапеции можно найти по формуле 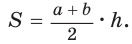 Пусть в трапеции ABCD основания
Пусть в трапеции ABCD основания 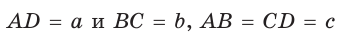 — боковые стороны,
— боковые стороны, 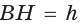 — высота (рис. 142). По свойству описанного четырехугольника АВ + CD = AD + ВС, откуда
— высота (рис. 142). По свойству описанного четырехугольника АВ + CD = AD + ВС, откуда 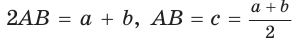 . Известно, что в равнобедренной трапеции
. Известно, что в равнобедренной трапеции 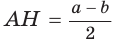 (можно опустить высоту СК и убедиться в этом). Из прямоугольного треугольника АНВ получаем:
(можно опустить высоту СК и убедиться в этом). Из прямоугольного треугольника АНВ получаем: 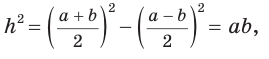
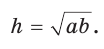 Отсюда
Отсюда 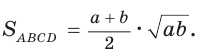 Ответ:
Ответ: 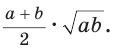
Замечание. Площадь описанной равнобедренной трапеции равна произведению среднего арифметического и среднего геометрического ее оснований.
Полезно запомнить!
Для описанной равнобедренной трапеции с основаниями 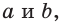 боковой стороной с, высотой h, средней линией
боковой стороной с, высотой h, средней линией 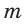 и радиусом
и радиусом 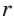 вписанной окружности (см. рис. 142) справедливы равенства:
вписанной окружности (см. рис. 142) справедливы равенства:
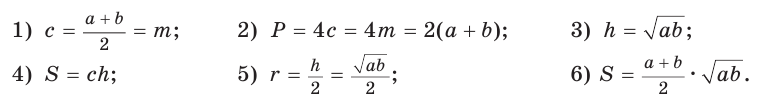
Дополнительные свойства и признаки вписанного четырехугольника
Теорема.
Около четырехугольника можно описать окружность тогда и только тогда, когда угол между его стороной и диагональю равен углу между противоположной стороной и другой диагональю.
Рис. 143
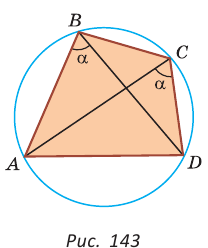
Доказательство:
1. Если четырехугольник ABCD вписан в окружность (рис. 143), то 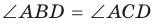 как вписанные углы, опирающиеся на одну и ту же дугу.
как вписанные углы, опирающиеся на одну и ту же дугу.
2. Докажем, что если в некотором четырехугольнике ABCD 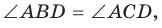 то около него можно описать окружность.
то около него можно описать окружность.
Опишем около треугольника ABD окружность.
В 8-м классе (В. В. Казаков. «Геометрия, 8», с. 186) было доказано свойство:
«Геометрическим местом точек плоскости, из которых данный отрезок AD виден под углом а, является объединение двух дуг окружностей: дуги ABD и ей симметричной относительно прямой AD, исключая точки 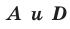 » . Данное свойство гарантирует, что вершины всех углов, равных углу ABD и лежащих по одну сторону от прямой AD, расположены на дуге ABD окружности. Поэтому окружность, описанная около треугольника ABD, пройдет и через вершину С. Теорема доказана.
» . Данное свойство гарантирует, что вершины всех углов, равных углу ABD и лежащих по одну сторону от прямой AD, расположены на дуге ABD окружности. Поэтому окружность, описанная около треугольника ABD, пройдет и через вершину С. Теорема доказана.
Обобщенная теорема Пифагора
В прямоугольном треугольнике 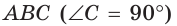 проведена высота СН, которая делит его на треугольники АСН и СВН, подобные между собой и подобные треугольнику
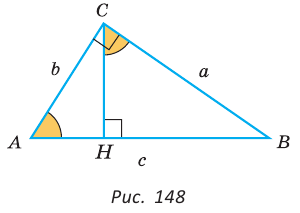
проведена высота СН, которая делит его на треугольники АСН и СВН, подобные между собой и подобные треугольнику 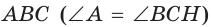 (рис. 148). Тогда теорема Пифагора
(рис. 148). Тогда теорема Пифагора 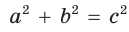 может звучать так: сумма квадратов гипотенуз
может звучать так: сумма квадратов гипотенуз  треугольников СВН и АСН равна квадрату гипотенузы треугольника АВС. И вообще, если
треугольников СВН и АСН равна квадрату гипотенузы треугольника АВС. И вообще, если 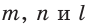 – соответствующие линейные элементы
– соответствующие линейные элементы 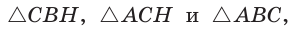 то можно сформулировать обобщенную теорему Пифагора:
то можно сформулировать обобщенную теорему Пифагора:
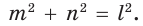
Действительно, из подобия указанных треугольников 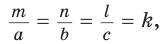 откуда
откуда 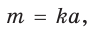
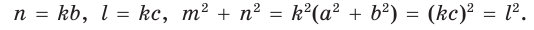
Пример:
Пусть  (см. рис. 148). Найдем
(см. рис. 148). Найдем 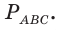 По обобщенной теореме Пифагора
По обобщенной теореме Пифагора 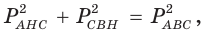 отсюда
отсюда 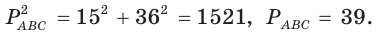
Ответ: 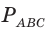 = 39.
= 39.
Формула Эйлера для окружностей
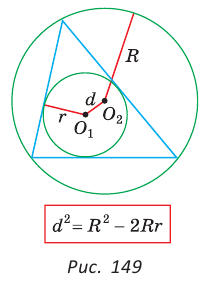
Для вписанной и описанной окружностей треугольника с радиусами 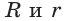 и расстоянием d между их центрами (рис. 149) справедлива формула Эйлера
и расстоянием d между их центрами (рис. 149) справедлива формула Эйлера
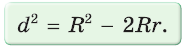
Проверим справедливость этой формулы на примере равнобедренного треугольника АВС, у которого АВ = ВС = 10, АС = 12 (рис. 150).
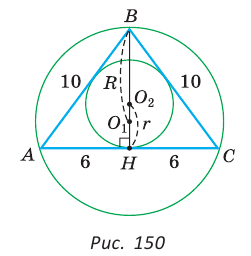
Вначале найдем расстояние между центрами указанных окружностей традиционным способом.
Проведем высоту ВН, длина которой будет равна 8 (пифагорова тройка 6, 8, 10). Центры описанной и вписанной окружностей — соответственно точки 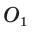 , и
, и 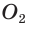 — лежат на прямой ВН (свойство равнобедренного треугольника). Тогда
— лежат на прямой ВН (свойство равнобедренного треугольника). Тогда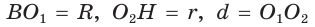 — расстояние между указанными центрами. Для нахождения радиуса описанной окружности воспользуемся формулой
— расстояние между указанными центрами. Для нахождения радиуса описанной окружности воспользуемся формулой 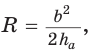 где b — боковая сторона,
где b — боковая сторона, 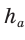 — высота, проведенная к основанию равнобедренного треугольника. Получим
— высота, проведенная к основанию равнобедренного треугольника. Получим 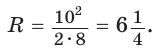 Радиус вписанной окружности
Радиус вписанной окружности 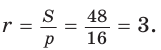 Так как
Так как 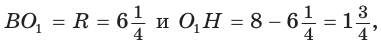 то
то 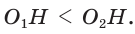 Искомое расстояние
Искомое расстояние 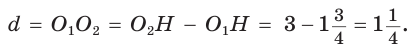
А теперь найдем d по формуле Эйлера: 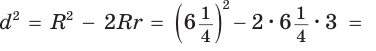
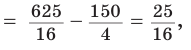 откуда
откуда 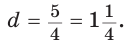 Как видим, формула Эйлера достаточно эффективна.
Как видим, формула Эйлера достаточно эффективна.
Запомнить:
- Центр описанной окружности треугольника (многоугольника) лежит в точке пересечения серединных перпендикуляров к его сторонам.
- Центр вписанной окружности треугольника (многоугольника) лежит в точке пересечения биссектрис его углов.
- Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы, а ее радиус равен половине гипотенузы:
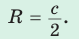
- Радиус вписанной окружности прямоугольного треугольника находится по формуле
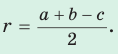
- Если четырехугольник вписан в окружность, то суммы его противоположных углов равны 180°. И обратно.
- Если четырехугольник описан около окружности, то суммы его противоположных сторон равны между собой. И обратно.
- Площадь треугольника и описанного многоугольника можно найти по формуле
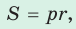 где
где 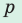 — полупериметр,
— полупериметр, 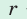 — радиус вписанной окружности.
— радиус вписанной окружности.
Справочная информация по описанной и вписанной окружности треугольника
Определение. Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника.
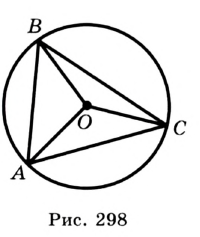
На рисунке 298 изображена окружность, описанная около треугольника. В этом случае также говорят, что треугольник вписан в окружность. Очевидно, что центр описанной окружности треугольника равноудален от всех его вершин. На рисунке 298 точка 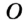 — центр окружности, описанной около треугольника
— центр окружности, описанной около треугольника 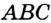 , поэтому
, поэтому 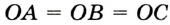 .
.
Теорема 21.1. Вокруг любого треугольника можно описать окружность.
Доказательство: Для доказательства достаточно показать, что для любого треугольника  существует точка
существует точка 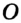 , равноудаленная от всех его вершин. Тогда точка
, равноудаленная от всех его вершин. Тогда точка 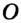 будет центром описанной окружности, а отрезки
будет центром описанной окружности, а отрезки 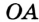 ,
, 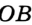 и
и 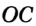 — ее радиусами.
— ее радиусами.
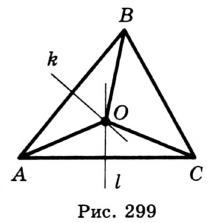
На рисунке 299 изображен произвольный треугольник  . Проведем серединные перпендикуляры
. Проведем серединные перпендикуляры  и
и  сторон
сторон 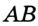 и
и 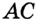 соответственно. Пусть точка
соответственно. Пусть точка 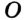 — точка пересечения этих прямых. Поскольку точка
— точка пересечения этих прямых. Поскольку точка  принадлежит серединному перпендикуляру
принадлежит серединному перпендикуляру  , то
, то 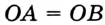 . Так как точка
. Так как точка 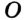 принадлежит серединному перпендикуляру
принадлежит серединному перпендикуляру 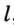 , то
, то 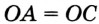 . Значит,
. Значит, 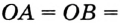
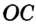 , т. е. точка
, т. е. точка  равноудалена от всех вершин треугольника.
равноудалена от всех вершин треугольника.
Заметим, что вокруг треугольника можно описать только одну окружность. Это следует из того, что серединные перпендикуляры 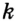 и
и 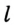 (рис. 299) имеют только одну точку пересечения. Следовательно, существует только одна точка, равноудаленная от всех вершин треугольника.
(рис. 299) имеют только одну точку пересечения. Следовательно, существует только одна точка, равноудаленная от всех вершин треугольника.
Следствие 1. Три серединных перпендикуляра сторон треугольника пересекаются в одной точке.
Следствие 2. Центр описанной окружности треугольника — это точка пересечения серединных перпендикуляров его сторон.
Определение. Окружность называют вписанной в треугольник, если она касается всех его сторон.
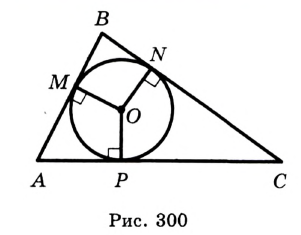
На рисунке 300 изображена окружность, вписанная в треугольник. В этом случае также говорят, что треугольник описан около окружности.
Точка  (рис. 300) — центр вписанной окружности треугольника
(рис. 300) — центр вписанной окружности треугольника  , отрезки
, отрезки  ,
,  ,
, 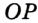 — радиусы, проведенные в точки касания,
— радиусы, проведенные в точки касания, 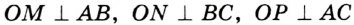 . Понятно, что центр вписанной окружности треугольника равноудален от всех его сторон.
. Понятно, что центр вписанной окружности треугольника равноудален от всех его сторон.
Теорема 21.2. В любой треугольник можно вписать окружность.
Доказательство: Для доказательства достаточно показать, что для любого треугольника  существует точка
существует точка  , удаленная от каждой его стороны на некоторое расстояние г. Тогда в силу следствия из теоремы 20.4 точка
, удаленная от каждой его стороны на некоторое расстояние г. Тогда в силу следствия из теоремы 20.4 точка  будет центром окружности радиуса г, которая касается сторон
будет центром окружности радиуса г, которая касается сторон  .
.
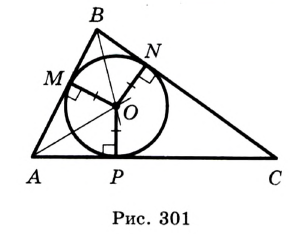
На рисунке 301 изображен произвольный треугольник  . Проведем биссектрисы углов
. Проведем биссектрисы углов  и
и  ,
, 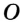 — точка их пересечения. Так как точка
— точка их пересечения. Так как точка  принадлежит биссектрисе угла
принадлежит биссектрисе угла  , то она равноудалена от сторон
, то она равноудалена от сторон 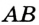 и
и 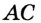 (теорема 19.2). Аналогично, так как точка
(теорема 19.2). Аналогично, так как точка  принадлежит биссектрисе угла
принадлежит биссектрисе угла  , то она равноудалена от сторон
, то она равноудалена от сторон 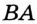 и
и  . Следовательно, точка
. Следовательно, точка  равноудалена от всех сторон треугольника.
равноудалена от всех сторон треугольника.
Заметим, что в треугольник можно вписать только одну окружность. Это следует из того, что биссектрисы углов  и
и  (рис. 301) пересекаются только в одной точке. Следовательно, существует только одна точка, равноудаленная от сторон треугольника.
(рис. 301) пересекаются только в одной точке. Следовательно, существует только одна точка, равноудаленная от сторон треугольника.
Следствие 1. Биссектрисы углов треугольника пересекаются в одной точке.
Следствие 2. Центр вписанной окружности треугольника — это точка пересечения его биссектрис.
Пример:
Докажите, что радиус окружности, вписанной в прямоугольный треугольник, определяется по формуле 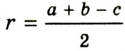 , где
, где  — радиус вписанной окружности,
— радиус вписанной окружности, 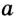 и
и 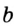 — катеты,
— катеты, 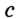 — гипотенуза.
— гипотенуза.
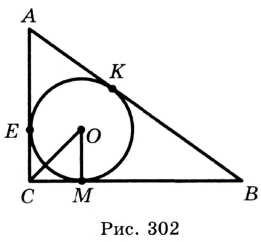
Решение:
В треугольнике  (рис. 302)
(рис. 302) 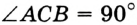 ,
,  ,
,  ,
,  , точка
, точка  — центр вписанной окружности,
— центр вписанной окружности,  ,
,  и
и  — точки касания вписанной окружности со сторонами
— точки касания вписанной окружности со сторонами 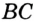 ,
, 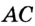 и
и 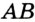 соответственно.
соответственно.
Отрезок 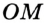 — радиус окружности, проведенный в точку касания. Тогда
— радиус окружности, проведенный в точку касания. Тогда 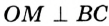 .
.
Так как точка  — центр вписанной окружности, то
— центр вписанной окружности, то  — биссектриса угла
— биссектриса угла  и
и  . Тогда
. Тогда  — равнобедренный прямоугольный,
— равнобедренный прямоугольный, 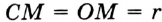 . Используя свойство отрезков касательных, проведенных к окружности из одной точки, получаем:
. Используя свойство отрезков касательных, проведенных к окружности из одной точки, получаем:
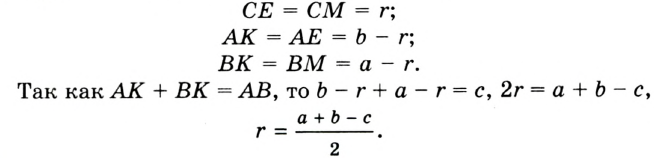
- Плоские и пространственные фигуры
- Взаимное расположение точек и прямых
- Сравнение и измерение отрезков и углов
- Первый признак равенства треугольников
- Треугольники и окружность
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
- Окружность и круг



