Свойства окружности, описанной вокруг трапеции
Содержание:
- Окружность, описанная около трапеции
-
Как найти радиус описанной окружности
- Если известны угол и диагональ трапеции
- Если известны диагональ, стороны трапеции и площадь одного из треугольников
- Если известны длины сторон треугольника
-
Как найти центр описанной окружности
- Если угол прямой
- Если угол острый
- Если угол тупой
- Задачи с решениями
Окружность, описанная около трапеции
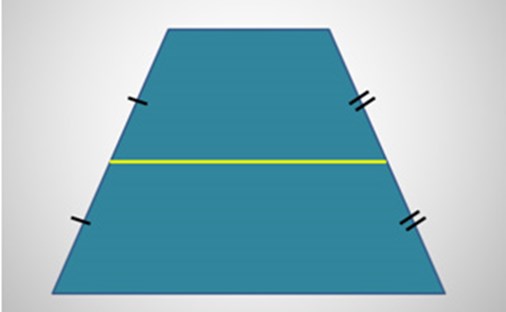
Трапеция — это выпуклый четырехугольник, две стороны которого параллельны, а две другие — не параллельны.
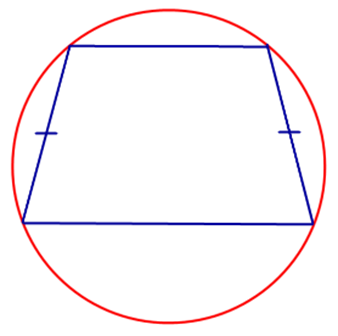
Около четырехугольника можно описать окружность, если сумма его противолежащих углов равна 180°. Поэтому окружность можно описать только вокруг равнобедренной трапеции.
Как найти радиус описанной окружности
Самый распространенный способ найти радиус окружности, описанной около трапеции — через радиус окружности, описанной около треугольника, имеющего 3 любые общие вершины с данной трапецией.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Каждая диагональ делит трапецию на два треугольника. Описанная окружность проходит через все вершины трапеции, значит она проходит через все вершины каждого из этих треугольников и также является для них описанной окружностью.
Если известны угол и диагональ трапеции
Формула 1
(R=frac а{2cdotsinalpha},)
где R — радиус описанной окружности,
а — сторона треугольника,
α — угол треугольника, противолежащий стороне а.
Например, если известна диагональ BD=а и острый угол трапеции ABCD ∠CDA=β, то можем найти радиус описанной окружности.
Рассмотрим треугольник BCD. Сторона BD известна. (∠BCD=180°-∠CDA=180°-β).
Радиус описанной окружности будет равен (frac а{2cdotsinleft(180^circ-betaright)}).
Если известны диагональ, стороны трапеции и площадь одного из треугольников
Формула 2
(R=frac{abc}{4S}),
где R — радиус описанной окружности,
а, b, c — стороны треугольника,
S — площадь треугольника.
Если известны длины сторон треугольника
Формула 3
(R=frac{abc}{4sqrt{pleft(p-aright)left(p-bright)left(p-cright)}},)
где R — радиус описанной окружности,
а, b, c — стороны треугольника,
p — ½ периметра треугольника.
Как найти центр описанной окружности
Центр описанной окружности может лежать как внутри трапеции, так и вне ее. Определить его местонахождение помогает угол между диагональю трапеции и боковой стороной.
Если угол прямой
Если диагональ трапеции перпендикулярна ее боковой стороне, то центр описанной окружности будет лежать на середине большего основания. Тогда большее основание будет равно диаметру описанной окружности.
Формула 4
(R=frac12а,)
где R — радиус описанной окружности,
а — большее основание трапеции.
Если угол острый
Если диагональ трапеции и боковая сторона образуют острый угол, то центр описанной около трапеции окружности лежит внутри трапеции.
Если угол тупой
Если диагональ трапеции и боковая сторона образуют тупой угол, то центр описанной около трапеции окружности будет лежать вне трапеции за ее большим основанием.
Задачи с решениями
Задача
Дано: трапеция с описанной окружностью. Периметр трапеции равен 22 см, а ее средняя линия — 5 см.
Найти: боковую сторону трапеции.
Решение: Так как около трапеции описана окружность, эта трапеция — равнобедренная. Удвоенная средняя линия трапеции равна сумме ее оснований (10 см). Сумма двух боковых сторон равна 22-10=12 (см). Боковая сторона трапеции равна 6 см.
Ответ: 6 см.
Примечание
Дано: основания трапеции ВС=11 см и AD=21 см. Диагональ трапеции ВD=20 см.
Найти: радиус описанной окружности.
Решение: найдем радиус окружности, описанной около (ΔABD. R=frac{BD}{2sinangle A}.)
- Трапеция ABCD равнобедренная, AB=CD, так как описать окружность можно только около равнобедренной трапеции.
- ВЕ — высота трапеции. Отрезок (АЕ=(21-11):2=5 (см)) по свойству равнобедренной трапеции. Отрезок ЕD=21-5=16 (см).
- Треугольник BED прямоугольный. ∠BED=90°. По теореме Пифагора (BE=sqrt{20^2-16^2}=12 (см).)
- Треугольник АBE также прямоугольный. ∠BED=90°. По теореме Пифагора (АВ=sqrt{5^2+12^2}=13 (см).)
- (sin∠BAD=frac{12}{13}) по определению синуса.
- (R=frac{BD}{2sinangle A}=10frac56 (см).)
Ответ: (10frac56 см.)
Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции – параллельные стороны
- Боковые стороны – две другие стороны
- Средняя линия – отрезок, соединяющий середины боковых сторон.
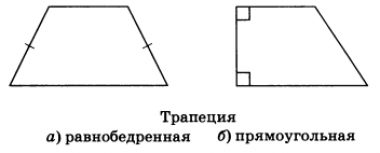
- Равнобедренная трапеция – трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a – h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a – c· cos α – d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 – 2 ad· cos β
d 2 = √ a 2 + c 2 – 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab – | a ( d 2 – c 2 ) |
| a – b |
| d 2 = | √ | c 2 + ab – | a ( c 2 – d 2 ) |
| a – b |
d 1 = √ h 2 + ( a – h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a – h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab – d 2 2
d 2 = √ c 2 + d 2 + 2 ab – d 1 2
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 – | ( | ( a – b ) 2 + c 2 – d 2 | ) | 2 |
| 2 | 2( a – b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p – a )( p – b )( p – a – c )( p – a – d ) |
| | a – b | |
где
| p = | a + b + c + d | – полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p – a )( p – c )( p – d 1) |
где
a – большее основание
Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d649e0e7ef1167e • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Радиус описанной окружности трапеции
Как найти радиус описанной окружности для трапеции?
В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.
I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции
Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.
В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул
где a — сторона треугольника, α — противолежащий ей угол;
либо по формуле
где a, b, c — стороны, S — площадь треугольника.
Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:
где синус угла A можно найти из прямоугольного треугольника ABF:
III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров
Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).
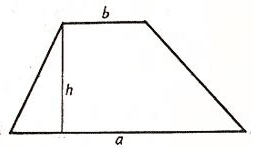
Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.
Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить
и приравнять правые части
Решив это уравнения относительно x, можно найти R.
IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.
точка O — середина AD
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.
I вариант нахождения радиуса для этого случая не изменяется.
Во II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.
Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.
[spoiler title=”источники:”]
http://mathvox.ru/geometria/mnogougolniki/glava-3-trapeciya-i-ee-svoistva/opisannaya-okrujnost-i-ravnobedrennaya-trapeciya-svoistvo-4/
[/spoiler]
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.

Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2.
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k2. - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ.
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b).
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2.
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 1800: α + β = 1800 и γ + δ = 1800.
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 900 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2.
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 1800 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2.
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2.
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ.
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*SАМЕ.
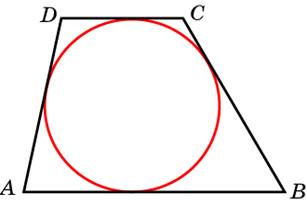
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2.
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ.
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab.
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 1800 – МЕТ = 1800 – КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной:
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.

Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 1500 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 1800. Поэтому КАН = 300 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 300. Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: SАКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см2.
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
где находится центр окружности описанной около трапеции
Ученик
(151),
на голосовании
7 лет назад
Голосование за лучший ответ
marat aminov
Просветленный
(32951)
7 лет назад
окружность можно описать только около равнобедренной трапеции. центр описанной окружности находится на прямой mn проходящей через центры оснований, а радиус окружности описанной около равнобедренной трапеции с основаниями a и b (b>a), боковой стороной c и диагональю d равен R=bcd/4√[p(p-b)(p-c)(p-d)], где р=(b+c+d)/2. точка пересечения дуги такого радиуса с центром в любой из вершин трапеции с прямой mn и есть центр описанной окружности.
PS. если боковая сторона и диагональ равнобедренной трапеции образуют прямой угол, то центр описанной окружности лежит в центре большего основания.
Ольга Гаврилова
Знаток
(422)
5 лет назад
Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
Как найти радиус описанной окружности для трапеции?
В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.
I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции
Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.
В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул
![]()
где a — сторона треугольника, α — противолежащий ей угол;
либо по формуле
![]()
где a, b, c — стороны, S — площадь треугольника.

Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:
![]()
или
![]()
где синус угла A можно найти из прямоугольного треугольника ABF:
![]()
III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров
 Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).
Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).
Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.
Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить
![]()
![]()
и приравнять правые части
![]()
![]()
![]()
Решив это уравнения относительно x, можно найти R.
IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.

![]()
точка O — середина AD
![]()
 Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.
I вариант нахождения радиуса для этого случая не изменяется.
 Во II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.
Во II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.
Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.