Найти центр и радиус окружности
Если окружность задана уравнением вида
найти центр (a;b) и радиус R такой окружности несложно.
Определить по уравнению окружности координаты её центра и радиуса:
Таким образом, центр данной окружности — точка (3;7), радиус R=2.
a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.
Центр окружности — (0;-3), радиус R=3.
Центр — в точке (6;0), радиус R=√5.
Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.
Чтобы найти центр и радиус окружности, заданной уравнением вида
нужно дополнить его до полных квадратов, чтобы привести к привычному виду.
Для этого сначала сгруппируем слагаемые
затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)
При a²+b²-c>0 это уравнение задаёт окружность с радиусом
При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).
При a²+b²-c
Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:
Центром этой окружности является точка (-5;3), радиус R=7.
Центр окружности — точка (2,5;0), радиус R=1,5.
окружность
Определение: Окружность – это линия второго порядка, которая представляет собой геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром.
Если центр находится в начале координат, то окружность задается каноническим уравнением второй степени вида: х2+у2=R2 , где R – радиус окружности; х,у – текущие координаты точек, лежащих на окружности.
Для вывода данного уравнения возьмем на окружности произвольную точку М(х;у). Отрезок ОМ=R является гипотенузой в прямоугольном треугольнике ОМР, а катеты определяются координатами х и у точки М. Уравнение окружности получается по теореме Пифагора: х2+у2=R2, которое называется каноническим уравнением окружности с несмещенным центром.
Если центр окружности находится в точке С(х0;у0), то уравнение окружности со смещенным центром будет иметь
Построение окружности выполняется с помощью циркуля.
эллипс
Определение: Эллипс – это линия второго порядка, которая представляет собой геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная и равная большой оси эллипса.
Эллипс с несмещенным центром задается каноническим уравнением второй степени вида:
где а и в – полуоси, х,у – текущие координаты точек, лежащих на эллипсе. Центр симметрии находится в начале координат. Осями симметрии служат координатные оси.
При рассмотрении эллипса возможны два случая:
- 1. Если ав, то а называется большая полуось, лежащая на координатной оси Ох, а в – малая полуось, лежащая на координатной оси Оу;
- 2. Если ав, то а называется малая полуось, лежащая на координатной оси Ох, а в-большая полуось, лежащая на координатной оси Оу.
Фокусы F1 и F2 всегда лежат на большой оси эллипса, причем симметрично относительно центра симметрии на расстоянии:
где величина “с” определяет фокусное расстояние.
Для характеристики формы эллипса вводится эксцентриситет.
Определение: Эксцентриситетом эллипса называется отношение фокусного расстояния к длине его большой полуоси:
=, если ав и =, если ва.
Значение эксцентриситета меняется в пределах 0??1. При этом форма эллипса изменяется от окружности (е=0, при а=в=R) и, вытягиваясь, вырождается в прямую (е=1, при а>>в).
Уравнение эллипса выводится из его основного свойства, представленного в определении. Возьмём на эллипсе произвольную точку М(х;у). Расстояния r1 и r2 от фокусов F1 и F2 до точки М(х;у) называются фокальными радиусами.
В соответствии с определением сумма фокальных радиусов есть величина постоянная, равная большой оси эллипса: r1 + r2 = 2а (при ав) – основное свойство эллипса. Для вывода уравнения эллипса необходимо выразить фокальные радиусы r1 и r2 через координаты точки М(х;у) и фокусов F1(с;0) и F2(-с;0)и подставить в это равенство.
Если центр симметрии смещен и находится в точке С(х0;у0), то уравнение эллипса со смещенным центром имеет вид:
Построение эллипса рассмотрим ниже на примерах.
Пример. Определить вид, параметры и построить линию, заданную уравнением:
Решение: 1. Это эллипс с несмещенным центром вида:
2. Найдем параметры: – большая полуось на оси Ох;
– малая полуось на оси Оу;
Фокусы F1(4.6;0) и F2(-4.6;0) лежат на большой оси, совпадающей с осью Ох, симметрично, на расстоянии с=4.6 относительно начала координат.
- 3. Построение эллипса (см. рисунок выше) выполним по этапам:
- 1) строим систему координат Оху;
- 2) на координатных осях симметрично относительно начала координат откладываем большую и малую полуоси (а=5, в=2) и показываем вершины эллипса А1,А2,В1,В2;
- 3) через вершины эллипса параллельно координатным осям строим осевой прямоугольник;
- 4) вписываем эллипс в осевой прямоугольник;
- 5) на большой оси, совпадающей с осью Ох, симметрично относительно начала координат показываем фокусы F1(4.6;0) и F2(-4.6;0).
Уравнение окружности.
Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.
В формулировке окружности упоминается расстояние между точкой окружности и центром.
Формула расстояния между двумя точками М1(х1; у1) и М2(х2; у2) имеет вид:
,
Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х0; у0) и радиусом r.
Отметим произвольную точку М(х; у) на этой окружности.
.
Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.
Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х0 ) 2 +(у – у0 ) 2 = r 2 .
Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х0; у0) и радиусом r имеет вид:
В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):
[spoiler title=”источники:”]
http://vuzlit.ru/884029/okruzhnost
http://www.calc.ru/Uravneniye-Okruzhnosti.html
[/spoiler]
Выделяют четыре
основных типа кривых второго порядка:
окружность,
эллипс, гипербола и парабола.
1. Окружность
Определение.
Окружностью
называется множество, состоящее из всех
точек плоскости, находящихся на равном
расстоянии R от фиксированной точки С.
Число R
называется радиусом
окружности, точка С
– центром.
Воспользуемся
определением окружности для вывода ее
уравнения.
П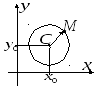
Рис. 5
усть точка
![]()
– центр окружности. Точка
![]()
– произвольная точка окружности, а
радиус этой окружности равен
![]() .
.
По определению
![]() ,
,
тогда, используя формулу вычисления
длины вектора
![]() ,
,
имеем
![]() ,
,
тогда
![]() .
.
Возведем обе части равенства в квадрат.
Тогда уравнение окружности с центром
в точке
![]()
и радиусом R
имеет вид:
![]()
каноническое
уравнение окружности
В частности,
уравнение окружности с центром в начале
координат и радиусом R
имеет вид:
![]() .
.
Пример
Составить
каноническое уравнение окружности,
центр которой находится в точке
![]() ,
,
а диаметр
![]() .
.
Решение:
Найдем радиус
![]() ,
,
тогда уравнение окружности имеет вид
![]()
или
![]() .
.
Пример
Построить окружность
по заданному уравнению
![]() .
.
Привести каноническое уравнение к
общему виду.
Решение:
П
Рис. 6
о заданному уравнению определяем,
что центр окружности
![]() ,
,
а радиус
![]() .
.
Теперь преобразуем каноническое
уравнение к общему виду
![]()
или
![]() ,
,
полученное уравнение является общим
уравнением окружности с центром в точке
![]()
и радиусом
![]() .
.
Возможно решение
обратной задачи: общее уравнение
преобразовать в каноническое.
2. Эллипс
Определение
1. Эллипсом
называется множество, состоящее из всех
точек плоскости, сумма расстояний от
каждой из которых до двух заданных точек
плоскости
![]()
и
![]() ,
,
называемых фокусами, есть величина
постоянная, большая, чем расстояние
между фокусами.
В случае, когда
фокусы эллипса
![]()
и
![]()
расположены
на оси Ox
(или на оси Oy)
симметрично относительно начала
координат, его уравнение называется
каноническим
и имеет
вид:
![]() .
.
Обозначим через
2с
расстояние между фокусами эллипса. Если
a >
b
(a <
b),
то фокусы эллипса расположены на оси
Ox
(на оси Oy)
и
![]()
![]()
(cм. рис. 7). Фокусы эллипса всегда лежат
на большей оси. Отрезки ОА
и ОВ
называются полуосями
эллипса. Точки пересечения линии эллипса
с осями координат А,
В,
А1,
В1
называются вершинами
эллипса.
Эллипс имеет две оси симметрии (в случае,
если эллипс задается каноническим
уравнением, оси симметрии совпадают с
осями координат) и центр симметрии (в
случае, если эллипс задается каноническим
уравнением, центр симметрии совпадает
с началом координат).
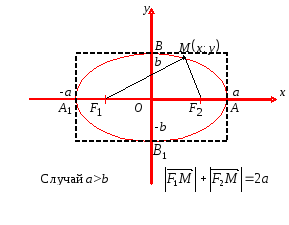
Рис. 7
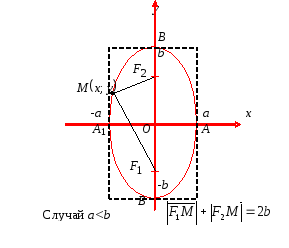
Для количественной
оценки формы эллипса введена величина,
называемая эксцентриситетом эллипса.
Определение
2.
Эксцентриситетом
эллипса называется величина, равная
отношению расстояния между фокусами к
длине его большей оси.
Обозначим
эксцентриситет эллипса через .
Пусть a >
b
(a <
b).
Тогда
![]()
(![]() ).
).
Так как 0 <
с < a (0 <
с < b)
, то 0 <
< 1. Чем ближе эксцентриситет к единице,
тем эллипс более вытянут вдоль большей
оси.
3. Гипербола
Определение
1. Гиперболой
называется множество, состоящее из всех
точек плоскости, модуль разности
расстояний от которых до двух фиксированных
точек
![]()
и
![]() ,
,
называемых фокусами, есть величина
постоянная, меньшая, чем расстояние
между фокусами, и отличная от нуля.
Каноническое
уравнение
гиперболы имеет вид:
![]() (1)
(1)
(в случае, если
фокусы
![]()
и
![]()
расположены
на оси Ох
симметрично относительно начала
координат, см. рис. 8) или
![]() (2)
(2)
(в случае, если
фокусы
![]()
и
![]()
расположены
на оси Оу
симметрично
относительно начала координат, см. рис.
9).
Гиперболы, заданные
уравнениями (1) и (2), называются сопряженными
относительно друг друга.
Обозначим через
2с
расстояние между фокусами гиперболы.
Тогда
![]() .
.
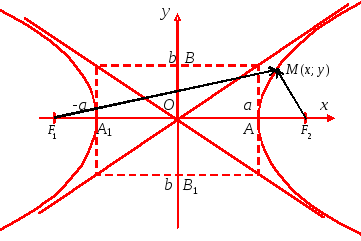
![]()
![]()

Рис. 8 Рис. 9
Точки А и А1 – вершины
гиперболы. Точки В и В1 –
вершины гиперболы.
Прямоугольник,
составленный прямыми
![]()
![]() ,
,
называется основным
прямоугольником гиперболы.
Его диагонали совпадают с прямыми
![]() ,
,
которые являются асимптотами
гиперболы. Отрезки ОА
= a и OB = b
называются полуосями
гиперболы. Ось координат, на которой
расположены фокусы гиперболы (и которую
пересекает гипербола) называется
действительной,
другая ось координат (с которой у
гиперболы нет общих точек) – мнимой.
Гипербола называется
равносторонней,
если длины осей равны
![]() .
.
Форму гиперболы
определяет отношение длин основного
прямоугольника. Для количественной
оценки формы гиперболы, как и в случае
эллипса, вводится понятие эксцентриситета.
Определение
2.
Эксцентриситетом
гиперболы называется величина, равная
отношению половины расстояния между
фокусами к длине действительной полуоси.
Обозначим
эксцентриситет гиперболы через .
Для гиперболы, заданной уравнением (1),
![]() ;
;
для гиперболы, заданной уравнением (2)
![]() .
.
Так как 0 <
а < с и
0 <
b
< с, то
> 1. Чем ближе эксцентриситет к единице,
тем основной прямоугольник гиперболы
более вытянут вдоль ее оси, соединяющей
вершины.
4. Парабола
Определение.
Параболой
называется множество, состоящее из всех
точек на плоскости, для которых расстояние
до некоторой фиксированной точки F,
называемой фокусом, равно расстоянию
до некоторой фиксированной прямой,
называемой директрисой.
На рисунках 10–13
представлены все простейшие случаи
расположения параболы и соответствующие
им канонические уравнения.
p
– параметр, он равен расстоянию между
фокусом и директрисой;
точка F
– фокус.
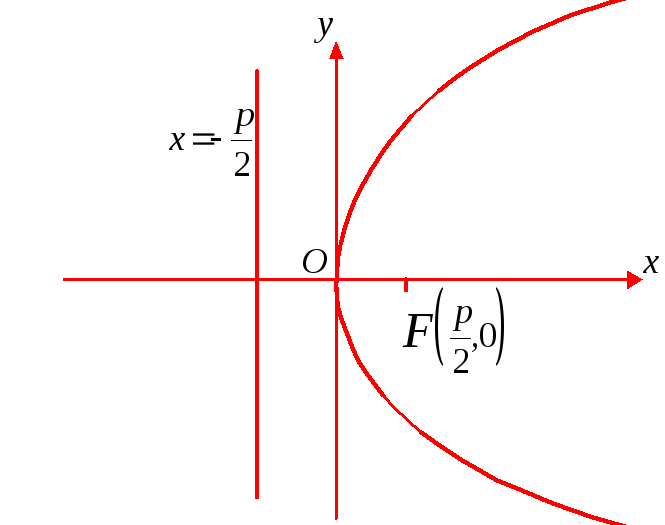

Рис. 10
Рис. 11
На рис. 10 парабола
![]() ;
;
уравнение директрисы
![]() .
.
На рис. 11 парабола
![]() ;
;
уравнение директрисы
![]() .
.
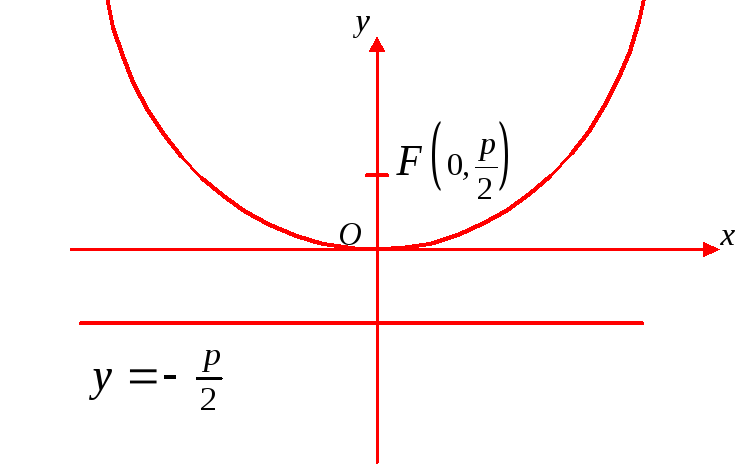
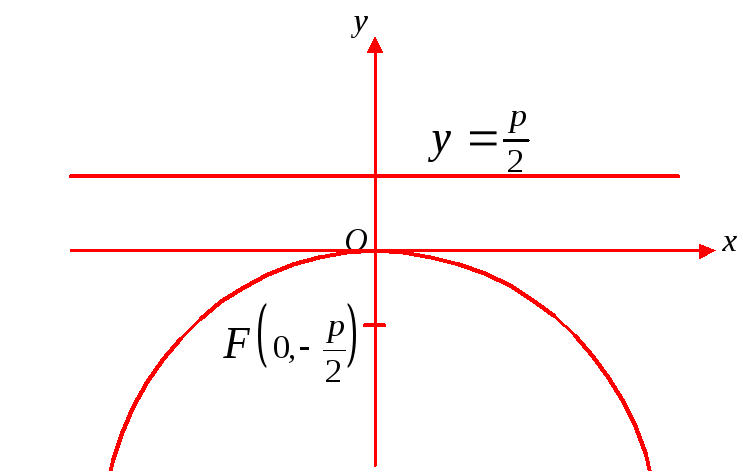
Рис. 12
Рис. 13
На рис. 12 парабола
![]() ;
;
уравнение директрисы
![]() .
.
На рис. 13 парабола
![]() ;
;
уравнение директрисы
![]() .
.
Пример
По заданному
каноническому уравнению
![]()
построить кривую,
найти координаты фокусов.
Решение:
З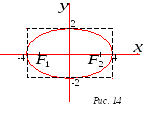 аданное
аданное
уравнение есть уравнение эллипса, где
![]() ,
,
![]() ,
,
следовательно,
![]() ,
,
![]() ,
,
тогда
![]() .
.
На оси
![]()
отметим точки
![]()
и
![]() ,
,
а на оси
![]()
отметим
![]()
и
![]()
это вершины эллипса.
Соединим полученные
точки плавной линией. Прямоугольных
участков быть не должно. Эллипс – это
сжатая окружность.
Найдем фокусы
эллипса, так как
![]() ,
,
то фокусы располагаются на оси
![]()
и имеют координаты
![]()
и
![]() .
.
Пример
Общее уравнение
![]()
кривой привести к каноническому виду,
построить кривую, найти координаты
фокусов.
Р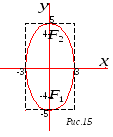 ешение:
ешение:
Перенесем свободный
член вправо
![]() .
.
Разделим слагаемое уравнения на 225,
получим
![]() ,
,
это уравнение
соответствует
каноническому уравнению эллипса, где
![]() ,
,
![]() ,
,
следовательно,
![]() ,
,
![]() ,
,
тогда
![]() .
.
На оси
![]()
отметим точки
![]()
и
![]() ,
,
а на оси
![]()
отметим
![]()
и
![]()
– это вершины эллипса.
Найдем фокусы
эллипса, так как
![]() ,
,
то фокусы располагаются на оси
![]()
и имеют координаты
![]()
и
![]() .
.
Пример
Дано каноническое
уравнение гиперболы
![]() .
.
Записать уравнение гиперболы, сопряженной
с заданной. Найти координаты фокусов и
построить обе гиперболы.
Решение:
Уравнение
![]()
соответствует гиперболе, у которой
действительная ось симметрии есть ось
![]() .
.
Следовательно, уравнение сопряженной
гиперболы
![]() ,
,
у которой действительная ось симметрии
есть ось
![]() .
.
Межфокусное расстояние у сопряженных
гипербол одинаковое, равно
![]() ,
,
где
![]() .
.
П
 одготовка
одготовка
к построению сопряженных гипербол
одинаковая. На осях координат строим
основной прямоугольник со сторонами
![]()
и
![]() .
.
Прямоугольник строится так, чтобы точка
пересечения его диагоналей совпадала
с началом координат. Продолжение
диагоналей являются асимптотами
гиперболы. В нашем случае уравнения
асимптот имеют вид:
![]() .
.
Для уравнения заданной гиперболы вершины
гиперболы
![]()
и
![]() ,
,
так же как и фокусы
![]()
и
![]() ,
,
находятся на оси
![]() .
.
Линия гиперболы касается вспомогательного
прямоугольника только в одной точке
(вершине) и плавно стремится к асимптотам.
Для уравнения сопряженной гиперболы
вершины гиперболы
![]()
и
![]() ,
,
так же как и фокусы
![]()
и
![]() ,
,
находятся на оси
![]() .
.
Рис. 16
Пример
Построить
по заданному уравнению параболы
![]() ,
,
определить координаты фокуса, составить
уравнение директрисы.
Решение:
Данное
уравнение
![]()
– это уравнение параболы с осью симметрии
![]() .
.
Для нахождения координат фокуса надо
найти параметр
![]() .
.
Сравнивая каноническое уравнение
параболы
![]()
и заданное уравнение
![]() ,
,
находим
![]() ,
,
откуда
![]() .
.
Следовательно,
![]()
и уравнение директрисы
![]() ,
,
а ветви параболы направлены вверх. Кроме
вершины
![]()
найдем еще хотя бы 4 точки, принадлежащие
данной параболе (рис. 17). Для этого
составим таблицу
-
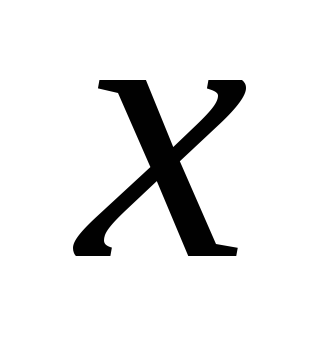
0
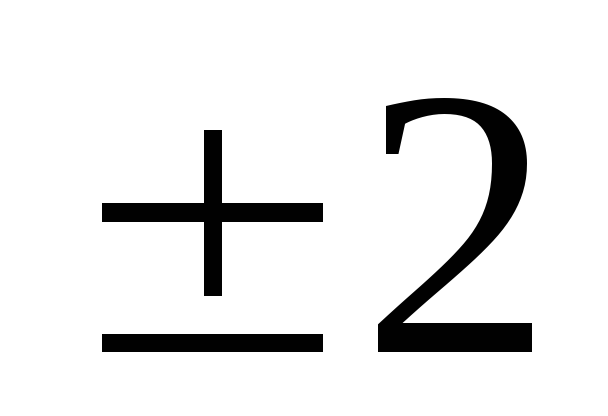
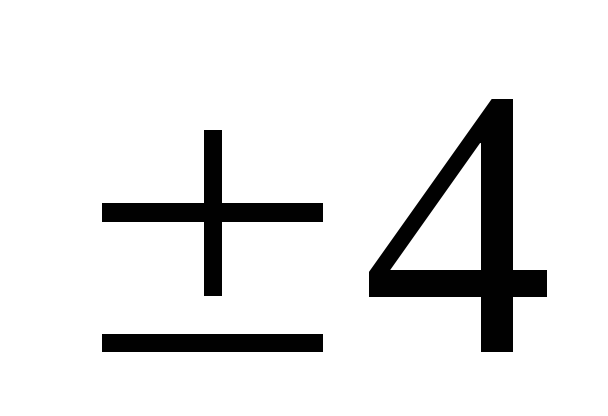

0
1
4
Пример
Привести
уравнение
![]()
к каноническому виду и выполнить задания
предыдущего примера.
Решение:
Преобразуем
уравнение к каноническому виду
![]() .
.
Это уравнение соответствует уравнению
![]() ,
,
то есть уравнению параболы с осью
симметрии
![]() .
.
Аналогично предыдущему примеру находим
![]() ,
,
откуда
![]() .
.
Следовательно,
![]()
и уравнение директрисы
![]() ,
,
а ветви параболы направлены влево. Кроме
вершины
![]()
найдем еще хотя бы 4 точки, принадлежащие
данной параболе (рис. 18). Для этого
составим таблицу
-
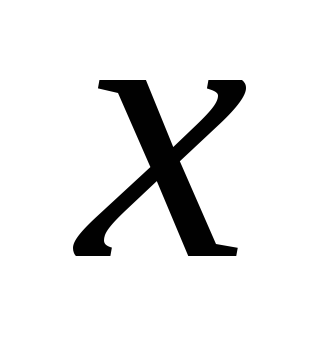
0
-1,5
-6

0
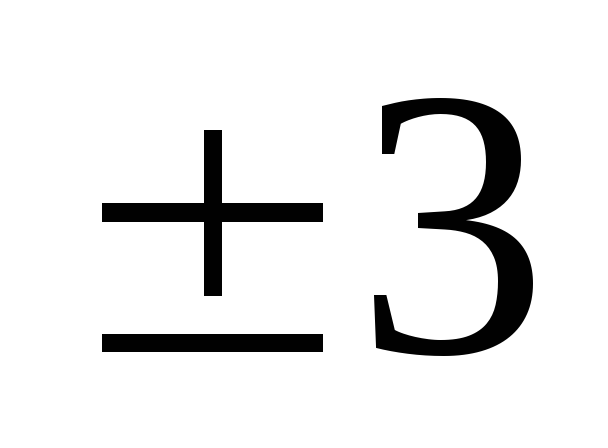
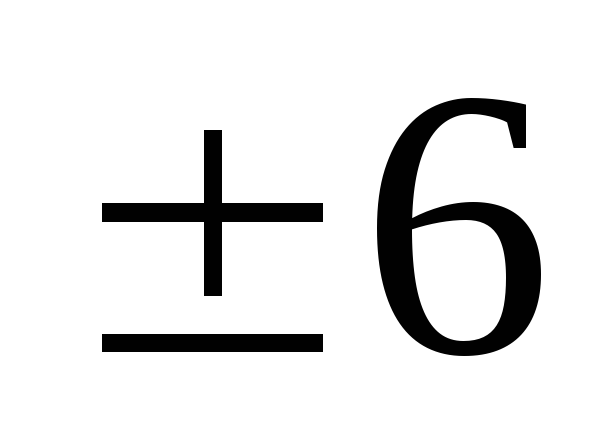
62
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Уравнение окружности
Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.
Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности
Равенство (1) есть уравнение окружности радиуса R с центром в точке С.
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.
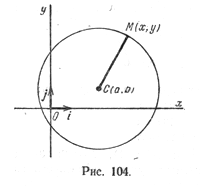
Так как |СМ| = ( sqrt <(x — a)^2 + (у — b)^2>), то уравнение (1) можно записать так:
(x — a) 2 + (у — b) 2 = R 2 (2)
Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение
есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).
Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид
Уравнение (3) называют каноническим уравнением окружности.
Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.
Непосредственной подстановкой значения радиуса в уравнение (3) получим
Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).
Подставив значение координат точки С и значение радиуса в формулу (2), получим
(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.
Задача 3. Найти центр и радиус окружности
Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.
Задача 4. Доказать, что уравнение
является уравнением окружности. Найти ее центр и радиус.
Преобразуем левую часть данного уравнения:
Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.
Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).
Напишем уравнение прямой АВ:
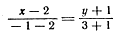 или 4х + 3y —5 = 0.
или 4х + 3y —5 = 0.
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:
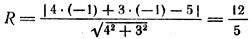
Напишем уравнение искомой окружности
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).
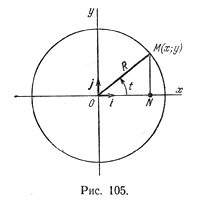
Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t
(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем
Найти центр и радиус окружности
Если окружность задана уравнением вида
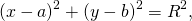
найти центр (a;b) и радиус R такой окружности несложно.
Определить по уравнению окружности координаты её центра и радиуса:
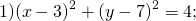
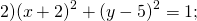
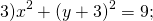
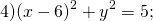
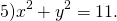
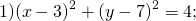
Таким образом, центр данной окружности — точка (3;7), радиус R=2.
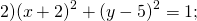
a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.
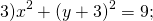
Центр окружности — (0;-3), радиус R=3.
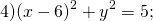
Центр — в точке (6;0), радиус R=√5.
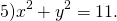
Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.
Чтобы найти центр и радиус окружности, заданной уравнением вида
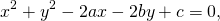
нужно дополнить его до полных квадратов, чтобы привести к привычному виду.
Для этого сначала сгруппируем слагаемые
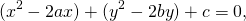
затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)
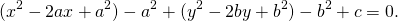
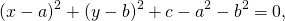
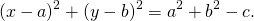
При a²+b²-c>0 это уравнение задаёт окружность с радиусом
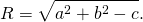
При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).
При a²+b²-c 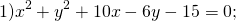
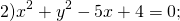
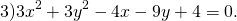
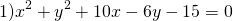
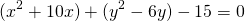
Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:
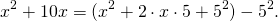
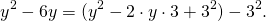
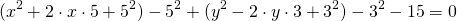
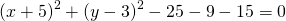
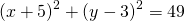
Центром этой окружности является точка (-5;3), радиус R=7.
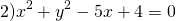
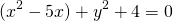
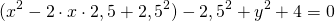
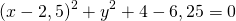
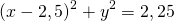
Центр окружности — точка (2,5;0), радиус R=1,5.
Нахождение центра и радиуса окружности по общему уравнению окружности
Этот калькулятор проверяет, является ли введенное уравнение общим уравнением окружности, и вычисляет координаты центра и радиуса окружности, если это возможно. Описание способа решения подобных задач находится под калькулятором

Нахождение центра и радиуса окружности по общему уравнению окружности
Уравнение НЕ является общим уравнением окружности
Приведение общего уравнения окружности к стандартному виду
Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде
Из этого уравнения достаточно легко найти центр окружности — это будет точка с координатами (a,b), и радиус окружности — это будет квадратный корень из правой части уравнения.
Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:
Это — уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.
Способ решения такого рода задач следующий:
Перегруппируем слагаемые уравнения
Как видим, выражение в конце это уравнение окружности в стандартном виде, из которого уже легко получить и координаты центра окружности и ее радиус. Если же справа получилось отрицательное число — значит заданное вначале уравнение не является уравнением окружности (бывают задачи и на такую проверку). Калькулятор тоже проверяет это условие.
Для решения обратной задачи — нахождения общего уравнения окружности по координатам центра и радиусу — можно использовать калькулятор Уравнение окружности по заданному центру и радиусу в различных формах
источники:
http://www.treugolniki.ru/najti-centr-i-radius-okruzhnosti/
http://planetcalc.ru/9507/
Задача №1. Определить центр и радиус окружности, заданной уравнением х²+у²-2х+4y-20=0.
Решение. Так как в заданном уравнении коэффициенты при х² и у² равны между собой и отсутствует член с произведением координат, го заданное уравнение действительно представляет собой уравнение окружности. Чтобы определить координаты центра и радиус окружности, необходимо уравнение привести к каноническому виду:
(х²-2х)+(y²+4у)=20, (x²-2х+1)+(у²+4х+4)=25, (x-1)²+(y+2)²=25.
Координаты центра и радиус окружности можно найти, не приводя данное уравнение к каноническому виду,
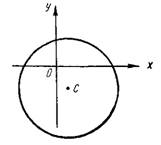
Рис.1
достаточно сравнить данное уравнение с уравнением окружности в общем виде:

Ответ: (1, —2), R = 5.
Задача №2. Составить уравнение окружности, проходя¬щей через точки А (—1;1) и В (1;-3), если центр ее лежит на прямой 2х-у+1=0.
Решение. Каноническое уравнение окружности:
(x-a)²+(y-b)² = r².
Так как окружность проходит через точки А и B, то координаты этих точек должны удовлетворять уравнению окружности. Имеем два уравнения:
(-1-а)² + (1-b)²=r², (1-а)² + (-3-b)² = r².
Если центр окружности лежит на прямой 2х-у+1=0, то координаты центра также должны удовлетворить уравнению прямой.
Имеем третье уравнение: 2а-b+1=0.

Рис.2
Решим систему уравнений:
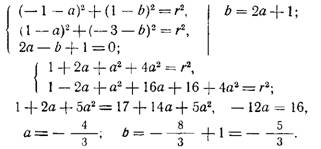
Таким образом, координаты центра окружности найдены:
![]()
Чтобы определить г², получим: г² = 1+2а+5а²,
![]()
Уравнение окружности:
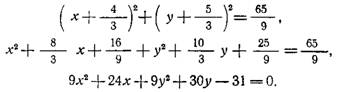
Ответ: 9х² + 9y² + 24x + 30у – 31 =0.
Задача №3. Составить уравнение окружности, если ее центр находится в точке С(5;4) и окружность отсекает от прямой х+2у-3=0 хорду, длина которой равна 8.
Решение. Искомое уравнение будет иметь вид:
(x-5)²+(у-4)²=r².
Определим расстояние центра С от данной прямой:
![]()
Так как радиус, перпендикулярный к хорде, делит ее пополам, то половина хорды будет равна 4 единицам.
Рис.3
По теореме Пифагора имеем:
г²=4²+CD²=16+20=36, r² = 36, r = 6.
Уравнение окружности: (х -5)²+(у – 4)² = 36.
Ответ: (х -5)²+(у – 4)² = 36.
Задача №4. Составить уравнение окружности, касающейся двух параллельных прямых 2х+у-5=0 и 2х+y+15=0, причем одной из них — в точке А(2; 1).
Решение. Определим диаметр окружности, для чего используем формулу расстояния точки от прямой
![]()
Уравнение прямой 2x+y+15=0, точка А(2; 1)
![]()
Воспользовавшись координатами точки A, можем составить такое уравнение:
(2 – а)²+(1 – b)² = 20.
Второе уравнение с неизвестными а и b получим, определив расстояние точки С от первой прямой
![]()
Поскольку точка С лежит по одну сторону от прямой
Рис. 4
вместе с началом координат, то расстояние АС<0.
Имеем систему уравнений:
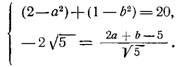
Решая полученную систему уравнений, найдем а=-2; b=-1.
Эту задачу рекомендуем решить самостоятельно другим способом.
Указания. Составить уравнение перпендикуляра А В к данным прямым и найти координаты точки В.
Ответ: (x+2)²+(у + 1)²=20.
Если окружность задана уравнением вида
![]()
найти центр (a;b) и радиус R такой окружности несложно.
Примеры.
Определить по уравнению окружности координаты её центра и радиуса:
![]()
![]()
![]()
![]()
![]()
Решение:
![]()
a=3, b=7, R²=4.
Таким образом, центр данной окружности — точка (3;7), радиус R=2.
![]()
a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.
![]()
a=0, b=-3, R²=9.
Центр окружности — (0;-3), радиус R=3.
![]()
a=6, b=0, R²=5.
Центр — в точке (6;0), радиус R=√5.
![]()
Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.
Чтобы найти центр и радиус окружности, заданной уравнением вида
![]()
нужно дополнить его до полных квадратов, чтобы привести к привычному виду.
Для этого сначала сгруппируем слагаемые
![]()
затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)
![]()
Отсюда
![]()
![]()
При a²+b²-c>0 это уравнение задаёт окружность с радиусом
![]()
При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).
При a²+b²-c<0 нет ни одной точки, удовлетворяющей этому уравнению.
Примеры.
Найти координаты центра и радиус окружности:
![]()
![]()
![]()
Решение:
![]()
Группируем слагаемые
![]()
Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:
![]()
Аналогично
![]()
Таким образом,
![]()
![]()
![]()
Центром этой окружности является точка (-5;3), радиус R=7.
![]()
![]()
![]()
![]()
![]()
Центр окружности — точка (2,5;0), радиус R=1,5.
![]()
Разделим обе части уравнения на 3:
![]()
Далее — аналогично
![]()
![]()
![]()
![]()
![]()
Центр этой окружности лежит в точке
![]()
