Центр окружности найти как точку
Быстрый способ, как найти центр окружности
В данном обзоре автор поделится с нами довольно простым способом, как быстро найти центр окружности.
Для этого нам потребуется всего два предмета: угольник и карандаш. Первым делом необходимо провести прямую линию в любом месте окружности.
Советуем также прочитать: как изготовить своими руками антенну для усиления 4G сигнала на даче или в частном доме.
После того, как начертили линию, измеряем длину, и делим это расстояние ровно пополам.
В данном случае длина линии составляет 210 мм. Разделив ее пополам, получаем 105 мм — ставим в этом месте отметку.
С помощью угольника проводим вторую линию, которая должна быть перпендикулярна первой (то есть проходить под углом 90 градусов).
Основные этапы работ
На следующем этапе проделываем те же операции с другой стороны окружности (только не параллельно, а немного в стороне).
Чертим линию, измеряем ее длину (в данном случае — 218 мм), делим пополам (109 мм) и откладываем в этом месте точку. После этого проводим перпендикулярную линию, как и в предыдущем случае.
Пересечение двух линий, которые мы чертили под углом 90 градусов, и будет являться центром круга.
Подробно об этом способе можно посмотреть на видео ниже. Статья подготовлена на основе видео с YouTube канала « ПОГРАНЕЦ 13 ».
Как найти Как найти центр окружности?
Как найти центр отверстия?
Через точки пересечения дуг проводят две прямые по направлению к центру до их пересечения в точке О. Точка пересечения этих прямых, и будет искомым центром отверстия.
Как найти центр окружности из уравнения?
Уравнение окружности ω (A; R) имеет вид (x – a) 2 + (y – b) 2 = R 2 , где a и b – координаты центра A окружности ω (A; R) .
Чем размечают отверстия?
Размечать центровые отверстия в деталях диаметром до 40 мм лучше при помощи специального приспособления, называемого колоколом. Оно состоит из корпуса, конического раструба и кернера, перемещаемого в корпусе.
Как найти центр окружности на плоской заготовки?
Есть и совсем простой способ нахождения центра плоской заготовки круглой формы. Всего-то нужно обвести её по периметру, положив на лист бумаги, затем вырезать по начерченной линии круг, согнуть его вчетверо и центр будет найден. Он находится точно на линии пересечения сгибов.
Как правильно разметить отверстия?
Разметка отверстий для сверления.
- Определить расположение отверстия по рабочему чертежу. Аккуратно отмерить расстояние отверстия от обоих краев доски. .
- Наколите центр отверстия шилом. .
- Если должны совпасть отверстия, просверленные в двух досках, зажмите обе доски в тисках.
Исследовательская работа по математике: «Как определить центр окружности»
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №1 с. Александров – Гай
Исследовательская работа по математике:
Подготовил: Амиров Марат, ученик 6 «а»
класса МБОУ СОШ №1 с. Александров – Гай
Руководитель: , учитель математики МБОУ СОШ №1 с. Александров — Гай
С. Александров – Гай
Глава 1 «Способы нахождения окружности» …………………………………..4
Глава 2 «Практическая часть»…………………………………………………..6
Список литературы и источников………………………………………………12
Окружность — совокупность точек, находящихся на равном расстоянии от одной точки, называемой центром. Однако в тех случаях, когда вам дана одна только окружность, нахождение ее центра может быть непростой задачей. Поэтому цель моей исследовательской работы: изучить способы определения центра окружности. Исходя из цели были поставлены задачи:
— найти самый простой способ определения центра окружности;
— сравнить несколько способов определения центра окружности;
— практические способы определения центра окружности.
Актуальность ислледовательской работы заключается в том, что в повседневной жизни людей часто приходится находить центр окружности, но не каждый знает как это правильно сделать. Поэтому изучение данной темы поможет найти правильное решение проблемы и определить оптимальный вариант для человека любой професии.
При написании исследовательской работы были использованны электронные источники и литература. Электронные источники помогли найти теоретический материал по теме, а учебники по математике были использованны для подбора задач и практической части работы.
Глава 1. Способы нахождения центра окружности.
1.Самый простой способ нахождения центра окружности — согнуть лист бумаги, на котором она начерчена, следя на просвет, чтобы окружность оказалась сложена точно пополам. Полученная линия сгиба будет одним из диаметров заданной окружности. Затем лист можно согнуть в другом направлении, получив тем самым второй диаметр. Точка их пересечения и будет центром окружности.
2. Для того чтобы найти центр окружности, надо сначала вписать ее в квадрат. То есть все стороны четырехугольника должны касаться круга. Для этого проведите с помощью линейки четыре ровные линии. Теперь соедините по диагонали два противоположных угла. Следите за тем, чтобы линия разбивала угол квадрата на две равные части. Соедините прямыми все 4 угла квадрата. Точка пересечения данных прямых и будет центром окружности.
3. Для любого треугольника центр описанной окружности находится в точке пересечения срединных перпендикуляров. Если этот треугольник — прямоугольный, то центр описанной окружности всегда совпадает с серединой гипотенузы. Следовательно, если вписать в окружность прямоугольный треугольник, то его гипотенуза будет диаметром этой окружности.
В качестве трафарета для этого способа подойдет любой прямой угол — школьный или строительный угольник, или просто лист бумаги. Поместите вершину прямого угла в любую точку окружности и сделайте отметки там, где стороны угла пересекают границу круга. Это конечные точки диаметра.
Тем же способом найдите второй диаметр. В точке их пересечения
4.На круглую деталь накладываем лист бумаги так, что бы один его угол находился на окружности или крае круга. И отмечаем точки, где лист соприкасается другими краями с кругом. Отмечаем эти точки.
Проводим прямую линию между отмеченными точками. Расстояние между ними является диаметром этого круга. Обрезаем лишнюю бумагу и проводим на детали прямую линию — диаметр.
Достаточно переместить наш треугольник в другое положение и нарисовать еще один диаметр круга, как тут же в точке пересечения диаметров мы и получим искомый центр окружности…
5. Диаметр и радиус окружности.
Диаметр окружности — это отрезок прямой, соединяющий пару наиболее удаленных друг от друга точек окружности, проходящий через центр окружности. Слово «диаметр» произошло от греческого слова «diametros» — поперечный. Обычно диаметр обозначается латинской буквой D или значком Ø.
Диаметр можно найти по формуле: D = 2R, где диаметр равен удвоенному радиусу окружности.
Радиус — расстояние от центра до любой точки окружности. Обозначается латинской R.
Если известен радиус окружности, допустим, он равен 8 см, то значит D = 2 * 8 = 16 см.
Радиус окружности определяется по формуле : R=D:2
» width=»390″ height=»299 >
Глава 2 «Практическая часть»
1) Прямой угол детали закруглен дугой радиуса R
Для решения задачи с центром в вершине прямого угла проводят окружность радиуса R, которая пересекает стороны прямого угла в точках А и В.
С центрами в точках А и В строят еще две окружности радиуса R; С – их точка пересечения. Дуга окружности радиуса R с центром в точке С и будет искомым закруглением.
Произвольный угол детали закруглить дугой радиуса R
Решение: На расстоянии R от сторон угла проводят соответствующие параллельные им прямые. О — их пересечение. Затем строим окружность с центром О, радиуса R
Даны две параллельные прямые и точка А между ними. Как построить окружность, касающуюся данных прямых и проходящих через данную точку?
1) Построим любую окружность, касающуюся двух прямых (центр окружности находим, разделив ее пополам)
2) Проведем через А прямую, равную данным. Она пересечет построенную окружность в точках В и С. Перед ними центр построенной окружности на АВ или АС.
Задачи на построение технического рисунка
Как при помощи слесарного разметочного угольника измерить недоступный диаметр круглой детали.
Можно ли прибором, изображенным на рисунке одним прикладыванием найти центр круга?
«Как найти центр окружности?» — вопрос, на который мне пришлось ответить в ходе исследования. Таким образом, я нашел несколько способов построения центра окружности: 1) центроискатель — прямой угол. Принцип работы: вписанный угол опирается на диаметр. 2) Центроискатель — угол с биссектрисой. Принцип работы: диаметр окружности лежит на биссектрисе угла, описанного около этой окружности.3)Центроискатель – пара взаимно перпендикулярных прямых. Принцип работы: диаметр, проведенный в точку касания, перпендикулярен касательной. 4)Центроискатель – пара взаимно перпендикулярных прямых. Принцип работы: хорда, перпендикулярная другой хорде и проходящая через ее середину, есть диаметр.
Соответственно цель моей работы достигнута: изучив несколько способов нахождения центра окружности возможно из каждого выбрать оптимальный вариант.
О, математика земная!
Гордись, прекрасная, собой,
Ты всем наукам мать родная,
И дорожат они тобой.
Твои расчеты величаво
Ведут к планетам корабли
Не ради праздничной забавы,
А ради гордости Земли!
Список использованной литературы и источников
1.Журнал «Математика в школе» №20 1989г.
Как построить окружность?
Как построить окружность?
Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.
Радиусом называется любой отрезок соединяющей точку окружности с ее центром.
Чтобы построить окружность необходимо знать уравнение окружности:
(х – а) 2 + (у – b) 2 = R 2
Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.
И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:
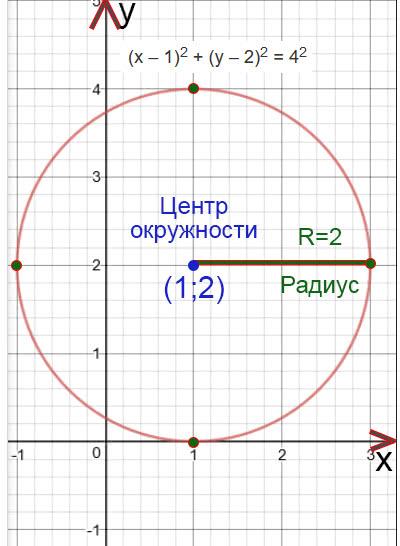
Пример №1:
(х – 1) 2 + (у – 2) 2 = 4 2
Найдем центр окружности:
х – 1=0
x=1
Центр окружности будет находится в точке (1;2)
Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2
Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность. 
Пример №2:
х 2 + (у + 1) 2 =1
Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2
Найдем центр окружности:
х=0
Центр окружности будет находится в точке (0;–1)
Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1
Построим окружность. 
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Круг. Окружность (центр, радиус, диаметр)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Данный урок посвящён изучению окружности и круга. Также учитель научит отличать замкнутые и незамкнутые линии. Вы познакомитесь с основными свойствами окружности: центром, радиусом и диаметром. Выучите их определения. Научитесь определять радиус, если известен диаметр, и наоборот.
[spoiler title=”источники:”]
http://tutomath.ru/uroki/kak-postroit-okruzhnost.html
http://interneturok.ru/lesson/matematika/3-klass/tema-umnozhenie-i-delenie/krug-okruzhnost-tsentr-radius-diametr
[/spoiler]
Download Article
Download Article
Finding the center of a circle can help you perform basic geometric tasks like finding the circumference or area. There are several ways to find the center point! You can draw crossed lines, you can draw overlapping circles, or you can use a straightedge and ruler.
Things You Should Know
- Measure out and draw a set of crossed lines inside of a circle to pinpoint the center.
- Sketch two separate sets of overlapping circles to identify the exact center point.
- Draw a square snugly around the circle. Sketch an “X” between all 4 corners of the square to find the circle’s center.
-
1
Draw a circle. Use a compass, or trace any circular object. The size of the circle does not matter. If you’re finding the center of an existing circle, then you don’t need to draw a new circle.
- A geometry compass is a tool specifically designed to draw and measure circles. Buy one in a school or office supply store![1]
- A geometry compass is a tool specifically designed to draw and measure circles. Buy one in a school or office supply store![1]
-
2
Sketch a chord between two points. A chord is a straight line segment that links any two points along the edge of a curve.[2]
Name the chord AB.- Consider using a pencil to sketch your lines. This way, you can erase the marks once you’ve found the center. Draw with a light touch so that it’ll be easier to erase.
Advertisement
-
3
Draw a second chord. This line should be parallel and equal in length to the first chord that you drew. Name this new chord CD.[3]
-
4
Make another line between A and C. This third chord (AC) should stretch through the center of the circle – but you will need to draw one more line to find the exact center point.
-
5
Join B and D. Draw one final chord (BD) across the circle between Point B and Point D. This new line should cross over the third chord (AC) that you drew.
-
6
Find the center. If you have drawn straight and accurate lines, then the center of the circle lies at the intersection of the crossed lines AC and BD.[4]
Mark the center point with a pen or pencil. If you only want the center point marked, then erase the four chords that you drew.
Advertisement
-
1
Draw a chord between two points. Use a ruler or straightedge to draw a straight line inside the circle, from one edge to another. The points that you use don’t matter. Label the two points A and B.
-
2
Use a compass to draw two overlapping circles. The circles should be the exact same size. Make A the center of one circle, and B the center of the other. Space the two circles so that they overlap like a Venn diagram.
- Draw these circles in pencil, not pen. The process will be simpler if you are able to erase these circles later on.
-
3
Draw a vertical line through the two points at which the circles intersect. There will be a point at the top and a point at the bottom of the “Venn diagram” space created between the overlap of the circles. Use a ruler to make sure that the line protrudes straight through these points. Finally, label the two points (C and D) at which this new line crosses the rim of the original circle. This line marks the diameter of the original circle.
-
4
Erase the two overlapping circles. This should clear up your work space for the next step of the process. Now, you should have a circle with two perpendicular lines running through it. Do not erase the center points (A and B) of these circles! You will be drawing two new circles.
-
5
Sketch two new circles. Use your compass to draw two equal circles: one with the point C at its center, and one with the point D. These circles, too, should overlap like a Venn diagram. Remember: C and D are the points at which the vertical line intersects the main circle.
-
6
Draw a line through the points at which these new circles intersect. This straight, horizontal line should cut through the overlap space of the two new circles. This line is the second diameter of your original circle, and it should be exactly perpendicular to the first diameter line.
-
7
Find the center. The intersection point of the two straight diameter lines is the exact center of the circle! Mark this center point for reference. If you want to clean up the page, feel free to erase the diameter lines and the non-original circles.
Advertisement
-
1
Draw two straight, intersecting tangent lines onto the circle. The lines can be completely random. However, the process will be easier if you make them roughly square or rectangular.[5]
-
2
Translate both of the lines to the other side of the circle. You will end up with four tangent lines forming a parallelogram or a rough rectangle.
-
3
Draw the diagonals of the parallelogram. The point where these diagonal lines intersect is the circle’s center.
-
4
Check the accuracy of the center with a compass. The center should be on target as long as you didn’t slip while translating the lines or when drawing the diagonals. Feel free to erase the parallelogram and diagonal lines.
Advertisement
Practice Problems and Answers
Add New Question
-
Question
How do you find the center of a circle if you’re only given the equation?
David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Academic Tutor
Expert Answer
-
Question
How do you find the center of the circle if you’re only given the endpoints of the diameter?
David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Academic Tutor
Expert Answer
-
Question
In the first method, what do I do if the chords are of different lengths?
It’s not easy to construct parallel chords of equal length. In practice, it would be a process of trial and error until you get the chords you need. But the real goal here is to find the center of a circle, and here’s a way to do it without worrying about equal and parallel chords: (1) draw any two or more chords; (2) perpendicularly bisect each chord (using either a compass or a ruler and right triangle; (3) the perpendicular bisectors will intersect at the circle’s center.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
You can also find the center of a circle by mathematically “completing the square.”[6]
This is useful if you are given a circle equation, but you aren’t working with a physical circle. -
Try using graph paper instead of blank or ruled paper. It might help to have the perpendicular lines and boxes for guidance.
-
If you have right angled square, place the corner anywhere along the circumference. Draw the 2 lines that intersect the circumference. Draw a line between those 2 points. Repeat on any other point on the circle. Where the lines intersect is the centrepoint.
Advertisement
-
A straightedge is not the same as a ruler. A straightedge can be any straight and even surface, but a ruler shows measurements. You can turn a straightedge into a functional ruler by marking it with inch or centimeter increments.
-
In order to find the true center of a circle, you must use a geometric compass and a straightedge.
Advertisement
Things You’ll Need
- Pencil
- Paper
- Straightedge
- Geometric compass
- Grid paper
References
About This Article
Article SummaryX
To find the center of a circle, start by drawing a straight line between 2 points on the circle. Don’t worry about trying to draw the straight line so it’s in the center — anywhere on the circle will do. Then, draw a second straight line that’s parallel to the first line on the opposite side of the circle. Next, draw a diagonal line from the first end of the first line to the opposite end of the second line. Repeat with the other two ends so that you’ve drawn an “X.” The point where the lines intersect is the center of the circle! If you want to learn how to draw overlapping circles to find the center, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 754,687 times.
Reader Success Stories
-
“I had a circular piece of wood that was a circular tabletop that I wanted to use for something else. I needed to…” more
Did this article help you?
Загрузить PDF
Загрузить PDF
Найдя центр круга или окружности, вы сможете решать различные геометрические задачи, например, на вычисление длины окружности или площади круга. Найти центр круга можно разными способами. Вы можете провести пересекающиеся отрезки; вы можете начертить пересекающиеся окружности; вы можете воспользоваться линейками.
-
1
Начертите окружность. Сделайте это при помощи циркуля. Радиус (диаметр) круга может быть любым. Если окружность вам дана, новую окружность чертить не нужно.
- Циркуль – это инструмент, предназначенный для черчения окружностей и их измерения. Циркуль можно купить в канцелярском магазине или в магазине для школьников.[1]
- Циркуль – это инструмент, предназначенный для черчения окружностей и их измерения. Циркуль можно купить в канцелярском магазине или в магазине для школьников.[1]
-
2
Проведите хорду. Хорда – это отрезок, соединяющий любые две точки, лежащие на окружности, и не проходящий через центр окружности.[2]
Обозначьте эту хорду как АВ.- Проводите прямые и отрезки при помощи карандаша, чтобы иметь возможность стереть их после нахождения центра окружности. Не давите на карандаш, чтобы вам было легче стереть нарисованные линии.
-
3
Проведите вторую хорду. Она должна быть параллельна и равна первой хорде АВ. Обозначьте эту хорду как CD.[3]
-
4
Соедините точки А и С. Эта третья хорда АС должна проходить через центр окружности, но для его нахождения вам понадобится провести четвертую хорду.
-
5
Соедините точки B и D. Это четвертая хорда BD, которая должна пересекаться с третьей хордой AC.
-
6
Найдите центр окружности. Если вы правильно провели все отрезки (хорды), то центр окружности – это точка пересечения хорд AC и BD.[4]
Отметьте центр окружности ручкой или карандашом. Если вам нужно отметить только центр окружности, сотрите четыре хорды, которые вы провели ранее.Реклама
-
1
Между двумя точками окружности проведите хорду. Воспользуйтесь линейкой, чтобы соединить две точки на окружности. Точки можно выбрать произвольно. Обозначьте точки как А и В.
-
2
При помощи циркуля начертите две пересекающиеся окружности. Окружности должны быть одного радиуса. Центром первой окружности сделайте точку А, а второй окружности – точку В. Чертите окружности так, чтобы они пересекались наподобие диаграммы Венна.
- Чертите окружности карандашом, а не ручкой, чтобы иметь возможность стереть их.
-
3
Проведите вертикальную прямую через точки пересечения начерченных окружностей. Окружности будут пересекаться в двух точках, которые расположены одна над другой. Проведите прямую при помощи линейки; убедитесь, что обе точки лежат на этой прямой. Точки, в которых эта прямая пересекает исходную окружность, обозначьте как С и D. Отрезок СD является диаметром исходной окружности.
-
4
Сотрите две начерченные вами окружности. Это необходимо для того, чтобы очистить пространство для последующих действий. Теперь на вашем листе останется исходная окружность и два перпендикулярных друг другу отрезка. Не стирайте центры стертых окружностей (эти центры расположены в точках А и В). Далее вы начертите две новые окружности.
-
5
Начертите две новые окружности. Для этого воспользуйтесь циркулем. Центром первой окружности будет точка С, а второй окружности – точка D. Эти окружности также должны пересекаться наподобие диаграммы Венна. Помните, что точки С и D – это точки пересечения вертикальной прямой с исходной окружностью.
-
6
Проведите прямую через две точки, в которых пересекаются начерченные вами окружности. Эта прямая будет расположена горизонтально. Полученный отрезок представляет собой второй диаметр исходной окружности и должен быть перпендикулярен первому диаметру.
-
7
Найдите центр окружности. Точка пересечения двух диаметров является центром исходной окружности. Отметьте эту точку. Если нужно, сотрите начерченные вами окружности и диаметры.
Реклама
-
1
К данной окружности проведите две касательные. Касательные можно провести к двум произвольным точкам окружности. Но вы облегчите себе работу, если проведете касательные под прямым или острым углом друг к другу.[5]
-
2
Теперь проведите еще две касательные, которые будут параллельны касательным, которые вы провели в предыдущем шаге. Таким образом, проведенные четыре касательные образуют подобие параллелограмма или прямоугольника.
-
3
Проведите диагонали параллелограмма. Точка пересечения этих диагоналей является центром окружности.
-
4
Проверьте правильность нахождения центра окружности при помощи циркуля. Центр окружности расположен строго в точке пересечения диагоналей, только если вы не допустили ошибку при проведении параллельных касательных или диагоналей. Сотрите параллелограмм и его диагонали.
Реклама
Советы
- Вместо чистого листа или листа в линейку работайте на листе в клетку. Так вам будет проще проводить перпендикулярные прямые.
- Центр окружности можно вычислить математически через дополнение до полного квадрата.[6]
Это работает в том случае, если вам дано уравнение окружности, а не сама окружность.
Реклама
Предупреждения
- Поверочная линейка немного отличается от обычной линейки. В отличие от обычной линейки на поверочной линейке нет шкалы. Вы можете превратить поверочную линейку в обычную, если нанесете на нее измерительную шкалу.
- Чтобы найти «истинный» центр окружности, используйте циркуль и поверочную линейку.
Реклама
Что вам понадобится
- Карандаш
- Бумага
- Линейка
- Циркуль
Об этой статье
Эту страницу просматривали 231 074 раза.
Была ли эта статья полезной?
Муниципальное
бюджетное общеобразовательное учреждение
средняя
общеобразовательная школа №1 с. Александров – Гай
Исследовательская
работа по математике:
Подготовил:
Амиров Марат, ученик 6 «а»
класса МБОУ СОШ №1 с.
Александров – Гай
Руководитель: Кушкумбаева
С.М., учитель математики МБОУ СОШ №1 с. Александров – Гай
С. Александров – Гай
2012
Содержание
Введение
…………………………………………………………………………..3
Глава
1 «Способы нахождения окружности» …………………………………..4
Глава
2 «Практическая часть»…………………………………………………..6
Заключение
………………………………………………………………………11
Список
литературы и источников………………………………………………12
Введение
Окружность — совокупность точек, находящихся на равном
расстоянии от одной точки, называемой центром. Однако в тех случаях, когда вам
дана одна только окружность, нахождение ее центра может быть непростой задачей. Поэтому
цель моей исследовательской работы: изучить способы определения центра
окружности. Исходя из цели были поставлены задачи:
– найти самый простой способ определения центра окружности;
– сравнить несколько способов определения центра окружности;
– практические способы определения центра окружности.
Актуальность ислледовательской работы заключается в том, что
в повседневной жизни людей часто приходится находить центр окружности, но не
каждый знает как это правильно сделать. Поэтому изучение данной темы поможет
найти правильное решение проблемы и определить оптимальный вариант для человека
любой професии.
При написании исследовательской работы были использованны электронные
источники и литература. Электронные источники помогли найти теоретический
материал по теме, а учебники по математике были использованны для подбора
задач и практической части работы.
Глава 1. Способы
нахождения центра окружности.
1.Самый простой способ нахождения центра окружности —
согнуть лист бумаги, на котором она начерчена, следя на просвет, чтобы окружность оказалась
сложена точно пополам. Полученная линия сгиба будет одним из диаметров заданной
окружности. Затем лист можно согнуть в другом направлении, получив тем самым
второй диаметр. Точка их пересечения и будет центром окружности.
2. Для того чтобы найти центр
окружности, надо сначала вписать ее в квадрат. То есть все стороны
четырехугольника должны касаться круга. Для этого проведите с помощью линейки
четыре ровные линии. Теперь соедините по диагонали два противоположных угла. Следите
за тем, чтобы линия разбивала угол квадрата на две равные части. Соедините
прямыми все 4 угла квадрата. Точка пересечения данных прямых и будет центром
окружности.
3. Для любого
треугольника центр описанной окружности находится в точке пересечения срединных
перпендикуляров. Если этот треугольник — прямоугольный, то центр описанной
окружности всегда совпадает с серединой гипотенузы. Следовательно, если вписать
в окружность прямоугольный треугольник, то его гипотенуза будет диаметром этой
окружности.
В качестве трафарета для этого способа подойдет любой прямой угол — школьный
или строительный угольник, или просто лист бумаги. Поместите вершину прямого
угла в любую точку окружности и сделайте отметки там, где стороны угла
пересекают границу круга. Это конечные точки диаметра.
Тем же способом найдите второй диаметр. В точке их пересечения
4.На круглую деталь
накладываем лист бумаги так, что бы один его угол находился на окружности или
крае круга. И отмечаем точки, где лист соприкасается другими краями с кругом.
Отмечаем эти точки.
Проводим прямую линию между
отмеченными точками. Расстояние между ними является диаметром этого круга.
Обрезаем лишнюю бумагу и проводим на детали прямую линию – диаметр.
Достаточно переместить наш
треугольник в другое положение и нарисовать еще один диаметр круга, как тут же
в точке пересечения диаметров мы и получим искомый центр окружности…
5.
Диаметр и радиус окружности.
Диаметр
окружности — это отрезок прямой, соединяющий пару наиболее удаленных друг от
друга точек окружности, проходящий через центр окружности. Слово
“диаметр” произошло от греческого слова “diametros” –
поперечный. Обычно диаметр обозначается латинской буквой D или значком Ø.
Диаметр можно найти
по формуле: D = 2R, где диаметр равен удвоенному радиусу окружности.
Радиус – расстояние от центра до любой точки окружности. Обозначается латинской
R.
Если известен радиус окружности, допустим, он равен 8 см, то значит D = 2 * 8 =
16 см.
Радиус окружности
определяется по формуле : R=D:2
Глава 2 «Практическая часть»
Задача 1.
1) Прямой
угол детали закруглен дугой радиуса R
Для решения задачи
с центром в вершине прямого угла проводят окружность радиуса R,
которая пересекает стороны прямого угла в точках А и В.
С
центрами в точках А и В строят еще две окружности радиуса R;
С – их точка пересечения. Дуга окружности радиуса R с центром в точке С и будет искомым закруглением.
Задача
2
Произвольный угол
детали закруглить дугой радиуса R
Решение: На расстоянии R от сторон
угла проводят соответствующие параллельные им прямые. О- их пересечение. Затем
строим окружность с центром О, радиуса R
Задача 3.
Даны две
параллельные прямые и точка А между ними. Как построить окружность, касающуюся
данных прямых и проходящих через данную точку?
Решение:
1)
Построим любую окружность, касающуюся двух
прямых (центр окружности находим, разделив ее пополам)
2)
Проведем через А прямую, равную данным.
Она пересечет построенную окружность в точках В и С. Перед ними центр
построенной окружности на АВ или АС.
Задачи
на построение технического рисунка
Задача 4.
Как при помощи слесарного
разметочного угольника измерить недоступный диаметр круглой детали.
Задача 5
Можно ли прибором,
изображенным на рисунке одним прикладыванием найти центр круга?
Заключение
«Как найти центр окружности?» – вопрос, на
который мне пришлось ответить в ходе исследования. Таким образом, я нашел
несколько способов построения центра окружности: 1) центроискатель – прямой
угол. Принцип работы: вписанный угол опирается на диаметр. 2) Центроискатель -угол
с биссектрисой. Принцип работы: диаметр окружности лежит на биссектрисе угла,
описанного около этой окружности.3)Центроискатель – пара взаимно
перпендикулярных прямых. Принцип работы: диаметр, проведенный в точку касания,
перпендикулярен касательной. 4)Центроискатель – пара взаимно перпендикулярных
прямых. Принцип работы: хорда, перпендикулярная другой хорде и проходящая через
ее середину, есть диаметр.
Соответственно цель моей работы
достигнута: изучив несколько способов нахождения центра окружности возможно из
каждого выбрать оптимальный вариант.
О, математика земная!
Гордись, прекрасная, собой,
Ты всем наукам мать родная,
И дорожат они тобой.
Твои расчеты величаво
Ведут к планетам корабли
Не ради праздничной забавы,
А ради гордости Земли
!
Список
использованной литературы и источников
1.Журнал
«Математика в школе» №20 1989г.
Как найти координаты центр окружности??
Ученик
(176),
закрыт
7 лет назад
Video
Просветленный
(28010)
10 лет назад
Инструкция
1
Аналитически окружность задается уравнением вида (x-x0)²+(y-y0)²=R², где x0 и y0 − координаты центра окружности, R − ее радиус. Итак, центр окружности (x0;y0) здесь задан в явном виде.
2
Пример. Установите центр фигуры, заданной в декартовой системе координат уравнением (x-2)²+(y-5)²=25.
Решение. Данное уравнение является уравнением окружности. Ее центр имеет координаты (2;5). Радиус такой окружности равен 5.
3
Уравнение x²+y²=R² соответствует окружности с центром в начале координат, то есть, в точке (0;0). Уравнение (x-x0)²+y²=R² означает, что центр окружности имеет координаты (x0;0) и лежит на оси абсцисс. Вид уравнения x²+(y-y0)²=R² говорит о расположении центра с координатами (0;y0) на оси ординат.
4
Общее уравнение окружности в аналитической геометрии запишется как: x²+y²+Ax+By+C=0. Чтобы привести такое уравнение к выше обозначенному виду, надо сгруппировать члены и выделить полные квадраты: [x²+2(A/2)x+(A/2)²]+[y²+2(B/2)y+(B/2)²]+C-(A/2)²-(B/2)²=0. Для выделения полных квадратов, как можно заметить, требуется добавлять дополнительные величины: (A/2)² и (B/2)². Чтобы знак равенства сохранялся, эти же величины надо вычесть. Прибавление и вычитание одного и того же числа не меняет уравнения.
5
Таким образом, получается: [x+(A/2)]²+[y+(B/2)]²=(A/2)²+(B/2)²-C. Из этого уравнения уже видно, что x0=-A/2, y0=-B/2, R=√[(A/2)²+(B/2)²-C]. Кстати, выражение для радиуса можно упростить. Домножьте обе части равенства R=√[(A/2)²+(B/2)²-C] на 2. Тогда: 2R=√[A²+B²-4C]. Отсюда R=1/2·√[A²+B²-4C].
6
Окружность не может быть графиком функции в декартовой системе координат, так как, по определению, в функции каждому x соответствует единственное значение y, а для окружности таких «игреков» будет два. Чтобы убедиться в этом, проведите перпендикуляр к оси Ox, пересекающий окружность. Вы увидите, что точек пересечения две.
7
Но окружность можно представить как объединение двух функций: y=y0±√[R²-(x-x0)²]. Здесь x0 и y0, соответственно, представляют собой искомые координаты центра окружности. При совпадении центра окружности с началом координат объединение функций принимает вид: y=√[R²-x²].
