Как найти центр описанной окружности прямоугольного треугольника

Описанная окружность — подробнее

Определение

Описанная окружность – такая окружность, что проходит через все три вершины треугольника, около которого она описана.

Свойства и центр описанной кружности

И вот, представь себе, имеет место удивительный факт:

Вокруг всякого треугольника можно описать окружность.

Почему этот факт удивительный?

Потому что треугольники ведь бывают разные!

И для всякого найдётся окружность, которая пройдёт через все три вершины, то есть описанная окружность.

Доказательство этого удивительного факта мы приведем чуть позже, а здесь заметим только, что если взять, к примеру, четырехугольник, то уже вовсе не для всякого найдётся окружность, проходящая через четыре вершины.

Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!

А есть только для прямоугольника:

Подробнее об этом смотри в статье о вписанных четырехугольниках!

Ну вот, а треугольник всякий и всегда имеет собственную описанную окружность! И даже всегда довольно просто найти центр этой окружности.

Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника.

Знаешь ли ты, что такое серединный перпендикуляр?

Серединный перпендикуляр — это прямая, проходящая через середину отрезка и перпендикулярная ему.

Прямая ( displaystyle a) – это серединный перпендикуляр к отрезку ( displaystyle AB).

А теперь посмотрим, что получится, если мы рассмотрим целых три серединных перпендикуляра к сторонам треугольника.

Вот оказывается (и это как раз и нужно доказывать, хотя мы и не будем), что все три перпендикуляра пересекутся в одной точке. Смотри на рисунок – все три серединных перпендикуляра пересекаются в одной точке ( displaystyle O).

Это и есть центр описанной около (вокруг) треугольника ( displaystyle ABC) окружности.

Как ты думаешь, всегда ли центр описанной окружности лежит внутри треугольника? Представь себе – вовсе не всегда!

Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи!

Вот так:

А вот если остроугольный, то внутри:

Что же делать с прямоугольным треугольником?

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.

Здорово, правда?

Если треугольник – прямоугольный, то не надо строить аж три перпендикуляра, а можно просто найти середину гипотенузы – и центр описанной окружности готов!

Да ещё с дополнительным бонусом:

В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.

Раз уж заговорили о радиусе описанной окружности: чему он равен для произвольного треугольника? И есть ответ на этот вопрос: так называемая теорема синусов.

А именно:

В произвольном треугольнике:
( Large displaystyle frac{a}{sin angle A}=2R)

Ну и, конечно,

( displaystyle begin{array}{l}frac{b}{sin angle B}=2R\frac{c}{sin angle C}=2Rend{array})

Так что ты теперь всегда сможешь найти и центр , и радиус окружности, описанной вокруг треугольника.

То есть чтобы найти радиус описанной окружности, нужно знать одну (!) сторону и один (!) противолежащий ей угол.

Хорошая формула? По-моему, просто отличная!

Доказательство теоремы

Теорема. Вокруг всякого треугольника можно описать окружность, при том единственным образом.

Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.

Смотри, вот так:

opisannaya okruzhnost vokrug okolo treugolnika

Давай наберёмся мужества и докажем эту теорему.

Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.

Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).

Геометрическое место точек, обладающих свойством «( displaystyle X)» — такое множество точек, что все они обладают свойством «( displaystyle X)» и никакие другие точки этим свойством не обладают.

Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы.

А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют.

В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:

Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудалённых от концов отрезка.

Тут множество – это серединный перпендикуляр, а свойство «( displaystyle X)» — это «быть равноудаленной (точкой) от концов отрезка».

Проверим? Итак, нужно удостовериться в двух вещах:

Всякая точка на серединном перпендикуляре находится на одинаковом расстоянии от концов отрезка
Всякая точка, которая равноудалена от концов отрезка – находится на серединном перпендикуляре к ему

Приступим:

Проверим 1. Пусть точка ( displaystyle M) лежит на серединном перпендикуляре к отрезку ( displaystyle AB).

Соединим ( displaystyle M) с ( displaystyle A) и с ( displaystyle B).Тогда линия ( displaystyle MK) является медианой и высотой в ( displaystyle Delta AMB).

Значит, ( displaystyle Delta AMB) – равнобедренный, ( displaystyle MA=MB) – убедились, что любая точка ( displaystyle M), лежащая на серединном перпендикуляре, одинаково удалена от точек ( displaystyle A) и ( displaystyle B).

Теперь 2. Почти точно так же, но в другую сторону. Пусть точка ( displaystyle M) равноудалена от точек ( displaystyle A) и ( displaystyle B), то есть ( displaystyle MA=MB).

Возьмём ( displaystyle K) – середину ( displaystyle AB) и соединим ( displaystyle M) и ( displaystyle K). Получилась медиана ( displaystyle MK). Но ( displaystyle Delta AMB) – равнобедренный по условию ( displaystyle (MA=MB)Rightarrow MK) не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка ( displaystyle M) — точно лежит на серединном перпендикуляре.

Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.

Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».

Рассмотрим треугольник ( displaystyle ABC). Проведём два серединных перпендикуляра ( displaystyle {{a}_{1}}) и ( displaystyle {{a}_{2}}), скажем, к отрезкам ( displaystyle AB) и ( displaystyle BC). Они пересекутся в какой-то точке, которую мы назовем ( displaystyle O).

А теперь, внимание!

Точка ( displaystyle O) лежит на серединном перпендикуляре ( displaystyle {{a}_{1}}Rightarrow OA=OB);
точка ( displaystyle O) лежит на серединном перпендикуляре ( displaystyle {{a}_{2}}Rightarrow OB=OC).
И значит, ( displaystyle OA=OB=OC) и ( displaystyle OA=OC).

Отсюда следует сразу несколько вещей:

Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 6. Описанная окружность. Многоугольники

Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства.

Около каких фигур можно, а вокруг каких нельзя описать окружность.

Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.

Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.

ЕГЭ 6. Вписанная окружность

В этом видео мы узнаем, что такое вписанная окружность, где находится её центр, и другие свойства.

В какие фигуры можно, а в какие нельзя вписать окружность. Научимся решать задачи на вписанную окружность.

Источник

Окружность вписана в n-угольник, если она касается всех сторон этого n-угольника (рис. 8.106).

Окружность описана около n-угольника, если все вершины n-угольника лежат на окружности (рис. 8.107).

Свойства вписанной окружности

1. Окружность можно вписать в любой треугольник.

2. Окружность можно вписать в четырехугольник, если суммы длин его противолежащих сторон равны.

Например, на рисунке 8.106 .

Так, окружность можно вписать в квадрат и в ромб, но нельзя вписать в параллелограмм и в прямоугольник.

Свойства описанной окружности

1. Окружность можно описать около любого треугольника.

2. Окружность можно описать около четырехугольника, если суммы его противолежащих углов равны.

Например, на рисунке 8.107 $LaTeX formula: angle A+angle C=angle B+angle D=180^{circ}$ .

Так, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

Расположение центров окружностей, описанных около треугольника:

1) центр окружности расположен на пересечении серединных перпендикуляров к сторонам треугольника;

2) если треугольник остроугольный, то центр окружности расположен в этом треугольнике:

а) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают (рис. 8.108);

б) в равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию (рис. 8.109);

3) если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы (рис. 8.110);

4) если треугольник тупоугольный, то центр окружности расположен вне треугольника (рис. 8.111).

Расположение центров окружностей, вписанных в треугольник:

1) центр окружности, вписанной в треугольник, расположен в этом треугольнике (рис. 8.112 – 8.115);

2) центром окружности является точка пересечения биссектрис треугольника;

3) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника.

Формулы для вычисления радиусов вписанной и описанной окружностей

Радиус окружности, описанной около многоугольника, как правило, обозначают , а радиус окружности, вписанной в многоугольник, обозначают :

1) для равностороннего треугольника со стороной :

$LaTeX formula: R=frac{a}{sqrt{3}}$ , (8.34)

$LaTeX formula: r=frac{a}{2sqrt{3}}$ ; (8.35)

2) для произвольного треугольника со сторонами и площадью :

$LaTeX formula: R=frac{abc}{4S}$ , (8.36)

$LaTeX formula: r=frac{2S}{a+b+c}$ ; (8.37)

3) для прямоугольного треугольника с катетами и гипотенузой :

$LaTeX formula: R=frac{c}{2}$ , (8.38)

$LaTeX formula: r=frac{a+b-c}{2}$ ; (8.39)

4) для квадрата со стороной и диагональю :

$LaTeX formula: R=frac{d}{2}$ , (8.40)

$LaTeX formula: r=frac{a}{2}$ ; (8.41)

5) для прямоугольника с диагональю :

$LaTeX formula: R=frac{d}{2}$ ; (8.42)

6) для ромба с высотой :

$LaTeX formula: r=frac{h}{2}$ ; (8.43)

7) для трапеции с высотой , при условии, что в трапецию можно вписать окружность:

$LaTeX formula: r=frac{h}{2}$ . (8.44)

Если около трапеции можно описать окружность, то, проведя диагональ трапеции и рассмотрев один из полученных треугольников со сторонами и площадью , по формуле $LaTeX formula: R=frac{abc}{4S}$ найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);

8) для правильного шестиугольника со стороной :

, (8.45)

$LaTeX formula: r=frac{asqrt{3}}{2}$ . (8.46)

Правильный шестиугольник состоит из шести правильных треугольников (рис. 8.117) и точка является центром вписанной в него и описанной около него окружностей.

Пример 1. Найдите сторону квадрата, если известно, что разность между площадью квадрата и площадью вписанного в него круга равна .

Решение. Так как площадь круга радиуса находят по формуле 8.32, а площадь квадрата со стороной находят по формуле $LaTeX formula: S=a^{2}$ , то согласно условию задачи запишем: $LaTeX formula: S_{square }-S_{bigcirc }=12$ , $LaTeX formula: pi r^{2}-a^{2}=2pi -8$ .

А так как $LaTeX formula: r=frac{a}{2}$ , то $LaTeX formula: frac{pi a^{2}}{4}-a^{2}=2pi -8$ , $LaTeX formula: pi a^{2}-4a^{2}=4(2pi -8)$ , $LaTeX formula: a^{2}(pi -4)=8(pi -4)$ , $LaTeX formula: a^{2}=8$ , .

Ответ: .

Пример 2. Площадь прямоугольника равна 4, а разность длин его смежных сторон рана 3. Найдите радиус окружности, описанной около этого прямоугольника.

Решение. Площадь прямоугольника со смежными сторонами и находят по формуле .

Пусть , тогда (рис. 8.118).

Получим: , $LaTeX formula: x^{2}+3x-4=0$ , откуда , следовательно, , .

По теореме Пифагора найдем диагональ прямоугольника: $LaTeX formula: d^{2}=1+16=17$ , . Согласно формуле 8.42 .

Ответ: .

Пример 3. Найдите радиус окружности, вписанной в ромб, если его диагонали равны 6 и 8.

Решение. По теореме Пифагора найдем сторону ромба (рис. 8.119):

$LaTeX formula: a^{2}=left (frac{d_{1}}{2} right )^{2}+left ( frac{d_{2}}{2} right )^{2}$ , $LaTeX formula: a^{2}=3^{2}+4^{2}$ , .

По формуле 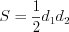$LaTeX formula: S=frac{1}{2}d_{1}d_{2}$ найдем площадь ромба: $LaTeX formula: S=frac{1}{2}cdot 6cdot 8=24$ .

Но площадь ромба можно найти и по формуле , а так как , то . Тогда , а .

Ответ: 2,4.

Пример 4. Найдите длину окружности, вписанной в правильный треугольник, если его площадь равна .

Решение. Площадь правильного треугольника со стороной находят по формуле: $LaTeX formula: S=frac{sqrt{3}a^{2}}{4}$ .

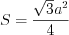Зная площадь треугольника, найдем его сторону: $LaTeX formula: frac{sqrt{3}a^{2}}{4}=4sqrt{3}$ , $LaTeX formula: a^{2}=16$ , .

По формуле 8.35 найдем радиус окружности, вписанной в этот треугольник: $LaTeX formula: r=frac{4}{2sqrt{3}}=frac{2}{sqrt{3}}$ .

По формуле 8.30 найдем длину окружности: $LaTeX formula: C=frac{4pi }{sqrt{3}}$ .

Ответ: $LaTeX formula: frac{4sqrt{3}pi }{3}$ .

Пример 5. Радиус окружности, описанной около равнобедренного прямоугольного треугольника равен 2. Найдите радиус окружности, вписанной в этот треугольник.

Решение. Радиус окружности, описанной около прямоугольного треугольника с гипотенузой находят по формуле 8.38. Тогда .

Так как треугольник равнобедренный, то его катеты и раны и по теореме Пифагора $LaTeX formula: c^{2}=2a^{2}$ , откуда $LaTeX formula: a=frac{C}{sqrt{2}}$ , $LaTeX formula: a=frac{4}{sqrt{2}}=2sqrt{2}$ .

Радиус окружности, вписанной в прямоугольный треугольник, находят по формуле 8.39. В нашем случае $LaTeX formula: r=frac{2a-c}{2}$ , $LaTeX formula: r=frac{4sqrt{2}-4}{2}=2sqrt{2}-2$ .

Ответ: .

Пример 6. Один из катетов прямоугольного треугольника равен 8, а радиус окружности, вписанной в треугольник равен 3. Найдите площадь треугольника.

Решение. Рассмотрим прямоугольный треугольник . Точка является центром вписанной в треугольник окружности (рис. 8.120).

Так как радиусы вписанной в треугольник окружности перпендикулярны сторонам треугольника в точках касания, то имеем квадрат со стороной 3. Если катет , а сторона квадрата , то .

Пусть отрезок . По свойству касательных и .

Тогда по теореме Пифагора $LaTeX formula: BC^{2}=AC^{2}+AB^{2}$ или $LaTeX formula: 25+10x+x^{2}=64+9+6x+x^{2}$ , откуда , .

Найдем катет : .

Найдем площадь треугольника: $LaTeX formula: S_{Delta ABC}=frac{1}{2}cdot ACcdot AB$ , $LaTeX formula: S_{Delta ABC}=frac{1}{2}cdot 8cdot 15=60$ .

Ответ: 60.

Пример 7. Окружность, центр которой расположен на большей стороне треугольника, делит эту сторону на отрезки 4 и 8 и касается двух других его сторон, длина одной из которых равна 6. Найдите радиус окружности, вписанной в этот треугольник (рис.8.121).

Решение. Согласно свойству биссектрисы треугольника запишем: $LaTeX formula: frac{6}{4}=frac{x}{8}$ , откуда .

Радиус окружности, вписанной в треугольник, найдем по формуле 8.37.

В свою очередь по формуле Герона найдем площадь треугольника. Так как , то .

Тогда $LaTeX formula: r=frac{18sqrt{15}}{30}=frac{3sqrt{15}}{5}=0,6sqrt{15}$ .

Ответ: .

Пример 8. В прямоугольную трапецию вписана окружность радиуса 3, которая в точке касания делит ее боковую сторону на отрезки 4 и 5. Найдите площадь трапеции.

Решение. Согласно условию задачи и рисунку 8.122, запишем: , .

По свойству четырехугольника, описанного около окружности, получим: , , .

Согласно формуле 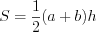$LaTeX formula: S=frac{1}{2}(a+b)h$ найдем площадь трапеции: $LaTeX formula: S=frac{1}{2}cdot 15cdot 6=45$ .

Ответ: 45.

Пример 9. Длины оснований равнобедренной трапеции относятся как , а длина ее высоты равна 17. Вычислите площадь круга, описанного около трапеции, если известно, что средняя линия трапеции равна ее высоте.

Решение. Рассмотрим равнобедренную трапецию (рис. 8.123) и проведем диагональ трапеции .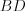

Радиус окружности, описанной около треугольника , найдем по формуле 8.36:

$LaTeX formula: R=frac{ABcdot BDcdot AD}{4cdot S_{triangle ABD}}=frac{ABcdot BDcdot AD}{4cdot frac{1}{2}cdot ADcdot BN}$ , $LaTeX formula: R=frac{ABcdot BD}{2cdot BN}$ .

Зная, что и вводя коэффициент пропорциональности , получим , .

Так как длина средней линии трапеции равна высоте трапеции, то $LaTeX formula: frac{1}{2}(5k +12k)=17$ , откуда . Тогда , .

Поскольку четырехугольник является прямоугольником, то , тогда $LaTeX formula: AN=KD=frac{1}{2}(24-10)=7$ .

Согласно теореме Пифагора запишем:

$LaTeX formula: AB=sqrt{AN^{2}+BN^{2}}$ , $LaTeX formula: AB=sqrt{17^{2}+7^{2}}=sqrt{338}$ ;

$LaTeX formula: BD=sqrt{BN^{2}+ND^{2}}$ , $LaTeX formula: BD=sqrt{17^{2}+17^{2}}=17sqrt{2}$ .

По формуле 8.36 найдем радиус окружности, описанной около треугольника , а, следовательно, и около трапеции :

$LaTeX formula: R=frac{sqrt{338}cdot 17sqrt{2}}{2cdot 17}=frac{2cdot 13}{2}=13$ .

Согласно формуле 8.32 найдем площадь круга: .

Ответ: .

Пример 10. В правильный шестиугольник вписана окружность и около него описана окружность. Найдите площадь образовавшегося кольца, если сторона шестиугольника равна .

Решение. По формуле 8.45 найдем радиус окружности, описанной около правильного шестиугольника: .

По формуле 8.46 найдем радиус окружности, вписанной в этот шестиугольник. Так как , то $LaTeX formula: r=frac{3}{2}$ .

Площадь круга находят по формуле 8.32. Тогда $LaTeX formula: S_{1}=3pi$ , а $LaTeX formula: S_{2}=frac{9pi}{4}$ .

Найдем площадь кольца: $LaTeX formula: S_{K}=S_{1}-S_{2}$ , $LaTeX formula: S_{K}=3pi -frac{9pi }{4}=frac{3pi }{4}$ .

Ответ: .

1. В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.

2. Не во всякий четырехугольник можно вписать окружность. Например, окружность можно вписать в ромб и квадрат, но нельзя вписать в параллелограмм и прямоугольник.

3. Не около всякого четырехугольника можно описать окружность. Например, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

4. Не во всякую трапецию можно писать окружность и не около всякой трапеции можно описать окружность. Описать окружность можно только около равнобедренной трапеции.

5. Если многоугольник правильный (все его стороны и все его углы равны между собой), то в него всегда можно вписать окружность и около него всегда можно описать окружность. Причем, центры этих окружностей совпадают.

Длину окружности радиуса находят по формуле:

. (8.30)

Площадь круга радиуса находят по формуле:

$LaTeX formula: S=pi R^{2}$ . (8.32)

Источник

Как описать окружность около прямоугольного треугольника

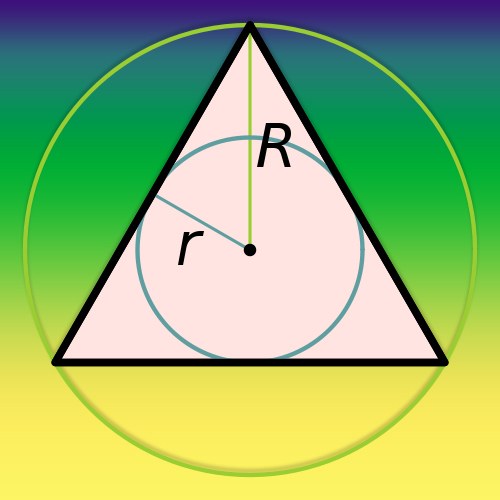
Треугольник – простейшая из плоских многоугольных фигур. Если величина какого-либо угла в его вершинах равна 90°, то треугольник называется прямоугольным. Около такого многоугольника можно начертить круг таким способом, чтобы каждая из трех вершин имела одну общую точку с его границей (окружностью). Эта окружность будет называться описанной, а наличие прямого угла значительно упрощает задачу ее построения.

Вам понадобится

Линейка, циркуль, калькулятор.

Инструкция

Начните с определения радиуса окружности, которую надо будет построить. Если есть возможность измерить длины сторон треугольника, то обратите внимание на его гипотенузу – сторону, лежащую напротив прямого угла. Измерьте ее и разделите полученное значение пополам – это и будет радиус описываемой около прямоугольного треугольника окружности.

Если длина гипотенузы неизвестна, но есть длины (a и b) катетов (двух сторон, прилегающих к прямому углу), то радиус (R) найдите с использованием теоремы Пифагора. Из нее вытекает, что этот параметр будет равен половине квадратного корня, извлеченного из суммы возведенных в квадрат длин катетов: R=½*√(a²+b²).

Если известна длина лишь одного из катетов (a) и величина прилегающего к нему острого угла (β), то для определения радиуса описанной окружности (R) используйте тригонометрическую функцию – косинус. В прямоугольном треугольнике она определяет соотношение длин гипотенузы и этого катета. Рассчитайте половину частного от деления длины катета на косинус известного угла: R=½*a/cos(β).

Если кроме длины одного из катетов (a) известна величина острого угла (α), лежащего напротив него, то для вычисления радиуса (R) воспользуйтесь другой тригонометрической функцией – синусом. Кроме замены функции и стороны в формуле ничего не изменится – разделите длину катета на синус известного острого угла, а результат поделите пополам: R=½*b/sin(α).

После нахождения радиуса любым из перечисленных способов определите центр описываемой окружности. Для этого отложите на циркуле полученное значение и установите его в любую вершину треугольника. Описывать полный круг нет необходимости, просто отметьте место его пресечения с гипотенузой – эта точка и будет центром окружности. Таково свойство прямоугольного треугольника – центр описанной около него окружности всегда находится в середине его самой длинной стороны. Начертите круг отложенного на циркуле радиуса с центром в найденной точке. На этом построение будет завершено.

Источники:

Описанная окружность для прямоугольного треугольника

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

ВИДЕОУРОК

Вписанная окружность
прямоугольного треугольника.

Радиус окружности,
вписанной в прямоугольный треугольник,

можно найти по формуле:

где r –
искомый радиус, а и b – катеты,

с – гипотенуза треугольника.

Радиус вписанной в
прямоугольный треугольник окружности

равен произведению катетов, делённому на сумму
катетов и гипотенузы,

где r –
искомый радиус, а и b – катеты,

с – гипотенуза треугольника.

Радиус вписанной в
прямоугольный треугольник окружности равен площади этого треугольника, делённой
на полупериметр:

где р – полупериметр

ЗАДАЧА:

Точка касания окружности, вписанной в прямоугольный треугольник,
делит один из катетов на отрезки 2 см и 8 см,
отсчитывая от вершины прямого угла. Найдите периметр треугольника.

РЕШЕНИЕ:

Начертим чертёж:

ВМ
= ВN = х.

(2 + х)² + (2 + 8)² = (8
+ х)²,

х² + 4х + 4
+ 100 =

= х² + 16х + 64,

12х = 40,

х =
¹⁰/₃ (см).

Р = (2 + 8) + (8 + ¹⁰/₃) + (¹⁰/₃ + 2) = 26²/₃ (см).

ЗАДАЧА:

Вписанная окружность прямоугольного треугольника АВС касается гипотенузы АВ в точке
К. Найдите радиус
вписанной окружности, если АК = 4 см, ВК
= 6 см.

РЕШЕНИЕ:

За свойством касательных имеем:

АК = АМ = 4 см,
ВК = ВN = 6 см.

Обозначим радиус вписанной окружности
через х:

СN = СM = NО = МО = х.

Тогда

АС =
(4 + х) см.
ВС = (6 + х) см,

АВ =
4 см +
6 см =
10 см.

По теореме Пифагора для треугольника АВС
можно записать соотношение:

(4 + х)² + (6 + х)² = 10².

Решим это квадратное уравнение:

16 + 8x + x²
+ 36 + 12x + x² = 100,

2x² + 20x + 52 – 100 = 0,

2x² + 20x – 48 = 0,

x² + 10x – 24 = 0,

x₁ = 2, x₂ = –10.

x₂не
удовлетворяет условию задачи.

ОТВЕТ: 2 см.

ЗАДАЧА:

Точка касания окружности, вписанной в прямоугольный треугольник,
делить гипотенузу на отрезки 8 см и 12
см. Найдите периметр треугольника.

РЕШЕНИЕ:

Начертим чертёж:

(8 + 12)²
= (8 + х)² + (12 + х)²,

400 = 64 + 16x + x²
+ x² + 24x + 144,

2x² + 40x – 192 = 0,

x² + 20x – 96 = 0,

x₁ = 4, x₂ = –24.

x₂не
подходит.

Р
= 8 + 12 + 12 + 4 + 4 + 8 = 48 (см).

ОТВЕТ: 48 см.

Описанная окружность
прямоугольного треугольника.

Центром окружности, описанной
вокруг прямоугольного треугольника, будет середина его гипотенузы.

Диаметр окружности,
описанной вокруг прямоугольного треугольника, равен его гипотенузе.

Медиана прямоугольного
треугольника, проведённая к его гипотенузе, равна половине гипотенузы и
является радиусом окружности, описанной около этого треугольника.

ОА = ОВ = ОС = R

Радиус описанной окружности равен половине
гипотенузы:

ЗАДАЧА:

Отрезок ВС – диаметр окружности, изображённой на рисунку.

Угол АВС = 55°.

Найдите
величину
угла АСВ
?

РЕШЕНИЕ:

ВС – диаметр,
поэтому ∠ ВАС = 90°,

∠ АСВ = 180° – (90° + 55°) = 35°.

ЗАДАЧА:

Перпендикуляр,
опущенный из точки окружности на его диаметр, делит диаметр на отрезки, разность
между которыми равна 5 см. Найдите радиус окружности, если длина перпендикуляра равна 6 см.

РЕШЕНИЕ:

Пусть АВ – диаметр окружности с
центром в точке О, СD ⊥ АВ,

где С – точка окружности,

СD = 6 см, АD = х см,

ВD – АD = 5 см.

Тогда

DВ = (х + 5) см.

Треугольник АСВ – прямоугольный (угол С прямой, так как
он вписанный и опирается на диаметр).

СD – перпендикуляр, проведений из вершины прямого угла на
гипотенузу. Тогда:

АD ∙ DВ = СD²,

х(х + 5) = 6²,

х²
+ 5х – 36 = 0,

x₁ = –9, x₂ = 4.

x₁не подходит.

Поэтому, АD = 4 см,

DВ = 4 + 5 = 9 (см).

АВ
= АD
+ DВ
=

=
4
+ 9 = 13 (см).

Тогда

r = АВ :
2 = 13 : 2 = 6,5 (см).

ОТВЕТ: 6,5 см

ЗАДАЧА:

Из точки на окружности проведены две перпендикулярные
хорды, разность между которыми равна 4 см. Найдите эти хорды, если радиус окружности равен 10
см.

РЕШЕНИЕ:

Пусть задана окружность радиуса R,

в
которой
проведены
хорды АВ и
АС (АВ ⊥ АС),

R = АО = ВО = СО =
10 см,

АС – АВ =
4
см.

Пусть АВ = х см, тогда

АС = (4
+ х) см.

Так как ∠ А = 90°, то треугольник
ВАС –
прямоугольный,
в
котором

ВС = 2ОВ= 2 ∙ 10 = 20 см.

Из
прямоугольного треугольника ВАС имеем:

АВ² + АС²
= ВС²,

х² + (4 + х)²
= 20²,

х² + 16 + 8х
+ х² = 400,

х² + 4х –
192 = 0,

х₁ = 12,

х₂
= –16 – не подходит.

Поэтому,
АВ = 12 см,

АС
= 4 + 12 = 16 (см).

ОТВЕТ: 12
см, 16 см

ЗАДАЧА:

Угол между биссектрисой и
медианой прямоугольного треугольника, проведёнными из вершины прямого угла,
равен 14°.
Найдите меньший угол этого треугольника.

РЕШЕНИЕ:

Начертим чертёж.

Так как треугольник
прямоугольный и медиана ВМ иcходит
из прямого угла В, то точка М является центром
описанной окружности вокруг треугольника
АВС.
Следовательно,

АМ
= МС = МВ = R,

где R –
радиус описанной окружности.

Найдём сначала угол МВС.
Учитывая, что BD – биссектриса, то

∠ DВС = ⁹⁰/₂ = 45°. Тогда

∠ МВС = ∠ МВD + ∠ DВС,

∠ МВС = 14° + 45° = 59°.

Рассмотрим
равнобедренный треугольник МВС со сторонами

МВ = МС,

в
котором углы при основании ВС равны, то есть

∠ С = ∠ МВС
= 59°.

Так
как сумма острых углов в прямоугольном треугольнике равна 90°, то

∠ А + ∠ С = 90°,

∠ А = 90° – ∠ С =

= 90° – 59° = 31°.

ЗАДАЧА:

Периметр
прямоугольного треугольника равен 72 м, а радиус вписанной в него окружности – 6 м. Найдите диаметр описанной окружности.

РЕШЕНИЕ:

DO = OF = OE = r = 6 м.

Поэтому AD =
AF =
6 м.

FC = EC, BD = BE (отрезки касательных, проведённых из
одной точки)

Пусть

BD = BE = x,

FC = EC = y,

Тогда

AB
= x + 6, AC = y + 6,

BC = x + y.

AB + AC + BC =

= x + 6 + y + 6
+ x + y = 72.

2x + 2y + 12 = 72,

2x + 2y = 60,

x + y = 30.

(x + y) – гипотенуза, или диаметр описанной окружности.

ОТВЕТ: 30 м.

ЗАДАЧА:

В окружности на расстоянии 6
см от его центра проведена хорда длинной 16
см. Найдите радиус окружности.

РЕШЕНИЕ:

Начертим чертёж:

Пользуясь теоремой
Пифагора, находим радиус.

ЗАДАЧА:

Две окружности, радиусы которых равны 4 см и 9 см, имеют внешнее касание. Найдите расстояние между
точками касания данных окружностей с их общей внешней касательной.

РЕШЕНИЕ:

ВК ⊥ АD, АК = 9 – 4 = 5 см.

Из ∆ ВКА:

Источник

Описанная окружность — подробнее

Доказательство теоремы

Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 6. Описанная окружность. Многоугольники

ЕГЭ 6. Вписанная окружность

Как описать окружность около прямоугольного треугольника

Вам также может понравиться

Формула как найти плошадь треугольника

Как найти номер тиража на билете мечталлион

Что такое сетевой ресурс недоступен как исправить

Добавить комментарий Отменить ответ