Элементы конуса
Определение. Вершина конуса – это точка (K), из которой исходят лучи.
Определение. Основание конуса – это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.
Определение. Образующей конуса (L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.
Формула. Длина образующей (L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора):
L2 = R2 + H2
Определение. Направляющая конуса – это кривая, которая описывает контур основания конуса.
Определение. Боковая поверхность конуса – это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.
Определение. Поверхность конуса состоит из боковой поверхности и основания конуса.
Определение. Высота конуса (H) – это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.
Определение. Ось конуса (a) – это прямая, проходящая через вершину конуса и центр основания конуса.
Определение. Конусность (С) конуса – это отношение диаметра основания конуса к его высоте. В случае усеченного конуса – это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:
где C – конусность, D – диаметр основания, d – диаметр меньшего основания и h – расстояние между основаниями.
Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса. Чем больше конусность, тем острее угол наклона. угол конуса α будет:
где R – радиус основы, а H – высота конуса.
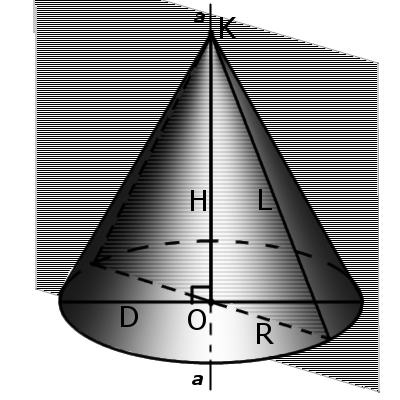
Определение. Осевое сечение конуса – это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника – это диаметр основания конуса.
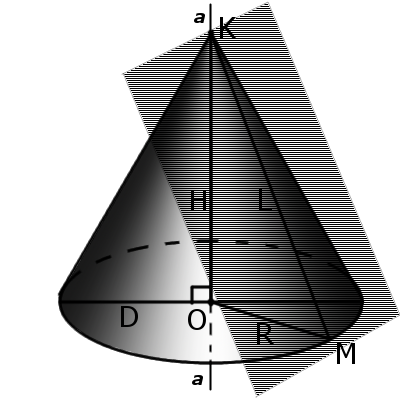
Определение. Касательная плоскость к конусу – это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.
Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим или параболическим конусом (последние два имеют бесконечный объем).
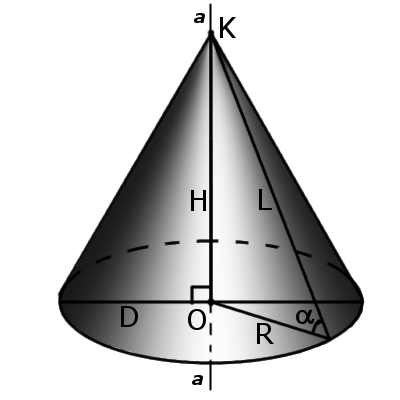
Определение. Прямой конус – это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.
Формула. Объём кругового конуса:
где R – радиус основы, а H – высота конуса.
Формула. Площадь боковой поверхности (Sb) прямого конуса через радиус R и длину образующей L:
Sb = πRL
Формула. Общая площадь поверхности (Sp) прямого кругового конуса через радиус R и длину образующей L:
Sp = πRL + πR2
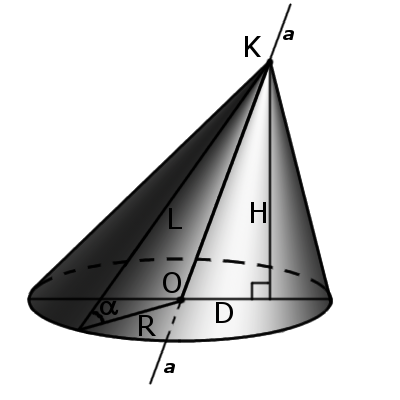
Определение. Косой (наклонный) конус – это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.
Формула. Объём любого конуса:
где S – площадь основы, а H – высота конуса.
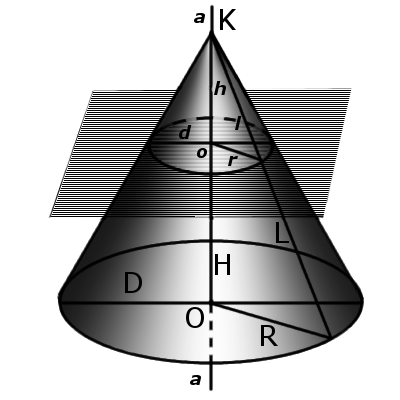
Определение. Усеченный конус – это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.
Формула. Объём усеченного конуса:
где S1 и S2 – площади меньшей и большей основы соответственно, а H и h – расстояние от вершины конуса до центра нижней и верхней основы соответственно.
Уравнение конуса
1. Уравнение прямого кругового конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | – | z2 | = 0 |
| a2 | a2 | c2 |
2. Уравнение прямого эллиптического конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | = | z2 |
| a2 | b2 | c2 |
Основные свойства кругового конуса
1. Все образующие прямого кругового конуса равны между собой.
2. При вращении прямоугольного треугольника вокруг своего катета на 360 ° образуется прямой круговой конус.
3. При вращении равнобедренного треугольника вокруг своей оси на 180 ° образуется прямой круговой конус.
4. В месте пересечения конуса плоскостью, параллельной основанию конуса, образуется круг. (см. Срезанный конус)
5. Если при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, то в месте пересечения образуется эллипс (рис. 3).
6. Если плоскость сечения проходит через основание, то в месте пересечения образуется парабола (рис. 4).
7. Если плоскость сечения проходит через вершину, то в месте пересечения образуется равнобедренный треугольник (см. Осевое сечение).
8. Центр тяжести любого конуса находится на одной четвертой высоты от центра основы.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 ноября 2022 года; проверки требуют 2 правки.
У этого термина существуют и другие значения, см. Конус (значения).
Ко́нус (через нем. Konus и лат. cōnus, от др.-греч. κώνος[1] — «сосновая шишка»[2]) — поверхность, образованная в пространстве множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса)[3].
Если направляющая конуса — замкнутая кривая, то коническая поверхность служит границей пространственного тела, которое также называют «конусом» (см. рисунок), а внутренность этой кривой называют «основанием конуса», если основание конуса представляет собой многоугольник, такой конус является пирамидой.
Иногда вместо лучей рассматривают прямые, тогда получается двойной конус, состоящий из двух симметричных относительно вершины частей.
Конус и связанные с ним конические сечения играют большую роль в математике, астрономии и других науках.
Связанные определения[править | править код]
- Боковая поверхность конуса — объединение образующих конуса; образующая поверхность конуса является конической поверхностью.
- Высота конуса — отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка).
- Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
- Конусность — соотношение высоты и диаметра основания конуса.
Типы конусов[править | править код]
-
Прямой круговой конус
-
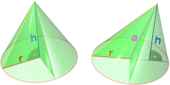
Прямой и косой круговые конусы с равным основанием и высотой: их объём одинаков
-
Усечённый прямой круговой конус
- Прямой конус — конус, основание которого имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром; при этом прямая, соединяющая вершину и центр основания, называется осью конуса.
- Косой (или наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
- Круговой конус — конус, основание которого является кругом.
- Конус вращения, или прямой круговой конус (часто под конусом подразумевают именно его) — конус, который можно получить вращением (то есть тело вращения) прямоугольного треугольника вокруг прямой, содержащей катет треугольника (эта прямая является осью конуса).
- Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом: последние два имеют бесконечный объём.
- Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.
- Равносторонний конус — конус вращения, образующая которого равна диаметру основания [4].
Свойства[править | править код]
- Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.
-
- где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.
- Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
- Телесный угол при вершине прямого кругового конуса равен
-
- где α — угол раствора конуса.
- Площадь боковой поверхности прямого кругового конуса равна
-
- а в общем случае
- где R — радиус основания,
— длина образующей,
— длина границы основания.
- Полная площадь поверхности (то есть сумма площадей боковой поверхности и основания) равна
- для прямого кругового конуса и
- для произвольного, где
— площадь основания.
- Объём кругового (не обязательно прямого) конуса равен
- Для усечённого кругового конуса (не обязательно прямого) объём равен:
-
- где
и
— радиусы соответственно нижнего и верхнего оснований,
— высота от плоскости нижнего основания,до верхнего основания.
- Для произвольного усечённого конуса (не обязательно прямого и кругового) объём равен:
-
- где
и
— площади соответственно верхнего (ближнего к вершине) и нижнего оснований,
и
— расстояния от плоскости соответственно верхнего и нижнего основания до вершины.
- Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).
Уравнение прямого кругового конуса[править | править код]
Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz:
- В сферической системе координат с координатами (r, φ, θ):
- В цилиндрической системе координат с координатами (r, φ, z):
-
или
- В декартовой системе координат с координатами (x, y, z):
-
- Это уравнение в каноническом виде записывается как
- где константы a, с определяются пропорцией
Отсюда видно, что боковая поверхность прямого кругового конуса представляет собой поверхность второго порядка (она носит название коническая поверхность). В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz) её уравнение имеет вид
- причём a/c и b/c равны полуосям эллипса. В наиболее общем случае, когда конус опирается на произвольную плоскую поверхность, можно показать, что уравнение боковой поверхности конуса (с вершиной в начале координат) задаётся уравнением
где функция
является однородной, то есть удовлетворяющей условию
для любого действительного числа α.
Развёртка[править | править код]
Развёртка прямого кругового конуса
Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.
В создании развёртки конуса могут использоваться всего две величины r и l. Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l, являющаяся радиусом сектора боковой поверхности. Угол сектора 
- φ = 360°·(r/l).
Вариации и обобщения[править | править код]
См. также[править | править код]
- Коническая поверхность
- Коническое сечение
- Конус (топология)
- Световой конус
Примечания[править | править код]
- ↑ Этимологический словарь русского языка Макса Фасмера
- ↑ «I κῶνος»
- ↑ Математический энциклопедический словарь, 1988, с. 288.
- ↑ Математический справочник. Дата обращения: 22 мая 2020. Архивировано 2 декабря 2020 года.
Литература[править | править код]
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — 2-е изд. — М.: Наука, 1970. — 720 с.
- Конус // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 288. — 847 с.
Конусом (прямым круговым конусом) называется тело, состоящее из круга (основания конуса), точки, не лежащей в плоскости этого круга (вершины конуса), и всех отрезков, соединяющих вершину конуса с точками основания.
Конус является телом вращения.
Конус
Рис.1
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.
Конус — тело, которое ограничено конической поверхностью и плоскостью, на которой лежат концы образующих конической поверхности.
Коническая поверхность — поверхность, которая образуется движением отрезка, один из концов которого неподвижен, а другой перемещается на плоскости вдоль некоторой кривой. Отрезки называют образующими конической поверхности, а кривую – направляющей. Неподвижная точка – вершина конической поверхности.
Боковая поверхность конуса — часть конической поверхности, ограниченная плоскостью.
Основание конуса — часть плоскости, отсекаемая боковой поверхностью конуса.
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания (См.Рис.1). В противном случае, конус называется наклонным. В школьном курсе изучается прямой круговой конус.
Круговой конус — конус, у которого в основании круг.
Прямой круговой конус (просто конус) — круговой конус, у которого прямая, соединяющая вершину конуса с центром круга, лежащего в основании, перпендикулярна плоскости основания.
Ось конуса — прямая, проходящая через вершину конуса и центр основания конуса.
Высота конуса — отрезок оси конуса, соединяющий вершину конуса с центром основания.
Конус можно рассматривать как тело, полученное вращением прямоугольного треугольника вокруг прямой, содержащей его катет.
Образующие конуса совпадают с образующими конической поверхности.
Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением. Плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью конуса.
См.Рис.2.
Рис.2
Развёртка боковой поверхности конуса — круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.
Площадь боковой поверхности (круглого) конуса равна произведению половины длины окружности основания (C) на образующую (l):
$$S_{бок}=frac{1}{2}cdot Cl=picdot rl$$
, где r – радиус основания, l – длина образующей.
Площадь полной поверхности конуса — сумма площадей основания конуса и его боковой поверхности, которая записывается формулой:
$$S_{полн}=picdot r(l+r)$$
, где r — радиус основания, l — длина образующей.
Объем всякого конуса равен трети произведения площади основания (S) на высоту (h):
$$V=frac{1}{3}cdot Sh$$
Объем круглого конуса:
$$V=frac{1}{3}cdot Sh=frac{1}{3}cdotpi r^2 cdot h$$
Усеченный конус – это часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания.
См.Рис.3.
Усечённый конус
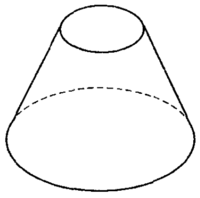
Рис.3
Формулы для усечённого конуса (См.Рис.4):
$$ S_{бок}=picdot lcdot (R+r)
\ S_{полн}=S_{бок}+pi(R^2+r^2)
\ V=frac{1}{3}picdot h(R^2+Rcdot r+r^2)
$$
Усечённый конус
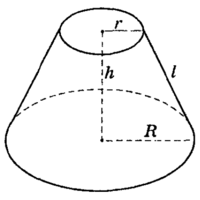
Рис.4
Пример 1. Высота конуса равна 4 , а длина образующей – 5. Найдите диаметр основания конуса.
Видео-решение.
Высота конуса равна 4 , а длина образующей – 5. Найдите диаметр основания конуса.
Определение и элементы конуса
Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние.
При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.
Обратите внимание!
Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.
Хотелось бы рассмотреть ещё несколько понятий по этой теме:
1. Под конусностью понимают отношение диаметра основания фигуры и её высоты:
Важно!
Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.
2. Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:
3. Касательная— это плоскость, которая соприкасается с образующей конуса. При этом важно, чтобы она была перпендикулярна осевому сечению.
Объем конуса
Объем конуса
равен трети от произведению площади его основания на высоту.
Формулы объема конуса:
где V – объем конуса, So – площадь основания конуса, R – радиус основания конуса, h – высота конуса, π = 3.141592.
Свойства кругового конуса
Выделяют несколько особенностей, которыми обладает фигура данного типа:
- Образующие кругового конуса равны друг другу.
- Чтобы найти центр тяжести фигуры, нужно её высоту поделить на четыре части.
- Место пересечения плоскости сечения и основы образует параболу. Если через вершину тела провести плоскость сечения, то получится равнобедренный треугольник.
Интересный факт!
Если вращать прямоугольный треугольник вокруг одного из катетов, то получится конус. При этом важно, чтобы угол вращения был не менее 360 градусов.
Построение развертки конуса на бумаге
Для выполнения этой задачи понадобится лист бумаги, карандаш, транспортир, линейка и циркуль.
В первую очередь начертим прямоугольный треугольник со сторонами 3 см, 4 см и 5 см. Его вращение вокруг катета в 3 см даст искомый конус. У фигуры r = 3 см, h = 4 см, g = 5 см.
Построение развертки начнем с рисования циркулем окружности радиусом r. Ее длина будет равна 6*pi см. Теперь рядом с ней нарисуем еще одну окружность, но уже радиусом g. Ее длина будет соответствовать 10*pi см. Теперь нам нужно от большой окружности отрезать круговой сектор. Его угол φ равен:
φ = 2*pi*r/g = 2*pi*3/5 = 216o.
Теперь откладываем транспортиром этот угол на окружности с радиусом g и проводим два радиуса, которые будут ограничивать круговой сектор.
Таким образом, мы построили развертку конуса с указанными параметрами радиуса, высоты и образующей.
Объём усечённого конуса
Это часть прямого конуса, которая находится в пространстве между основой и плоскостью, параллельной этому основанию. В общем виде выглядит следующим образом:
Объём данного тела можно вычислить по формуле:
Важно! S и S1 это площади соответствующих основ, которые равняются ПR2 и ПR12 При нахождении этих значений поможет онлайн калькулятор.
Онлайн-калькулятор
Общее определение конуса
Конус – это тело, образованное совокупностью всех лучей, исходящих из точки пространства и пересекающих плоскость.
Точка, из которой лучи исходят, получила название вершины конуса. В случае, когда основанием конуса является многоугольник, он превращается в пирамиду.
Рассмотрим некоторые важные понятия.
Образующей конуса называется отрезок, который соединяет любую точку границы основания конуса, с его вершиной. Высотой конуса является перпендикуляр, который опущен из вершины к основанию тела.
Конус бывает нескольких типов:
Прямой, если его основание – одна из таких фигур, как эллипс или круг. Обязательным условием является проецирование вершины конуса в центр основания.
Косой – у него центр фигуры, которая находится в основании, не совпадает с проекцией вершины на это самое основание.
Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.
Усеченный – область конуса, лежащая между основанием и сечением плоскости, которая параллельна основанию и пересекает данный конус.
Площадь усечённого конуса
Для нахождения данного параметра нужно воспользоваться формулами:
- площади боковой поверхности усечённого конуса Sбок;
- полной площади усечённой фигуры Sпол, которая равна сумме площадей двух оснований и площади боковой поверхности:
Здесь l — длина образующей, а R и r — радиусы большего и меньшего оснований соответственно.
Связанные определения для конуса
Образующая конуса. Отрезок, соединяющий вершину и границу основания, называется образующей конуса.
Образующая поверхность конуса. Объединение образующих конуса называется образующей (или боковой) поверхностью конуса.
Коническая поверхность. Образующая поверхность конуса является конической поверхностью.
Высота конуса (H). Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.
Угол раствора конуса. Угол раствора конуса – угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
Прямой конус. Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то конус называется прямым. При этом прямая, соединяющая вершину и центр основания, называется осью конуса.
Косой (наклонный) конус. Косой (наклонный) конус – конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
Круговой конус. Круговой конус – конус, основание которого является кругом.
Прямой круговой конус. Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).
Эллиптическим конус. Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).
Усечённый конус. Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.
Получение фигуры с помощью вращения
Перед тем как перейти к рассмотрению развертки поверхности конуса, полезно узнать, как с помощью вращения можно получить эту пространственную фигуру.
Предположим, что у нас имеется прямоугольный треугольник со сторонами a, b, c. Первые две из них являются катетами, c — это гипотенуза. Поставим треугольник на катет a и начнем его вращать вокруг катета b. Гипотенуза c при этом опишет коническую поверхность. Эта простая методика получения конуса изображена ниже на схеме.
Очевидно, что катет a будет радиусом основания фигуры, катет b — его высотой, а гипотенуза c соответствует образующей круглого прямого конуса.
Объем фигуры
Если взять прямую пирамиду и увеличивать на бесконечности число сторон ее основания, то форма основания будет стремиться к окружности, а боковая поверхность пирамиды будет приближаться к конической поверхности. Эти рассуждения позволяют использовать формулу для объема пирамиды при расчете аналогичной величины для конуса. Объем конуса может быть найден по формуле:
V = 1/3*h*So.
Справедлива эта формула всегда, независимо от того, что собой представляет основание конуса, имеющее площадь So. Более того, формула применима также для наклонного конуса.
Поскольку мы изучаем свойства прямой фигуры с круглым основанием, то для определения его объема можно пользоваться таким выражением:
V = 1/3*h*pi*r2.
Справедливость формулы очевидна.
Как рассчитать угол конуса
| Элементы конуса | Расчетные формулы | Элементы конуса | Расчетные формулы |
| K | K = (D-d)/ lK = 2tga | D | D = K× l + dD = 2× l×tga + d |
| a | tga = (D-d)/ 2ltga = K / 2 | d | d = D – 2× l×tgad = D – K× l |
Угол a вычисляют по тригонометрической функции тангенса.
Нормальные конические поверхности должны быть изготовлены по стандартным размерам, некоторые из которых указаны в табл.4.
Кроме этих поверхностей, различают также конусы Морзе и метрические конусы. Наружные конусы Морзе выполняют на хвостовой части сверл (см. рис.6
), зенкеров, разверток, центров, а внутренние конусы – в отверстиях шпинделей, оправок, переходных втулок, в которые эти инструменты устанавливают. Существуют семь номеров конусов Морзе (от до
6
) со своими размерами и углами наклона
a
. Наименьшим является конус Морзе (
1:19,212
), наибольшим – конус Морзе
6
(
1:19,18
). Их размеры приведены в стандарте СТ СЭВ 147-75. Недостатком конусов Морзе следует считать разные углы наклона
a
у различных номеров.
Таблица 4
Стандартные размеры конусов деталей
| Конусность K | Угол конуса 2a | Угол наклона a | Обозначение конусности |
| 1:100 1:50 1:20 1:10 1:3 1:1,866 1:1,207 1:0,866 | 0 0 34¢23² 1 0 8¢45² 2 0 51¢51² 5 0 43¢29² 18 0 55¢30² 30 0 45 0 60 0 | 0 0 17¢12² 0 0 34¢23² 1 0 25¢56² 2 0 51¢45² 9 0 27¢45² 15 0 22 0 30¢ 30 0 | 1:100 1:50 1:20 1:10 1:3 30 0 45 0 60 0 |
Метрические конусы 4, 6, 80, 100, 120, 160, 200
(см. тот же стандарт) имеют одинаковую конусность
1:20
(и угол
a
), а номер конуса обозначает размер диаметра большого основания.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения:
Да какие ж вы математики, если запаролиться нормально не можете.
8256 – | 7223 – или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock! и обновите страницу (F5)
очень нужно
Конусность – отношение разности диаметров двух поперечных сечений кругового конуса к расстоянию между ними.
Конусность имеет двойной Уклон: k=2i Конусность на чертеже может быть указана в градусной мере, в радианах и в процентах. Заданы конусность пробки крана 1:5, диаметр D=BC=20 мм, длина l=35 мм.
Необходимо построить очертание пробки крана одним из двух способов: Первый способ. Из формулы k=2i находим i=1:10. Отмечаем точки BC и строим треугольник DKP так, чтобы KP:BK=1:10. Продолжив BP до пересечения с осью конуса, получим вершину конуса S. Точку S соединяем с точкой C. Отложив по оси пробки от BC отрезок l=35 мм и проведя через конец этого отрезка прямую, перпендикулярную к оси , получим диаметр d=EF=13 мм торца пробки; Второй способ. Из формулы k=(D-d)/l находим d=EF=20-35/5=13 мм; Величина угла при вершине конуса:
здесь угол φ представлен в радианах.
где L – расстояние от большого сечения до вершины S конуса, а отношение: D/(2L) = tgφ Пусть задана конусность например 1 : 2,5 откуда i=1:5 и tgφ=0,2 тогда перевод ее в градусы выполняется по формулам:
Конусность стандартизована. ГОСТ 8593-81 устанавливает нормальные конусности и углы конусов
| Обозна- чение | конуса | Конус- | ность | Угол | конуса | Угол | уклона |
| Ряд 1 | Ряд 2 | Угл. ед. | Рад. | Угл. ед. | Рад. | ||
| 1:500 | 1:500 | 0,0020000 | 6`52,5″ | 0,0020000 | 3`26,25″ | 0,0010000 | |
| 1:200 | 1:200 | 0,0050000 | 17`11,3″ | 0,0050000 | 8`25,65″ | 0,0025000 | |
| 1:100 | 1:100 | 0,0100000 | 34`22,6″ | 0,0100000 | 17`11,3″ | 0,0050000 | |
| 1:50 | 1:50 | 0,0200000 | 1°8`45,2″ | 0,0199996 | 34`22,6″ | 0,0099998 | |
| 1:30 | 1:30 | 0,0333333 | 1°54`34,9″ | 0,0333304 | 57`17,45″ | 0,0166652 | |
| 1:20 | 1:20 | 0,0500000 | 2°51`51,1″ | 0,0499896 | 1°25`55,55″ | 0,0249948 | |
| 1:15 | 1:15 | 0,0666667 | 3°49`5,9″ | 0,0666420 | 1°54`32,95″ | 0,0333210 | |
| 1:12 | 1:12 | 0,0833333 | 4°46`18,8″ | 0,0832852 | 2°23`9,4″ | 0,0416426 | |
| 1:10 | 1:10 | 0,1000000 | 5°43`29,3″ | 0,0999168 | 2°51`44,65″ | 0,0499584 | |
| 1:8 | 1:8 | 0,1250000 | 7°9`9,6″ | 0,1248376 | 3°34`34,8″ | 0,0624188 | |
| 1:7 | 1:7 | 0,1428571 | 8°10`16,4″ | 0,1426148 | 4°5`8,2″ | 0,0713074 | |
| 1:6 | 1:6 | 0,1666667 | 9°31`38,2″ | 0,1662824 | 4°45`49,1″ | 0,0831412 | |
| 1:5 | 1:5 | 0,2000000 | 11°25`16,3″ | 0,1993374 | 5°42`38,15″ | 0,0996687 | |
| 1:4 | 1:4 | 0,2500000 | 14°15`0,1″ | 0,2487100 | 7°7`30,05″ | 0,1243550 | |
| 1:3 | 1:3 | 0,3333333 | 18°55`28,7″ | 0,3302972 | 9°27`44,35″ | 0,1651486 | |
| 30° | 1:1,866025 | 0,5358985 | 30° | 0,5235988 | 15° | 0,2617994 | |
| 45° | 1:1,207107 | 0,8284269 | 45° | 0,7853982 | 22°30` | 0,3926991 | |
| 60° | 1:0,866025 | 1,1547010 | 60° | 1,0471976 | 30° | 0,5235988 | |
| 75° | 1:0,651613 | 1,5346532 | 75° | 1,3089970 | 37°30` | 0,6544985 | |
| 90° | 1:0,500000 | 2,0000000 | 90° | 1,5707964 | 45° | 0,7853982 | |
| 120° | 1:0,288675 | 3,4641032 | 120° | 2,0943952 | 60° | 1,0471976 |
Конусности и углы конусов должны соответствовать указанным на чертеже и в таблице. При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.
Конусность поверхности
обозначается на чертеже: – надписью Конусность с указанием ее величины; – указывающей на нее стрелкой с полкой где пишется: – Конусность с указанием ее величины; – знак конусности и ее величина.
В машиностроении, наряду с цилиндрическими, широко применяются детали с коническими поверхностями в виде наружных конусов или в виде конических отверстий. Например, центр токарного станка имеет два наружных конуса, из которых один служит для установки и закрепления его в коническом отверстии шпинделя; наружный конус для установки и закрепления имеют также сверло, зенкер, развертка и т. д. Переходная втулка для закрепления сверл с коническим хвостовиком имеет наружный конус и коническое отверстие
Читать также: Как точить резцы по дереву
Понятие о конусе и его элементах
Элементы конуса . Если вращать прямоугольный треугольник АБВ вокруг катета АБ (рис. 202, а), то образуется тело АВГ, называемое полным конусом
. Линия АБ называется осью или
высотой конуса
, линия АВ —
образующей конуса
. Точка А является
вершиной конуса
.
При вращении катета БВ вокруг оси АБ образуется поверхность круга, называемая основанием конуса
.
Угол ВАГ между боковыми сторонами АВ и АГ называется углом конуса
и обозначается 2α. Половина этого угла, образуемая боковой стороной АГ и осью АБ, называется
углом уклона конуса
и обозначается α. Углы выражаются в градусах, минутах и секундах.
Если от полного конуса отрезать его верхнюю часть плоскостью, параллельной егооснованию (рис. 202, б), то получим тело, называемое усеченным конусом
. Оно имеет два основания верхнее и нижнее. Расстояние OO1 по оси между основаниями называется
высотой усеченного конуса
. Так как в машиностроении большей частью приходится иметь дело с частями конусов, т. е. усеченными конусами, то обычно их просто называют конусами; дальше будем называть все конические поверхности конусами.
Связь между элементами конуса. На чертеже указывают обычно три основных размера конуса: больший диаметр D, меньший — d и высоту конуса l (рис. 203).
Иногда на чертеже указывается только один из диаметров конуса, например, больший D, высота конуса l и так называемая конусность. Конусностью называется отношение разности диаметров конуса к его длине. Обозначим конусность буквой K, тогда
Если конус имеет размеры: D =80 мм, d = 70 мм и l = 100 мм, то согласно формуле (10):
Это значит, что на длине 10 мм диаметр конуса уменьшается на 1 мм или на каждый миллиметр длины конуса разница между его диаметрами изменяется на
Иногда на чертеже вместо угла конуса указывается уклон конуса
. Уклон конуса показывает, в какой мере отклоняется образующая конуса от его оси. Уклон конуса определяется по формуле
где tg α — уклон конуса; D — диаметр большого основания конуса в мм; d — диаметр малого основания конуса в мм; l — высота конуса в мм.
Пользуясь формулой (11), можно при помощи тригонометрических таблиц определить угол а уклона конуса.
Уклон конуса и конусность обычно выражают простой дробью, например: 1 : 10; 1 : 50, или десятичной дробью, например, 0,1; 0,05; 0,02 и т. д.
Способы получения конических поверхностей на токарном станке
На токарном станке обработка конических поверхностей производится одним из следующих способов: а) поворотом верхней части суппорта; б) поперечным смещением корпуса задней бабки; в) с помощью конусной линейки; г) с помощью широкого резца.
3. Обработка конических поверхностей поворотом верхней части суппорта
При изготовлении на токарном станке коротких наружных и внутренних конических поверхностей с большим углом уклона нужно повернуть верхнюю часть суппорта относительно оси станка под углом α уклона конуса (см. рис. 204). При таком способе работы подачу можно производить только от руки, вращая рукоятку ходового винта верхней части суппорта, и лишь в наиболее современных токарных станках имеется механическая подача верхней части суппорта.
Для установки верхней части суппорта 1 на требуемый угол можно использовать деления, нанесенные на фланце 2 поворотной части суппорта (рис. 204). Если угол α уклона конуса задан по чертежу, то верхнюю часть суппорта повертывают вместе с его поворотной частью на требуемое число делений, обозначающих градусы. Число делений отсчитывают относительно риски, нанесенной на нижней части суппорта.
Если на чертеже угол α не дан, а указаны больший и меньший диаметры конуса и длина его конической части, то величину угла поворота суппорта определяют по формуле (11)
Способ обтачивания конических поверхностей поворотом верхней части суппорта имеет следующие недостатки: он допускает обычно применение только ручной подачи, что отражается на производительности труда и чистоте обработанной поверхности; позволяет обтачивать сравнительно короткие конические поверхности, ограниченные длиной хода верхней части суппорта.
Обработка конических поверхностей способом поперечного смещения корпуса задней бабки
Для получения конической поверхности на токарном станке необходимо при вращении заготовки вершину резца перемещать не параллельно, а под некоторым углом к оси центров. Этот угол должен равняться углу α уклона конуса. Наиболее простой способ получения угла между осью центров и направлением подачи — сместить линию центров, сдвинув задний центр в поперечном направлении. Путем смещения заднего центра в сторону резца (на себя) в результате обтачивания получают конус, у которого большее основание направлено в сторону передней бабки; при смещении заднего центра в противоположную сторону, т. е. от резца (от себя), большее основание конуса окажется со стороны задней бабки (рис. 205).
Смещение корпуса задней бабки определяют по формуле
где S — смещение корпуса задней бабки от оси шпинделя передней бабки в мм; D — диаметр большого основания конуса в мм; d — диаметр малого основания конуса в мм; L — длина всей детали или расстояние между центрами в мм; l — длина конической части детали в мм.
Смещение корпуса задней бабки производят, используя деления 1 (рис 206), нанесенные на торце опорной плиты, и риску 2 на торце корпуса задней бабки.
Если на торце плиты делений нет, то смещают корпус задней бабки, пользуясь измерительной линейкой, как показано на рис. 207.
Читать также: Отличие вгп трубы от электросварной
Преимущество обработки конических поверхностей путем смещения корпуса задней бабки заключается в том, что этим способом можно обтачивать конусы большой длины и вести обтачивание с механической подачей.
Недостатки этого способа: невозможность растачивать конические отверстия; потеря времени на перестановку задней бабки; возможность обрабатывать лишь пологие конусы; перекос центров в центровых отверстиях, что приводит к быстрому и неравномерному износу центров и центровых отверстий и служит причиной брака при вторичной установке детали в этих же центровых отверстиях.
Неравномерного износа центровых отверстий можно избежать, если вместо обычного применять специальный шаровой центр (рис. 208). Такие центры используют преимущественно при обработке точных конусов.
5. Обработка конических поверхностей с применением конусной линейки
Для обработки конических поверхностей с углом уклона а до 10—12° современные токарные станки обычно имеют особое приспособление, называемое конусной линейкой. Схема обработки конуса с применением конусной линейки приводится на рис. 209.
К станине станка прикреплена плита 11, на которой установлена конусная линейка 9. Линейку можно поворачивать вокруг пальца 8 под требуемым углом а к оси обрабатываемой детали. Для закрепления линейки в требуемом положении служат два болта 4 и 10. По линейке свободно скользит ползун 7, соединяющийся с нижней поперечной частью 12 суппорта при помощи тяги 5 и зажима 6. Чтобы эта часть суппорта могла свободно скользить по направляющим, ее отсоединяют от каретки 3, вывинчивая поперечный винт или отсоединяя от суппорта его гайку.
Если сообщить каретке продольную подачу, то ползун 7, захватываемый тягой 5, начнет перемещаться вдоль линейки 9. Так как ползун скреплен с поперечными салазками суппорта, то они вместе с резцом будут перемещаться параллельно линейке 9. Благодаря этому резец будет обрабатывать коническую поверхность с углом уклона, равным углу α поворота конусной линейки.
После каждого прохода резец устанавливают на глубину резания с помощью рукоятки 1 верхней части 2 суппорта. Эта часть суппорта должна быть повернута на 90° относительно нормального положения, т. е. так, как это показано на рис. 209.
Если даны диаметры оснований конуса D и d и его длина l, то угол поворота линейки можно найти по формуле (11).
Подсчитав величину tg α, легко определить значение угла α по таблице тангенсов. Применение конусной линейки имеет ряд преимуществ: 1) наладка линейки удобна и производится быстро; 2) при переходе к обработке конусов не требуется нарушать нормальную наладку станка, т. е. не нужно смещать корпус задней бабки; центры станка остаются в нормальном положении, т. е. на одной оси, благодаря чему центровые отверстия в детали и центры станка не срабатываются; 3) при помощи конусной линейки можно не только обтачивать наружные конические поверхности, но и растачивать конические отверстия; 4) возможна работа е продольным самоходом, что увеличивает производительность труда и улучшает качество обработки.
Недостатком конусной линейки является необходимость отсоединять салазки суппорта от винта поперечной подачи. Этот недостаток устранен в конструкции некоторых токарных станков, у которых винт не связан жестко со своим маховичком и зубчатыми колесами поперечного самохода.
Обработка конических поверхностей широким резцом
Обработку конических поверхностей (наружных и внутренних) с небольшой длиной конуса можно производить широким резцом с углом в плане, соответствующим углу α уклона конуса (рис. 210). Подача резца может быть продольная и поперечная.
Однако использование широкого резца на обычных станках возможно только при длине конуса, не превышающей примерно 20 мм. Применять более широкие резцы можно лишь на особо жестких станках и деталях, если это не вызывает вибрации резца и обрабатываемой детали.
7. Растачивание и развертывание конических отверстий
Обработка конических отверстий является одной из наиболее трудных токарных работ; она значительно труднее, чем обработка наружных конусов.
Обработку конических отверстий на токарных станках в большинстве случаев производят растачиванием резцом с поворотом верхней части суппорта и реже с помощью конусной линейки. Все подсчеты, связанные с поворотом верхней части суппорта или конусной линейки, выполняются так же, как при обтачивании наружных конических поверхностей.
Если отверстие должно быть в сплошном материале, то сначала сверлят цилиндрическое отверстие, которое затем растачивают резцом на конус или обрабатывают коническими зенкерами и развертками.
Чтобы ускорить растачивание или развертывание, следует предварительно просверлить отверстие сверлом, диаметр d, которого на 1—2 мм меньше диаметра малого основания конуса (рис. 211, а). После этого рассверливают отверстие одним (рис. 211, б) или двумя (рис. 211, в) сверлами для получения ступеней.
После чистового растачивания конуса его развертывают конической разверткой соответствующей конусности. Для конусов с небольшой конусностью выгоднее производить обработку конических отверстий непосредственно после сверления набором специальных разверток, как показано на рис. 212.
Режимы резания при обработке отверстий коническими развертками
Конические развертки работают в более тяжелых условиях, чем цилиндрические: в то время как цилиндрические развертки снимают незначительный припуск небольшими режущими кромками, конические развертки режут всей длиной их режущих кромок, расположенных на образующей конуса. Поэтому при работе коническими развертками применяют подачи и скорости резания меньше, чем при работе цилиндрическими развертками.
При обработке отверстий коническими развертками подачу производят вручную, вращая маховичок задней бабки. Необходимо следить за тем, чтобы пиноль задней бабки перемещалась равномерно.
Подачи при развертывании стали 0,1—0,2 мм/об, при развертывании чугуна 0,2—0,4 мм/об.
Скорость резания при развертывании конических отверстий развертками из быстрорежущей стали 6—10 м/мин.
Читать также: Схема мощного зарядного устройства для автомобильного аккумулятора
Для облегчения работы конических разверток и получения чистой и гладкой поверхности следует применять охлаждение. При обработке стали и чугуна применяют эмульсию или сульфофрезол.
Измерение конических поверхностей
Поверхности конусов проверяют шаблонами и калибрами; измерение и одновременно проверку углов конуса производят угломерами. На рис. 213 показан способ проверки конуса с помощью шаблона.
Наружные и внутренние углы различных деталей можно измерять универсальным угломером (рис. 214). Он состоит из основания 1, На котором на дуге 130 нанесена основная шкала. С основанием 1 жестко скреплена линейка 5. По дуге основания перемещается сектор 4, несущий нониус 3. К сектору 4 посредством державки 7 может быть прикреплен угольник 2, в котором, в свою очередь, закрепляется съемная линейка 5. Угольник 2 и съемная линейка 5 имеют возможность перемещаться по грани сектора 4.
Путем различных комбинаций в установке измерительных деталей угломера можно производить измерение углов от 0 до 320°. Величина отсчета по нониусу 2′. Отсчет, полученный при измерении углов, производится по шкале и нониусу (рис. 215) следующим образом: нулевой штрих нониуса показывает число градусов, а штрих нониуса, совпадающий со штрихом шкалы основания, — число минут. На рис. 215 со штрихом шкалы основания совпадает 11-й штрих нониуса, что означает 2’Х 11 = 22′. Следовательно, угол в данном случае равен 76°22′.
На рис. 216 показаны комбинации измерительных деталей универсального угломера, позволяющие производить измерение различных углов от 0 до 320°.
Для более точной проверки конусов в серийном производстве применяют специальные калибры. На рис. 217, а показан кониче-ский калибр-втулка для проверки наружных конусов, а на рис. 217, б—конический калибр-пробка для проверки конических отверстий.
На калибрах делаются уступы 1 и 2 на торцах или наносятся риски 3, служащие для определения точности проверяемых поверхностей.
На. рис. 218 приводится пример проверки конического отверстия калибром-пробкой.
Для проверки отверстия калибр (см. рис. 218), имеющий уступ 1 на определенном расстоянии от торца 2 и две риски 3, вводят с легким нажимом в отверстие и проверяют, нет ли качания калибра в отверстии. Отсутствие качания показывает, что угол конуса правилен. Убедившись, что угол конуса правилен, приступают к проверке его размера. Для этого наблюдают, до какого места калибр войдет в проверяемую деталь. Если конец конуса детали совпадает с левым торцом уступа 1 или с одной из рисок 3 или находится между рисками, то размеры конуса правильны. Но может случиться, что калибр войдет в деталь настолько глубоко, что обе риски 3 войдут в отверстие или оба торца уступа 1 выйдут из него наружу. Это показывает, что диаметр отверстия больше заданного. Если, наоборот, обе риски окажутся вне отверстия или ни один из торцов уступа не выйдет из него, то диаметр отверстия меньше требуемого.
Для точной проверки конусности применяют следующий способ. На измеряемой поверхности детали или калибра проводят мелом или карандашом две-три линии вдоль образующей конуса, затем вставляют или надевают калибр на деталь и повертывают его на часть оборота. Если линии сотрутся неравномерно, это значит, что конус детали обработан неточно и необходимо его исправить. Стирание линий по концам калибра говорит о неправильной конусности; стирание линий в средней части калибра показывает, что конус имеет небольшую вогнутость, причиной чего обычно является неточное расположение вершины резца по высоте центров. Вместо меловых линий можно нанести на всю коническую поверхность детали или калибра тонкий слой специальной краски (синьки). Такой способ дает большую точность измерения.
Брак при обработке конических поверхностей и меры его предупреждения
При обработке конических поверхностей, помимо упомянутых видов брака для цилиндрических поверхностей, дополнительно возможны следующие виды брака: 1) неправильная конусность; 2) отклонения в размерах конуса; 3) отклонения в размерах диаметров оснований при правильной конусности; 4) непрямолинейность образующей конической поверхности.
1. Неправильная конусность получается главным образом вследствие неточного смещения корпуса задней бабки, неточного поворота верхней части суппорта, неправильной установки конусной линейки, неправильной заточки или установки широкого резца. Следовательно, точной установкой корпуса задней бабки, верхней части суппорта или конусной линейки перед началом обработки можно брак предупредить. Этот вид брака исправим только в том случае, если ошибка во всей длине конуса направлена в тело детали, т. е. все диаметры у втулки меньше, а у конического стержня больше требуемых.
2. Неправильный размер конуса при правильном угле его, т. е. неправильная величина диаметров по всей длине конуса, получается, если снято недостаточно или слишком много материала. Предупредить брак можно только внимательной установкой глубины резания по лимбу на чистовых проходах. Брак исправим, если снято недостаточно материала.
3. Может получиться, что при правильной конусности и точных размерах одного конца конуса диаметр второго конца неправилен. Единственной причиной является несоблюдение требуемой длины всего конического участка детали. Брак исправим, если деталь излишне длинна. Чтобы избежать этого вида брака, необходимо перед обработкой конуса тщательно проверить его длину.
4. Непрямолинейность образующей обрабатываемого конуса получается при установке резца выше (рис. 219, б) или ниже (рис. 219, в) центра (на этих рисунках для большей наглядности искажения образующей конуса показаны в сильно преувеличенном виде). Таким образом, и этот вид брака является результатом невнимательной работы токаря.
Что это — конус?
С точки зрения геометрии речь идет о пространственной фигуре, которая образована совокупностью прямых отрезков, соединяющих некоторую точку пространства со всеми точками плавной плоской кривой. Этой кривой может быть окружность или эллипс. На рисунке ниже показан конус.
Вам будет интересно:Советские вещи: фото и описание
Представленная фигура не обладает объемом, поскольку стенки ее поверхности имеют бесконечно малую толщину. Однако если ее заполнить веществом и ограничить сверху не кривой, а плоской фигурой, например кругом, то мы получим твердое объемное тело, которое также принято называть конусом.
Форму конуса можно часто встретить в жизни. Так, ею обладает мороженое-рожок или полосатые черно-оранжевые дорожные конусы, которые выставляют на проезжую часть для привлечения внимания участников движения.
Площадь поверхности
При изучении поверхности любой объемной фигуры удобно пользоваться ее разверткой на плоскость. Конус не является исключением. Для круглого конуса развертка показана ниже.
Мы видим, что развертка фигуры состоит из двух частей:
- Круга, который образует основание конуса.
- Сектора круга, являющегося конической поверхностью фигуры.
Площадь круга найти легко, и соответствующая формула известна каждому школьнику. Говоря о круговом секторе, заметим, что он является частью круга с радиусом g (длина генератрисы конуса). Длина дуги этого сектора равна длине окружности основания. Эти параметры позволяют однозначно определить его площадь. Соответствующая формула имеет вид:
S = pi*r2 + pi*r*g.
Первое и второе слагаемые в выражении — это конуса основания и боковой поверхности площади соответственно.
Если длина генератрисы g неизвестна, но дана высота h фигуры, тогда формулу можно переписать в виде:
S = pi*r2 + pi*r*√(r2 + h2).
Геометрические элементы, составляющие конус
Чтобы лучше понимать вопрос, что такое конус, следует привести геометрические названия элементов этой пространственной фигуры.
Конус ограничен двумя поверхностями. Первая называется основанием. Она представляет собой плоскость, которая ограничена отмеченной выше кривой. Например, это может быть круг или эллипс. Вторая поверхность является боковой для фигуры и называется конической. Она не лежит в одной плоскости, однако может быть развернута в плоскую фигуру, о чем будет сказано ниже.
Одним из важных элементов конуса является его вершина. Эта точка ограничивает коническую поверхность. С ней соединяются все точки кривой основания.
Отрезок, который вершину соединяет с основанием, называется генератрисой, или образующей конуса. В свою очередь, кривая, ограничивающая основание, получила название директрисы, или направляющей фигуры.
Площади конической поверхности и основания в сумме дают общую площадь конуса. Объем пространства, который ограничивают указанные две поверхности, является объемом конуса.
Фигура конус
Приведем максимально общее определение конуса. Под этой фигурой понимают поверхность, которая образована в результате соединения прямыми отрезками некоторой точки пространства со всеми точками данной кривой. При этом указанная точка в пространстве не должна находиться в плоскости кривой. Например, если кривая будет иметь форму параболы, то полученная описанным способом фигура будет называться параболическим конусом, если кривая — эллипс, то конус будет эллиптическим, и так далее.
Дав геометрическое определение, что такое конус, приведем фото, которое показывает наглядно возможные формы этой фигуры.
Взглянув на это фото, многие увидели в нем форму детской шапки, которую носил Буратино, вафельный стаканчик от мороженого в виде рожка или предупредительный оранжево-черный полосатый дорожный конус.
Введите радиус основания и высоту конуса
| Радиус конуса r |
| Высота конуса h |
| Результат |
| Расчет объема куба, пирамиды, конуса, цилиндра, шара (объема всех фигур). |
| Объемы фигур |
| Радиус: |
| Высота: |
| Конус – геометрическое тело, которое состоит из круга (основание конуса), точки, не лежащей в плоскости этого круга (вершина конуса), и всех точек, соединяющих вершину конуса с точками основания. Формула объема конуса: , где R – радиус основания, h – высота конуса |
Объем конуса через радиус
Данный треугольник
для получения конуса должен вращаться вокруг одного из своих
катетов
, который является не только осью вращения, но и высотой конуса.
Второй
же катет становится радиусом полученной в результате вращения окружности-основания конуса, а гипотенуза будет апофемой (высотой опущенной под прямым углом к линии окружности, а не центру).
Технически взаимосвязь конуса
с цилиндром идентична взаимосвязи пирамиды с кубом (параллелепипедом), единственное, что вывод
формулы
проходит через отношения интегралов их сферических углов, но тем не менее, он точно также как и пирамида занимает одну треть цилиндра, в который он может быть вписан.
Поэтому его объем
равен произведению площади основания на высоту, деленному на три, или произведению числом
π
на квадрат радиуса и высоту, деленному на три.
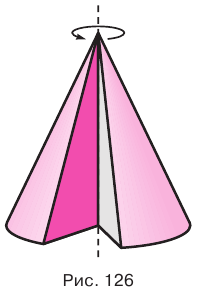
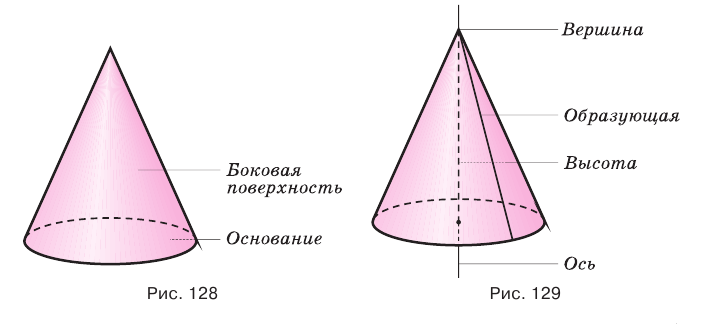
Конусом называется тело, полученное вращением прямоугольного треугольника вокруг оси, проходящей через один из его катетов (рис. 126).
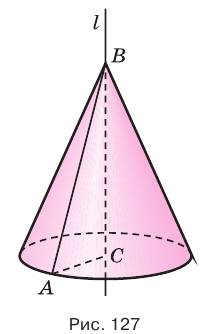
На рисунке 127 показано образование конуса при вращении прямоугольного треугольника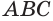 
вокруг прямой 
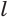, которой принадлежит катет 
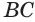. При этом ломаная 
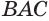описывает поверхность конуса, гипотенуза 
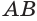— боковую поверхность, а катет 
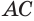— основание конуса (рис. 128). Саму гипотенузу 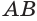называют образующей конуса, неподвижную точку 
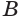— вершиной конуса, прямую, проходящую через неподвижный катет 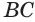, — осью конуса, а перпендикуляр, опущенный из вершины конуса на основание, — высотой конуса (рис. 129). Основание высоты конуса совпадает с центром основания конуса.
Поверхность конуса можно развернуть на плоскость, в результате получится сектор, представляющий боковую поверхность конуса, и круг, представляющий основание конуса. На рисунке 130 представлены конус и его развертка.
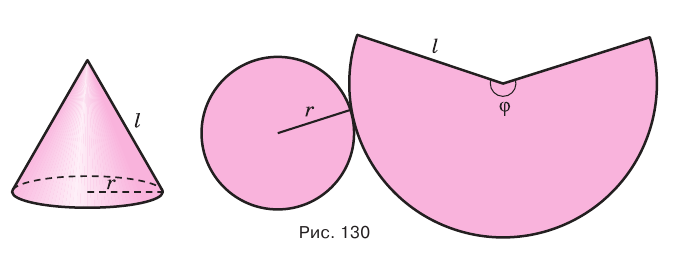
Теорема 5.
Боковая поверхность конуса равна произведению полуокружности его основания и образующей:
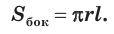
Доказательство проведите самостоятельно, используя рисунок 130.
Важной пространственной конфигурацией, которая часто встречается в задачах, является сочетание конуса с плоскостью.
Если конус пересечь плоскостью, параллельной основанию, то получится круг (рис. 131), а если плоскостью, проходящей через вершину, то — равнобедренный треугольник, у которого боковые стороны являются образующими конуса (рис. 132).
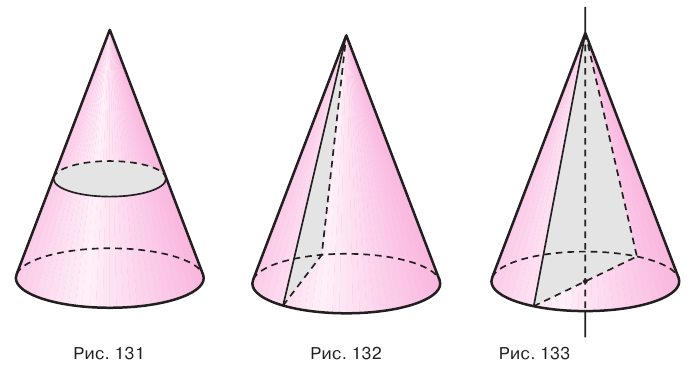
Осевое сечение конуса, т. е. сечение плоскостью, проходящей через ось конуса, является равнобедренным треугольником, у которого основание равно диаметру основания конуса (рис. 133).
Проведем через вершину конуса секущую плоскость и будем ее поворачивать вокруг прямой, перпендикулярной оси конуса (рис. 134). При этом основание треугольника-сечения будет укорачиваться, а его боковые стороны сближаться до того момента, пока не совпадут. Получим плоскость, целиком содержащую образующую и не имеющую с конусом других общих точек. Такая плоскость называется касательной плоскостью конуса.
Теорема 6.
Если плоскость касается конуса по некоторой образующей, то ей перпендикулярна плоскость, проходящая через эту образующую и ось конуса.
Доказательство:
Пусть плоскость 
касается конуса с осью 
по образующей 
(рис. 135). Докажем, что плоскость, содержащая эту образующую и ось , перпендикулярна плоскости .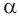
Проведем прямую 
, которая перпендикулярна образующей 
, пересекает ось конуса в точке 
, отличной от вершины 
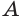. Через точку 
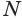проведем плоскость 
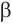, перпендикулярную оси , она пересечет конус по кругу с центром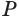 
и плоскость 
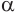— по прямой 
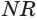, касающейся окружности с центром 
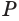. Эта касательная по свойству касательной к окружности перпендикулярна радиусу 
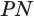соответствующей окружности. Но этот радиус является проекцией наклонной 
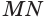на плоскость 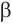, поэтому по теореме о трех перпендикулярах прямая 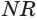перпендикулярна наклонной 
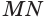, т. е. прямой .
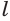Таким образом, прямая 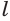перпендикулярна прямым и 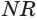, которые пересекаются и лежат в плоскости 
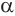, поэтому по признаку перпендикулярности прямой и плоскости прямая перпендикулярна плоскости 
. Значит, плоскость 
, содержащая прямую , перпендикулярна плоскости .
Теорема 6 выражает свойство касательной плоскости конуса.
Теорема 7.
Плоскость касается конуса, если она проходит через его образующую и перпендикулярна плоскости, проходящей через эту образующую и ось конуса.
Доказательство:
Пусть плоскость проходит через образующую конуса с осью и перпендикулярна плоскости (рис. 136). Докажем, что плоскость касается конуса, т. е. что точки образующей , и только они, являются общими точками конуса и плоскости .
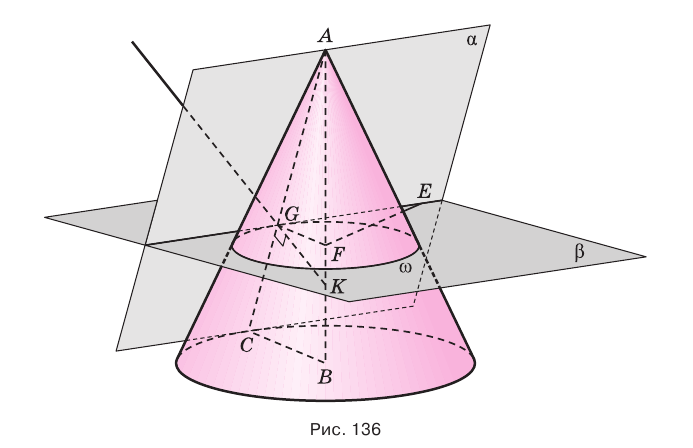
Точки образующей принадлежат и конусу, и плоскости . Пусть 
— какая-либо точка плоскости вне образующей . Через эту точку проведем плоскость 
, перпендикулярную оси , она пересекает поверхность конуса по окружности 
с центром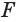 
, образующую — в некоторой точке 
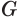и плоскость — по прямой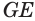 
. Пусть 
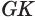— прямая, которая перпендикулярна плоскости и пересекает ось в точке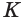 
. Тогда по теореме о трех перпендикулярах прямая 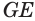, проведенная в плоскости 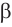через основание наклонной 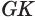перпендикулярно к ней, перпендикулярна ее проекции 
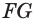. Значит, 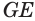— касательная к окружности , и поэтому точка находится вне окружности , а значит, и вне конуса.
Теорема 7 выражает признак касательной плоскости конуса.
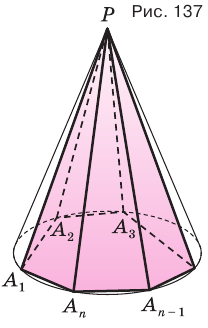
Пусть есть конус с вершиной 
(рис. 137). Впишем в основание конуса многоугольник 
и через его вершины 
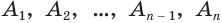проведем образующие 
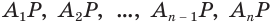. В результате получим тело 
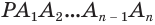, являющееся пирамидой. Ее называют пирамидой, вписанной в конус, а сам конус — конусом, описанным около пирамиды.
Если основание конуса вписано в основание пирамиды, а боковая поверхность конуса касается боковых граней пирамиды, то говорят, что пирамида описана около конуса, или конус вписан в пирамиду (рис. 138).
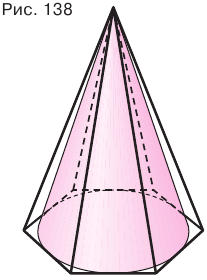
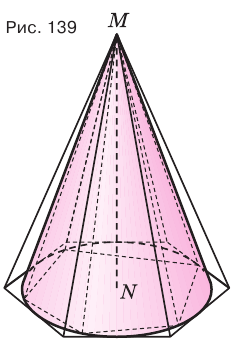
Теорема 8.
Объем конуса равен третьей доле произведения площади Рис. 139 т его основания и высоты:
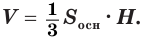
Доказательство:
Пусть есть конус с осью 
(рис. 139). В него впишем правильную пирамиду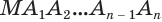 
, а около него опишем правильную пи-рамиду 
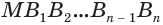. В соответствии с теоремой 4 объем первой пирамиды равен третьей доле произведения площади многоугольника 
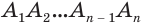и высоты 
пирамиды, т. е. высоты конуса, а объем второй — произведению площади многоугольника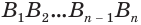 
и той же высоты. Объем самого конуса заключен между этими числами.
Будем увеличивать количество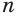 
сторон оснований пирамид. Тогда объем первой пирамиды будет увеличиваться, объем второй — уменьшаться, причем их разность стремится к нулю, если значение переменной 
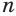неограниченно увеличивается. То число, к которому приближаются объемы обеих пирамид, принимается за объем конуса.
В описанном процессе высота 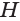пирамиды не изменяется, а площади обоих многоугольников — 
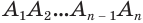и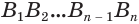 
— стремятся к площади 
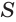круга, являющегося основанием конуса. Значит, объем 
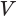конуса равен третьей доле произведения площади 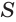основания конуса и его высоты :
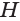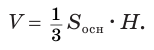
Теорема 9.
Если конус пересечь плоскостью, параллельной его основанию, то:
- а) образующая и высота разделяются на пропорциональные части;
- б) площади сечения и основания относятся как квадраты их расстояний от вершины.
Используя рисунок 140, докажите эту теорему самостоятельно.
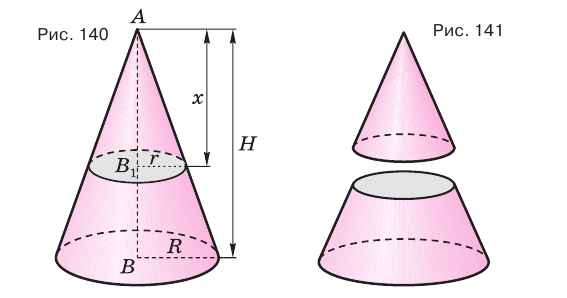
Секущая плоскость, параллельная основанию конуса, разделяет его на две части (рис. 141). Одна из этих частей также является конусом, а другая — телом, которое называется усеченным конусом.
Основание данного конуса и круг, полученный в сечении, называют основаниями усеченного конуса, а отрезок образующей данного конуса, заключенный между его основанием и секущей плоскостью, — образующей усеченного конуса (рис. 142). Высотой усеченного конуса называется перпендикуляр, проведенный из какой-либо точки одного его основания к плоскости другого основания.
Усеченный конус можно получить вращением прямоугольной трапеции вокруг боковой стороны, к которой прилежат прямые углы (рис. 143).
Пример:
Найдем боковую поверхность усеченного конуса. Пусть есть усеченный конус, у которого радиусы основани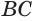й 
и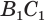 
равны 
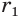и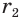 
соответственно, а образующая 
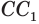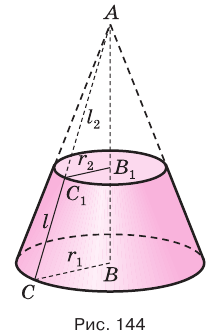
равна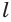 
(рис. 144).
Достроим его до полного конуса. Достроенная часть представляет собой конус, у которого радиус основания равен 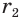. Пусть образующая 
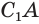достроенного конуса равна 
.
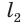Боковую поверхность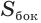 
усеченного конуса можно получить как разность боковых поверхносте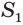й 
и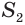 
полного и достроенного конусов. Пусть 
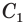и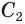 
— длины окружностей нижнего и верхнего оснований усеченного конуса.
Тогда:
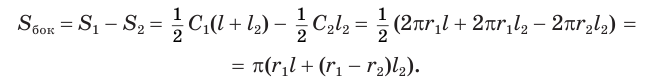
Найдем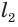 
, учитывая подобие треугольников 
и 
:
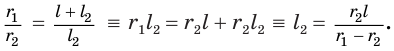
Значит,
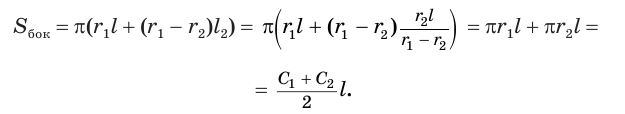
Таким образом, боковая поверхность усеченного конуса равна произведению полусуммы длин окружностей его оснований и образующей.
Пример:
Используя рисунок 144, можно, как и для усеченной пирамиды (см. параграф 9), доказать, что объем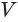 
усеченного конуса равен третьей доле произведения высоты 
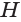конуса и суммы площаде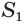й 
и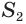 
оснований конуса и их среднего геометрического 
:
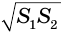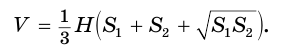
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Возникновение геометрии
- Призма в геометрии
- Цилиндр в геометрии
- Пирамида в геометрии
