Как найти центр ова

Как определить центр окружности

Окружность — совокупность точек, находящихся на равном расстоянии от одной точки, называемой центром. Однако в тех случаях, когда вам дана одна только окружность, нахождение ее центра может быть непростой задачей.

Инструкция

Самый простой способ нахождения центра окружности — согнуть лист бумаги, на котором она начерчена, следя на просвет, чтобы окружность оказалась сложена точно пополам. Полученная линия сгиба будет одним из диаметров заданной окружности. Затем лист можно согнуть в другом направлении, получив тем самым второй диаметр. Точка их пересечения и будет центром окружности.Этот способ, конечно же, годится только для случаев, когда окружность изображена на листе бумаги, бумагу можно сгибать, и есть возможность следить за точностью сгиба на просвет.

Предположим, что заданная окружность начерчена на твердом материале, или же это круглая деталь, которую нет возможности согнуть. В этом случае для нахождения ее центра вам понадобится линейка.Диаметр, по определению этого слова — самый длинный из всех отрезков, которые можно провести между двумя точками одной окружности. Середина любого диаметра окружности совпадает с ее центром.Наложив линейку на заданную окружность, зафиксируйте нулевую отметку в любой точке окружности. Таким образом вы измерите некоторую секущую, то есть отрезок, соединяющий две точки этой окружности. Затем медленно поворачивайте линейку, следя за изменением ширины отрезка. Она будет возрастать, пока секущая не превратится в диаметр, после чего снова начнет уменьшаться. Отметив момент максимума, вы найдете диаметр, а значит, и центр.

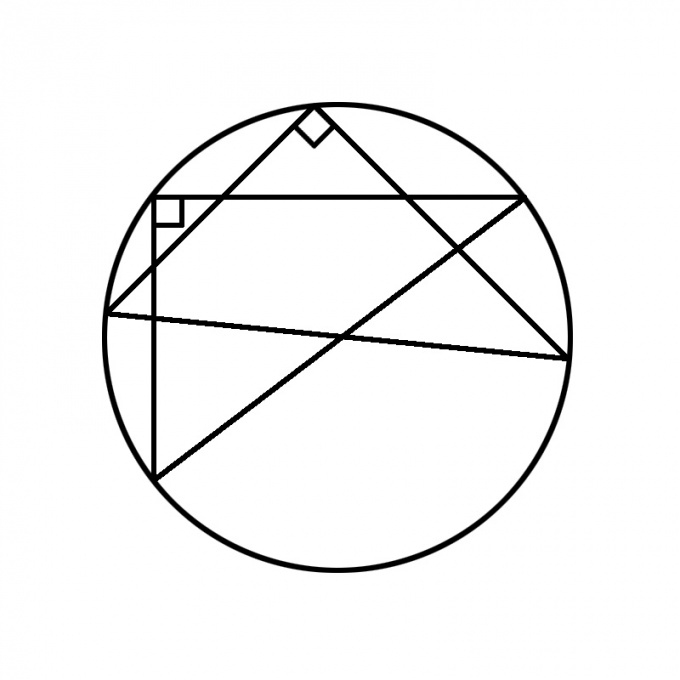
Для любого треугольника центр описанной окружности находится в точке пересечения срединных перпендикуляров. Если этот треугольник — прямоугольный, то центр описанной окружности всегда совпадает с серединой гипотенузы. Следовательно, если вписать в окружность прямоугольный треугольник, то его гипотенуза будет диаметром этой окружности.В качестве трафарета для этого способа подойдет любой прямой угол — школьный или строительный угольник, или просто лист бумаги. Поместите вершину прямого угла в любую точку окружности и сделайте отметки там, где стороны угла пересекают границу круга. Это конечные точки диаметра.Тем же способом найдите второй диаметр. В точке их пересечения находится центр окружности.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

План урока:

Понятие окружности и круга

Касательная к окружности

Взаимное расположение двух окружностей

Понятие окружности и круга

Тарелки, шины, колеса и монеты – все эти предметы имеют одинаковую форму, их называют круглыми. Этот термин понятен каждому, однако в геометрии каждое понятие надо строго определять. Дадим строгое определение понятию окружности:

Та точка, от которой равноудалены все точки, образующие окруж-ть, именуется центром окружности. Обратите внимание, что сам центр частью окружности НЕ считается. Расстояние, отделяющее точки окруж-ти от ее центра, именуют радиусом окружности. Получается, что для построения окруж-ти достаточно знать только ее радиус и центр. Выглядит она так:

Для построения окруж-ти используется специальный инструмент – циркуль. Он представляет собой два длинных стрежня, которые соединены шарниром. На конце одного стержня находится иголка, на конце другого – грифель карандаша или иной пишущий предмет. Сначала необходимо выставить расстояние между концами стержней – оно будет равно радиусу окруж-ти. Потом иголку ставят в центр будущей окруж-ти, после чего поворачивают циркуль так, что его пишущий конец оставил на бумаге след:

Отрезок, соединяющий две точки окруж-ти, именуется хордой. Хорда, проходящая через центр окруж-ти, именуется диаметром окружности.

Особо отметим, что сам диаметр также считается хордой.

Непосредственно из определения окруж-ти вытекает первое важное её свойство – все радиусы, построенные в одной окруж-ти, равны друг другу.

Так как центр окруж-ти делит ее диаметр на два отрезка, каждый из которых – это радиус, то диаметр окружности равен двум ее радиусам:

Традиционно диаметр обозначается буквой D, а радиус – буквой R. Получается, что справедлива формула:

D = 2R

Очевидно, что диаметр длиннее, чем любая другая хорда окружности, не являющаяся диаметром. Докажем это. Пусть хорда AВ не проходит через О, центр окруж-ти (он почти всегда обозначается именно этой буквой). Тогда можно построить ∆AВО:

Мы знаем про неравенство треугольника, согласно которому любая сторона треугольника меньше суммы двух других. В данном случае можно записать, что

AB < OA + OB

ОА и ОВ – радиусы. Обозначив их буквой R, получим, что

AB < R + R

AB < 2R

Величина 2R как раз равна диаметру, то есть

AB < D

ч. т. д.

Ещё раз сформулируем простейшие свойства окруж-ти:

Задание. AВ и СD – диаметры окружности. Верно ли, что BD = АС?

Решение. Выполним построение по условию задачи:

Заметим, что отрезки ОА, ОВ, ОС и ОD одинаковы, ведь они являются радиусами одной окруж-ти:

В итоге получается, что у ∆АОС и ∆ВОD одинаковы две стороны образованный ими угол. Тогда по первому признаку равенства треуг-ков они равны:

Отсюда вытекает, что одинаковы и отрезки АС и BD.

Ответ: верно.

Задание. AВ и CD – диаметры, проходящие через точку О. Длина ВС составляет 13, а АВ – 16. Вычислите периметр ∆АОD.

Решение.

Чтобы вычислить периметр, нужно узнать длины всех сторон треугольника, то есть AD, OD и ОА. Как и в предыдущей задаче, хорды ВС и AD оказываются одинаковыми, так как ∆ОВС и ∆ОАD равны:

AB = DC = 13

Нам известен отрезок AВ, который является диаметром. Поделив его на два, узнаем и радиус:

Задание. Точки А и В на окруж-ти выбраны так, что радиусы АО и ВО пересекаются под углом 40°. Найдите ∠ОВА.

Решение.

Заметим, что в ∆ОAВ есть две одинаковые стороны. Это ОА и ОВ, которые являются радиусами и потому одинаковы. Значит, ∆ОAВ равнобедренный, причем AВ – это его основание. Но тогда углы при основании должны быть одинаковы:

Задание. Угол между радиусом ОА и хордой AВ составляет 60°. AВ имеет длину 29. Каков радиус окруж-ти?

Решение. Исследуем ∆ОAВ. ОВ и ОА являются радиусами одной длины, поэтому он равнобедренный. Тогда ∠ОAВ и ∠ОВА одинаковы:

В итоге получили, что у ∆ОAВ все углы составляют по 60°. Из этого вытекает, что он равносторонний, то есть все его стороны, в частности AВ и ОВ, одинаковы:

OB = AB = 29

Ответ: 29.

Выделяют ещё несколько элементов окруж-ти. Всякие две точки окруж-ти разбивают ее на две кривые линии, которые именуются дугами окружности. Для обозначения дуг используется символ ⋃, после которого пишутся три буквы. Первая и третья буквы указывают на концы дуги, а вторая буква – на какую-либо точку между ними:

Но иногда дугу обозначают только двумя буквами, указывая только ее концы: ⋃AВ. Так поступают, когда ясно, о какой именно из двух дуг идет речь.

Часть плоскости, ограниченная окруж-тью, именуется кругом. То есть окруж-ть – это лишь линия, граница круга, имеющая длину, не имеющая площади. Круг же, наоборот, обладает какой-то площадью, но не имеет длины. На рисунке точка А принадлежит кругу, но НЕ принадлежит окруж-ти:

Очевидно, что любая точка внутри окруж-ти ближе к ее центру, чем точки на самой окруж-ти. Действительно, через центр O и точку A внутри окруж-ти можно построить прямую, которая пересечет окруж-ть в некоторой точке B:

Ясно, что

OB = OA + AB

Значит, отрезок ОВ длиннее ОА. Точки на самой окруж-ти обычно также считают частью круга. Таким образом, круг представляет собой множество точек, удаленных от некоторого центра не более чем на величину заданного радиуса.

Круг можно разделить на две части, либо проведя хорду, либо построив два радиуса. В первом случае образуется фигура, которую называют сегментом. Во втором случае образуется сектор окружности:

Касательная к окружности

Возможно три варианта расположения прямой и окруж-ти относительно друг друга. Если расстояние между центром окруж-тии прямой меньше радиуса, то у них обязательно будут две общие точки. В таком ситуации прямую именуют секущей:

Если же расстояние между прямой и центром окруж-ти больше радиуса, то тогда никаких точек пересечения не будет:

Наконец, возможен особый случай, когда расстояние между прямой и центром окруж-ти в точности равно радиусу. Тогда окруж-ть и прямая будут иметь только одну общую точку. Прямую же в такой ситуации называют касательной к окружности:

Общая точка касательной и окруж-ти именуется точкой касания. Сформулируем одну важную теорему, которая представляет собой основное свойство касательной:

Действительно, предположим, что это утверждение ошибочно, и радиус может образовать с касательной угол, отличный от 90°. Тогда из центра окруж-ти опустим перпендикуляр на прямую, и он упадет на нее в точке B, не совпадающую с точкой касания A. Далее от В на прямой AВ отложим отрезок ВA₁, который будет равен AВ.

Получается, что в ∆АОА₁ ОВ одновременно высота (ведь ОВ – это перпендикуляр) и медиана (ведь AВ = ВА₁). Но это возможно лишь в том случае, если ∆АОА₁ – равнобедренный, то есть АО = А₁О. Отсюда вытекает, что точка А₁ находится на том же расстоянии от О, что и точка А, поэтому она также должна принадлежать окруж-ти. Но тогда прямая имеет уже 2 общие точки с окруж-тью, А и А₁, а потому по определению она уже не касательная, ч. т. д.

Оказывается, верна и обратная теорема, которая представляет собой признак касательной.

Действительно, пусть прямая, описанная в теореме, не является касательной. Тогда она имеет не одну, а 2 общие точки с окруж-тью, которые можно обозначить буквами А и А₁:

Заметим, что ∆АОА₁ равнобедренный, так как две его стороны, ОА и ОА₁, представляют собой одинаковые радиусы. Тогда и углы при его основании одинаковы. Если один из них составляет 90°, то и другой также будет составлять 90°. Однако треугольник с двумя прямыми углами не может существовать. Полученное противоречие показывает, что прямая должна быть не секущей, а касательной, ч. т. д.

Из каждой точки плоскости, не принадлежащей кругу, можно провести не одну, а сразу 2 касательных к окруж-ти:

Докажем, что образовавшиеся отрезки AВ и АС (их называют отрезками касательных) одинаковы. Посмотрим на ∆АОС и ∆АОВ. Они прямоугольные, ведь

по свойству касательной. Также у них общая гипотенуза АО и одинаковые катеты ОС и ОВ, которые одинаковы как радиусы одной окруж-ти. Получается, что ∆АOС и ∆АOВ равны, AВ = АС. Также можно запомнить, что и ∠OАС = ∠OAВ, то есть OА оказывается биссектрисой ∠СAВ.

Задание. Угол между двумя касательными к одной окруж-ти составляет 39°.Каков угол между радиусами, построенными к точкам касания?

Решение. Обозначим точки касания буквами С и B, а точку их пересечения буквой А:

Теперь посмотрим на четырехугольник AВОС. Сумма углов в нем, как и во всяком выпуклом четырехугольнике, составляет 360°. По условию известен ∠A, а ∠B и ∠C составляют по 90°. Зная три угла, легко найдем и четвертый:

Задание. Радиус окруж-ти ОМ делит хорду AB пополам. Докажите, что эта хорда будет параллельна касательной к окружности в точке С.

Решение: Обозначим точку касания как С, а середину хорды буквой Н:

Проведем из центра радиусы к точкам А и В. В результате мы получим ∆ОAВ, который оказывается равнобедренным, ведь радиусы ОА и ОВ одинаковы. Так как радиус ОС делит AВ пополам, то он является медианой. Но в равнобедренном треуг-ке медиана, проведенная к основанию, ещё и высота, поэтому прямые ОС и AВ перпендикулярны. В свою очередь касательная также перпендикулярна радиусу. Получается, что хорда и касательная одновременно перпендикулярны третьей прямой, значит, они параллельны, ч. т. д.

Задание. Касательная проходит через точку А окруж-ти. Хорда AВ равна радиусу окруж-ти. Какой угол образуют хорда и касательная?

Решение. Соединим точки А и В с центром окруж-ти:

Хорда по условию имеет такую же длину, как и радиусы, поэтому в ∆ОAВ оказывается три одинаковых стороны. Следовательно, он равносторонний, а у него все углы составляют по 60°. В частности,

∠BAO = 60°

Нам надо найти ∠СAВ. ∠САО должен быть прямым как угол между радиусом и касательной, но ∠САО также является суммой ∠СAВ и ∠ВАО, что позволяет найти ∠СAВ:

Задание. В окруж-ти проведены радиус ОВ длиной 5 и перпендикулярная ему хорда АС, которая отсекает от радиуса отрезок BD длиной 1. Какова длина этой хорды?

Решение:

Сначала можно найти длину OD:

OD = OB – BD = 5 -1 = 4

Теперь исследуем ∆АОD. Он прямоугольный, при этом мы знаем длину его гипотенузы ОА и катет OD. Значит, по теореме Пифагора можно найти и второй катет:

Так как ∆ОАС – равнобедренный, то высота OD– это также и медиана, поэтому DC = AВ = 3. (Примечание: вообще всегда хорда, перпендикулярная диаметру, делится им на одинаковых отрезка). Тогда

AC = DC + AB = 3 + 3 = 6

Ответ: 6.

Задание. Через центр окруж-ти О проходит секущая ОА, а AВ – касательная. Найдите величину радиуса ОВ, если AВ = 12, АО = 13.

Решение. Выполним построение:

Ясно, что угол между отрезками AВ и ОВ должен быть прямым по свойству касательной. Тогда ∆АОВ оказывается прямоугольным, и для него справедлива теорема Пифагора. С ее помощью легко найдем неизвестный нам катет ОВ:

Задание. Длина хорды окружности составляет 72, и находится эта хорда на расстоянии 27 от центра окруж-ти. Каков диаметр этой окруж-ти?

Решение. Ещё раз напомним, что расстояние между точкой и некоторым отрезком – это длина перпендикуляра, опущенного из этой точки на отрезок. С учетом этого построим рисунок:

Здесь отрезок ОН – это как раз перпендикуляр к хорде AВ. Так как ОА и ОВ – радиусы, то ∆ОAВ – равнобедренный, и ОН в нем – это высота, проведенная к основанию. Значит, она является и медианой тоже, то есть делит AВ пополам. Это позволяет найти АН:

AH = AB/2 = 72/2 = 36

∆АОН – прямоугольный, и в нем нам известны оба катета. По теореме Пифагора можно найти и гипотенузу ОА:

Отрезок АО является радиусом. Нам надо в ответе указать диаметр. Диаметр вдвое длиннее радиуса, то есть он равен 45•2 = 90.

Ответ:90.

Задание. Хорда МК образует с касательной КH угол 83°. Найдите угол между этой хордой и радиусом ОМ.

Решение. 

Заметим, что ∠ОКН составляет 90°, так как он образован касательной НК и радиусом ОК. Но он состоит из двух углов, ∠МКН и ∠МКО. Так как ∠МКН известен, то можно найти и ∠МКО:

Задание. Точка А находится на расстоянии 8 от центра окруж-ти. Если из точки А провести касательные к окруж-ти, то они образуют угол в 60°. Каков радиус окруж-ти?

Решение:

По условию ∠ВАС = 60°. ОА разбивает этот угол пополам, то есть

∠OAB = ∠OАС = 30°

Посмотрим на ∆AВО. Он прямоугольный, и ∠ОAВ = 30°. Известно, что в прямоугольном треугольнике с углом 30° напротив этого угла находится катет, который вдвое короче гипотенузы. Но гипотенуза в ∆AВО – это ОА, значит, катет ОВ в 2 раза меньше:

OB = OA/2 = 8/2 = 4

ОВ – это и есть искомый нами радиус окруж-ти.

Ответ: 4.

Взаимное расположение двух окружностей

Касаться друг друга могут не только прямая и окруж-ть, но и две окруж-ти. Это значит, что у них есть ровно одна общая точка. Докажем важное утверждение:

Действительно, предположим обратное, что окруж-ти с центрами в точках О₁ и О₂ касаются в точке К, но точки О₁, О₂ и К НЕ лежат на одной прямой. Тогда можно построить ∆О₁КО₂, причем отрезки О₁К и О₂К будут радиусами соответствующих окруж-тей:

Отложим от точки О₁ луч так, чтобы он образовывал с О₁О₂ угол, равный ∠О₂О₁K, но не совпадал с лучом ОК. Аналогично отложим луч и от О₂ так, чтобы он образовал с О₂О₁ угол, равный ∠О₁О₂К. Эти лучи пересекутся в некоторой точке M:

У ∆О₁О₂К и ∆О₁О₂М есть общая сторона О₁О₂, а прилегающие к ней углы одинаковы. По 2-ому признаку равенства треугольников они оказываются равными. То есть

O₁K = O₁M = R₁

O₂K = O₂M = R₂

Выходит, что точка М лежит на том же расстоянии от О₁, что и K. Значит, по определению окруж-ти, она принадлежит окруж-ти с центром в О₁ и радиусом R₁. Аналогично М лежит на том же расстоянии от О₂, что и К. Значит, она также принадлежит и второй окруж-ти, с центром в О₂. То есть М принадлежит обеим окруж-тям, а значит, является их общей точкой. Но тогда оказывается, что у окруж-тей уже есть сразу две общие точки, М и К, а изначально мы предположили, что они только касаются, то есть имеют 1 общую точку. Противоречие означает, что точки О₁, О₂ и K обязательно должны лежать на одной прямой, ч. т. д.

Очевидно, что когда три точки лежат на прямой, то каждая из низ либо лежит между двумя другими, либо находится «с краю», то есть по одну сторону от двух других точек. В связи с этим возможны два принципиально различных случая касания окружностей. В первом случае точка касания находится между центрами окруж-тей. Тогда говорят, что окруж-ти касаются внешним образом:

Важно заметить, что при внешнем касании двух окружностей расстояние между их центрами равно сумме их радиусов:

O₁O₂ = O₁K + O₂K

Во втором случае одна из окруж-тей находится внутри другой, в таком случае говорят, что окруж-ти касаются внутренним образом. Такое расположение окруж-тей означает, что точка касания находится «с краю»:

При внутреннем касании двух окружностей расстояние между их центрами – это уже разность их радиусов:

O₁O₂ = O₁K – O₂K

Заметим, что если в точке касания двух окружностей провести ещё и касательную прямую, то она, во-первых, окажется общей касательной для обоих окруж-тей, а во-вторых, будет перпендикулярна линии, соединяющей их центра:

Однако окруж-ти (не обязательно касающиеся друг друга) могут иметь и другие общие касательные, которые соприкасаются с ними в различных точках. Важно отличать внешние и внутренние касательные. Если обе окруж-ти лежат по одну сторону от касающейся их прямой, то эту прямую именуют внешней касательной. Обычно можно построить сразу две таких внешних касательных:

Однако касательную можно провести и так, что окруж-ти окажутся по разные стороны от нее. В этом случае ее называют уже внутренней касательной:

Задание. Две окруж-ти соприкасаются в точке К. Построена общая касательная к этим окруж-тям, которая касается первой окруж-ти в точке А, а второй – в точке В. Длины хорд АК и ВК равны 15 и 8. Найдите длину отрезка AВ.

Решение:

Решение. Выполним дополнительное построение – проведем общую касательную к окруж-тям через точку К:

Получается, что АМ и КМ – это отрезки касательных, проведенные из одной точки. Мы знаем, что они должны быть одинаковыми:

AM = KM

По той же логике одинаковую длину имеют и отрезки ВМ и КВ, ведь это также касательные к одной окруж-ти, проведенные из одной точки:

BM = KM

В итоге получается, что на рисунке есть два равнобедренных треугольника, ∆АМК и ∆КМВ. Значит, углы при их основании одинаковы. Вместе же они образуют ∆AВК. Попытаемся найти в нем ∠АКВ. Пусть ∠МАК = α, а ∠AВК = β. Тогда можно записать, что

Заметим, что сумма углов в ∆AВК должна составлять 180°, то есть можно записать уравнение:

Задание. Центры окруж-тей, радиусы которых составляют 3 и 10, находятся на расстоянии 25 друг от друга. К ним построена внешняя касательная, касающаяся их в точках А и В. Какова длина отрезка AВ?

Решение. Построим к точкам касания окружностей радиусы, а также проведем через центр меньшей окруж-ти прямую О₂Н, параллельную касательной:

Радиусы перпендикулярны касательным. Так как О₂Н параллельна AВ, то она также должна быть перпендикулярна радиусам. Получается, что в четырехугольнике AВО₂Н все углы прямые, то есть это прямоугольник. Его противоположные стороны одинаковы, поэтому нам достаточно найти длину НО₂. Также заметим, что одинаковы и стороны АН и ВО₂:

AH = BO₂ = 3

Тогда можно найти и длину НО₁:

HO₁ = AO₁ – AH = 10 – 3 = 7

Заметим, что ∆НО₁О₂ прямоугольный, поэтому длину его катета НО₂ можно найти по теореме Пифагора:

Ответ: 24.

Задание. В окруж-ти на радиусе О₁А (его длина составляет 10) отмечена точка К на расстоянии 4 от центра окруж-ти О₁. Построена ещё одна окруж-ть, которая касается как исходной окруж-ти, так и отрезка О₁А в точке К. Какой у неё радиус?

Решение: Соединим центры обоих окруж-тей прямой, которая также пройдет через их точку касания. Также построим радиус О₂К:

Обозначим искомый нами радиус буквой R. Теперь посмотрим на отрезок О₁О₂. С одной стороны, его можно найти как разность радиусов окруж-тей:

Задание на построение. Постройте три окруж-ти, которые касаются друг друга внешним образом. Известны радиусы окруж-тей, они составляют 2, 3 и 4 см.

Решение. Для построения окруж-тей надо лишь знать их центры и величины их радиусов. Радиусы уже известны. Если окруж-ти касаются внешним образом, то расстояние между их центрами равно сумме их радиусов. Значит, в данном случае эти расстояния составят:

2 + 3 = 5 см

2 + 4 = 6 см

3 + 4 = 7 см

Но если расстояния между центрами составляют 5, 6 и 7 см, то это значит, что они образуют треугольник, стороны которого имеют такую же длину. Значит, нам надо просто построить треугольник со сторонами 5, 6 и 7 см, а строить треугольник по известным сторонам мы уже научились в 7 классе:

Сегодня мы узнали многие свойства окруж-ти, а также касательных к ней. Однако это только малая часть геометрических знаний об окруж-ти. В будущих уроках мы узнаем об соотношениях между углами, которые можно в ней провести, вписанных и описанных многоугольниках, вычислениях площадей окруж-ти и способах ее построения.

Уверен, у каждого домашнего мастера был случай, когда ему нужно было сделать разметку какой-нибудь круглой заготовки и найти центр ее основания. Казалось бы, это очень просто сделать, но некоторые мастера долго не могут найти выход в данной ситуации. Сегодня я покажу вам два простых решения, с помощью которых можно быстро и точной найти центр любой окружности.

1. Первый способ подойдет для разметки небольших заготовок. В качестве примера я возьму заглушку от пластиковой трубы диаметром 50 мм.

Для того, чтобы найти центр окружности заглушки, не нужны будут какие-то математические вычисления и сложные манипуляции. Нам понадобятся всего лишь строительный угольник и обычная линейка (или второй угольник), которые есть в любой мастерской.

Складываем вместе угольник и линейку, так чтобы образовался угол в 45 градусов.

Затем, придерживая одной рукой угольник и линейку, прикладываем их к круглой заготовке (заглушке) так, чтобы она вплотную соприкасалась с двумя сторонами угольника.

Теперь берем карандаш и чертим на заглушке первую линию, потом немного ее поворачиваем и делаем вторую метку (достаточно провести две линии, но для уверенности можно поставить три метки).

Все задача решена! Точка пересечения этих двух линий и будет центром данной окружности. Данный способ один из самых быстрых и простых.

2. Второй способ подойдет, если окружность имеет большой диаметр или она расположена на плоскости. Для примера я обвел карандашом крышку от кастрюли. В этом случае тоже все очень просто. Для начала выбираем любую точку на окружности.

Потом от этой точки чертим две линии до пересечения с окружностью так, чтобы у нас получился прямой угол (90 градусов). Для построения данных линий проще всего воспользоваться угольником (если окружность очень большая, линии можно продлить с помощью линейки).

А теперь все очень просто, соединяем точки, в которых пересекаются линии с окружностью и измеряем длину получившегося отрезка. Его середина и будет центром окружности. Уверен, многие помнят это из уроков по геометрии. Середина гипотенузы прямого треугольника вписанного в окружность, является центром этой окружности.

Как найти центры овала?

опокоп аукау

Ученик

(90),
на голосовании

5 лет назад

Есть зеркало, хочу ему сделать раму из фанеры, для этого хочу найти его центры чтобы эта рама была со всех сторон одинакого шире, как это сделать?