Как найти центр трапеции
Трапецией называется четырехугольник, у которого только одна пара противолежащих сторон параллельна. Найти центр трапеции очень просто. Следуйте пошаговой инструкции ниже.

Вам понадобится
- Карандаш, линейка
Инструкция
Возьмите линейку. С ее помощью найдите середину одного основания трапеции. Основание трапеции – это одна из параллельных сторон. Измерьте длину основания, разделите ее на два. Отмерьте от начала основания по ее длине найденную величину и поставьте точку.Так же измерьте и длину второго основания трапеции. В результате на двух параллельных сторонах у вас будут отметки точно на их серединах.
Соедините найденные в предыдущем шаге середины оснований прямой линией. Сделайте это с помощью карандаша и линейки.Теперь точки, обозначающие середины трапеции, соединены прямой.
Найдите середину прямой линии, которую вы провели в предыдущем шаге.Для этого с помощью линейки измерьте длину линии и разделите ее на два.От любого из оснований трапеции отмерьте по этой линии половину ее длины и поставьте точку.Эта точка является центром трапеции.
Видео по теме
Полезный совет
Чтобы проверить правильность расчетов, вырежьте трапецию из бумаги, проведите все вышеописанные действия, чтобы найти ее центр, и поместите трапецию на кончик карандаша или на зубочистку. Острие карандаша/зубочистки должно приходиться точно на центр трапеции.
Если центр трапеции найден верно, бумажная фигура не будет падать с кончика карандаша или с зубочистки.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Трапеция – это четырехугольник, у которого две стороны параллельны друг другу. Высотой трапеции называют линию, перпендикулярную основаниями, для удобства ее часто проводят из тупого угла трапеции на большее основание. Средняя линия трапеции – это линия, которая параллельна основаниям, и разделяет боковые стороны ровно пополам. Среднюю линию трапеции можно найти средним арифметическим оснований – сложив их и разделив на два.
Площадь трапеции в самом простом виде – это произведение средней линии на высоту, или если раскрыть формулу средней линии, то произведение полусуммы оснований на высоту.
Доказательством этой формулы будет служить представление площади трапеции, как суммы площадей двух треугольников полученных при проведении диагонали.

Площади этих треугольников будут равны соответственно  и
и  (для того, чтобы нарисовать высоту во втором треугольнике, необходимо будет продлить основание b). Площадь трапеции будет равна сумме полученных выражений, где мы вынесем высоту за скобку, и получим искомую формулу:
(для того, чтобы нарисовать высоту во втором треугольнике, необходимо будет продлить основание b). Площадь трапеции будет равна сумме полученных выражений, где мы вынесем высоту за скобку, и получим искомую формулу:

Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с помощью метода подстановки.

Проведя две высоты в трапеции, получаем по бокам прямоугольные треугольники с известными гипотенузами и неизвестными катетами x и y.
Таким образом x+y=d-b, y=d-b-x.
Одинаковый катет у обоих треугольников – высота, которую мы ищем. Через теорему Пифагора в прямоугольных треугольниках выражаем высоту  и
и  . Приравнивая, получаем a2-x2=c2-y2 или x2-y2=a2-c2.
. Приравнивая, получаем a2-x2=c2-y2 или x2-y2=a2-c2.
x2-(d-b-x)2=a2-c2 – Подставляем вместо х полученное выше выражение d-b-y.
x2-d2+bd+dx-b2+bd-bx-x2+dx-bx=a2-c2 – Раскрываем скобки.
x2-d2+2bd+2dx-b2-2bx-x2=a2-c2 – Приводим подобные слагаемые.
2dx-2bx=a2-c2+d2+b2-2bd – Переносим все вправо, оставляя слева только y.
2x(d-b)=a2-c2+(d-b)2 – Выносим общие множители.
Подставляем обратно y в формулу высоты  .
.
Формула площади трапеции через стороны будет выглядеть так:

Площадь трапеции через диагонали и угол между ними считается условным делением трапеции на четыре треугольника, точно также как и площадь любого произвольного четырехугольника.
Площадь равнобедренной трапеции можно найти еще одним способом, если даны угол при основании и радиус вписанной окружности. Дело в том, что центр вписанной окружности, откуда берет свое начало радиус, находится точно в центре трапеции, таким образом, приравнивая высоту и диаметр окружности (либо удвоенный радиус). Также одно из свойств трапеции, описанной вокруг окружности – это равенство суммы оснований и суммы боковых сторон, значит, мы сможем найти среднюю линию, зная боковые стороны. Проведя высоту, из прямоугольного треугольника получаем боковую сторону  и среднюю линию
и среднюю линию 
Тогда площадь трапеции равна 
Преподаватель который помогает студентам и школьникам в учёбе.
Площадь трапеции – определение и вычисление с примерами решения
Теорема (о площади трапеции). Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Доказательство:
Пусть 
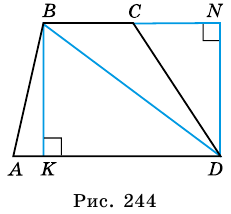
Докажем, что площадь 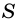 трапеции можно найти по формуле:
трапеции можно найти по формуле:
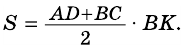
1) Диагональ 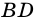 разбивает трапецию на два треугольника
разбивает трапецию на два треугольника 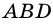 и
и 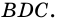 Поэтому
Поэтому 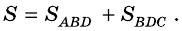
2) 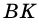 – высота треугольника
– высота треугольника 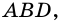 поэтому
поэтому 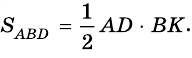
3) Проведем в трапеции высоту 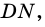 она является и высотой треугольника
она является и высотой треугольника 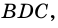 поэтому
поэтому 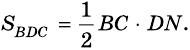
4) 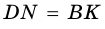 (как высоты трапеции). Следовательно,
(как высоты трапеции). Следовательно,
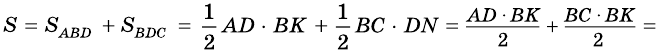
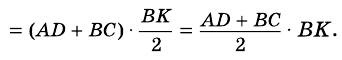
В общем виде формулу площади 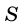 трапеции можно записать так:
трапеции можно записать так:
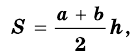
где 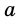 и
и 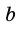 – основания трапеции,
– основания трапеции, 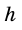 – ее высота.
– ее высота.
Следствие. Площадь трапеции равна произведению ее средней линии на высоту.
Пример:
В трапеции 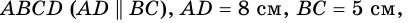
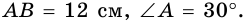 Найдите площадь трапеции.
Найдите площадь трапеции.
Решение:
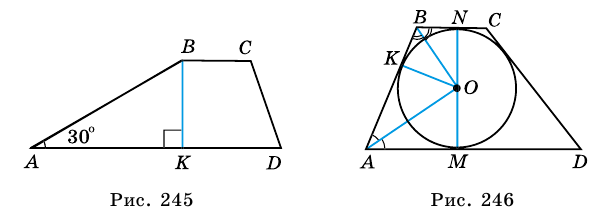
1) Проведем в трапеции 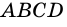 высоту
высоту 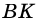
(рис. 245). В 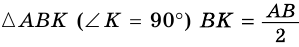 (по свойству катета, противолежащего углу 30°). Следовательно,
(по свойству катета, противолежащего углу 30°). Следовательно, 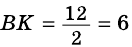 (см).
(см).
2) 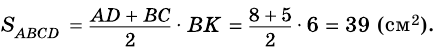
Ответ. 39 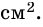
Пример:
Периметр трапеции 60 см, а одна из боковых сторон точкой касания вписанной окружности делится на отрезки 9 см и 4 см. Найдите площадь трапеции.
Решение:
1) Так как трапеция является описанной около окружности (рис. 246), то
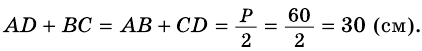
2) Центр вписанной окружности – точка 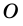 – является точкой пересечения биссектрис углов трапеции, следовательно, и углов
– является точкой пересечения биссектрис углов трапеции, следовательно, и углов 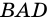 и
и 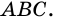 Поэтому
Поэтому 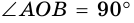 (задача 214, с. 43).
(задача 214, с. 43).
3) Точка 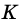 – точка касания окружности со стороной
– точка касания окружности со стороной 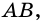 поэтому
поэтому 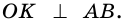 Следовательно,
Следовательно, 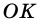 – радиус окружности и высота прямоугольного треугольника
– радиус окружности и высота прямоугольного треугольника 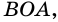 проведенная к гипотенузе. По теореме о средних пропорциональных отрезках в прямоугольном треугольнике имеем:
проведенная к гипотенузе. По теореме о средних пропорциональных отрезках в прямоугольном треугольнике имеем: 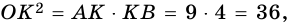 откуда
откуда 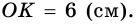
4) 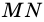 — диаметр окружности, а также высота трапеции, поэтому
— диаметр окружности, а также высота трапеции, поэтому 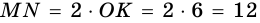 (см).
(см).
5) Следовательно, 
Ответ. 180 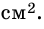
Площадь трапеции
Часто для вычисления площади некоторого многоугольника его разбивают на несколько треугольников и находят искомую площадь как сумму площадей этих треугольников. Именно такой подход можно применить для вывода формулы площади трапеции.
Теорема (формула площади трапеции) Площадь трапеции равна произведению полусуммы ее оснований на высоту:
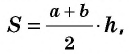
где 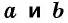 — основания трапеции,
— основания трапеции, 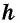 — высота трапеции.
— высота трапеции.
Доказательство:
Пусть дана трапеция 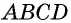 с основаниями
с основаниями 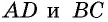 и высотой
и высотой 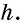 Диагональ
Диагональ 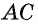 делит ее на два треугольника
делит ее на два треугольника 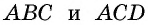 (рис. 151).
(рис. 151).
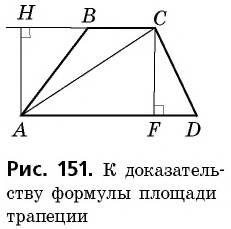
Проведем высоты этих треугольников 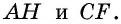 Обе они являются высотами трапеции, т.е. равны
Обе они являются высотами трапеции, т.е. равны 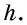 Имеем:
Имеем:
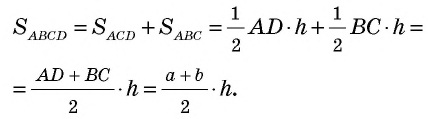
Теорема доказана.
Следствие
Площадь трапеции равна произведению средней линии на высоту.
- Центральные и вписанные углы
- Углы и расстояния в пространстве
- Подобие треугольников
- Решение прямоугольных треугольников
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
- Трапеция и ее свойства
Площадь трапеции
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь трапеции
Чтобы найти площадь трапеции воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Через длины оснований и высоту

Чему равна площадь трапеции, если:
основание a =
основание b =
высота h =
Ответ: S =
0
ед.²
Округление ответа:
Чему равна площадь трапеции если известны основания a и b, а также высота h?
Формула
S = ½ ⋅ (a + b) ⋅ h
Пример
Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:
S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²
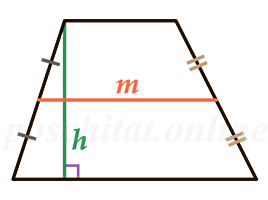
Через среднюю линию и высоту
Чему равна площадь трапеции, если:
средняя линия m =
высота h =
Ответ: S =
0
ед.²
Округление ответа:
Чему равна площадь трапеции если известны средняя линия m и высота h?
Формула
S = m ⋅ h
Пример
Если у трапеции средняя линия m = 6 см, а высота h = 4 см, то её площадь:
S = 6 ⋅ 4 = 24 см²
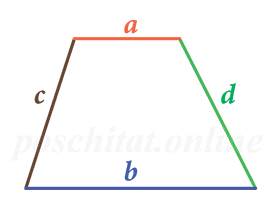
Через длины сторон и оснований
Чему равна площадь трапеции, если:
основание a =
основание b =
сторона c = сторона d =
Ответ: S =
0
ед.²
Округление ответа:
Чему равна площадь трапеции если известны основания a и b, а также стороны c и d?
Формула
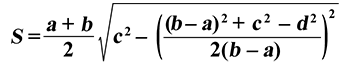
Пример
Если у трапеции основание a = 2 см, основание b = 6 см, сторона c = 4 см, а сторона d = 7 см, то её площадь:
S ≈ 13.555 см²
Через диагонали и угол между ними
Чему равна площадь трапеции, если:
диагональ d1 =
диагональ d2 =
угол α =
Ответ: S =
0
ед.²
Округление ответа:
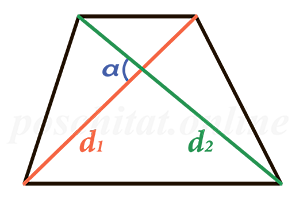
Чему равна площадь трапеции если известны диагонали d1 и d2 и угол между ними α?
Формула
S = ½ ⋅ d1 ⋅ d2 ⋅ sin(α)
Пример
Если у трапеции одна диагональ d1 = 5 см, другая диагональ d2 = 7 см, а угол между ними ∠α = 30°, то её площадь:
S = ½ ⋅ 5 ⋅ 7 ⋅ sin (30) = 17.5 ⋅ 0.5= 8.75 см²
Площадь равнобедренной трапеции
Через среднюю линию, боковую сторону и угол при основании
Чему равна площадь трапеции, если:
средняя линия m =
сторона c =
угол α =
Ответ: S =
0
ед.²
Округление ответа:
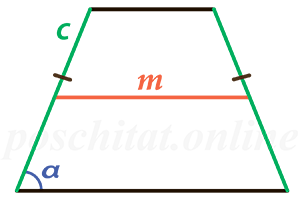
Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?
Формула
S = m ⋅ c ⋅ sin(α)
Пример
Если у равнобедренной трапеции средняя линия m = 6 см, сторона c = 4 см, а угол при основании ∠α = 30°, то её площадь:
S = 6 ⋅ 4 ⋅ sin (30) = 24 ⋅ 0.5 = 12 см²
Через радиус вписанной окружности
Чему равна площадь трапеции, если:
радиус r =
угол α =
Ответ: S =
0
ед.²
Округление ответа:
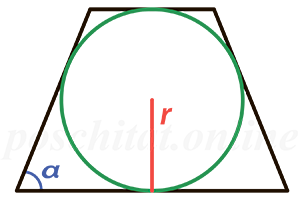
Чему равна площадь равнобедренной трапеции если радиус вписанной окружности r, a угол при основании α?
Формула
S = 4⋅r² ⁄ sin(α)
Пример
Если у равнобедренной трапеции радиус вписанной окружности r = 5 см, а угол при основании ∠α = 30°, то её площадь:
S = 4 ⋅ 5² / sin (30) = 100 / 0.5 = 200 см²
См. также

|
xC |
F1 x1 F2 x2 |
и yC |
F1 y1 F2 y2 |
. |
|
F1 F2 |
||||
|
F1 F2 |
Этот способ определения центра тяжести плоской фигуры, из которой вырезана некоторая часть, называется способом отрицательных площадей.
Аналогичный прием, называемый способом отрицательных объемов, применяется при вычислении координат центра тяжести однородного тела, полученного вырезанием из тела
|
объемом 1 с центром тяжести |
C1 (x1 , y1 , z1 ), части объемом 2 с центром |
|||||
|
тяжестиC2 (x2 , y2 , z2 ). Тогда |
||||||
|
x 1x1 2 x2 |
; |
y |
1 y1 2 y2 ; |
z |
C |
1z1 2 z2 . |
|
C |
1 2 |
C |
1 2 |
1 2 |
||
Центры тяжести некоторых линий, плоских фигур и тел
Центр тяжести площади треугольника. Разбивая площадь треугольника на ряд узких полосок, параллельных одной из сторон треугольника, убеждаемся, что центры тяжести всех полосок лежат на медиане треугольника (рис. 1.1.76).
Из этого следует, что центр тяжести С площади треугольника находится на этой медиане, а следовательно, и на других медианах, т. е. в точке пересечения его медиан и
CK 13 BK .
Центр тяжести площади трапеции. Обозначим параллельные стороны трапеции АЕ = а, BD = b, а высоту трапеции h (рис. 1.1.77). Центр тяжести площади трапеции должен лежать на прямой FK, соединяющей середины параллельных сторон трапеции. Эта прямая является линией центров тяжести полосок бесконечно малой ширины, параллельных основаниям трапеции, на которые можно разбить площадь трапеции.
Для определения координаты центра тяжести площади трапеции разобьем трапецию на два треугольника АВЕ и EBD, площади и координаты центров тяжести которых соответственно
|
F ah |
и |
F bh |
; |
y h |
и |
y |
2 |
2 h. |
||
|
1 |
2 |
2 |
2 |
1 |
3 |
3 |
||||
Центр тяжести трапеции должен находиться на прямой С1С2 , соединяющей центры
тяжести рассматриваемых треугольников. Из этого следует. что центр тяжести площади трапеции находится в точке пересечения прямых FK и С1С2 .
61

Координату центра тяжести площади трапеции определяем по формуле
|
ah |
h |
bh |
2 |
||||||||
|
y |
F1 y1 F2 y2 |
2 |
3 |
2 |
3 h |
h(a 2b) . |
|||||
|
C |
ah bh |
||||||||||
|
F1 F2 |
3(a b) |
||||||||||
|
2 2 |
Центр тяжести площади трапеции можно построить и графическим способом. Для этого отложим на продолжении стороны BD отрезок DL = a и на продолжении стороны АЕ
отрезок АN = b (рис. 1.1.78).
Рис. 1.1.78
Соединим точки N и L прямой. Покажем, что точка С пересечения прямых NL и FК является центром тяжести площади трапеции. Опустим из точки С на прямую АЕ перпендикуляр CJ и определим его длину.
Действительно,
|
CJ |
CK |
CJ h CK |
||||||||
|
h |
FK , откуда |
FK . |
||||||||
|
Из подобия треугольников NCK и LCF |
CF |
|||||||||
|
CK |
||||||||||
|
. |
||||||||||
|
a b |
a b |
|||||||||
|
По свойству пропорции |
2 |
2 |
||||||||
|
CK |
CK CF |
|||||||||
|
3 a |
3 b |
, |
||||||||
|
a b |
||||||||||
|
2 |
2 |
2 |
откуда
a b CK (CK CF) 3 2 3 ,
2 a 2 b
или
|
CK FK |
a 2b |
, |
CJ h CK |
h(a 2b) |
yC . |
|
|
3(a b) |
||||||
|
FK |
3(a b) |
Полученный результат показывает, что точка С действительно является центром тяжести площади трапеции.
Центр тяжести дуги окружности. Возьмем дугу АВ окружности радиусом R с центральным углом 2 (рис. 1.1.79).
62

Так как ось х является осью симметрии этой дуги, то центр тяжести дуги лежит на этой оси и положение его определяется только координатой xC :
|
xC xi |
li |
. |
|||||||||||||
|
L |
|||||||||||||||
|
Длина дуги L R 2 , |
где 2 – центральный угол в радианах. Разбиваем всю дугу на |
||||||||||||||
|
бесконечно малые элементы длиной li и вычисляем координату xC : |
|||||||||||||||
|
xC |
1 |
xi li |
1 |
xi |
li cos |
1 |
R yi |
R |
yi |
R |
AB R |
2Rsin . |
|||
|
cos i |
L |
||||||||||||||
|
L |
L |
L |
L |
2R |
Окончательно получаем
xC R sin ,
где – половина центрального угла, рад.
Так как sin , то центр тяжести дуги лежит внутри сектора АОВ.
Центр тяжести площади сектора круга.
Разбиваем сектор круга, соответствующий центральному углу 2 , на бесчисленное множество элементарных секторов (рис. 1.1.80).
Каждый элементарный сектор можно рассматривать как треугольник высотой R и основанием R , центр тяжести которого находится на расстоянии 32 R от центра круга.
Очевидно, что центр тяжести площади сектора АОВ совпадает с центром тяжести дуги окружности радиусом r 23 R . Имеем
|
xC r |
sin |
или xC |
2 |
R |
sin |
. |
|
3 |
||||||
63

Центр тяжести объема четырехгранной пирамиды.
Разобьем пирамиду плоскостями, параллельными основанию ABD, на бесчисленное множество тонких треугольных пластинок (рис. 1.1.81).
|
Рис. 1.1.81 |
||||
|
Рис. 1.1.82 |
||||
|
Рис. 1.1.83 |
||||
Центры тяжести этих пластинок лежат на прямой ЕК, соединяющей вершину E пирамиды с центром тяжести К ее основания. Очевидно, что центр тяжести объема пирамиды должен лежать на этой же прямой. Аналогично центр тяжести объема пирамиды должен лежать и на прямой AL, соединяющей вершину А пирамиды с центром тяжести L грани BED.
Следовательно, центр тяжести объема пирамиды находится в точке С пересечения прямых ЕК и AL.
|
Так как KF |
1 |
AF |
и |
LF |
1 EF , т. к. KL || AE и KF |
1 |
AE . |
||
|
3 |
3 |
3 |
|||||||
|
Из этого следует, что ACE подобен KCL , а потому |
|||||||||
|
CK |
KL |
1 |
, EC 3CK , |
EK EC CK 4CK , |
|||||
|
EC |
AE |
3 |
откуда CK 14 EK .
Таким образом, центр тяжести объема четырехгранной пирамиды лежит на отрезке, соединяющем вершину пирамиды с центром тяжести основания, на расстоянии ¼ длины этого отрезка от центра тяжести основания.
Если из центра тяжести объема пирамиды опустить перпендикуляр на основание, то длина его составит ¼ высоты пирамиды.
Полученный результат можно применить и к многогранной пирамиде (рис. 1.1.82), так как ее можно разбить на четырехгранные пирамиды, разбив многоугольник ее основания на треугольники.
Так как конус представляет собой предел многогранной пирамиды, то расстояние от центра тяжести его объема до основания составляет ¼ его высоты (рис. 1.1.83).
1.1.6.Контрольные вопросы.
1.Что изучает механика?
2.Какие абстракции механики Вы знаете?
64
3.Дать определение материальной точке.
4.Какое тело называют абсолютно твердым?
5.Что подразумевают под понятием «система материальных точек»?
6.Сформулируйте основные аксиомы статики.
7.Что такое связь?
8.Какая система сил называется сходящейся?
9.Сформулируйте теорему о трех непараллельных силах.
10.Укажите способы решения задач на равновесие системы сходящихся сил.
11.Каково условие равновесия системы сходящихся сил?
12.Запишите уравнения равновесия системы сходящихся сил.
13.Какие способы сложения сил Вы знаете?
14.Как вычисляется момент силы относительно точки?
15.Чем отличаются понятия «момент силы как вектор» и «алгебраический момент силы»?
16.Как найти момент силы относительно оси?
17.Как соотносятся понятия «момент силы относительно оси» и «момент силы относительно точки»?
18.Что такое пара сил?
19.Как определяется момент пары сил?
20.Сформулируйте теорему Вариньона о моменте равнодействующей.
21.Дать определение алгебраическому моменту силы.
22.Дать определение алгебраическому моменту пары сил.
23.Что такое статически определимые и статически неопределимые системы тел?
24.Как определить внутренние усилия в стержнях?
25.Укажите способы расчета ферм.
26.Запишите условия равновесия тел с учетом трения скольжения и трения качения.
27.Что такое конус трения?
28.Как найти центр параллельных сил?
29.Что такое центр тяжести твердого тела?
30.Как вычислить координаты центра тяжести?
31.Запишите формулы для определения координат центра тяжести однородных тел: объема, площади, линии.
32.Укажите способы вычисления центра тяжести однородных тел.
1.1.7. Тестовые задания
С1. Механикой называется наука: а) о формах движения материи;
65
б) о формах движения вещества и поля; в) о простейших формах движения вещества и поля;
г) о движении, приводящем к переходу вещества в поле.
С2. К абстракциям теоретической механики относятся:
а) материальная точка, абсолютно твердое тело, система материальных тел и точек; б) материальная точка, деформируемое тело, система материальных тел и точек; в) геометрическая точка, тело, система тел и точек;
г) материальная точка, абсолютно твердое и деформируемое тело, система материальных точек.
С3. Материальной точкой называется: а) тело маленьких размеров;
б) материальное тело, размерами которого в условиях данной задачи можно пренебречь;
в) тело небольших размеров с незначительной массой; г) тело, размерами и массой которого в условиях данной задачи можно пренебречь.
С4. Абсолютно твердым телом называется:
а) тело, расстояние между двумя любыми точками которого остается неизменным при данных связях;
б) тело, размеры которого не изменяются при покое тела; в) тело, с незначительными размерами;
г) тело, расстояние между двумя любыми точками которого остается неизменным.
С5. Системой материальных точек называется: а) тело с однородной структурой; б) тело неправильной формы;
в) совокупность материальных точек, положение и движение которых взаимосвязаны;
г) точки, соединенные гибкими связями.
С6. Сила – это:
а) мера механического взаимодействия двух тел; б) ограничение для движения других тел; в) мера инерциальных свойств тела; г) мера деформации тела.
С7. Системой сил называется:
а) совокупность сил, приложенных к системе материальных точек; б) совокупность сил, приложенных к выделенному объекту; в) совокупность сил, подчиняющихся третьему закону Ньютона;
г) силы, равные по величине и прямо противоположные по направлению.
С8. Эквивалентными называются системы сил:
а) приложенные к двум материальным точкам разной массы и вызывающие одинаковое движение;
б) приложенные к двум точкам одинаковой массы и вызывающие одно и то же движение;
в) действующие на абсолютно твердое тело, если каждая из них порознь, уравновешивает одну и ту же систему сил;
г) приложенные к абсолютно твердому телу и приводящие его в состояние покоя.
С9. Несвободным называется твердое тело: а) имеющее шесть степеней свободы;
б) движение которого ограничено другими телами; 66
в) связанное реакциями связей; г) деформируемое другими телами.
С10. Системой сходящихся сил называется:
а) система сил, приложенных в одной точке; б) система сил, расположенных в пересекающихся плоскостях; в) соосная система сил;
г) система сил, линии действия которых пересекаются в одной точке.
С11. Если тело находится в равновесии под действием системы трех непараллельных сил, лежащих в одной плоскости, то:
а) эта система сил может быть заменена одной силой; б) эта система сил может быть заменена одной силой и главным моментом этих сил;
в) эта система сил может быть заменена главным моментом этих сил; г) линии действия этих сил пересекаются в одной точке.
С12. Моментом сил относительно точки является:
а) вектор, равный векторному произведению силы и плеча силы относительно точки;
б) произведение силы на плечо; в) произведение силы на плечо, взятое с соответствующим знаком;
г) вектор, равный векторному произведению радиуса – вектора и силы.
С13. Пара сил – это:
а) система двух параллельных сил, равных по величине и прямо противоположных по направлению;
б) момент, приложенный к телу; в) силы, линии действия которых параллельны; г) система двух сил.
С14. Алгебраический момент силы находится по формуле:
а) m = F h; б) m = F h sin ; в) m = F r;
г) m = F h sin .
С15. Условие равновесия плоской системы сил
а) M 0 R 0 ;
б) M = 0 R 0 ; в) M 0 ;
г) R 0 .
С16. Универсальная форма уравнений равновесия плоской системы сил
|
Fix |
0 |
mA (Fi ) 0 |
|||||||
|
m |
; |
m |
; |
||||||
|
а) |
(F ) 0 |
б) |
(F ) 0 |
||||||
|
m |
A |
i |
m |
B |
i |
||||
|
B |
(F ) 0 |
B |
(F ) 0 |
||||||
|
i |
i |
67
|
Fix |
0 |
|||
|
в) |
F |
0 |
; |
|
|
iy |
||||
|
m |
A |
(F ) 0 |
||
|
i |
Fix 0
Fiy 0
г) mX (Fi ) 0m (F ) 0
Y i
1.2.КИНЕМАТИКА
1.2.1Кинематика точки
Вопросы:
1.Введение в кинематику.
2.Пространство и время в классической механике.
3.Система отсчета.
4.Способы задания движения точки: векторный, координатный, естественный.
5.Скорость точки и ее определение при различных способах задания движения.
6.Ускорение точки.
7.Определение модуля и направления ускорения.
8.Касательное и нормальное ускорения точки, их физический смысл.
9.Равномерное и равнопеременное движение точки.
Введение в кинематику
Кинематикой называется раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение.
В кинематике изучается движение точки или тела независимо от причин, вызывающих или изменяющих его, т. е. независимо от тел.
Под движением точки, механическим движением, понимают изменение положения точки или тела в пространстве. Движение точки или тела происходит в пространстве с изменением времени. При этом пространство предполагается трехмерным эвклидовым. Его свойства во всех точках и направлениях одинаковы и не зависят от тел, находящихся в нем, и от их движений. Такое пространство называют абсолютным.
Чтобы характеризовать движение какой-либо точки или тела, нужно сравнить их положение с положением какого-либо другого тела, называемого телом отсчета.
Систему координат, неизменно связанную с телом отсчета, называют системой отсчета.
Если положение точки или тела в выбранной системе отсчета не изменяется, т. е. не изменяются координаты точки или координаты всех точек тела, то точка или тело относительно взятой системы отсчета находится в покое. Если же положение точки или тела относительно выбранной системы отсчета изменяется, т. е. изменяются координаты точки или координаты каких-либо точек тела, то точка или тело по отношению к взятой системе отсчета движется.
Движение точки или тела всегда является относительным движением (относительно какой-либо системы отсчета). Например, если положение точки задается тремя декартовыми координатами в системе координат, неизменно связанной с Землей, то при изменении этих координат точка движется относительно Земли.
Время принято считать одинаковым во всех системах отсчета, независимо от их движения. Это время называют абсолютным. Начало отсчета времени, т. е. тот момент времени, с которого начинается его счет, можно выбирать применительно к условиям задачи.
68

Рис. 1.2.1
Единицы для измерения расстояния и времени также можно выбирать применительно к условиям задачи. Основной единицей времени является секунда (с), расстояния – метр (м).
В кинематике движение задают относительно какой-либо системы отсчета. Задать движение точки или тела относительно какой-либо системы отсчета – значит дать условия, позволяющие найти положение точки или тела в любой момент времени относительно этой
|
системы отсчета. |
||
|
Кинематика разделяется на кинематику точки и кинематику твердого тела. |
||
|
M3 |
Движущаяся точка описывает в пространстве |
|
|
некоторую линию. |
||
|
M2 |
Эта линия, представляющая собой геометрическое |
|
|
M1 |
место последовательных положений движущейся точки |
|
|
в рассматриваемой системе отсчета, называется |
||
|
r3 |
траекторией точка. |
|
|
По виду траектории все движения точки делятся |
||
|
M |
r2 |
на прямолинейные и криволинейные. |
|
r1 |
Существуют три способа задания движения точки: |
естественный, векторный и координатный.
r
Векторный способ задания движения точки
Положение точки в пространстве однозначно определяется заданием радиуса вектора r, проведенного из некоторого неподвижного центра О в данную точку
М (рис. 1.2.1).
Для определения движения точки нужно знать, как изменяется с течением времени радиус-вектор r , т. е. должна быть задана вектор-функция r аргумента t:
r = r (t).
Траектория точки является геометрическим местом концов радиуса-вектора r движущейся точки.
Линия, образованная концами переменного вектора, начало которого находится в определенной точке пространства, называется годографом этого вектора. Следовательно, траектория точки М является годографом ее радиуса-вектора r .
Координатный способ задания движения точки. Уравнения движения точки в декартовых координатах
|
M |
Положение точки М в системе отсчета Oxyz |
||||||
|
Z |
определяется тремя декартовыми |
координатами |
|||||
|
ZM |
точки х, у, z (рис. 1.2.2). При движении точки М ее |
||||||
|
координаты изменяются с течением времени. |
|||||||
|
Следовательно, координаты х, у, z движущейся |
|||||||
|
точки М являются функциями времени t: |
|||||||
|
0 |
YM |
Y |
x f1 (t) |
||||
|
y |
f2 (t) . |
||||||
|
XM |
|||||||
|
z |
f3 (t) |
уравнениями |
|||||
|
X |
Эти уравнения |
называются |
|||||
|
Рис. 1.2.2 |
движения точки в декартовых координатах. |
||||||
|
69 |

Этими уравнениями определяется движение точки.
Уравнения движения, определяющие координаты точки в любой момент времени, можно рассматривать как параметрические уравнения траектории точки. При исключении параметра t из уравнений движения получаются уравнения траектории точки в координатной форме.
|
Естественный способ задания движения точки |
S |
||
|
При этом способе задания движения дается |
О |
М |
|
|
траектория точки, т. е. линия, по которой движется |
|||
|
– |
+ |
||
|
точка. Траекторию можно задать уравнением |
|||
|
относительно взятой системы отсчета или иными |
|||
|
геометрическими характеристиками. Например, при |
Рис. 1.2.3 |
||
|
изучении движения точки по поверхности Земли в |
|||
|
качестве траектории может быть часть какого-либо |
меридиана, параллели или какой-либо другой отрезок линии в системе координат, неизменно связанной с Землей.
Положение точки на заданной траектории определяют следующим образом. Некоторую точку траектории принимают за начало отсчета расстояний. На траектории устанавливают направление положительных и отрицательных отсчетов расстояний. Положение точки на траектории определяют расстоянием ОМ = s (рис. 1.2.3), измеряемым по траектории и взятым с соответствующим знаком.
Для числового определения расстояния необходимо выбрать единицу измерения расстояний. Для измерения времени необходимо выбрать единицу измерения времени и начало отсчета времени. Обычно за начало отсчета времени принимают момент начала движения или момент, когда движущаяся точка находится в начале отсчета расстояний.
При движении точки расстояние s изменяется с изменением t. Поэтому величина s является функцией t, т. е. s = f(t). Эту зависимость s = f(t) называют законом изменения расстояний, или уравнением движения точки по траектории. Функция времени s = f(t) является непрерывной.
Если дано уравнение движения точки по траектории s = f(t) , то движение точки задано. Можно найти положение точки в любой момент времени. Для этого в уравнение движения s = f(t) подставим значение времени t и получим значение s. Отложив расстояние s, найдем положение точки.
Рассмотренный способ задания движения точки называют естественным; его также можно назвать способом задания движения точки при известной траектории.
Важно отметить, что для уравнения движения s = f(t) нужно выбирать определенные единицы измерения расстояния и времени. При других единицах уравнение становится иным.
Скорость точки
Определение скорости точки при задании ее движения векторным способом. Вектор скорости точки
Скорость – это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.
Вектор скорости точки в данный момент равен векторной производной от радиусавектора точки по времени:
70
Соседние файлы в папке Прикладная механика [РТФ, Новикова, 4 семестр]
- #
06.08.2022105 б1desktop.ini
- #
06.08.202289 б3Решебник Яблонского 1985 год. Задание С3.url
- #
- #
- #
06.08.202284 б1Электронная библиотека полнотекстовых учебных и научных изданий УлГТУ.url

