Как найти центр плоскости треугольника

Центр треугольника

Треугольник — наиболее распространенная форма деталей в сферах машиностроения и строительства. Точка пересечения 3-х медиан считается центром треугольника. На эту точку приходится также центр тяжести и центр симметрии предметов треугольной формы. При разработке дизайнерских, инженерных проектов очень важно точно рассчитать центр тяжести элементов металлической или бетонной конструкции.

Существует несколько понятий центра для треугольника.

Инцентр — точка пересечения его биссектрис. Это — центр описанной около треугольника окружности.

Ортоцентр — точка пересечения его высот.

Центр тяжести,центр масс или центроид (обозн. М) — точка пересечения медиан треугольника.

Рассмотрим треугольник. Определим середины его сторон и соединим их с противолежащими углами. Точка пересечения медиан и будет центром тяжести тр-ка. Медиана делится этой точкой в пропорции 2:1 , (считая от вершины тр-ка).

Как найти центр треугольника

Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.

Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан.

Центр равностороннего треугольника является также центром вписанной и описанной окружности.

Центроид расположен на отрезке, соединяющем ортоцентр и центр описанной окружности. Центроид делит отрезок 2:1.

Быстро найти центр треугольника G можно с помощью онлайн калькулятора. Для этого:

• ввести в поле калькулятора координаты вершин треугольника;
• нажать кнопку Вычислить. Калькулятор вычислит значение центра треугольника G.

Центр тяжести треугольника

Этот онлайн калькулятор находит центроид, или барицентр (центр тяжести) треугольника по координатам его вершин

Центр тяжести (центр масс, барицентр) треугольника для треугольника с равномерно распределённой массой (или в вершинах которого находятся равные массы) находится в центроиде треугольника. Центроидом называется точка пересечения медиан треугольника. Центроид относится к так называемым замечательным точкам треугольника. Например, помимо того, что он является центром тяжести, он также делит каждую медиану в отношении 2:1, считая от вершины, а три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника.

Чтобы вычислить положение центра тяжести по координатам вершин треугольника, достаточно вычислить среднее арифметическое координат вершин по оси x и по оси y, что и делает калькулятор ниже.

Центры тяжести многоугольников и многогранников

Центром тяжести (или центром масс) некоторого тела называется точка, обладающая тем свойством, что если подвесить тело за эту точку, то оно будет сохранять свое положение.

Ниже рассмотрены двумерные и трёхмерные задачи, связанные с поиском различных центров масс — в основном с точки зрения вычислительной геометрии.

В рассмотренных ниже решениях можно выделить два основных факта. Первый — что центр масс системы материальных точек равен среднему их координат, взятых с коэффициентами, пропорциональными их массам. Второй факт — что если мы знаем центры масс двух непересекающихся фигур, то центр масс их объединения будет лежать на отрезке, соединяющем эти два центра, причём он будет делить его в то же отношении, как масса второй фигуры относится к массе первой.

Двумерный случай: многоугольники

На самом деле, говоря о центре масс двумерной фигуры, можно иметь в виду одну из трёх следующих задач:

• Центр масс системы точек — т.е. вся масса сосредоточена только в вершинах многоугольника.
• Центр масс каркаса — т.е. масса многоугольника сосредоточена на его периметре.
• Центр масс сплошной фигуры — т.е. масса многоугольника распределена по всей его площади.

Каждая из этих задач имеет самостоятельное решение, и будет рассмотрена ниже отдельно.

Центр масс системы точек

Это самая простая из трёх задач, и её решение — известная физическая формула центра масс системы материальных точек:

где — массы точек, — их радиус-векторы (задающие их положение относительно начала координат), и — искомый радиус-вектор центра масс.

В частности, если все точки имеют одинаковую массу, то координаты центра масс есть среднее арифметическое координат точек. Для треугольника эта точка называется центроидом и совпадает с точкой пересечения медиан:

Для доказательства этих формул достаточно вспомнить, что равновесие достигается в такой точке , в которой сумма моментов всех сил равна нулю. В данном случае это превращается в условие того, чтобы сумма радиус-векторов всех точек относительно точки , домноженных на массы соответствующих точек, равнялась нулю:

и, выражая отсюда , мы и получаем требуемую формулу.

Центр масс каркаса

Будем считать для простоты, что каркас однороден, т.е. его плотность везде одна и та же.

Но тогда каждую сторону многоугольника можно заменить одной точкой — серединой этого отрезка (т.к. центр масс однородного отрезка есть середина этого отрезка), с массой, равной длине этого отрезка.

Теперь мы получили задачу о системе материальных точек, и применяя к ней решение из предыдущего пункта, мы находим:

где — точка-середина -ой стороны многоугольника, — длина -ой стороны, — периметр, т.е. сумма длин сторон.

Для треугольника можно показать следующее утверждение: эта точка является точкой пересечения биссектрис треугольника, образованного серединами сторон исходного треугольника. (чтобы показать это, надо воспользоваться приведённой выше формулой, и затем заметить, что биссектрисы делят стороны получившегося треугольника в тех же соотношениях, что и центры масс этих сторон).

Центр масс сплошной фигуры

Мы считаем, что масса распределена по фигуре однородно, т.е. плотность в каждой точке фигуры равна одному и тому же числу.

Случай треугольника

Утверждается, что для треугольника ответом будет всё тот же центроид, т.е. точка, образованная средним арифметическим координат вершин:

Случай треугольника: доказательство

Приведём здесь элементарное доказательство, не использующее теорию интегралов.

Первым подобное, чисто геометрическое, доказательство привёл Архимед, но оно было весьма сложным, с большим числом геометрических построений. Приведённое здесь доказательство взято из статьи Apostol, Mnatsakanian “Finding Centroids the Easy Way”.

Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид.

Разобьём данный треугольник на четыре, соединив середины сторон, как показано на рисунке:

Четыре получившихся треугольника подобны треугольнику с коэффициентом .

Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого лежит в точке пересечения его диагоналей (поскольку это фигура, симметричная относительно обеих диагоналей, а, значит, её центр масс обязан лежать на каждой из двух диагоналей). Точка находится посередине общей стороны треугольников №1 и №2, а также лежит на медиане треугольника :

Пусть теперь вектор — вектор, проведённый из вершины к центру масс треугольника №1, и пусть вектор — вектор, проведённый из к точке (которая, напомним, является серединой стороны, на которой она лежит):

Наша цель — показать, что вектора и коллинеарны.

Обозначим через и точки, являющиеся центрами масс треугольников №3 и №4. Тогда, очевидно, центром масс совокупности этих двух треугольников будет точка , являющаяся серединой отрезка . Более того, вектор от точки к точке совпадает с вектором .

Искомый центр масс треугольника лежит посередине отрезка, соединяющего точки и (поскольку мы разбили треугольник на две части равных площадей: №1-№2 и №3-№4):

Таким образом, вектор от вершины к центроиду равен . С другой стороны, т.к. треугольник №1 подобен треугольнику с коэффициентом , то этот же вектор равен . Отсюда получаем уравнение:

Таким образом, мы доказали, что вектора и коллинеарны, что и означает, что искомый центроид лежит на медиане, исходящей из вершины .

Более того, попутно мы доказали, что центроид делит каждую медиану в отношении , считая от вершины.

Случай многоугольника

Перейдём теперь к общему случаю — т.е. к случаю мноугоугольника. Для него такие рассуждения уже неприменимы, поэтому сведём задачу к треугольной: а именно, разобьём многоугольник на треугольники (т.е. триангулируем его), найдём центр масс каждого треугольника, а затем найдём центр масс получившихся центров масс треугольников.

Окончательная формула получается следующей:

где — центроид -го треугольника в триангуляции заданного многоугольника, — площадь -го треугольника триангуляции, — площадь всего многоугольника.

Триангуляция выпуклого многоугольника — тривиальная задача: для этого, например, можно взять треугольники , где .

Случай многоугольника: альтернативный способ

С другой стороны, применение приведённой формулы не очень удобно для невыпуклых многоугольников, поскольку произвести их триангуляцию — сама по себе непростая задача. Но для таких многоугольников можно придумать более простой подход. А именно, проведём аналогию с тем, как можно искать площадь произвольного многоугольника: выбирается произвольная точка , а затем суммируются знаковые площади треугольников, образованных этой точкой и точками многоугольника: . Аналогичный приём можно применить и для поиска центра масс: только теперь мы будем суммировать центры масс треугольников , взятых с коэффициентами, пропорциональными их площадям, т.е. итоговая формула для центра масс такова:

где — произвольная точка, — точки многоугольника, — центроид треугольника , — знаковая площадь этого треугольника, — знаковая площадь всего многоугольника (т.е. ).

Трёхмерный случай: многогранники

Аналогично двумерному случаю, в 3D можно говорить сразу о четырёх возможных постановках задачи:

• Центр масс системы точек — вершин многогранника.
• Центр масс каркаса — рёбер многогранника.
• Центр масс поверхности — т.е. масса распределена по площади поверхности многогранника.
• Центр масс сплошного многогранника — т.е. масса распределена по всему многограннику.

Центр масс системы точек

Как и в двумерном случае, мы можем применить физическую формулу и получить тот же самый результат:

который в случае равных масс превращается в среднее арифметическое координат всех точек.

Центр масс каркаса многогранника

Аналогично двумерному случаю, мы просто заменяем каждое ребро многогранника материальной точкой, расположенной посередине этого ребра, и с массой, равной длине этого ребра. Получив задачу о материальных точках, мы легко находим её решение как взвешенную сумму координат этих точек.

Центр масс поверхности многогранника

Каждая грань поверхности многогранника — двухмерная фигура, центр масс которой мы умеем искать. Найдя эти центры масс и заменив каждую грань её центром масс, мы получим задачу с материальными точками, которую уже легко решить.

Центр масс сплошного многогранника

Случай тетраэдра

Как и в двумерном случае, решим сначала простейшую задачу — задачу для тетраэдра.

Утверждается, что центр масс тетраэдра совпадает с точкой пересечения его медиан (медианой тетраэдра называется отрезок, проведённый из его вершины в центр масс противоположной грани; таким образом, медиана тетраэдра проходит через вершину и через точку пересечения медиан треугольной грани).

Почему это так? Здесь верны рассуждения, аналогичные двумерному случаю: если мы рассечём тетраэдр на два тетраэдра с помощью плоскости, проходящей через вершину тетраэдра и какую-нибудь медиану противоположной грани, то оба получившихся тетраэдра будут иметь одинаковый объём (т.к. треугольная грань разобьётся медианой на два треугольника равной площади, а высота двух тетраэдров не изменится). Повторяя эти рассуждения несколько раз, получаем, что центр масс лежит на точке пересечения медиан тетраэдра.

Эта точка — точка пересечения медиан тетраэдра — называется его центроидом. Можно показать, что она на самом деле имеет координаты, равные среднему арифметическому координат вершин тетраэдра:

(это можно вывести из того факта, что центроид делит медианы в отношении )

Таким образом, между случаями тетраэдра и треугольника принципиальной разницы нет: точка, равная среднему арифметическому вершин, является центром масс сразу в двух постановках задачи: и когда массы находится только в вершинах, и когда массы распределены по всей площади/объёму. На самом деле, этот результат обобщается на произвольную размерность: центр масс произвольного симплекса (simplex) есть среднее арифметическое координат его вершин.

Случай произвольного многогранника

Перейдём теперь к общему случаю — случаю произвольного многогранника.

Снова, как и в двумерном случае, мы производим сведение этой задачи к уже решённой: разбиваем многогранник на тетраэдры (т.е. производим его тетраэдризацию), находим центр масс каждого из них, и получаем окончательный ответ на задачу в виде взвешенной суммы найденных центров масс.

[spoiler title=”источники:”]

http://planetcalc.ru/9363/

http://e-maxx.ru/algo/gravity_center

[/spoiler]

Была ли эта статья полезной?

Точка в треугольнике, которую можно рассматривать как его середину при некоторых критериях

В геометрии, центр треугольника (или центр треугольника ) – это точка на плоскости, которая в некотором смысле является центром треугольника, аналогичным центрам квадраты и кружки, то есть точка, которая по какой-то мере находится в середине рисунка. Например, центроид, центр окружности, центр окружности и ортоцентр были известны древним грекам и могут быть полученные простыми конструкциями.

Каждый из этих классических центров обладает тем свойством, что он инвариантен (точнее, эквивариантен ) относительно преобразований подобия. Другими словами, для любого треугольника и любого преобразования подобия (например, вращение, отражение, растяжение или перевод ) центр преобразованного треугольника совпадает с точкой преобразованного центра исходного треугольника. Эта инвариантность является определяющим свойством центра треугольника. Он исключает другие хорошо известные точки, такие как точки Брокара, которые не являются инвариантными при отражении и поэтому не могут считаться центрами треугольников.

Все центры равностороннего треугольника совпадают в его центроиде, но обычно они отличаются друг от друга в разносторонних треугольниках. Определения и свойства тысяч центров треугольников собраны в Энциклопедии центров треугольников.

Содержание

• 1 История
• 2 Формальное определение
  • 2.1 Домен по умолчанию
  • 2.2 Другие полезные домены
  • 2.3 Симметрия домена
• 3 Примеры
  • 3.1 Окружной центр
  • 3.2 1-й изогонический центр
  • 3.3 Точка Ферма
• 4 Не примеры
  • 4.1 Точки Брокара
• 5 Позиционные векторы
• 6 Некоторые хорошо известные центры треугольников
  • 6.1 Центры классических треугольников
  • 6.2 Последние центры треугольников
• 7 Общие классы центров треугольников
  • 7.1 Центр Кимберлинга
  • 7.2 Центр полиномиального треугольника
  • 7.3 Центр правильного треугольника
  • 7.4 Центр большого треугольника
  • 7.5 Центр трансцендентного треугольника
• 8 Разное
  • 8.1 Равнобедренные и равносторонние треугольники
  • 8.2 Excenters
  • 8.3 Биантосимметричные функции
  • 8.4 Новые центры из старого
  • 8.5 Неинтересные центры
  • 8.6 Барицентрические координаты
  • 8.7 Бинарные системы
  • 8.8 Бисимметрия и инвариантность
  • 8.9 Альтернатива t erminology
• 9 центров гиперболических треугольников
• 10 центров тетраэдров и n-симплексных центров
• 11 См. также
• 12 Примечания
• 13 Внешние ссылки

История

Хотя древние Греки открыли классические центры треугольника, они не сформулировали никакого определения центра треугольника. После древних греков, несколько особых точек, связанных с треугольником, таких как точка Ферма, центр из девяти точек, точка Лемуана, точка Жергонна и точка Фейербаха. Во время возрождения интереса к геометрии треугольника в 1980-х годах было замечено, что эти особые точки обладают некоторыми общими свойствами, которые теперь составляют основу для формального определения центра треугольника. По состоянию на 1 сентября 2020 года Кларк Кимберлинг Энциклопедия центров треугольников содержит аннотированный список из 39 474 центров треугольников.

Формальное определение

A вещественнозначная функция f трех вещественных переменных a, b, c может иметь следующие свойства:

• Однородность: f (ta, tb, tc) = tf (a, b, c) для некоторой константы n и для всех t>0.
• Бисимметрия во второй и третьей переменных: f (a, b, c) = f (a, c, b).

Если ненулевое f имеет оба этих свойства, оно называется функция центра треугольника . Если F представляет собой треугольник центр функции и, Ь, с боковыми длинами опорного треугольника, то точка, трилинейной координата являются F (а, б, в): F (B, C, a): f (c, a, b) называется центром треугольника .

. Это определение гарантирует, что центры треугольников подобных треугольников удовлетворяют критериям инвариантности, указанным выше. По соглашению цитируется только первая из трех трилинейных координат центра треугольника, поскольку две другие получаются путем циклической перестановки точек a, b, c. Этот процесс известен как цикличность .

Каждая функция центра треугольника соответствует уникальному центру треугольника. Это соответствие не является биективным. Различные функции могут определять один и тот же центр треугольника. Например, функции f 1 (a, b, c) = 1 / a и f 2 (a, b, c) = bc обе соответствуют центроиду. Две функции центра треугольника определяют один и тот же центр треугольника тогда и только тогда, когда их отношение является функцией, симметричной относительно a, b и c.

Даже если функция центра треугольника хорошо определена везде, то же самое нельзя всегда сказать о соответствующем центре треугольника. Например, пусть f (a, b, c) равно 0, если a / b и a / c оба рациональны, и 1 в противном случае. Тогда для любого треугольника с целыми сторонами центр связанного треугольника оценивается как 0: 0: 0, что не определено.

Домен по умолчанию

В некоторых случаях эти функции не определены для всего ℝ. Например, трилинейные линии X 365 – это a: b: c, поэтому a, b, c не могут быть отрицательными. Кроме того, чтобы изобразить стороны треугольника, они должны удовлетворять неравенству треугольника. Таким образом, на практике каждая функция домен ограничена областью ℝ, где a ≤ b + c, b ≤ c + a и c ≤ a + b. Эта область T является областью всех треугольников и областью по умолчанию для всех функций на основе треугольников.

Другие полезные области

Существуют различные случаи, когда может быть желательно ограничить анализ областью меньшего размера, чем T . Например:

• Центры X 3, X 4, X 22, X 24, X 40 сделайте конкретную ссылку на острые треугольники,., а именно на ту область T, где a ≤ b + c, b ≤ c + a, c ≤ a + b.
• При различении точки Ферма и X 13 важна область треугольников с углом, превышающим 2π / 3,. другими словами треугольников, для которых a>b + bc + c или b>c + ca + a или c>a + ab + b.
• Область, имеющая большую практическую ценность, поскольку она плотна в T, но исключает все тривиальные треугольники (т.е. точки) и вырожденные треугольники. (т.е. линии) – это набор всех разносторонних треугольников. Он получается удалением плоскостей b = c, c = a, a = b из T.

Симметрия домена

Не каждое подмножество D⊆ Tявляется жизнеспособным доменом. Для подтверждения теста на бисимметрию D должен быть симметричным относительно плоскостей b = c, c = a, a = b. Для поддержки цикличности он также должен быть инвариантным относительно 2π / 3 поворотов вокруг прямой a = b = c. Самой простой областью является прямая (t, t, t), которая соответствует набору всех равносторонних треугольников.

Примеры

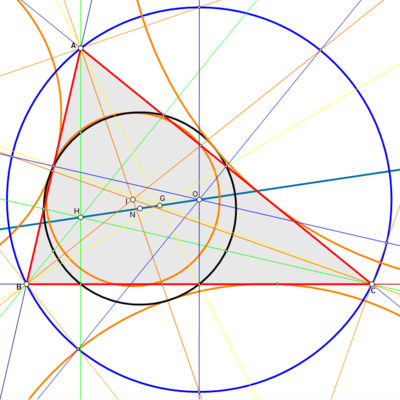Треугольник (ΔABC) с центроидом (G), центром (I), центром описанной окружности (O), ортоцентр (H) и центр из девяти точек (N)

Центр окружности

Точка пересечения серединных перпендикуляров сторон треугольника ABC – это центр окружности. Трилинейные координаты центра описанной окружности следующие:

a (b + c – a): b (c + a – b): c (a + b – c).

Пусть f (a, b, c) = а (б + с – а). Тогда

f (ta, tb, tc) = (ta) ((tb) + (tc) – (ta)) = t (a (b + c – a)) = tf (a, b, c) (однородность)

f (a, c, b) = a (c + b – a) = a (b + c – a) = f (a, b, c) (бисимметрия)

так что f – функция центра треугольника. Поскольку соответствующий центр треугольника имеет те же трилинейи, что и центр описанной окружности, следует, что центр описанной окружности является центром треугольника.

1-й изогонический центр

Пусть A’BC будет равносторонним треугольником, имеющим основание BC и вершину A ‘на отрицательной стороне BC, и пусть AB’C и ABC’ построены аналогичным образом равносторонними треугольниками на основе на двух других сторонах треугольника ABC. Тогда прямые AA ‘, BB’ и CC ‘совпадают, и точка совпадения – это 1-й изогональный центр. Его трилинейные координаты:

csc (A + π / 3): csc (B + π / 3): csc (C + π / 3).

Выражая эти координаты через a, b и c, получаем единицу можно проверить, что они действительно удовлетворяют определяющим свойствам координат центра треугольника. Следовательно, 1-й изогонический центр также является центром треугольника.

Точка Ферма

Пусть

f (a, b, c) = {1, если a 2>b 2 + bc + c 2 (эквивалентно A>2 π / 3), 0, если b 2>c 2 + ca + a 2 или c 2>a 2 + ab + b 2 (эквивалентно B>2 π / 3 или C>2 π / 3), csc ⁡ (A + π / 3) в противном случае (эквивалентно, ни один угол при вершине не превышает 2 π / 3). { displaystyle f (a, b, c) = { begin {cases} 1 quad { text {if}} a ^ {2}>b ^ {2} + bc + c ^ {2} ({ text {эквивалентно}} A>2 pi / 3), \ 0 quad { text {if}} b ^ {2}>c ^ {2} + ca + a ^ {2} { text { или}} c ^ {2}>a ^ {2} + ab + b ^ {2} ({ text {эквивалентно}} B>2 pi / 3 { text {или}} C>2 pi / 3), \ csc (A + pi / 3) quad { text {иначе}} ({ text {эквивалентно, что ни один угол при вершине не превышает}} 2 pi /3).end{cases} }}

Тогда f является бисимметричным и однородным, поэтому это функция центра треугольника. Более того, центр соответствующего треугольника совпадает с вершиной с тупым углом, когда любой угол вершины ds 2π / 3, а с 1-м изогоническим центром в противном случае. Следовательно, центр этого треугольника – не что иное, как точка Ферма.

Непримеры

Точки Брокара

Трилинейные координаты первой точки Брокара – c / b: a / c : б / у. Эти координаты удовлетворяют свойствам однородности и цикличности, но не бисимметрии. Итак, первая точка Брокара не является (в общем) центром треугольника. Вторая точка Брокара имеет трилинейные координаты b / c: c / a: a / b; применимы аналогичные замечания.

Первая и вторая точки Брокара – это одна из многих бицентрических пар точек, пар точек, определенных из треугольника со свойством, что пара (но не каждая отдельная точка) сохраняется при сходстве с треугольником. Несколько бинарных операций, таких как средняя точка и трилинейное произведение, при применении к двум точкам Брокара, а также к другим бицентрическим парам, создают центры треугольников.

Векторы положения

Центры треугольников можно записать следующим образом:

P = w A A + w B B + w C C w A + w B + w C. { displaystyle P = { frac {w_ {A} A + w_ {B} B + w_ {C} C} {w_ {A} + w_ {B} + w_ {C}}}.}

Здесь, P, A, B, C { displaystyle P, A, B, C}– векторы положения, и координаты w A, w B, w C { displaystyle w_ {A}, w_ {B}, w_ {C}}– скаляры, определение которых соответствует каждому центральному экземпляру, можно увидеть в следующей таблице, где, a, b, c { displaystyle a, b, c}– длины сторон, и S { displaystyle S}– площадь треугольника, для получения которой можно использовать формулу Герона.

	вес A { displaystyle w_ {A}}	w B { displaystyle w_ {B}}	w C { displaystyle w_ {C}}	w A + w B + w C { displaystyle w_ {A} + w_ {B} + w_ {C}}
Incenter	a { displaystyle a}	b { displaystyle b}	c { displaystyle c}	a + b + c { displaystyle a + b + c}
Excenter	– a { displaystyle -a}	b { displaystyle b}	c { displaystyle c}	b + c – a { displaystyle b + ca}
a { displaystyle a}	– b { displaystyle -b}	c { displaystyle c}	c + a – b { displaystyle c + ab}
a { displaystyle a}	b { displaystyle b}	– c { displaystyle -c}	a + b – c { displaystyle a + bc}
Центроид	1 { displaystyle 1}	1 { displaystyle 1}	1 { displaystyle 1}	3 { displaystyle 3}
Circumcenter	a 2 (b 2 + c 2 – a 2) { displaystyle a ^ {2} (b ^ {2} + c ^ {2} -a ^ {2})}	b 2 (c 2 + a 2 – b 2) { displaystyle b ^ {2} (c ^ {2} + a ^ {2} -b ^ {2})}	c 2 (a 2 + b 2 – c 2) { displaystyle c ^ {2} (a ^ {2} + b ^ {2} -c ^ {2})}	16 S 2 { displaystyl e 16S ^ {2}}
Ортоцентр	a 4 – (b 2 – c 2) 2 { displaystyle a ^ {4} – (b ^ {2} -c ^ {2}) ^ {2 }}	b 4 – (c 2 – a 2) 2 { displaystyle b ^ {4} – (c ^ {2} -a ^ {2}) ^ {2}}	c 4 – ( a 2 – b 2) 2 { displaystyle c ^ {4} – (a ^ {2} -b ^ {2}) ^ {2}}	16 S 2 { displaystyle 16S ^ {2}}

a ≡ BC ¯ = (BC →, BC →), { displaystyle a эквив { overline {BC}} = { sqrt {({ vec {BC}}, { vec {BC}}) }},}

b ≡ CA ¯ = (CA →, CA →), { displaystyle b Equiv { overline {CA}} = { sqrt {({ vec {CA}}, { vec {CA}})}},}

c ≡ AB ¯ = (AB →, AB →), { displaystyle c Equiv { overline {AB}} = { sqrt {({ vec {AB} }, { vec {AB}})}},}

16 S 2 = (a 2 + b 2 + c 2) 2 – 2 (a 4 + b 4 + c 4). { displaystyle 16S ^ {2} = (a ^ {2} + b ^ {2} + c ^ {2}) ^ {2} -2 (a ^ {4} + b ^ {4} + c ^ { 4}).}

Некоторые хорошо известные центры треугольников

Классические центры треугольников

Энциклопедия. Центров треугольников. ссылка	Имя	Стандартный символ	Трилинейные координаты	Описание
X1	Incenter	I	1: 1: 1	Пересечение биссектрисы угла. Центр вписанной окружности треугольника.
X2	Центроид	G	bc: ca: ab	Пересечение медиан. Центр масс однородной треугольной пластинки.
X3	Круговой центр	O	cos A: cos B: cos C	Пересечение серединного перпендикуляра стороны. Центр описанной окружности треугольника.
X4	Ортоцентр	H	tan A: tan B: tan C	Пересечение высот.
X5	Девятиточечный центр	N	cos (B – C): cos (C – A): cos (A – B)	Центр круга, проходящего через среднюю точку каждой стороны, основание каждой высоты и среднюю точку между ортоцентром и каждой вершиной.
X6	Точка симмедианы	K	a: b: c	Пересечение симмедиан – отражение каждой медианы относительно соответствующей биссектрисы угла.
X7	Точка Жергонна	Ge	bc / (b + c – a): ca / ​​(c + a – b): ab / (a ​​+ b – c)	Пересечение линий, соединяющих каждую вершину до точки, где вписанная окружность касается противоположной стороны.
X8	Точка Нагеля	Na	(b + c – a) / a: (c + a – b) / b: (a + b – c) / c	Пересечение линий, соединяющих каждую вершину до точки соприкосновения вневписанной окружности с противоположной стороны.
X9	Mittenpunkt	M	b + c – a: c + a – b: a + b – c	Различные эквивалентные определения.
X10	Центр Шпикера	Sp	bc (b + c): ca (c + a): ab (a + b)	Центр среднего треугольника. Центр масс равномерного треугольного каркаса.
X11	Точка Фейербаха	F	1 – cos (B – C): 1 – cos (C – A): 1 – cos (A – B)	Точка, в которой окружность с девятью точками касается касательной к вписанному кругу.
X13	Точка Ферма	X	csc (A + π / 3): csc (B + π / 3): csc (C + π / 3) *	Точка, которая представляет собой наименьшую возможную сумму расстояний из вершин.
X15. X16	Изодинамические точки	S. S ′	sin (A + π / 3): sin (B + π / 3): sin (C + π / 3). sin (A – π / 3): sin (B – π / 3): sin (C – π / 3)	Центры инверсии, которые превращают треугольник в равносторонний треугольник.
X17. X18	Очки Наполеона	N. N ′	сек (A – π / 3): сек (B – π / 3): сек (C – π / 3). сек (A + π / 3): sec (B + π / 3): sec (C + π / 3)	Пересечение линий, соединяющих каждую вершину с центром равностороннего треугольника, направленного наружу (первая точка Наполеона) или внутрь (вторая точка Наполеона), установленная на противоположной стороне.
X99	Точка Штейнера	S	bc / (b – c): ca / ​​(c – a): ab / (a ​​- b)	Различные эквивалентные определения.

(*): фактически 1-й изогонический центр, но также и точка Ферма, когда A, B, C ≤ 2π / 3

Центры недавних треугольников

В следующей таблице более поздних центров треугольников, никаких специальных обозначений для различных точек не упоминается. Также для каждого центра указывается только первая трилинейная координата f (a, b, c). Остальные координаты можно легко получить, используя свойство цикличности трилинейных координат.

Энциклопедия. центров треугольников. ссылка	Имя	Функция центра. f (a, b, c)	Год описания
X21	Точка Шиффлера	1 / (cos B + cos C)	1985
X22	точка Эксетера	a (b + c – a)	1986
X111	Точка парирования	a / (2a – b – c)	начало 1990-х
X173	Точка конгруэнтных изоселизаторов	tan (A / 2) + sec (A / 2)	1989
X174	Yff центр конгруэнтности	сек (A / 2)	1987
X175	Изопериметрическая точка	– 1 + сек (A / 2) cos (B / 2) cos (C / 2)	1985
X179	Первая точка Аджима-Мальфатти	сек (A / 4)
X181	точка Аполлония	a (b + c) / (b + c – a)	1987
X192	точка равных параллелий	bc (ca + ab – bc)	1961
X356	Центр Морли	cos (A / 3) + 2 cos (B / 3) cos (C / 3)
X360	Нулевая точка Хофштадтера	A / a	1992

Общие классы треугольных центров

Кимберлинг-центр

В честь Кларка Кимберлинга, создавшего онлайн-энциклопедию более чем 32 000 центров треугольников, центры треугольников, перечисленные в энциклопедии, вместе называются центрами Кимберлинга.

Центр полиномиального треугольника

Центр треугольника P называется центром полиномиального треугольника, если трилинейные координаты P могут быть выражается в виде многочленов от a, b и c.

Центр правильного треугольника

Центр треугольника P называется точкой правильного треугольника, если трилинейные координаты P могут быть выражены как полиномы от Δ, a, b и c, где Δ – площадь треугольника.

Центр большого треугольника

Центр треугольника P называется центром большого треугольника, если трилинейные координаты P могут быть выражены в форме f (A): f (B): f (C) где f (A) является функцией только угла A и не зависит от других углов или длин сторон.

Центр трансцендентного треугольника

Центр треугольника P равен называется трансцендентным треугольным центром, если P не имеет трилинейного представления с использованием только алгебраических функций от a, b и c.

Разное

Равнобедренные и равносторонние треугольники

Пусть f – функция центра треугольника. Если две стороны треугольника равны (скажем, a = b), то

f (a, b, c) = f (b, a, c) { displaystyle f (a, b, c) = f (b, a, c)}(поскольку a = b)

= f (b, c, a) { displaystyle quad quad quad quad = f (b, c, a) }(по бисимметрии)

, поэтому два компонента центра соответствующего треугольника всегда равны. Следовательно, центры всех треугольников равнобедренного треугольника должны лежать на его линии симметрии. В равностороннем треугольнике все три компонента равны, поэтому все центры совпадают с центроидом. Итак, как и у круга, равносторонний треугольник имеет уникальный центр.

Excenters

Пусть

f (a, b, c) = {- 1, если a ≥ b и a ≥ c, 1 в противном случае. { displaystyle f (a, b, c) = { begin {case} -1 quad { text {if}} a geq b { text {and}} a geq c, \; ; ; 1 quad { text {else}}. End {ases}}}

Легко видеть, что это функция центра треугольника, и (при условии, что треугольник разносторонний) соответствующий центр треугольника является центром противоположного до наибольшего угла при вершине. Два других специалиста могут быть выбраны аналогичными функциями. Однако, как указано выше, только одна из сторон равнобедренного треугольника и ни одна из сторон равностороннего треугольника никогда не может быть центром треугольника.

Биантисимметричные функции

Функция f биантисимметрична, если f (a, b, c) = −f (a, c, b) для всех a, b, c. Если такая функция также не равна нулю и однородна, легко видеть, что отображение (a, b, c) → f (a, b, c) f (b, c, a) f (c, a, b) функция центра треугольника. Соответствующим центром треугольника является f (a, b, c): f (b, c, a): f (c, a, b). По этой причине определение функции центра треугольника иногда включает ненулевые однородные биантисимметричные функции.

Новые центры из старого

Любую функцию треугольного центра f можно нормализовать, умножив ее на симметричную функцию от a, b, c, так что n = 0. A нормализованная функция центра треугольника имеет тот же центр треугольника, что и исходная, а также более сильное свойство: f (ta, tb, tc) = f (a, b, c) для всех t>0 и всех (a, b, c). Вместе с нулевой функцией нормализованные функции центра треугольника образуют алгебру при сложении, вычитании и умножении. Это дает простой способ создавать новые центры треугольников. Однако различные нормализованные функции центра треугольника часто определяют один и тот же центр треугольника, например f и (abc) (a + b + c) f.

Неинтересные центры

Предположим, что a, b, c – действительные переменные, и пусть α, β, γ – любые три действительные константы. Пусть

f (a, b, c) = {α, если a < b and a < c (equivalently the first variable is the smallest), γ if a>b и a>c (эквивалентно первая переменная самая большая), β в противном случае (эквивалентно первая переменная находится посередине). { displaystyle f (a, b, c) = { begin {case} alpha quad { text {if}} a b { text {and}} a>c quad { text {(эквивалентно первая переменная самая большая)}}, \ beta quad ; { text {else}} quad ; quad quad , quad { text {(эквивалентно первая переменная находится посередине)}}. end {ases}}}

Тогда f равно a функция центра треугольника, а α: β: γ – соответствующий центр треугольника, если стороны контрольного треугольника помечены так, что < b < c. Thus every point is potentially a triangle center. However the vast majority of triangle centers are of little interest, just as most continuous functions are of little interest. The Энциклопедия центров треугольников представляет собой постоянно расширяющийся список интересных.

Барицентрические координаты

Если f – функция центра треугольника, то также af и соответствующий центр треугольника af (a, b, c): bf (b, c, a): cf (c, a, b). Поскольку это в точности барицентрические координаты центра треугольника, соответствующего f, следует, что центры треугольников с таким же успехом можно было бы определить в терминах барицентрических, а не трилинейных. На практике переключиться с одной системы координат на другую несложно.

Двоичные системы

Помимо точки Ферма и 1-го изогонического центра, существуют и другие пары центров. Другая система образована X 3 и центром тангенциального треугольника. Рассмотрим функцию центра треугольника, задаваемую формулой

f (a, b, c) = {cos ⁡ (A), если треугольник острый, cos ⁡ (A) + sec ⁡ (B) sec ⁡ (C), если угол при вершине в A тупой, cos ⁡ (A) – sec ⁡ (A), если любой из углов в B или C тупой. { Displaystyle е (a, b, c) = { begin {case} соз (A) quad ; quad ; quad ; quad ; quad ; quad ; , , { text {если треугольник острый}}, \ cos (A) + sec (B) sec (C) quad { text {если угол при вершине в}} A { text {равен obtuse}}, \ cos (A) – sec (A) quad ; quad ; quad ; , { text {если любой из углов в}} B { text {или} } C { text {тупой}}. End {ases}}}

Для соответствующего центра треугольника есть четыре различных возможности:

• cos (A): cos (B): cos (C), если справочный треугольник острый (это также центр описанной окружности).
• [cos (A) + sec (B) sec (C)]: [cos (B) – sec (B)]: [cos ( C) – sec (C)], если угол в A тупой.
• [cos (A) – sec (A)]: [cos (B) + sec (C) sec (A)]: [cos (C) – sec (C)], если угол в B тупой.
• [cos (A) – sec (A)]: [cos (B) – sec (B)]: [ cos (C) + sec (A) sec (B)], если угол в точке C тупой.

Обычный расчет показывает, что в каждом случае эти трилинейные линии представляют центр тангенциального треугольника. Таким образом, эта точка является центром треугольника, который является близким спутником центра описанной окружности.

Бисимметрия и инвариантность

Отражение треугольника меняет порядок его сторон на обратный. На изображении координаты относятся к треугольнику (c, b, a) и (используя “|” в качестве разделителя) отражение произвольной точки α: β: γ есть γ | β | α. Если f – функция центра треугольника, отражение его центра треугольника равно f (c, a, b) | f (b, c, a) | f (a, b, c), которая по бисимметрии совпадает с f (c, b, a) | f (b, a, c) | е (а, в, б). Поскольку это также центр треугольника, соответствующий f относительно треугольника (c, b, a), бисимметрия гарантирует, что все центры треугольника инвариантны относительно отражения. Поскольку повороты и сдвиги можно рассматривать как двойные отражения, они также должны сохранять центры треугольников. Эти свойства инвариантности служат обоснованием для определения.

Альтернативная терминология

Некоторые другие названия для расширения: равномерное масштабирование, изотропное масштабирование, гомотетия и гомотезия.

Центры гиперболических треугольников

Изучение центров треугольников традиционно связано с евклидовой геометрией, но центры треугольников также можно изучать в гиперболической геометрии. Используя гиротригонометрию, можно вычислить выражения для тригонометрических барицентрических координат, которые имеют одинаковую форму как для евклидовой, так и для гиперболической геометрии. Чтобы выражения совпадали, выражения не должны включать в себя спецификацию суммы углов, равной 180 градусов.

Центры тетраэдров и центры n-симплексов

Обобщение центров треугольников на более высокие измерения – центры тетраэдров или многомерных симплексов.

См. также

• Центральная линия
• Энциклопедия центров треугольников

Примечания

1. ^Кимберлинг, Кларк. «Центры треугольников». Проверено 23 мая 2009. В отличие от квадратов и кругов, треугольники имеют множество центров. Древние греки нашли четыре: центр тяжести, центр тяжести, центр окружности и ортоцентр. Пятый центр, обнаруженный намного позже, – это точка Ферма. После этого в литературу были добавлены точки, которые теперь называются центром девяти точек, точкой симедианы, точкой Жергонна и точкой Фейербаха. В 1980-х годах было замечено, что эти особые точки обладают некоторыми общими свойствами, которые теперь составляют основу формального определения центра треугольника
2. ^Kimberling, Clark (11 апреля 2018 г.) [1994]. «Центральные точки и центральные линии на плоскости треугольника». Математический журнал. 67 (3): 163–187. doi : 10.2307 / 2690608. JSTOR 2690608.
3. ^Кимберлинг, Кларк. «Это ЧАСТЬ 20: Центры X (38001) – X (40000)». Энциклопедия треугольных центров.
4. ^Вайсштейн, Эрик В.. «Центр треугольника». MathWorld – Интернет-ресурс Wolfram. Проверено 25 мая 2009 г.
5. ^Вайсштейн, Эрик У. «Функция центра треугольника». MathWorld – Интернет-ресурс Wolfram. Проверено 1 июля 2009 г.
6. ^Бицентрические пары точек, Энциклопедия центров треугольников, дата обращения 2012-05-02
7. ^Вайсштейн, Эрик У. «Kimberling Center». MathWorld – Интернет-ресурс Wolfram. Проверено 25 мая 2009 г.
8. ^Вайсштейн, Эрик У. «Центр Большого Треугольника». MathWorld – Интернет-ресурс Wolfram. Проверено 25 мая 2009 г.
9. ^Гиперболические барицентрические координаты, Абрахам А. Унгар, Австралийский журнал математического анализа и приложений, AJMAA, том 6, выпуск 1, статья 18, стр. 1-35, 2009
10. ^Центры гиперболических треугольников: специальный релятивистский подход, Abraham Ungar, Springer, 2010
11. ^ Барицентрическое исчисление в евклидовой и гиперболической геометрии: сравнительное введение, Abraham Ungar, World Scientific, 2010

Внешние ссылки

• Манфред Эверс, О центрах и центральных линиях треугольников в эллиптической плоскости
• Манфред Эверс, О геометрии треугольника в эллиптической и расширенной гиперболической плоскости
• Кларк Кимберлинг, Центры треугольников из Университета Эвансвилля
• Пол Ю, Экскурсия по геометрии треугольника из Атлантического университета Флориды.