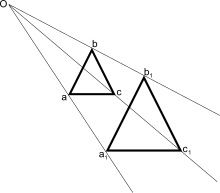
Рисунок 1: Точка O является внешним центром подобия для двух треугольников. Размер каждой фигуры пропорционален её расстоянию до центра подобия.
Центр подобия (или центр гомотетии) — это точка, из которой по меньшей мере две геометрически подобные фигуры можно видеть как масштабирование[en] (растяжение/сжатие) друг друга. Если центр внешний, две фигуры похожи друг на друга прямо — их углы одни и те же в смысле вращения. Если центр внутренний, две фигуры являются изменёнными в размерах отражениями друг друга — их углы противоположны.

Рисунок 2: Две геометрические фигуры относительно внешнего центра подобия S. Углы в соответствующих точках те же самые и имеют тот же смысл. Например, углы ABC и A’B’C’ оба равны по размерам и по направлению (по часовой стрелке/против часовой стрелки).
Многоугольники[править | править код]

Внешний (сверху) и внутренний (внизу) центры подобия двух окружностей (выделены красным) показаны как зелёные точки.
Если две геометрические фигуры имеют центр подобия, они подобны друг другу. Другими словами, они должны иметь те же самые углы в соответствующих точках и отличаются только их относительными размерами. Центр подобия и две фигуры не обязательно должны принадлежать одной плоскости. Он может относиться к трёхмерной проекции[en] из центра подобия.
Центры подобия могут быть внешние или внутренние. Если центр внутренний, две геометрические фигуры являются изменёнными в размерах зеркальными отражениями друг друга. Говоря техническим языком, они имеют противоположную хиральность. Направленный по часовой стрелке угол одной фигуры будет соответствовать углу против часовой стрелки на другой. И наоборот, если центр подобия внешний, две фигуры прямо пропорциональны друг другу — их углы имеют тот же смысл.
Окружности[править | править код]
Окружности геометрически подобны друг другу и зеркально симметричны. Пара окружностей имеет оба типа центров подобия, внешний и внутренний, если только центры не совпадают или окружности имеют одинаковый радиус. Эти особые случаи трактуются как общие случаи. Эти два центра подобия лежат на прямой, проходящей через центры двух данных окружностей, которая называется линией центров (Рисунок 3). Окружности с нулевым радиусом можно тоже включать в рассмотрение (смотрите особые случаи), как и отрицательные радиусы, при этом происходит смена ролей внешних и внутренних центров подобий.
Вычисление центра подобия[править | править код]

Рисунок 3: Две окружности имеют оба вида центров подобия, внутренний (I) и внешний (E). Радиусы окружностей (r1 и r2) пропорциональны расстоянию (d) от каждого центра подобия. Точки A1 и A2 гомологичны, как точки B1 и B2.
Для данной пары окружности внутренний и внешний центры подобия можно найти различными путями. В аналитической геометрии внутренний центр подобия является средним взвешенным центров окружностей, где вес соответствует радиусу противоположной окружности – расстояние от центра окружности до внутренней точки подобия пропорциональны противоположным радиусам. Если обозначить центры окружностей 






Внешний центр можно получить из того же уравнения, если принять один из радиусов отрицательным. Какой бы радиус мы не приняли отрицательным, будем иметь то же самое уравнение:
Обобщая, если взять радиусы с одним и тем же знаком (оба положительны или оба отрицательных), получим внутренний центр, в то время как радиусы с разными знаками (один положительный, а другой отрицательный) дадут внешний центр подобия. Заметим, что уравнение для внутреннего центра остаётся верным для любых значений (если только оба радиуса не равны нулю или в сумме радиусы не дают нуль), но уравнение для внешних центров требует, чтобы радиусы были различны, иначе получим деление на ноль.
В элементарной геометрии, если нарисованы два параллельных диаметра, по одному в окружности, они будут составлять один и тот же угол α с линией центров. Прямые A1A2 и B1B2, проведённые через соответствующие конечные точки радиусов, являющиеся гомологичными токами, пересекают друг друга и линию центров во внешнем центре подобия. Прямые же A1B2 и B1A2, проведённые через одну конечную точку и противоположную конечную точку, пересекают друг друга и линию центров во внутреннем центре подобия.
Особые случаи[править | править код]
Если окружности имеют один и тот же радиус (но разные центры), не существует внешнего центра подобия в аффинной плоскости — в аналитической геометрии это приводит к делению на нуль, а в классической геометрии прямые 

Если окружности имеют один и тот же центр, но различные радиусы, внешний и внутренний центры подобия совпадают с общим центром окружностей. Это можно видеть из аналитической формулы, а также как предел двух центров подобия при движении центров друг к другу при сохранении радиусов, пока центры не совпадут.
Если один радиус равен нулю, а другой нулю не равен (точка и окружность), и внешний, и внутренний центры подобия совпадают с точкой (центром окружности нулевого радиуса).
Если две окружности идентичны (имеют один центр и одинаковые радиусы), внутренний центр подобия — это их общий центр, но нет хорошо определённого внешнего центра. В пределе, когда две окружности равного радиуса двигаются друг к другу до совпадения центров, внешний центр подобия находится на бесконечности и потому может быть где угодно, а потому никакого внешнего центра подобия для таких окружностей не существует.
Если оба радиуса равны нулю (две точки), но точки различны, внешний центр подобия можно определить как точку на бесконечности, соответствующую прямой, проходящей через линию центров, но в этом случае нет внутреннего центра.
Гомологичные и антигомологичные точки[править | править код]

Рисунок 4: Прямые через соответствующие антигомологичные точки пересекаются на радикальных осях двух заданных окружностей (зелёные и синие). Точки Q и P′ антигомологичны, как и S и R′. Эти четыре точки лежат на окружности, которая пересекает две данные окружности. Прямые через точки пересечения новой окружности с двумя заданными окружностями должны пересекаться в радикальном центре G трёх окружностей, который лежит на радикальных осях двух заданных окружностей.
В общем случае луч, исходящий из центра подобия, пересекает каждую окружность в двух местах. Из этих четырёх точек две гомологичны, если радиусы, проведённые из них, составляют один и тот же угол с линией центров, т.е. точки A1 и A2 на рисунке 3. Точки, которые лежат на одной прямой с центром подобия, но не гомологичные, называются антигомологичными,[1] как, например, точки Q и P′ на рисунке 4.
Пары антигомологичных точек, лежащих на окружности[править | править код]
Если два луча из одного центра подобия пересекают окружности, любой набор антигомологичных точек лежит на окружности.
Пусть даны треугольники EQS и EQ′S′ (рисунок 4).
Они подобны, поскольку имеют общий угол ∠QES=∠Q′ES′ и 
Из этого подобия следует, что ∠ESQ=∠ES′Q′=α.
Вследствие теоремы о вписанном угле ∠EP′R′=∠ES′Q′.
∠QSR′=180°-α, поскольку это дополнительный угол для ∠ESQ.
В четырёхугольнике QSR′P′ ∠QSR′+∠QP′R′=180°-α+α=180°, что означает, что четырёхугольник вписан.
Из теоремы о секущих следует, что EQ•EP′=ES•ER′.
Тем же способом можно показать, что PRS′Q′ может быть вписан в окружность и EP•EQ′=ER•ES′.
Доказательство аналогично доказательству для внутреннего центра подобия I.
PIR~P′IR′, следовательно, ∠RPI=∠IP′R′=α.
∠RS′Q′=∠PP′R′=α (теорема о вписанном угле).
Сегмент RQ′ виден под тем же углом из P и S′ что означает, что R, P, S′ и Q′ лежат на окружности.
Тогда из теоремы о пересекающихся хордах IP•IQ′=IR•IS′.
Похожим образом можно показать, что QSP′R′ может быть вписан в окружность и IQ•IP′=IS•IR′.
Связь с радикальными осями[править | править код]
Две окружности имеют радикальные оси, прямые, состоящие из точек, из которых отрезки от точки до точки касания обеих окружностей имеют одну длину. Обобщённо, любая точка на радикальной оси имеет свойство, что её степени относительно окружностей равны. Радикальная ось всегда перпендикулярна линии центров, и если две окружности пересекаются, их радикальная ось проходит через точки пересечения окружностей. Для трёх окружностей можно определить три радикальные оси, для каждой пары окружностей (C1/C2, C1/C3 и C2/C3). Замечателен факт, что эти три радикальные оси пересекаются в одной точке, радикальном центре. Касательные отрезки, проведённые из радикального центра до всех трёх окружностей, будут иметь одну и ту же длину.
Любые две пары антигомологичных точек могут быть использованы для нахождения точки на радикальной оси. Пусть два луча проведены из внешнего центра подобия E, как на рисунке 4. Эти лучи пересекают две заданные окружности (зелёная и синяя на рисунке 4) в двух парах антигомологичных точек, Q и P′ для первого луча, и S и R′ для второго луча. Эти четыре точки лежат на одной окружности, которая пересекает обе заданные окружности. По определению, прямая QS является радикальной осью для новой окружности и зелёной окружности, в то время как прямая P′R′ является радикальной осью для новой окружности и синей окружности. Эти две прямые пересекаются в точке G, которая является радикальным центром трёх окружностей — новой окружности и двух исходных. Таким образом, точка G также лежит на радикальной оси двух исходных окружностей.
Касательные окружности и антигомологичные точки[править | править код]
Для любой пары антигомологичных точек двух окружностей существует третья окружность, которая касается исходных окружностей в антигомологичных точках.
Обратное также верно — любая окружность, касающаяся двух других окружностей, касается их в антигомологичных точках.

Рисунок 5: Любая окружность, касающаяся двух других окружностей, касается их в антигомологичных точках
Пусть наши две окружности имеют центры O1 и O2 (Рисунок 5). Пусть E — их внешний центр подобия.
Строим произвольный луч из точки E, который пересекает две окружности в точках P, Q, P′ и Q′.
Продлим O1Q и O2P′ до пересечения (в точке
T1).
Легко показать, что треугольники O1PQ и O2P′Q′ подобны. Эти треугольники равнобедренны, поскольку O1P=O1Q (радиус), потому
∠O1PQ=∠O1QP=∠O2P′Q′=∠O2Q′P′=∠T1QP′=∠T1P′Q.
Но тогда T1P′Q также будет равнобедренным, и можно построить окружность с центром в T1 и радиусом T1P′=T1Q. Эта окружность касается двух исходных окружностей в точках Q и P′.
Аналогично доказывается утверждение для другой пары антигомологичных точек (P и Q′), а также для случая внутреннего центра подобия.

Рисунок 6: Семейство касательных окружностей для внешнего центра подобия

Рисунок 7: Семейство касательных окружностей для внутреннего центра подобия
Если мы построим касательные окружности для каждой возможной пары антигомологичных точек, мы получим два семейства окружностей — для каждого центра подобия. Семейство окружностей для внешнего центра подобия таково, что окружности этого семейства либо содержат обе исходные окружности внутри себя, либо ни одной (рисунок 6). С другой стороны, окружности из семейства для внутреннего центра содержат всегда одну из исходных окружностей (рисунок 7).

Рисунок 8: Радикальные оси касательных окружностей проходят через радикальный центр
Все окружности из семейства касательных окружностей имеют общий радикальный центр и он совпадает с центром подобия.
Для того, чтобы это показать, представим два луча из центра подобия, пересекающие заданные окружности (рисунок 8). Существуют две касательные окружности T1 и T2, которые касаются исходных окружностей в антигомологичных точках. Как мы уже показали, эти точки лежат на окружности C, а потому эти два луча являются радикальными осями для C/T1 и C/T2. Точка пересечения этих радикальных осей должна лежать также на радикальной оси T1/T2. Эта точка пересечения — центр подобия E.
Если две касательные окружности касаются в антигомологичных точках, лежащих на прямой через точку подобия, как на рисунке 5, то из-за подобия 
Центр подобия трёх окружностей[править | править код]
Любая пара окружностей имеет два центра подобия, поэтому три окружности будут иметь шесть центров подобия, по два на каждую пару (различных) окружностей. Интересно, что все эти шесть точек лежат на четырёх прямых, по три точки на каждой прямой. Вот один из способов показать это.

Рисунок 9: В случае трёх окружностей три центра подобия (для каждой пары окружностей) лежат на одной прямой
Представим на плоскости три окружности (рисунок 9). Добавим для каждого центра окружностей точку на перпендикуляре к плоскости, отстоящую от исходного центра на расстояние, равное соответствующему радиусу. Точки можно добавить с любой стороны плоскости. Три полученные точки определяют плоскость. В этой плоскости мы построим три прямых через каждую пару точек. Эти прямые пересекают плоскость окружностей в точках HAB, HBC и HAC. Поскольку геометрическим местом точек, которые принадлежат обеим непараллельным плоскостям, является прямая, эти три точки будут лежать на одной прямой. Из подобия треугольников HABAA′ и HABBB′ мы видим, что 
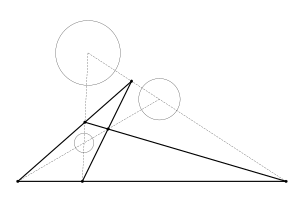
Рисунок 10: Все шесть центров подобия (точек) трёх окружностей лежат на четырёх прямых (жирные линии)
Повторяя процесс для различных комбинаций центров подобия (в нашем методе они определяются сторонами, с которых мы выбираем точки относительно плоскости), получим четыре прямых — по три центра подобия на каждой прямой (рисунок 10).
Существует и другой метод доказательства.

Рисунок 11: Синяя прямая является радикальной осью двух касающихся окружностей C1 и C2 (светло-красные). Каждая пара исходных окружностей имеет центр подобия, лежащий на радикальной оси двух касающихся окружностей. Поскольку радикальные оси — прямые, это означает, что три центра подобия лежит на одной прямой
Пусть C1 и C2 — пара сопряжённых окружностей ко всем трём исходным окружностям (рисунок 11). Под сопряжённостью здесь мы понимаем, что окружности принадлежат тому же самому семейству для одной из пары исходных окружностей. Как мы уже видели, радикальная ось любых двух касательных окружностей из одного класса проходит через центр подобия двух исходных окружностей. Поскольку касательные окружности являются общими для всех трёх пар исходных окружностей, их центры подобия лежат на радикальной оси C1 и C2, т.е. на одной прямой.
Это свойство используется в общем решении Жозефа Диаса Жергонна задачи Аполлония. Если даны три окружности, можно найти центры подобия, а затем радикальные оси пар искомых окружностей. Естественно, имеется бесконечно много окружностей с одними и теми же радикальными осями, так что нужна дополнительная работа, чтобы определить в точности, какая пара окружностей является решением.
См. также[править | править код]
- Подобие
- Гомотетия
- Радикальная ось двух окружностей, Радикальный центр
- Задача Аполлония
Примечания[править | править код]
- ↑ Weisstein.
Литература[править | править код]
- Johnson RA. Advanced Euclidean Geometry: An Elementary treatise on the geometry of the Triangle and the Circle. — New York: Dover Publications, 1960.
- Paul Kunkel. The tangency problem of Apollonius: three looks. — 2007. — Т. 22, вып. 1. — С. 34–46. — doi:10.1080/17498430601148911.
- Eric W. Weisstein. Antihomologous Points. MathWorld–A Wolfram Web Resource.

Рисунок 1: Точка O является внешним центром подобия для двух треугольников. Размер каждой фигуры пропорционален её расстоянию до центра подобия.
Центр подобия (или центр гомотетии) — это точка, из которой по меньшей мере две геометрически подобные фигуры можно видеть как масштабирование[en] (растяжение/сжатие) друг друга. Если центр внешний, две фигуры похожи друг на друга прямо — их углы одни и те же в смысле вращения. Если центр внутренний, две фигуры являются изменёнными в размерах отражениями друг друга — их углы противоположны.

Рисунок 2: Две геометрические фигуры относительно внешнего центра подобия S. Углы в соответствующих точках те же самые и имеют тот же смысл. Например, углы ABC и A’B’C’ оба равны по размерам и по направлению (по часовой стрелке/против часовой стрелки).
Многоугольники
Внешний (сверху) и внутренний (внизу) центры подобия двух окружностей (выделены красным) показаны как зелёные точки.
Если две геометрические фигуры имеют центр подобия, они подобны друг другу. Другими словами, они должны иметь те же самые углы в соответствующих точках и отличаются только их относительными размерами. Центр подобия и две фигуры не обязательно должны принадлежать одной плоскости. Он может относиться к трёхмерной проекции[en] из центра подобия.
Центры подобия могут быть внешние или внутренние. Если центр внутренний, две геометрические фигуры являются изменёнными в размерах зеркальными отражениями друг друга. Говоря техническим языком, они имеют противоположную хиральность. Направленный по часовой стрелке угол одной фигуры будет соответствовать углу против часовой стрелки на другой. И наоборот, если центр подобия внешний, две фигуры прямо пропорциональны друг другу — их углы имеют тот же смысл.
Окружности
Окружности геометрически подобны друг другу и зеркально симметричны. Пара окружностей имеет оба типа центров подобия, внешний и внутренний, если только центры не совпадают или окружности имеют одинаковый радиус. Эти особые случаи трактуются как общие случаи. Эти два центра подобия лежат на прямой, проходящей через центры двух данных окружностей, которая называется линией центров (Рисунок 3). Окружности с нулевым радиусом можно тоже включать в рассмотрение (смотрите особые случаи), как и отрицательные радиусы, при этом происходит смена ролей внешних и внутренних центров подобий.
Вычисление центра подобия

Рисунок 3: Две окружности имеют оба вида центров подобия, внутренний (I) и внешний (E). Радиусы окружностей (r1 и r2) пропорциональны расстоянию (d) от каждого центра подобия. Точки A1 и A2 гомологичны, как точки B1 и B2.
Для данной пары окружности внутренний и внешний центры подобия можно найти различными путями. В аналитической геометрии внутренний центр подобия является средним взвешенным центров окружностей, где вес соответствует радиусу противоположной окружности – расстояние от центра окружности до внутренней точки подобия пропорциональны противоположным радиусам. Если обозначить центры окружностей [math]displaystyle{ C_1 }[/math] и [math]displaystyle{ C_2 }[/math] как [math]displaystyle{ (x_1, y_1) }[/math] и [math]displaystyle{ (x_2, y_2) }[/math] и их радиусы как [math]displaystyle{ r_1 }[/math] и [math]displaystyle{ r_2 }[/math], а центр подобия [math]displaystyle{ (x_0, y_0), }[/math], имеем:
- [math]displaystyle{ (x_0, y_0) = frac{r_2}{r_1 + r_2}(x_1, y_1) + frac{r_1}{r_1 + r_2}(x_2, y_2). }[/math]
Внешний центр можно получить из того же уравнения, если принять один из радиусов отрицательным. Какой бы радиус мы не приняли отрицательным, будем иметь то же самое уравнение:
- [math]displaystyle{ (x_e, y_e) = frac{-r_2}{r_1 – r_2}(x_1, y_1) + frac{r_1}{r_1 – r_2}(x_2, y_2). }[/math]
Обобщая, если взять радиусы с одним и тем же знаком (оба положительны или оба отрицательных), получим внутренний центр, в то время как радиусы с разными знаками (один положительный, а другой отрицательный) дадут внешний центр подобия. Заметим, что уравнение для внутреннего центра остаётся верным для любых значений (если только оба радиуса не равны нулю или в сумме радиусы не дают нуль), но уравнение для внешних центров требует, чтобы радиусы были различны, иначе получим деление на ноль.
В элементарной геометрии, если нарисованы два параллельных диаметра, по одному в окружности, они будут составлять один и тот же угол α с линией центров. Прямые A1A2 и B1B2, проведённые через соответствующие конечные точки радиусов, являющиеся гомологичными токами, пересекают друг друга и линию центров во внешнем центре подобия. Прямые же A1B2 и B1A2, проведённые через одну конечную точку и противоположную конечную точку, пересекают друг друга и линию центров во внутреннем центре подобия.
Особые случаи
Если окружности имеют один и тот же радиус (но разные центры), не существует внешнего центра подобия в аффинной плоскости — в аналитической геометрии это приводит к делению на нуль, а в классической геометрии прямые [math]displaystyle{ A_1A_2 }[/math] и [math]displaystyle{ B_1B_2 }[/math] параллельны линии центров (как для секущих прямых, так и для касательных), а потому не могут пересекаться. Внешний центр подобия можно определить в проективной плоскости как точку на бесконечности, соответствующую пересечению прямых.
Если окружности имеют один и тот же центр, но различные радиусы, внешний и внутренний центры подобия совпадают с общим центром окружностей. Это можно видеть из аналитической формулы, а также как предел двух центров подобия при движении центров друг к другу при сохранении радиусов, пока центры не совпадут.
Если один радиус равен нулю, а другой нулю не равен (точка и окружность), и внешний, и внутренний центры подобия совпадают с точкой (центром окружности нулевого радиуса).
Если две окружности идентичны (имеют один центр и одинаковые радиусы), внутренний центр подобия — это их общий центр, но нет хорошо определённого внешнего центра. В пределе, когда две окружности равного радиуса двигаются друг к другу до совпадения центров, внешний центр подобия находится на бесконечности и потому может быть где угодно, а потому никакого внешнего центра подобия для таких окружностей не существует.
Если оба радиуса равны нулю (две точки), но точки различны, внешний центр подобия можно определить как точку на бесконечности, соответствующую прямой, проходящей через линию центров, но в этом случае нет внутреннего центра.
Гомологичные и антигомологичные точки

Рисунок 4: Прямые через соответствующие антигомологичные точки пересекаются на радикальных осях двух заданных окружностей (зелёные и синие). Точки Q и P′ антигомологичны, как и S и R′. Эти четыре точки лежат на окружности, которая пересекает две данные окружности. Прямые через точки пересечения новой окружности с двумя заданными окружностями должны пересекаться в радикальном центре G трёх окружностей, который лежит на радикальных осях двух заданных окружностей.
В общем случае луч, исходящий из центра подобия, пересекает каждую окружность в двух местах. Из этих четырёх точек две гомологичны, если радиусы, проведённые из них, составляют один и тот же угол с линией центров, т.е. точки A1 и A2 на рисунке 3. Точки, которые лежат на одной прямой с центром подобия, но не гомологичные, называются антигомологичными,[1] как, например, точки Q и P′ на рисунке 4.
Пары антигомологичных точек, лежащих на окружности
Если два луча из одного центра подобия пересекают окружности, любой набор антигомологичных точек лежит на окружности.
Пусть даны треугольники EQS и EQ′S′ (рисунок 4).
Они подобны, поскольку имеют общий угол ∠QES=∠Q′ES′ и [math]displaystyle{ frac{EQ}{EQ^prime}=frac{ES}{ES^prime} }[/math], поскольку E является центром подобия.
Из этого подобия следует, что ∠ESQ=∠ES′Q′=α.
Вследствие теоремы о вписанном угле ∠EP′R′=∠ES′Q′.
∠QSR′=180°-α, поскольку это дополнительный угол для ∠ESQ.
В четырёхугольнике QSR′P′ ∠QSR′+∠QP′R′=180°-α+α=180°, что означает, что четырёхугольник вписан.
Из теоремы о секущих следует, что EQ•EP′=ES•ER′.
Тем же способом можно показать, что PRS′Q′ может быть вписан в окружность и EP•EQ′=ER•ES′.
Доказательство аналогично доказательству для внутреннего центра подобия I.
PIR~P′IR′, следовательно, ∠RPI=∠IP′R′=α.
∠RS′Q′=∠PP′R′=α (теорема о вписанном угле).
Сегмент RQ′ виден под тем же углом из P и S′ что означает, что R, P, S′ и Q′ лежат на окружности.
Тогда из теоремы о пересекающихся хордах IP•IQ′=IR•IS′.
Похожим образом можно показать, что QSP′R′ может быть вписан в окружность и IQ•IP′=IS•IR′.
Связь с радикальными осями
Две окружности имеют радикальные оси, прямые, состоящие из точек, из которых отрезки от точки до точки касания обеих окружностей имеют одну длину. Обобщённо, любая точка на радикальной оси имеет свойство, что её степени относительно окружностей равны. Радикальная ось всегда перпендикулярна линии центров, и если две окружности пересекаются, их радикальная ось проходит через точки пересечения окружностей. Для трёх окружностей можно определить три радикальные оси, для каждой пары окружностей (C1/C2, C1/C3 и C2/C3). Замечателен факт, что эти три радикальные оси пересекаются в одной точке, радикальном центре. Касательные отрезки, проведённые из радикального центра до всех трёх окружностей, будут иметь одну и ту же длину.
Любые две пары антигомологичных точек могут быть использованы для нахождения точки на радикальной оси. Пусть два луча проведены из внешнего центра подобия E, как на рисунке 4. Эти лучи пересекают две заданные окружности (зелёная и синяя на рисунке 4) в двух парах антигомологичных точек, Q и P′ для первого луча, и S и R′ для второго луча. Эти четыре точки лежат на одной окружности, которая пересекает обе заданные окружности. По определению, прямая QS является радикальной осью для новой окружности и зелёной окружности, в то время как прямая P′R′ является радикальной осью для новой окружности и синей окружности. Эти две прямые пересекаются в точке G, которая является радикальным центром трёх окружностей — новой окружности и двух исходных. Таким образом, точка G также лежит на радикальной оси двух исходных окружностей.
Касательные окружности и антигомологичные точки
Для любой пары антигомологичных точек двух окружностей существует третья окружность, которая касается исходных окружностей в антигомологичных точках.
Обратное также верно — любая окружность, касающаяся двух других окружностей, касается их в антигомологичных точках.

Рисунок 5: Любая окружность, касающаяся двух других окружностей, касается их в антигомологичных точках
Пусть наши две окружности имеют центры O1 и O2 (Рисунок 5). Пусть E — их внешний центр подобия.
Строим произвольный луч из точки E, который пересекает две окружности в точках P, Q, P′ и Q′.
Продлим O1Q и O2P′ до пересечения (в точке
T1).
Легко показать, что треугольники O1PQ и O2P′Q′ подобны. Эти треугольники равнобедренны, поскольку O1P=O1Q (радиус), потому
∠O1PQ=∠O1QP=∠O2P′Q′=∠O2Q′P′=∠T1QP′=∠T1P′Q.
Но тогда T1P′Q также будет равнобедренным, и можно построить окружность с центром в T1 и радиусом T1P′=T1Q. Эта окружность касается двух исходных окружностей в точках Q и P′.
Аналогично доказывается утверждение для другой пары антигомологичных точек (P и Q′), а также для случая внутреннего центра подобия.

Рисунок 6: Семейство касательных окружностей для внешнего центра подобия

Рисунок 7: Семейство касательных окружностей для внутреннего центра подобия
Если мы построим касательные окружности для каждой возможной пары антигомологичных точек, мы получим два семейства окружностей — для каждого центра подобия. Семейство окружностей для внешнего центра подобия таково, что окружности этого семейства либо содержат обе исходные окружности внутри себя, либо ни одной (рисунок 6). С другой стороны, окружности из семейства для внутреннего центра содержат всегда одну из исходных окружностей (рисунок 7).

Рисунок 8: Радикальные оси касательных окружностей проходят через радикальный центр
Все окружности из семейства касательных окружностей имеют общий радикальный центр и он совпадает с центром подобия.
Для того, чтобы это показать, представим два луча из центра подобия, пересекающие заданные окружности (рисунок 8). Существуют две касательные окружности T1 и T2, которые касаются исходных окружностей в антигомологичных точках. Как мы уже показали, эти точки лежат на окружности C, а потому эти два луча являются радикальными осями для C/T1 и C/T2. Точка пересечения этих радикальных осей должна лежать также на радикальной оси T1/T2. Эта точка пересечения — центр подобия E.
Если две касательные окружности касаются в антигомологичных точках, лежащих на прямой через точку подобия, как на рисунке 5, то из-за подобия [math]displaystyle{ frac{EP}{EP^prime}=frac{EQ}{EQ^prime}; {EP}cdot{EQ^prime}={EQ}cdot{EP^prime} }[/math]. Но тогда степени точки E по отношению к двум касательным окружностям равны, что означает, что E принадлежит радикальной оси.
Центр подобия трёх окружностей
Любая пара окружностей имеет два центра подобия, поэтому три окружности будут иметь шесть центров подобия, по два на каждую пару (различных) окружностей. Интересно, что все эти шесть точек лежат на четырёх прямых, по три точки на каждой прямой. Вот один из способов показать это.

Рисунок 9: В случае трёх окружностей три центра подобия (для каждой пары окружностей) лежат на одной прямой
Представим на плоскости три окружности (рисунок 9). Добавим для каждого центра окружностей точку на перпендикуляре к плоскости, отстоящую от исходного центра на расстояние, равное соответствующему радиусу. Точки можно добавить с любой стороны плоскости. Три полученные точки определяют плоскость. В этой плоскости мы построим три прямых через каждую пару точек. Эти прямые пересекают плоскость окружностей в точках HAB, HBC и HAC. Поскольку геометрическим местом точек, которые принадлежат обеим непараллельным плоскостям, является прямая, эти три точки будут лежать на одной прямой. Из подобия треугольников HABAA′ и HABBB′ мы видим, что [math]displaystyle{ frac{H_{AB}B}{H_{AB}A}=frac{r_B}{r_A} }[/math] (здесь rA,B — радиусы), а потому HAB является центром подобия двух соответствующих окружностей. Мы можем сделать то же самое для HBC и HAC.

Рисунок 10: Все шесть центров подобия (точек) трёх окружностей лежат на четырёх прямых (жирные линии)
Повторяя процесс для различных комбинаций центров подобия (в нашем методе они определяются сторонами, с которых мы выбираем точки относительно плоскости), получим четыре прямых — по три центра подобия на каждой прямой (рисунок 10).
Существует и другой метод доказательства.

Рисунок 11: Синяя прямая является радикальной осью двух касающихся окружностей C1 и C2 (светло-красные). Каждая пара исходных окружностей имеет центр подобия, лежащий на радикальной оси двух касающихся окружностей. Поскольку радикальные оси — прямые, это означает, что три центра подобия лежит на одной прямой
Пусть C1 и C2 — пара сопряжённых окружностей ко всем трём исходным окружностям (рисунок 11). Под сопряжённостью здесь мы понимаем, что окружности принадлежат тому же самому семейству для одной из пары исходных окружностей. Как мы уже видели, радикальная ось любых двух касательных окружностей из одного класса проходит через центр подобия двух исходных окружностей. Поскольку касательные окружности являются общими для всех трёх пар исходных окружностей, их центры подобия лежат на радикальной оси C1 и C2, т.е. на одной прямой.
Это свойство используется в общем решении Жозефа Диаса Жергонна задачи Аполлония. Если даны три окружности, можно найти центры подобия, а затем радикальные оси пар искомых окружностей. Естественно, имеется бесконечно много окружностей с одними и теми же радикальными осями, так что нужна дополнительная работа, чтобы определить в точности, какая пара окружностей является решением.
См. также
- Подобие
- Гомотетия
- Радикальная ось двух окружностей, Радикальный центр
- Задача Аполлония
Примечания
- ↑ Weisstein.
Литература
- Johnson RA. Advanced Euclidean Geometry: An Elementary treatise on the geometry of the Triangle and the Circle. — New York: Dover Publications, 1960.
- Paul Kunkel. The tangency problem of Apollonius: three looks. — 2007. — Т. 22, вып. 1. — С. 34–46. — doi:10.1080/17498430601148911.
- Eric W. Weisstein. Antihomologous Points. MathWorld–A Wolfram Web Resource.

In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (enlarging or reducing), possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other.
|
|
|
|
|
For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, rectangles are not all similar to each other, and isosceles triangles are not all similar to each other. This is because two ellipses can have different width to height ratios, two rectangles can have different length to breadth ratios, and two isosceles triangles can have different base angles.

Figures shown in the same color are similar
If two angles of a triangle have measures equal to the measures of two angles of another triangle, then the triangles are similar. Corresponding sides of similar polygons are in proportion, and corresponding angles of similar polygons have the same measure.
Two congruent shapes are similar, with a scale factor of 1. However, some school textbooks specifically exclude congruent triangles from their definition of similar triangles by insisting that the sizes must be different if the triangles are to qualify as similar.[citation needed]
Similar triangles[edit]
Two triangles, △ABC and △A′B′C′ are similar if and only if corresponding angles have the same measure: this implies that they are similar if and only if the lengths of corresponding sides are proportional.[1] It can be shown that two triangles having congruent angles (equiangular triangles) are similar, that is, the corresponding sides can be proved to be proportional. This is known as the AAA similarity theorem.[2] Note that the “AAA” is a mnemonic: each one of the three A’s refers to an “angle”. Due to this theorem, several authors simplify the definition of similar triangles to only require that the corresponding three angles are congruent.[3]
There are several criteria each of which is necessary and sufficient for two triangles to be similar:
- Any two pairs of angles are congruent,[4] which in Euclidean geometry implies that all three angles are congruent:[5]
-
- If ∠BAC is equal in measure to ∠B′A′C′, and ∠ABC is equal in measure to ∠A′B′C′, then this implies that ∠ACB is equal in measure to ∠A′C′B′ and the triangles are similar.
- All the corresponding sides are proportional:[6]
-
- AB/A′B′ = BC/B′C′ = AC/A′C′. This is equivalent to saying that one triangle (or its mirror image) is an enlargement of the other.
- Any two pairs of sides are proportional, and the angles included between these sides are congruent:[7]
-
- AB/A′B′ = BC/B′C′ and ∠ABC is equal in measure to ∠A′B′C′.
This is known as the SAS similarity criterion.[8] The “SAS” is a mnemonic: each one of the two S’s refers to a “side”; the A refers to an “angle” between the two sides.
Symbolically, we write the similarity and dissimilarity of two triangles△ABC and △A′B′C′ as follows:[9]
There are several elementary results concerning similar triangles in Euclidean geometry:[10]
- Any two equilateral triangles are similar.
- Two triangles, both similar to a third triangle, are similar to each other (transitivity of similarity of triangles).
- Corresponding altitudes of similar triangles have the same ratio as the corresponding sides.
- Two right triangles are similar if the hypotenuse and one other side have lengths in the same ratio.[11] There are several equivalent conditions in this case, such as the right triangles having an acute angle of the same measure, or having the lengths of the legs (sides) being in the same proportion.
Given a triangle △ABC and a line segment DE one can, with a ruler and compass, find a point F such that △ABC ~ △DEF. The statement that point F satisfying this condition exists is Wallis’s postulate[12] and is logically equivalent to Euclid’s parallel postulate.[13] In hyperbolic geometry (where Wallis’s postulate is false) similar triangles are congruent.
In the axiomatic treatment of Euclidean geometry given by George David Birkhoff (see Birkhoff’s axioms) the SAS similarity criterion given above was used to replace both Euclid’s parallel postulate and the SAS axiom which enabled the dramatic shortening of Hilbert’s axioms.[8]
Similar triangles provide the basis for many synthetic (without the use of coordinates) proofs in Euclidean geometry. Among the elementary results that can be proved this way are: the angle bisector theorem, the geometric mean theorem, Ceva’s theorem, Menelaus’s theorem and the Pythagorean theorem. Similar triangles also provide the foundations for right triangle trigonometry.[14]
Other similar polygons[edit]
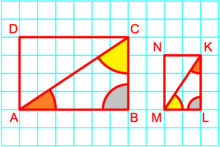
The concept of similarity extends to polygons with more than three sides. Given any two similar polygons, corresponding sides taken in the same sequence (even if clockwise for one polygon and counterclockwise for the other) are proportional and corresponding angles taken in the same sequence are equal in measure. However, proportionality of corresponding sides is not by itself sufficient to prove similarity for polygons beyond triangles (otherwise, for example, all rhombi would be similar). Likewise, equality of all angles in sequence is not sufficient to guarantee similarity (otherwise all rectangles would be similar). A sufficient condition for similarity of polygons is that corresponding sides and diagonals are proportional.
For given n, all regular n-gons are similar.
Similar curves[edit]
Several types of curves have the property that all examples of that type are similar to each other. These include:
- Lines (any two lines are even congruent)
- Line segments
- Circles
- Parabolas[15]
- Hyperbolas of a specific eccentricity[16]
- Ellipses of a specific eccentricity[16]
- Catenaries
- Graphs of the logarithm function for different bases
- Graphs of the exponential function for different bases
- Logarithmic spirals are self-similar
In Euclidean space[edit]
A similarity (also called a similarity transformation or similitude) of a Euclidean space is a bijection f from the space onto itself that multiplies all distances by the same positive real number r, so that for any two points x and y we have
where “d(x,y)” is the Euclidean distance from x to y.[17] The scalar r has many names in the literature including; the ratio of similarity, the stretching factor and the similarity coefficient. When r = 1 a similarity is called an isometry (rigid transformation). Two sets are called similar if one is the image of the other under a similarity.
As a map f : ℝn → ℝn, a similarity of ratio r takes the form
where A ∈ On(ℝ) is an n × n orthogonal matrix and t ∈ ℝn is a translation vector.
Similarities preserve planes, lines, perpendicularity, parallelism, midpoints, inequalities between distances and line segments.[18] Similarities preserve angles but do not necessarily preserve orientation, direct similitudes preserve orientation and opposite similitudes change it.[19]
The similarities of Euclidean space form a group under the operation of composition called the similarities group S.[20] The direct similitudes form a normal subgroup of S and the Euclidean group E(n) of isometries also forms a normal subgroup.[21] The similarities group S is itself a subgroup of the affine group, so every similarity is an affine transformation.
One can view the Euclidean plane as the complex plane,[22] that is, as a 2-dimensional space over the reals. The 2D similarity transformations can then be expressed in terms of complex arithmetic and are given by f(z) = az + b (direct similitudes) and f(z) = az + b (opposite similitudes), where a and b are complex numbers, a ≠ 0. When |a| = 1, these similarities are isometries.
Area ratio and volume ratio[edit]

The tessellation of the large triangle shows that it is similar to the small triangle with an area ratio of 5. The similarity ratio is 5/h = h/1 = √5. This can be used to construct a non-periodic infinite tiling.
The ratio between the areas of similar figures is equal to the square of the ratio of corresponding lengths of those figures (for example, when the side of a square or the radius of a circle is multiplied by three, its area is multiplied by nine — i.e. by three squared). The altitudes of similar triangles are in the same ratio as corresponding sides. If a triangle has a side of length b and an altitude drawn to that side of length h then a similar triangle with corresponding side of length kb will have an altitude drawn to that side of length kh. The area of the first triangle is, A = 1/2bh, while the area of the similar triangle will be A′ = 1/2(kb)(kh) = k2A. Similar figures which can be decomposed into similar triangles will have areas related in the same way. The relationship holds for figures that are not rectifiable as well.
The ratio between the volumes of similar figures is equal to the cube of the ratio of corresponding lengths of those figures (for example, when the edge of a cube or the radius of a sphere is multiplied by three, its volume is multiplied by 27 — i.e. by three cubed).
Galileo’s square–cube law concerns similar solids. If the ratio of similitude (ratio of corresponding sides) between the solids is k, then the ratio of surface areas of the solids will be k2, while the ratio of volumes will be k3.
Similarity with a center[edit]

Example where each similarity
composed with itself several times successively
has a center at the center of a regular polygon that it shrinks.

Example of direct similarity of center S
decomposed into a rotation of 135° angle
and a homothety that halves areas.
Examples of direct similarities that have each a center.
If a similarity has exactly one invariant point: a point that the similarity keeps unchanged, then this only point is called “center” of the similarity.
On the first image below the title, on the left, one or another similarity shrinks a regular polygon into a concentric one, the vertices of which are each on a side of the previous polygon. This rotational reduction is repeated, so the initial polygon is extended into an abyss of regular polygons. The center of the similarity is the common center of the successive polygons. A red segment joins a vertex of the initial polygon to its image under the similarity, followed by a red segment going to the following image of vertex, and so on to form a spiral. Actually we can see more than three direct similarities on this first image, because every regular polygon is invariant under certain direct similarities, more precisely certain rotations the center of which is the center of the polygon, and a composition of direct similarities is also a direct similarity. For example we see the image of the initial regular pentagon under a homothety of negative 

Below the title on the right, the second image shows a similarity decomposed into a rotation and a homothety. Similarity and rotation have the same angle of +135 degrees modulo 360 degrees. Similarity and homothety have the same ratio 



This direct similarity that transforms triangle EFA into triangle ATB can be decomposed into a rotation and a homothety of same center S in several manners. For example, 



With 








How to construct the center S of direct similarity 




In general metric spaces[edit]

In a general metric space (X, d), an exact similitude is a function f from the metric space X into itself that multiplies all distances by the same positive scalar r, called f ‘s contraction factor, so that for any two points x and y we have
Weaker versions of similarity would for instance have f be a bi-Lipschitz function and the scalar r a limit
This weaker version applies when the metric is an effective resistance on a topologically self-similar set.
A self-similar subset of a metric space (X, d) is a set K for which there exists a finite set of similitudes { fs}s∈S with contraction factors 0 ≤ rs < 1 such that K is the unique compact subset of X for which
-

A self-similar set constructed with two similitudes z’=0.1[(4+i)z+4] and z’=0.1[(4+7i)z*+5-2i]
These self-similar sets have a self-similar measure μD with dimension D given by the formula
which is often (but not always) equal to the set’s Hausdorff dimension and packing dimension. If the overlaps between the fs(K) are “small”, we have the following simple formula for the measure:
Topology[edit]
In topology, a metric space can be constructed by defining a similarity instead of a distance. The similarity is a function such that its value is greater when two points are closer (contrary to the distance, which is a measure of dissimilarity: the closer the points, the lesser the distance).
The definition of the similarity can vary among authors, depending on which properties are desired. The basic common properties are
- Positive defined:
- Majored by the similarity of one element on itself (auto-similarity):
More properties can be invoked, such as reflectivity (

Note that, in the topological sense used here, a similarity is a kind of measure. This usage is not the same as the similarity transformation of the § In Euclidean space and § In general metric spaces sections of this article.
Self-similarity[edit]
Self-similarity means that a pattern is non-trivially similar to itself, e.g., the set {…, 0.5, 0.75, 1, 1.5, 2, 3, 4, 6, 8, 12, …} of numbers of the form {{math|{2i, 3·2i}} where i ranges over all integers. When this set is plotted on a logarithmic scale it has one-dimensional translational symmetry: adding or subtracting the logarithm of two to the logarithm of one of these numbers produces the logarithm of another of these numbers. In the given set of numbers themselves, this corresponds to a similarity transformation in which the numbers are multiplied or divided by two.
Psychology[edit]
|
This section needs expansion. You can help by adding to it. (July 2021) |
The intuition for the notion of geometric similarity already appears in human children, as can be seen in their drawings.[23]
See also[edit]
- Congruence (geometry)
- Hamming distance (string or sequence similarity)
- Helmert transformation
- Inversive geometry
- Jaccard index
- Proportionality
- Basic proportionality theorem
- Semantic similarity
- Similarity search
- Similarity (philosophy)
- Similarity space on numerical taxonomy
- Homoeoid (shell of concentric, similar ellipsoids)
- Solution of triangles
Notes[edit]
- ^ Sibley 1998, p. 35.
- ^ Stahl 2003, p. 127. This is also proved in Euclid’s Elements, Book VI, Proposition 4.
- ^ For instance, Venema 2006, p. 122 and Henderson & Taimiņa 2005, p. 123.
- ^ Euclid’s Elements, Book VI, Proposition 4.
- ^ This statement is not true in non-Euclidean geometry where the triangle angle sum is not 180 degrees.
- ^ Euclid’s Elements, Book VI, Proposition 5.
- ^ Euclid’s Elements, Book VI, Proposition 6.
- ^ a b Venema 2006, p. 143.
- ^ Posamentier, Alfred S.; Lehmann, Ingmar (2012). The Secrets of Triangles. Prometheus Books. p. 22.
- ^ Jacobs 1974, pp. 384–393.
- ^ Hadamard, Jacques (2008). Lessons in Geometry, Vol. I: Plane Geometry. American Mathematical Society. Theorem 120, p. 125. ISBN 978-0-8218-4367-3.
- ^ Named for John Wallis (1616–1703)
- ^ Venema 2006, p. 122.
- ^ Venema 2006, p. 145.
- ^ a proof from academia.edu
- ^ a b The shape of an ellipse or hyperbola depends only on the ratio b/a
- ^ Smart 1998, p. 92.
- ^ Yale 1968, p. 47 Theorem 2.1.
- ^ Pedoe 1988, pp. 179–181.
- ^ Yale 1968, p. 46.
- ^ Pedoe 1988, p. 182.
- ^ This traditional term, as explained in its article, is a misnomer. This is actually the 1-dimensional complex line.
- ^ Cox, Dana Christine (2008). Understanding Similarity: Bridging Geometric and Numeric Contexts for Proportional Reasoning (Ph.D.). Kalamazoo, Michigan: Western Michigan University. ISBN 978-0-549-75657-6. S2CID 61331653.
References[edit]
- Henderson, David W.; Taimiņa, Daina (2005). Experiencing Geometry/Euclidean and Non-Euclidean with History (3rd ed.). Pearson Prentice-Hall. ISBN 978-0-13-143748-7.
- Jacobs, Harold R. (1974). Geometry. W. H. Freeman and Co. ISBN 0-7167-0456-0.
- Pedoe, Dan (1988) [1970]. Geometry/A Comprehensive Course. Dover. ISBN 0-486-65812-0.
- Sibley, Thomas Q. (1998). The Geometric Viewpoint/A Survey of Geometries. Addison-Wesley. ISBN 978-0-201-87450-1.
- Smart, James R. (1998). Modern Geometries (5th ed.). Brooks/Cole. ISBN 0-534-35188-3.
- Stahl, Saul (2003). Geometry/From Euclid to Knots. Prentice-Hall. ISBN 978-0-13-032927-1.
- Venema, Gerard A. (2006). Foundations of Geometry. Pearson Prentice-Hall. ISBN 978-0-13-143700-5.
- Yale, Paul B. (1968). Geometry and Symmetry. Holden-Day.
Further reading[edit]
- Cederberg, Judith N. (2001) [1989]. “Chapter 3.12: Similarity Transformations”. A Course in Modern Geometries. Springer. pp. 183–189. ISBN 0-387-98972-2.
- Coxeter, H. S. M. (1969) [1961]. “§5 Similarity in the Euclidean Plane”. pp. 67–76. “§7 Isometry and Similarity in Euclidean Space”. pp. 96–104. Introduction to Geometry. John Wiley & Sons.
- Ewald, Günter (1971). Geometry: An Introduction. Wadsworth Publishing. pp. 106, 181.
- Martin, George E. (1982). “Chapter 13: Similarities in the Plane”. Transformation Geometry: An Introduction to Symmetry. Springer. pp. 136–146. ISBN 0-387-90636-3.
External links[edit]
- Animated demonstration of similar triangles
Построение центра преобразования подобия
Избранные в опросы теории преобразований подобия плоскости. §5. Построение центра преобразования подобия.
З. А. Скопец, Л. И. Кузнецова
Библиотека учителя математики.
ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ.
СБОРНИК СТАТЕЙ.
Избранные в опросы теории преобразований подобия плоскости.
З. А. Скопец, Л. И. Кузнецова
Текст для быстрого ознакомления (формулы и чертежи качественнее отображаются в PDF файле ниже):
Скачать бесплатно в PDF формате «Сборник статей: Преподавание геометрии в 6-8 классах» на странице Учебники Скачать.
На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
§5. Построение центра преобразования подобия.
Для представления подобия композицией
гомотетии и перемещения так, чтобы
центры гомотетии и поворота совпадали
или чтобы центр гомотетии принадлежал
оси симметрии, необходимо
207 Построение центра преобразований подобия.
уметь строить центр подобия, заданного двумя парами соответственных
точек. Знание способов построения центра, знание его свойств находит
эффективное применение и при решении задач.
Способы построения центра очень разнообразны. Мы рассмотрим
лишь некоторые из них.
1. Принадлежность центра подобия окружности Аполлония.
Пусть преобразование подобия задано двумя парами точек
(Л; Лх) и ( В Вх). Если М — центр подобия, то выполняется равенство
М А 1 ‘ . М А = М В 1 : M B — k , т. е. М принадлежит
множествам точек, отношение расстояний которых до двух данных
точек (Лх и Л, и В ) — величина постоянная. Центр преобразования
подобия есть точка пересечения двух окружностей Аполлония,
построенных для отрезков А Х А и В г В и отношения k . Если
окружности пересекутся (рис. 30), то одна из точек пересечения —•
центр преобразования подобия первого рода, другая — центр
преобразования подобия второго рода. Если окружности касаются
(что возможно тогда и только тогда, когда ( А А г ) || ( В В ^ ) ) , то центры
подобий первого и второго рода совпадают (рис. 31). Если отрезки
А А х и В В 1 параллельны и конгруэнтны, то пары точек (Л; Лх)
и ( В ; В г ) задают перенос и переносную симметрию. Точки, делящие
отрезки ЛХЛ и В Х В в отношении, равном 1, внешним образом, не
существуют. Поэтому не существуют соответствующие окружности
Аполлония, а значит, не существуют и центры (рис. 32).
2. Принадлежность центра преобразования подобия множеству
точек пересечения прямых пучка параллельных со своими образами
при подобии.
При доказательстве существования центра у любого подобия,
отличного от перемещения, было выяснено, что центр принадлежит
прямой, которая является множеством точек пересечения прямых
пучка параллельных со своими образами при преобразовании подобия.
На основании этого свойства центра можно указать два
способа его построения. Один из них уже рассмотрен в процессе
доказательства существования центра. Рассмотрим второй способ.
Пусть а и b — прямые одного пучка параллельных, а с и d —
другого. Прямые а и b пересекаются со своими образами в точках
А и В , a c n d — в точках С и D . Точка S = ( А В ) f) ( C D ) есть центр
преобразования подобия.
Рассмотренное свойство центра дает следующий простой способ
его построения.
Если преобразование подобия задано парами точек (Л; А х ) и
( В ; В г ) , то строим квадраты ABCD и Л1В1С101 (одинаково или
противоположно ориентированные в зависимости от рода подобия,
центр которого находим). Прямые ЛВ и CD принадлежат одному
пучку параллельных, а прямые AD и ВС — другому. Образы
этих прямых — соответственно (Л^) и (CjDi), (Л^О и { В Х С Х ) .
Если ( А В ) П ( А А ) = М , ( C D ) П (№) = N , ( A D ) П ( А ^ ) = Р ,
( В С ) П (BjCx) = Q, то ( M N ) П ( P Q ) — $ — центр преобразования
подобия (рис. 33).
208 Построение центра преобразований подобия.
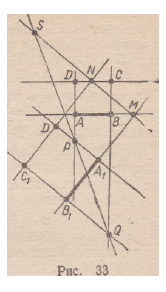
Построение центра преобразования подобия
Построение центра в данном случае не
зависит от рода подобия. Оно использует
только аффинные свойства подобий и применимо
для построения неподвижной точки
любого аффинного преобразования.
3. Принадлежность центра преобразования
подобия множеству точек пересечения
прямых центрального пучка со своими
образами.
При отыскании множеств точек пересечения
прямых центрального пучка со своими
образами при подобии используются метрические
свойства преобразований подобия
— угол между любым лучом и его образом
при преобразовании подобия первого
рода — величина постоянная, прямая и ее
образ при подобии второго рода равнонак-
лонены к каждой из двойных прямых. Предварительно
докажем следующие теоремы.
Т е о р е м а 1 . Множество точек пересечения прямых централь-
ного пучка со своими образами при преобразовании подобия первого
рода есть окружность, проходящая через центр пучка, образ центра
пучка и центр подобия.
Д о к а з а т е л ь с т в о . Пусть задано преобразование подобия
первого рода, точка М — его центр, ср — угол поворота. Рассмотрим
пучок прямых с центром в точке S, ПмФ (S) = Sx (рис. 34).
Если а — произвольная прямая пучка с центром S, ах — ее образ
при заданном подобии, то (а^а^ = ф, если |ф| ^90°, и (а, аг) =
= 180° — ф, если 90° < | Ф | < 180°. Следовательно, точка А =
= а П % принадлежит окружности SS± М.
Обратно, если точка В принадлежит окружности SSxM, то
sl ((55), ( S . B ) ) =Ф, если | ф | < 9 0 ° , и ((SB), ( S X B ) ) = 180° — ф,
если 90° < |ф| ^ 180° (теорема об измерении вписанных углов).
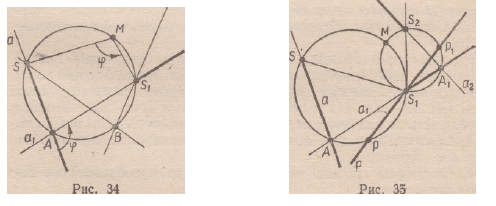
Построение центра
209 Построение центра преобразований подобия.
Построение центра преобразования подобия второго рода
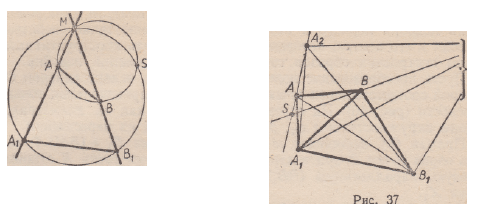
1) Построение центра преобразования подобия второго рода,
вообще говоря, не является самостоятельной задачей, так как может
быть сведено к построению центра гомотетии. В самом деле,
если 5 — центр преобразования подобия П = Н % ° S a , где S 6 а ,
то имеем:
п2 = (Я* о S a r = Я* о sa о Я* о S a = Я| о 5а о о Я* = Я**.
210 Построение центра преобразований подобия.
Поэтому для построения центра подобия П, заданного парами точек
(Л; Л,) и ( В ; В х ) , достаточно построить Л 2 = П (Лх) и В2
=П ( B t).
Точка пересечения прямых ЛЛ2 и SS2 искомая (рис. 37).
2) В отличие от преобразования подобия первого рода подобие
второго рода имеет две взаимно перпендикулярные двойные прямые,
пересекающиеся в центре подобия. Поэтому построение центра
может быть сведено к построению двойных прямых.
Пусть преобразование подобия второго рода задано парами
точек (Л; А г ) и ( В ; В г ) . В § 4, п. 10 было отмечено, что одна из
двойных прямых делит отрезок ЛХЛ и [ B X B в отношении k внутренним
образом, другая — в отношении k внешним образом. Построив
двойные прямые, найдем точку их пересечения. Она и будет искомой
(рис. 39).
Построение образов точек при преобразовании подобия
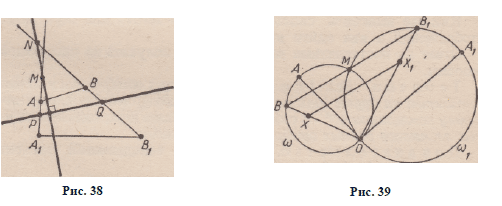
Построение образов точек при преобразовании подобия
211 Построение центра преобразований подобия.
В процессе отыскания способов построения центров преобразований
подобия первого и второго рода получены такие свойства
подобия и его центра, которые позволяют указать конструктивный
прием построения образов точек при преобразовании подобия.
Пусть преобразование подобия первого рода задано центром О
и парой соответственных точек (Л; Лх), а X — произвольная точка
плоскости (рис. 40). На отрезках ОА и О А г , как на диаметрах,
строим окружности со и сolt М — вторая точка их пересечения.
Прямая О Х пересекает ю в точке В . Точка В г £ (В М ) П ®i
есть образ точки В при заданном подобии. Через точку X строим
прямую, параллельную (В В х ). Она пересекает (05х) в искомой
точке Х х .
С преобразованием подобия второго рода связаны пары гипербол.
Если одна пара таких гипербол построена, то построение образов
точек при подобии второго рода выполняется совершенно
аналогично соответствующим построениям для подобий первого
рода.
Свойства подобий в объеме, достаточном для решения широкого
круга задач, рассмотрены. Далее мы остановимся еще на одном
понятии, связанном с преобразованиями, и покажем (позднее),
как оно применяется при решении задач.
212 Построение центра преобразований подобия.
На главную страницу Библиотека учителя математики. ПРЕПОДАВАНИЕ ГЕОМЕТРИИ В 6—8 КЛАССАХ. СБОРНИК СТАТЕЙ.
Похожие статьи:
Школьная Математика. Школьный курс математики. Школьная математика скачать. Школьные учебники по математике.
Школьные задачи по математике. Математика 1 класс. Математика 2 КЛАСС. Математика 3 КЛАСС.
Построение центра

Рисунок 1: Точка О является внешним гомотетическим центром для двух треугольников. Размер каждой фигуры пропорционален ее расстоянию от гомотетического центра.
В геометрия, а гомотетический центр (также называемый центр сходства или центр подобия) – точка, из которой не менее двух геометрически подобный цифры можно рассматривать как расширение или сокращение друг друга. Если центр внешний, эти две фигуры напрямую похожи друг на друга; их углы имеют одинаковое направление вращения. Если центр внутренний, две фигуры являются зеркальными отражениями друг друга; их углы имеют противоположный смысл.

Рисунок 2: Две геометрические фигуры, связанные внешним гомотетическим центром S. Углы в соответствующих точках одинаковы и имеют одинаковый смысл; например, углы ABC и A’B’C ‘оба по часовой стрелке и равны по величине.
Общие многоугольники

Внешний (вверху) и внутренний (внизу) гомотетические центры двух окружностей (красные) показаны черными точками.
Если две геометрические фигуры имеют гомотетический центр, они аналогичный для другого; другими словами, они должны иметь одинаковые углы в соответствующих точках и отличаться только их относительным масштабом. Гомотетический центр и две фигуры не обязательно должны лежать в одной плоскости; они могут быть связаны проекция из гомотетического центра.
Гомотетические центры могут быть внешними или внутренними. Если центр находится внутри, две геометрические фигуры являются зеркальным отражением друг друга; на техническом языке у них есть противоположные хиральность. Угол по часовой стрелке на одном рисунке соответствует углу против часовой стрелки на другом. И наоборот, если центр внешний, две фигуры прямо похожи друг на друга; их углы имеют одинаковый смысл.
Круги
Круги геометрически подобны друг другу и зеркально симметричны. Следовательно, пара окружностей имеет оба типа гомотетических центров, внутренний и внешний, если только центры не равны или не равны радиусы; эти исключительные случаи рассматриваются после общая позиция. Эти два центра гомотетики лежат на линии, соединяющей центры двух данных окружностей, которая называется прямой. линия центров (Рисунок 3). Также могут быть включены круги с нулевым радиусом (см. Исключительные случаи), и также можно использовать отрицательный радиус, переключая внешний и внутренний.
Вычислительные центры гомотетики

Рисунок 3: Два круга имеют оба типа гомотетических центров, внутренние (я) и внешний (E). Радиусы окружностей (р1 и р2) пропорциональны расстоянию (d) от каждого гомотетического центра. Точки А1 и А2 гомологичны, как и точки B1 и B2.
Для данной пары кругов внутренние и внешние центры гомотетики могут быть найдены различными способами. В аналитическая геометрия внутренний гомотетический центр – это средневзвешенное центров кругов, взвешенных по радиусу противоположного круга – расстояние от центра круга до внутреннего центра пропорционально этому радиусу, поэтому взвешивание пропорционально противоположный радиус. Обозначение центров кругов 






Внешний центр можно вычислить по тому же уравнению, но с учетом одного из радиусов отрицательным; любой из них дает одно и то же уравнение, а именно:
В более общем смысле, если взять оба радиуса с одинаковым знаком (оба положительные или оба отрицательные), получится внутренний центр, а радиусы с противоположными знаками (один положительный, а другой отрицательный) – внешний центр. Обратите внимание, что уравнение для внутреннего центра действительно для любых значений (кроме случаев, когда оба радиуса равны нулю или один являются отрицательными для другого), но уравнение для внешнего центра требует, чтобы радиусы были разными, иначе оно включает деление на ноль.
В синтетическая геометрия, нарисованы два параллельных диаметра, по одному на каждый круг; они имеют одинаковый угол α с линией центров. Линии А1А2 и B1B2 проведенные через соответствующие концы этих радиусов, которые являются гомологичными точками, пересекают друг друга и линию центров в внешний гомотетический центр. И наоборот, линии А1B2 и B1А2 проведенный через одну конечную точку и противоположную конечную точку своего аналога, пересекает друг друга и линию центров в внутренний гомотетический центр.
Как предельный случай этой конструкции прямая касательная к обеим окружностям (прямая касательная) проходит через один из центров гомотетики, поскольку образует прямые углы с обоими соответствующими диаметрами, которые, таким образом, параллельны; видеть касательные к двум окружностям для подробностей. Если круги попадают на противоположные стороны линии, она проходит через внутренний гомотетический центр, как в А2B1 на рисунке выше. И наоборот, если круги попадают на одну сторону от линии, она проходит через внешний гомотетический центр (не показан).
Особые случаи
Если круги имеют одинаковый радиус (но разные центры), они не имеют внешнего гомотетического центра в аффинная плоскость: в аналитической геометрии это приводит к делению на ноль, тогда как в синтетической геометрии линии 

Если круги имеют один и тот же центр, но разные радиусы, и внешний, и внутренний совпадают с общим центром кругов. Это можно увидеть из аналитической формулы, а также является пределом для двух гомотетических центров, поскольку центры двух окружностей меняются до совпадения, сохраняя радиусы равными. Однако здесь нет линии центров, и синтетическая конструкция терпит неудачу, поскольку две параллельные линии совпадают.
Если один радиус равен нулю, а другой не равен нулю (точка и круг), и внешний, и внутренний центр совпадают с точкой (центром круга нулевого радиуса).
Если два круга идентичны (один и тот же центр, одинаковый радиус), внутренний центр является их общим центром, но нет четко определенного внешнего центра – собственно, функция из пространства параметров двух кругов на плоскости к внешнему центру имеет несъемный разрыв на геометрическом месте одинаковых окружностей. В пределе двух окружностей с одинаковым радиусом, но с разными центрами, движущимися к одному и тому же центру, внешний центр – это бесконечно удаленная точка, соответствующая наклону линии центров, которая может быть чем угодно, поэтому для всех возможных ограничений не существует. пары таких кругов.
И наоборот, если оба радиуса равны нулю (две точки), но точки различны, внешний центр может быть определен как бесконечно удаленная точка, соответствующая наклону линии центров, но четко определенного внутреннего центра нет.
Гомологические и антигомологические точки

Рисунок 4: Линии, проходящие через соответствующие антигомологические точки, пересекаются на радикальной оси двух данных окружностей (зеленого и синего). Точки Q и П’ антигомологичны, как и S и Р’. Эти четыре точки лежат на окружности, которая пересекает две заданные окружности; линии, проходящие через точки пересечения нового круга с двумя заданными кругами, должны пересекаться в радикальный центр грамм трех кругов, лежащих на радикальная ось из двух данных кружков.
В общем, луч, исходящий из гомотетического центра, пересекает каждую из его окружностей в двух местах. Две из этих четырех точек считаются гомологичный если проведенные к ним радиусы составляют один и тот же угол с линией, соединяющей центры, например, точки Q и Q ′ на рисунке 4. Точки, которые коллинеарны относительно гомотетического центра, но нет гомологичными считаются антигомологичный,[1] например, очки Q и П’ на рисунке 4.
Пары антигомологических точек лежат на окружности
Когда два луча из одного и того же гомотетического центра пересекают окружности, каждый набор антигомологических точек лежит на окружности.
Рассмотрим треугольники EQS и EQ′S ′ (Рисунок 4).
Они похожи, потому что оба угла долей ∠QES = ∠Q′ES ′ и 
Таким же образом можно показать, что PRS′Q ′ можно вписать в круг и EP · EQ ′ = ER · ES ′.
Доказательство аналогично для внутреннего гомотетического центра. я.
ПИР ~ П′ИР ′ тогда ∠RPI = ∠IP′R ′ = α.∠RS′Q ′ = ∠PP′R ′ = α (теорема о вписанном угле). RQ ′ виден под тем же углом из п и S ′ что значит R, P, S ′ и Q ′ лежать по кругу. теорема о пересечении хорд IP · IQ ′ = IR · IS ′.по аналогии QSP′R ′ можно вписать в круг и IQ · IP ′ = IS · IR ′.
Связь с радикальной осью
Два круга имеют радикальная ось, которая представляет собой линию точек, от которой касательные к обеим окружностям имеют одинаковую длину. В более общем смысле, каждая точка на радикальной оси обладает свойством полномочия относительно окружностей равны. Радикальная ось всегда перпендикулярна линии центров, и если две окружности пересекаются, их радикальная ось – это линия, соединяющая их точки пересечения. Для трех окружностей можно определить три радикальные оси, по одной для каждой пары окружностей (C1/C2, C1/C3, и C2/C3); примечательно, что эти три радикальные оси пересекаются в одной точке, радикальный центр. Все касательные, проведенные от радикального центра к трем окружностям, будут иметь одинаковую длину.
Любые две пары антигомологических точек можно использовать, чтобы найти точку на радикальной оси. Рассмотрим два луча, исходящие из внешнего гомотетического центра. E на рисунке 4. Эти лучи пересекают два заданных круга (зеленый и синий на рисунке 4) в двух парах антигомологических точек, Q и П’ для первого луча, и S и Р’ для второго луча. Эти четыре точки лежат на одной окружности, которая пересекает обе заданные окружности. По определению линия QS является радикальной осью нового круга с зеленым заданным кругом, тогда как прямая P′R ′ – радикальная ось нового круга с выделенным синим кружком. Эти две прямые пересекаются в точке грамм, который является радикальным центром нового круга и двух данных окружностей. Следовательно, точка грамм также лежит на радикальной оси двух данных окружностей.
Касательные круги и антигомологические точки
Для каждой пары антигомологических точек двух окружностей существует третья окружность, которая касается данных и касается их в антигомологических точках.
Верно и обратное: каждая окружность, касающаяся двух других окружностей, касается их в паре антигомологических точек.

Рисунок 5: Каждая окружность, касающаяся двух данных окружностей, касается их в паре антигомологических точек.
Пусть у наших двух кругов есть центры О1 и О2 (Рисунок 5). E является их внешним гомотетическим центром. Построим произвольный луч из E который пересекает два круга в P, Q, P ′ и Q ′.Продлевать О1Q и О2П’ пока они не пересекутся Т1Несложно доказать, что треугольники О1PQ и О2P′Q ′ похожи из-за гомотетия. Они также равнобедренный потому что О1P = O1Q (радиус ), следовательно∠O1PQ = ∠O1QP = ∠O2P′Q ′ = ∠O2Q′P ′ = ∠T1QP ′ = ∠T1P′Q.Таким образом Т1P′Q также равнобедренный, и можно построить круг с центром Т1 и радиус Т1P ′ = T1Q. Эта окружность касается двух заданных окружностей в точках Q и П’.
Доказательство для другой пары антигомологических точек (п и Q ′), как и в случае внутреннего гомотетического центра аналогично.

Рисунок 6: Семейство касательных окружностей для внешнего гомотетического центра

Рисунок 7: Семейство касательных окружностей для внутреннего гомотетического центра
Если мы построим касательные окружности для каждой возможной пары антигомологических точек, мы получим два семейства окружностей – по одному для каждого гомотетического центра. Семейство окружностей внешнего гомотетического центра таково, что каждая касательная окружность либо содержит обе даны круги или нет (Рисунок 6). С другой стороны, круги из другого семейства всегда содержат только один из данных кругов (рисунок 7).

Рисунок 8: Коренная ось касательных окружностей проходит через радикальный центр
Все окружности из касательного семейства имеют общий радикальный центр и совпадает с гомотетическим центром.
Чтобы показать это, рассмотрим два луча из центра гомотетии, пересекающие данные окружности (рис. 8). Два касательных круга Т1 и Т2 существуют, которые касаются данных окружностей в антигомологических точках. Как мы уже показали, эти точки лежат на окружности C и, таким образом, два луча являются радикальными осями для C/Т1 и C/Т2. Тогда точка пересечения двух радикальных осей также должна принадлежать радикальной оси Т1/Т2. Эта точка пересечения является гомотетическим центром E.
Если две касательные окружности касаются коллинеарных пар антигомологических точек – как на рисунке 5 – то из-за гомотетии
Гомотетические центры трех кругов
Любая пара кругов имеет два центра подобия, следовательно, три круга будут иметь шесть центров подобия, по два для каждой отдельной пары данных кругов. Примечательно, что эти шесть точек лежат на четырех линиях, по три точки на каждой линии. Вот один из способов показать это.

Рисунок 9: В конфигурации с тремя кругами три центра гомотетики (по одному для каждой пары кругов) лежат на одной линии.
Рассмотрим самолет из трех кругов (рисунок 9). Сместите каждую центральную точку перпендикулярно плоскости на расстояние, равное соответствующему радиусу. Центры могут быть смещены в любую сторону от плоскости. Три точки смещения определяют одну плоскость. На этой плоскости мы проводим по три линии через каждую пару точек. Линии пронизывают плоскость окружностей в точках ЧАСAB, ЧАСдо н.э и ЧАСAC. Поскольку локус точек, которые являются общими для двух различных и непараллельных плоскостей, является прямой, то обязательно эти три точки лежат на такой прямой. Из подобия треугольников ЧАСABAA ′ и ЧАСABBB ′ Мы видим, что 

Рисунок 10: Все шесть гомотетических центров (точки) трех кругов лежат на четырех линиях (толстые линии).
Повторение описанной выше процедуры для различных комбинаций гомотетических центров (в нашем методе это определяется стороной, на которую мы смещаем центры окружностей) даст в общей сложности четыре линии – по три гомотетических центра на каждой линии (рис. 10).
Вот еще один способ доказать это.

Рисунок 11: Синяя линия – радикальная ось двух касательных окружностей. C1 и C2 (розовый). Каждая пара данных окружностей имеет гомотетический центр, который принадлежит радикальной оси двух касательных окружностей. Поскольку радикальная ось – это линия это означает, что три гомотетических центра коллинеарны
Позволять C1 и C2 – пара сопряженных окружностей, касающихся все три заданных круга (рисунок 11). Под сопряжением мы подразумеваем, что обе касательные окружности принадлежат одному семейству по отношению к любой из данных пар окружностей. Как мы уже видели, радикальная ось любых двух касательных окружностей из одного семейства проходит через гомотетический центр двух данных окружностей. Поскольку касательные окружности являются общими для всех трех пар данных окружностей, их гомотетические центры все принадлежат радикальной оси C1 и C2 например, они лежат на одной линии.
Это свойство эксплуатируется в Джозеф Диас Жергонн общее решение Проблема Аполлония. Учитывая три окружности, можно найти центры гомотетики и, таким образом, радикальную ось пары окружностей решения. Конечно, существует бесконечно много окружностей с одинаковой радикальной осью, поэтому проводится дополнительная работа, чтобы точно определить, какие две окружности являются решением.
Смотрите также
- теорема о перехвате
- Сходство (геометрия)
- Гомотетическая трансформация
- Радикальная ось, радикальный центр
- Проблема Аполлония
Рекомендации
- ^ Вайсштейн, Эрик В., Антигомологические точки, MathWorld – Веб-ресурс Wolfram
- Джонсон Р.А. (1960). Продвинутая евклидова геометрия: элементарный трактат о геометрии треугольника и круга. Нью-Йорк: Dover Publications.
- Кункель, Пол (2007), «Проблема касания Аполлония: три взгляда» (PDF), Бюллетень БШМ: Журнал Британского общества истории математики, 22 (1): 34–46, Дои:10.1080/17498430601148911


















