Как найти центр прямоугольника онлайн

Centroid of rectangle is defined as the center point where all the diagonals intersect each other. The diagonals of the rectangle intersect at width b/2 from x – axis and at height h/2 from y – axis. It can also be termed as the geometric center. Centroid can be located in the shape or figure using various methods like plumb line method, balancing methodn etc., Make use of this online centroid of rectangle calculator to find the centroid value of the rectangle shape with its length and width.

Centroid of rectangle is defined as the center point where all the diagonals intersect each other. The diagonals of the rectangle intersect at width b/2 from x – axis and at height h/2 from y – axis. It can also be termed as the geometric center. Centroid can be located in the shape or figure using various methods like plumb line method, balancing methodn etc., Make use of this online centroid of rectangle calculator to find the centroid value of the rectangle shape with its length and width.

Информация по назначению калькулятора

Прямоугольник – это двумерная геометрическая фигура, имеющая 4 стороны и 4 угла. Две его стороны сходятся под прямым углом. Таким образом, прямоугольник имеет 4 угла, каждый из которых равен 90 градусов. Противоположные стороны прямоугольника имеют одинаковую длину и параллельны. Две стороны называются параллельными, когда расстояние между ними остается одинаковым во всех точках.

Поскольку все углы прямоугольника равны, его можно назвать равноугольным четырехугольником.

Некоторые свойства прямоугольника отмечены далее:

⇒ Прямоугольник – это четырехугольник.

⇒ Противоположные стороны прямоугольника равны и параллельны друг другу.

⇒ Внутренний угол прямоугольника в каждой вершине равен 90°.

⇒ Сумма всех внутренних углов равна 360°.

⇒ Диагонали делят пополам друг друга.

⇒ Длина диагоналей равна.

⇒ Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.

⇒ Все прямоугольники являются параллелограммами, но не все параллелограммы являются прямоугольниками.

Онлайн калькулятор поможет найти параметры прямоугольника, такие как:

• Длины сторон
• Периметр

– равен сумме всех 4х сторон (P=AB+BC+CD+DA)

• Площадь

– равна произведению двух сторон (S=AB*BC)

• Диагонали

– Диагональ разрезает прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а две смежные стороны прямоугольника образуют две другие стороны треугольника.(AC=√(AB² + BC²))

• Углы

– всегда равны 90 градусов

• Радиус Описанной окружности
• Диаметр Описанной окружности
• Длина Описанной окружности
• Площадь Описанной окружности

Диаметр описанной окружности прямоугольника равен длине его диагонали

(x,y) = (x2 + x1)/2, (y2+y1)/2

3 ответов

The center of rectangle is the mid point of the diagonal end points of rectangle. 
Here the midpoint is ( (x1 +x2)/2 ,(y1 + y2)/2 ).
that means xCenter = (x1 +x2)/2
           yCenter = (y1 + y2)/2

centre (x,y) =  new Point((boundRect.tl().x+boundRect.br().x)/2,(boundRect.tl().y+boundRect.br().y)/2)

Центр описанной окружности в прямоугольнике

Прямоугольник. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Можно дать и другое определение прямоугольника.

Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.

Свойства прямоугольника

Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.

• 1. Стороны прямоугольника являются его высотами.
• 2. Все углы прямоугольника прямые.
• 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
• 4. Диагонали прямоугольника равны.
• 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.

Длиной прямоугольника называется более длинная пара его сторон.

Шириной прямоугольника называется более короткая пара его сторон.

Диагональ прямоугольника

Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

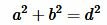(1)

Из равенства (1) найдем d:

.

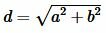(2)

Пример 1. Стороны прямоугольника равны . Найти диагональ прямоугольника.

Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:

Ответ:

Окружность, описанная около прямоугольника

Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Формула радиуса окружности описанной около прямоугольника

Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.

Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть

Подставляя (3) в (2), получим:

Пример 2. Стороны прямоугольника равны . Найти радиус окружности, описанной вокруг прямоугольника.

Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:

Ответ:

Периметр прямоугольника

Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Периметр прямоугольника вычисляется формулой:

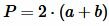(5)

где ( small a ) и ( small b ) − стороны прямоугольника.

Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.

Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:

Ответ:

Формулы сторон прямоугольника через его диагональ и периметр

Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).

Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:

(6)

(7)

Из формулы (7) найдем ( small b ) и подставим в (6):

(8)

(9)

Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):

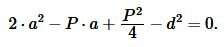(10)

Вычислим дискриминант квадратного уравнения (10):

Сторона прямоугольника вычисляется из следующих формул:

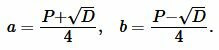(12)

После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).

Примечание. Легко можно доказать, что

( frac >d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*).

Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим , в (11):

Подставляя значения и в первую формулу (12), получим:

Найдем другую сторону ( small b ) из формулы (8). Подставляя значения и в формулу, получим:

Ответ: ,

Признаки прямоугольника

Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.

Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.

Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.

Описанная окружность

Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема

Около любого треугольника можно описать окружность.

Доказательство

Дано: произвольный АВС.

Доказать: около АВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.

Замечание 1

Около треугольника можно описать только одну окружность.

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Около четырехугольника не всегда можно описать окружность.

Доказательство

Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

В любом вписанном четырехугольнике сумма противоположных углов равна 180 0 .

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Если сумма противоположных углов четырехугольника равна 180 0 , то около него можно описать окружность.

Доказательство

Дано: четырехугольник АВСD, BАD + BСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)

Углы ВFD и FDE — вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.

BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .

Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 — ( В + F). (2)

В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)

F и ВFD — смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 — ВFD = 180 0 — ВАD. (4)

Подставим (3) и (4) в (2), получим:

С = 180 0 — (ЕF + 180 0 — ВАD) = 180 0 — ЕF — 180 0 + ВАD = (ВАD — ЕF), следовательно, СВАD.

А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.

Примечание:

Окружность всегда можно описать:

Поделись с друзьями в социальных сетях:

Прямоугольник

Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам). Площадь прямоугольника равна произведению его смежных сторон. Диагонали прямоугольника равны. Вторая формула нахождения площади прямоугольника исходит из формулы площади четырехугольника через диагонали.

Прямоугольник — это четырехугольник, у которого каждый угол является прямым.

Квадрат — это частный случай прямоугольника.

Прямоугольник имеет две пары равных сторон. Длина наиболее длинных пар сторон называется длиной прямоугольника, а длина наиболее коротких — шириной прямоугольника.

Свойства прямоугольника

1. Прямоугольник — это параллелограмм

Свойство объясняется действием признака 3 параллелограмма (то есть ( angle A = angle C ) , ( angle B = angle D ) )

2. Противоположные стороны равны

( AB = CD,enspace BC = AD )

3. Противоположные стороны параллельны

( AB parallel CD,enspace BC parallel AD )

4. Прилегающие стороны перпендикулярны друг другу

( AB perp BC,enspace BC perp CD,enspace CD perp AD,enspace AD perp AB )

5. Диагонали прямоугольника равны

Согласно свойству 1 прямоугольник является параллелограммом, а значит ( AB = CD ) .

Следовательно, ( triangle ABD = triangle DCA ) по двум катетам ( ( AB = CD ) и ( AD ) — совместный).

Если обе фигуры — ( ABC ) и ( DCA ) тождественны, то и их гипотенузы ( BD ) и ( AC ) тоже тождественны.

Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.

( Rightarrow AB = CD ) , ( AC = BD ) по условию. ( Rightarrow triangle ABD = triangle DCA ) уже по трем сторонам.

Получается, что ( angle A = angle D ) (как углы параллелограмма). И ( angle A = angle C ) , ( angle B = angle D ) .

Выводим, что ( angle A = angle B = angle C = angle D ) . Все они по ( 90^ ) . В сумме — ( 360^ ) .

6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон

Это свойство справедливо в силу теоремы Пифагора.

7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника

( triangle ABC = triangle ACD, enspace triangle ABD = triangle BCD )

Прямоугольник

Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам). Площадь прямоугольника равна произведению его смежных сторон. Диагонали прямоугольника равны. Вторая формула нахождения площади прямоугольника исходит из формулы площади четырехугольника через диагонали.

Прямоугольник — это четырехугольник, у которого каждый угол является прямым.

Квадрат — это частный случай прямоугольника.

Прямоугольник имеет две пары равных сторон. Длина наиболее длинных пар сторон называется длиной прямоугольника, а длина наиболее коротких — шириной прямоугольника.

Свойства прямоугольника

1. Прямоугольник — это параллелограмм

Свойство объясняется действием признака 3 параллелограмма (то есть ( angle A = angle C ) , ( angle B = angle D ) )

2. Противоположные стороны равны

( AB = CD,enspace BC = AD )

3. Противоположные стороны параллельны

( AB parallel CD,enspace BC parallel AD )

4. Прилегающие стороны перпендикулярны друг другу

( AB perp BC,enspace BC perp CD,enspace CD perp AD,enspace AD perp AB )

5. Диагонали прямоугольника равны

Согласно свойству 1 прямоугольник является параллелограммом, а значит ( AB = CD ) .

Следовательно, ( triangle ABD = triangle DCA ) по двум катетам ( ( AB = CD ) и ( AD ) — совместный).

Если обе фигуры — ( ABC ) и ( DCA ) тождественны, то и их гипотенузы ( BD ) и ( AC ) тоже тождественны.

Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.

( Rightarrow AB = CD ) , ( AC = BD ) по условию. ( Rightarrow triangle ABD = triangle DCA ) уже по трем сторонам.

Получается, что ( angle A = angle D ) (как углы параллелограмма). И ( angle A = angle C ) , ( angle B = angle D ) .

Выводим, что ( angle A = angle B = angle C = angle D ) . Все они по ( 90^ <circ>) . В сумме — ( 360^ <circ>) .

6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон

Это свойство справедливо в силу теоремы Пифагора.

7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника

( triangle ABC = triangle ACD, enspace triangle ABD = triangle BCD )

Как найти центр описанной окружности в прямоугольнике

Ключевые слова: окружность, описанная окружность, центр окружности, вписанная окружность, треугольник, четырехугольник, вневписанная окружность

Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон.

Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.

Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.
Сам многоугольник в таком случае называется описанным около данной окружности.
Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.

Для произвольного многоугольника невозможно вписать в него и описать около него окружность.
Для треуголь ника это всегда возможно.

Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а её центр находится внутри окружности

• Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
• В любой треугольник можно вписать окружность, и только одну.
• Радиус вписанной в треугольник окружности равен отношению площади треугольника и его полупериметра: $$r = frac

  $$ , где S – площадь треугольника, а $$p =frac<2>$$ – полупериметр треугольника.