Как найти центр пятиугольник - Сайт, где вы сможете решить свои вопросы

Бывают задачи на построение и нахождение некоторых геометрических параметров правильного пятиугольника. Построить фигуру непросто. Для этого математики рекомендуют несколько методик, позволяющих выполнить операцию более точно или за короткий промежуток времени. У фигуры есть свойства, а также формулы, позволяющие найти ее геометрические характеристики.

Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто. Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:

S = (5/12) * R * d.

Высота правильного пятиугольника (h) — отрезок, проведенный из центра на любую из сторон. Она делит ее на две равные части, поскольку является биссектрисой и медианой равнобедренного треугольника. У последнего две стороны — радиусы описанной окружности, а третья — сторона пентагона. Высота называется также апофемой и проекцией на «а». Вычисляется ее значение по формуле h = a * tg(72) / 2.

Величина Ф является отношением площади пентагона (S) к площади (S1) правильного пятиугольника, полученного при пересечении диагоналей первого: S / S1 = Ф^4 = 3Ф + 2 = (3 * 5^(1/2) + 7) / 2. Длина диагонали находится по такому соотношению: d = [Ф * 5^(1/2) * R]^(1/2).

Таким образом, при решении задач необходимо знать основные признаки, свойства, соотношения и формулы для нахождения основных характеристик пентагона. Практика обязательна, поскольку теоретические знания без практического применения бесполезны.

Окружность, вписанная в правильный многоугольник

На этом занятии мы рассмотрим следующую тему – «Окружность, вписанная в правильный многоугольник». В первую очередь дадим определение правильному многоугольнику. После чего докажем теорему о том, что внутри любого правильного многоугольника можно вписать окружность, и притом только одну. Кроме того, рассмотрим следствия из этой теоремы.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»

Правильные многоугольники

Многоугольник – замкнутая ломаная линия. В школьной планиметрии изучают плоские линии, без самопересечений. Часть плоскости, ограниченная этой линией, также называется многоугольником. В этом смысле многоугольник имеет площадь. Многоугольник с n вершинами, а значит и с n сторонами, называется n-угольником.
Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.

На этом рисунке

1 – простая (без самопересечений) ломаная линия, имеет 6 звеньев и 7 вершин;
2 – шестизвенная ломаная, имеющая одно самопересечение;
3 – выпуклый многоугольник, пятиугольник;
4 – невыпуклый многоугольник, десятиугольник.

Итак, слово “правильный” в условии задачи сразу говорит нам о том, что все стороны и все углы многоугольника одинаковые. Количество углов (вершин) и количество сторон определяем по названию многоугольника. Далее в формулах и задачах будем обозначать это количество символом n.

и так далее.

правильный пятиугольник.

Чтобы построить другие правильные многоугольники, задайте количество сторон n (от 3-ёх до 12-ти).

Многоугольники можно вписывать в окружность или описывать вокруг неё. Однако, это получается не для всех и не всегда. Говоря математическим языком, не всегда существует окружность, которая удовлетворяет определению.

Если многоугольник вписан в окружность, то можно сказать, что окружность описана около многоугольника, или, наобррот, если многоугольник описан около окружности, то окружность вписана в него. Такие формулировки тоже встречаются в условиях геометрических задач. Чтобы не путаться запомним – вписанная фигура находится внутри описанной около неё.

Четырехугольник вписан в окружность.

Четырехугольник описан около окружности.

Рассмотрим другие примеры.

Произвольный прямоугольник всегда можно вписать в окружность, но описать нельзя. Описать получится только тогда, когда прямоугольник – это квадрат.

Параллелограмм нельзя вписать в окружность. Описать можно только ромб.

В окружность можно вписать только равнобочную трапецию, описать около окружности тоже можно не всякую трапецию.

Существование вписанной и описанной окружности для произвольных многоугольников связано с величинами их углов и сторон. Есть специальные теоремы, позволяющие определить будет ли многоугольник являться вписанным и/или описанным. Сейчас мы на них останавливаться не будем. Сейчас важно отметить следующее:

Треугольник вписан в зеленую окружность, описан вокруг синей.

Пятиугольник вписан в зеленую окружность, описан вокруг синей.

Правильные многоугольники имеют центр, точнее совпадающие в одной точке центр симметрии, центр тяжести, центры вписанной и описанной окружностей. Если соединить с центром правильного n-угольника его вершины, то многоугольник разобьется на n равных равнобедренных треугольников.

Боковые стороны этих треугольников (на рисунке – зелёные отрезки) будут равны радиусу описанной окружности (R), а их основания (на рисунке – красные отрезки) равны стороне многоугольника (a).

Пользуясь таким чертежом, можно вычислять различные отрезки и углы в многоугольнике на основе знаний о равнобедренных треугольниках.
Например, угол AOB в пятиугольнике равен 360/5 = 72° (360° – полный круг). Угол OAB равен углу OBA и равен (180 − 72)/2 = 54°. Угол CAB = 2×54 = 108°. Сумма всех углов при вершинах пятиугольника 5×108 = 540°.

При решении задач на правильный многоугольник, часто бывает удобно дорисовать внешнюю (описанную) или внутреннюю (вписанную) окружность даже, если они не упоминаются в условии, и соединить вершины и точки касания с центром. Получатся равнобедренные или прямоугольные треугольники, о которых много известно, поэтому задачу будет решать легко.

Синие треугольники равнобедренные потому, что их боковые стороны это радиусы одной и той же окруюности.

Оранжевые треугольники прямоугольные потому, что касательная к окружности перпендикулярна её радиусу.

На ОГЭ по математике в 9-ом классе и на ЕГЭ в 11-ом встречаются задачи с правильными многоугольниками, часто они включают в себя и вписанную или описанную окружность.

Задачи на правильные многоугольники

Внимание: задачи с решениями, но они временно скрыты. Сначала сделайте попытку решить задачу самостоятельно, и только после этого нажимайте кнопки “Посмотреть ответ” и “Посмотреть решение”. Cовпадать обязан только ответ. Способ решения может отличаться.

Доказать, что площадь правильного n-угольника можно вычислить по формуле S = pr, где p – полупериметр многоугольника, r – радиус вписанной окружности.

Ответ: S = pr

Середины сторон правильного восьмиугольника ABCDEFGH последовательно соединили. Какую часть площади исходного многоугольника занимает получившийся многоугольник KLMNPQRS ?
Ответ дайте в процентах, округлив до целых.

Примечание: Отношение сторон многоугольников можно найти иначе, например, достроить другие внутренние отрезки и рассмотреть прямоугольные треугольники.

Ответ: 85

В круг вписан правильный шестиугольник ABCDEF. Найти площадь круга, если радиус окружности, вписанной в треугольник ADE, равен r.

Определим площадь треугольника ADE двумя способами:
через произведение катетов [S = frac<cdot> <2>= frac><2>cdotfrac<2>cdotfrac<1> <2>= frac><8>; ] и через полупериметр и заданный радиус вписанной окружности [S = frac<2>cdot r = frac<2>cdot big(frac><2>+frac<2>+ xbig) = frac + 3) > <4>]

Теперь можно составить уравнение и решить его относительно х.
[ frac> <8>= frac + 3)> <4>] [ frac> <2>= frac + 3)> <1>] [x = frac <2r(sqrt<3>+ 3)><sqrt<3>> = 2r(1 + sqrt<3>)] Так как AD = x – диаметр окружности, то её площадь можно найти по формуле [S = frac <pi d^2> <4>= frac <pi (2r)^2 (1 + sqrt<3>)^2> <4>= pi r^2(1 +2 sqrt <3>+ 3) = pi r^2(4 + 2sqrt<3>) = 2pi r^2(2 + sqrt<3>)]

Ответ: 2πr 2 (2 + √3 _ )

Найти отношение площади правильного двадцатичетырёхугольника, вписанного в некоторую окружность, к площади правильного двенадцатиугольника, вписанного в ту же окружность.

Ответ: 4sin15° ≈ 1,04

Точка O – центр правильного шестиугольника ABCDEF, в котором AC = 10,5. Найдите радиус окружности, касающейся окружностей, описанных около треугольников AOB, COD и EOF.

Примечание: Если Вы не догадались использовать свойство медиан треугольника, то можно рассматривать треугольники AOC, AOH и т.п., теорему косинусов или теорему Пифагора. Ответ будет получен с чуть большим объёмом вычислений.

Ответ: 7

Точка O – центр правильного шестиугольника ABCDEF со стороной 7. Найдите радиус окружности, касающейся окружностей, описанных около треугольников BOD, DOF и BOF.

[spoiler title=”источники:”]

http://interneturok.ru/lesson/geometry/9-klass/dlina-okruzhnosti-i-ploschad-kruga/okruzhnost-vpisannaya-v-pravilnyy-mnogougolnik

http://mathematichka.ru/school/geom_figures/Regular_polygon_1.html

[/spoiler]

Источник

Как построить и нарисовать правильный пятиугольник по окружности

Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.

Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.

Параметры правильного пятиугольника

Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:

сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:

с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

Построение пентагона

Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.

Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:

Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:

Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

Интересные факты

В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.

Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.

Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.

Правильный пятиугольник

По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.

Так как все углы правильного n-угольника равны между собой, каждый внутренний угол правильного пятиугольника равен 540º:5=108º (в частности, ∠A₂A₁A₅=108º).

Сумма внешних углов многоугольника, взятых по одному при каждой вершине, равна 360º. Поскольку все внешние углы правильного пятиугольника равны между собой, градусная мера каждого, например, угла 1, равна

∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).

Каждый центральный угол правильного пятиугольника, например, угол A₁O A₂, равен

Как и любой другой правильный многоугольник, правильный пятиугольник вписан в окружность и описан около окружности.

Соединив центр правильного многоугольника с его вершинами, получим пять равных равнобедренных треугольников.

Основанием каждого такого треугольника равно стороне 5-угольника, боковые стороны равны радиусу описанной окружности, угол при вершине — центральному углу 5-угольника.

$[{A_1}{A_5} = a,]$

$[{A_1}O = {A_5}O = R,]$

$[angle {A_1}O{A_5} = {72^o}.]$

Проведём из вершины высоту OF.

По свойству равнобедренного треугольника, OF является также медианой и биссектрисой треугольника A₁OA₅, то есть

$[{A_1}F = frac{1}{2}{A_1}{A_5} = frac{a}{2},]$

$[angle {A_1}OF = frac{1}{2}angle {A_1}O{A_2} = {36^o}.]$

Рассмотрим прямоугольный треугольник A₁OF.

$[sin angle {A_1}OF = frac{{{A_1}F}}{{{A_1}O}},]$

$[{A_1}O = frac{{{A_1}F}}{{sin angle {A_1}OF}},]$

$[R = frac{{frac{a}{2}}}{{sin {{36}^o}}} = frac{a}{{2sin {{36}^o}}}.]$

$[sin {36^o} = sqrt {frac{{5 - sqrt 5 }}{8}} ,]$

$[R = frac{a}{{2sqrt {frac{{5 - sqrt 5 }}{8}} }} = frac{{asqrt 8 }}{{2sqrt {5 - sqrt 5 } }} = frac{{a cdot 2sqrt 2 }}{{2sqrt {5 - sqrt 5 } }} = ]$

$[ = frac{{asqrt 2 }}{{sqrt {5 - sqrt 5 } }} = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{sqrt {5 - sqrt 5 } cdot sqrt {5 + sqrt 5 } }} = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{sqrt {{5^2} - {{(sqrt 5 )}^2}} }} = ]$

$[ = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{sqrt {20} }} = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{2sqrt 5 }} = ]$

$[ = frac{{asqrt 2 cdotsqrt {5 + sqrt 5 } cdotsqrt 5 }}{{2sqrt 5 cdotsqrt 5 }} = frac{{asqrt {50 + 10sqrt 5 } }}{{10}}.]$

Таким образом, формула радиуса описанной около правильного пятиугольника окружности —

Сколько горизонтальных линий у правильного Пентагона?

У правильного пятиугольника есть 5 стороны и 5 линии симметрии. Количество линий симметрии в правильном многоугольнике равно количеству сторон.

Кроме того, как найти центр пятиугольника?

к найдите что собой представляет центр регулярного пятиугольник/ шестиугольник: разделите сторону пополам, поместив точку циркуля на каждую из точек и нарисовав дугу с радиусом чуть более половины длины стороны.

Таким образом, что такое прямоугольный Пентагон? Мы определяем «прямоугольный пятиугольник”Как домообразную целочисленную выпуклую плоскую фигуру, состоящую из треугольника с основанием B и сторонами u и v, выходящего на прямоугольник ширины B и высоты d: Таким образом, если треугольник тупой или прямой, то основанием может быть только его самая длинная сторона.

Сколько горизонтальных линий у правильного Пентагона?

Каковы углы пятиугольника?

Все стороны одинаковой длины (конгруэнтны), и весь интерьер углов одинакового размера (конгруэнтные). Чтобы найти меру интерьера углов, мы знаем, что сумма всех углов 540 градусов (сверху) А их пять углов Итак, мера интерьера угол регулярного пятиугольник это 108 градусов.

Все стороны пятиугольника равны?

Обычный пятиугольник один с все равно и углов. Его интерьер углов 108 градусов и его внешний вид углов 72 градуса. Нерегулярныйпятиугольник это форма, которая не имеет равные стороныи / или углов и поэтому не указалиуглов.

Как нарисовать пятиконечную звезду?

Нарисуйте перевернутую букву «V». Начните с левой нижней части вашего рисунка, подойдите к точке и опустите карандаш вниз и вправо.
Проведите влево прямую линию под углом вверх.
Нарисуйте прямую горизонтальную линию поперек вашего рисунка, заканчивающуюся справа.

Есть ли у Пентагона равные стороны?

Пентагоны могут быть правильными или неправильными, а также выпуклыми или вогнутыми. Обычный пятиугольник едино со всеми равные стороны и углы. Его внутренние углы составляют 108 градусов, а внешние — 72 градуса. Нерегулярный пятиугольник это форма, которая делает не иметь равные стороны и / или углы и поэтому не иметь указанные углы.

Сколько углов у пятиугольника?

Что в форме пятиугольника?

Треугольник	Квадратный
Пятиугольник	Икосагон

Сколько треугольников в пятиугольнике?

Сколько углов у круга?

Все части круг находятся на равном расстоянии от центра круг. Сторона должна состоять из линии и двух углов, по одному с каждой стороны линии. Квадрат состоит из четырех сторон: четырех линий и четырех сторон. углов. Шестиугольник, состоящий из шести сторон и шестиуглов.

Является ли шестиугольник правильным многоугольником?

A шестиугольник это пример многоугольник, или многогранной формы. А правильный шестиугольник имеет шесть сторон, которые все равны или равны по размеру. А правильный шестиугольник выпуклый, что означает, что точкишестиугольник все указывают наружу. Все углы правильный шестиугольник совпадают и измеряют 120 градусов.

Что такое многоугольник?

A многоугольник любое двумерное формировать формируется прямыми линиями. Треугольники, четырехугольники, пятиугольники и шестиугольники — все это примеры полигонов. Название говорит вам, сколько сторон формировать имеет. Например, треугольник имеет три стороны, а четырехугольник — четыре стороны. Это то, что делает многоугольник.

Что такое фигура с четырьмя вершинами?

Четырехугольник — это замкнутая фигура с 4 стороны. некоторые формы которые классифицируются как четырехугольники: квадрат, прямоугольник, параллелограмм, ромб и трапеция. Это квадрат. Оно имеет 4 прямые углы и 4 равные стороны. Оно имеет 4 стороны и Вершины 4.

Как нарисовать шестиугольник внутри круга?

к рисовать a шестиугольникначните с обводки чего-нибудь круглого, чтобы получился круг. Затем с помощью линейки рисовать горизонтальная линия через центр круг. Далее берем линейку и рисовать «x» над круг поэтому он разделен на 6 равных частей.

Сколько существует типов шестиугольников?

In геометрия, а шестиугольник можно определить как многоугольник с шестью сторонами. Двумерная форма имеет 6 сторон, 6 вершин и 6 углов. Мы можем найти форму шестиугольник ввокруг нас соты и футбольный мяч.

Как нарисовать ромб?

Шаг 1: Начните с рисования клюва пингвина.
Шаг 2: Нарисуйте голову.
Шаг 3: Нарисуйте тело и основание ступней.
Шаг 4: Нарисуйте перья на спине и хвосте.
Шаг 5: Нарисуйте крыло и лапы пингвина.

Как нарисовать ромб?

пятиугольник имеет 5 сторон. К найдите ценность интерьера угол в А пятиугольник, используйте следующее формула, чтобы найти сумма всего интерьерауглов. Разделите это число на 5, чтобы определять ценность каждого интерьера угол. Каждый интерьер угол составляет 108 градусов.

Является ли треугольник правильным многоугольником?

A правильный многоугольник — это многоугольник где все стороны и углы одинаковы. Равносторонний треугольник — это правильный многоугольник. У него все одинаковые стороны и одинаковые углы. Равнобедренный треугольник имеет две равные стороны и два равных угла.

Что такое четырехугольник?

четырехугольник. В геометрии евклидовой плоскости aчетырехугольник многоугольник с четырьмя ребрами (или сторонами) и четырьмя вершинами или углами. Иногда термин четырехугольник используется по аналогии с треугольником, а иногда четырехугольник для согласованности с пятиугольником (5-гранный), шестиугольником (6-гранный) и так далее.

Что такое многоугольник?

A многоугольник любое двумерное формироватьформируется прямыми линиями. Треугольники, четырехугольники, пятиугольники и шестиугольники — все это примеры полигонов. Название говорит вам, сколько сторон формировать имеет. Например, треугольник имеет три стороны, а четырехугольник — четыре стороны. Это то, что делает многоугольник.

Что такое 6-сторонний многоугольник?

В геометрии шестиугольник (от греческого? Ξ hex, «шесть» и γωνία, gonía, «угол, угол») — это шесть–двусторонний многоугольник or 6-гон. Сумма внутренних углов любого простого (несамопересекающегося) шестиугольника составляет 720 °.

Как называется 9-сторонняя форма?

Как нарисовать восьмиугольник?

Шаг 1. Разделите на три части. Разделите длину на три части.
Шаг 2: Разделите на 9 квадратов. Нарисуйте по разметке 9 маленьких квадратов.
Шаг 3: сделайте восьмиугольник из 9 квадратов. Нарисуйте линии так, чтобы восьмиугольник был виден в 9 квадратах.
Шаг 4: Сотрите форму восьмиугольника.

Как называется девятиугольная форма?

В геометрии девятиугольник (/ ˈn? N? G? N /) или enneagon (/ ˈ? Ni? G? N /) является 9–односторонняя многоугольник или 9-угольник. Название нонагон — это префиксная гибридная формация, от латинского (nonus, «девятый» + гонон), используемая эквивалентно, засвидетельствованная уже в 16 веке во французском nonogone и в английском языке с 17 века.

Как называется девятиугольная форма?

Шаг 1: Проведите прямую AB длиной 6 см.
Шаг 2: Используя транспортир, нарисуйте угол 57 ° от точки A. Отметьте точку D так, чтобы AD = 6 см.
Шаг 3: Используя линейку и установленный квадрат, проведите линию BC так, чтобы она была параллельна AD. Отметьте точку C так, чтобы BC = 6 см.
Шаг 4: Соедините точку D с точкой C.

Как нарисовать параллелограмм?

Собери свои инструменты.
Ознакомьтесь с инструкциями по решению вашей математической задачи.
Проведите линию с помощью линейки.
Обозначьте длину одной стороны.
Установите транспортир.
Измерьте угол.
Нарисуйте следующую сторону параллелограмма.
Повторите для следующей стороны.

Как называется 7-сторонняя форма?

В геометрии семиугольник — это семиугольник.односторонняя многоугольник 7-гон. Гептагон иногда называют семиугольником, используя «sept-» (элизия septua-, числового префикса латинского происхождения, а не hepta-, числового префикса греческого происхождения; оба являются родственными) вместе с греческим суффиксом «-agon Означает угол.

Как называется 3-сторонняя форма?

A 3–двусторонняя форма is под названием треугольник. Треугольники — это многоугольники с тремя сторонами, поэтому любыемногоугольник с трех сторон под названием треугольник. Есть

Источник

I wondered, is there a geometrical way to find the center of a pentagon or a hexagon? I’m not talking about equal sides, just polygons with 5 or 6 corners.

Like, with a triangle you can take the intersection of two medians to find the center. With a quadrilateral, the center is the intersection of the bimedians.

Is it possible to construct the center of pentagons and hexagons in a similar way?

Edit: Apparently is rather difficult, so I probably have to settle for a formula to calculate the centroid. I always learned that the $x$ and $y$ values of the centroid are just the mean values of the $x_i$ and $y_i$ values of the corners respectively, but Wikipedia says otherwise (Wiki):

$C_x = dfrac{1}{6A} displaystyle sum_{i=0}^{n-1} (x_i+x_{i+1})(x_iy_{i+1}-x_{i+1}y_i)$

$C_y = dfrac{1}{6A} displaystyle sum_{i=0}^{n-1} (y_i+y_{i+1})(x_iy_{i+1}-x_{i+1}y_i)$

Where $A = dfrac{1}{2} displaystyle sum_{i=0}^{n-1} (x_iy_{i+1}-x_{i+1}y_i)$

I’m not entirely sure, but wouldn’t those $(x_iy_{i+1}-x_{i+1}y_i)$ terms cancel out because you divide by the summation over the same interval? That would leave:

$C_x = dfrac{1}{12} displaystyle sum_{i=0}^{n-1} (x_i+x_{i+1})$

which is rubbish, except for when your polygon has 6 corners — and that’s exactly the case on the source from Wikipedia, here.

Therefore I wonder, is my math correct and is this formula just a very elaborate way to calculate the centroid of a hexagon (and no other polygons), or is it just coincidence? If so, please explain the formula.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 ноября 2020 года; проверки требуют 22 правки.

Иное название этого понятия — «Пентагон»; см. также другие значения.

Пятиугольник
Правильный пятиугольник
Тип	Правильный многоугольник
Рёбра	5
Символ Шлефли	{5}
Диаграмма Коксетера — Дынкина
Вид симметрии	Диэдрическая группа (D₅)
Площадь	${displaystyle {frac {t^{2}{sqrt {25+10{sqrt {5}}}}}{4}}=}$ ${displaystyle {frac {5R^{2}}{4}}{sqrt {frac {5+{sqrt {5}}}{2}}};}$
Внутренний угол	108°
Свойства
выпуклый, вписанный, Равносторонний, равноугольный^[en], изотоксальный
Медиафайлы на Викискладе

Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Свойства[править | править код]

У правильного пятиугольника угол равен

$alpha ={frac {(n-2)}{n}}cdot 180^{circ }={frac {3}{5}}cdot 180^{circ }=108^{circ }$

Площадь правильного пятиугольника рассчитывается по любой из формул:

$S={frac {5}{4}}t^{2}{mathop {{mathrm {ctg}}}},{frac {pi }{5}}={frac {{sqrt 5}{sqrt {5+2{sqrt {5}}}}}{4}}t^{2}={frac {5}{12}}Rd={frac {5}{2}}R^{2}sin {frac {2pi }{5}}=5r^{2}{mathop {{mathrm {tg}}}},{frac {pi }{5}}$

где

— радиус описанной окружности,

— радиус вписанной окружности,

— диагональ,

— сторона.

Высота правильного пятиугольника:

${displaystyle h={frac {operatorname {tg} ,72^{circ }}{2}}t={frac {sqrt {5+2{sqrt {5}}}}{2}}tapprox 1{,}5388417685876268t}$

Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу ${frac {1+{sqrt {5}}}{2}}$ .

Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:

Сторона:

${displaystyle t=R{sqrt {frac {5-{sqrt {5}}}{2}}}approx 1{,}1755705045849463~R}$

Радиус вписанной окружности:

${displaystyle r={frac {{sqrt {5}}{sqrt {5+2{sqrt {5}}}}}{10}}tapprox 0{,}6881909602355869~t}$

Радиус описанной окружности:

${displaystyle R={frac {{sqrt {1}}0{sqrt {5+{sqrt {5}}}}}{10}}tapprox 0{,}85065080835204~t}$

Диагональ:

${displaystyle d={sqrt {Phi {sqrt {5}}}}R={frac {{sqrt {5}}+1}{2}}tapprox 1{,}9021130325903073~Rapprox 1{,}618033988749895~t}$

Площадь:

${displaystyle S={frac {{sqrt {5}}{sqrt {5+2{sqrt {5}}}}}{4}}t^{2}approx 1{,}7204774005889671~t^{2}}$

Правильным пятиугольником невозможно заполнить плоскость без промежутков (см. также Паркет)
Отношение площадей правильного пятиугольника и другого правильного пятиугольника, образованного пересечением диагоналей исходного (середина пятиугольной звезды)

${displaystyle {frac {S}{s}}=Phi ^{4}=3Phi +2={frac {3{sqrt {5}}+7}{2}}approx 6{,}854101966249685}$

где

— отношение золотого сечения.

Построение[править | править код]

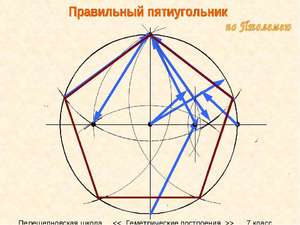
Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

Вот один из методов построения правильного пятиугольника в заданной окружности:

Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
Постройте точку C посередине между O и B.
Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
Постройте правильный пятиугольник AEGHF.

Построение правильного пятиугольника
Построение правильного пятиугольника
Построение правильного пятиугольника
Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

Получение с помощью полоски бумаги[править | править код]

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

Узел из полоски бумаги, образующий пятиугольник

В природе[править | править код]

В природе не существует кристаллов с гранями в форме правильного пятиугольника, но исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K
показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.^[1]
Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.
Пентасимметрией обладают иглокожие (например морские звёзды) и некоторые растения. См. также Закономерности в природе.

Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как мушмула германская

Интересные факты[править | править код]

Этот раздел представляет собой неупорядоченный список разнообразных фактов о предмете статьи.

Пожалуйста, приведите информацию в энциклопедический вид и разнесите по соответствующим разделам статьи. Списки предпочтительно основывать на вторичных обобщающих авторитетных источниках, содержащих критерий включения элементов в список. (24 июля 2020)

Здание Министерства обороны США, известное как Пентагон

Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.
Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
Правильный пятиугольник со всеми его диагоналями является проекцией правильного пятиячейника (4-симплекса).
Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.

См. также[править | править код]

Золотое сечение
Пятиугольник
Пентаэдр
Пентаграмма
Государственный знак качества СССР

Примечания[править | править код]

↑ A one-dimensional ice structure built from pentagons. Nature Materials. 8 March 2009 Архивная копия от 22 апреля 2009 на Wayback Machine (англ.)

Источник

Правильный пятиугольник

Правильный пятиугольник — это такой пятиугольник у которого все пять сторон равны и его пять углов равны.

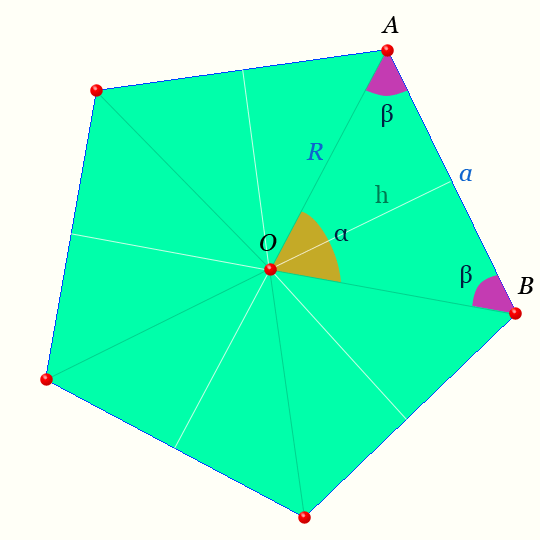
Правильный пятиугольник

Центр правильного пятиугольника — на рисунке точка O равноудалена от вершин.

Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.

Отрезки OA, OB — радиусы правильного пятиугольника.

Обозначения на рисунке для правильного пятиугольника

n=5	число сторон и вершин правильного пятиугольника,	шт
α	центральный угол правильного пятиугольника,	радианы, °
β	половина внутреннего угла правильного пятиугольника,	радианы, °
γ	внутренний угол правильного пятиугольника,	радианы, °
a	сторона правильного пятиугольника,	м
R	радиусы правильного пятиугольника,	м
p	полупериметр правильного пятиугольника,	м
L	периметр правильного пятиугольника,	м
h	апофемы правильного пятиугольника,	м

Основные формулы для правильного пятиугольника

Периметр правильного пятиугольника

[ L = 5a ]

Полупериметр правильного пятиугольника

[ p = frac{5}{2}a ]

Центральный угол правильного пятиугольника в радианах

[ α = frac{2}{5}π ]

Центральный угол правильного пятиугольника в градусах

[ α = frac{360°}{5} = 72° ]

Половина внутреннего угла правильного пятиугольника в радианах

[ β = frac{3}{10}π ]

Половина внутреннего угла правильного пятиугольника в градусах

[ β = frac{3}{10}180° = 54° ]

Внутренний угол правильного пятиугольника в радианах

[ γ = 2β = frac{3}{5}π ]

Внутренний угол правильного пятиугольника в градусах

[ γ = frac{3}{5}180° = 108° ]

Площадь правильного пятиугольника

[ S = ph = frac{5}{2}ha ]

Или учитывая формулу Площади правильного пятиугольника получим

[ S = frac{5}{2} a sqrt{Big(frac{a}{2 sin(π/5)}Big)^2-frac{a^2}{4}} ]

Отсюда получим апофему правильного пятиугольника

[ h = sqrt{Big(frac{a}{2 sin(π/5)}Big)^2-frac{a^2}{4}} ]

Правильный пятиугольник	стр. 269

Источник

Окружность, вписанная в правильный многоугольник

Правильные многоугольники

Задачи на правильные многоугольники

Как построить и нарисовать правильный пятиугольник по окружности

Параметры правильного пятиугольника

Построение пентагона

Интересные факты

Правильный пятиугольник

Сколько горизонтальных линий у правильного Пентагона?

Сколько горизонтальных линий у правильного Пентагона?

Каковы углы пятиугольника?

Все стороны пятиугольника равны?

Как нарисовать пятиконечную звезду?

Есть ли у Пентагона равные стороны?

Сколько углов у пятиугольника?

Что в форме пятиугольника?

Сколько треугольников в пятиугольнике?

Сколько углов у круга?

Является ли шестиугольник правильным многоугольником?

Что такое многоугольник?

Что такое фигура с четырьмя вершинами?

Как нарисовать шестиугольник внутри круга?

Сколько существует типов шестиугольников?

Как нарисовать ромб?

Как нарисовать ромб?

Является ли треугольник правильным многоугольником?

Что такое четырехугольник?

Что такое многоугольник?

Что такое 6-сторонний многоугольник?

Как называется 9-сторонняя форма?

Как нарисовать восьмиугольник?

Как называется девятиугольная форма?

Как называется девятиугольная форма?

Как нарисовать параллелограмм?

Как называется 7-сторонняя форма?

Как называется 3-сторонняя форма?

Свойства[править | править код]

Построение[править | править код]

Получение с помощью полоски бумаги[править | править код]

В природе[править | править код]

Интересные факты[править | править код]

См. также[править | править код]

Примечания[править | править код]

Правильный пятиугольник

Обозначения на рисунке для правильного пятиугольника

Основные формулы для правильного пятиугольника

Правильный пятиугольник

Вам также может понравиться

Как найти кучму в последнем сталкере

Как найти управу на вайлдберриз

Кольцо матери воландеморта как нашли

Добавить комментарий Отменить ответ