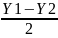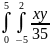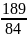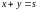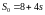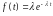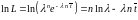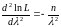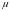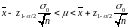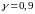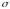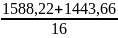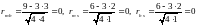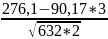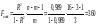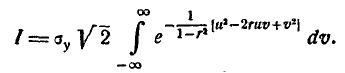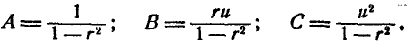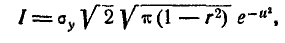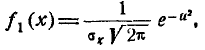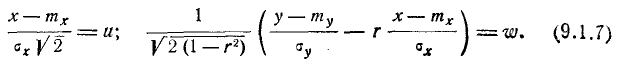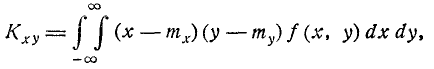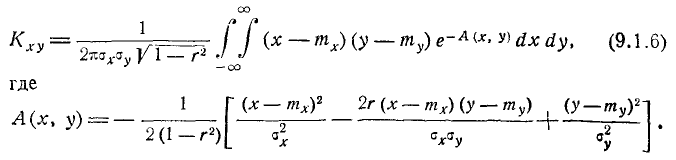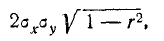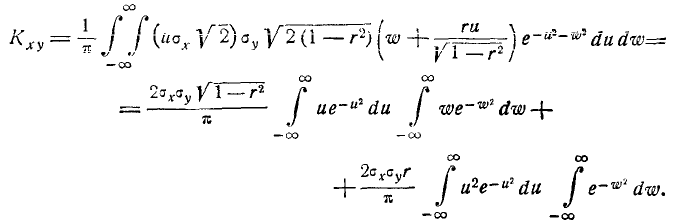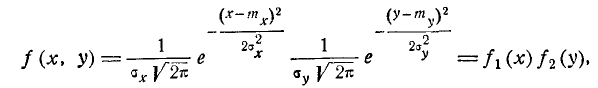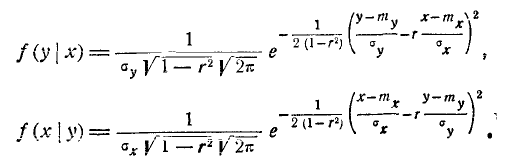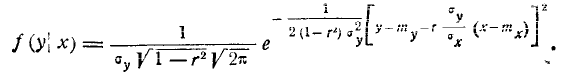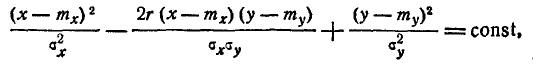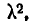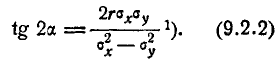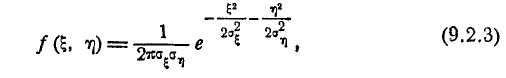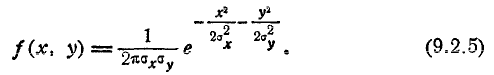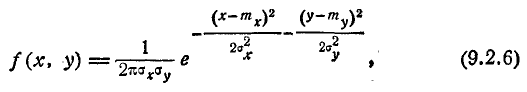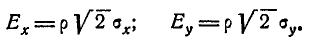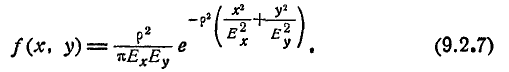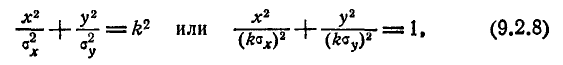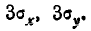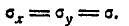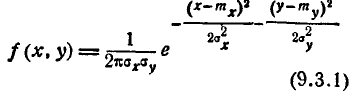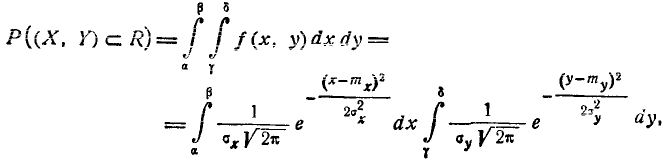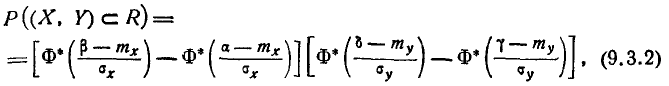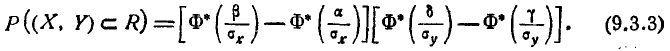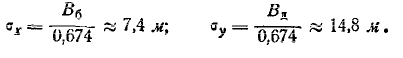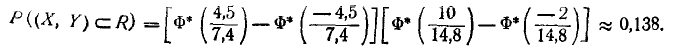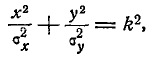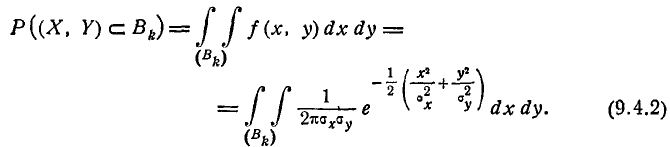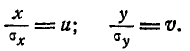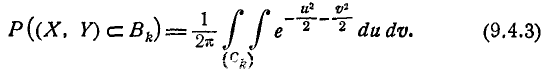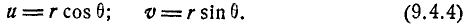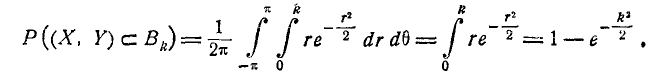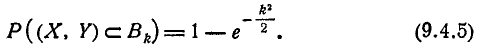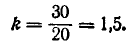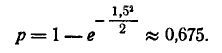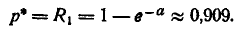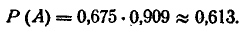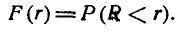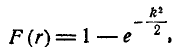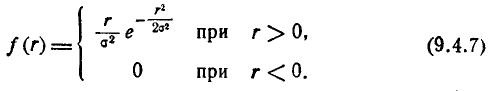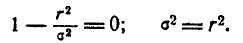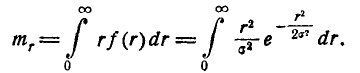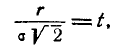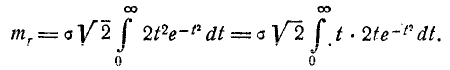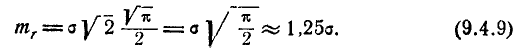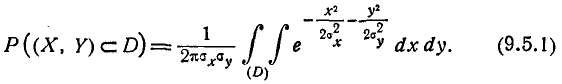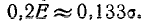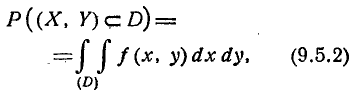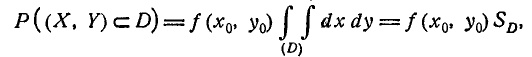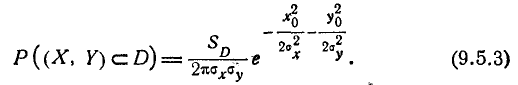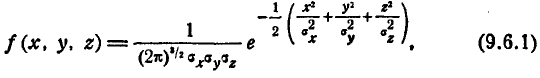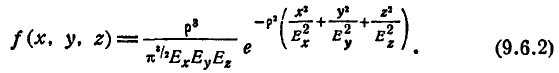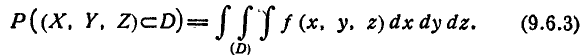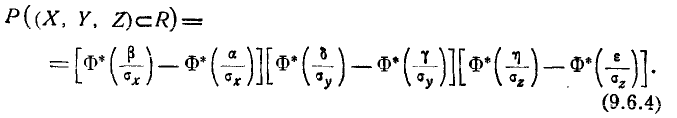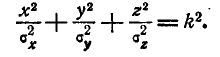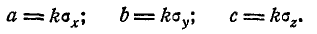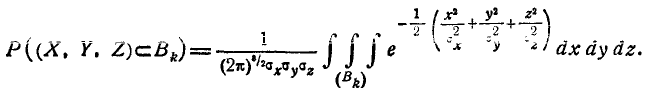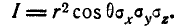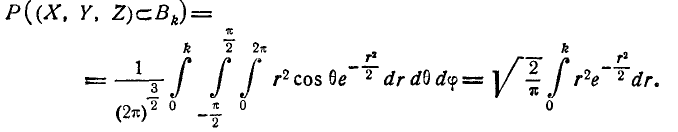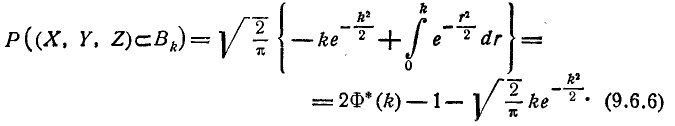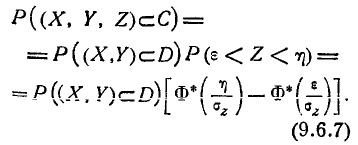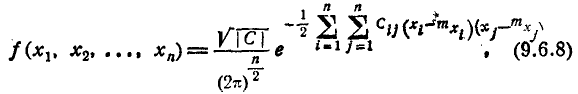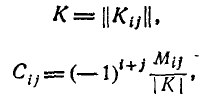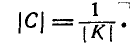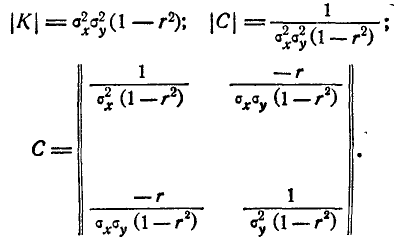-
Вычислить
условное математическое ожидание
M[X/Y = 0]
и дисперсию D[X/Y = 0]. -
Построить ковариационную и корреляционную матрицы.
-
Установить
закон распределения случайных величин:
S = X + Y
и Z = XY.
-
Найти центр рассеивания случайного вектора (X, y).


Функция
плотности совместного равномерного
распределения в области G
постоянна и равна F(X,Y)
=
=
=

Одномерные
плотности вероятности распределения
X
и Y
FX(x)
=
(x,y)dy
=
dy
=
=
, 0 ≤ x ≤5
FY(y)
=
(x,y)dx
=
dx
=
=
, – 5 ≤ y ≤ 2
Так
как F(X,Y)
=
=
*
= FX(x)*FY(y),
X
и Y
независимы.
Случайные
величины X
и Y
также распределены равномерно.
Математические ожидания равны
M(X)
=
*Fx(x)dx
=
dx
=
=

M(Y)
=
*Fy(y)dy
=
dx
=
= –
= –

То
же получим по формулам для равномерного
распределения:
M(X)
=
=
=
M(X)
=
=
= –
Центр
рассеивания случайного вектора (X, Y):
M(X,Y)
= (M(X),M(Y))
= (
,
–
)
-
Вычислить
условное математическое ожидание
M[X/Y = 0] и дисперсию D[X/Y = 0].
Условная
плотность вероятности φx(x/y)
=
=
=
Плотность
вероятности X
при условии Y=0:
φx(x/y
= 0) =
Условное
математическое ожидание
M(X/Y
= 0) =
φx(x/y
= 0)dx
=
dx
=
=
условная
дисперсия.
D(X/Y
= 0) =
φx(x/y
= 0)dx
– (M(X/Y
= 0))2
=
dx
– 5 =
– 5 =
– 5 = =
= 1,25
-
Построить ковариационную и корреляционную матрицы.
Найдем
ковариацию X
и Y.
K
(X,Y)
= K
(Y,X)
=
x-M(X))(y-M(Y))f(x,y)dxdy
=
yf(x,y)dxdy
– mxmy
=
dxdy
– mxmy
=
dx
dy
– M(X)M(Y)
= M(X)M(Y)
– M(X)M(Y)
= 0
Найдем
дисперсии X
и Y
по одномерным законам распределения.
D(X)
= M ((X – M(X))2)
=
X2fx(x)dx
– (M(X))2
=
dx
–
=
–
=
–
=
=
=
2,08
D(y)
= M ((Y – M(Y))2)
=
Y2fy(y)dy
– (M(Y))2
=
dy
–
=
–
=
–
=
=
= 4,08
То
же получим по формулам для равномерного
распределения:
D(X)
=
=
=
D(Y)
=
=
=
Ковариационная
матрица
.
K
=

Коэффициент
корреляции
.
Корреляционная
матрица
.
-
По
определению функции распределения,
.

Вероятность
того, что X+Y<s,
равна отношению площади S0
той части прямоугольника G,
которая лежит ниже прямой
,
к площади всего прямоугольника, равной
35.
Из
рисунков видим, что
при
s
≤ -5
,
при -5< s
≤ 0 S0
=
,
при 0 < s
≤ 2 S0
= 7+4s,
при
2< s ≤ 7 S0
=
, при
s > 7 S0
= 35
при
,
при
,
при
,
при
,
при
.

Плотность
вероятности

2)
.

Вероятность
того, что X·Y<z,
равна отношению площади S0
той части прямоугольника, которая лежит
ниже гиперболы
,
к площади всего прямоугольника, равной
35.
Из
рисунков видим, что
при
z
≤ -25 S0
= 0
при
-25 < z < 0 S0
=
5
–
)dy
= (5y – z
)
z/55
= z + 25 – z
,
при
0 < z ≤ 15
S0
= 35 –
5
–
)dy
= 35 – (5y – z
)
2z/5
= 35 – (10 – z – z
)
= 25 + z +

При
z
>
10 S0
= 35

Плотность
вероятности
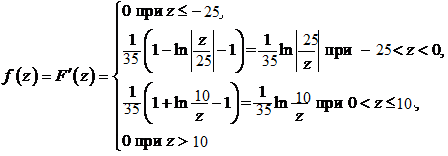
.
Задача
3.
Пусть
время до отказа рассматриваемого изделия
подчиняется экспоненциальному закону
с параметром ,
где
— неизвестный параметр. По результатам
испытаний образцов изделий получена
выборка:
70.8
с, 362.23 с, 62.44 с, 76.91 с, 56.71 с, 88.05 с, 74.87 с,
103.84 с.
Найти
оценку параметра ,
используя различные способы.
Плотность вероятности
экспоненциального закона распределения
,
λ – неизвестный параметр.
1) Метод моментов
Объем выборки
.
Выборочная средняя
является точечной оценкой математического
ожидания.
=
I
=
= 111,981 c
Математическое
ожидание экспоненциального распределения
выразим через его параметр.
M(t)
=
f(t)dt
=
λe–λtdt
= |u
= t,
du
= dt;
dv
= λe-λt
dt,
v
=
e-λt
dt
= – e-λt|
= – t*e-λt|
+
-λtdt
= 0 –
e-λt|0∞
=
.
Приравнивая мат. ожидание его выборочной
оценке, получим оценку неизвестного
параметра распределения.
=
*
=
=
= 0,00893 c-1
2)
Метод наибольшего правдоподобия
Функция
правдоподобия
,
t
i
– варианты выборки,
.
.
Логарифмическая
функция правдоподобия:
.
Найдем
первую производную по λ:
.
Приравняв
её нулю, найдем критическую точку:
.
Найдем
вторую производную по λ:
.
Вторая
производная всюду отрицательна,
следовательно,
– точка максимума и она принимается в
качестве оценки наибольшего правдоподобия
неизвестного параметра λ.
*
=
=
= 0,00893 c-1
3)
Метод квантилей.
Найдем
медиану (квантиль 0,5) выборки.
Упорядочим
выборку по возрастанию:
70.8
с, 362.23 с, 62.44 с, 76.91 с, 56.71 с, 88.05 с, 74.87 с,
103.84 с.
Медиана
выборки Me
=
=
= 66,81
Теоретический
квантиль 0,5 находится из условия
.
Функция
распределения экспоненциального
распределения
.

Оценку параметра
находим, приравнивая теоретическую и
выборочную медиану:
= Me
λ*
=
=
= 0,001 c-1
Задача 4.
Пусть
определяется величина H
с помощью измерительного прибора.
Среднеквадратичное отклонение погрешности
измерения 0
равно 10 мм.
По результатам измерений получена
следующая выборка:
420.8
мм, 406 мм, 441.2 мм, 419.5 мм, 424.2 мм, 434.7 мм.
Считая,
что H ~ N(, 0),
определить доверительный интервал для
параметра
с уровнем доверия 0.9.
Доверительный
интервал для оценки параметра
нормально распределенной случайной
величины с известным среднеквадратическим
отклонением
имеет вид
,
– квантиль нормального распределения.
Объем выборки
.
Выборочная средняя
=
i
=
= 424,4 мм
По заданному уровню
доверия
определяется
.
По таблице квантилей
нормального распределения, находим
квантиль порядка
.

z1-α/2
=
= 6,7 мм;
424,4 – 6,7 < µ <
424,4 + 6,7
(мм);
417,7 < µ < 431,1 (мм).
C
вероятностью 0,9 параметр
находится в интервале: 417,7 < µ < 431,1
(мм).
Задача
5.
Пусть
измеряемая величина Y ~ N(,
)
является пределом прочности при
растяжении материала (Ст. 3). По результатам
испытаний образцов получена выборка:
414.8
МПа, 424.5 МПа, 424.2 МПа, 425.7 МПа, 427.8 МПа, 427.8
МПа.
Установить
доверительные интервалы для
и
с уровнем значимости 0.1.
Пусть
измеряемая величина Y ~ N(,
)
является пределом прочности при
растяжении материала (Ст. 3). По результатам
испытаний образцов получена выборка:
433.2
МПа, 410.2 МПа, 443.3 МПа, 400 МПа, 417.1 МПа, 411
МПа.
Установить
доверительные интервалы для
и
с уровнем значимости 0.1.
Объем выборки
.
Выборочная средняя
=
i
=
= 424,1 МПа
Выборочная
дисперсия
=
i2
– (
)2
=
– 424,12
=
– 179860 = 48 МПа
Исправленное
среднеквадратическое отклонение
s
=
=
= 7,6 МПа
1)
Доверительный интервал для параметра
случайной величины, распределённой по
нормальному закону с неизвестным
среднеквадратическим отклонением,
имеет вид
.
– квантиль
распределения Стьюдента с
степенями свободы порядка
.
По
таблице,
.
t1-α/2,
n-1
=
= 6,25 МПа;
48
– 6,25 = 41,75 МПа;
48 + 6,25 =
54,25 МПа;
41,75
< µ < 54,25 МПа;
C
вероятностью 0,9 параметр
находится в интервале41,75 < µ < 54,25 МПа.
2)
Доверительный интервал для
среднеквадратического отклонения
случайной величины
,
распределённой по нормальному закону,
имеет вид
.
По
таблице находим квантили распределения
с
степенями свободы.
.
.
C
вероятностью 0,9 параметр
находится в интервале
.
Задача
6.
Данные
измерения величины y
в зависимости от факторов m,
b
и s
представлены в табл. 1 и 2.
Таблица
1
Значения
y
в зависимости от m,
b
и s
|
№ опыта |
m, |
b, |
s, |
y, |
|
1 |
5 |
1 |
1 |
47.48 |
|
2 |
1 |
1 |
1 |
34.71 |
|
3 |
5 |
5 |
1 |
107.75 |
|
4 |
1 |
5 |
1 |
97.18 |
|
5 |
5 |
1 |
3 |
85.18 |
|
6 |
1 |
1 |
3 |
73.18 |
|
7 |
5 |
5 |
3 |
142.52 |
|
8 |
1 |
5 |
3 |
132.82 |
Таблица
2
Данные
специальной серии опытов по измерению
величины y
|
№ опыта |
m, |
b, |
s, |
y, |
|
1 |
3 |
3 |
2 |
91.83 |
|
2 |
3 |
3 |
2 |
89.09 |
|
3 |
3 |
3 |
2 |
90.5 |
|
4 |
3 |
3 |
2 |
89.44 |
|
5 |
3 |
3 |
2 |
89.97 |
|
6 |
3 |
3 |
2 |
90.78 |
|
7 |
3 |
3 |
2 |
91.62 |
|
8 |
3 |
3 |
2 |
88.6 |
Используя
данные из этих таблиц, найти экспериментальную
зависимость y(m, b, s).
В качестве первого приближения следует
выбрать линейную регрессионную модель
вида
y(m, b, s) = 01 + 1
m + 2
b + 3
s + e,
где
0, 1, 2, 3
— коэффициенты регрессии; 1, m, b, s
— базисные функции (F0 = 1,
F1 = m,
F2 = b,
F3 = s);
e
— случайная величина.
Решение
Сначала
найдем стандартизированные коэффициенты
методом наименьших квадратов из системы
.
– вектор коэффициентов
парной корреляции между зависимой
переменной
и объясняющими переменными;
– матрица коэффициентов
парной корреляции между объясняющими
переменными;
– вектор
стандартизированных коэффициентов.
|
№ опыта |
m, |
m2 |
b, |
b2 |
s, |
s2 |
y, |
y2 |
m·b |
m·s |
b·s |
y·m |
y·b |
y·s |
|
1 |
5 |
25 |
1 |
1 |
1 |
1 |
47.48 |
2254 |
5 |
5 |
1 |
237 |
47.48 |
47.48 |
|
2 |
1 |
1 |
1 |
1 |
1 |
1 |
34.71 |
1205 |
1 |
1 |
1 |
34,71 |
34.71 |
34.71 |
|
3 |
5 |
25 |
5 |
25 |
1 |
1 |
107.75 |
11610 |
25 |
5 |
5 |
538,75 |
538,75 |
107.75 |
|
4 |
1 |
1 |
5 |
25 |
1 |
1 |
97.18 |
9444 |
5 |
1 |
5 |
97,18 |
485,9 |
97.18 |
|
5 |
5 |
25 |
1 |
1 |
3 |
9 |
85.18 |
7256 |
5 |
15 |
3 |
425,9 |
85.18 |
255,54 |
|
6 |
1 |
1 |
1 |
1 |
3 |
9 |
73.18 |
5355 |
1 |
3 |
3 |
73,18 |
73.18 |
219,54 |
|
7 |
5 |
25 |
5 |
25 |
3 |
9 |
142.52 |
20312 |
25 |
15 |
15 |
712,6 |
712,6 |
427,56 |
|
8 |
1 |
1 |
5 |
25 |
3 |
9 |
132.82 |
17641 |
5 |
3 |
15 |
132,82 |
664,1 |
398,46 |
|
Σ |
24 |
104 |
24 |
104 |
16 |
40 |
720.82 |
75077 |
72 |
48 |
48 |
2252,14 |
2642,52 |
1588,22 |
Табл.2.
Данные специальной серии опытов по
измерению величины y.
|
№ опыта |
m, |
m2 |
b, |
b2 |
s, |
s2 |
y, |
y2 |
m·b |
m·s |
b·s |
y·m |
y·b |
y·s |
|
1 |
3 |
9 |
3 |
9 |
2 |
4 |
91.83 |
8432,75 |
9 |
6 |
6 |
275.49 |
275.49 |
183.66 |
|
2 |
3 |
3 |
2 |
89.09 |
7937,03 |
267.27 |
267.27 |
178.18 |
||||||
|
3 |
3 |
3 |
2 |
90.5 |
8190,25 |
271.5 |
271.5 |
181 |
||||||
|
4 |
3 |
3 |
2 |
89.44 |
8000 |
268.32 |
268.32 |
178.88 |
||||||
|
5 |
3 |
3 |
2 |
89.97 |
8094,6 |
269.91 |
269.91 |
179.94 |
||||||
|
6 |
3 |
3 |
2 |
90.78 |
8241,01 |
272.34 |
272.34 |
181.56 |
||||||
|
7 |
3 |
3 |
2 |
91.62 |
8394,22 |
274.86 |
274.86 |
183.24 |
||||||
|
8 |
3 |
3 |
2 |
88.6 |
7850 |
265.8 |
265.8 |
177.2 |
||||||
|
Σ |
24 |
72 |
24 |
72 |
16 |
32 |
721,83 |
65139,86 |
72 |
48 |
48 |
2165,49 |
2165,49 |
1443,66 |
По
табл.1 и 2 находим выборочные средние
и дисперсии
n
= 8 + 8 = 16
.
=
= 90,17;
=
= 276,1;
=
= 300,5;
=
= 189,49;

σy2
=
– 90,172
= 8763 – 8131 = 632
Находим
коэффициенты парной корреляции
.
.
rym
=
=
0,157;
ryb
=
= 0,844; rys
=
= 0,364


Факторы
m,
b,
s
попарно некоррелированы. Получили
,
откуда
b1
= 0,157; b2
= 0,844; b3
= 0,364
Находим
оценки коэффициентов уравнения регрессии
y(m, b, s) = 01 + 1
m + 2
b + 3
s + e
по
формулам
,
.
β
1*
= 0,157*
= 2,79; β2*
= 0,844 *
= 15; β3*
= 0,364
*
= 12,94;
β4*
= 90,17 – 2,79*3 – 15*3 – 12,94*2 = 90,17 – 79,25 = 10,92
Выборочное
уравнение линейной регрессии
x
(m,b,s) = 10,92 + 2,79m + 15b + 12,94s
Проверим соответствие
регрессионной модели результатам
эксперимента.
Множественный
коэффициент корреляции
=
0,932
Множественный
коэффициент детерминации
R2
= R2y
mbs
= 0,9322
= 0,869
Оценка
значимости уравнения регрессии.
Проверим
основную гипотезу
при альтернативной гипотезе
.
Наблюдаемое
значение
–
статистики
*
= 6,63*4 = 26,53
Критическая
точка распределения Фишера

при
уровне значимости
(доверительная вероятность 0,95)
.
.
Основная гипотеза отвергается. Коэффициент
детерминации и уравнение регрессии в
целом значимы. Линейная модель хорошо
соответствует экспериментальным данным.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нормальный закон распределения для системы случайных величин с примерами решения и образцами выполнения
Нормальный закон распределения для системы случайных величин:
Нормальный закон на плоскости
Из законов распределения системы двух случайных величин имеет смысл специально рассмотреть нормальный закон, как имеющий наибольшее распространение на практике. Так как система двух случайных величин изображается случайной точкой на плоскости, нормальный закон для системы двух величин часто называют «нормальным законом на плоскости».
В общем случае плотность нормального распределения двух случайных величин выражается формулой
Этот закон зависит от пяти параметров: 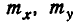
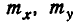
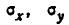
Для того чтобы убедиться в этом, найдём прежде всего плотность распределения для каждой из величин, входящих в систему. Согласно формуле (8.4.2)
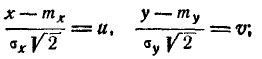
Из интегрального исчисления известно, что
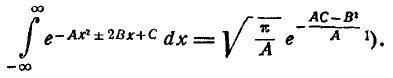
Подставляя эти значения в формулу (9.1.3), имеем:
или, учитывая (9.1.2),
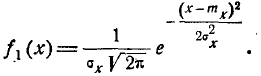
Таким образом, величина X подчинена нормальному закону с центром рассеивания 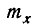
Аналогично покажем, что
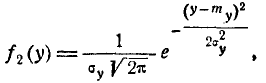
т. е. величина Y подчинена нормальному закону с центром рассеивания 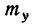
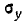
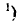
Остаётся доказать, что параметр r в формуле (9.1.1) представляет собой коэффициент корреляции величин X и У. Для этого вычислим корреляционный момент:
где 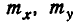
Произведём в двойном интеграле (9.1.6) замену переменных, положив:
Якобиан преобразования равен
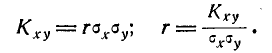
Таким образом, доказано, что параметр r в формуле (9.1.1) представляет собой коэффициент корреляции величин X и Y.
Предположим теперь, что случайные величины X и Y, подчинённые нормальному закону на плоскости, не коррелированы; положим в формуле (9.1.1) r = 0. Получим:
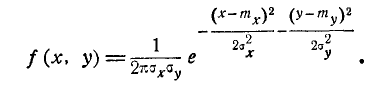
Легко убедиться, что случайные величины (X, Y), подчинённые закону распределения с плотностью (9.1.9), не только не коррелированы, но и независимы. Действительно,
т. е. плотность распределения системы равна произведению плотностей распределения отдельных величин, входящих в систему, а это значит, что случайные величины (Х,У) независимы.
Таким образом, для системы случайных величин, подчинённых нормальному закону, из некоррелированности величин вытекает также их независимость. Термины «некоррелированные» и «независимые» величины для случая нормального распределения эквивалентны. При 
Проанализируем одно из этих условных законов распределения, например f(yx). Для этого преобразуем выражение плотности f(yx) к виду:
Очевидно, это есть плотность нормального закона с центром рассеивания
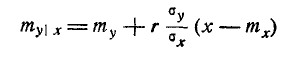
и средним квадратическим отклонение
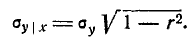
Формулы (9.1.10) и (9.1.11) показывают, что в условном законе распределения величины У при фиксированном значении X = х от этого значения зависит только математическое ожидание, но не дисперсия.
Величина 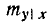
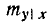
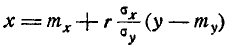
есть линия регрессии X и Y. Линии регрессии совпадают только при наличии линейной функциональной зависимости Y от X. При независимых X и Y линии регрессии параллельны координатным осям.
Рассматривая выражение (9.1.1) для плотности нормального распределения на плоскости, мы видим, что нормальный закон на плоскости полностью определяется заданием пяти параметров: двух координат центра рассеивания 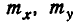
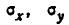
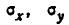
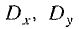
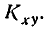
Так как на практике нормальный закон весьма распространён, то очень часто для полной характеристики закона распределения системы оказывается достаточно задать минимальное число — всего пять — числовых характеристик.
Эллипсы рассеивания. Приведение нормального закона к каноническому виду
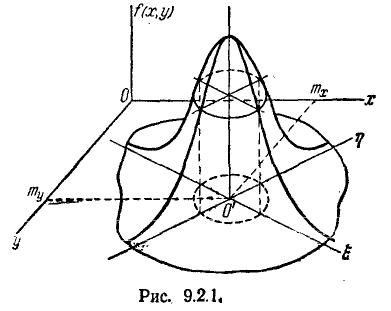
Рассмотрим поверхность распределения, изображающую функцию (9.1.1). Она имеет вид холма, вершина которого находится над точкой (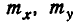
В сечении поверхности распределения плоскостями, параллельными оси f (х, у), получаются кривые, подобные нормальным кривым распределения. В сечении поверхности распределения плоскостями, параллельными плоскости хОу, получаются эллипсы. Напишем уравнение проекции такого эллипса на плоскость хОу.
или, обозначая константу
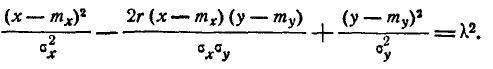
Уравнение эллипса (9.2.1) можно проанализировать обычными методами аналитической геометрии. Применяя их, убеждаемся, что центр эллипса (9.2.1) находится в точке с координатами (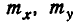
Это уравнение даёт два значения углов: а и 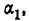
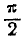
Таким образом, ориентация эллипса (9.2.1) относительно координатных осей находится в прямой зависимости от коэффициента корреляции г системы (X. Y): если величины не коррелированы (т. е. в данном случае и независимы), то оси Симметрия эллипса параллельны координатным осям; в противном случае они составляют с координатными осями некоторый угол.
Пересекая поверхность распределения плоскостями, параллельными плоскости хОу, и проектируя сечения на плоскость хОу, мы получим целое семейство подобных и одинаково расположенных эллипсов с общим центром (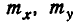
Известно, что уравнение эллипса принимает наиболее простой, так называемый «канонический» вид, если координатные оси совпадают с осями симметрии эллипса. Для того чтобы привести уравнение эллипса рассеивания к каноническому виду, достаточно перенести начало координат в точку (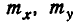
Каноническая форма нормального закона на плоскости имеет вид:
где 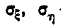
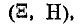
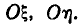
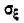
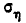
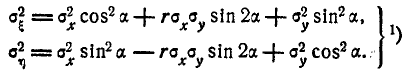
Обычно, рассматривая нормальный закон на плоскости, стараются заранее выбрать координатные оси Ох, Оу так, чтобы они совпали с гласными осями рассеивания. При этом средние квадратические отклонения по осям 
В некоторых случаях координатные оси выбирают параллельно главным осям рассеивания, но начало координат с центром рассеивания не совмещают. При этом случайные величины (X, Y) также оказываются независимыми, но выражение нормального закона имеет вид:
где 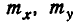
Перейдём в канонической форме нормального закона (9.2.5) от средних квадратических отклонений к вероятным отклонениям:
Величины Ех, Еу называются главными вероятными отклонениями. Подставляя выражения 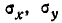
В такой форме нормальный закон часто применяется в теории стрельбы.
Напишем уравнение эллипса рассеивания в каноническом виде:
где k — постоянное число. Из уравнения видно, что полуоси эллипса рассеивания пропорциональны главным средним квадратическим отклонениям (а значит, и главным вероятным отклонениям).
Назовём «единичным» эллипсом рассеивания тот из эллипсов равной плотности вероятности, полуоси которого равны главным средним квадратическим отклонениям 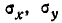
Кроме единичного эллипса рассеивания иногда рассматривают ещё «полный» эллипс рассеивания, под которым понимают тот из эллипсов равной плотности вероятности, в который с практической достоверностью укладывается все рассеивание. Размеры этого эллипса, разумеется, зависят от того, что понимать под «практической достоверностью». В частности, если принять за «практическую достоверность» вероятность порядка 0,99, то «полным эллипсом рассеивания» можно считать эллипс с полуосями
Рассмотрим специально один частный случай, когда главные средние квадратические отклонения равны друг другу:
Тогда все эллипсы рассеивания обращаются в круги, и рассеивание называется круговым. При круговом рассеивании каждая из осей, проходящих через центр рассеивания, может быть принята за главную ось рассеивания, или, другими словами, направление главных осей рассеивания неопределённо. При некруговом рассеивании случайные величины X, Y, подчинённые нормальному закону на плоскости, независимы тогда и только тогда, когда координатные оси параллельны главным осям рассеивания; при круговом рассеивании случайные величины ( X, Y ) независимы при любом выборе прямоугольной системы координат. Эта особенность кругового рассеивания приводит к тому, что оперировать с круговым рассеиванием гораздо удобнее, чем с эллиптическим. Поэтому на практике, где только возможно, стремятся приближённо заменять некруговое рассеивание круговым.
Вероятность попадания в прямоугольник со сторонами, параллельными главным осям рассеивания
Пусть случайная точка (Х , Y ) на плоскости подчинена нормаль- нормальному закону
При этом главные оси рассеивания параллельны координатным осям и величины X и У независимы.
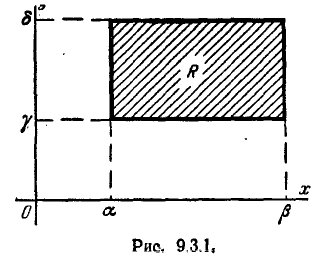
Требуется вычислить вероятность попадания случайной точки (X, Y) в прямоугольник R, стороны которого параллельны координатным осям хОу, а следовательно и главным осям рассеивания (рис. 9.3.1). Согласно обшей формуле (8.3.4) имеем
откуда, применяя формулу (6.3.3) для вероятности попадания на уча- участок, находим:
где Ф*(х) — нормальная функция распределения. Если нормальный закон на плоскости дан в канонической форме, то 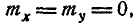
Если стороны прямоугольника не параллельны координатным осям, то формулы (9.3.2) и (9.3.3) уже неприменимы. Только при круговом рассеивании вероятность попадания в прямоугольник любой ориентации вычисляется по формулам (9.3.2) или (9.3.3).
Формулы (9.3.2) и (9.3.3) широко применяются при вычислении вероятностей попадания в цели: прямоугольные, близкие к прямоугольным, составленные из прямоугольников или приближённо заменяемые таковыми.
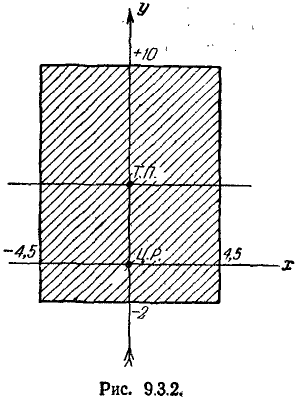
Пример:
Производится стрельба с самолёта по прямоугольному щиту размером 9 м X12 м, лежащему на земле горизонтально. Главные вероятные отклонения: в продольном направлении 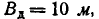
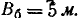
Решение:
На чертеже (рис. 9.3.2) наносим мишень, точку прицеливания (т. п.) и центр рассеивания (ц. р.). Через ц. р. проводим главные рассеивания: по направлению полёта и перпендикулярно к нему.
Перейдём от главных вероятных отклонений 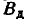
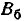
По формуле (9.3.3) имеем:
Вероятность попадания в эллипс рассеивания
К числу немногих плоских фигур, вероятность попадания в которые может быть вычислена в конечном виде, принадлежит эллипс рассеивания (эллипс равной плотности).
Пусть нормальный закон на плоскости задан в канонической форме:
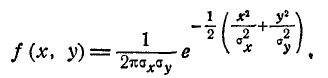
Рассмотрим эллипс рассеивания 
где параметр k представляет собой отношение полуосей эллипса рассеивания к главным средним квадратическим отклонениям. По общей формуле (8.3.3) имеем:
Сделаем в интеграле (9.4.2) замену переменных
Этой подстановкой эллипс 
Перейдём в интеграле (9.4.3) от декартовой системы координат к полярной, положив
Якобиан преобразования (9.4.4) равен r. Производя замену переменных, получим:
Таким образом, вероятность попадания случайной точки в эллипс рассеивания, полуоси которого равны k средним квадратическим отклонениям, равна:
В качестве примера найдём вероятность попадания случайной точки, распределённой по нормальному закону на плоскости хОу, в единичный эллипс рассеивания, полуоси которого равны средним квадратическим отклонениям:
Для такого эллипса k=l. Имеем:
Пользуясь таблицей 2 приложения, находим:
Формула (9.4.5) чаще всего применяется для вычисления вероятности попадания в круг при круговом рассеивании.
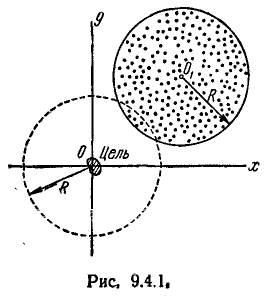
Пример:
На пути быстро движущейся малоразмерной цели площади 1,2 м ставится осколочное поле в форме плоского диска радиуса R =30 м. Внутри диска плотность осколков постоянна и равна 2 оск./м2. Если цель накрыта диском, то число осколков, попадающих в неё, можно считать распределённым по закону Пуассона. В силу малости цели можно рассматривать её как точечную и считать, что она или полностью накрывается осколочным полем (если её центр попадает в круг), или совсем не накрывается (если её центр не попадает в круг). Попадание осколка гарантирует поражение цели. При прицеливании центр круга 
Решение:
Чтобы цель была поражена осколками, необходимо совмещение двух событий: 1) попадание цели (точки О) в осколочное поле (круг радиуса R) и 2) поражение цели при условии, что попадание произошло.
Вероятность попадания цели в круг, очевидно, равна вероятности того, что центр круга (случайная точка 
Применим формулу (9.4.5). Имеем:
Вероятность попадания цели в осколочное поле равна:
Далее найдём вероятность поражения цели р* при условии, что она накрыта осколочным диском. Среднее число осколков а, попадающих в накрытую полем цель, равно произведению площади цели на плотность поля осколков:
Условная вероятность поражения цели р* есть не что иное, как вероятность попадания в неё хотя бы одного осколка. Пользуясь формулой (5.9.5) главы 5, имеем:
Вероятность поражения цели равна:
Воспользуемся формулой (9.4.5) для вероятности попадания в круг, чтобы вывести одно важное для практики распределение: так называемое распределение Релея.
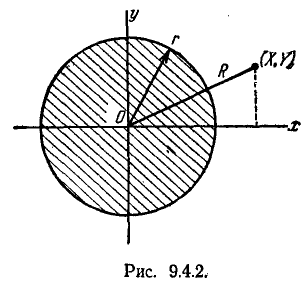
Рассмотрим на плоскости хОу (рис. 9.4.2) случайную точку (X, Y), рассеивающуюся вокруг начала координат О по круговому нормальному закону со средним квадратическим отклонением с. Найдём закон распределения случайной величины R — расстояния от точки (X, Y) до начала координат, т. е. длины случайного вектора с составляющими X, Y.
Найдём сначала функцию распределения F(r) величины R. По определению
Это есть не что иное, как вероятность попадания случайной точки (X, Y) внутрь круга радиуса r (рис. 9.4.2). По формуле (9.4.5) эта вероятность равна:
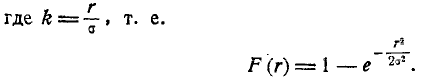
Данное выражение функции распределения имеет смысл только при положительных значениях r; при отрицательных г нужно положить F(r)=0.
Дифференцируя функцию распределения F(r) по r , найдём плотность распределения
Закон Релея (9.4.7) встречается в разных областях практики: в стрельбе, радиотехнике, электротехнике и др.
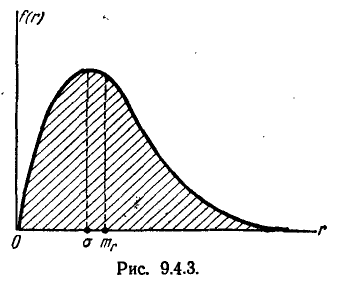
График функции f( r ) (плотности закона Релея) приведён на рис. 9.4.3.
Найдём числовые характеристики величины R, распределённой по закону Релея, а именно: её моду 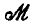
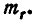
Корень этого уравнения и есть искомая мода
Таким образом, наивероятнейшее значение расстояния R случайной точки (X, У) от начала координат равно среднему квадратическому отклонению рассеивания.
Математическое ожидание 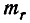
Производя замену переменной
Интегрируя по частям, найдём математическое ожидание расстояния R:
Вероятность попадания в область произвольной формы
При стрельбе ударными снарядами вычисление вероятности попадания в цель сводится к вычислению вероятности попадания случайной точки (X, Y) в некоторую область D. Пусть случайная точка (X, Y) подчинена нормальному закону в каноническом виде. Вероятность попадания точки (X, Y) в область D выражается интегралом
В отдельных частных случаях (например, когда область D есть прямоугольник со сторонами, параллельными главным осям рассеивания, или эллипс рассеивания, а также в некоторых других, имеющих меньшее практическое значение) интеграл (9.5.1) может быть выражен через известные функции; в общем же случае этот интеграл через известные функции не выражается. На практике для вычисления вероятности попадания в область произвольной формы применяются следующие приближенные способы.
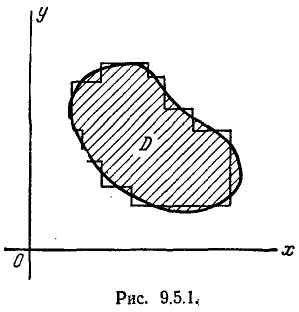
1.Область D приближённо заменяется областью, составленной из х прямоугольников, стороны которых параллельны главным осям рассеивания (рис. 9.5.1). Вероятность попадания в каждый из таких п прямоугольников вычисляется по формуле (9.3.3). Этот способ можно рекомендовать тогда, когда число прямоугольников, на которые приближённо разбивается цель D, не слишком велико.
2.Вся плоскость хОу с помощью некоторой системы линий (прямых или кривых) заранее разбивается на ряд ячеек, вероятности попадания в которые могут быть выражены точно через известные функции, и вычисляется вероятность попадания в каждую ячейку. Такая система линий с соответствующими ей вероятностями попадания в ячейки называется сеткой рассеивания. Работа с сеткой заключается в том, что изображение сетки накладывается на изображение цели, после чего производится суммирование вероятностей попадания в ячейки, накрытые целью; если цель накрывает часть ячейки, то берётся часть вероятности попадания в ячейку, пропорциональная накрытой площади.
Сетку рассеивания можно применять двояким образом: а) строить цель в масштабе сетки, б) строить сетку в масштабе цели.
Если цель имеет сложные очертания и, особенно, если она сравнительно невелика, бывает обычно удобнее построить на изображении цели в том же масштабе ту часть сетки, которая занята целью. Если же цель имеет сравнительно простые очертания и довольно велика (занимает значительную часть полного эллипса рассеивания),
обычно удобнее построить цель в масштабе сетки. Так как стандартная сетка строится для кругового рассеивания, а на практике рассеивание в общем случае круговым не является, при построении Цели в масштабе сетки приходится в общем случае пользоваться Двумя разными масштабами по осям Ох и Оу. При этом способе удобно иметь в распоряжении сетку рассеивания, выполненную на прозрачной бумаге, и накладывать её на перестроенное изображение цели. Прямолинейная сетка рассеивания для одного координатного угла дана на рис. 9.5.2. Сторона ячейки равна
В ячейках проставлены вероятности попадания в них, выраженные в сороковых долях процента.
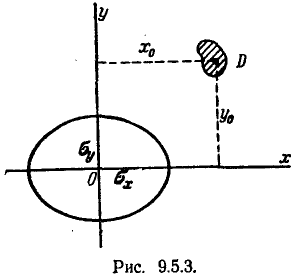
3.В случае, когда размеры области D невелики по сравнению со средними квадратическими отклонениями (не превышают 0,5—1 с. к. о. в направлении соответствующих осей), вероятность попадания в эту область может быть приближённо вычислена по формуле, не содержащей операции интегрирования. Рассмотрим на плоскости хОу малую цель D произвольной формы (рис. 9.5.3).
Допустим, что размеры этой цели невелики по сравнению х с вероятными отклонениями Ех, Еу, По общей формуле (8.3.3) имеем:
где f(x, у) — плотность распределения системы (X, Y). Применим к интегралу (9.5.2) теорему о среднем значении:
где 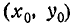
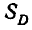
При сравнительно малых размерах области D плотность распределения f(x, у) в пределах этой области изменяется мало и практически может быть принята постоянной. Тогда в качестве точки 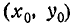
Формулы типа (9.5.3) широко применяются на практике. Для областей, наибольшие размеры которых не превышают 0,5 среднего квадратического отклонения в соответствующем направлении, они дают вполне приемлемые по точности результаты. В отдельных случаях их применяют и для более крупных областей (порядка одного с. к. о.). При условии внесения некоторых поправок (а именно, замены величин 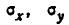
Нормальный закон в пространстве трёх измерений. Общая запись нормального закона для системы произвольного числа случайных величин
При исследовании вопросов, связанных со стрельбой дистанционными снарядами, приходится иметь дело с законом распределения точек разрыва дистанционного снаряда в пространстве. При условии применения обычных дистанционных взрывателей этот закон распределения может считаться нормальным.
В данном п° мы рассмотрим лишь каноническую форму нормального закона в пространстве:
где 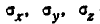
При решении задач, связанных со стрельбой дистанционными снарядами, иногда приходится вычислять вероятность разрыва дистанционного снаряда в пределах заданной области D. В общем случае эта вероятность выражается тройным интегралом:
Интеграл (9.6.3) обычно не выражается через элементарные функции. Однако существует ряд областей, вероятность попадания в которые вычисляется сравнительно просто.
- Вероятность попадания в прямоугольный параллелепипед со сторонами, параллельными главным осям рассеивания
Пусть область R представляет собой прямоугольный параллелепипед, ограниченный абсциссами 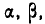
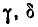
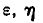
2. Вероятность попадания в эллипсоид равной плотности
Рассмотрим эллипсоид равной плотности 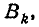
Полуоси этого эллипсоида пропорциональны главным средним квадратическим отклонениям:
Пользуясь формулой (9.6.1) для f(x, у,z ), выразим вероятность
попадания в эллипсоид
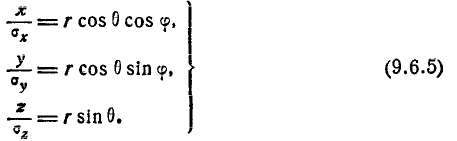
Перейдём от декартовых координат к полярным (сферическим) заменой переменных
Якобиан преобразования (9.6.5) равен:
Переходя к новым переменным, имеем:
Интегрируя по частям, получим:
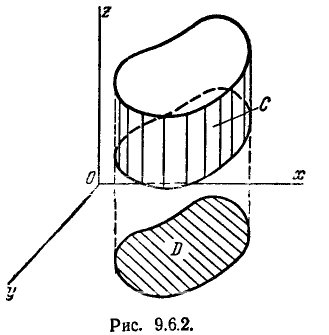
3. Вероятность попадания в цилиндрическую область с образующей, параллельной одной из главных осей рассеивания
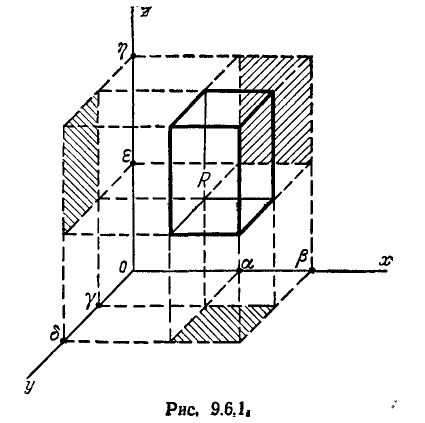
Рассмотрим цилиндрическую область С, образующая которой параллельна одной из главных осей рассеивания (например, оси Oz), а направляющая есть контур произвольной области D на плоскости хОу (рис. 9.6.2).
Пусть область С ограничена двумя плоскостями 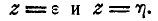
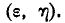
Вероятность 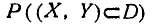
На формуле (9.6.7) основан следующий способ вычисления вероятности попадания в пространственную областьG произвольной формы: область G приближённо разбивается на ряд цилиндрических областей 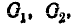
В заключение данной главы напишем общее выражение для нормального закона в пространстве любого числа измерений n. Плотность распределения такого закона имеет вид:
где С — определитель матрицы 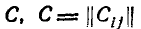
где |К|—определитель корреляционной матрицы, a 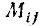
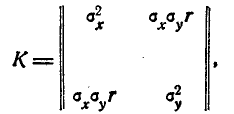
Из общего выражения (9.6.8) вытекают все формы нормального закона для любого числа измерений ц для любых видов зависимости между случайными величинами. В частности, при n = 2 (рассеивание на плоскости) корреляционная матрица есть
где r — коэффициент корреляции. Отсюда
Подставляя определитель матрицы С и её члены в (9.6.8), получим формулу (9.1.1) для нормального закона на плоскости, с которой мы начали п°9.1.
Решение заданий и задач по предметам:
Дополнительные лекции по теории вероятностей:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Числовые характеристики СЛУЧАЙНОГО ВЕКТОРА
Для двумерного случайного вектора (X, Y) вводятся следующие числовые характеристики.
Начальным моментом порядка r + s случайного вектора (X, Y) называется действительное число nr,s, определяемое формулой:
nr,s = M[X r Y s ] =
Начальный момент nr,s существует, если интеграл (соответственно ряд) в правой части равенства абсолютно сходится.
Центральным моментом порядка r + s случайного вектора (X, Y) называется действительное число mr,s определяемое формулой
mr,s = M[(X-mX) r (Y-mY) s ] =
Центральный момент mr,s существует, если интеграл (соответственно ряд) в правой части равенства абсолютно сходится. Вектор с неслучайными координатами (DX, DY) = (m2,0, m0,2) называется дисперсией случайного вектора.
Центральный момент m1,1 называется корреляционным моментом (ковариацией): KXY = M[] = M[(X-mX)?(Y-mY)] = M[XY]-mX mY.
Коэффициентом корреляции двух случайных компонентов X и Y случайного вектора является нормированная ковариация
3. |KXY| £ , (|rXY | £ 1).
Ковариационный момент и коэффициент корреляции определяет степень линейной зависимости между X и Y. Условие |rXY | = 1 необходимо и достаточно, чтобы СВ X и Y были связаны линейной зависимостью Х = a?Y + b, где a и b – константы. СВ, для которых KXY = 0 (rXY = 0), называются некоррелированными. Из независимости случайных величин Х и Y вытекает их некоррелированность (обратное, вообще говоря, неверно).
Условным математическим ожиданием компоненты Х при условии, что Y приняла одно из своих возможных значений yj, называется действительное число определяемое формулой:
mX/Y = M[X/Y = yj] =
где Рi /Y = yj> = , pij = Рi ,Y = yj>.
Условной дисперсией компоненты Х при условии, что Y приняла одно из своих возможных значений yj, называется действительное число определяемое формулой:
DX/Y = D[X/Y = yj] =
Приведенные выше формулы для числовых характеристик двумерного случайного вектора без труда обобщаются на случай n-мерного случайного вектора (Х1, Х2, . Хn). Так, например, вектор с неслучайными координатами (m1, m2, . mn), где mi – математическое ожидание СВ Хi, определяемое формулой
mi = M[Xi] =, называется центром, рассеивания случайного вектора.
Ковариационной матрицей n-мерного случайного вектора = (Х1, Х2, . Хn) называется симметрическая матрица, элементы которой представляют собой ковариации соответствующих пар компонент случайного вектора:
где Кij = M[] – ковариация i-й и j-й компонент.
Очевидно, что Кii = М[Xi 2 ] -дисперсия i-й компоненты.
Корреляционной матрицей n-мерного случайного вектора называется симметрическая матрица, составленная из коэффициентов корреляции соответствующих пар компонент случайного вектора:
rij = – коэффициент корреляции i-й и j-й компоненты.
Задача 1. Закон распределения случайного вектора (X, Y) задан в следующем виде:
| Y
X |
1 | 2 | 3 |
| 1 | 1/9 | 1/9 | 1/9 |
| 2 | 0 | 1/6 | 1/6 |
| 3 | 0 | 0 | 1/3 |
1. Вычислить условное математическое ожидание M[X/Y = 2] и дисперсию D[X/Y = 2].
2. Найти центр рассеивания случайного вектора (X, Y).
3. Построить ковариационную и корреляционную матрицы.
Задача 2. Координаты X, Y случайного положения точки на плоскости имеют
совместное равномерное распределение внутри области G = <(x, y) | -1£ x £ 2, 1 £ y £ 2>.
Записать общее выражение для ПР и для ФР вероятности случайного вектора (X,Y).
Найти центр рассеивания (mX, mY)и вычислить дисперсию (DX, DY) совместного распределения координат.
Построить ковариационную и корреляционную матрицы.
Двумерные дискретные/непрерывные случайные величины
Страницы работы
Содержание работы
РГР2. Случайные величины.
Двумерные дискретные случайные величины
· Описать закон распределения случайного вектора (X,Y)
· Описать законы распределения отдельных компонент
· Найти ковариационную (корреляционную) матрицу
· Найти условные законы и условные мат. ожидания
· Найти функцию распределения
· Установить зависимость компонент X и Y
Двумерные непрерывные случайные величины
1. выражение для
2. одномерные плотности
3. центр рассеивания
4. сделать вывод о зависимости X и Y
5. найти
6. плотности условных распределений
Пусть () – вероятностное пространство (- пространство элементарных событий, S – -алгебра событий, -вероятности событий); – множество вещественных чисел.
Будем обозначать случайную величину, – принимаемые этой величиной значения.
Определение. Случайной величиной называется числовая функция, определённая на пространстве элементарных событий , которая каждому элементарному событию ставит в соответствие число : , причем функция должна быть такова, чтобы событие принадлежало -алгебре событий S, то есть для любого определена вероятность .
Определение. Функцией распределения случайной величины называется функция , которая равна вероятности события :
Тогда есть неубывающая, непрерывная слева функция, удовлетворяющая свойствам:
1.
2.
3.
Дискретные случайные величины
Определение. Случайная величина, принимающая конечное или счётное число значений, называется дискретной.
Определение. Закон распределения дискретной случайной величины представляет собой таблицу, в которой значениям, принимаемым случайной величиной, сопоставлены их вероятности, причём, события образуют полную группу событий, то есть (условие нормировки):
[spoiler title=”источники:”]
http://scicenter.online/teoriya-veroyatnostey-scicenter/chislovyie-harakteristiki-sluchaynogo-145641.html
http://vunivere.ru/work48716
[/spoiler]
Макеты страниц
Определение 1. Распределение двумерной случайной величины называется нормальным, если плотность распределения этой величины выражается формулой,

График этой функции есть поверхность, изображенная на рис. 446.

Рис. 446,
Центром рассеивания случайной величины с законом распределения (1) является точка 

Перепишем формулу (1) так:

Таким образом, f(x, у) можно рассматривать как произведение двух плотностей нормальных распределений случайных величин х и у. Как и в случае одномерной случайной величины, определим главные вероятные отклонения двумерной случайной величины 


Подставляя 


Рассмотрим линии уровня поверхности (4)

(при этом будет 




Полным эллипсом рассеивания называется эллипс, полуоси которого равны 

В следующем параграфе мы установим, что вероятность попадания двумерной случайной величины в полный эллипс рассеивания равна 0,97, т. е. практически попадание достоверно.
1. Дисперсия и среднее квадратическое отклонение случайной величины и их свойства.
2. Случайная величина X имеет распределение:

3. Интегральная функция распределения случайного вектора (X,Y):
Найти центр рассеивания случайного вектора.
4. Из колоды в 36 карт выбирают 4. Какова вероятность того, что среди них будет три туза?
5. Производится стрельба по некоторой цели, вероятность попадания в которую при каждом выстреле равна 0,6. Стрельба прекращается при первом попадании в цель. Найти вероятность того, что будет произведено не более четырех выстрелов.
Download (PDF, 198KB)
21 февраля, 2014
Posted In: Билет, Математика, СибГУТИ, Теория вероятности
Метки: Билет № 18