Разложение функций в степенные ряды. Ряд Тейлора
Общая постановка задачи разложения функции в ряд в комплексной области формулируется так же, как и в действительной области. А именно, для заданной функции , определенной в области
и удовлетворяющий в ней него которым дополнительным условиям, требуется найти ряд вида
который бы сходился в области
и его сумма в этой области совпадала с
.
Постановка задачи разложения функции в степенной ряд
Для функции , аналитической в области
, найти ряд
, сходящийся к
в круге
, принадлежащем области
, то есть
(3.15)
Равенство (3.15) означает, что является суммой ряда в круге
.
Для решения задачи нужно, очевидно, найти коэффициенты ряда по заданной функции ; найти круг сходимости ряда и установить сходимость ряда именно к
. Последнее, напомним, означает, что для точек круга выполняется неравенство
для любого
и
.
Все поставленные вопросы решаются с помощью следующей теоремы.
Теорема Тейлора о разложении функции в степенной ряд
Теорема 3.4. Функция, аналитическая в области , в окрестности каждой точки
этой области представляется в виде степенного ряда (3.15), радиус сходимости
которого не меньше, чем расстояние от точки
до границы области
. Коэффициенты ряда вычисляются по формуле
(3.16)
где — произвольный контур, принадлежащий области
и охватывающий точку
, в частности,
— окружность
или по формуле
(3.17)
На основании теоремы можно сформулировать алгоритм решения поставленной выше задачи и вывод — утверждение.
Алгоритм разложения аналитической функции в степенной ряд
1. Найти производные от данной функции: .
2. Вычислить значения производных в точке ; записать коэффициенты по формуле (3.17). Составить ряд по степеням
с этими коэффициентами, который соответствует данной функции
3. Найти область сходимости полученного ряда и записать разложение (3.15).
Если функция не имеет конечных особых точек, то ряд сходится к ней во всей плоскости, .
Утверждение 3.3
1. Функция, аналитическая в точке , раскладывается в окрестности этой точки в степенной ряд.
2. На границе круга сходимости ряда есть хотя бы одна особая точка функции, т.е. радиус сходимости круга равен расстоянию от центра разложения до ближайшей особой точки функции.
3. Степенной ряд в круге сходимости является рядом Тейлора для своей суммы, т.е. коэффициенты ряда вычисляются по формулам (3.16), (3.17).
Примеры разложения функций по степеням z
Пример 3.13. Записать разложения по степеням функций
.
Решение
Задачу решаем по вышеприведенному алгоритму.
1. Найдем производные:
В поставленной задаче . По формуле (3.17) имеем
3. Нетрудно убедиться, что все составленные ряды сходятся во всей комплексной плоскости, . В результате получаем формулы, которые ранее были приняты за определения соответствующих функций:
В результате получены так называемые основные разложения.
Пример 3.14. Записать разложения по степеням функций: а)
; б)
.
Решение
Задачу можно решать, пользуясь алгоритмом, а можно использовать формулы (3.13) для суммы членов геометрической профессии. Заданные функции являются аналитическими во всей комплексной плоскости за исключением одной точки . Для каждого случая получаем:
заметим, что здесь
для
.
Пример 3.15. Записать разложения по степеням функций: а)
; б)
.
Решение
Разложения записываются для однозначных ветвей многозначного выражения. Выбор ветви определяется заданием функции в точке .
a) Функция определена во всей комплексной плоскости за исключением , т.е. в двусвязной области
. Чтобы получить односвязную область из
, проведем разрез, соединяющий точки
и
. Из условия
следует, что точка
должна быть внутренней точкой области. Поэтому выбираем разрез, не проходящий через
. например по лучу
. В полученной односвязной области, где
, функция
является однозначной аналитической функцией. Далее решаем задачу по алгоритму.
1. Находим производные (формулу устанавливаем по индукции):
2. По формуле (3.17):
3. Находим радиус сходимости ряда: , где
. В результате получаем
б) Функция определена всюду в
за исключением
, т.е. в двусвязной области. В односвязной области, полученной из
путем разреза по лучу
, функция является однозначной , аналитической. Задачу можно решать, как и выше, т.е. по алгоритму, а можно использовать полученный выше результат, введя обозначение
. Для
, удовлетворяющих неравенству
имеем разложение
. Заменяя
на
, получаем результат
Разложения основных функция в степенной ряд
Разложения, полученные в результате решения примеров 3.13-3.15, носят название основных (табличных) разложений. Выпишем их:
Основные разложения позволяют при решении примеров на разложение функции в ряд Тейлора не пользоваться сформулированным выше алгоритмом, сложность которого связана с техникой дифференцирования и составления формулы общего члена.
Утверждение 3.4. При разложении функции в ряд Тейлора используются основные (табличные) разложения и действия над рядами. Радиус сходимости ряда может быть получен по виду раскладываемой функции без использования формулы общего члена ряда и формул для нахождения радиуса. Радиус сходимости ряда, полученного при разложении данной функции в окрестности точки , равен расстоянию от центра разложения — точки
до ближайшей особой точки функции. Если функция является аналитической всюду, то
.
Пример 3.16. Разложить по степеням функции комплексного переменного:
Решение
а) Обозначим через
и, используя табличное разложение для функции
, получим ответ:
, то есть
.
б) Запишем функцию в виде произведения и, используя разложение для
, получим ответ:
, то есть
.
в) Чтобы воспользоваться одним из основных разложений, применим тригонометрическую формулу — формулу “понижения”. Получим:
Заметим, что свободный член разложения в этой записи встречается дважды, поэтому нужно привести подобные члены. Для этого в записи рада отделим слагаемое при — свободный член:
В результате имеем .
Из этого разложения можно найти значение производной любого порядка функции в точке
, так как эти значения связаны формулой (3.17) с коэффициентами разложения:
. Поэтому, учитывая, что в разложении присутствуют только четные степени, заключаем, что все производные нечетных порядков от
в точке
равны нулю, а производная, например, десятого порядка не равна нулю. Найдем ее, используя равенство
, где
— коэффициент в разложении
при
, т.е. в записанном выше разложении нужно взять
. Получим
г) Функция определена всюду, кроме . В односвязной области, например в плоскости с разрезом по лучу
, где
, возможно выделение однозначных ветвей многозначного выражения
(рис. 3.1). Выбираем ту ветвь, для которой
, то есть из
получаем
. Разложим аналитическую функцию
по степеням
в круге
; радиус круга
— расстояние от центра разложения
до граничной точки
.
Чтобы воспользоваться основным разложением, преобразуем функцию следующим образом:
Тогда, обозначая через
и используя основное разложение для
, получаем
при условии
, т.е. в круге
.
Пример 3.17. Разложить в окрестности точки ветвь функции
, для которой
.
Решение
Функция определена всюду в
, кроме точек
, т.е. в трехсвязной области — плоскости с выколотыми точками
и
. Чтобы получить односвязную область, проведем разрезы по лучам, выходящим из этих точек. Например, луч из точки
выберем параллельным мнимой оси,
, а луч из точки
— по действительной оси:
. В полученной односвязной области (рис. 3.2) каждая ветвь является аналитической функцией и раскладывается в ряд в круге
(
— расстояние от
до границы). Здесь ветвь задается условием:
, то есть из
при
.
Далее, чтобы использовать основное разложение, преобразуем функцию:
Для числа в силу выбора ветви берем
, а функции
и
раскладываем в ряды, как в предыдущем примере:
В области , принадлежащей выбранной односвязной области, сходятся оба ряда. Используя свойство сложения рядов, получаем окончательный результат:
При разложении функции в ряд в окрестности точки , т.е. по степеням
, удобно использовать замену
и полученную после замены функцию раскладывать по степеням
.
Пример 3.18. Разложить по степеням функции: a)
; б)
в)
.
Решение
а) Обозначим через
, и, используя тригонометрическую формулу для функции
, получим:
. Здесь
и
— постоянные величины, а для функций
и
используем основные разложения. В результате получим
то есть ряд вида , где коэффициент
определяется следующим образом:
для
и
для
.
б) Можно, как и выше, использовать вспомогательную переменную, а можно сделать то же самое, применив простое преобразование: . Здесь
— постоянная величина, функция
раскладывается в ряд как функция
по степеням
. Получаем ответ:
, или
.
в) Обозначая через
, получаем функцию
. Разложение этой функции по степеням
найдено в примере 3.16:
Возвращаясь к исходной переменной, получаем разложение исходной функции в круге (рис. 3.3):
Пример 3.19. Разложить по степеням функции:
.
Решение
Данные функции являются простейшими рациональными (элементарными) дробями. Для их разложения используется формула суммы членов бесконечно убывающей геометрической прогрессии . В первом случае формула используется непосредственно, при
, во втором — после преобразования
получаем
. Разложение заданных функций имеет вид
(3.18)
(3.19)
Соотношения (3.18),(3.19) обобщают формулу , которая получается из них при
.
При разложении дроби замечаем, что она является производной от
, то есть
, поэтому ее разложение можно получить, используя дифференцирование ряда:
Ответ удобнее записать в виде .
Очевидно, повторяя процедуру дифференцирования, можно получить разложение элементарных дробей вида при любом натуральном
.
Алгоритм разложения рациональных дробей в ряд Тейлора
Рассмотрим примеры на разложение в ряд Тейлора рациональных дробей
где и
— многочлены. Первые этапы решения задачи аналогичны этапам интегрирования этих дробей. Приведем полный алгоритм.
1. Если дробь неправильная , следует выделить целую часть дроби многочлен.
2. Правильную рациональную дробь разложить на элементарные дроби:
а) записать дробь в виде суммы элементарных дробей вида с неопределенными коэффициентами
, где
— корень знаменателя,
— его кратность;
б) найти неопределенные коэффициенты.
3. Разложить элементарные дроби в степенные ряды. Основными приемами при этом являются применение формул (3.13),(3.18),(3.19) и правила дифференцирования ряда (см. пример 3.19)).
При разложении по степеням можно предварительно ввести вспомогательную переменную
.
Пример 3.20. Разложить по степеням функции: а)
; б)
.
Решение
а) Воспользуемся алгоритмом.
1. Дробь неправильная, поэтому выделяем целую часть: .
2. Полученная правильная дробь является элементарной дробью.
3. Записываем разложение элементарной дроби и получаем:
Для разложения дроби можно было использовать формулу (3.19) при
.
Для нахождения окончательного ответа нужно сделать преобразование приведения подобных членов, так как в полученном выражении свободный член встречается дважды. Имеем
, то есть
.
б) Воспользуемся алгоритмом.
1. Дробь неправильная, выделяем целую часть. Можно, как и выше, применить преобразование дроби:
Можно для выделения целой части применить метод деления “углом”, или, обозначая i + 2 = t, произвести почленное деление на одночлен
2,3. Записываем разложение заданной функции, используя формулу (3.19) для правильной дроби:
Окончательный ответ: .
Получен ряд вида , где
. Нетрудно проверить равенство:
.
Пример 3.21. Функцию разложить в ряд Тейлора в окрестности точки
, если а)
; б)
.
Решение
а) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Раскладываем ее на элементарные дроби. Для этого представим дробь в виде
где и
— неопределенные коэффициенты, которые находим из тождества
Полагая последовательно и
, получаем
.
Записываем дробь в виде суммы дробей: .
3. Раскладываем по степеням г каждую элементарную дробь:
В общей области сходимости — круге — записываем сумму рядов разложение исходной дроби:
б) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Разложение дроби на элементарные получено в предыдущем пункте:
3. Раскладываем по степеням каждую элементарную дробь:
Записываем разложение исходной дроби в круге
При разложении по степеням, можно было сделать замену
в исходной дроби.
Радиусы сходимости в обоих случаях можно определить заранее, до записи» разложения — по виду функции. Ее особыми точками являются точки и
. В первом случае ближайшей к точке
является точка
, расстояние между точками равно единице и, следовательно,
; во втором — обе особые точки удалены от
на расстояние, равное двум, и
.
Пример 3.22. Разложить по степеням функции (рациональные дроби): а)
; б)
.
Решение
а) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Раскладываем правильную дробь на элементарные дроби, предварительно разложив знаменатель на множители:
, где
и
.
Представим дробь в виде . Находим коэффициенты
и
из тождества
, т.е. из системы
Дробь представлена в виде суммы: .
3. Раскладываем элементарные дроби по степеням
Записываем ответ:
б) Воспользуемся алгоритмом.
1,2. Раскладываем дробь на элементарные:
, где
— неопределенные коэффициенты.
Находим коэффициенты из тождества .
Приравнивая коэффициенты при одинаковых степенях , имеем
3. Раскладываем элементарные дроби по степеням
Для исходной дроби получаем разложение:
или, складывая ряды: .
Окончательный ответ: .
Пример 3.23. Разложить по степеням функции: а)
; б)
.
Решение
Обе дроби правильные; раскладывать на более простые нет необходимости. Используя основные разложения, получаем ответы:
а) ;
б) или
.
Пример 3.24. Используя разложение функции по степеням
, найти значение производной седьмого порядка в точке
.
Решение
Пример 3.25. Записать разложение функций a) и б)
по степеням
до члена, содержащего
.
Решение
а) Применим метод подстановки ряда в ряд, используя основные разложения для функций и
. Имеем
, или, подставляя:
где . Записывать большее число слагаемых нет необходимости, так как уже у следующего (первого отброшенного) младшая степень равна
.
Возведение в степень рядов, как и перемножение рядов, производится по правилам действий с многочленами, в частности применяется формула бинома Ньютона:
Так как младшая степень выражения
равна трем, следовательно,
— шести, то для записи результата следует взять из первых двух скобок по два слагаемых, а из остальных по одному, т.е.
Приводя подобные члены, получим окончательный ответ:
или .
Разложение, очевидно, можно получить, вычисляя коэффициенты разложения по формуле (3.17), что более громоздко.
б) Разложение можно получить, используя формулу (3.17) для коэффициентов либо произведя деление ряда
на ряд
методом деления “утлом” или методом неопределенных коэффициентов.
Применим последний прием. Разложение по степеням
ищем в виде
По определению деления имеем тождество
Перемножаем ряды справа и приравниваем коэффициенты полученного ряда известным коэффициентам при соответствующих степенях ряда, записанного слева. Получаем систему уравнений
из которой находим коэффициенты .
Ответ получаем в виде . Это разложение справедливо в круге
, так как
— ближайшая к
особая точка функции тангенса
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
1°. Ряд Тейлора. Функция однозначная и аналитическая в точке
разлагается (то есть является суммой) в окрестности этой точки в степенной ряд – ряд Тейлора
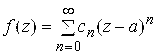
Где коэффициенты вычисляются по формулам
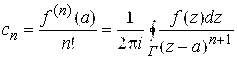
, (5.11)
Где Г – окружность с центром в точке , целиком лежащая в области аналитичности
. Областью сходимости ряда является круг с центром в точке разложения радиуса R, равном расстоянию от центра разложения до ближайшей осо бой точки – точки, в которой
теряет аналитичность.
Теорема Тейлора. Функция , аналитическая в круге
однозначно представима в нем своим рядом Тейлора (5.10), коэффициенты которого определяются по формулам (5.11).
Из этой теоремы и теоремы о возможности дифференцирования степенного ряда в круге сходимости любое число раз следует, что разложение функции в степенной ряд единственно. Это означает, что по любому методу разложения функции в степенной ряд мы получаем одно и то же разложение – ряд Тейлора. При ряд (5.10) называется рядом Маклорена.
При решении многих задач рекомендуется пользоваться следующими разложениями элементарных функций:
1) 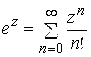
; 2)
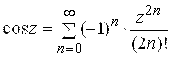
;
3) 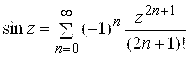
; 4)
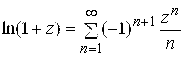
; (5.12)
5) 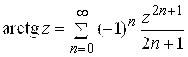
; 6)
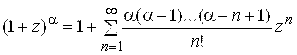
,
; 7)
;
8) 
Для непосредственного разложения функции в степенной ряд (ряд Тейлора), необходимо найти закон получения производной N-го порядка (подобные примеры опустим).
Пример 1. Разложить в ряд по степеням функцию
.
Решение. Рассмотрим сначала следующее преобразование данной логарифмической функции . Воспользуемся разложением 4) из (5.12) для
, полагая
. Так как разложение 4) имеет место при
, то наше разложение будет иметь место при
. Таким образом, для
:

Часто при разложении функций в ряд удобно пользоваться дифференцированием или интегрированием известных разложений, а при разложении рациональной дроби – разложением ее на простейшие.
Пример 2. Разложить в ряд по степеням Z функцию 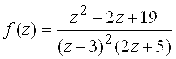
Решение. Разложим на простейшие дроби:

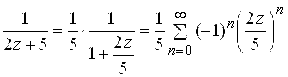
и

. Замечая, что
и применяя теорему о возможном почленном дифференцировании степенного ряда в круге сходимости, получим

. Складывая ряды для
и
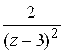

.
2°. Ряды Лорана.
Определение. Рядом Лорана называется ряд (5.6)
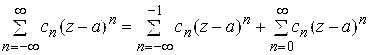
При этом ряд 


.
Теорема Лорана. Если функция аналитична в кольце
, то в этом кольце она единственным образом представима в виде ряда Лорана (5.6), коэффициенты которого вычисляются по формулам:

(5.13)
Заметим, что из этой теоремы “кольца разложимости” определяются через расстояния от центра разложения до двух “соседних” особых точек . Вычисление контурных интегралов (5.14), как правило, достаточно затруднительно. Поэтому для разложения функций в ряды Лорана используются различные искусственные приемы.
Пример 1. Разложить в ряд Лорана в кольце функцию

Решение. Преобразуем данную функцию:

Первые два слагаемых в правой части (1) имеют нужный вид, так как представляют собой степени разности . Последние два слагаемых запишем в виде:



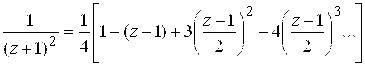
Подставляя (2) и (3) в (1), после несложных преобразований получим разложение в кольце
в ряд Лорана:

Пример 2. Разложить в ряд Лорана функцию в окрестности
.
Решение. Для любого комплексного имеем
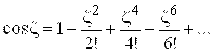
Полагая , получим:
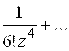
. В данном случае “кольцо” представляет собой всю комплексную плоскость с одной выброшенной точкой
:
.
Пример 3. Рассмотреть различные разложения в ряд Лорана функции .
Решение. Функция имеет две особые точки:
и
. Следовательно, имеется три “кольца” с центром в точке
, в каждом из которых
является аналитической: а) круг
; б) кольцо
; в)
– внешность круга
. Найдем ряды Лорана для функции
В каждом из этих “колец”. Представим предварительно функцию в виде суммы простейших дробей:
(1). а)разложение в круге
. Преобразуем (1) следующим образом:
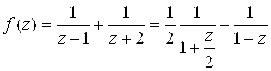
,
(3);

(4). Подставляя эти разложения в (2), получим:
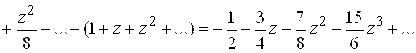
. б) разложение в кольце
. Ряд (4) для функции
остается сходящимся в этом кольце, так как
. Ряд (3) для функции
расходится для
. Поэтому преобразуем
следующим образом:


(6). Этот ряд сходится, если
, то есть при
. Подставляя (4) и (6) в (5), найдем

. Ряд (4) для функции
при
расходится, а ряд (6) для функции
будет сходиться, так как, если
, то и подавно
. Функцию
представим в таком виде


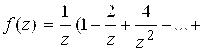
. Заметим, что этот пример показывает, что для одной и той же функции ряд Лорана, вообще говоря, имеет разный вид для разных колец.
Пример 4. Разложить в ряд Лорана функцию 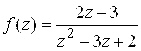
Решение. Особые точки функции: . а) разложение
в окрестности точки
, то есть в кольце
. Представим функцию
в виде суммы простейших дробей:
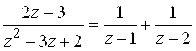

, получим

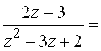
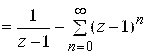
в окрестности точки
, то есть в кольце
. Имеем

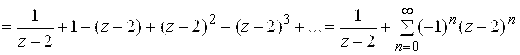
| < Предыдущая | Следующая > |
|---|
Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций. Частный случай разложения в ряд Тейлора в нулевой точке называется рядом Маклорена.
Ряд Тейлора был известен задолго до публикаций Брука Тейлора[1] — его использовали ещё в XIV веке в Индии[2], а также в XVII веке Грегори и Ньютон.
Ряды Тейлора применяются при аппроксимации функции многочленами.
В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Обобщением понятия ряда Тейлора в функциональном анализе является ряд Фантапье.
Определение[править | править код]
1. Многочленом Тейлора функции 



,
используемая в приближённых вычислениях, как обобщение следствия теоремы Лагранжа о среднем значении дифференцируемой функции:
- при
верно
.
При записи суммы использованы обозначение 


2. Рядом Тейлора в точке 



с общим членом
, зависящим от параметра
.
Другими словами, рядом Тейлора функции 


.[3]
Как указано ниже в примерах, наличия бесконечной дифференцируемости функции 


3. Рядом Тейлора в точке 


удовлетворяющей в некоторой окрестности 

называется степенной ряд
.
В отличие от вещественного случая, из условий следует, что найдётся такое значение радиуса 


4. В случае 
называется рядом Маклорена.
Аналитическая функция[править | править код]
1. Функция 








то есть 


Функция называется аналитической на промежутке (на множестве), если она является аналитической в каждой точке этого промежутка (множества).
2. Степенной ряд 


Если в 



Таким образом, для аналитической в точке 




Следствие. Функция 




3. Вопрос: будет ли для произвольной бесконечно дифференцируемой в точке 






Ответ: нет.
Существуют бесконечно дифференцируемые функции вещественной переменной, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности

Примеры. Функции вещественной переменной 

являются бесконечно дифференцируемыми в точке 
Следовательно, ряды Тейлора всех этих функций с параметром 
Однако, для любого 


в которых функции отличны от 
Таким образом, эти функции не являются в точке 
Доказательство
Доказательство проведём для функции 
Функция 
для всех 
Для 

Функция 



дополненная пределами слева
и справа 

Найдём производную функции 

По определению:

Поскольку для 

то
докажем, что для произвольного 

Применение правила Лопиталя непосредственно к частям
не приводит к результату.
Выполним замену переменной: 

Пусть 
Применяя правило Лопиталя 




.
Таким образом,
.
Найдём (для 
производных функции 
И так далее. Во всех случаях, очевидно,
получается произведение
на сумму целых отрицательных степеней

Конечная сумма
бесконечно малых является бесконечно малой.
Таким образом,

Вычисляя последовательно по определению (как выше) производные 

обнаруживаем, что все производные в
точке 
Область сходимости ряда Тейлора[править | править код]
Ряд Тейлора, являясь степенным рядом, имеет в качестве области сходимости круг (с центром в точке 
и интервал (с центром в точке 
1. Например, функция 





2. Радиус сходимости ряда Тейлора можно определить, например, по формуле Даламбера:
.
3. Рассмотрим для примера экспоненциальную функцию 



4. От параметра — точки разложения 
Например, разложим в общем случае (для произвольного 


Можно доказать с помощью формулы суммы геометрической прогрессии, что данный ряд, как функция аргумента 


Действительно,
.
Область сходимости ряда может быть задана неравенством 





Формула Тейлора[править | править код]
Предположим, что функция 









Достаточно легко доказать, что такой многочлен имеет вид 








Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
Различные формы остаточного члена[править | править код]
В форме Лагранжа:
В форме Коши:
В интегральной форме:
Ослабим предположения:
- В асимптотической форме (форме Пеано, локальной форме):
Критерий аналитичности функции[править | править код]
Основной источник: [5]
Предположим, что некоторую функцию 



Во-первых, необходимым условием аналитичности функции является сходимость ряда Тейлора в некоторой непрерывной области. Действительно, если ряд Тейлора сходится всего в одной точке, то это точка 

Во-вторых, по формуле Тейлора в ряд Тейлора с остаточным членом может быть разложена любая (а не только аналитическая) функция, бесконечно дифференцируемая в окрестности, содержащей точку 





Очевидно, что функция 






В качестве примера рассмотрим экспоненциальную функцию 



Остаточный член разложения этой функции в форме Лагранжа имеет вид 



Здесь используется, что на фиксированном промежутке экспонента ограничена некоторым числом 
Причем, как видно, предел остаточного члена равен нулю для любых 

Ряды Маклорена некоторых функций[править | править код]
- Гиперболические функции[6][10]:
- Обратные гиперболические функции[6][11]:
Формула Тейлора для функции двух переменных[править | править код]
Пусть функция 


Введём дифференциальный оператор
.
Тогда разложение (формула Тейлора) функции 



где 
Следует иметь в виду, что операторы 
в 



Аналогичным образом формула строится для функций любого числа переменных, меняется только число слагаемых в операторе 
В случае функции одной переменной 
Формула Тейлора многих переменных[править | править код]
Для получения формулы Тейлора функции 



Тогда разложение (формула Тейлора) функции по степеням 

где 

Для функции 


В другой форме ряд Тейлора можно записать таким образом:

Пример разложения в ряд Маклорена функции трёх переменных[править | править код]
Найдём выражение для разложения в ряд Тейлора функции трёх переменных 




Разложение в ряд Тейлора запишется в виде
Учитывая, что
получим
Например, при 
Примечания[править | править код]
- ↑ Taylor, Brook, Methodus Incrementorum Directa et Inversa [Direct and Reverse Methods of Incrementation] (London, 1715), pages 21-23 (Proposition VII, Theorem 3, Corollary 2). Translated into English in D. J. Struik, A Source Book in Mathematics 1200—1800 (Cambridge, Massachusetts: Harvard University Press, 1969), pages 329—332.
- ↑ Gupta R. C. The Madhava-Gregory series, Math. Education 7 (1973), B67-B70.
- ↑ Запорожец Г. И. «Руководство к решению задач по математическому анализу» — С. 371
- ↑ Н.С. Пискунов. Дифференциальное и интегральное исчисления. — Мифрил, 1996. — С. Том 1, глава 4, параграф 6.
- ↑ Н.С. Пискунов. Дифференциальное и интегральное исчисления для втузов. — тринадцатое. — МОСКВА “НАУКА”, 1985. — С. Том 2, глава 16, параграф 16.
- ↑ 1 2 3 4 5 6 Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. — 4-е изд. — М.: Наука, 1963.
- ↑ Цукер Р. Тригонометрические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 37—43. — 832 с. — 50 000 экз.
- ↑ Цукер Р. Обратные тригонометрические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 44—47. — 832 с. — 50 000 экз.
- ↑ При значении x, близком к 1, эта расчётная формула сходится медленно, т.е. даёт большую погрешность при приближении функции суммой первых нескольких членов ряда. Поэтому можно воспользоваться формулой
где
- ↑ Цукер Р. Гиперболические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 48—49. — 832 с. — 50 000 экз.
- ↑ Цукер Р. Обратные гиперболические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 50—53. — 832 с. — 50 000 экз.
Литература[править | править код]
- Ильин В. А., Садовничий В. А., Сендов Б. Х. Математический анализ, ч. 1, изд. 3, ред. А. Н. Тихонов. М.: Проспект, 2004.
- Камынин Л. И. Математический анализ. Т. 1, 2. — 2001.
- Киселёв В. Ю., Пяртли А. С., Калугина Т. Ф. Высшая математика. Первый семестр, Интерактивный компьютерный учебник.
- Маркушевич А. И. Теория аналитических функций. В 2 т. — Изд. 2-е. — М.: Наука, 1967. — Т. 1: Начала теории. — 486 с.
- Нарасимхан Р. Анализ на действительных и комплексных многообразиях. — пер. с англ. Е. М. Чирки. — М.: Мир, 1971. — 232 с.
- Петрова С. С., Романовска Д. А. К истории открытия ряда Тэйлора. // Историко-математические исследования. — М.: Наука, 1980. — № 25. — С. 10—24.
- Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов. В 2 т. — Изд. 13-е. — М.: Наука, Главная редакция физико-математической литературы, 1985. — Т. 1. — 432 с.
- Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов. В 2 т. — Изд. 13-е. — М.: Наука, Главная редакция физико-математической литературы, 1985. — Т. 2. — 560 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. В 3 т. — Изд. 8-е. — М.: ФИЗМАТЛИТ, 2003. — Т. I. — 680 с. — ISBN ISBN 5-9221-0156-0.
Степенные ряды в форме рядов Тейлора и Маклорена
Степенные ряды и, в частности, ряды Тейлора являются одним из видов функциональных рядов.
Степенной ряд в общем виде записывается как:
a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n+…=∑k=0∞ak(x−x0)ka_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n+ldots=sumlimits_{k=0}^{infty} a_k(x-x_0)^k
где a0,a1,…,an,…a_0, a_1, ldots, a_n, ldots – постоянные, коэффициенты ряда,
x0x_0 – центр интервала сходимости ряда ∣x−x0∣<R|x-x_0|<R,
RR – радиус сходимости, когда для частичных сумм Sn(x)S_n(x) существует предел, сумма ряда S(x)S(x):
Sn(x)=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n,limn→∞Sn(x)=S(x)S_n(x)= a_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n, quad limlimits_{n to infty } S_n (x) = S (x)
Возьмем функцию действительной переменной f(x)f(x), которая является бесконечно дифференцируемой в точке x0x_0. Такую функцию можно разложить в степенной ряд следующего вида:
f(x)=f(x0)+f′(x0)1!(x−x0)+f′′(x0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=∑k=0∞f(k)(x0)k!(x−x0)kf(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +dfrac{f{”}(x_0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
Этот ряд по степеням двучлена (x−x0)(x-x_0) называют рядом Тейлора.
В случае x0=0x_0=0 полученный степенной ряд:
f(x)=f(0)+f′(0)1!x+f′′(0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=∑k=0∞f(k)(x0)k!(x−x0)kf(x)=f(0)+dfrac{f{‘}( 0)}{1!} x +dfrac{f{”}(0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
называют рядом Маклорена.
Ряд Тейлора можно записать в другом виде. Полагая:
x−x0=t,f(x)=f(x0+t)=g(t)x-x_0=t, quad f(x)=f(x_0+t)=g(t)
ряд Тейлора
f(x)=f(x0+t)=f(0)+f′(x0)1!t+f′′(x0)2!t2+…+f(n)(x0)n!tn+…=∑k=0∞f(k)(x0)k!tkf(x)=f(x_0+t)=f(0)+dfrac{f{‘}(x_ 0)}{1!} t +dfrac{f{”}(x_0)}{2!}t^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}t^k
сводится к ряду Маклорена:
g(t)=g(0)+g′(0)1!t+…+g(n)(0)n!tn+…=∑k=0∞g(k)(0)k!tkg(t)=g(0)+dfrac{g{‘}( 0)}{1!}t +ldots+dfrac{g^{(n)}(0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{g^{(k)}(0)}{k!}t^k
Как и в случае произвольного степенного ряда, ряды Тейлора и Маклорена имеют интервал сходимости.
Пример
Разложим в ряд Тейлора функцию:
f(x)=1xf(x)=dfrac{1}{x}
в окрестности точки x0=1x_0=1.
С помощью замены:
x−x0=x−1=tx-x_0=x-1=t
функция сводится к виду:
f(x)=f(t+1)=11+tf(x)=f(t+1)=dfrac {1}{1+t}
Полученное выражение при ∣t∣<1|t|<1 является суммой бесконечно убывающей геометрической прогрессии знаменателем (−t)(-t), и ряд записывается в виде:
11+t=1−t+t2−t3+…+(−1)ntn+…=∑k=0∞(−1)ktkdfrac {1}{1+t}=1-t+t^2-t^3+ldots+(-1)^{n}t^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}t^{k}
Возвращаясь к переменной xx, получаем разложение по степеням двучлена (x−1)(x-1):
1x=1−(x−1)+(x−1)2−(x−1)3+…+(−1)n(x−1)n+…=∑k=0∞(−1)k(x−1)k,∣x−1∣<1dfrac {1}{x}=1-(x-1)+ (x-1)^2-(x-1)^3+ldots+(-1)^{n}(x-1)^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}(x-1)^{k}, quad |x-1|<1
Формула Тейлора
Следствием разложения функции в степенной ряд является соответствующая формула Тейлора. Если функция f(x)f(x) имеет в точке x0x_0 производные до nn –го порядка включительно, то функцию f(x)f(x) можно представить с помощью формулы Тейлора:
f(x)=f(x0)+f′(x0)1!(x−x0)+…+f(n)(x0)n!(x−x0)n+Rn(x)f(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +R_n (x)
или
f(x)=∑k=0nf(k)(x0)k!(x−x0)k+Rn(x)f(x)= sumlimits_{k=0}^{n} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k +R_n (x),
где функция Rn(x)R_n (x) называется остаточным членом.
Формы остаточного члена
Существует несколько форм для остаточного члена. В частности, если f(x)f(x) дифференцируема (n+1)(n+1) раз в окрестности x0x_0, то Rn(x)R_n (x) может быть представлена в форме Лагранжа:
Rn(x)=f(n+1)(ξ)(n+1)!xn+1,x<ξ<x0R_n (x)=dfrac {f^{(n+1)}(xi)}{(n+1)!} x^{n+1}, quad x<xi<x_0 или x<ξ<x0x<xi<x_0.
Если функция f(x)f(x) дифференцируема (n−1)(n-1) раз в окрестности x0=0x_0=0, то Rn(x)R_n(x) может быть представлена в форме Пеано:
Rn(x)=o((x−x0)n)R_n(x)=o((x-x_0)^n).
Учитывая, что ряд Тейлора можно свести к ряду Маклорена, запишем формулу Тейлора для основных элементарных функций в окрестности x0=0x_0=0 и укажем соответствующие интервалы сходимости.
Показательная функция:
ex=1+x1!+x22!+x33!+…+xnn!+o(xn),∣x∣<∞e^x=1+dfrac{x}{1!} +dfrac{x^2}{2!} +dfrac{x^3}{3!}+ldots+dfrac{x^n}{n!}+o(x^n),quad |x|<infty
Тригонометрические функции:
sinx=x1!−x33!+x55!−x77!+…+(−1)n+1x2n−1(2n−1)!+o(x2n),∣x∣<∞sin x=dfrac{x}{1!} -dfrac{x^3}{3!} +dfrac{x^5}{5!} -dfrac{x^7}{7!} +ldots+dfrac{(-1)^{n+1}x^{2n-1}}{(2n-1)!}+ o(x^{2n}),quad |x|<infty
cosx=1−x22!+x44!−x66!+…+(−1)n+1x2n(2n)!+o(x2n+1),∣x∣<∞cos x=1 -dfrac{x^2}{2!} +dfrac{x^4}{4!} -dfrac{x^6}{6!} +ldots+dfrac{(-1)^{n+1}x^{2n}}{(2n)!}+ o(x^{2n+1}),quad |x|<infty
arctgx=x−x33+x55−x77+…+(−1)nx2n+12n+1+o(x2n+2),∣x∣≤1arctg x=x-dfrac{x^3}{3} +dfrac{x^5}{5} -dfrac{x^7}{7} +ldots+dfrac{(-1)^{n}x^{2n+1}}{2n+1}+ o(x^{2n+2}),quad |x|le{1}
Логарифмическая функция:
ln(1+x)=x1!−x22!+x33!−…+(−1)n+1xnn!+o(xn),x∈(−1;1]ln (1+x)=dfrac{x}{1!} -dfrac{x^2}{2!} +dfrac{x^3}{3!} -ldots+dfrac{(-1)^{n+1}x^{n}}{n!}+ o(x^n),quad xin (-1;1]
Степенная функция:
(1+x)α=1+α1!x+α(α−1)2!x2+α(α−1)(α−2)3!x3+…+α(α−1)…(α−n+1)n!xn+o(xn)(1+x)^alpha=1+dfrac{alpha }{1!}x+dfrac{alpha (alpha -1)}{2!}x^2 +dfrac{alpha (alpha -1)( alpha -2)}{3!} x^3 +ldots+dfrac{alpha (alpha -1) ldots ( alpha-n+1)} {n!} {x^n}+ o(x^n)
Пример 1
Разложим, используя формулу Тейлора, функцию
f(x)=(x+1)ln(x2+2x+2)f(x)=(x+1)ln (x^2+2x+2)
в окрестности точки x0=−1x_0=-1 с точностью до o((x+1)7)o((x+1)^7).
Выполнив замену переменной
x−x0=x+1=tx-x_0=x+1=t
получаем:
g(t)=tln(1+t2)g(t)=tln(1+t^2)
Используя разложение логарифмической функции, получаем:
g(t)=t(t21!−(t2)22!+(t2)33!+o((t2)3))=t3−t52+t76+o(t7)g(t)=t left( dfrac{t^2}{1!}-dfrac{(t^2)^2}{2!}+dfrac{(t^2)^3}{3!}+o((t^2)^3) right)=t^3-dfrac{t^5}{2}+dfrac{t^7}{6}+o(t^7)
Выполняем далее обратную замену переменной:
f(x)=(x+1)3−(x+1)52+(x+1)76+o((x+1)7)f(x)= (x+1)^3-dfrac{(x+1)^5}{2}+dfrac{(x+1)^7}{6}+o((x+1)^7)
Пример 2
Разложим, используя формулу Тейлора, функцию
f(x)=(x2−4x)cos(2x−4)f(x)=(x^2-4x)cos{(2x-4)}
в окрестности точки x0=2x_0=2 с точностью до o((x−5)5)o((x-5)^5).
Выполнив замену переменной:
x−x0=x−2=t,x=t+2x-x_0=x-2=t, quad x=t+2
получаем:
g(t)=(t2−4)cos2tg(t)=(t^2-4)cos{2t}
Используя разложение тригонометрической функции, получаем:
g(t)=(t2−4)(1−(2t)22!−(2t)44!+o(t5))=(t2−4)(1−2t2+2t43+o(t5))g(t) =(t^2-4) left( 1-dfrac{(2t)^2}{2!}-dfrac{(2t)^4}{4!}+o(t^5) right) =(t^2-4) left( 1-2t^2+dfrac{2t^4}{3}+o(t^5) right)
Раскрываем скобки, ограничиваясь слагаемыми со степенью t не выше пяти:
g(t)=(t2−2t4)−(4−8t2+8t43+o(t5))=−4+9t2−143t4+o(t5)g(t) =(t^2-2t^4)- left( 4-8t^2+dfrac{8t^4}{3}+o(t^5) right) =-4+9t^2-dfrac{14}{3} t^4+o(t^5)
Выполняя обратную замену переменной, получаем:
f(x)=−4+9(x−2)2−143(x−2)4+o((x−2)5)f(x)=-4+9(x-2)^2-dfrac{14}{3}(x-2)^4+o((x-2)^5)
Применение формулы Тейлора при x, стремящемся к бесконечности
При необходимости представить функцию с помощью формулы Тейлора при x→∞x to infty с точностью до o(1xn)oleft( dfrac {1} {x^n}right), последовательно:
- выполняем замену переменной t=1xt=dfrac{1}{x};
- полученную функцию g(t)g(t) представляем с помощью формулы Тейлора с необходимой точностью;
- с помощью обратной замены переменных находим искомое выражение для f(x)f(x).
Пример
Разложим, используя формулу Тейлора, функцию
f(x)=2x−x2−1f(x)=2x-sqrt{x^2-1}
с точностью до o(1×3)oleft( dfrac {1} {x^3}right) при x→+∞x to +infty.
Выполнив замену переменной
t=1x,x=1tt=dfrac{1}{x}, quad x=dfrac{1}{t}
получаем:
g(t)=2t−1t2−1=2−(1−t2)1/2tg(t)=dfrac {2}{t}-sqrt {dfrac{1}{t^2}-1}=dfrac{2-(1-t^2)^{1/2}}{t}
Учитывая требуемую точность o(t3)o(t^3), используем разложение степенной функции в ряд Тейлора с точностью до o(t4)o(t^4):
g(t)=2−(1−t22−t48)+o(t4)t=1t+t2−t38+o(t3)g(t)=dfrac {2-left( 1-dfrac{t^2}{2}-dfrac{t^4}{8}right)+o(t^4)}{t}=dfrac{1}{t}+dfrac{t}{2}-dfrac{t^3}{8}+o(t^3)
Выполняя обратную замену переменной, находим:
f(x)=x+12x−18×3+o(1×3),x→+∞f(x)=x+dfrac{1}{2x}- dfrac {1}{8x^3}+ oleft( dfrac {1} {x^3}right), quad x to +infty
Применение формула Тейлора при вычислении пределов
С помощью разложения функции с использованием формулы Тейлора при вычислении пределов можно избавиться от неопределённостями различного вида. Проиллюстрируем использование формулы Тейлора на примере вычисления предела функции с неопределенностью вида (00)left( dfrac {0} {0}right).
Пример 1
Вычислим, используя формулу Тейлора, предел:
limx→1ex−ecos(x−1)sin(x−1)limlimits_{x to 1 } dfrac {e^{x}-e cos{(x-1)}}{sin {(x-1)}}
Заменим ex{e^{x}} и тригонометрические функции их разложениями в степенные ряды в окрестности x0=1x_0=1, находим:
limx→1ex−ecos(x−1)sin(x−1)=limx→1(e+e(x−1)+e(x−1)22!+e(x−1)33!+…)−e(1−(x−1)22!+…)(x−1)−(x−1)33!+…=elimx→1(x−1)+(x−1)2+(x−1)36+…(x−1)−(x−1)36+…=elimx→11+(x−1)+(x−1)26+…1−(x−1)26+…=elimlimits_{x to 1 } dfrac {e^{x}-e cos{(x-1)}}{sin {(x-1)}}=limlimits_{x to 1} dfrac {left(e+e(x-1)+dfrac{e(x-1)^2}{2!}+dfrac{e(x-1)^3}{3!} +ldots right)-eleft( 1-dfrac{(x-1)^2}{2!}+ ldots right)} {(x-1)-dfrac{(x-1)^3}{3!}+ ldots}= elimlimits_{x to 1 } dfrac {(x-1)+(x-1)^2+ dfrac{(x-1)^3}{6}+ldots} {(x-1)- dfrac{(x-1)^3}{6}+ldots} =e limlimits_{x to 1 } dfrac {1+(x-1) +dfrac{(x-1)^2}{6}+ldots} {1- dfrac{(x-1)^2}{6}+ldots} =e
Тест по теме «Формула и ряд Тейлора»
Введение
Теория функций комплексной переменной (ТФКП) дошла до наших дней почти в том виде, в котором оставил нам ее создатель великий французский математик Огюстен Коши (1789–1857 гг.).
ТФКП как продолжает, так и расширяет идеи математического анализа функций действительной переменной. Обычные определения, известные из алгебры чисел и математического анализа функций действительной переменной, остаются почти без изменений, но их содержание меняется весьма существенным образом. Хорошо известно, что уже обычные простейшие операции над действительными числами могут вывести за пределы их области. И решения большинства алгебраических уравнений не могут быть выражены только обычными действительными числами. Поэтому приходится расширять область действительных чисел, а таким расширением этой области и является область комплексных чисел.
Основное понятие комплексного анализа аналитическая функция. Это понятие позволяет доказать теоремы о существовании производных любого порядка от этих функций, о независимости интегралов от формы пути интегрирования. Позволяет сравнительно единообразно вычислять сложные интегралы с помощью вычетов и многое другое.
В данных методических указаниях изложены основные вопросы теории функций комплексной переменной в соответствии с действующими рабочими программами для студентов всех направлений подготовки бакалавров инженерно-технических специальностей вуза.
Каждый из выделенных параграфов содержит краткое изложение основных теоретических сведений, практическое руководство по решению стандартных математических задач. В конце предлагаются варианты заданий для расчетно-графической работы.
1. Функциональные ряды в комплексной области.
Степенные ряды
Пусть 
. Функциональным рядом в комплексной области называется выражение

где . Функции

называются членами ряда. Функциональный ряд (1) называется сходящимся в точке


, если сходится числовой ряд

точек, в которых функциональный ряд (1) сходится, называется областью сходимости ряда, а функция

– суммой функционального ряда (1).
Функциональный ряд вида

где ,

– комплексная переменная, называется степенным рядом в комплексной области. Числа

– его центром.
Область определения степенного ряда – вся комплексная плоскость. Очевидно, что в точке 
Теорема 1 (Абеля). Если степенной ряд (2) сходится в точке , то он сходится абсолютно при любом
, удовлетворяющем условию

Областью сходимости ряда (2) является круг с центром в точке . Радиус сходимости степенного ряда может быть найден по формулам:


если указанные пределы существуют.
Если 
Если 
, а в его внешности, т. е. во всей комплексной плоскости, кроме точки
, ряд расходится.
На окружности 
Пример 1.1. Найти радиус сходимости степенного ряда: 
Решение. Воспользуемся формулой (3). Имеем


Пример 1.2. Найти круг сходимости степенного ряда: 
Решение. Воспользуемся формулой (4). Имеем



Следовательно, 
2. Разложение функций в ряд Тейлора
Теорема 2 (о разложении аналитической функции в степенной ряд). Пусть – аналитическая функция в области
,

– расстояние от
до границы
. Тогда в круге
функция
разлагается в степенной ряд


называемый рядом Тейлора функции . При этом коэффициенты ряда удовлетворяют соотношениям

при любых ,

Первый отличный от нуля член ряда Тейлора называется главным членом разложения в ряд Тейлора, а его степень – порядком главного члена.
Из этой теоремы следует еще одно определение аналитической функции.
Функция называется аналитической в точке
, если она разлагается в степенной ряд в некоторой окрестности точки
.
Функция называется аналитической в области
, если она разлагается в степенной ряд в некоторой окрестности каждой точки
.
Ряды Тейлора некоторых элементарных функций:

; (7)

; (8)

; (9)

; (10)

; (11)

. (12)
Формула (12) называется суммой бесконечной геометрической прогрессии и является следствием (11) при 
Пример 2.1. Разложить функцию 
и определить радиус сходимости ряда.
Решение. Найдем коэффициенты ряда Тейлора, пользуясь формулой (5):

Таким образом

Поскольку функция аналитична на всей комплексной плоскости, то по теореме 2 этот ряд сходится также при всех

Пример 2.2. Разложить функцию 
и определить радиус сходимости ряда.
Решение. Преобразуем данную функцию:

Обозначим 
при
. Получим:

Из условия следует, что полученный ряд сходится при


Пример 2.3. Разложить функцию 
и определить радиус сходимости ряда.
Решение. Найдем нули знаменателя дроби: 
. Так как

, то данная функция аналитична в круге
как частное двух аналитических функций. Представим данную функцию в виде суммы простейших дробей:

Каждое слагаемое разложим в ряд по степеням , пользуясь формулой (12):

,

.
Складывая полученные разложения и учитывая аналитичность функции в круге
, получаем:

.
Пример 2.4. Разложить функцию 
и определить радиус сходимости ряда.
Решение. Преобразуем данную функцию и воспользуемся разложением (9):

Полученный ряд сходится на всей комплексной плоскости, так как ряд (9) сходится при всех 
3. Ряд Лорана
Рядом Лорана называется выражение

где ,

, если на этом множестве сходятся оба функциональных ряда:

и

Суммой ряда Лорана (13) называется сумма 
и

, если на этом множестве абсолютно сходятся ряды (14) и (15).
Ряды Лорана позволяют изучать функции, аналитические в кольцах , где
,
.
Теорема 3 (о сходимости ряда Лорана). Ряд Лорана сходится абсолютно внутри кольца , где
– радиус сходимости степенного ряда (15), а


если .
Теорема 4 (Лорана). Функция , аналитическая в кольце
, представляется в этом кольце сходящимся рядом Лорана

где

,
.
Главная часть ряда Лорана сходится во внешности круга с центром в точке и радиусом
, где
, как и в случае степенных рядов, может быть найден (если существуют соответствующие пределы) по формулам:

или
. (19)
При эта область вырождается в в несобственную точку
, а при
– во всю плоскость, за исключением, возможно,

Пример 3.1. Найти область сходимости ряда 
Решение. Найдем круг сходимости правильной части ряда, т. е. ряда 

то это круг . Для ряда

представляющего собой главную часть данного ряда,

поэтому его область сходимости 

Пример 3.2. Разложить функцию 

Решение. Записав функцию в виде

замечаем, что данная функция является аналитической на всей комплексной плоскости, за исключением точек 
, в которых знаменатель дроби обращается в нуль. Эти точки лежат на границе данного кольца

Рис. 1
Это означает, что в самом кольце функция аналитическая и, следовательно, по теореме 4 разлагается в ряд Лорана с центром в точке . Для получения этого разложения представим функцию в виде
, где


Функция аналитична в большем круге
. Разложим ее в ряд Тейлора с центром в точке
. Преобразуем
следующим образом:

Положим 

.
Функция 
, но этот ряд сходится лишь в круге

следующим образом:

Положим 

Этот ряд сходится при 
. Окончательно получаем:

.
Пример 3.3. Найти все возможные разложения в ряд Лорана по степеням функции

Решение. Данная функция является аналитической на всей комплексной плоскости, за исключением точек 
, в которых знаменатель дроби обращается в нуль. Следовательно, по теореме 4 она разлагается в ряд Лорана в любом кольце с центром в точке
, не содержащем точку
. Получаем два кольца:

. Найдем разложение функции в ряд Лорана в кольце
. Имеем

В кольце :

Таким образом, получены два разложения данной функции в ряд Лорана по степеням :

,

.
4. Изолированные особые точки аналитических функций
Точка 
, если функция
аналитична в этой точке. Если функция
не является аналитической в точке
, но аналитична в некоторой ее проколотой окрестности
, то точка
называется изолированной особой точкой функции
.
Так как проколотую окрестность точки можно рассматривать как частный случай кольца, то функция
разлагается в нем в ряд Лорана по степеням
. В зависимости от вида этого ряда различают три типа изолированных особых точек.
Изолированная особая точка для функции
называется
1) устранимой, если указанный ряд Лорана содержит только правильную часть:
;
2) полюсом, если главная часть ряда Лорана содержит лишь конечное число членов:

причем ,
. Число
называется порядком полюса, при
полюс называется простым.
3) существенно особой, если главная часть ряда Лорана содержит бесконечное число членов:

причем для бесконечного числа отрицательных номеров
.
Во многих вопросах комплексного анализа удобно рассматривать расширенную комплексную плоскость, т. е. плоскость, дополненную символической точкой .
Точка 
, если
аналитична в области

является изолированной особой точкой функции


или существенно особой точкой функции
в зависимости от того, является ли точка
устранимой особой точкой, полюсом порядка
или существенно особой точкой функции

Разложим 
и произведем замену переменной 

который называется рядом Лорана функции в окрестности бесконечно удаленной точки. Ряд


в окрестности бесконечно удаленной точки. Если главная часть разложения отсутствует, то точка



. При этом, если

функции

является нулем порядка
функции
.
Теорема 5 (о связи между нулем и полюсом). Точка является полюсом порядка
функции
тогда и только тогда, когда она является нулем порядка
функции

Теорема 6 (о существенно особой точке). Если существует окрестность существенно особой точки аналитической функции
, в которой
, то точка
является существенно особой и для функции

Теорема 7 (Сохоцкого). Если – существенно особая точка функции
, то для любого


, сходящаяся к точке
, такая что

Функция, аналитическая на всей комплексной плоскости, называется целой. Целая функция, для которой точка 
всюду, кроме полюсов, называется мероморфной в
.
На практике при определении вида особых точек часто бывает полезен следующий простой факт:
если – нуль порядка
аналитической функции
, а функция
аналитична в точке
и
, то
– полюс порядка
функции

Пример 4.1. Найти изолированные особые точки функции 
Решение. Данная функция представляет собой частное двух аналитических на всей комплексной плоскости функций, поэтому ее особыми точками могут быть только нули знаменателя. Найдем их:

,

Причем они являются простыми нулями.
Так как числитель ни в одной из этих точек не обращается в нуль, то по теореме 5 точки 
,

Пример 4.2. Найти изолированные особые точки функции 
Решение. Данная функция как частное двух аналитических на всей комплексной плоскости функций может иметь особой точкой только нуль знаменателя, т. е. . Однако точка
является также и нулем числителя. Поэтому для выяснения вида особенности разложим функцию в ряд Лорана по степеням
:

Ряд не содержит отрицательных степеней , поэтому
– устранимая особая точка.
Пример 4.3. Найти изолированные особые точки функции 
Решение. Данная функция определена и дифференцируема на всей комплексной плоскости, за исключением точки . Это изолированная особая точка. Запишем ряд Лорана для функции
в окрестности точки
, пользуясь разложением (7) для функции
, полагая
:

Ряд содержит бесконечно много членов с отрицательными степенями. Поэтому точка – существенно особая.
Пример 4.4. Найти изолированные особые точки функции 
Решение. Данная функция есть частное двух аналитических на всей комплексной плоскости функций. Поэтому ее особыми точками являются нули знаменателя:

.
Так как числитель дроби в нуль не обращается, то эти точки являются полюсами. Определим порядки полюсов по порядкам нулей функции

Вычислим:
,


,


Следовательно, точки 
) являются нулями второго порядка функции
и, по теореме 5, полюсами второго порядка функции
.
Вид изолированной особенности характеризует поведение функции в окрестности этой особенности:
если – устранимая особая точка функции
, то существует конечный предел функции
в точке
;
если – полюс, то

если же – существенно особая точка, то указанного предела не существует.
Эти свойства являются характеристическими, т. е. справедливы и обратные утверждения.
Пример 4.5. Найти изолированные особые точки функции 
Решение. Единственная особая точка данной функции – (см. пример 4.2). Так как

т. е. функция имеет конечный предел в точке , то
является устранимой особой точкой данной функции.
5. Вычеты и их применение
Пусть – изолированная особая точка однозначной аналитической функции
и
– окружность


, кроме точки
. Интеграл от функции
по такой окружности
, деленный на
, называется вычетом функции
в точке
и обозначается

Таким образом, по определению

Вычислять вычеты, исходя из определения, довольно трудно. Поэтому на практике применяются следующие утверждения:
Теорема 8 (о вычете относительно изолированной особой точки). Вычет функции в изолированной особой точке
равен коэффициенту при

:
.
Если точка – полюс, то для определения вычета иногда можно и не находить разложение функции в ряд Лорана. Имеются более простые способы.
Теорема 9 (о вычете относительно полюса). Пусть – полюс порядка
функции
. Тогда

Следствие. Если – простой полюс функции
, то
. (21)
Вычисление вычета в простом полюсе еще более упрощается, если имеет вид:

где ,

. Тогда

Пример 5.1. Вычислить вычеты функции 
Решение. В примере 4.3 установлено, что точка – существенно особая точка данной функции, и получено разложение функции в ряд Лорана в окрестности этой точки:

следовательно,

Пример 5.2. Вычислить вычеты функции 
Решение. Особыми точками данной функции являются нули знаменателя – простой полюс и
– полюс второго порядка. Найдем вычет относительно точки
по формуле (21):

Для определения вычета относительно точки воспользуемся формулой (20) при


Теория вычетов находит широкое применение благодаря следующему утверждению:
Теорема 10 (о вычетах). Пусть функция является аналитической в области
всюду, за исключением конечного числа точек
,
. Пусть замкнутый контур
содержится в области
и не проходит через особые точки. Тогда интеграл от функции
по контуру
равен сумме вычетов функции относительно всех особых точек
(

, умноженной на
:

Теорема 11 (о вычетах на расширенной комплексной плоскости). Пусть функция является аналитической на расширенной комплексной плоскости, кроме конечного числа точек

,
,…,
. Тогда

Пример 5.3. Вычислить интеграл 
Решение. Особыми точками подынтегральной функции 
,

. Из них внутри окружности
лежат только две:

. Поэтому по теореме 10

Обе эти точки являются для данной функции простыми полюсами. Воспользуемся формулой (22):


Следовательно,

Пример 5.4. Вычислить интеграл 
Решение. Внутри окружности 
и

:

Для определения вычета в точке 
, тогда

Так как функция аналитична в круге
, то ее можно разложить в этом круге в степенной ряд:
,
.
Тогда

или

.
В полученном разложении коэффициент при равен нулю, т. е.


Варианты заданий для РГР
Задание 1. Разложить функцию в ряд по степеням

1. а) ,


.
2. а) ,


.
3. а) ,


.
4. а) ,


.
5. а) ,


.
6. а) ,


.
7. а) ,


.
8. а) ,


.
9. а) ,


.
10. а) 
; б)

.
11. а) 
; б)

.
12. а) 
; б)

.
13. а) 
; б)

.
14. а) 
; б)

.
15. а) 


.
16. а) 
; б)

.
17. а) 
; б)

.
18. а) 
; б)

.
19. а) 
; б)

.
20. а) 
; б)

.
21. а) 
; б)

.
22. а) 
; б)

.
23. а) 
; б)

.
24. а) 
; б)

.
25. а) 
; б)

.
26. а) 
; б)

.
27. а) 
; б)

.
28. а) 
; б)

.
29. а) 
; б)

.
30. а) 
; б)

.
Задание 2. Разложить функцию в ряд Лорана в указанном кольце.
1. 
;
2. 
;
3. 
;
4. 
;
5. 
;
6. 
;
7. 
;
8. 
;
9. 
;
10. 
;
11. 
;
12. 
;
13. 
;
14. 
;
15. 
;
16. 
;
17. 
;
18. 
;
19. 
;
20. 
;
21. 
;
22. 
;
23. 
;
24. 
;
25. 
;
26. 
;
27. 
;
28. 
;
29. 
;
30. 
.
Задание 3. Найти все возможные разложения функции в ряд Лорана по степеням

1. 
;
2. 
;
3. 
;
4. 
;
5. 
;
6. 
;
7. 
;
8. 
;
9. 
;
10. 
;
11. 
;
12. 
;
13. 
;
14. 
;
15. 
;
16. 
;
17. 
;
18. 
;
19. 
;
20. 
;
21. 
;
22. 
;
23. 
;
24. 
;
25. 
;
26. 
;
27. 
;
28. 
;
29. 
;
30. 
.
Задание 4. Найти изолированные особые точки функции и определить их вид.
1. 
2. 
3. 
4. ;
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. ;
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
Задание 5. Вычислить вычеты функции относительно каждой из ее особых точек.
1. 
2. 
3. 
4. 
5. 
6. ;
7. ;
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
Задание 6. Вычислить интеграл.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
Литература
1. Волковыский Л. И., Лунц Г. Л., Араманович И. Г. Сборник задач по теории функций комплексного переменного. – М.: ФИЗМАТЛИТ, 2004.
2. Леонтьева Т. А. Лекции по теории функций комплексного переменного. – М.: Научный мир. 2004.
3. Лунц Г. Л., Эльсгольц Л. Э. Функции комплексного переменного (с элементами операционного исчисления). – М.: Лань, 2002.
4. Морозова В. Д. Теория функций комплексного переменного. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2009.
5. Пантелеев А. В., Якимова А. С. Теория функций комплексного переменного и операционное исчисление в примерах и задачах. – М.: Вузовская книга, 2012.
6. Письменный Д. Т. Конспект лекций по высшей математике, 1, 2 часть. – М.: 2004.
7. Письменный Д. Т. Сборник задач по высшей математике, 1, 2 часть. – М.: 2004.
8. Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. – М.: ФИЗМАТЛИТ, 2005.
9. Шабунин М. И. Сборник задач по теории функций комплексного переменного. – М.: БИНОМ. Лаборатория знаний. 2006.
Антоненкова О. Е., Часова Н. А.
МАТЕМАТИКА
Теория функций
комплексной переменной
Методические указания и задания к расчетно-графической работе
для студентов всех направлений подготовки бакалавров
очной формы обучения
Формат Объем Тираж Заказ
Брянск, Станке Димитрова 3, Редакционно-издательский отдел
Отпечатано: Печатный цех БГИТА
Наташа — контент-маркетолог и блогер, но все это не мешает ей оставаться адекватным человеком. Верит во все цвета радуги и не верит в теорию всемирного заговора. Увлекается «нефрохиромантией» и тайно мечтает воссоздать дома Александрийскую библиотеку.
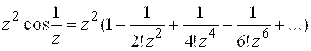



















![{displaystyle R_{n}(x)={(x-a)^{n+1} over (n+1)!}f^{(n+1)}[a+theta (x-a)]qquad p=n+1;qquad 0<theta <1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a9581ea19ed64de9723d6f3725f0470e9a0f23c)
![{displaystyle R_{n}(x)={(x-a)^{n+1}(1-theta )^{n} over n!}f^{(n+1)}[a+theta (x-a)]qquad p=1;qquad 0<theta <1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/616cdc3cb043af06990a174a073b35ea0e3fbee1)

![{displaystyle R_{n}(x)=o[(x-a)^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7eca3be3644e41dedb8f25e26357ddb9a08386d)



![R_n(x,y)=dfrac {mathrm{T}^{(n+1)} f(xi,zeta)} {(n+1)!}, xi in [x_0,x], zeta in [y_0,y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/144e134c30b8d4c579305c2bbaf6591647deb6c9)





















