Сфера, вписанная в пирамиду

Биссекторная плоскость. Основное свойство биссекторной плоскости
Определение 1. Биссекторной плоскостью двугранного угла называют такую плоскость, которая проходит через ребро двугранного угла и делит этот угол на два равных двугранных угла (рис. 1).
Утверждение 1. Точка, расположенная внутри двугранного угла, находится на одном и том же расстоянии от граней этого угла тогда и только тогда, когда она лежит на биссекторной плоскости.
Доказательство. Рассмотрим произвольную точку O, расположенную внутри двугранного угла, и проведем через эту точку плоскость δ , перпендикулярную к ребру AB двугранного угла (рис. 2).
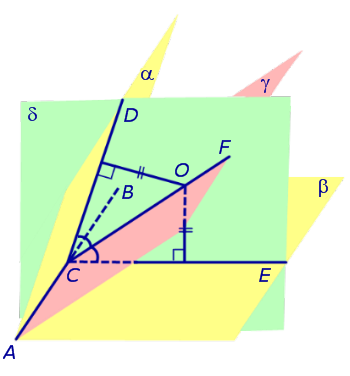
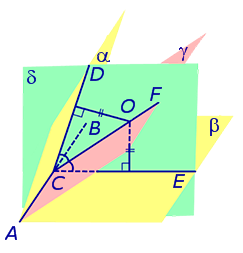
Плоскость δ пересекает ребро AB двугранного угла в точке C, а грани двугранного угла α и β по лучам CD и CE соответственно. Угол DCE является линейным углом двугранного угла. Биссекторная плоскость γ пересекает плоскость δ по биссектрисе CF линейного угла DCE .
Таким образом, справедливость утверждения вытекает из соответствующих теорем о свойствах биссектрисы угла. Доказано.
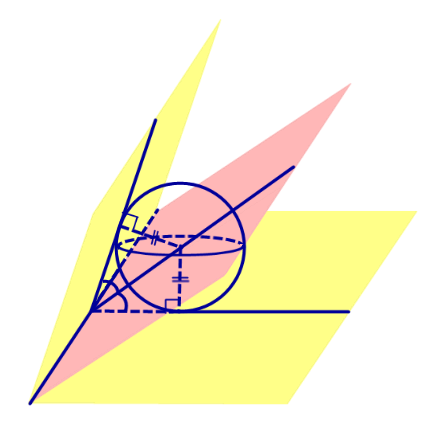
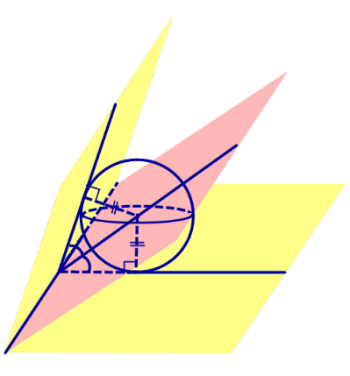
Следствие 1. Если сфера, расположенная внутри двугранного угла, касается каждой из плоскостей граней этого угла, то центр сферы находится на биссекторной плоскости двугранного угла (рис. 3).

Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы
Определение 2. Сферой, вписанной в пирамиду, называют такую сферу, которая касается плоскостей всех граней пирамиды, причем точки касания лежат на гранях пирамиды (рис. 4).
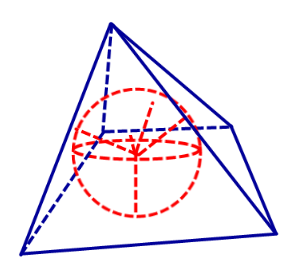

Определение 3. Если сфера вписана в пирамиду, то пирамиду называют описанной около сферы.
Если сфера вписана в пирамиду, то она касается граней каждого внутреннего двугранного угла, образованного соседними гранями пирамиды. В соответствии со следствием 1 центр вписанной в пирамиду сферы должен находиться в точке пересечения биссекторных плоскостей всех внутренних двугранных углов, образованных соседними гранями пирамиды.
Если у пирамиды нет точки, в которой пересекаются биссекторные плоскости всех внутренних двугранных углов, образованных соседними гранями пирамиды, то в такую пирамиду нельзя вписать сферу.
Замечание 1. Для того, чтобы проверить, можно ли в пирамиду вписать сферу, достаточно проверить, существует ли точка пересения биссекторных плоскостей всех внутренних двугранных углов при основании пирамиды. Если такая точка существует, то она будет равноудалена как от основания пирамиды, так и от каждой из боковых граней.
Рассмотрим несколько типов пирамид, в которые можно вписать сферу.
Утверждение 2. Если у пирамиды SA1A2 . An основание O перпендикуляра, опущенного из вершины S на плоскость основания пирамиды, лежит внутри многоугольника A1A2 . An , а все боковые грани пирамиды наклонены под одним и тем же углом к плоскости основания пирамиды, то в такую пирамиду можно вписать сферу.
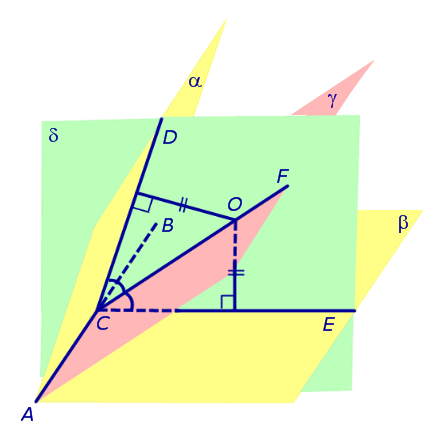
Доказательство. Пусть все боковые грани пирамиды наклонены к плоскости основания под углом φ , а высота пирамиды равна h. Рассмотрим, например, боковую грань SA1A2 и проведем в ней высоту SB (рис. 5).
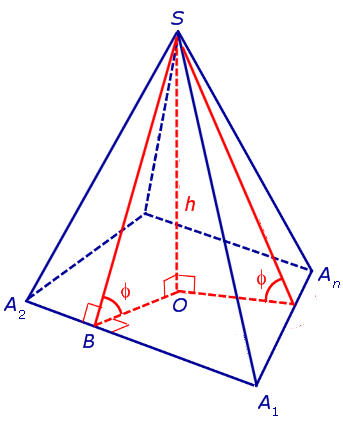
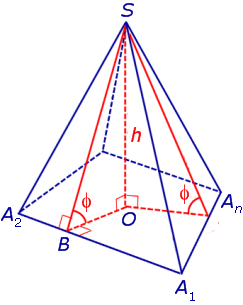
По теореме о трех перпендикулярах отрезок OB перпендикулярен ребру A1A2 . Следовательно, угол SBO является линейным углом двугранного угла между боковой гранью SA1A2 и плоскостью основания пирамиды и равен φ. Биссекторная плоскость этого двугранного угла пересекает высоту пирамиды в точке O’ (рис. 6).
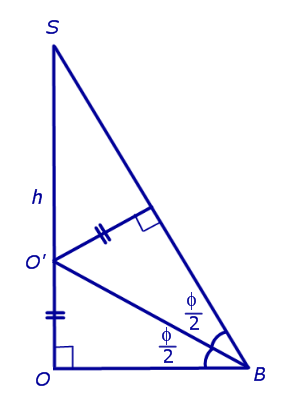
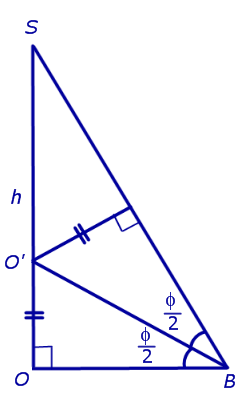
Катет OB прямоугольного треугольника SOB выражается через высоту пирамиды h и угол φ по формуле
Катет OO’ прямоугольного треугольника OO’B выражается через высоту пирамиды h и угол φ по формуле
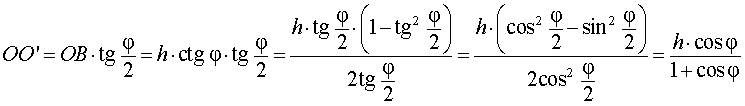
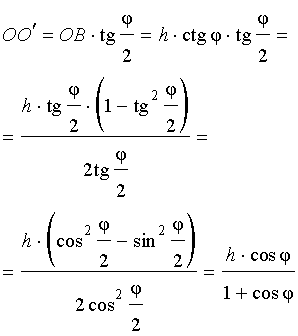
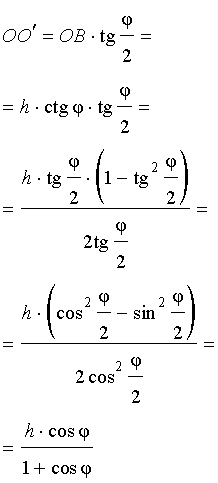
Поскольку длина отрезка OO’ не зависит от выбора боковой грани пирамиды, то биссекторные плоскости всех внутренних двугранных углов при основании пирамиды пересекаются в точке O’, которая и является центром вписанной в пирамиду сферы.
Доказательство утверждения 2 завершено.
Поскольку у любой правильной пирамиды все внутренние двугранные углы при основании равны, то справедливо
Следствие 2. В любую правильную пирамиду можно вписать сферу, причем ее радиус R выражается через высоту пирамиды h и внутренний двугранный угол при основании пирамиды φ по формуле
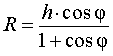 |
(1) |
Радиус сферы, вписанной в правильную n – угольную пирамиду
Решение. Рассмотрим правильную n – угольную пирамиду SA1A2 . An и обозначим символом O’ центр вписанной в пирамиду сферы, а буквой O – центр основания пирамиды. Проведем плоскость через высоту пирамиды SO и апофему SB какой-либо боковой грани (рис. 7).
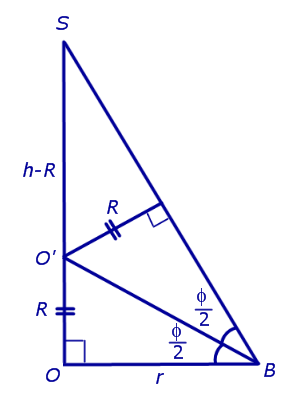
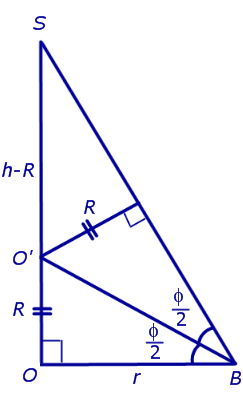
Буквой R на рисунке 7 обозначен радиус вписанной в пирамиду сферы, буквой r – радиус вписанной в основание пирамиды окружности, а буквой φ – внутренний двугранный угол при основании пирамиды. Из прямоугольного треугольника OSB получаем
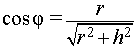 |
(2) |
В силу следствия 2 из формул (1) и (2) получаем
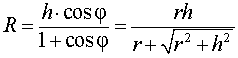
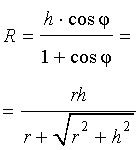
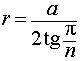
из формулы (3) получаем соотношение
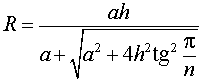
Ответ. 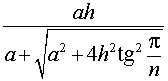
Следствие 3. Радиус сферы, вписанной в правильную треугольную пирамиду с высотой h и ребром основания a, равен
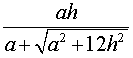
Следствие 4. Радиус сферы, вписанной в правильный тетраэдр с ребром a, равен
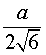
Следствие 5. Радиус сферы, вписанной в правильную четырехугольную пирамиду с высотой h и ребром основания a, равен
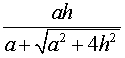
Следствие 6. Радиус сферы, вписанной в правильную шестиугольную пирамиду с высотой h и ребром основания a, равен
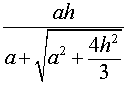
Сфера, вписанная в треугольную пирамиду.
Формула для радиуса вписанной сферы
Утверждение 3. В любую треугольную пирамиду можно вписать сферу.
Доказательство. Доказательство этого утверждения напоминает планиметрическое доказательство возможности вписать окружность в произвольный треугольник.
Действительно, пусть SABC – произвольный тетраэдр. Биссекторная плоскость внутреннего двугранного угла с ребром AC и биссекторная плоскость внутреннего двугранного угла с ребром AB пересекаются по некоторой прямой, проходящей через вершину A. Биссекторная плоскость внутреннего двугранного угла в ребром BC пересекает эту прямую в единственной точке O , которая и является центром вписанной сферы (рис. 8).
Получим формулу, позволяющую вычислить радиус вписанной в тетраэдр SABC сферы. Для этого заметим, что объем пирамиды SABC равен сумме объемов пирамид OABC, OSCA, OSAB, OSCB, причем высота каждой из пирамид OABC, OSCA, OSAB, OSCB равна радиусу R вписанной в пирамиду SABC сферы. Если обозначить площади граней тетраэдра SABC символами
а объемы пирамид SABC, OABC, OSCA, OSAB, OSCB – символами
то справедливы следующие равенства:
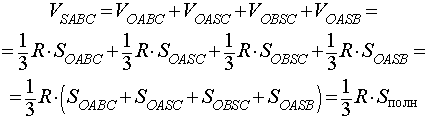
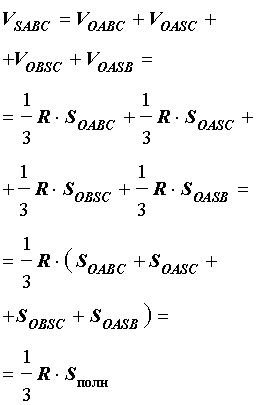
где символом Sполн обозначена площадь полной поверхности пирамиды SABC.
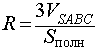
Замечание 2. Если в пирамиду (необязательно треугольную) можно вписать сферу, то, рассуждая аналогично, можно получить следующую формулу для радиуса вписанной в пирамиду сферы
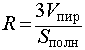
где символами Vпир и Sполн обозначены объем и площадь полной поверхности пирамиды соответственно.
Центр вписанной окружности в тетраэдре
ТЕТРАЭДР. ВИДЫ ТЕТРАЭДРОВ
Тетраэдр является одним из простейших многогранников, гранями которого являются четыре треугольника. Его можно считать пространственным аналогом треугольника. Рассмотрим свойства треугольников и аналогичные им свойства тетраэдров.
Теорема 1. Биссектрисы треугольника пересекаются в одной точке – центре вписанной окружности.
Теорема 1′. Биссектральные плоскости двугранных углов тетраэдра пересекаются в одной точке – центре вписанной сферы.
Доказательство. Пусть ABCD – тетраэдр. Пересечением биссектральных плоскостей двугранных углов с ребрами AB, AC,и BC (рис. 1) является точка O, равноудаленная от всех граней тетраэдра. Следовательно, эта точка принадлежит биссектральным плоскостям остальных двугранных углов тетраэдра и является центром вписанной сферы.
Теорема 2. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке – центре описанной окружности.
Теорема 2′. Плоскости, проходящие через середины ребер тетраэдра и перпендикулярные этим ребрам, пересекаются в одной точке – центре описанной сферы.
Доказательство. Пусть ABCD – тетраэдр. Пересечением плоскостей, проходящих через середины ребер AD, BD, и CD является точка O, равноудаленная от всех вершин тетраэдра. Следовательно, эта точка принадлежит остальным плоскостям и является центром описанной сферы.
Теорема 2″. Прямые, перпендикулярные граням тетраэдра, и проходящие через центры их описанных окружностей, пересекаются в одной точке – центре описанной сферы.
Доказательство. Каждая такая прямая является геометрическим местом точек, равноудаленных от вершин соответствующей грани тетраэдра. Поэтому центр описанной сферы будет принадлежать всем этим прямым.
Заметим, что не у всякого тетраэдра прямые, проходящие через центры вписанных в грани окружностей и перпендикулярные этим граням, пересекаются в одной точке. Ответ на то, когда это происходит, дает следующая теорема.
Теорема 2”’. У тетраэдра существует сфера, касающаяся всех его ребер, тогда и только тогда, когда суммы противоположных ребер этого тетраэдра равны.
Доказательство. Пусть у тетраэдра ABCD существует сфера, касающаяся его ребер. Обозначим через a, b, c и d расстояния от соответствующих вершин тетраэдра до точек касания. Тогда AB = a + b, CD = c + d. Следовательно, AB + CD = a + b + c + d. Аналогично, AC + BD = a + b + c + d, AD + BC = a + b + c + d. Таким образом, суммы противоположных ребер тетраэдра равны.
Обратно. Предположим, что суммы противоположных ребер тетраэдра ABCD равны. Впишем в треугольник ABC окружность. Обозначим через X точку касания этой окружности стороны AB (рис. 2) .
Тогда AX = (AB + AC – BC):2. Так как AC – BC = AD – BD, то AX = (AB + AD – BD):2. Следовательно, точка X является точкой касания окружности, вписанной в треугольник ABD . Через центры этих двух окружностей проведем перпендикуляры. Они лежат в одной плоскости, проходящей через X и перпендикулярной AB. Точка O их пересечения будет равноудалена от сторон треугольников ABC и ABD. Таким образом, любые два перпендикуляра, проходящие через центры окружностей, вписанных в грани тетраэдра, пересекаются. Из этого следует, что или они лежат в одной плоскости, или пересекаются в одной точке. Поскольку они не лежат в одной плоскости, то значит, они пересекаются в одной точке O , равноудаленной от всех ребер тетраэдра, т.е. O – центр сферы, касающейся всех ребер данного тетраэдра.
Теорема 3. Медианы треугольника пересекаются в одной точке, называемой центроидом треугольника и делятся в этой точке в отношениии 2 : 1.
Теорема 3′. Отрезки, соединяющие вершины тетраэдра с точками пересечения медиан противоположных граней, пересекаются в одной точке – центроиде тетраэдра и делятся в этой точке в отношении 3 : 1, считая от вершины.
Доказательство. Пусть ABCD – тетраэдр, O – точка пересечения медиан треугольника ABC, P – точка пересечения медиан треугольника BCD, R – точка пересечения отрезков DO и AP (рис. 3) .
Рассмотрим треугольник AQD. Точки O и P делят соответствующие стороны в отношении 2 : 1. Покажем, что точка R делит DO и AP в отношении 3 : 1. В треугольнике APQ проведем OS параллельно AP. Она разделит отрезок PQ в отношении 2 : 1. Если отрезок SQ принять за единицу, то отрезок DP будет равен 6. Отрезки DR и RQ относятся также как DP и PS, т.е. DR : RQ = 6 : 2 = 3 : 1. Аналогичным образом доказывается, что точка R делит отрезок AP в отношении 3 : 1. Отрезки, соединяющие вершины B и C с точками пересечения медиан противоположных граней также будут делить отрезок DO в отношении 3 : 1 и, следовательно, будут проходить через точку O . Что и требовалось доказать.
Теорема 4. Отрезки, соединяющие середины противоположных ребер тетраэдр, пересекаются в одной точке – центроиде.
Доказательство. Достаточно заметить, что в предыдущем доказательстве медиана треугольника AQD, проведенная из вершины Q, проходит через центроид O .
Теорема 5. Для цетроида O треугольника ABC имеет место равенство .
Теорема 5′. Для цетроида O тетраэдра ABCD имеет место равенство .
Теорема 6. Пусть a произвольная прямая, проходящая через центроид треугольника ABC. Будем считать одну из полуплоскостей, на которые эта прямая разбивает плоскость, положительной, а другую отрицательной. Тогда сумма расстояний от вершин треугольника до прямой a, взятых со знаком + или – в зависимости от того, какой полуплоскости принадлежит вершина, равна нулю.
Теорема 6′. Пусть произвольная плоскость, проходящая через центроид тетраэдра ABCD. Будем считать одно из полупространств, на которые эта плоскость разбивает пространство, положительным, а другое отрицательным. Тогда сумма расстояний от вершин тетраэдра до плоскости , взятых со знаком + или – в зависимости от того, какому полупространству принадлежит вершина, равна нулю.
Теорема 7. Пусть a произвольная прямая. Будем считать одну из полуплоскостей, на которые эта прямая разбивает плоскость, положительной, а другую отрицательной. Тогда сумма расстояний от вершин треугольника до прямой a, взятых со знаком + или – в зависимости от того, какой полуплоскости принадлежит вершина, равна утроенному расстоянию от центроида треугольника до прямой a .
Теорема 7′. Пусть a произвольная плоскость. Будем считать одно из полупространств, на которые эта плоскость разбивает пространство, положительным, а другое отрицательным. Тогда сумма расстояний от вершин тетраэдра до плоскости a , взятых со знаком + или – в зависимости от того, какому полупространству принадлежит вершина, равна учетверенному расстоянию от центроида тетраэдра до данной плоскости.
Теорема 8′ (Менелая). Пусть на ребрах AB, BC, CD и AD тетраэдра ABCD взяты соответственно точки A 1 , B 1 , C 1 и D 1 . Для того чтобы эти точки лежали в одной плоскости, необходимо и достаточно, чтобы выполнялось равенство
Доказательство. Пусть точки A 1 , B 1 , C 1 и D 1 лежат в одной плоскости (рис. 4). Опустим из вершин тетраэдра перпендикуляры AA ’ , BB ’ , CC ’ , DD ’ на эту плоскость. Тогда AA 1 : A 1 B = AA ’ : BB ’ , BB 1 : B 1 C = BB ’ : CC ’ , CC 1 : C 1 D = CC ’ : DD ’ , DD 1 : D 1 A = DD ’ : AA ’ . Откуда и следует требуемое равенство.
Обратно, пусть выполняется указанное равенство. Через точки A 1 , B 1 , C 1 проведем плоскость. Она пересечет ребро AD в некоторой точке D ’ . Для точек A 1 , B 1 , C 1 и D ’ также выполняется указанное равенство. Из этого следует, что DD 1 : D 1 A = DD ’ : D ’ A и, значит, D 1 и D ’ совпадают, т.е. A 1 , B 1 , C 1 и D 1 лежат в одной плоскости.
Теорема 9′ (Чевы). Пусть на ребрах AB, BC, CD и AD тетраэдра ABCD взяты соответственно точки A 1 , B 1 , C 1 и D 1. Плоскости ABC 1 , BCD 1 , CDA 1 и DAB 1 пересекаются в одной точке тогда и только тогда, когда
Доказательство. По предыдущей теореме выполнимость указанного равенства равносильна тому, что точки A 1 , B 1 , C 1 и D 1 лежат в одной плоскости. При этом точка пересечения этих плоскостей является точкой пересечения диагоналей четырехугольника A 1 B 1 C 1 D 1 .
Рассмотрим теперь некоторые специальные тетраэдры.
Равногранным тетраэдром называется тетраэдр, у которого все грани равны.
Теорема 10. Для любого остроугольного треугольника существует равногранный тетраэдр, грани которого равны данному треугольнику.
Доказательство. Пусть ABC – произвольный остроугольный треугольник. Через его вершины проведем прямые, параллельные противоположным сторонам (рис. 5).
Они образуют треугольник A 1 B 1 C 1 , разбитый на четыре треугольника, равных исходному. Ясно, что A 1 B 1 C 1 представляет собой развертку равногранного тетраэдра.
Теорема 11. Тетраэдр является равногранным тогда и только тогда, когда у него центры вписанной и описанной сфер совпадают.
Доказательство. Пусть в тетраэдре ABCD центрами вписанной и описанной сфер является точка O . P и Q – и точки касания вписанной сферы граней ABC и BCD (рис.6) . Заметим, что P и Q являются центрами окружностей, описанных около треугольников ABC и BCD соответственно. Из этого, в частности, следует, что треугольник ABC – остроугольный. Кроме того, треугольники BP C и BQ C равны. Углы BAC и BDC равны половинам углов BP C и BQ C , и следовательно также равны. Таким образом, плоские углы при вершине D равны углам треугольника ABC. Значит, в сумме они составляют 180 0 . Аналогично, плоские углы при остальных вершинах тетраэдра в сумме составляют 180 0 . Поэтому развертка этого тетраэдра имеет вид, указанный в теореме 1. Следовательно, тетраэдр равногранный.
Покажем обратное, пусть ABCD – равногранный тетраэдр, O – цетр описанной сферы. Тогда плоскости граней пересекают описанную сферу по окружностям одинакового радиуса. Следовательно, расстояния от точки O до граней тетраэдра равны и, значит O – центр вписанной сферы.
Прямоугольным тетраэдром называется тетраэдр, у которого все плоские углы при какой-нибудь вершине прямые.
Теорема 12. Основанием высоты прямоугольного тетраэдра, проведенной из вершины с прямыми плоскими углами, является точка пересечения высот противоположной грани.
Теорема 13. (Пифагора) Квадрат площади грани прямоугольного тетраэдра, лежащей против вершины с прямыми плоскими углами, равен сумме квадратов площадей остальных граней этого тетраэдра.
Доказательство. Пусть ABCD – прямоугольный тетраэдр (рис. 7). Плоские углы при вершине D прямые. Можно было бы обозначить ребра, выходящие из вершины D через a, b, c, а затем воспользоваться формулой Герона для нахождения площади треугольника ABC .
Мы рассмотрим другой способ. Имеем S ADB = S ABC cos ; S ACD = S ABC cos ; S BCD = S ABC cos , где , , – соответствующие двугранные углы, равные углам C DO, BDO и A DO . Таким образом, cos , cos , cos составляют координаты единичного вектора, поэтому cos 2 + cos 2 + cos 2 = 1. Значит , S 2 ABC = S 2 ABD + S 2 BCD + S 2 ACD . Что и требовалось доказать.
Ортогональным называется тетраэдр, у которого противоположные ребра попарно перпендикулярны.
Ортоцентрическим называется тетраэдр, у которого высоты или их продолжения пересекаются в одной точке – ортоцентре третаэдра.
Теорема 14. Тетраэдр является ортогональным тогда и только тогда, когда отрезки, соединяющие середины противоположных ребер, равны.
Доказательство. Пусть ABCD – тетраэдр. A 1 , B 1, C 1, D 1 – середины двух пар противоположных ребер (рис. 8).
Тогда A 1 B 1 D 1 C 1 – параллелограмм. Его диагонали равны тогда и только тогда, когда он – прямоугольник, т.е. AC BD .
Теорема 2. Тетраэдр является ортогональным тогда и только тогда, когда он является ортоцентрическим.
Доказательство. Пусть ABCD – ортогональный тетраэдр (рис. 9). DD 2 – высота, опущенная из вершины D. Плоскость CDD 2 перпендикулярна AB и, следовательно, DC 1 и CC 1 – высоты треугольников ABC и ABD. Высоты DD 2 и CC 2 треугольника C 1 CD пересекаются.
Таким образом, произвольные пары высот тетраэдра пересекаются в одной точке. Но попарно пересекающиеся прямые или лежат в одной плоскости, или пересекаются в одной точке. В нашем случае прямые не лежат в одной плоскости и, следовательно, пересекаются в одной точке O .
Обратно, пусть высоты тетраэдра ABCD пересекаются в одной точке O. Тогда DD 2 ABC и, следовательно, DD 2 ABC . Аналогично, CC 2 ABD и, следовательно, CC 2 AB . Таким образом, AB перпендикулярна плоскости COD и, следовательно, AB CD. Аналогично показывается перпендикулярность остальных противоположных ребер.
Теорема 3. Тетраэдр является ортогональным тогда и только тогда, когда одна из его высот проходит через ортоцентр соответствующей грани.
Доказательство. Необходимость вытекает из Теоремы 2. Покажем достаточность. Пусть D 2 – ортоцентр грани ABC, DD 2 – высота тетраэдра ABCD. Тогда BC перпендикулярна плоскости AA 1 D и, следовательно, BC перпендикулярна AD. Аналогично показывается перпендикулярность остальных противоположных ребер.
Теорема 4. В ортогональном тетраэдре окружности 9-ти точек всех граней лежат на одной сфере (сфера 24 точек).
Доказательство. Рассмотрим сферу с центром в центроиде тетраэдра и диаметром, равным отрезкам, соединяющим середины противоположных ребер. Эта сфера проходит через середины всех ребер тетраэдра и, следовательно, содержит окружности 9 точек всех граней.
Литература
1. Адамар Ж. Элементарная геометрия. Часть II. Стереометрия. – М.: Учпедгиз, 1938.
2. Перепелкин Д.И. Курс элементарной геометрии. Часть II. Геометрия в пространстве. – М.-Л.: Гостехиздат, 1949.
3. В.В.Прасолов, И.Ф.Шарыгин. Задачи по стереометрии. – М.: Наука, 1989.
4. Д.О.Шклярский, Н.Н.Ченцов, И.М.Яглом. Избранные задачи и теоремы элементарной математики. Часть 3. – М.: Государственное издательство технико-теоретической литературы, 1954.
Тетраэдр.
Тетраэдр – это частный случай правильной треугольной пирамиды.
Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.
Медиана тетраэдра – это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).
Бимедиана тетраэдра – это отрезок, который соединяет середины рёбер, что скрещиваются (соединяет середины сторон треугольника, который есть одной из граней тетраэдра).
Высота тетраэдра – это отрезок, который соединяет вершину и точку противоположной грани и перпендикулярен этой грани (т.е. это высота, проведенная от всякой грани, кроме того, совпадает с центром описанной окружности).
Свойства тетраэдра.
Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.
Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.
Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.
Типы тетраэдров.
Правильный тетраэдр – это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.
У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.
Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.
Правильный тетраэдр – это один из 5-ти правильных многогранников.
Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:
– Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.
– Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.
– Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.
– Каркасный тетраэдр — тетраэдр, который таким условиям:
- есть сфера, которая касается каждого ребра,
- суммы длин ребер, что скрещиваются равны,
- суммы двугранных углов при противоположных ребрах равны,
- окружности, которые вписаны в грани, попарно касаются,
- каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
- перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.
– Соразмерный тетраэдр, бивысоты у него одинаковы.
– Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.
Формулы для определения элементов тетраэдра.
Высота тетраэдра:
где h – высота тетраэдра, a – ребро тетраэдра.
Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.
где V – объем тетраэдра, a – ребро тетраэдра.
Основные формулы для правильного тетраэдра:
Где S – Площадь поверхности правильного тетраэдра;
h – высота, опущенная на основание;
r – радиус вписанной в тетраэдр окружности;
[spoiler title=”источники:”]
http://vasmirnov.ru/Lecture/Tetrahed/Tetrahed.htm
http://www.calc.ru/Tetraedr.html
[/spoiler]
Тема “Разные задачи на многогранники, цилиндр,
конус и шар” является одной из самых сложных в
курсе геометрии 11 класса. Перед тем, как решать
геометрические задачи, обычно изучают
соответствующие разделы теории, на которые
ссылаются при решении задач. В учебнике
С.Атанасяна и др. по данной теме (стр. 138) можно
найти только определения многогранника,
описанного около сферы, многогранника,
вписанного в сферу, сферы, вписанной в
многогранник, и сферы, описанной около
многогранника. В методических рекомендациях к
этому учебнику (см. книгу “Изучение геометрии в
10–11-х классах” С.М.Саакяна и В.Ф.Бутузова, стр.159)
сказано, какие комбинации тел рассматриваются
при решении задач № 629–646, и обращается внимание
на то, что “при решении той или иной задачи
прежде всего нужно добиться того, чтобы учащиеся
хорошо представляли взаимное расположение
указанных в условии тел”. Далее приводится
решение задач №638(а) и №640.
Учитывая все выше сказанное, и то, что наиболее
трудными для учащихся являются задачи на
комбинацию шара с другими телами, необходимо
систематизировать соответствующие
теоретические положения и сообщить их учащимся.
Определения.
1. Шар называется вписанным в многогранник, а
многогранник описанным около шара, если
поверхность шара касается всех граней
многогранника.
2. Шар называется описанным около
многогранника, а многогранник вписанным в шар,
если поверхность шара проходит через все вершины
многогранника.
3. Шар называется вписанным в цилиндр, усеченный
конус (конус), а цилиндр, усеченный конус (конус) –
описанным около шара, если поверхность шара
касается оснований (основания) и всех образующих
цилиндра, усеченного конуса (конуса).
(Из этого определения следует, что в любое
осевое сечение этих тел может быть вписана
окружность большого круга шара).
4. Шар называется описанным около цилиндра,
усеченного конуса (конуса), если окружности
оснований (окружность основания и вершина)
принадлежат поверхности шара.
(Из этого определения следует, что около
любого осевого сечения этих тел может быть
описана окружность большего круга шара).
Общие замечания о положении центра
шара.
1. Центр шара, вписанного в многогранник, лежит в
точке пересечения биссекторных плоскостей всех
двугранных углов многогранника. Он расположен
только внутри многогранника.
2. Центр шара, описанного около многогранника,
лежит в точке пересечения плоскостей,
перпендикулярных ко всем ребрам многогранника и
проходящих через их середины. Он может быть
расположен внутри, на поверхности и вне
многогранника.
Комбинация шара с призмой.
1. Шар, вписанный в прямую призму.
Теорема 1. Шар можно вписать в прямую
призму в том и только в том случае, если в
основание призмы можно вписать окружность, а
высота призмы равна диаметру этой окружности.
Следствие 1. Центр шара, вписанного в прямую
призму, лежит в середине высоты призмы,
проходящей через центр окружности, вписанной в
основание.
Следствие 2. Шар, в частности, можно вписать
в прямые: треугольную, правильную,
четырехугольную (у которой суммы
противоположных сторон основания равны между
собой) при условии Н = 2r, где Н – высота призмы, r –
радиус круга, вписанного в основание.
2. Шар, описанный около призмы.
Теорема 2. Шар можно описать около
призмы в том и только в том случае, если призма
прямая и около ее основания можно описать
окружность.
Следствие 1. Центр шара, описанного около
прямой призмы, лежит на середине высоты призмы,
проведенной через центр круга, описанного около
основания.
Следствие 2. Шар, в частности, можно описать:
около прямой треугольной призмы, около
правильной призмы, около прямоугольного
параллелепипеда, около прямой четырехугольной
призмы, у которой сумма противоположных углов
основания равна 180 градусов.
Из учебника Л.С.Атанасяна на комбинацию шара с
призмой можно предложить задачи № 632, 633, 634, 637(а),
639(а,б).
Комбинация шара с пирамидой.
1. Шар, описанный около пирамиды.
Теорема 3. Около пирамиды можно описать
шар в том и только в том случае, если около ее
основания можно описать окружность.
Следствие 1. Центр шара, описанного около
пирамиды лежит в точке пересечения прямой,
перпендикулярной основанию пирамиды, проходящей
через центр окружности, описанной около этого
основания, и плоскости, перпендикулярной любому
боковому ребру, проведенной через сере дину
этого ребра.
Следствие 2. Если боковые ребра пирамиды
равны между собой (или равно наклонены к
плоскости основания), то около такой пирамиды
можно описать шар.Центр этого шара в этом случае
лежит в точке пересечения высоты пирамиды (или ее
продолжения) с осью симметрии бокового ребра,
лежащей в плоскости бокового ребра и высоты.
Следствие 3. Шар, в частности, можно описать:
около треугольной пирамиды, около правильной
пирамиды, около четырехугольной пирамиды, у
которой сумма противоположных углов равна 180
градусов.
2. Шар, вписанный в пирамиду.
Теорема 4. Если боковые грани пирамиды
одинаково наклонены к основанию, то в такую
пирамиду можно вписать шар.
Следствие 1. Центр шара, вписанного в
пирамиду, у которой боковые грани одинаково
наклонены к основанию, лежит в точке пересечения
высоты пирамиды с биссектрисой линейного угла
любого двугранного угла при основании пирамиды,
стороной которого служит высота боковой грани,
проведенная из вершины пирамиды.
Следствие 2. В правильную пирамиду можно
вписать шар.
Из учебника Л.С.Атанасяна на комбинацию шара с
пирамидой можно предложить задачи № 635, 637(б), 638,
639(в),640, 641.
Комбинация шара с усеченной
пирамидой.
1. Шар, описанный около правильной усеченной
пирамиды.
Теорема 5. Около любой правильной
усеченной пирамиды можно описать шар. (Это
условие является достаточным, но не является
необходимым)
2. Шар, вписанный в правильную усеченную
пирамиду.
Теорема 6. В правильную усеченную
пирамиду можно вписать шар в том и только в том
случае, если апофема пирамиды равна сумме апофем
оснований.
На комбинацию шара с усеченной пирамидой в
учебнике Л.С.Атанасяна есть всего лишь одна
задача (№ 636).
Комбинация шара с круглыми телами.
Теорема 7. Около цилиндра, усеченного
конуса (прямых круговых), конуса можно описать
шар.
Теорема 8. В цилиндр (прямой круговой)
можно вписать шар в том и только в том случае,
если цилиндр равносторонний.
Теорема 9. В любой конус (прямой
круговой) можно вписать шар.
Теорема 10. В усеченный конус (прямой
круговой) можно вписать шар в том и только в том
случае, если его образующая равна сумме радиусов
оснований.
Из учебника Л.С.Атанасяна на комбинацию шара с
круглыми телами можно предложить задачи № 642, 643,
644, 645, 646.
Для более успешного изучения материала данной
темы необходимо включать в ход уроков устные
задачи:
1. Ребро куба равно а. Найти радиусы шаров:
вписанного в куб и описанного около него. (r = a/2, R =
a![]() 3).
3).
2. Можно ли описать сферу (шар) около: а) куба; б)
прямоугольного параллелепипеда; в) наклонного
параллелепипеда, в основании которого лежит
прямоугольник; г) прямого параллелепипеда; д)
наклонного параллелепипеда? (а) да; б) да; в) нет;
г) нет; д) нет)
3. Справедливо ли утверждение, что около любой
треугольной пирамиды можно описать сферу? (Да)
4. Можно ли описать сферу около любой
четырехугольной пирамиды? (Нет, не около любой
четырёхугольной пирамиды)
5. Какими свойствами должна обладать пирамида,
чтобы около нее можно было описать сферу? (В её
основании должен лежать многоугольник, около
которого можно описать окружность)
6. В сферу вписана пирамида, боковое ребро
которой перпендикулярно основанию. Как найти
центр сферы? (Центр сферы – точка пересечения
двух геометрических мест точек в пространстве.
Первое – перпендикуляр, проведённый к плоскости
основания пирамиды, через центр окружности,
описанной около него. Второе – плоскость
перпендикулярная данному боковому ребру и
проведённая через его середину)
7. При каких условиях можно описать сферу около
призмы, в основании которой – трапеция? (Во-первых,
призма должна быть прямой, и, во-вторых, трапеция
должна быть равнобедренной, чтобы около неё
можно было описать окружность)
8. Каким условиям должна удовлетворять призма,
чтобы около нее можно было описать сферу?
(Призма должна быть прямой, и её основанием
должен являться многоугольник, около которого
можно описать окружность)
9. Около треугольной призмы описана сфера, центр
которой лежит вне призмы. Какой треугольник
является основанием призмы? (Тупоугольный
треугольник)
10. Можно ли описать сферу около наклонной
призмы? (Нет, нельзя)
11. При каком условии центр сферы, описанной
около прямой треугольной призмы, будет находится
на одной из боковых граней призмы? (В основании
лежит прямоугольный треугольник)
12. Основание пирамиды – равнобедренная
трапеция .Ортогональная проекция вершины
пирамиды на плоскость основания – точка,
расположенная вне трапеции. Можно ли около такой
трапеции описать сферу? (Да, можно. То что
ортогональная проекция вершины пирамиды
расположена вне её основания, не имеет значения.
Важно, что в основании пирамиды лежит
равнобедренная трапеция – многоугольник, около
которого можно описать окружность)
13. Около правильной пирамиды описана сфера. Как
расположен ее центр относительно элементов
пирамиды? (Центр сферы находится на
перпендикуляре, проведенном к плоскости
основания через его центр)
14. При каком условии центр сферы, описанной
около прямой треугольной призмы, лежит: а) внутри
призмы; б) вне призмы? (В основании призмы: а)
остроугольный треугольник; б) тупоугольный
треугольник)
15. Около прямоугольного параллелепипеда, ребра
которого равны 1 дм, 2 дм и 2 дм, описана сфера.
Вычислите радиус сферы. (1,5 дм)
16. В какой усеченный конус можно вписать сферу? (В
усечённый конус, в осевое сечение которого можно
вписать окружность. Осевым сечением конуса
является равнобедренная трапеция, сумма её
оснований должна равняться сумме её боковых
сторон. Другими словами, у конуса сумма радиусов
оснований должна равняться образующей)
17. В усеченный конус вписана сфера. Под каким
углом образующая конуса видна из центра сферы? (90
градусов)
18. Каким свойством должна обладать прямая
призма, чтобы в нее можно было вписать сферу? (Во-первых,
в основании прямой призмы должен лежать
многоугольник, в который можно вписать
окружность, и, во-вторых, высота призмы должна
равняться диаметру вписанной в основание
окружности)
19. Приведите пример пирамиды, в которую нельзя
вписать сферу? (Например, четырёхугольная
пирамида, в основании которой лежит
прямоугольник или параллелограмм)
20. В основании прямой призмы лежит ромб. Можно
ли в эту призму вписать сферу? (Нет, нельзя, так
как около ромба в общем случае нельзя описать
окружность)
21. При каком условии в прямую треугольную
призму можно вписать сферу? (Если высота призмы
в два раза больше радиуса окружности, вписанной в
основание)
22. При каком условии в правильную
четырехугольную усеченную пирамиду можно
вписать сферу? (Если сечением данной пирамиды
плоскостью, проходящей через середину стороны
основания перпендикулярно ей, является
равнобедренная трапеция, в которую можно вписать
окружность)
23. В треугольную усеченную пирамиду вписана
сфера. Какая точка пирамиды является центром
сферы? (Центр вписанной в данную пирамиду сферы
находится на пересечении трёх биссектральных
плоскостей углов, образованных боковыми гранями
пирамиды с основанием)
24. Можно ли описать сферу около цилиндра
(прямого кругового)? (Да, можно)
25. Можно ли описать сферу около конуса,
усеченного конуса (прямых круговых)? (Да, можно,
в обоих случаях)
26. Во всякий ли цилиндр можно вписать сферу?
Какими свойствами должен обладать цилиндр, чтобы
в него можно было вписать сферу? (Нет, не во
всякий: осевое сечение цилиндра должно быть
квадратом)
27. Во всякий ли конус можно вписать сферу? Как
определить положение центра сферы, вписанной в
конус? (Да, во всякий. Центр вписанной сферы
находится на пересечении высоты конуса и
биссектрисы угла наклона образующей к плоскости
основания)
Автор считает, что из трех уроков, которые
отводятся по планированию на тему “Разные
задачи на многогранники, цилиндр, конус и шар”,
два урока целесообразно отвести на решение задач
на комбинацию шара с другими телами. Теоремы,
приведенные выше, из-за недостаточного
количества времени на уроках доказывать не
рекомендуется. Можно предложить учащимся,
которые владеют достаточными для этого навыками,
доказать их, указав (по усморению учителя) ход или
план доказательства.
Автор надеется, что материал этой статьи
поможет молодым коллегам при подготовке к урокам
по данной теме.
Чтобы легко справиться с решением задач на шар, вписанный в пирамиду, полезно разобрать небольшой теоретический материал.
Шар вписан в пирамиду (или сфера вписана в пирамиду) — значит, шар (сфера) касаются каждой грани пирамиды. Плоскости, содержащие грани пирамиды, являются касательными плоскостями шара. Отрезки, соединяющие центр шара с точками касания, перпендикуляры к касательным плоскостям. Их длины равны радиусу шара. Центр вписанного в пирамиду шара — точка пересечения бисекторных плоскостей двугранных углов при основании (то есть плоскостей, делящих эти углы пополам).
Чаще всего в задачах речь идет о шаре, вписанном в правильную пирамиду. Шар можно вписать в любую правильную пирамиду. Центр шара в этом случае лежит на высоте пирамиды. При решении задачи удобно провести сечение пирамиды и шара плоскостью, проходящей через апофему и высоту пирамиды.
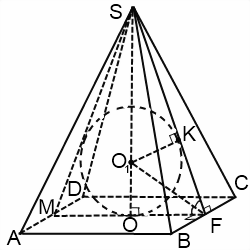
Если пирамида четырехугольная или шестиугольная, сечение представляет собой равнобедренный треугольник, боковые стороны которого — апофемы, а основание — диаметр вписанной в основание окружности.
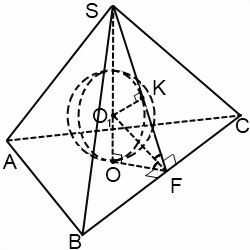
Если пирамида треугольная или пятиугольная, достаточно рассмотреть лишь часть этого сечения — прямоугольный треугольник, катеты которого — высота пирамиды и радиус вписанной в основание пирамиды окружности, а гипотенуза — апофема.
В любом случае, в итоге приходим к рассмотрению соответствующего прямоугольного треугольника и других связанных с ним треугольников.
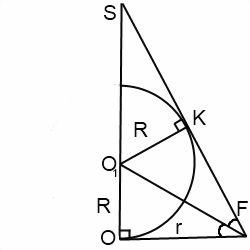 Итак, в прямоугольном треугольнике SOF катет SO=H — высота пирамиды, катет OF=r — радиус вписанной в основание пирамиды окружности, гипотенуза SF=l — апофема пирамиды. O1- центр шара и, соответственно, окружности, вписанной в треугольник, полученный в сечении (мы рассматриваем его часть). Угол SFO — линейный угол двугранного угла между плоскостью основания и плоскостью боковой грани SBC. Точки K и O — точки касания, следовательно, O1K перпендикулярен SF. OO1=O1K=R — радиусу шара.
Итак, в прямоугольном треугольнике SOF катет SO=H — высота пирамиды, катет OF=r — радиус вписанной в основание пирамиды окружности, гипотенуза SF=l — апофема пирамиды. O1- центр шара и, соответственно, окружности, вписанной в треугольник, полученный в сечении (мы рассматриваем его часть). Угол SFO — линейный угол двугранного угла между плоскостью основания и плоскостью боковой грани SBC. Точки K и O — точки касания, следовательно, O1K перпендикулярен SF. OO1=O1K=R — радиусу шара.
Прямоугольные треугольники OO1F и KO1F равны (по катетам и гипотенузе). Отсюда KF=OF=r.
Прямоугольные треугольники SKO1 и SOF подобны (по острому углу S), откуда следует, что
![]()
В треугольнике SOF применим свойство биссектрисы треугольника:
![]()
Из прямоугольного треугольника OO1F
![]()
При решении задач на шар, вписанный в правильную пирамиду, будет полезным еще одно рассуждение.
![]()
![]()
![]()
Теперь найдем отношение объема пирамиды к площади ее поверхности:
![]()
![]()
Таким образом, радиус вписанного шара выражается через объем пирамиды и ее полную поверхность:
![]()
Все эти рассуждения верны не только для правильной пирамиды, но и для пирамиды, основание высоты которой совпадает с центром вписанной в основание окружности (то есть для пирамиды, у которой все двугранные углы при основании равны).
03
Мар 2014
Категория: 13 (С2) Стереометр. задачиСтереометрия
C2 (№16). Сфера вписана в пирамиду
2014-03-03
2015-09-04
В новом формате ЕГЭ по математике задание значится как «Задание №14»
Задача С2 Т/Р №65 А. Ларина.
В треугольной пирамиде длины двух непересекающихся ребер равны 12 и 4, а остальные ребра имеют длину 7. В пирамиду вписана сфера. Найти расстояние от центра сферы до ребра длины 12.
Решение:

Пусть нам дана пирамида с основанием
, равными ребрами
Центр вписанной сферы равноудален от всех граней пирамиды, поэтому является точкой пересечения биссекторных плоскостей всех двугранных углов пирамиды + показать
В частности, центр сферы лежит на некоторой прямой
(
– середины
соответственно), по которой пересекаются биссекторные плоскости двугранных углов с ребрами

При построении биссекторной плоскости двугранного угла при ребре мы опирались на то, что линейный угол упомянутого двугранного – это угол
, ведь
и
– высоты/медианы/биссектрисы равнобедренных треугольников. При этом треугольник
также равнобедренный. Аналогично с биссекторной плоскостью при ребре
Заметим, построенная плоскость перпендикулярна прямой
по признаку перпендикулярности прямой и плоскости. А значит, любая прямая этой плоскости (
) будет перпендикулярна прямой
, в частности,
– и есть искомое расстояние.
Также, из того, что перпендикулярна прямой
следует, что
по признаку перпендикулярности плоскостей. Нам это еще пригодится.
Можно провести и третью биссекторную плоскость, чтобы «зафиксировать» точку , но мы обойдемся и без этого при решении задачи.

Очевидно, высота пирамиды лежит в плоскости
(плоскость
перпендикулярна плоскости основания, а значит, прямая, в ней лежащая, и при этом перпендикулярная прямой пересечения плоскостей, перпендикулярна плоскости основания (по свойству перпендикулярных плоскостей)).
Найдем высоту пирамиды из треугольника
Заметим,
Распишем дважды площадь треугольника , используя разные высоты:

Найдем радиус вписанной в пирамиду сферы, используя формулу (кстати, мы ее уже применяли (доказательство там же)):
Прежде
Тогда
Стало быть,
Наконец, из подобия треугольников ,
(
– точка касания сферы и плоскости основания) по двум углам имеем:

где
Откуда
Ответ:
Для самостоятельной проработки
В треугольной пирамиде боковое ребро
перпендикулярно плоскости основания
, и его длина равна
. Ребра
и
равны
, а ребро
равно
. Найдите расстояние от центра вписанной в пирамиду сферы до вершины
.
Ответ: + показать
![]()
+ показать
Автор: egeMax |
Один комментарий
Печать страницы


Описанные шары
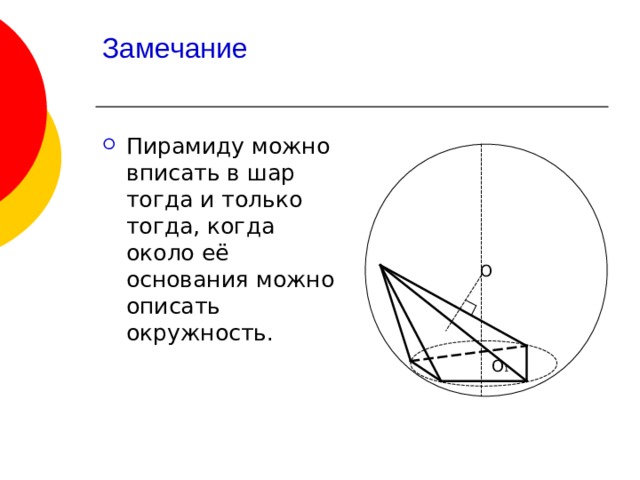
- Сфера называется описанной около многогранника, если на ней лежат все его вершины.
- Центр шара, описанного около многогранника, лежит в точке пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящих через их середины. Он может находится внутри, на поверхности и вне многогранника.
О
О 1
Замечание
- Пирамиду можно вписать в шар тогда и только тогда, когда около её основания можно описать окружность.
О
О 1

- Следствие 1. Центр шара, описанного около пирамиды, лежит в точке пересечения прямой, перпендикулярной основанию пирамиды, проходящей через центр окружности, описанной около этого основания, и плоскости, перпендикулярной любому боковому ребру, проведенной через середину этого ребра.
- Следствие 2. Если боковые рёбра пирамиды равны между собой (или равно наклонены к плоскости основания), то около такой пирамиды можно описать шар.
- Следствие 3. Шар, в частности можно описать:
– около треугольной пирамиды
– около правильной пирамиды
– около четырёхугольной пирамиды, у которой сумма противоположных углов основания равна 180 ° .
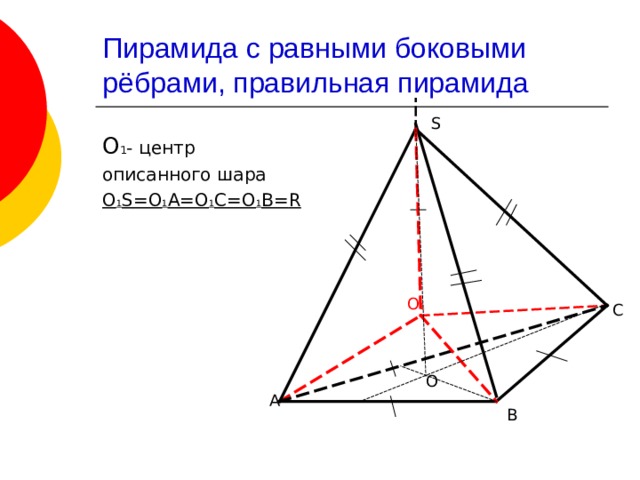
Пирамида с равными боковыми рёбрами, правильная пирамида
S
О 1 – центр
описанного шара
О 1 S =О 1 А=О 1 С=О 1 В= R
О 1
С
О
В
А
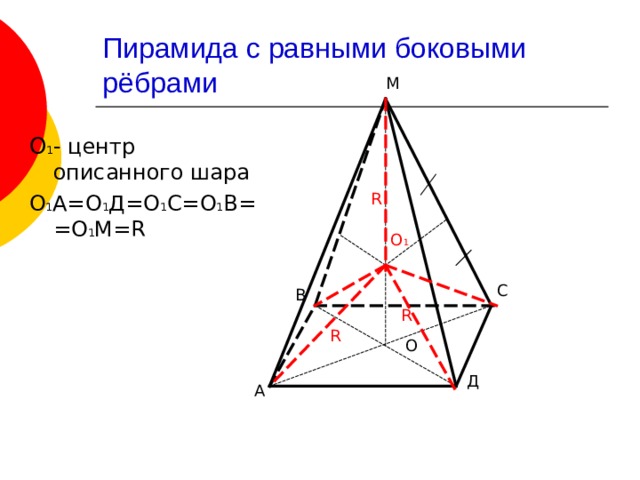
Пирамида с равными боковыми рёбрами
М
О 1 – центр описанного шара
О 1 А=О 1 Д=О 1 С=О 1 В==О 1 М= R
R
О 1
С
В
R
R
О
Д
А

Основание пирамиды – равнобедренная трапеция
S
О 1 – центр описанной окружности
О 1 В=О 1 А=О 1 Д=
=О 1 С=О 1 S = R
АД || ВС
АВ=СД
∟ А + ∟ С =180 °
∟ В + ∟ Д = 180 °
R
О 1
R
R
В
С
О
А
Д
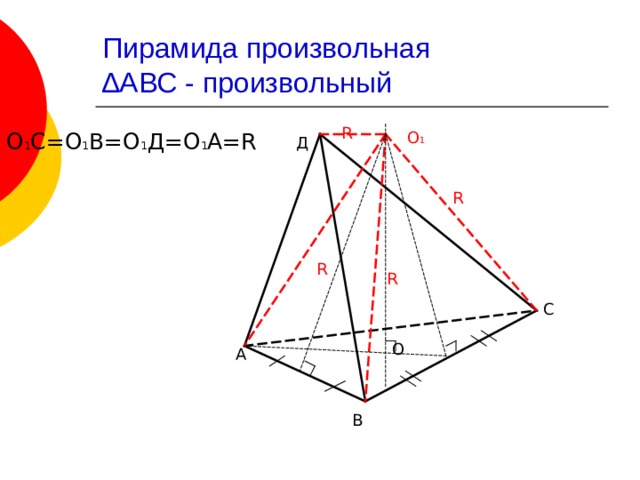
Пирамида произвольная ∆АВС – произвольный
R
О 1
О 1 С=О 1 В=О 1 Д=О 1 А= R
Д
R
R
R
С
О
А
В
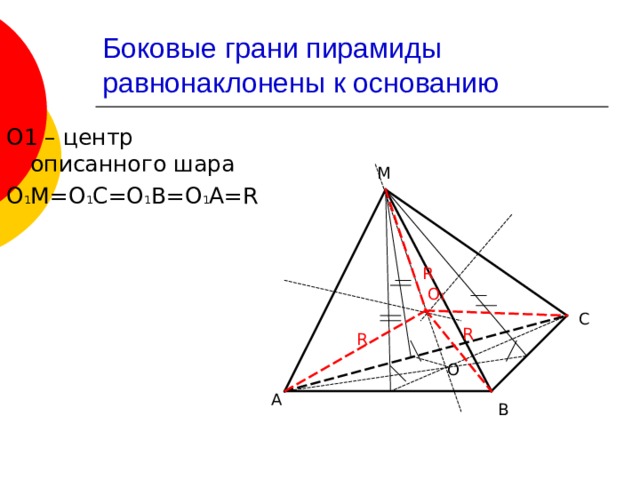
Боковые грани пирамиды равнонаклонены к основанию
О1 – центр описанного шара
О 1 М=О 1 С=О 1 В=О 1 А= R
М
R
О 1
С
R
R
О
А
В
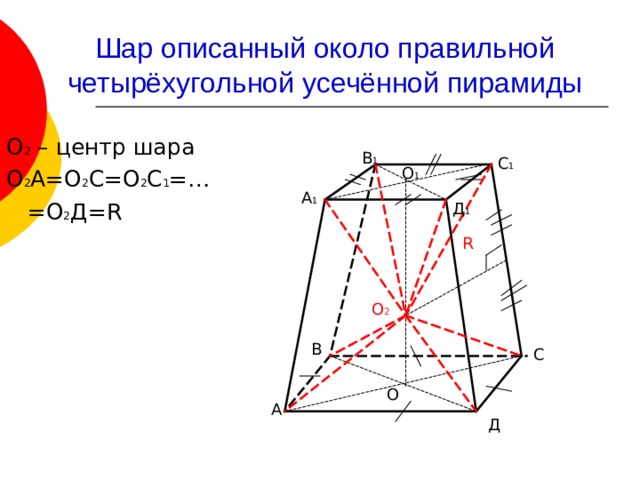
Шар описанный около правильной четырёхугольной усечённой пирамиды
О 2 – центр шара
О 2 А=О 2 С=О 2 С 1 =…
=О 2 Д= R
В 1
С 1
О 1
А 1
Д 1
R
О 2
В
С
О
А
Д
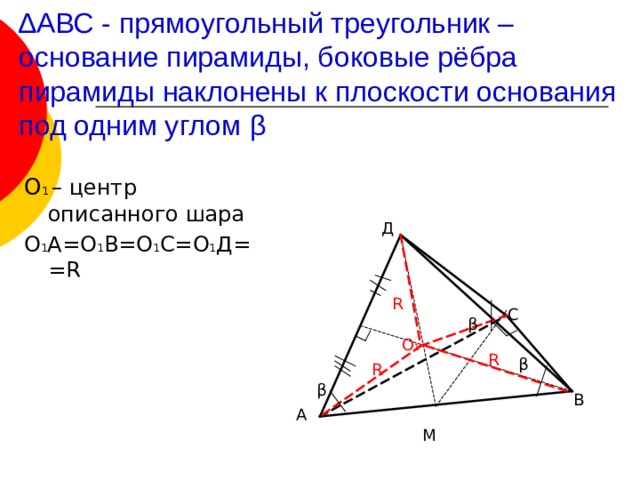
∆ АВС – прямоугольный треугольник – основание пирамиды, боковые рёбра пирамиды наклонены к плоскости основания под одним углом β
О 1 – центр описанного шара
О 1 А=О 1 В=О 1 С=О 1 Д= =R
Д
R
С
β
О 1
R
β
R
β
В
А
М

- Сфера называется вписанной в многогранник, если она касается всех его граней.
- Центр шара, вписанного в многогранник, лежит в точке пересечения биссекторных плоскостей всех двугранных углов многогранника. Он расположен только внутри многогранника.
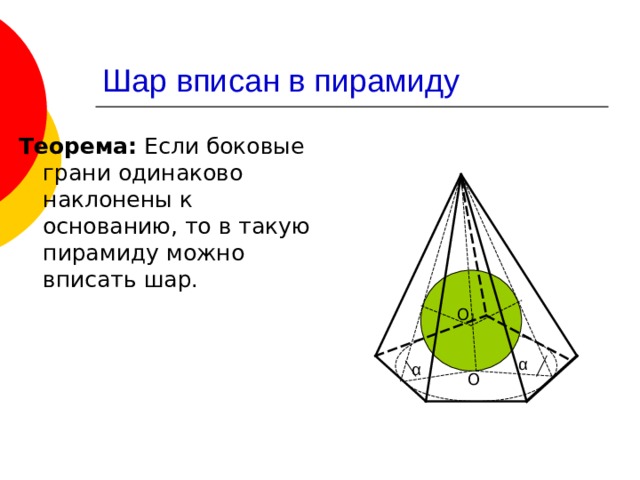
Теорема: Если боковые грани одинаково наклонены к основанию, то в такую пирамиду можно вписать шар.
О 1
α
α
О

Следствие 1. Центр шара, вписанного в пирамиду, у которой боковые грани одинаково наклонены к основанию, лежит в точке пересечения высоты пирамиды с биссектрисой линейного угла любого двугранного угла при основании пирамиды, стороной которого служит высота боковой грани, проведенная из вершины пирамиды.
Следствие 2. В правильную пирамиду можно вписать шар.
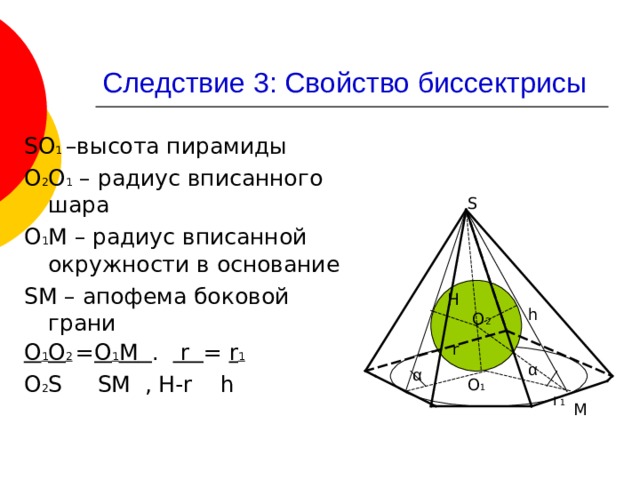
Следствие 3: Свойство биссектрисы
SO 1 – высота пирамиды
О 2 О 1 – радиус вписанного шара
О 1 М – радиус вписанной окружности в основание
SM – апофема боковой грани
О 1 О 2 = О 1 М . r = r 1
О 2 S SM , H-r h
S
H
h
О 2
r
α
α
О 1
r 1
М
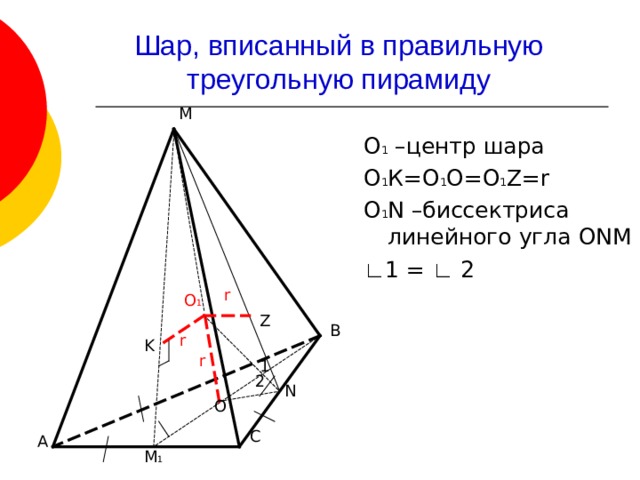
Шар, вписанный в правильную треугольную пирамиду
М
О 1 –центр шара
О 1 К=О 1 О=О 1 Z=r
О 1 N –биссектриса линейного угла ONM
∟ 1 = ∟ 2
r
О 1
Z
В
r
K
r
1
2
N
О
С
А
М 1
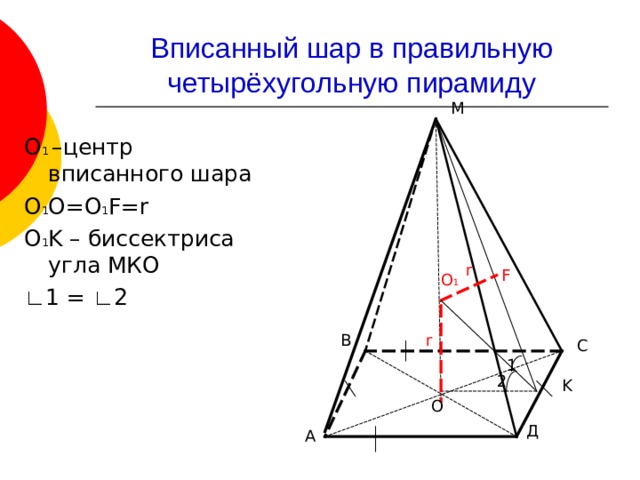
Вписанный шар в правильную четырёхугольную пирамиду
M
О 1 –центр вписанного шара
О 1 О=О 1 F=r
О 1 K – биссектриса угла МКО
∟ 1 = ∟ 2
r
F
О 1
В
r
С
1
2
K
O
Д
А
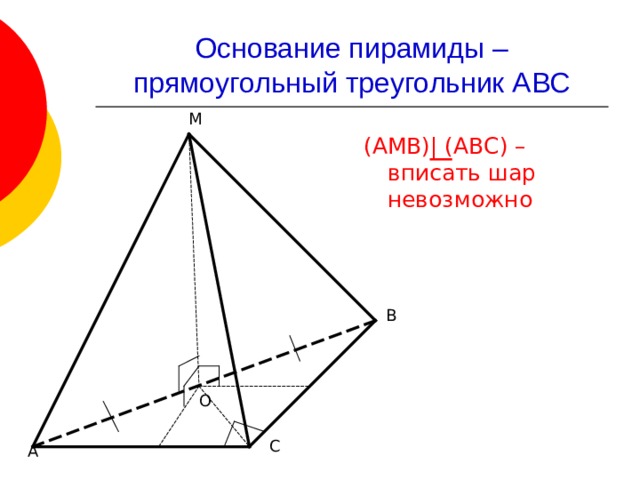
Основание пирамиды – прямоугольный треугольник АВС
М
(АМВ) | (АВС) – вписать шар невозможно
В
О
С
А
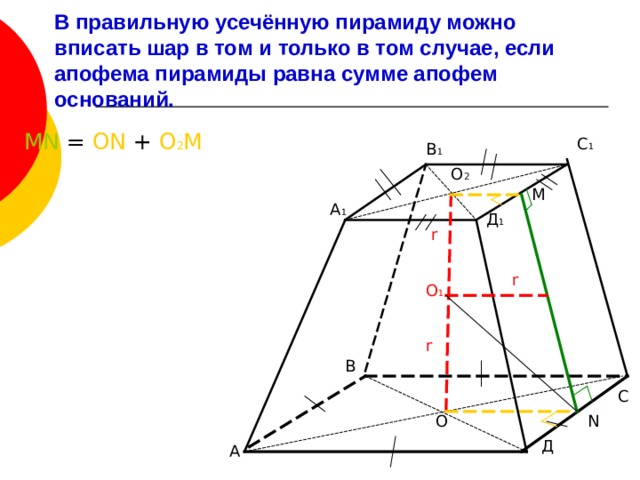
В правильную усечённую пирамиду можно вписать шар в том и только в том случае, если апофема пирамиды равна сумме апофем оснований.
MN = ON + O 2 M
С 1
В 1
О 2
М
А 1
Д 1
r
r
О 1
r
В
С
О
N
Д
А
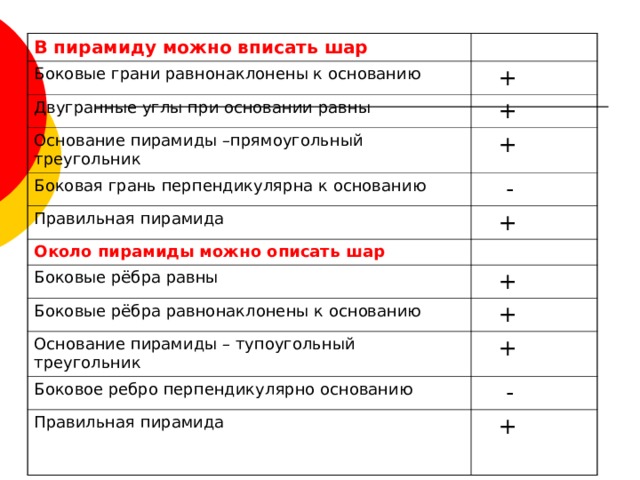
В пирамиду можно вписать шар
Боковые грани равнонаклонены к основанию
+
Двугранные углы при основании равны
+
Основание пирамиды –прямоугольный треугольник
+
Боковая грань перпендикулярна к основанию
–
Правильная пирамида
Около пирамиды можно описать шар
+
Боковые рёбра равны
+
Боковые рёбра равнонаклонены к основанию
+
Основание пирамиды – тупоугольный треугольник
+
Боковое ребро перпендикулярно основанию
–
Правильная пирамида
+

Для правильного тетраэдра со стороной а:
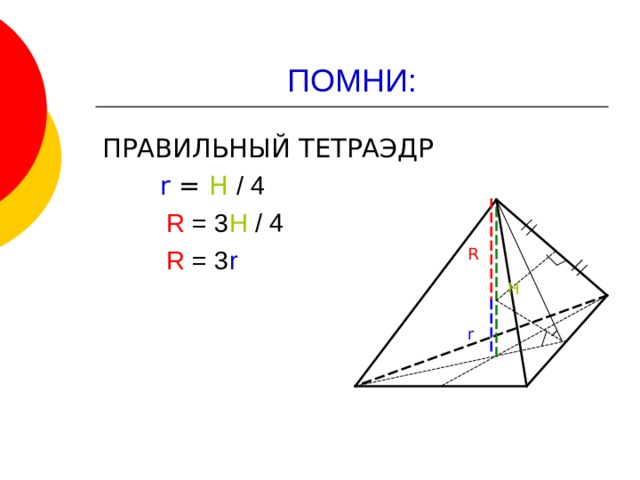
ПРАВИЛЬНЫЙ ТЕТРАЭДР
r = H / 4
R = 3 H / 4
R = 3 r
R
H
r
ПРОВЕРКА ТЕСТА № 2 Построить центр описанного шара
В
1.
О 1
С
О
Д
А
Построить центр описанного шара
М
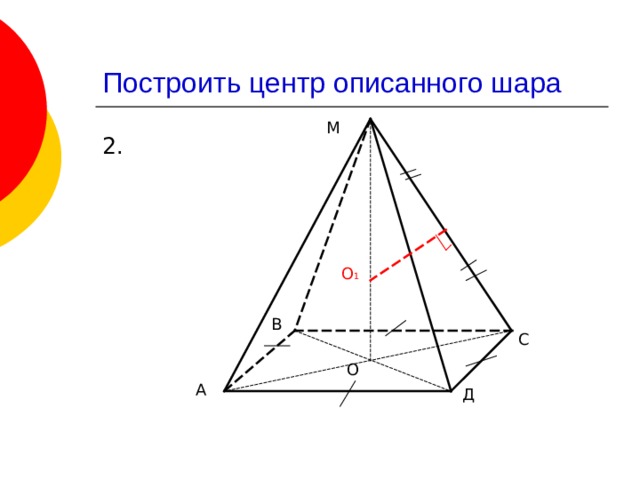
2.
О 1
В
С
О
А
Д
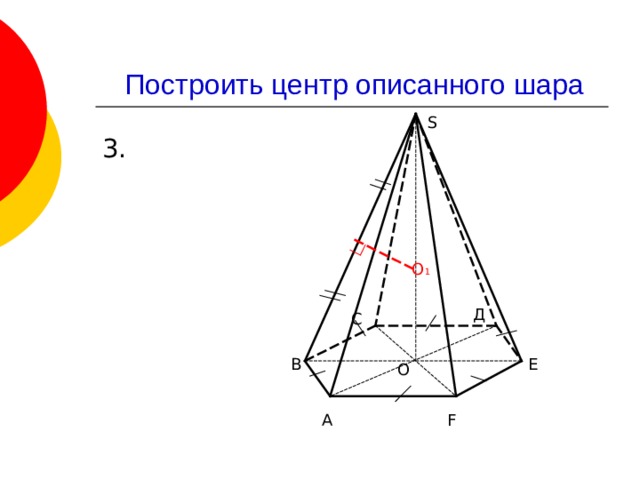
Построить центр описанного шара
S
О 1
Д
С
В
Е
О
А
F
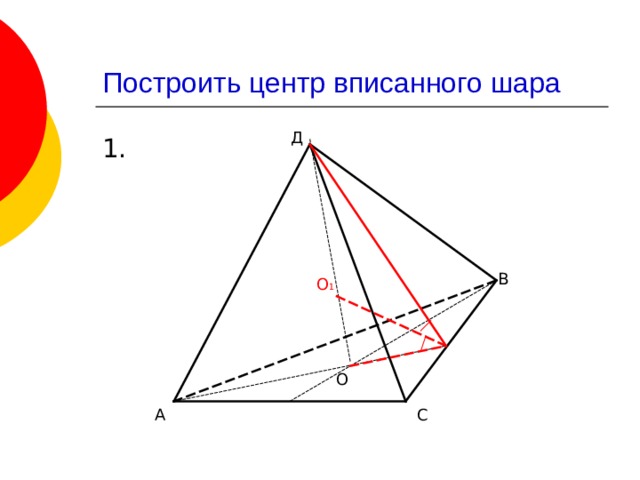
Построить центр вписанного шара
Д
В
О 1
О
С
А
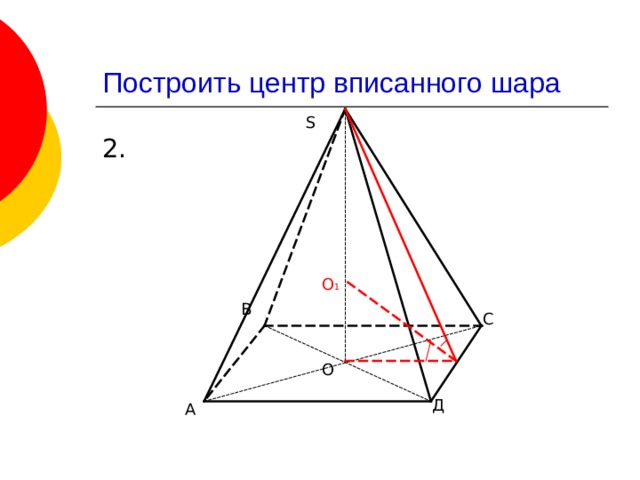
Построить центр вписанного шара
S
О 1
В
С
О
Д
А
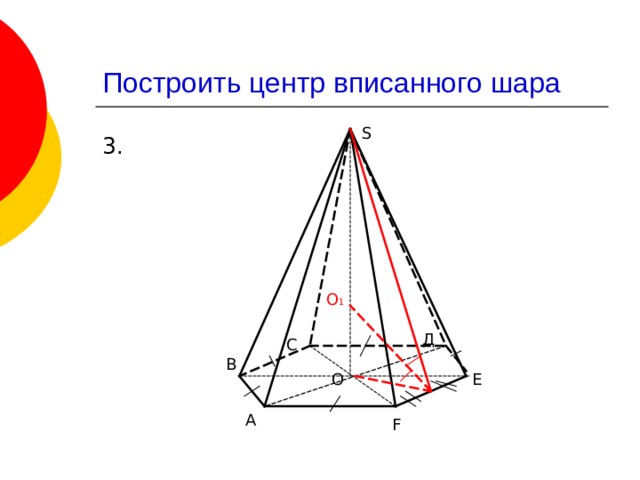
Построить центр вписанного шара
S
3.
О 1
Д
С
В
О
Е
А
F

СПАСИБО ЗА УРОК!
