Как найти центр шара формула

Сфера, шар, сегмент и сектор. Формулы и свойства сферы

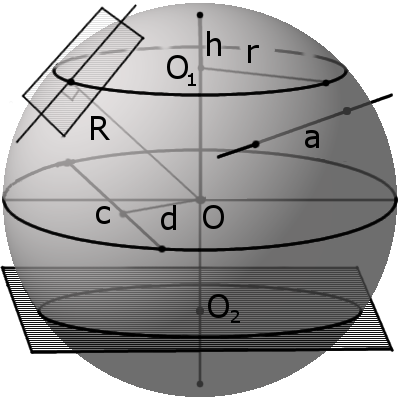
Формула. Объём шара:

V =	4	π R 3 =	1	π D 3
3	6

S = 4 π R 2 = π D 2

Уравнение сферы

x 2 + y 2 + z 2 = R 2

( x – x ₀) 2 + ( y – y ₀) 2 + ( z – z ₀) 2 = R 2

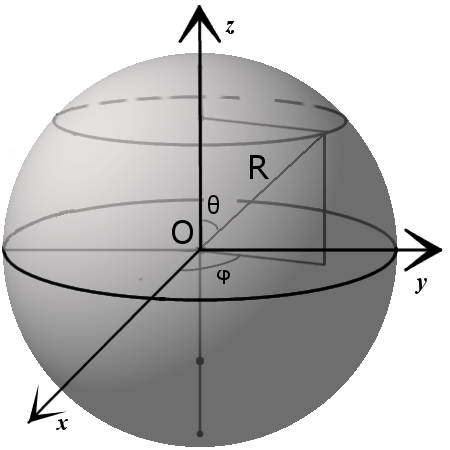
Основные свойства сферы и шара

Секущая, хорда, секущая плоскость сферы и их свойства

d m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m r такого круга можно найти по формуле:

где R – радиус сферы (шара), m – расстояние от центра шара до секущей плоскости.

Касательная, касательная плоскость к сфере и их свойства

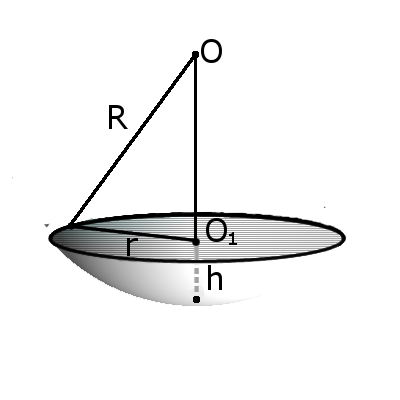
Формула. Объём сегмента сферы с высотой h через радиус сферы R:

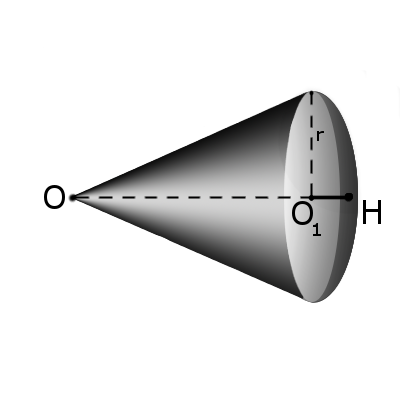
S = π R(2 h + √ 2 h R – h 2 )

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Урок №8. Сфера и шар

Перечень вопросов, рассматриваемых в теме:

• что такое сфера, какие у неё есть элементы (центр, радиус, диаметр сферы);
• что такое шар и его элементы;
• уравнение сферы;
• формула для нахождения площади поверхности сферы;
• взаимное расположение сферы и плоскости;
• теорема о радиусе сферы, который проведён в точку касания и теорему обратную данной.

Глоссарий по теме:

Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.

Круг – это часть плоскости, ограниченная окружностью.

Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

– уравнение сферы радиуса R и центром С(x₀; y₀; z₀).

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Сегмент шара – это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Основные теоретические факты

По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.

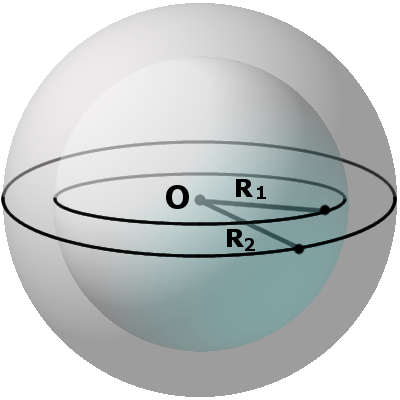
Рисунок 1 – Сфера с центром в точке О и радиусом R

Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

Сферу можно получить ещё одним способом – вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.

2. Уравнение сферы

Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.

Пусть сфера имеет центром точку С (x₀; y₀; z₀) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:

МС=

Исходя из понятия уравнения поверхности, следует, что если точка М лежит на данной сфере, то МС=R, или МС 2 =R 2 , то есть координаты точки М удовлетворяют уравнению:

.

Это выражение называют уравнением сферы радиуса R и центром С(x₀; y₀; z₀).

3. Взаимное расположение сферы и плоскости

Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.

1. Пусть dR. Если расстояние от центра сферы до плоскости меньше радиуса сферы, тогда сфера и плоскость пересекаются, и сечение сферы плоскостью есть окружность.

2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.

3. Пусть dR. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Рассмотрим случай касания более подробно.

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Теорема (свойство касательной плоскости).

Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Теорема (признак касательной плоскости):

Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.

4. Основные формулы

Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:

Формула для вычисления площади поверхности сферы и ее элементов:

S=4πR 2 – площадь сферы.

S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

– площадь поверхности сектора с высотой h.

Примеры и разбор решения заданий тренировочного модуля

1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.

Площадь круга вычисляется по формуле: S_кр=πR 2 .

Площадь поверхности шара вычисляется по формуле: S_сф=4πR 2 . Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.

2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.

Площадь сферы равна S_сф=4πR 2 . То есть S_сф=100π.

По условию площадь круга некоторого радиуса r также равна 100π. Значит, r 2 =100, то есть r=10.

3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15

Окружность, вписанная в треугольник, является сечением сферы.

Найдем ее радиус.

Площадь треугольника с известными сторонами можно вычислить по формуле Герона:

С другой стороны, S=p·r.

Теперь найдем расстояние от центра шара до секущей плоскости.

4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.

Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.

Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.

Урок «Сфера. Уравнение сферы»

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Продолжаем изучение сферы.

На прошлых занятиях вы познакомились с определением сферы и шара.

Вспомним, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Данная точка — центр сферы.

Заданное расстояние — радиус сферы.

Прежде чем вывести уравнение сферы, познакомимся с понятием уравнения поверхности в пространстве.

Зададим прямоугольную систему координат Оxyz и некоторую поверхность F.

Уравнением поверхности F называется уравнение с тремя переменными x, y, z, если этому уравнению удовлетворяют координаты всех точек поверхности F и не удовлетворяют координаты точки, не принадлежащей этой поверхности.

1.Рассмотрим сферу радиуса R и с центром С(x0; y0; z0).

2.Найдём расстояние от произвольной точки М(x; y; z) до центра С( x0 ; y0 ; z0) по формуле для вычисления расстояния между двумя точками с заданными координатами.

3. Если точка М лежит на сфере, то отрезок МС равен радиусу R, то есть

4.В случае если точка М не принадлежит данной сфере, то R≠МС, значит, координаты точки М не удовлетворяют уравнению R2=(x-x0)2+(y-y0)2+(z-z0)2.

5. Таким образом, в прямоугольной системе координат Оxyz уравнение сферы с центром

С (x0 ; y0 ; z0) и радиусом R имеет вид:

Применим полученные знания при решении задач.

Записать уравнение сферы с центром в точке А, которая проходит через точку N, если А(-2;2;0) и N(5;0;-1).

1.Запишем уравнение сферы с центром

А (x0 ; y0 ; z0) и радиусом R:

2.Подставим соответствующие координаты центра сферы А в данное уравнение:

Уравнение сферы с центром в точке А с координатами (-2;2;0) примет вид:

3.Так как сфера проходит через точку N с координатами (5;0;-1), то её координаты удовлетворяют уравнению сферы, подставим координаты этой точки в полученное уравнение:

Таким образом, уравнение сферы с центром в точке А, которая проходит через точку N имеет вид:

Сфера задана уравнением:

1) Найти координаты центра и радиус сферы;

2) Найти значение m, при котором точки

А (0; m;2) и В (1;1; m-2) принадлежат данной сфере.

1. Уравнение данной сферы имеет вид:

x2+ y2+ z2+2y-4z=4 или x2+ y2+2y + z2-4z=4

Выделим полный квадрат для переменных y и z, для этого прибавим и одновременно вычтем 1 и 4 в левой части уравнения:

x2+ y2+2y+1-1 + z2-4z+4-4=4

Уравнение примет вид:

x2+( y+1)2+( z-2)2-5=4 или

Таким образом, центр сферы имеет координаты:

О (0;-1;2), радиус равен R=√9=3

2.Уравнение сферы с центром в точке О (0;-1;2) и радиусом R=3 имеет вид:

Точки А (0; m;2) и В (1;1; m-2) принадлежат данной сфере, значит их координаты удовлетворяют уравнению сферы. Подставим координаты этих точек в уравнение сферы и решим систему уравнений:

Упростим полученные уравнения, раскрывая скобки и приводя подобные слагаемые:

Таким образом, мы получили 4 значения m:

Несложно проверить, что при m=-4 и m=6 координаты точек А и В не удовлетворяют уравнению сферы. Проверьте самостоятельно.

Итак, при m=2 точки А (0; m;2) и В (1;1; m-2) принадлежат сфере, заданной уравнением

x2+ y2+ z2+2y-4z=4 с центром в точке

О (0;-1;2) и радиусом R=3.

–> –>

АвторДата добавленияРазделПодразделПросмотровНомер материала

Инфоурок

07.11.2014

Геометрия

Видеоурок

51859

1003

© 2022 Проект «Уроки математики»

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

[spoiler title=”источники:”]

http://resh.edu.ru/subject/lesson/4034/conspect/

http://urokimatematiki.ru/urok-sfera-uravnenie-sferi-1003.html

[/spoiler]

Центр тяжести (центр масс):

Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.

Центр тяжести – геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.

На каждую точку тела в поле сил тяжести действует сила, а на все тело – равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.

Центр масс (центр инерции) – точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе  внешние силы.

При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.

Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.

При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, – параллельными.

Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.

 Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.

Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.

Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.

Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.

1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О – середине стержня.

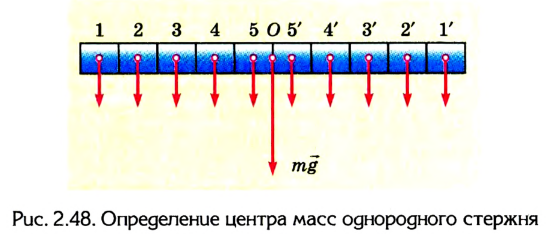
Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.

Центр тяжести однородного стержня расположен в середине стержня.

2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).

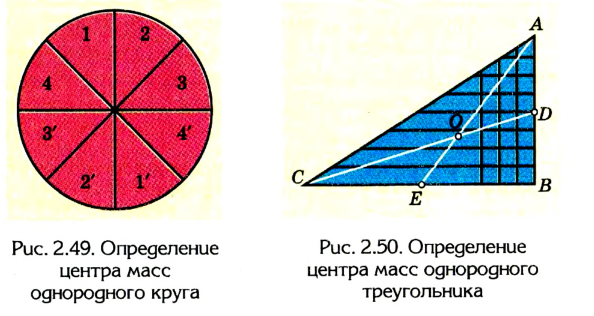
Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.

Центр тяжести однородного круга совпадает с его центром.

Центр тяжести однородного треугольника находится в точке пересечения его медиан.

3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.

Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.

4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).

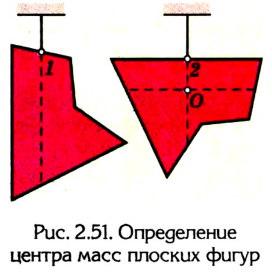
Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.

Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.

Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.

• Заказать решение задач по физике

Центр тяжести тела и центр масс тела

Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.

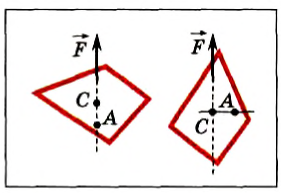
Рис. 151

Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.

Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m₁ и m₂, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:

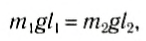
или

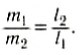
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:

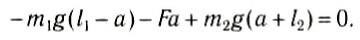
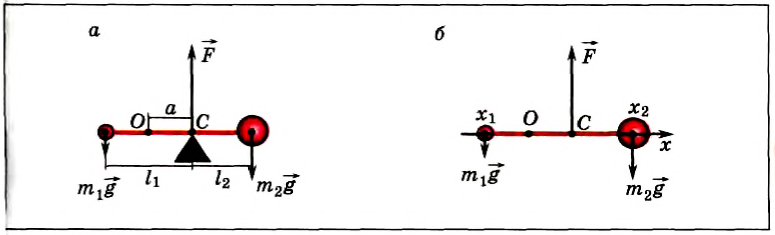
Рис. 152

Поскольку F=(m₁ + m₂)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.

Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х₁, х_с и х₂. Запишем условие моментов относительно точки О:

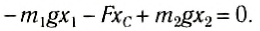
Отсюда

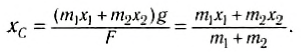
При выводе этой формулы было использовано значение силы F = (m₁ + m₂) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии х_с, определенном формулой (2).

Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.

Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.

Если произвольное тело можно разбить на n элементов, массы которых m₁, m₂…,    m_n, и если известны координаты центров масс этих элементов x₁, x₂…,   x_n относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:

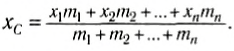
Естественно, что такие же соотношения можно записать и для у_с и z_c. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m₁ = 2m₂). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C₁) и линейки (C₂).

Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х₁ = 0, y₁ =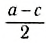, а координаты центра масс линейки: 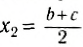, y₂ = 0 .
По формуле (3):    .

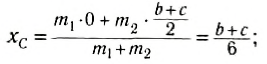
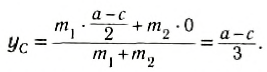
Таким образом, центр масс угольника находится вне тела.

Главные выводы:

1. Центр тяжести — точка, в которой приложена сила тяжести.
2. Центр масс симметричных однородных тел находится в их геометрическом центре.
3. Координаты центра масс тела можно вычислить по формуле (3).

Шар – это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Граница шара называется шаровой поверхностью или сферой. Точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, который соединяет центр шара с точкой шаровой поверхности, тоже называется радиусом. Проходящий через центр шара отрезок, который соединяет две точки шаровой поверхности, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.

Шар является телом вращения, так же как конус и цилиндр. Шар получается при вращении полукруга вокруг  его диаметра как оси.

Площадь поверхности шара можно найти по формулам:

S = 4 πr²

S = πd²,

где r – радиус шара, d – диаметр шара.

Объём шара находится по формуле:

V = 4 / 3 πr³,

где r – радиус шара.

Теорема. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

Исходя из данной теоремы, если шар с центром O и радиусом R пересечён плоскостью α, то в сечении получается круг радиуса r с центром K. Радиус сечения шара плоскостью можно найти по формуле

 

Из формулы видно, что плоскости, равноудалённые от центра, пересекают шар по равным кругам. Радиус сечения тем больше, чем ближе секущая плоскости к центру шара, то есть чем меньше расстояние ОК. Наибольший радиус имеет сечение плоскостью, проходящей через центр шара. Радиус этого круга равен радиусу шара.

Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью, называется большим кругом, а сечение сферы – большим кругом, а сечение сферы – большой окружностью.

Теорема. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.

Плоскость, которая и проходит через точку А шаровой поверхности и перпендикулярна радиусу, проведённому в точку А, называется касательной плоскостью. Точка А называется точкой касания.

Теорема. Касательная плоскость имеет с шаром только одну общую точку – точку касания.

Прямая, которая проходит через точку А шаровой поверхности перпендикулярно к радиусу, проведённому в эту точку, называется касательной.

Теорема. Через любую точку шаровой поверхности проходит бесконечно много касательных, причём все они лежат в касательной плоскости шара.

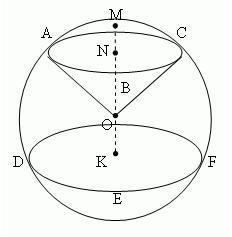Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Круг ABC – основание шарового сегмента. Отрезок MN перпендикуляра, проведенного из центра N круга ABC до пересечения со сферической поверхностью, – высота шарового сегмента. Точка M – вершина шарового сегмента.

Площадь поверхности шарового сегмента можно вычислить по формуле:

S = 2πRh,

где R – радиус большого круга, h – высота шарового сегмента.

Объём шарового сегмента можно найти по формуле:

V = πh²(R – 1/3h),

где R – радиус большого круга, h – высота шарового сегмента.

Шаровой сектор получается из шарового сегмента и конуса, следующим образом. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.

Шаровой сектор – это часть шара, ограниченная кривой поверхностью сферического сегмента (на нашем рисунке – это AMCB) и конической поверхностью (на рисунке – это OABC), основанием которой служит основание сегмента (ABC), а вершиной – центр шара O.

Объем шарового сектора находится по формуле:

V = 2/3 πR²H.

Шаровый слой – это часть шара, заключённая между двумя параллельными плоскостями (на рисунке плоскостями ABC и DEF), пересекающими сферическую поверхность. Кривая поверхность шарового слоя называется шаровым поясом (зоной). Круги  ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Сфера в геометрии — элементы, формулы, свойства с примерами

Сферой называется поверхность, полученная вращением окружности вокруг какого-либо ее диаметра (рис. 180). Центр этой окружности называется центром сферы.

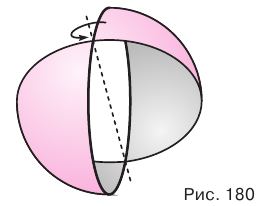
Отрезок, соединяющий центр сферы с любой ее точкой, называется радиусом сферы, отрезок, соединяющий две точки сферы, — хордой сферы, а хорда, которой принадлежит центр сферы, — диаметром сферы (рис. 181).

Из определения сферы следует, что все ее точки равноудалены от центра сферы. Поэтому все радиусы сферы равны друг другу.

Теоремы

Теорема 1.

Сечение сферы плоскостью есть окружность, центр которой совпадает с основанием перпендикуляра, опущенного из центра сферы на секущую плоскость.

Доказательство:

Пусть сфера с центром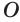

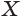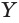Пусть и — произвольные точки линии пересечения сферы с плоскостью 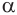. Треугольник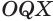и и 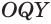оба прямоугольные, так как отрезок 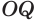перпендикулярен плоскости 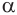, а значит, и отрезкам 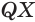и 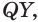лежащим в этой плоскости.

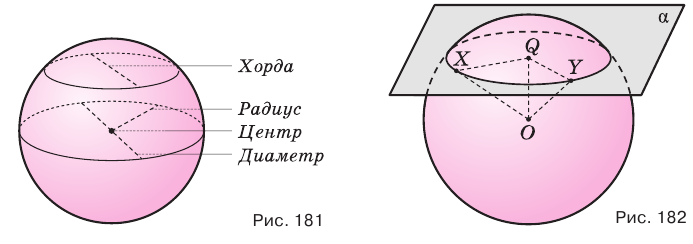
Отрезок 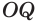является общим катетом, а гипотенузы этих треугольников равны как радиусы сферы. Поэтому треугольник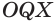и и 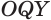равны друг другу, а значит, 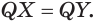Получили, что любые две точки линии пересечения сферы плоскостью 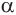равноудалены от основания перпендикуляра, опущенного из центра сферы на эту плоскость. Значит, эта линия является окружностью с центром .

Следствие. Радиус 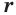сечения сферы плоскостью удовлетворяет условию 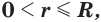где 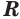— радиус сферы.

Сечение имеет наибольший радиус 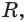если секущая плоскость проходит через центр сферы, это сечение называют большой окружностью, а ограниченный ею круг — большим кругом.

Плоскость, имеющая со сферой единственную общую точку, называется касательной плоскостью сферы. Общая точка сферы и касательной плоскости называется точкой касания.

Прямая касательной плоскости сферы, проходящая через точку касания, имеет со сферой единственную общую точку. Такая прямая называется касательной прямой сферы.

Теорема 2.

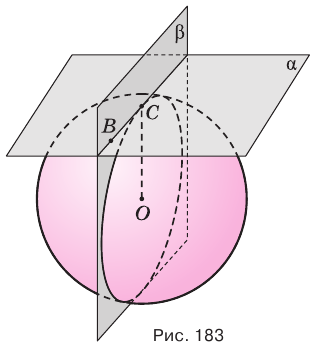
Касательная плоскость сферы перпендикулярна радиусу, проведенному в точку касания.

Доказательство:

Пусть плоскость 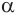касается сферы с центром 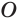в точке (рис. 183). Пусть 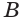— произвольная точка плоскости 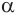, отличная от точки . Через точки 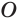, , 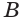проведем плоскость 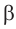, она по теореме 1 пересекает сферу по окружности. По отношению к этой окружности прямая 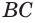является касательной, так как точка — их единственная общая точка. По свойству касательной к окружности радиус 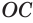перпендикулярен прямой 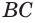. Таким образом, радиус 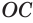перпендикулярен любой прямой 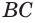, проведенной в плоскости а через ее точку . 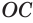Значит, радиус перпендикулярен плоскости .

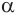Теорема 3.

Если плоскость проходит через точку сферы и перпендикулярна радиусу, проведенному в эту точку, то она является касательной плоскостью сферы.

Доказательство:

Пусть плоскость проходит через точку сферы и перпендикулярна радиусу 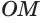(рис. 184). Пусть 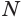— произвольная точка плоскости , отличная от точки . Треугольник 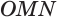прямоугольный с гипотенузой 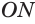, и она длиннее катета. Поэтому точка 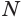расположена вне сферы. Получается, что любая точка плоскости , кроме точки , не принадлежит сфере. Значит, точка — единственная общая точка плоскости и сферы, а поэтому плоскость является касательной плоскостью сферы.

Теоремы 2 и 3 выражают соответственно свойство и признак касательной плоскости сферы.

Теорема 4.

Две сферы пересекаются по окружности, плоскость которой перпендикулярна прямой, проходящей через центры сфер.

Доказательство:

Пусть имеются две пересекающиеся сферы с центрам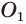и 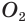и , и 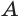— какая-либо их общая точка (рис. 185). Через точку 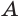проведем плоскость 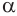, перпендикулярную прямой 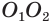. Пусть эта плоскость пересекает прямую 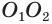в точке . В соответствии с теоремой 1 плоскость 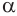пересекает одну и другую сферы по окружности с центром . Получили, что окружность с центром является общей окружностью данных сфер.

Других общих точек данные окружности не имеют. Допустим, что это не так. Пусть 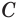— какая-либо общая точка сфер, не принадлежащая окружности с центром . Через точк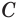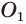и , и 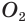проведем плоскость, которая пересечет сферы по окружностям с центрам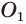и и 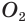. Эти окружности пересекаются в двух точках, которые принадлежат окружности с центром , и вместе с этим им обеим принадлежит точка .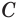

Но это противоречит утверждению о том, что две окружности имеют не более двух общих точек.

Прежде чем доказывать утверждение о поверхности сферы, обобщим утверждения о боковых поверхностях конуса, усеченного конуса и цилиндра.

Теорема 5.

Боковая поверхность конуса, усеченного конуса, цилиндра равна боковой поверхности цилиндра с той же высотой и радиусом основания, равным длине перпендикуляра, соединяющего середину образующей с точкой на оси этого тела.

Доказательство:

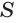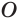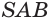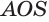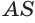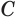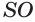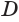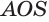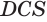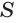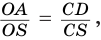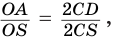Пусть есть конус с вершиной , основанием которого является круг с центром . Пусть — осевое сечение конуса (рис. 186). В плоскости к образующей из ее середины возведем перпендикуляр, который пересечет ось в некоторой точке . Прямоугольные треугольники и подобны, так как у них угол при вершине общий. Поэтому или или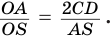

Отсюда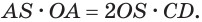

С учетом этого для боковой поверхности 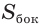конуса будем иметь:

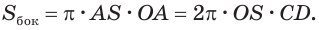
Пусть есть усеченный конус, полученный вращением прямоугольной трапеции 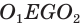со средней линией 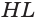вокруг боковой стороны 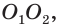которая перпендикулярна основаниям 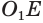и 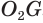, отрезок 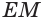— проекция 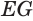на основание 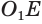(рис. 187).

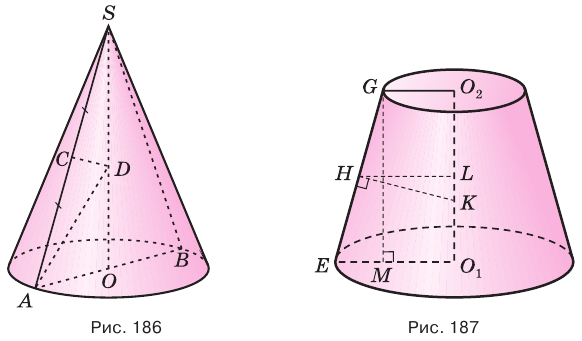
В плоскости 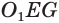к образующей 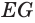усеченного конуса из ее середины 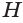возведем перпендикуляр, который пересечет ось 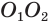в некоторой точке 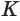. Прямоугольные треугольник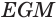и и 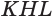подобны, так как их стороны попарно перпендикулярны. Поэтому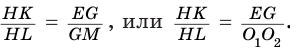

Отсюда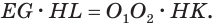

С учетом этого для боковой поверхности 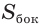усеченного конуса будем иметь:

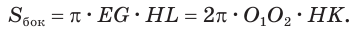
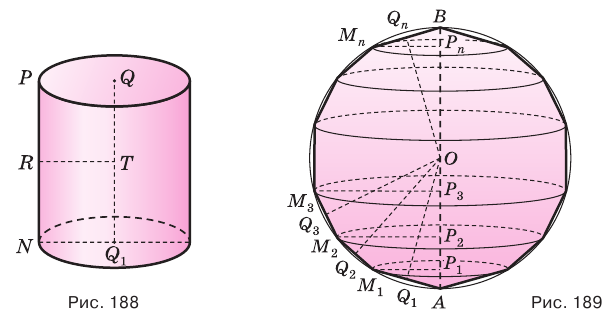
Для цилиндра утверждение очевидно (рис. 188).

Теорема 6.

Поверхность сферы равна учетверенной площади большого круга:

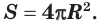
Доказательство:

Пусть есть сфера, образованная вращением полуокружности 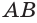вокруг своего диаметра (рис. 189). Впишем в эту дугу ломаную 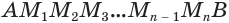с равными звеньями и из точек 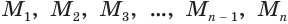опустим перпендикуляры 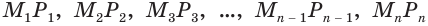на диаметр 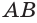. Пусть — середины звеньев ломаной. Тогда — серединные перпендикуляры к этим звеньям. При вращении вокруг 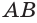звенья ломаной будут описывать или конусы, или усеченные конусы, или цилиндр. Поэтому, в соответствии с теоремой 5, для образовавшейся поверхности 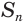получим

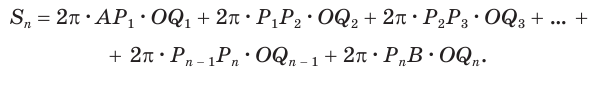
Учтем, что отрезки 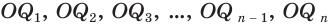все равны друг другу:

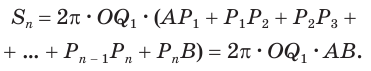
Пусть радиус сферы равен 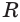. Тогда 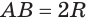. Будем неограниченно увеличивать количество звеньев ломаной. Тогда отрезок 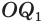будет стремиться к радиусу сферы, а выражение 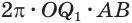— к выражению 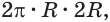т. е. к выражению 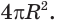Этот предел и принимается в качестве площади поверхности сферы.

Учитывая, что 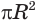выражает площадь большого круга, получим, что поверхность сферы равна учетверенной площади большого круга.

Уравнение сферы

Определение: Сферой радиуса R называется множество всех точек пространства, расстояние от каждой из которых до данной точки (центра) равно R.

Выведем уравнение сферы. Пусть 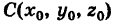— центр сферы радиуса 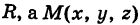— произвольная точка, лежащая на этой сфере (рис. 204). Тогда СМ = R. По формуле расстояния между двумя точками имеем

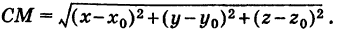
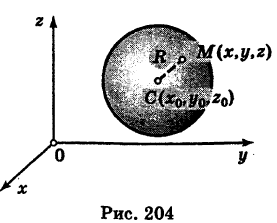
Приравнивая это выражение R, получим уравнение сферы

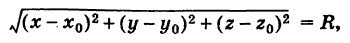
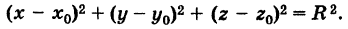
Если центр сферы совпадает с началом координат, то х₀ = 0, у₀ = 0, 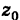= 0 и уравнение сферы принимает вид

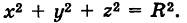
Пример:

Определить координаты центра и радиус сферы

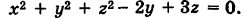
Решение:

Объединяя члены, содержащие одноименные текущие координаты, и дополняя их до полных квадратов, будем иметь

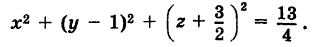
Следовательно, центр сферы находится в точке 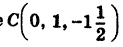и радиус ее

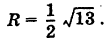
Заметим, что совокупность

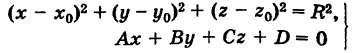
уравнений сферы и плоскости определяет окружность, по которой пересекаются плоскость и сфера (если это множество не пусто). В частности, если 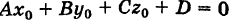, то совокупность этих уравнений изображает окружность большого круга.

Уравнение окружности можно также писать в параметрическом виде.

Пример:

Написать параметрические уравнения меридиана сферы

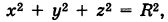
проходящего через полюсы 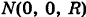и 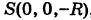, если плоскость меридиана образует угол а с координатной плоскостью Охг (рис. 205).

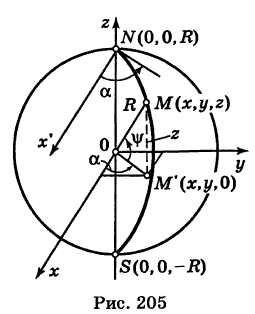
Решение:

За параметр текущей точки 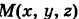меридиана примем угол 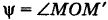— широту этой точки, где 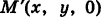— проекция точки М на координатную плоскость Оху . Так как 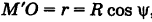, то из рис. 205 имеем

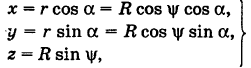
где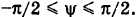

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Уравнение сферы

Определение. Сферой называется множество всех точек, расположенных на расстоянии от заданной точки . Точка называется центром сферы, — радиусом сферы.

Если точка — произвольная точка сферы, то по формуле расстояния между двумя точками имеем:

Это уравнение сферы с центром в точке и радиусом .

Если центр сферы находится в начале координат, то уравнение сферы радиуса имеет вид:

Как видно из рисунка, пересечение этой сферы с координатной плоскостью является ее большой окружностью.

Задача пример №47

Запишите уравнение сферы, радиус которой равен , а центр расположен в точке .

Решение:

Задача пример №48

Представьте фигуру, которая получается при пересечении сферы с плоскостью .

Решение:

радиус сферы . Учитывая в уравнении сферы, что получим : ;

Пересечение плоскости и данной сферы является окружность с центром в точке (0; 0; 12) и радиусом .

Плоскость, имеющая со сферой только одну общую точку, называется плоскостью, касательной к сфере.

Например, плоскость касается сферы в точке (0;0;13). Плоскость, касательная к сфере, в точке касания перпендикулярна радиусу сферы.

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Математика: полный курс решений задач в виде лекций

Другие темы которые вам помогут понять математику:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Координаты на сфере

Положение точки на сфере удобнее всего задавать так, как это делается в географии. На данной сфере радиуса R выберем какие-нибудь две диаметрально противоположные точки, одну из них N назовем условно се­верным полюсом, другую S — южным. Какой-нибудь из «меридианов» (кратчайший путь по сфере из S в N) назовем начальным меридиа­ном; проходящую через центр О сферы и пер­пендикулярную оси SN плоскость назовем экваториальной, а пересечение ее со сферой — экватором, на экваторе изберем направление, скажем против часовой стрелки, если смот­реть из N. Положение любой точки М на сфере определяется двумя координатами, одна из них, назовем ее долготой,—угол φ между плоскостью начального меридиана и плоскостью, проходя­щей через М и ось SN (угол должен отсчиты­ваться в направлении, соответствующем вы­бранному на экваторе). Широтой точки М бу­дем называть угол θ между радиусом ОМ и плоскостью экватора ( θ считается положитель­ным для точек северного полушария и отри­цательным для южного). Будем писать: М < φ ; θ >, ставя на первое место долготу, на второе — широту.

Пример. Проверьте правильность коор­динатного обозначения точек на рис. 21.

Все точки с одинаковой долготой φ ₀ запол­няют меридиан, уравнение которого поэтому φ = φ ₀. Все точки с одинаковой широтой θ ₀ заполняют параллель θ = θ ₀. Уравнение, связывающее текущие координаты φ и θ , опреде­ляет, как и в плоской геометрии, кривую; не­равенство, соответствующее этому уравнению, определяет одну или несколько областей, на которые эта кривая разделяет сферу. Так, не­равенство θ < 0 определяет южную полусферу, θ >0—северную; θ =0 есть уравнение экватора. Если сферу отнести к декартовым коорди­натам в пространстве, приняв центр О сферы за начало, ось SN — за ось z, ось х направив через точку <0; 0>, ось у — через<90°; 0>, то декарто­вы координаты х, y, z любой точки М сферы легко выразить через долготу и широту этой точки. Для этого выразим сначала координаты ее проекции М₁на плоскость Оху, где обычным образом расположим полярную систему коор­динат. Из рис. 21 видно, что для М₁(х; у; 0) полярный радиус r=Rcos θ , а полярный угол φ совпадает с долготой точки М. Кроме того,

z=Rsin θ . Приняв во внимание формулы (11), получим:

По этим формулам вычисляют декартовы коор­динаты точки М (х; у; z), если известны ее координаты φ и θ на сфере.

На эти же формулы можно взглянуть и с другой точки зрения. Будем считать со и 6 пе­ременными, придавая им всевозможные значе­ния в естественных пределах 0 ≤ φ <360°, -90° ≤ θ≤ +90°; тогда точка М< φ ; θ > будет пе­ремещаться по сфере, занимая всевозможные положения. Это напоминает параметрические уравнения линии, в которых декартовы коор­динаты х, y, z выражены через один перемен­ный параметр t. Разница лишь в том, что те­перь х, у, z выражены через два параметра, поэтому получается не линия (одномерное обра­зование), а поверхность (образование дву­мерное). Подобные уравнения называют пара­метрическими уравнениями поверхности; пере­менные параметры чаще всего здесь обозначают буквами и и v. Итак, уравнения сферы запи­шем в виде:

Если из этих уравнений исключить параметры и, v (для этого проще всего возвести (13) в квадрат и сложить; к сожалению, исключе­ние переменных не всегда так просто), полу­чим обычное ее уравнение x 2 + y 2 +z 2 =R 2 .

Уверен, у каждого домашнего мастера был случай, когда ему нужно было сделать разметку какой-нибудь круглой заготовки и найти центр ее основания. Казалось бы, это очень просто сделать, но некоторые мастера долго не могут найти выход в данной ситуации. Сегодня я покажу вам два простых решения, с помощью которых можно быстро и точной найти центр любой окружности.

1. Первый способ подойдет для разметки небольших заготовок. В качестве примера я возьму заглушку от пластиковой трубы диаметром 50 мм.

Для того, чтобы найти центр окружности заглушки, не нужны будут какие-то математические вычисления и сложные манипуляции. Нам понадобятся всего лишь строительный угольник и обычная линейка (или второй угольник), которые есть в любой мастерской.

Складываем вместе угольник и линейку, так чтобы образовался угол в 45 градусов.

Затем, придерживая одной рукой угольник и линейку, прикладываем их к круглой заготовке (заглушке) так, чтобы она вплотную соприкасалась с двумя сторонами угольника.

Теперь берем карандаш и чертим на заглушке первую линию, потом немного ее поворачиваем и делаем вторую метку (достаточно провести две линии, но для уверенности можно поставить три метки).

Все задача решена! Точка пересечения этих двух линий и будет центром данной окружности. Данный способ один из самых быстрых и простых.

2. Второй способ подойдет, если окружность имеет большой диаметр или она расположена на плоскости. Для примера я обвел карандашом крышку от кастрюли. В этом случае тоже все очень просто. Для начала выбираем любую точку на окружности.

Потом от этой точки чертим две линии до пересечения с окружностью так, чтобы у нас получился прямой угол (90 градусов). Для построения данных линий проще всего воспользоваться угольником (если окружность очень большая, линии можно продлить с помощью линейки).

А теперь все очень просто, соединяем точки, в которых пересекаются линии с окружностью и измеряем длину получившегося отрезка. Его середина и будет центром окружности. Уверен, многие помнят это из уроков по геометрии. Середина гипотенузы прямого треугольника вписанного в окружность, является центром этой окружности.