Как найти центр шара по уравнению

Урок «Сфера. Уравнение сферы»

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Продолжаем изучение сферы.

На прошлых занятиях вы познакомились с определением сферы и шара.

Вспомним, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Данная точка — центр сферы.

Заданное расстояние — радиус сферы.

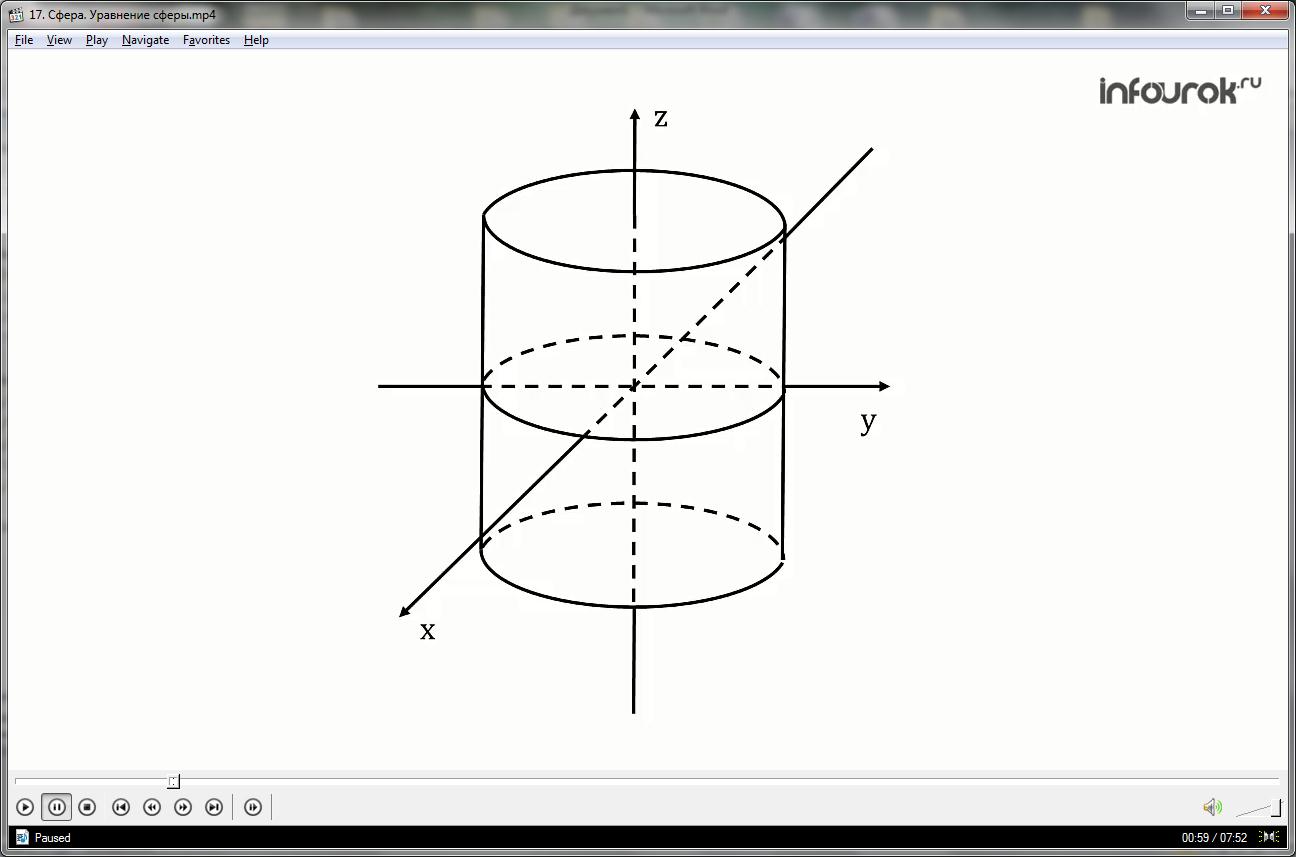
Прежде чем вывести уравнение сферы, познакомимся с понятием уравнения поверхности в пространстве.

Зададим прямоугольную систему координат Оxyz и некоторую поверхность F.

Уравнением поверхности F называется уравнение с тремя переменными x, y, z, если этому уравнению удовлетворяют координаты всех точек поверхности F и не удовлетворяют координаты точки, не принадлежащей этой поверхности.

1.Рассмотрим сферу радиуса R и с центром С(x0; y0; z0).

2.Найдём расстояние от произвольной точки М(x; y; z) до центра С( x0 ; y0 ; z0) по формуле для вычисления расстояния между двумя точками с заданными координатами.

3. Если точка М лежит на сфере, то отрезок МС равен радиусу R, то есть

4.В случае если точка М не принадлежит данной сфере, то R≠МС, значит, координаты точки М не удовлетворяют уравнению R2=(x-x0)2+(y-y0)2+(z-z0)2.

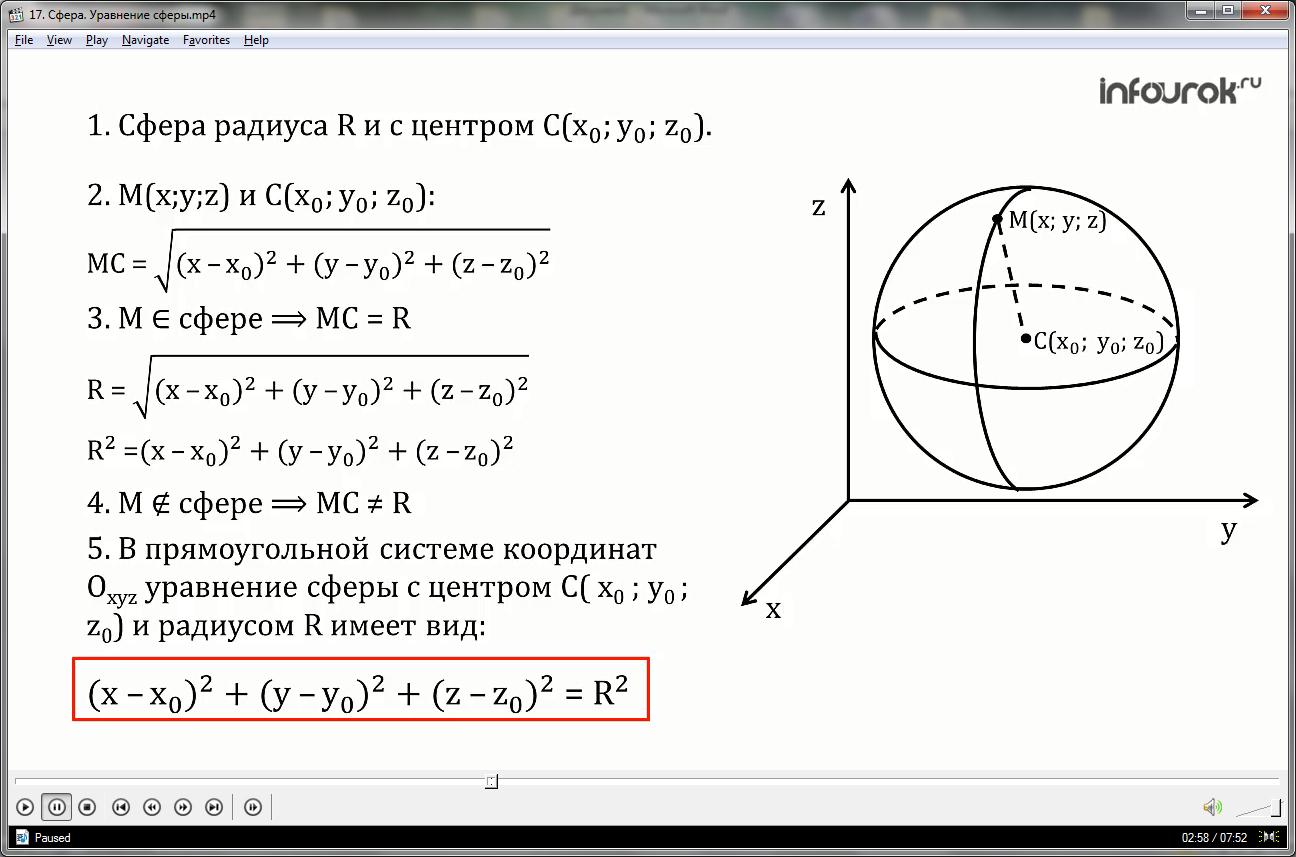
5. Таким образом, в прямоугольной системе координат Оxyz уравнение сферы с центром

С (x0 ; y0 ; z0) и радиусом R имеет вид:

Применим полученные знания при решении задач.

Записать уравнение сферы с центром в точке А, которая проходит через точку N, если А(-2;2;0) и N(5;0;-1).

1.Запишем уравнение сферы с центром

А (x0 ; y0 ; z0) и радиусом R:

2.Подставим соответствующие координаты центра сферы А в данное уравнение:

Уравнение сферы с центром в точке А с координатами (-2;2;0) примет вид:

3.Так как сфера проходит через точку N с координатами (5;0;-1), то её координаты удовлетворяют уравнению сферы, подставим координаты этой точки в полученное уравнение:

Таким образом, уравнение сферы с центром в точке А, которая проходит через точку N имеет вид:

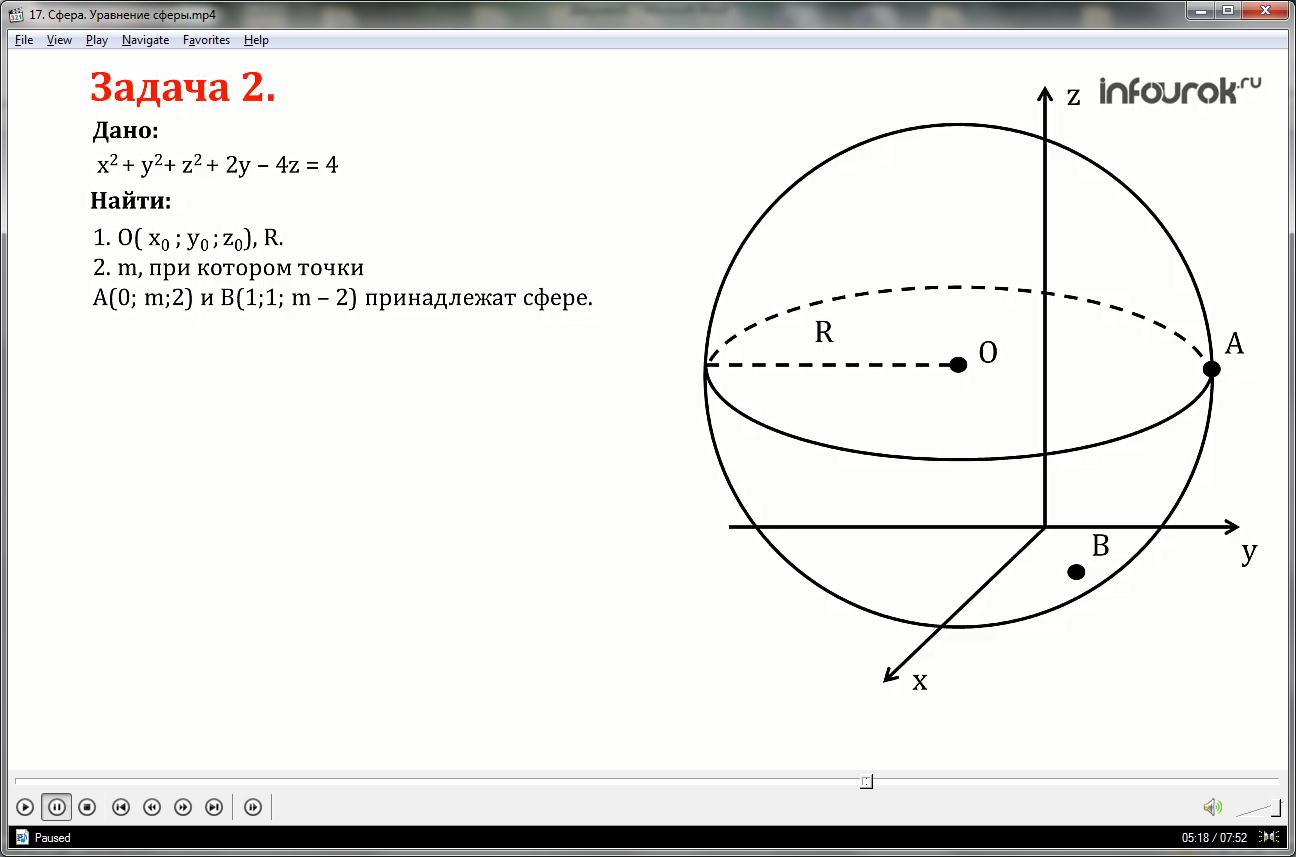
Сфера задана уравнением:

1) Найти координаты центра и радиус сферы;

2) Найти значение m, при котором точки

А (0; m;2) и В (1;1; m-2) принадлежат данной сфере.

1. Уравнение данной сферы имеет вид:

x2+ y2+ z2+2y-4z=4 или x2+ y2+2y + z2-4z=4

Выделим полный квадрат для переменных y и z, для этого прибавим и одновременно вычтем 1 и 4 в левой части уравнения:

x2+ y2+2y+1-1 + z2-4z+4-4=4

Уравнение примет вид:

x2+( y+1)2+( z-2)2-5=4 или

Таким образом, центр сферы имеет координаты:

О (0;-1;2), радиус равен R=√9=3

2.Уравнение сферы с центром в точке О (0;-1;2) и радиусом R=3 имеет вид:

Точки А (0; m;2) и В (1;1; m-2) принадлежат данной сфере, значит их координаты удовлетворяют уравнению сферы. Подставим координаты этих точек в уравнение сферы и решим систему уравнений:

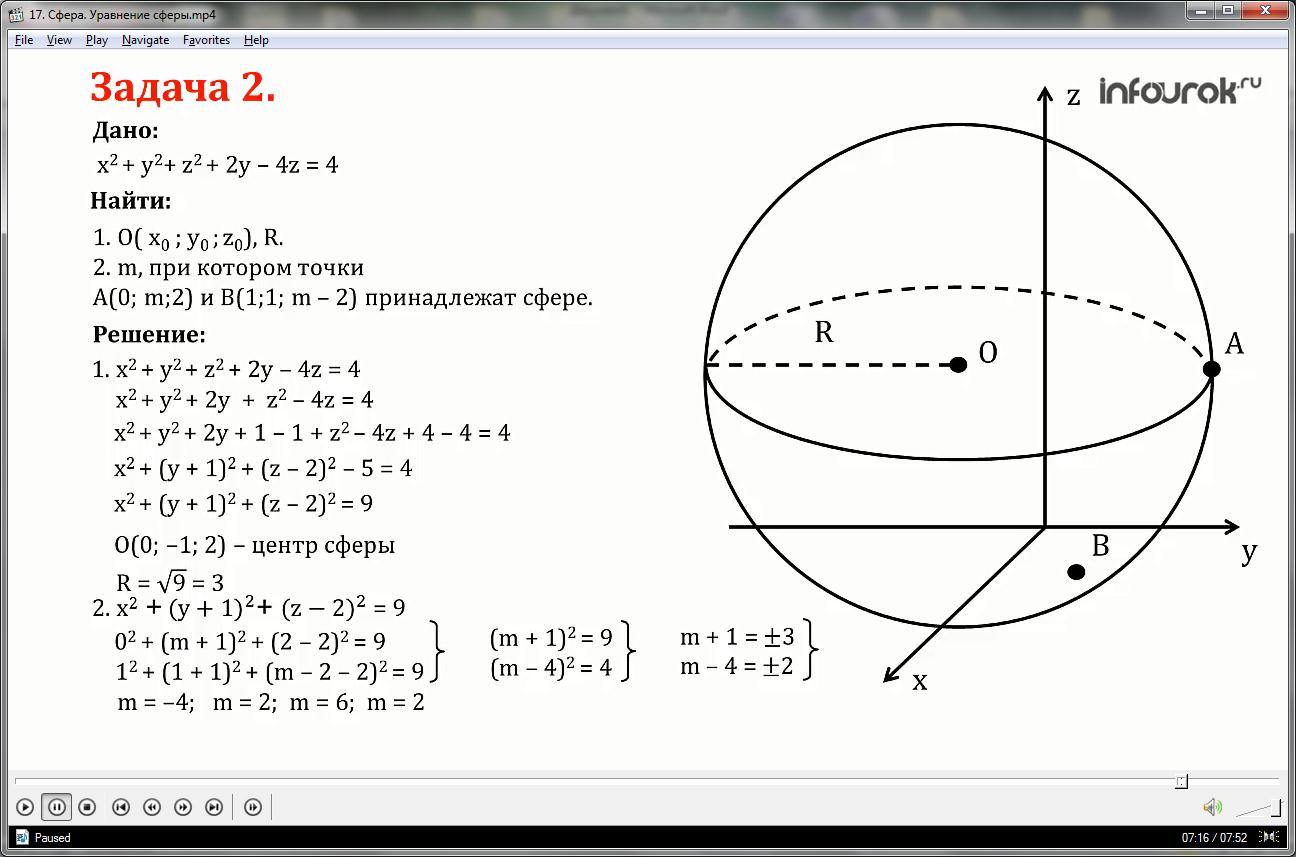
Упростим полученные уравнения, раскрывая скобки и приводя подобные слагаемые:

Таким образом, мы получили 4 значения m:

Несложно проверить, что при m=-4 и m=6 координаты точек А и В не удовлетворяют уравнению сферы. Проверьте самостоятельно.

Итак, при m=2 точки А (0; m;2) и В (1;1; m-2) принадлежат сфере, заданной уравнением

x2+ y2+ z2+2y-4z=4 с центром в точке

О (0;-1;2) и радиусом R=3.

—> —>

Инфоурок

07.11.2014

Геометрия

Видеоурок

51611

1003

АвторДата добавленияРазделПодразделПросмотровНомер материала

© 2022 Проект «Уроки математики»

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

Сфера, шар, сегмент и сектор. Формулы и свойства сферы

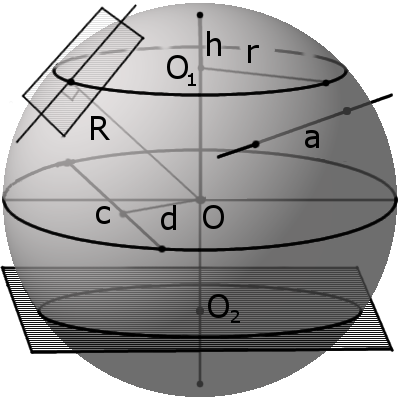
Формула. Объём шара:

V =	4	π R 3 =	1	π D 3
3	6

S = 4 π R 2 = π D 2

Уравнение сферы

x 2 + y 2 + z 2 = R 2

( x — x ₀) 2 + ( y — y ₀) 2 + ( z — z ₀) 2 = R 2

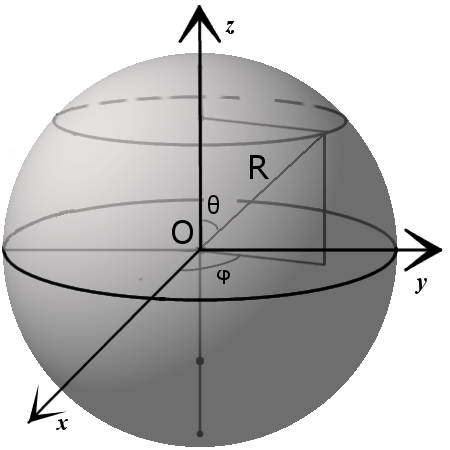
Основные свойства сферы и шара

Секущая, хорда, секущая плоскость сферы и их свойства

d m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m r такого круга можно найти по формуле:

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Касательная, касательная плоскость к сфере и их свойства

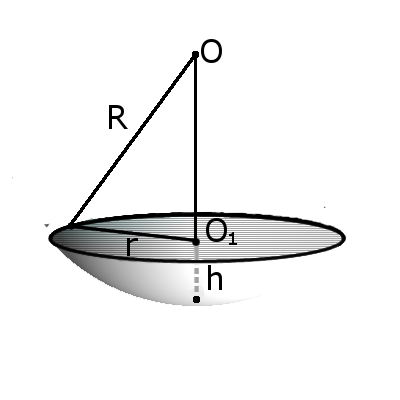
Формула. Объём сегмента сферы с высотой h через радиус сферы R:

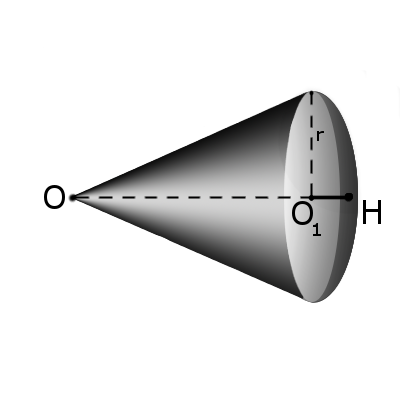
S = π R(2 h + √ 2 h R — h 2 )

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Урок №8. Сфера и шар

Перечень вопросов, рассматриваемых в теме:

• что такое сфера, какие у неё есть элементы (центр, радиус, диаметр сферы);
• что такое шар и его элементы;
• уравнение сферы;
• формула для нахождения площади поверхности сферы;
• взаимное расположение сферы и плоскости;
• теорема о радиусе сферы, который проведён в точку касания и теорему обратную данной.

Глоссарий по теме:

Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.

Круг – это часть плоскости, ограниченная окружностью.

Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

– уравнение сферы радиуса R и центром С(x₀; y₀; z₀).

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Основные теоретические факты

По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.

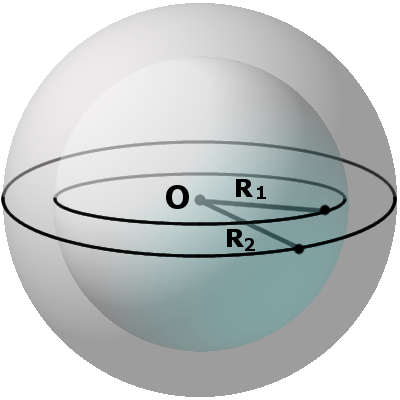
Рисунок 1 – Сфера с центром в точке О и радиусом R

Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

Сферу можно получить ещё одним способом — вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.

2. Уравнение сферы

Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.

Пусть сфера имеет центром точку С (x₀; y₀; z₀) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:

МС=

Исходя из понятия уравнения поверхности, следует, что если точка М лежит на данной сфере, то МС=R, или МС 2 =R 2 , то есть координаты точки М удовлетворяют уравнению:

.

Это выражение называют уравнением сферы радиуса R и центром С(x₀; y₀; z₀).

3. Взаимное расположение сферы и плоскости

Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.

1. Пусть dR. Если расстояние от центра сферы до плоскости меньше радиуса сферы, тогда сфера и плоскость пересекаются, и сечение сферы плоскостью есть окружность.

2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.

3. Пусть dR. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Рассмотрим случай касания более подробно.

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Теорема (свойство касательной плоскости).

Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Теорема (признак касательной плоскости):

Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.

4. Основные формулы

Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:

Формула для вычисления площади поверхности сферы и ее элементов:

S=4πR 2 – площадь сферы.

S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

– площадь поверхности сектора с высотой h.

Примеры и разбор решения заданий тренировочного модуля

1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.

Площадь круга вычисляется по формуле: S_кр=πR 2 .

Площадь поверхности шара вычисляется по формуле: S_сф=4πR 2 . Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.

2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.

Площадь сферы равна S_сф=4πR 2 . То есть S_сф=100π.

По условию площадь круга некоторого радиуса r также равна 100π. Значит, r 2 =100, то есть r=10.

3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15

Окружность, вписанная в треугольник, является сечением сферы.

Найдем ее радиус.

Площадь треугольника с известными сторонами можно вычислить по формуле Герона:

С другой стороны, S=p·r.

Теперь найдем расстояние от центра шара до секущей плоскости.

4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.

Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.

Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.

На этом уроке мы вспомним понятия сферы и шара. Дадим
их определения. Рассмотрим их основные элементы. А также выведем уравнение
сферы радиуса  с
центром в точке .

Итак, рассмотрим понятия сферы и шара. В окружающем
мире предметы имеют очень разнообразные формы. Среди них встречаются так
называемые «круглые тела». Особое место среди круглых тел занимает шар.

Итак, шар – это геометрическое тело.

Форму, близкую к форме шара, имеют шарики
мороженного, снежный ком, бусинки, светильники.

Некоторые архитектурные сооружения.

Декоративным растениям также придают форму шара.

Поверхность шара называют сферой. Можно
сказать, что сфера – это как-бы оболочка или граница шара. Как
окружность, есть граница круга, так и сфера – это граница шара.

Представление о сфере дают полые круглые
предметы, например, мячи (футбольный, баскетбольный, волейбольный и т.д.), шарики
для украшения ёлки, мыльные пузыри.

А также ставший популярным видом отдыха в наше время
«аквазорбинг». Зорб даёт представление о сфере.

Сфера входит в число наиболее привлекательных
пространственных фигур. Использование в строительстве и архитектуре
конструкций, имеющих форму сферы, придает сооружениям особое величие и служит
подтверждением тому, что сфера – достаточно гармоничная геометрическая фигура.

Чтобы уяснить разницу между понятиями шар и сфера,
давайте внимательно посмотрим на экран.

Перед вами изображены воздушный шар и бильярдный шар. Отметим,
что оба этих предмета называют шарами. Однако в первом случае мы имеем дело со
сферой, а во втором с полноценным шаром со своим содержимым внутри.

Определение:

Сферой
называется поверхность, состоящая из всех точек пространства, расположенных на
данном расстоянии от данной точки.

А теперь назовём основные элементы сферы.

Данная точка называется центром сферы (в
нашем случае это точка О), а данное расстояние – радиусом сферы.
Радиус сферы часто обозначают латинской буквой .

Любой отрезок, соединяющий центр и какую-нибудь точку
сферы, также называется радиусом сферы. Все радиусы одной сферы равны
между собой.

Хордой
сферы называется отрезок, соединяющий две точки сферы.

Отрезок, соединяющий две точки сферы и проходящий
через её центр, называется диаметром сферы. Любой диаметр сферы равен
двум радиусам .

Тело, ограниченное сферой, называется шаром.

Определение:

Шар – это
совокупность всех точек пространства, находящихся от центра на расстоянии, не
больше заданного.

Центр, радиус, хорда и диаметр сферы называются также
центром, радиусом, хордой и диаметром шара.

Т.е. отрезок, соединяющий любую точку сферы с центром
шара, называется радиусом шара.

Отрезок, соединяющий две точки сферы называется хордой
шара.

Отрезок, соединяющий две точки сферы и проходящий
через центр шара, называется диаметром шара. Диаметр шара равен двум
радиусам .

Рассмотрим чертёж.

Перед нами математическое изображение шара. Точка О –
это центр шара. Все точки поверхности шара одинаково удалены от
центра шара. Понятно, что шар радиуса  с
центром О содержит все точки пространства, расположенные от точки О на
расстоянии, не превышающем  (включая
саму точку О), и не содержит других точек.

Хотелось бы обратить внимание на то, что шар может
быть получен путём вращения полукруга вокруг его диаметра.

При этом сфера образуется в результате вращения
полуокружности вокруг её диаметра.

Задача: отрезок
 –
хорда сферы, не проходящая через центр сферы .
Вычислите расстояние от центра сферы до середины хорды ,
если радиус сферы равен  см,
а длина хорды  равна
 см.

Решение: обозначим
середину хорды  точкой
.

Рассмотрим .
Он равнобедренный, т.е. ,
так как .
А как мы знаем, все радиусы одной сферы равны между собой. Отсюда,  (см).

Теперь рассмотрим .
Он прямоугольный, так как отрезок  является
серединным перпендикуляром проведённым к хорде .
Его катет  (см).

Воспользовавшись теоремой Пифагора найдём катет ,
который как раз таки и есть расстояние от центра сферы до середины хорды .
Получаем, что  (см).

Запишем ответ.

Перейдём к уравнению сферы.

Для начала вспомним, что уравнение с тремя переменными
,
,
 называется
уравнением поверхности ,
если этому уравнению удовлетворяют координаты любой точки поверхности  и
не удовлетворяют координаты никакой точки, не лежащей на этой поверхности.

Напомним, что уравнение плоскости, проходящей через
точку  и
перпендикулярной к ненулевому вектору  имеет
следующий вид:

где

Теперь давайте выведем уравнение сферы радиуса  с
центром в точке .

Напомним, что расстояние от произвольной точки  до
точки  вычисляется
по формуле:

Если точка  лежит
на данной сфере, то расстояние ,
или ,
т.е. координаты точки  удовлетворяют
уравнению:

Если же точка  не
лежит на данной сфере, то расстояние ,
или ,
т.е. координаты точки  не
удовлетворяют уравнению сферы.

Следовательно, в прямоугольной системе координат
уравнение сферы радиуса  с
центром в точке :

Если уравнение относительно прямоугольных координат  определяет
поверхность в пространстве, то ею является сфера.

Задача: напишите
уравнение сферы с центром в точке  радиусом
равным  см.

Решение: запишем
уравнение сферы в общем виде, где ,
 и
 –
координаты центра сферы.

Подставим заданные координаты центра сферы в
уравнение. Получим, что уравнение данной нам сферы выглядит так:

Запишем ответ.

Задача: найдите
координаты центра и радиус сферы, заданной уравнением: .

Решение: запишем
уравнение сферы в общем виде, где ,
 и
 –
координаты центра сферы.

Тогда не трудно заметить, что координаты центра сферы
будут равны 2, – 1, 0.

А радиус заданной сферы равен .

Не забудем записать ответ.

Задача: какую
поверхность определяет уравнение

 ?

Решение: запишем
уравнение сферы в общем виде, где ,
 и
 –
координаты центра сферы.

Преобразуем наше уравнение.

Разделим почленно это уравнение на 4.

Получим, .

Затем выделим полные квадраты. Получим, .
 

Преобразуем слагаемые получившегося выражения.
Получим, .

Теперь сравним последнее уравнение с уравнением сферы
в общем виде. Заметим, что исходное уравнение определяет сферу с центром в
точке  и .

Запишем ответ.

Итоги:

На этом уроке мы вспомнили понятия сферы и шара. Узнали,
что сферой называется поверхность, состоящая из всех точек пространства,
расположенных на данном расстоянии от данной точки. А шар – это совокупность
всех точек пространства, находящихся от центра на расстоянии, не больше
заданного. Назвали основные элементы сферы и шара. А также вывели уравнение
сферы радиуса  с
центром в точке .

План урока:

Понятие сферы и шара

Уравнение сферы

Пересечение сферы плоскостью

Касательная плоскость к сфере

Пересечение двух сфер

Площадь сферы

Вписанные и описанные сферы

Понятие сферы и шара

Люди постоянно сталкиваются с предметами, имеющими форму шара. В большинстве спортивных игр (баскетболе, большом и настольном теннисе, футболе) используются мячи, которые по форме как раз являются шарами. Такую же форму имеют многие фрукты – яблоки, апельсины, мандарины. Более того, известно, что Земля, другие планеты и звезды, большинство крупных спутников также представляют собой шары.

Важно отличать шар от сферы. Сферой называют только поверхность шара. Сам же шар является объемной фигурой, к нему относят всю часть пространства, ограниченную сферой.

Дадим строгие определения сферы и шара:

Отрезок, соединяющий точку на сфере с ее центром, именуется радиусом сферы. Он же называется и радиусом шара, заключенного внутри этой сферы.

Проходящий через центр сферы отрезок, чьи концы принадлежат сфере, именуется диаметром сферы. Сама сфера считается частью шара, также как и окружность считается частью круга.Показывают шар или сферу на рисунке так:

Из определения сферы явно вытекает тот факт, что все ее радиусы одинаковы. Это в свою очередь означает, что центр сферы – это середина диаметра, и диаметр вдвое длиннее радиуса.

Заметим, что сфера является телом вращения. Она получается при повороте полуокружности вокруг ее диаметра:

Уравнение сферы

В планиметрии мы уже изучали уравнения линии. Так назывались ур-ния с двумя переменными, каждое решение которых соответствовало точке на координатной плос-ти, принадлежавшей заданной линии. Если же точка не принадлежала линии, то ее координаты решением соответствующего ур-ния не являлись. В частности, нам удалось получить уравнения прямой и окружности.

Аналогично в стереометрии вводится понятие уравнения поверхности. Так как в пространстве используются уже три координаты (х, у и z), то ур-ния поверхности содержат три переменных. Координаты всякой точки, принадлежащей поверхности, будут являться решениями ур-ния этой поверхности. И наоборот, координаты точки, не принадлежащей поверхности, будут обращать ур-ние поверхности в неверное равенство.

Выведем ур-ние сферы. Пусть ее центр располагается в точке С с координатами (х₀, у₀, z₀), а радиус обозначен как R. Возьмем произвольную точку А на сфере. По определению сферы расстояние между А и С должно составлять R:

Мы уже знаем формулу для расчета расстояния между А и С:

Точки, координаты которых удовлетворяют этому неравенству, находятся от центра сферы на расстоянии меньше ее радиуса. Это значит, что они находятся внутри сферы, то есть принадлежат шару, чьей поверхностью является рассматриваемая сфера. Если же координаты точки удовлетворяют неравенству

то можно утверждать, что точка находится вне пределов сферы, то есть она не принадлежит ни сфере, ни шару.

Задание. Напишите уравнение сферы, центр которой располагается в точке (2; – 4; 7) и чей радиус равен 3.

Решение. Здесь мы просто подставляем координаты центра сферы и ее радиус в ур-ние сферы:

Задание. Есть сфера с радиусом 9, чей центр располагается в точке О(2; 3; 4). Определите, какие из следующих точек будут принадлежать этой сфере: А(1; 7; – 4), В(0; 6; 10), С(– 2; – 1; 11), D(5; 6; 8).

Решение. Сначала составляем уравнение сферы, описанной в условии:

Равенство неверное, значит, В не располагается на сфере (более того, раз 49 < 81, то можно утверждать, что точка располагается внутри сферы). Далее проверяем точку С(– 2; – 1; 11):

Задание. Докажите, что ур-ние

является ур-нием сферы, после чего определите радиус этой сферы.

Решение. Здесь необходимо выполнить некоторые преобразования ур-ния, чтобы оно стало похожим на ур-ние сферы. Для этого используем формулы квадратов суммы и разности:

Пересечение сферы плоскостью

Рассмотрим ситуацию, когда секущая плоскость α пересекает сферу. Нас в первую очередь интересует форма получающегося сечения. Опустим из точки О, центра сферы, перпендикуляр ОН на секущую плос-ть (пока мы рассматриваем случай, когда секущая плос-ть проходит не через О):

Буквами А и В обозначим любые две точки сечения, которые принадлежат одновременно и сфере, и плос-ти α. Теперь сравним ∆ОНА и ∆ОНВ. Они прямоугольные, ведь ОН – перпендикуляр к α. При этом у них есть общий катет ОН и одинаковые гипотенузы ОА и ОВ (это радиусы одной сферы).Тогда эти ∆ОНА и ∆ОНВ одинаковы, и поэтому

AH = BH

Мы выбрали точки А и В произвольно, и они оказались равноудаленными от Н. Значит, А и В находятся на одной окруж-ти с центром Н. Легко показать и обратное – любая точка этой окруж-ти будет лежать и на сфере (попробуйте сделать этот сами). Значит, сечение имеет форму окруж-ти, причем ее центр – это основание перпендикуляра, проведенного из О на α.

Обозначим длину перпендикуляра ОН буквой h, радиус сферы буквой R и радиус сечения буквой r. Тогда, используя теорему Пифагора, мы можем составить формулу для расчета радиуса r сечения:

Видно, что чем длиннее перпендикуляр h(он представляет собой расстояние от О до α), тем меньше радиус сечения. Тогда ясно, что наибольший радиус будет у того сечения, которое проходит через центр О. Действительно, если сечение проходит через О, то все его точки по определению сферы будут удалены на расстояние R от О. Но уже по другому определению такое множество точек – окруж-ть с центром в О и радиусом R. Плос-ть, проходящая через центр сферы, именуется диаметральной плоскостью, а само сечение именуют большой окружностью сферы. Радиус большой окруж-ти совпадает с радиусом самой сферы.

Задание. Сфера с радиусом 41 пересечена плос-тью, которая находится на расстоянии 9 от центра этой сферы. Найдите площадь сечения.

Решение. Опустим из центра сферы О перпендикуляр ОН на секущую плос-ть, тогда по условию ОН = 9. Пусть А – точка на сечении, тогда ОА = 41. ∆ОНА – прямоугольный, поэтому мы можем найти радиус АН:

Теперь площадь сечения можно рассчитать по известной формуле площади круга:

Ответ: 1600π.

Задание. Докажите, что если через три точки сферы провести окруж-ть, то все точки этой окруж-ти будут также принадлежать сфере.

Решение. Пусть на сфере есть точки А, В, С. Проведем через них окруж-ть L. Надо доказать, что произвольная точка D, принадлежащая этой окруж-ти, также будет находиться на сфере.

Через точки А, В и С можно провести единственную плос-ть АВС. Она будет секущей для сферы, ведь она имеет с ней как минимум три общих точки – А, В и С. Формой этого сечения будет некоторая окруж-ть L₁. L₁ обязательно будет проходить через А, В и С. Но через любые три точки можно провести не более одной окружности, поэтому L и L₁ совпадают. Значит, D, принадлежащая по условию L, будет также принадлежать и L₁. Но L₁– это сечение, все его точки, в том числе и D, принадлежат сфере, ч. т. д.

Есть смысл запомнить доказанное утверждение:

Задание. На сфере радиусом 13 отмечены точки А, В и С так, что АВ = 6, ВС = 8 и АС = 10. Каково расстояние между центром сферы и плос-тью АВС?

Решение. Сначала заметим, что ∆АВС является прямоугольным, ведь его стороны удовлетворяют теореме Пифагора:

Напомним одного из свойств прямоугольного треугольника – центр окруж-ти, описанной около него, совпадает с серединой его гипотенузы. То есть если через точки А, В и С провести окруж-ть, то ее центр Н будет серединой АВ, и поэтому

Теперь заметим, что эта описанная окруж-ть должна быть сечением сферы. Это значит, что ОН – перпендикуляр к плос-ти АВС, ведь центр сечения должен лежать на перпендикуляре к плос-ти, проведенном из О. Тогда ∆ОНС – прямоугольный, и ОН – искомое нами расстояние. ОС – радиус сферы. Рассчитаем по теореме Пифагора ОН:

Касательная плоскость к сфере

Плос-ть, имеющая со сферой строго одну общую точку, именуется касательной плоскостью к сфере.

Действительно, если плос-ть касается окруж-ти, то точка касания А должна располагаться на расстоянии R от центра сферы О, где R– радиус сферы. Все остальные точки касательной плос-ти находятся вне пределов сферы, то есть должны находиться от О на расстоянии, превышающем R. Это значит, что отрезок ОА должен быть кратчайшим отрезком, соединяющим О и касательную плос-ть. Но мы знаем, что кратчайший отрезок между плос-тью и точкой – это как раз перпендикуляр, опущенный из точки на плос-ть.

Справедливо и обратное утверждение:

Доказательство. Если радиус ОА – перпендикуляр к плос-ти α, то он является кратчайшим расстоянием между плос-тью и центром О. Тогда все остальные точки плос-ти располагаются на большем расстоянии от О, чем точка А. Это значит, что они не располагаются на сфере. Значит, у сферы и плос-ти α одна общая точка А, а потому α по определению – касательная плос-ть.

По аналогии с касательной плос-тью существует понятие касательной прямой к сфере.

Касательная к сфере обладает почти теми же свойствами, что и касательная к окруж-ти.

Доказательство. Пусть m– касательная прямая к сфере с центром О. обозначим точку касания как А. Далее через прямую m и центр О проведем плос-ть α. Нам надо показать, что ОА⊥m:

Плос-ть α будет диаметральной плос-тью. Сечение будет иметь форму окруж-ти с центром О и радиусом ОА. Прямая m будет касательной к этой окруж-ти, ведь она имеет с ней общую точку А, а второй общей точки m и окруж-ть иметь не могут, ведь такая бы точка была бы также общей для m и сферы, а m по определению имеет лишь одну общую точку со сферой. Напомним, что касательная к окруж-ти перпендикулярна радиусу, то есть m⊥ОА, ч. т. д.

Будет верным и обратное утверждение:

Для доказательства используем ту же картинку. Известно, что m⊥ОА, надо показать, что m– касательная к сфере. Проведем через пересекающиеся прямые m и ОА плос-ть α. Она снова окажется диаметральной плоскостью, и снова сечением будут окруж-ть с радиусом ОА. По признаку касательной, который мы изучали в планиметрии, m– касательная к этой окруж-ти, ведь m⊥ОА. То есть в плос-ти α есть лишь одна общая точка m и сферы. В других плос-тях у них не может быть общих точек, так как m полностью принадлежит α. В итоге у m и сферы только одна общая точка, а потому m– касательная к сфере, ч. т. д.

Рассмотрим ещё одно утверждение:

Сначала разберемся с понятием отрезков касательных. Пусть из точки А, лежащей вне сферы, к ней проведены две касательные, а точки касания обозначены буквами В и С. Тогда АВ и АС как раз и будут отрезками касательных:

Докажем, что эти отрезки одинаковы. Для этого к точкам касания проведем радиусы ОВ и ОС. Теперь сравним ∆АВО и ∆АСО. Они прямоугольные, ведь ОВ⊥АВ по свойству касательной, и ОС⊥АС. Гипотенуза АО у этих треугольников общая, а катеты ОВ и ОС – это одинаковые радиусы. Получается, что ∆АВО и ∆АСО равны, а потому отрезки АВ и АС одинаковы.

Задание. Дан шар радиусом 10 см, к которому проведена касательная плос-ть α. Через точку касания проведена секущая плос-ть β, образующая с α угол в 30°. Вычислите площадь сечения шара плос-тью β.

Решение. Обозначим точку касания как А. Опустим из центра сферы о перпендикуляр ОН на плос-ть β. Тогда отрезок АН будет радиусом сечения. Так как угол между плос-тями α и β составляет 30° (на рисунке он показан как ∠НАС), то

Ответ: 25π см².

Задание. Некоторое тело представляет собой шар, внутри которого есть полость, также имеющая форму шара, причем центры этих шаров совпадают. Докажите, что площадь сечения этого тела, проходящего через центр шаров, совпадает с площадью сечения, являющегося касательной к внутреннему шару.

Решение. Обозначим радиус большей сферы как R, а радиус меньшей (внутренней сферы) как r. Площадь центрального сечения в виде кольца (показано синим цветом) представляет собой разницу между площадью большого круга с радиусом R и малого с радиусом r:

Задание. Сфера радиусом 5 см касается каждой стороны треугольника со сторонами 13, 14 и 15 см. Каково расстояние между центром этой сферы и плос-тью треугольника?

Решение. Обозначим вершины треугольника точками А, В и С. Пусть

AB = 13

AC = 14

BC = 15

Заметим, что плос-ть АВС – секущая, а само сечение имеет форму окруж-ти. Эта окруж-ть будет касаться сторон ∆АВС, то есть она является вписанной окруж-тью. Как вычислить ее радиус НK?

Напомним одну из формул для расчета площади треугольника:

Площадь ∆АВС можно найти по формуле Герона. Предварительно найдем полупериметр ∆АВС:

Пересечение двух сфер

Пусть есть две пересекающиеся сферы с центрами в точках О₁ и О₂ с радиусами R₁ и R₂ соответственно. Какую форму будет иметь линия L, по которой они пересекаются?

Эта линия является множеством точек, которые принадлежат как первой, так и второй сфере. Обозначим две произвольные точки этой линии буквами А и В:

Проведем радиусы О₁А, О₁В, О₂А и О₂В. Теперь сравним ∆АО₁О₂ и ∆ВО₁О₂. Сторона О₁О₂ у них общая, а другие стороны попарно равны как радиусы сфер:

Получается, что ∆АО₁О₂ и ∆ВО₁О₂ равны. Теперь из точек А и В опустим высоты на прямую О₁О₂. Из равенства ∆АО₁О₂ и ∆ВО₁О₂ вытекает два факта:

• эти высоты упадут в одну точку Н;
• эти высоты будут одинаковы, то есть АН = НВ.

Другими словами, А и В равноудалены от Н. Получается, что точки А и В находятся на окруж-ти, центр которой – точка Н. Заметим, что О₁О₂ – перпендикуляр к плоскости окружности, ведь О₁О₂⊥АН и О₁О₂⊥ВН.

Точки А и В были выбраны произвольно, поэтому можно утверждать, что любые точки линии L будут находиться на одной окруж-ти. Докажем и обратное утверждение – любая точка, лежащая на этой окруж-ти, будет принадлежать линии L. Возьмем на окруж-ти какую-нибудь точку С и построим радиус НС:

Теперь сравним ∆О₁НС и ∆О₁НА. Они прямоугольные, ведь О₁Н – перпендикуляр к плос-ти окружности. Катет О₁Н у них общий, а катеты АН и НС одинаковы как радиусы окруж-ти. Значит, ∆О₁НС и ∆О₁НА равны, и потому

Это равенство означает, что С принадлежит сфере с центром в О₁. Аналогично рассмотрев ∆О₂НС и ∆О₂НА, можно показать, что С также принадлежит и второй сфере. Тогда С принадлежит пересечению этих сфер.

Итак, всякая точка линии L лежит на окруж-ти с центром Н, и наоборот, каждая точка этой окруж-ти лежит на линии L. Это означает, что L как раз и является этой окружностью.

Отметим ещё один факт: по неравенству треугольника отрезок О₁О₂ должен быть меньше суммы отрезков О₁А и О₂А, то есть суммы радиусов сфер.

Задание. Сферы имеют радиусы 25 см и 29 см, а расстояние между их центрами составляет 36 см. Вычислите радиус окруж-ти, по которой они пересекаются.

Решение. Пусть А – одна их точек сечения. Искомый радиус обозначим как АН. В итоге получим такую картинку:

Площадь сферы

Сферическая поверхность, как и всякая другая ограниченная поверхность, имеет какую-то площадь. Напомним, что для вычисления площадей цилиндрической и конической поверхности мы строили их плоские развертки и находили площади уже этих разверток, используя формулы из планиметрии. Оказывается, что для сферы построить такую развертку невозможно. Мы не будем доказывать строго этот факт, но он известен из географии – любая карта Земли, которая как раз и должна быть разверткой сферической поверхности нашей планеты, является неточной и сильно искажает форму и размеры континентов. Если бы существовал способ построить точную развертку, то и географические карты не имели бы таких искажений.

Однако вычислить площадь сферы всё же можно по известной формуле:

Сейчас мы не будем доказывать эту формулу. Отметим лишь, что для ее получения необходимо использовать интегралы.

Задание. Какова площадь сферы с радиусом 5 см?

Решение. Просто используем формулу:

Ответ: 100π см².

Вписанные и описанные сферы

Если каждая точка многогранника лежит на поверхности сферы, то говорят, что многогранник вписан в сферу. Тогда сферу именуют описанной, а многогранник – вписанным.

Если же сфера касается каждой грани многогранника, то уже наоборот, сфера вписана в многогранник. Тогда уже сфера будет вписанной фигурой, а многогранник – описанной.

Заметим, что не в каждый многогранник может быть вписанным или описанным. Например, в куб вписать сферу можно, а в прямоугольный параллелепипед, измерения которого отличаются, уже вписать сферу не получится.

Надо отметить, что в сферу можно вписать не только в многогранник, но и другие геометрические фигуры, в частности конус и цилиндр. Здесь нужно уточнить (без доказательства), что если касание плос-ти и сферы происходит только в одной точке, то цилиндрическая и коническая поверхности касаются сферы уже по окруж-ти.

Задание. Правильная пирамида вписана в сферу. Докажите, высота этой пирамиды проходит через центр сферы.

Решение. Опустим из центра сферы О перпендикуляр ОН на основание пирамиды. Далее возьмем произвольную вершину Х основания пирамиды, и соединим ее с Н отрезком ХН. По теореме Пифагора можно вычислить длину ХН (радиус сферы ОХ обозначим, буквой R):

Получилось, что расстояние ХН не зависит от самой точки Х. То есть все вершины основания равноудалены от точки, то есть Н – центр описанной около основания окруж-ти. Это означает, что перпендикуляр ОН одновременно является высотой правильной пирамиды, ч. т. д.

Задание. Вычислите радиус описанной сферы, в которую вписан правильный тетраэдр со стороной а.

Решение. Правильный тетраэдр можно считать правильной треугольной пирамидой, поэтому (согласно предыдущей задаче) из центра сферы О можно опустить перпендикуляр на основание АВС, который упадет в точку Н – центр основания. Так как тетраэдр правильный, то ∆АВС – равносторонний, то есть Н – эта точка пересечения и медиан, и высот. Опустим из А высоту АК, она пройдет через Н. Так как АК – ещё и медиана, то

Далее найдем длину АН. Вспомним, что АН – медиана, а точка пересечения медиан Н делит их в отношении 2:1. Это значит, что

Буквой R здесь обозначен радиус описанной сферы. Осталось применить теорему Пифагора к ∆АНD:

Задание. Докажите что вокруг любого тетраэдра можно описать сферу.

Решение. Обозначим вершины произвольного тетраэдра буквами А, В, С и D. Далее на грани АВС отметим точку К – центр окруж-ти, описанной около ∆АВС. Аналогично на грани АВD отметим Н – центр окруж-ти, описанной около ∆АВD:

Напомним, что центры описанных окружностей располагаются в той точке, где пересекаются серединные перпендикуляры. Это значит, что если мы из К и Н опустим перпендикуляры на ребро АВ, то эти перпендикуляры будут серединными, то есть они попадут в одну точку М, являющуюся серединой ребра АВ.

Мы получили плос-ть НМК. Заметим, что НМК⊥АВ по признаку перпендикулярности прямой и плоскости, так как АВ⊥МН и АВ⊥МК. Но тогда АВС⊥МНК уже по признаку перпендикулярности плоскостей, ведь АВС проходит через АВ, являющийся перпендикуляром к НМК. По той же причине и АВD⊥НМК.

Далее проведем через К перпендикуляр m к АВС. Он должен будет принадлежать НМК, ведь НМК⊥АВD. Аналогично и через Н проведем перпендикуляр n к АВD, который также будет принадлежать НМК.

В плос-ти НМК есть две прямые, mи n. Они либо параллельны, либо пересекаются. Но перпендикуляры к двум плос-тям могут быть параллельны только в случае, если сами эти плос-ти параллельны (или совпадают). Но АВС и АВD непараллельны и не совпадают, поэтому m и n непаралелльны, то есть они пересекаются в какой-то точке О.

Покажем, что точка О равноудалена от всех вершин тетраэдра. Сравним ∆АОК и ∆СОК. Они прямоугольные, ведь ОК – перпендикуляр к АВС. ОК – общий катет, а катеты АК и СК одинаковы как радиусы описанной окруж-ти. Значит, ∆АОК и ∆СОК равны, ОА = ОС. Аналогично рассмотрев ∆АОК и ∆ВОК, приходим к выводу, что ОА = ОВ. Далее рассматриваем ∆ОНD и ∆ОНА и получаем, что ОА = ОD. Эти три равенства все вместе означают, что О равноудалена от точек А, В, С и D. А это значит, что на сфере с центром О и радиусом ОА будут лежать все вершины тетраэдра, то есть такая сфера окажется описанной, ч. т. д.

Примечание. Несложно доказать, что описанная сфера будет единственной. Действительно, если бы около тетраэдра можно было описать две различных сферы, то они пересекались бы в точках А, В, С и D. Сферы пересекаются по окруж-ти, то есть А, В, С и D должны лежать на одной окруж-ти, но это невозможно, ведь они не располагаются в одной плос-ти. Значит, двух описанных сфер существовать не может.

Доказанное в задаче утверждение можно сформулировать несколько иначе:

Сегодня мы изучили сферу – одну из важнейших геометрических фигур. Именно сферическую форму имеют звезды и планеты. Жидкость, оказавшаяся в невесомости, также принимает форму шара. Важно запомнить, что сечение сферы имеет форму окруж-ти, и касательные к сфере обладают почти такими ми же свойствами, как и касательные к окруж-ти в планиметрии.