Чтобы легко справиться с решением задач на шар, вписанный в пирамиду, полезно разобрать небольшой теоретический материал.
Шар вписан в пирамиду (или сфера вписана в пирамиду) — значит, шар (сфера) касаются каждой грани пирамиды. Плоскости, содержащие грани пирамиды, являются касательными плоскостями шара. Отрезки, соединяющие центр шара с точками касания, перпендикуляры к касательным плоскостям. Их длины равны радиусу шара. Центр вписанного в пирамиду шара — точка пересечения бисекторных плоскостей двугранных углов при основании (то есть плоскостей, делящих эти углы пополам).
Чаще всего в задачах речь идет о шаре, вписанном в правильную пирамиду. Шар можно вписать в любую правильную пирамиду. Центр шара в этом случае лежит на высоте пирамиды. При решении задачи удобно провести сечение пирамиды и шара плоскостью, проходящей через апофему и высоту пирамиды.
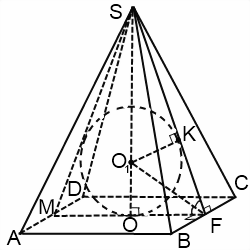
Если пирамида четырехугольная или шестиугольная, сечение представляет собой равнобедренный треугольник, боковые стороны которого — апофемы, а основание — диаметр вписанной в основание окружности.
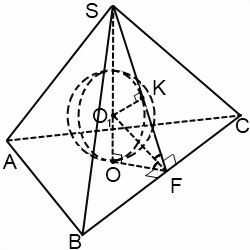
Если пирамида треугольная или пятиугольная, достаточно рассмотреть лишь часть этого сечения — прямоугольный треугольник, катеты которого — высота пирамиды и радиус вписанной в основание пирамиды окружности, а гипотенуза — апофема.
В любом случае, в итоге приходим к рассмотрению соответствующего прямоугольного треугольника и других связанных с ним треугольников.
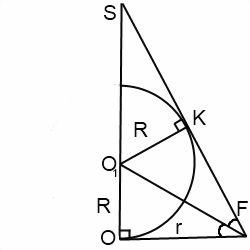 Итак, в прямоугольном треугольнике SOF катет SO=H — высота пирамиды, катет OF=r — радиус вписанной в основание пирамиды окружности, гипотенуза SF=l — апофема пирамиды. O1- центр шара и, соответственно, окружности, вписанной в треугольник, полученный в сечении (мы рассматриваем его часть). Угол SFO — линейный угол двугранного угла между плоскостью основания и плоскостью боковой грани SBC. Точки K и O — точки касания, следовательно, O1K перпендикулярен SF. OO1=O1K=R — радиусу шара.
Итак, в прямоугольном треугольнике SOF катет SO=H — высота пирамиды, катет OF=r — радиус вписанной в основание пирамиды окружности, гипотенуза SF=l — апофема пирамиды. O1- центр шара и, соответственно, окружности, вписанной в треугольник, полученный в сечении (мы рассматриваем его часть). Угол SFO — линейный угол двугранного угла между плоскостью основания и плоскостью боковой грани SBC. Точки K и O — точки касания, следовательно, O1K перпендикулярен SF. OO1=O1K=R — радиусу шара.
Прямоугольные треугольники OO1F и KO1F равны (по катетам и гипотенузе). Отсюда KF=OF=r.
Прямоугольные треугольники SKO1 и SOF подобны (по острому углу S), откуда следует, что
![]()
В треугольнике SOF применим свойство биссектрисы треугольника:
![]()
Из прямоугольного треугольника OO1F
![]()
При решении задач на шар, вписанный в правильную пирамиду, будет полезным еще одно рассуждение.
![]()
![]()
![]()
Теперь найдем отношение объема пирамиды к площади ее поверхности:
![]()
![]()
Таким образом, радиус вписанного шара выражается через объем пирамиды и ее полную поверхность:
![]()
Все эти рассуждения верны не только для правильной пирамиды, но и для пирамиды, основание высоты которой совпадает с центром вписанной в основание окружности (то есть для пирамиды, у которой все двугранные углы при основании равны).


Описанные шары
- Сфера называется описанной около многогранника, если на ней лежат все его вершины.
- Центр шара, описанного около многогранника, лежит в точке пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящих через их середины. Он может находится внутри, на поверхности и вне многогранника.
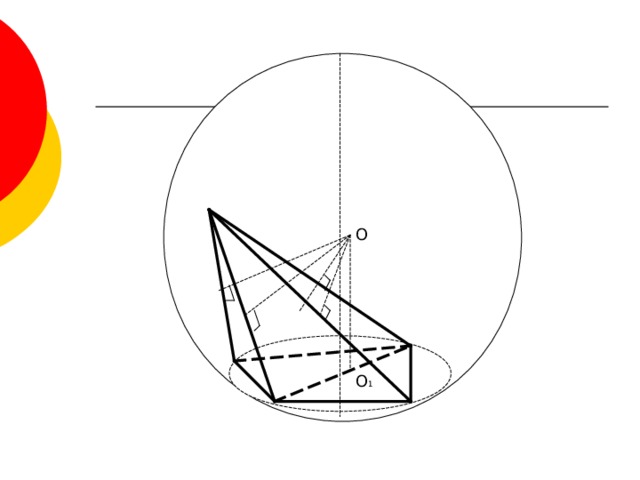
О
О 1
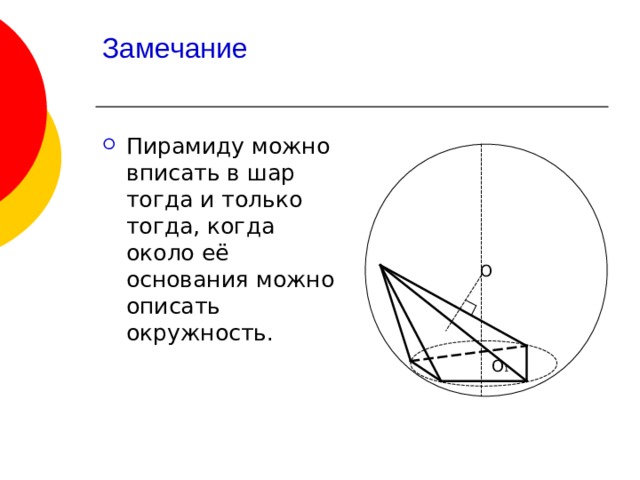
Замечание
- Пирамиду можно вписать в шар тогда и только тогда, когда около её основания можно описать окружность.
О
О 1

- Следствие 1. Центр шара, описанного около пирамиды, лежит в точке пересечения прямой, перпендикулярной основанию пирамиды, проходящей через центр окружности, описанной около этого основания, и плоскости, перпендикулярной любому боковому ребру, проведенной через середину этого ребра.
- Следствие 2. Если боковые рёбра пирамиды равны между собой (или равно наклонены к плоскости основания), то около такой пирамиды можно описать шар.
- Следствие 3. Шар, в частности можно описать:
– около треугольной пирамиды
– около правильной пирамиды
– около четырёхугольной пирамиды, у которой сумма противоположных углов основания равна 180 ° .
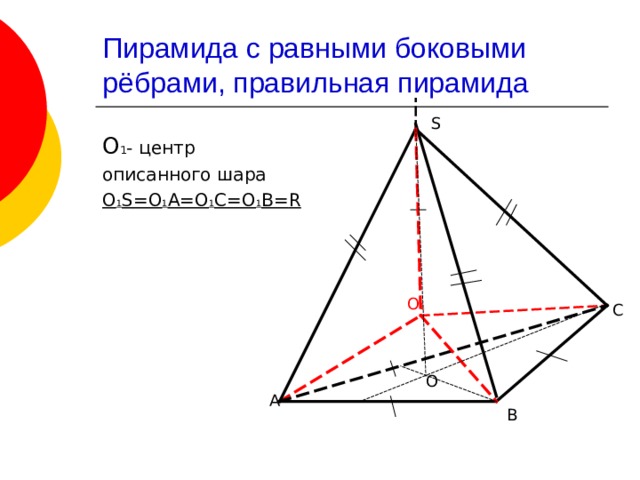
Пирамида с равными боковыми рёбрами, правильная пирамида
S
О 1 – центр
описанного шара
О 1 S =О 1 А=О 1 С=О 1 В= R
О 1
С
О
В
А
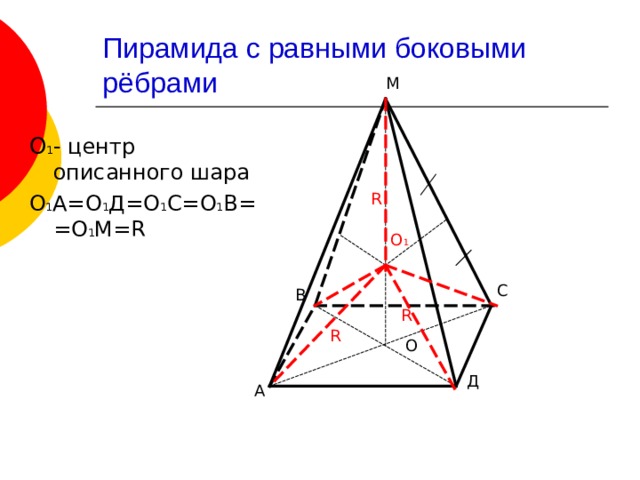
Пирамида с равными боковыми рёбрами
М
О 1 – центр описанного шара
О 1 А=О 1 Д=О 1 С=О 1 В==О 1 М= R
R
О 1
С
В
R
R
О
Д
А

Основание пирамиды – равнобедренная трапеция
S
О 1 – центр описанной окружности
О 1 В=О 1 А=О 1 Д=
=О 1 С=О 1 S = R
АД || ВС
АВ=СД
∟ А + ∟ С =180 °
∟ В + ∟ Д = 180 °
R
О 1
R
R
В
С
О
А
Д
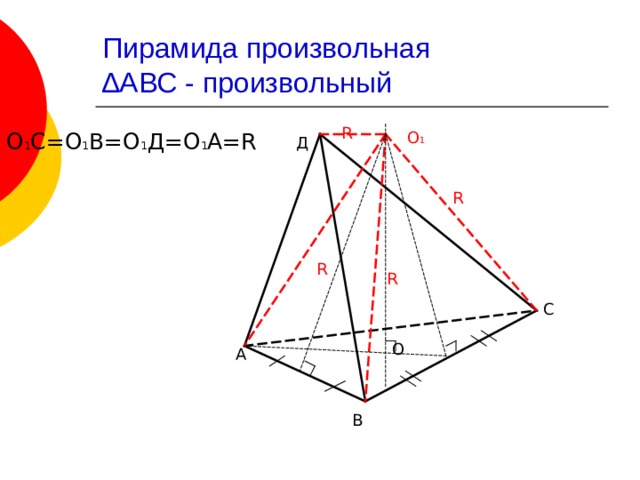
Пирамида произвольная ∆АВС – произвольный
R
О 1
О 1 С=О 1 В=О 1 Д=О 1 А= R
Д
R
R
R
С
О
А
В
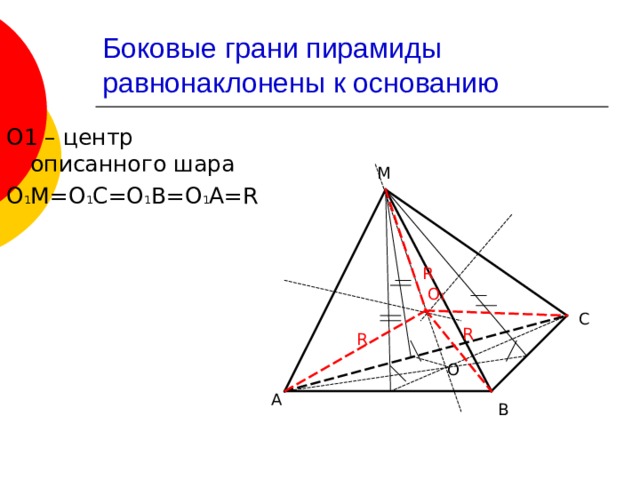
Боковые грани пирамиды равнонаклонены к основанию
О1 – центр описанного шара
О 1 М=О 1 С=О 1 В=О 1 А= R
М
R
О 1
С
R
R
О
А
В
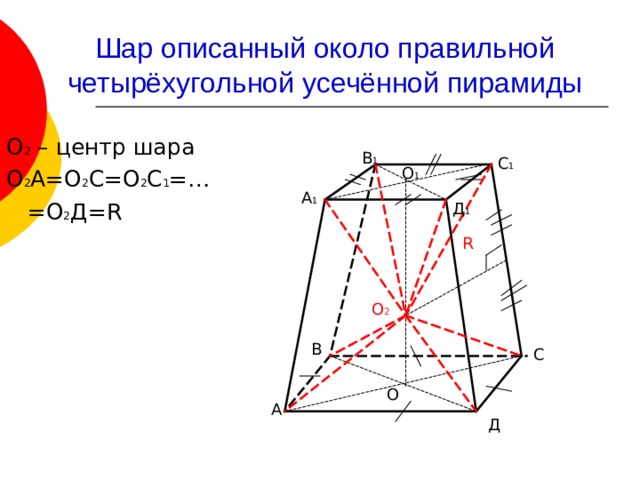
Шар описанный около правильной четырёхугольной усечённой пирамиды
О 2 – центр шара
О 2 А=О 2 С=О 2 С 1 =…
=О 2 Д= R
В 1
С 1
О 1
А 1
Д 1
R
О 2
В
С
О
А
Д
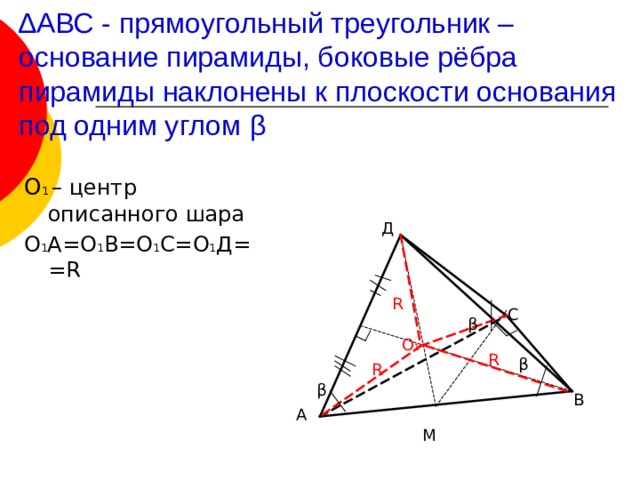
∆ АВС – прямоугольный треугольник – основание пирамиды, боковые рёбра пирамиды наклонены к плоскости основания под одним углом β
О 1 – центр описанного шара
О 1 А=О 1 В=О 1 С=О 1 Д= =R
Д
R
С
β
О 1
R
β
R
β
В
А
М

- Сфера называется вписанной в многогранник, если она касается всех его граней.
- Центр шара, вписанного в многогранник, лежит в точке пересечения биссекторных плоскостей всех двугранных углов многогранника. Он расположен только внутри многогранника.
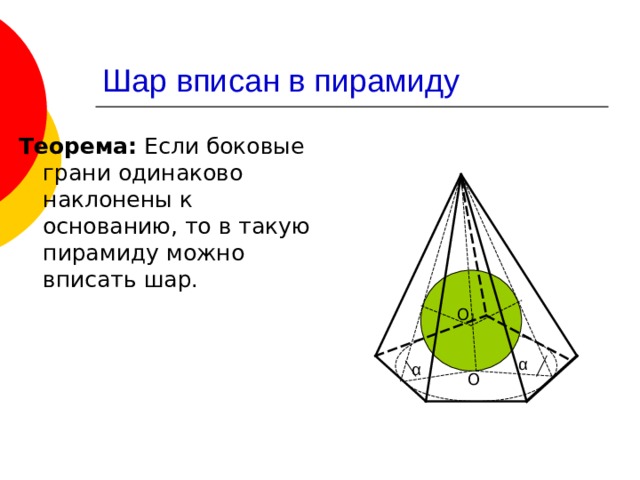
Теорема: Если боковые грани одинаково наклонены к основанию, то в такую пирамиду можно вписать шар.
О 1
α
α
О

Следствие 1. Центр шара, вписанного в пирамиду, у которой боковые грани одинаково наклонены к основанию, лежит в точке пересечения высоты пирамиды с биссектрисой линейного угла любого двугранного угла при основании пирамиды, стороной которого служит высота боковой грани, проведенная из вершины пирамиды.
Следствие 2. В правильную пирамиду можно вписать шар.
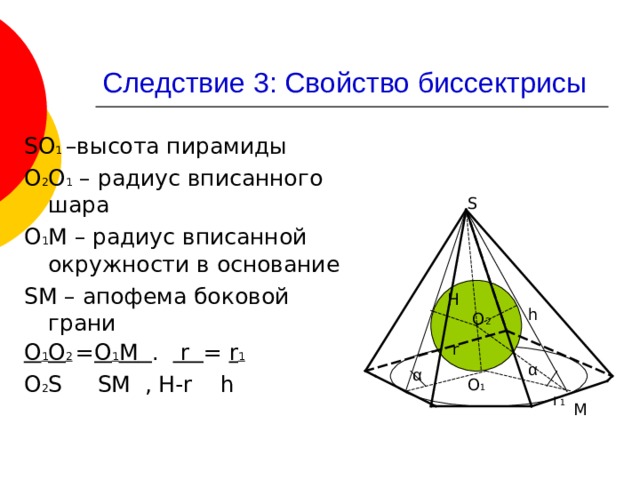
Следствие 3: Свойство биссектрисы
SO 1 – высота пирамиды
О 2 О 1 – радиус вписанного шара
О 1 М – радиус вписанной окружности в основание
SM – апофема боковой грани
О 1 О 2 = О 1 М . r = r 1
О 2 S SM , H-r h
S
H
h
О 2
r
α
α
О 1
r 1
М
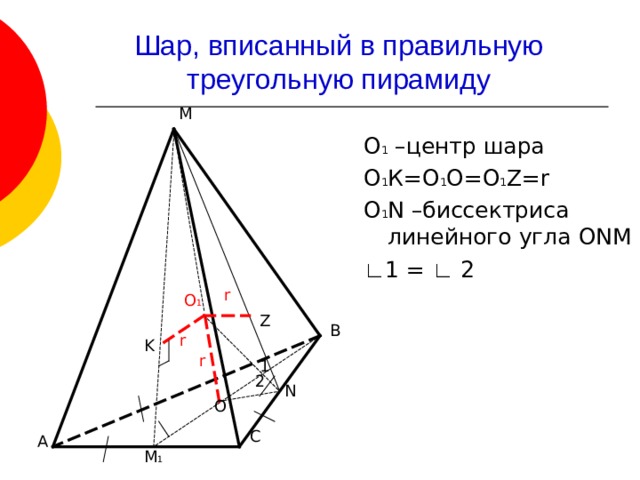
Шар, вписанный в правильную треугольную пирамиду
М
О 1 –центр шара
О 1 К=О 1 О=О 1 Z=r
О 1 N –биссектриса линейного угла ONM
∟ 1 = ∟ 2
r
О 1
Z
В
r
K
r
1
2
N
О
С
А
М 1
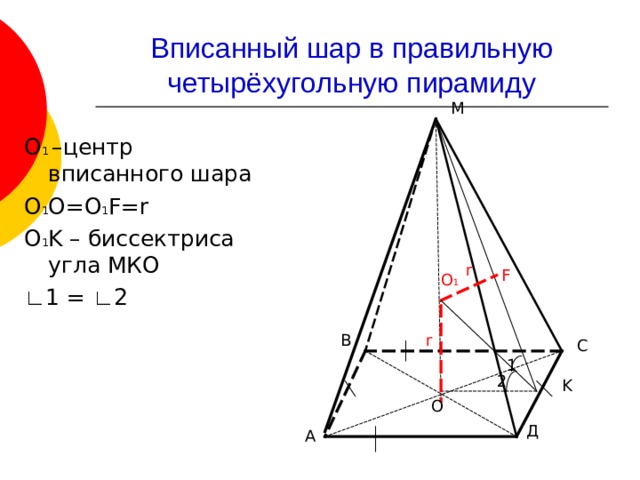
Вписанный шар в правильную четырёхугольную пирамиду
M
О 1 –центр вписанного шара
О 1 О=О 1 F=r
О 1 K – биссектриса угла МКО
∟ 1 = ∟ 2
r
F
О 1
В
r
С
1
2
K
O
Д
А
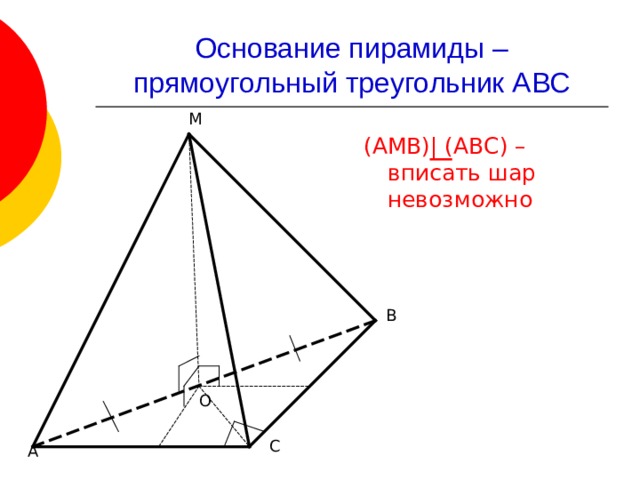
Основание пирамиды – прямоугольный треугольник АВС
М
(АМВ) | (АВС) – вписать шар невозможно
В
О
С
А
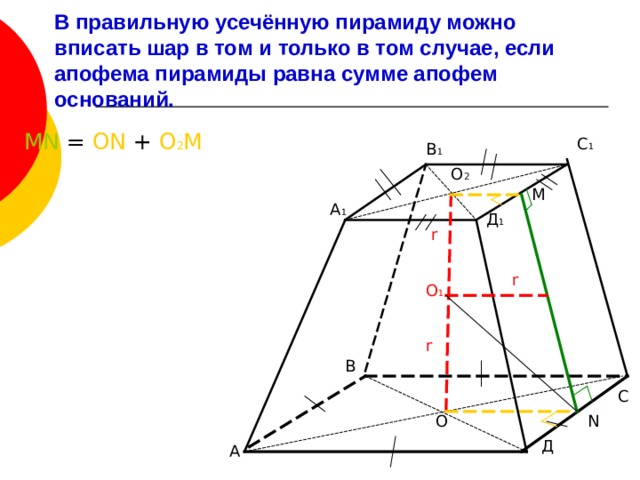
В правильную усечённую пирамиду можно вписать шар в том и только в том случае, если апофема пирамиды равна сумме апофем оснований.
MN = ON + O 2 M
С 1
В 1
О 2
М
А 1
Д 1
r
r
О 1
r
В
С
О
N
Д
А
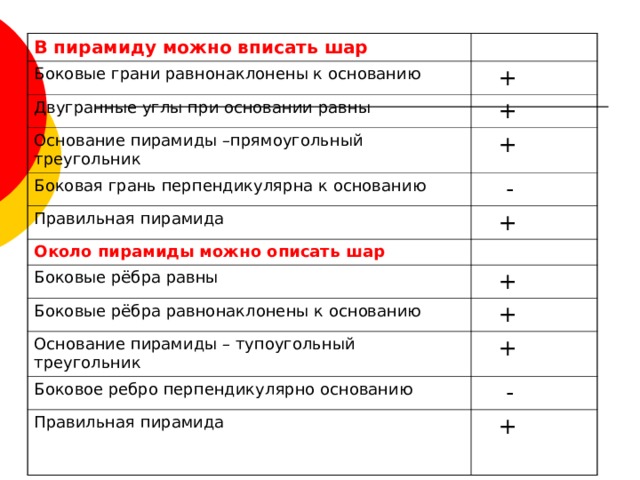
В пирамиду можно вписать шар
Боковые грани равнонаклонены к основанию
+
Двугранные углы при основании равны
+
Основание пирамиды –прямоугольный треугольник
+
Боковая грань перпендикулярна к основанию
–
Правильная пирамида
Около пирамиды можно описать шар
+
Боковые рёбра равны
+
Боковые рёбра равнонаклонены к основанию
+
Основание пирамиды – тупоугольный треугольник
+
Боковое ребро перпендикулярно основанию
–
Правильная пирамида
+

Для правильного тетраэдра со стороной а:
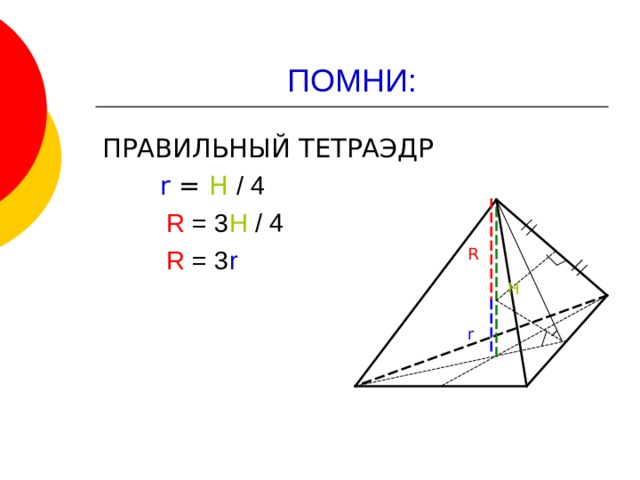
ПРАВИЛЬНЫЙ ТЕТРАЭДР
r = H / 4
R = 3 H / 4
R = 3 r
R
H
r
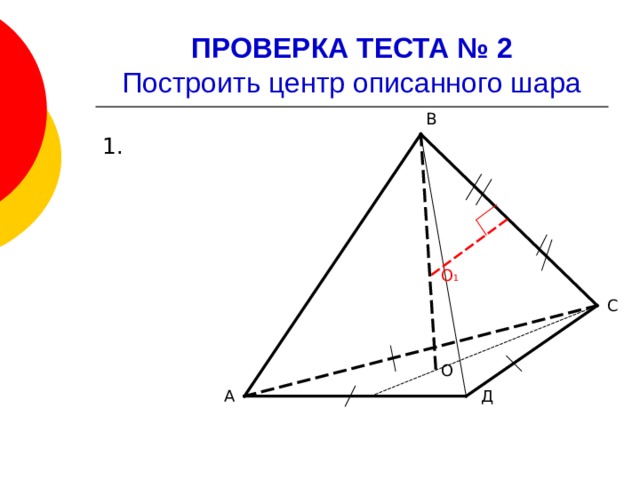
ПРОВЕРКА ТЕСТА № 2 Построить центр описанного шара
В
1.
О 1
С
О
Д
А
Построить центр описанного шара
М
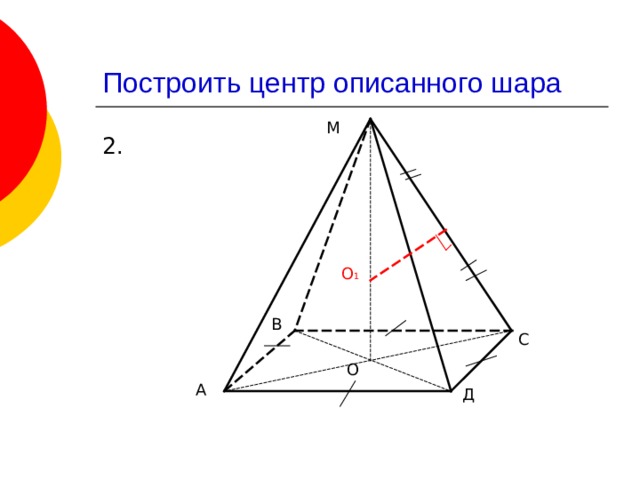
2.
О 1
В
С
О
А
Д
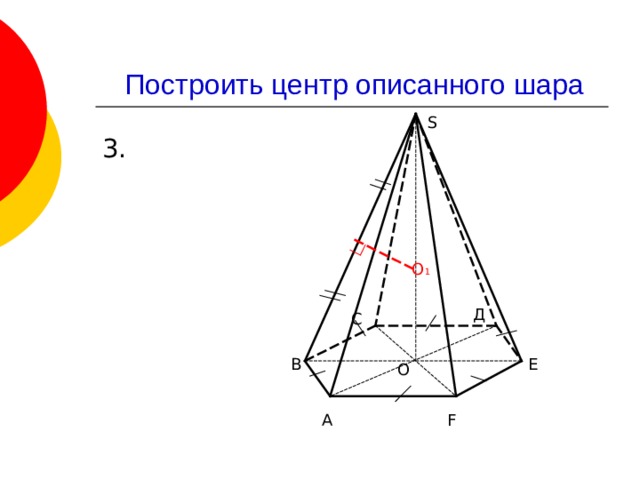
Построить центр описанного шара
S
О 1
Д
С
В
Е
О
А
F
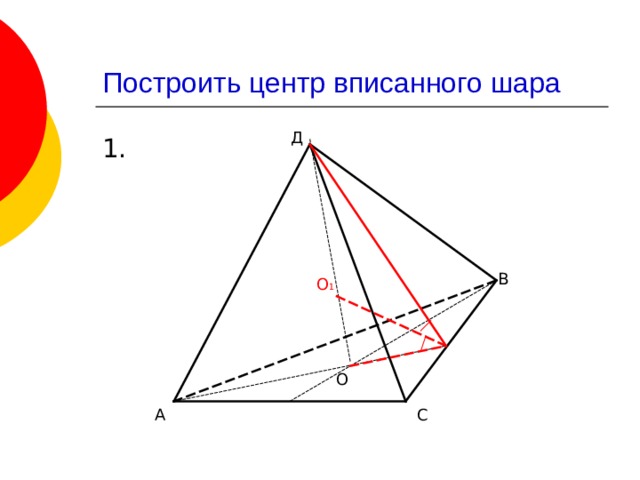
Построить центр вписанного шара
Д
В
О 1
О
С
А
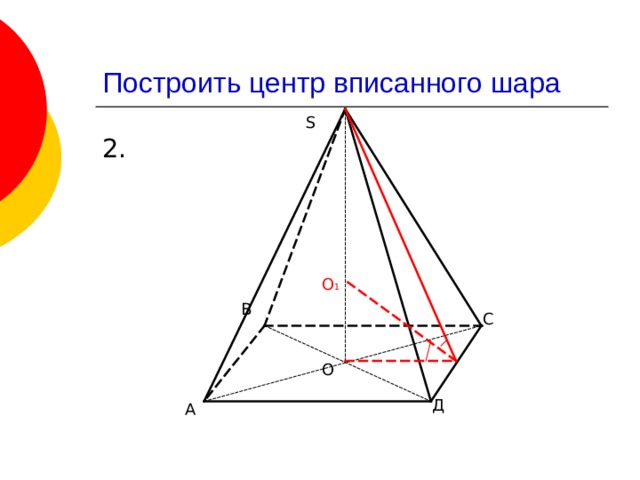
Построить центр вписанного шара
S
О 1
В
С
О
Д
А
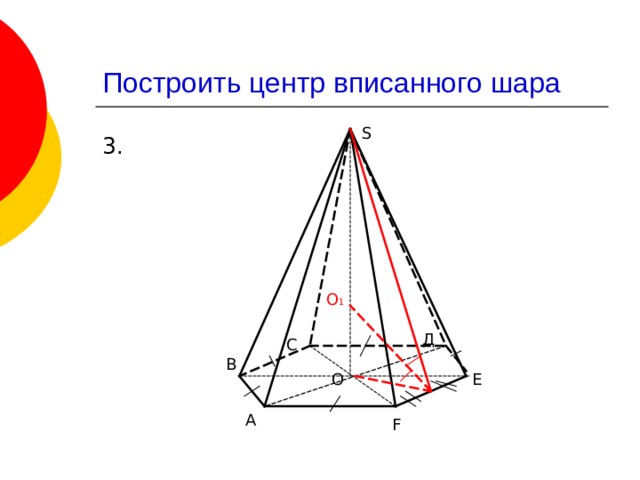
Построить центр вписанного шара
S
3.
О 1
Д
С
В
О
Е
А
F

СПАСИБО ЗА УРОК!
Тема “Разные задачи на многогранники, цилиндр,
конус и шар” является одной из самых сложных в
курсе геометрии 11 класса. Перед тем, как решать
геометрические задачи, обычно изучают
соответствующие разделы теории, на которые
ссылаются при решении задач. В учебнике
С.Атанасяна и др. по данной теме (стр. 138) можно
найти только определения многогранника,
описанного около сферы, многогранника,
вписанного в сферу, сферы, вписанной в
многогранник, и сферы, описанной около
многогранника. В методических рекомендациях к
этому учебнику (см. книгу “Изучение геометрии в
10–11-х классах” С.М.Саакяна и В.Ф.Бутузова, стр.159)
сказано, какие комбинации тел рассматриваются
при решении задач № 629–646, и обращается внимание
на то, что “при решении той или иной задачи
прежде всего нужно добиться того, чтобы учащиеся
хорошо представляли взаимное расположение
указанных в условии тел”. Далее приводится
решение задач №638(а) и №640.
Учитывая все выше сказанное, и то, что наиболее
трудными для учащихся являются задачи на
комбинацию шара с другими телами, необходимо
систематизировать соответствующие
теоретические положения и сообщить их учащимся.
Определения.
1. Шар называется вписанным в многогранник, а
многогранник описанным около шара, если
поверхность шара касается всех граней
многогранника.
2. Шар называется описанным около
многогранника, а многогранник вписанным в шар,
если поверхность шара проходит через все вершины
многогранника.
3. Шар называется вписанным в цилиндр, усеченный
конус (конус), а цилиндр, усеченный конус (конус) –
описанным около шара, если поверхность шара
касается оснований (основания) и всех образующих
цилиндра, усеченного конуса (конуса).
(Из этого определения следует, что в любое
осевое сечение этих тел может быть вписана
окружность большого круга шара).
4. Шар называется описанным около цилиндра,
усеченного конуса (конуса), если окружности
оснований (окружность основания и вершина)
принадлежат поверхности шара.
(Из этого определения следует, что около
любого осевого сечения этих тел может быть
описана окружность большего круга шара).
Общие замечания о положении центра
шара.
1. Центр шара, вписанного в многогранник, лежит в
точке пересечения биссекторных плоскостей всех
двугранных углов многогранника. Он расположен
только внутри многогранника.
2. Центр шара, описанного около многогранника,
лежит в точке пересечения плоскостей,
перпендикулярных ко всем ребрам многогранника и
проходящих через их середины. Он может быть
расположен внутри, на поверхности и вне
многогранника.
Комбинация шара с призмой.
1. Шар, вписанный в прямую призму.
Теорема 1. Шар можно вписать в прямую
призму в том и только в том случае, если в
основание призмы можно вписать окружность, а
высота призмы равна диаметру этой окружности.
Следствие 1. Центр шара, вписанного в прямую
призму, лежит в середине высоты призмы,
проходящей через центр окружности, вписанной в
основание.
Следствие 2. Шар, в частности, можно вписать
в прямые: треугольную, правильную,
четырехугольную (у которой суммы
противоположных сторон основания равны между
собой) при условии Н = 2r, где Н – высота призмы, r –
радиус круга, вписанного в основание.
2. Шар, описанный около призмы.
Теорема 2. Шар можно описать около
призмы в том и только в том случае, если призма
прямая и около ее основания можно описать
окружность.
Следствие 1. Центр шара, описанного около
прямой призмы, лежит на середине высоты призмы,
проведенной через центр круга, описанного около
основания.
Следствие 2. Шар, в частности, можно описать:
около прямой треугольной призмы, около
правильной призмы, около прямоугольного
параллелепипеда, около прямой четырехугольной
призмы, у которой сумма противоположных углов
основания равна 180 градусов.
Из учебника Л.С.Атанасяна на комбинацию шара с
призмой можно предложить задачи № 632, 633, 634, 637(а),
639(а,б).
Комбинация шара с пирамидой.
1. Шар, описанный около пирамиды.
Теорема 3. Около пирамиды можно описать
шар в том и только в том случае, если около ее
основания можно описать окружность.
Следствие 1. Центр шара, описанного около
пирамиды лежит в точке пересечения прямой,
перпендикулярной основанию пирамиды, проходящей
через центр окружности, описанной около этого
основания, и плоскости, перпендикулярной любому
боковому ребру, проведенной через сере дину
этого ребра.
Следствие 2. Если боковые ребра пирамиды
равны между собой (или равно наклонены к
плоскости основания), то около такой пирамиды
можно описать шар.Центр этого шара в этом случае
лежит в точке пересечения высоты пирамиды (или ее
продолжения) с осью симметрии бокового ребра,
лежащей в плоскости бокового ребра и высоты.
Следствие 3. Шар, в частности, можно описать:
около треугольной пирамиды, около правильной
пирамиды, около четырехугольной пирамиды, у
которой сумма противоположных углов равна 180
градусов.
2. Шар, вписанный в пирамиду.
Теорема 4. Если боковые грани пирамиды
одинаково наклонены к основанию, то в такую
пирамиду можно вписать шар.
Следствие 1. Центр шара, вписанного в
пирамиду, у которой боковые грани одинаково
наклонены к основанию, лежит в точке пересечения
высоты пирамиды с биссектрисой линейного угла
любого двугранного угла при основании пирамиды,
стороной которого служит высота боковой грани,
проведенная из вершины пирамиды.
Следствие 2. В правильную пирамиду можно
вписать шар.
Из учебника Л.С.Атанасяна на комбинацию шара с
пирамидой можно предложить задачи № 635, 637(б), 638,
639(в),640, 641.
Комбинация шара с усеченной
пирамидой.
1. Шар, описанный около правильной усеченной
пирамиды.
Теорема 5. Около любой правильной
усеченной пирамиды можно описать шар. (Это
условие является достаточным, но не является
необходимым)
2. Шар, вписанный в правильную усеченную
пирамиду.
Теорема 6. В правильную усеченную
пирамиду можно вписать шар в том и только в том
случае, если апофема пирамиды равна сумме апофем
оснований.
На комбинацию шара с усеченной пирамидой в
учебнике Л.С.Атанасяна есть всего лишь одна
задача (№ 636).
Комбинация шара с круглыми телами.
Теорема 7. Около цилиндра, усеченного
конуса (прямых круговых), конуса можно описать
шар.
Теорема 8. В цилиндр (прямой круговой)
можно вписать шар в том и только в том случае,
если цилиндр равносторонний.
Теорема 9. В любой конус (прямой
круговой) можно вписать шар.
Теорема 10. В усеченный конус (прямой
круговой) можно вписать шар в том и только в том
случае, если его образующая равна сумме радиусов
оснований.
Из учебника Л.С.Атанасяна на комбинацию шара с
круглыми телами можно предложить задачи № 642, 643,
644, 645, 646.
Для более успешного изучения материала данной
темы необходимо включать в ход уроков устные
задачи:
1. Ребро куба равно а. Найти радиусы шаров:
вписанного в куб и описанного около него. (r = a/2, R =
a![]() 3).
3).
2. Можно ли описать сферу (шар) около: а) куба; б)
прямоугольного параллелепипеда; в) наклонного
параллелепипеда, в основании которого лежит
прямоугольник; г) прямого параллелепипеда; д)
наклонного параллелепипеда? (а) да; б) да; в) нет;
г) нет; д) нет)
3. Справедливо ли утверждение, что около любой
треугольной пирамиды можно описать сферу? (Да)
4. Можно ли описать сферу около любой
четырехугольной пирамиды? (Нет, не около любой
четырёхугольной пирамиды)
5. Какими свойствами должна обладать пирамида,
чтобы около нее можно было описать сферу? (В её
основании должен лежать многоугольник, около
которого можно описать окружность)
6. В сферу вписана пирамида, боковое ребро
которой перпендикулярно основанию. Как найти
центр сферы? (Центр сферы – точка пересечения
двух геометрических мест точек в пространстве.
Первое – перпендикуляр, проведённый к плоскости
основания пирамиды, через центр окружности,
описанной около него. Второе – плоскость
перпендикулярная данному боковому ребру и
проведённая через его середину)
7. При каких условиях можно описать сферу около
призмы, в основании которой – трапеция? (Во-первых,
призма должна быть прямой, и, во-вторых, трапеция
должна быть равнобедренной, чтобы около неё
можно было описать окружность)
8. Каким условиям должна удовлетворять призма,
чтобы около нее можно было описать сферу?
(Призма должна быть прямой, и её основанием
должен являться многоугольник, около которого
можно описать окружность)
9. Около треугольной призмы описана сфера, центр
которой лежит вне призмы. Какой треугольник
является основанием призмы? (Тупоугольный
треугольник)
10. Можно ли описать сферу около наклонной
призмы? (Нет, нельзя)
11. При каком условии центр сферы, описанной
около прямой треугольной призмы, будет находится
на одной из боковых граней призмы? (В основании
лежит прямоугольный треугольник)
12. Основание пирамиды – равнобедренная
трапеция .Ортогональная проекция вершины
пирамиды на плоскость основания – точка,
расположенная вне трапеции. Можно ли около такой
трапеции описать сферу? (Да, можно. То что
ортогональная проекция вершины пирамиды
расположена вне её основания, не имеет значения.
Важно, что в основании пирамиды лежит
равнобедренная трапеция – многоугольник, около
которого можно описать окружность)
13. Около правильной пирамиды описана сфера. Как
расположен ее центр относительно элементов
пирамиды? (Центр сферы находится на
перпендикуляре, проведенном к плоскости
основания через его центр)
14. При каком условии центр сферы, описанной
около прямой треугольной призмы, лежит: а) внутри
призмы; б) вне призмы? (В основании призмы: а)
остроугольный треугольник; б) тупоугольный
треугольник)
15. Около прямоугольного параллелепипеда, ребра
которого равны 1 дм, 2 дм и 2 дм, описана сфера.
Вычислите радиус сферы. (1,5 дм)
16. В какой усеченный конус можно вписать сферу? (В
усечённый конус, в осевое сечение которого можно
вписать окружность. Осевым сечением конуса
является равнобедренная трапеция, сумма её
оснований должна равняться сумме её боковых
сторон. Другими словами, у конуса сумма радиусов
оснований должна равняться образующей)
17. В усеченный конус вписана сфера. Под каким
углом образующая конуса видна из центра сферы? (90
градусов)
18. Каким свойством должна обладать прямая
призма, чтобы в нее можно было вписать сферу? (Во-первых,
в основании прямой призмы должен лежать
многоугольник, в который можно вписать
окружность, и, во-вторых, высота призмы должна
равняться диаметру вписанной в основание
окружности)
19. Приведите пример пирамиды, в которую нельзя
вписать сферу? (Например, четырёхугольная
пирамида, в основании которой лежит
прямоугольник или параллелограмм)
20. В основании прямой призмы лежит ромб. Можно
ли в эту призму вписать сферу? (Нет, нельзя, так
как около ромба в общем случае нельзя описать
окружность)
21. При каком условии в прямую треугольную
призму можно вписать сферу? (Если высота призмы
в два раза больше радиуса окружности, вписанной в
основание)
22. При каком условии в правильную
четырехугольную усеченную пирамиду можно
вписать сферу? (Если сечением данной пирамиды
плоскостью, проходящей через середину стороны
основания перпендикулярно ей, является
равнобедренная трапеция, в которую можно вписать
окружность)
23. В треугольную усеченную пирамиду вписана
сфера. Какая точка пирамиды является центром
сферы? (Центр вписанной в данную пирамиду сферы
находится на пересечении трёх биссектральных
плоскостей углов, образованных боковыми гранями
пирамиды с основанием)
24. Можно ли описать сферу около цилиндра
(прямого кругового)? (Да, можно)
25. Можно ли описать сферу около конуса,
усеченного конуса (прямых круговых)? (Да, можно,
в обоих случаях)
26. Во всякий ли цилиндр можно вписать сферу?
Какими свойствами должен обладать цилиндр, чтобы
в него можно было вписать сферу? (Нет, не во
всякий: осевое сечение цилиндра должно быть
квадратом)
27. Во всякий ли конус можно вписать сферу? Как
определить положение центра сферы, вписанной в
конус? (Да, во всякий. Центр вписанной сферы
находится на пересечении высоты конуса и
биссектрисы угла наклона образующей к плоскости
основания)
Автор считает, что из трех уроков, которые
отводятся по планированию на тему “Разные
задачи на многогранники, цилиндр, конус и шар”,
два урока целесообразно отвести на решение задач
на комбинацию шара с другими телами. Теоремы,
приведенные выше, из-за недостаточного
количества времени на уроках доказывать не
рекомендуется. Можно предложить учащимся,
которые владеют достаточными для этого навыками,
доказать их, указав (по усморению учителя) ход или
план доказательства.
Автор надеется, что материал этой статьи
поможет молодым коллегам при подготовке к урокам
по данной теме.
Пирамида, вписанная в шар
Шар называют описанным около пирамиды, если все вершины пирамиды принадлежат поверхности шара. Пирамиду в этом случае называют вписанной в шар (рис. 1).
|
|
|
|
Рис. 1. Пирамида, вписанная в шар |
Рис. 2. Пирамида, вписанная в шар |
Несложно заметить, что вершины основания пирамиды лежат в одной плоскости, значит, они должны принадлежать одной окружности описанного шара. Таким образом, необходимым условием для того, чтобы вписать пирамиду в шар, является то, что многоугольник основания является вписанным (рис. 2).
Докажем, что это является также и достаточным условием.
Разветвление: доказательство
Заметим, что если основание пирамиды можно вписать в окружность, то ГМТ равноудаленных от вершин основания – перпендикуляр к плоскости основания, проведенный через центр описанной окружности (рис. 3). Осталось найти на этой прямой точку, которая равноудалена от вершин основания и от вершины пирамиды. Для этого рассмотрим любую вершину ![]() основания и вершину
основания и вершину ![]() пирамиды. ГМТ точек, равноудаленных от них, – плоскость, проходящая через середину
пирамиды. ГМТ точек, равноудаленных от них, – плоскость, проходящая через середину ![]() перпендикулярно ему. Но эта плоскость не может быть параллельна перпендикуляру к плоскости основания – в противном случае, точка
перпендикулярно ему. Но эта плоскость не может быть параллельна перпендикуляру к плоскости основания – в противном случае, точка ![]() лежала бы в основании (рис. 4). Значит, условие вписанности основания является необходимым и достаточным.
лежала бы в основании (рис. 4). Значит, условие вписанности основания является необходимым и достаточным.
Любая треугольная пирамида, а также любая правильная пирамида могут быть вписаны в шар.
Задача №1
Условие. Найти радиус шара, в который вписана правильная треугольная пирамида, все ребра которой равны 2 (рис. 5).
|
|
|
|
Рис. 5. Иллюстрация к задаче 1 |
Рис. 6. Треугольник |
Решение
Рассмотрим пирамиду ![]() , все ребра которой равны 2. Пусть
, все ребра которой равны 2. Пусть ![]() – центр основания,
– центр основания, ![]() – центр шара. Тогда очевидно, что
– центр шара. Тогда очевидно, что ![]() лежит на
лежит на ![]() , причем
, причем ![]() . И пусть
. И пусть ![]() – середина
– середина ![]() .
.
Рассмотрим плоскость ![]() (рис. 6). По теореме Пифагора из треугольника
(рис. 6). По теореме Пифагора из треугольника ![]() высота
высота ![]() равна
равна ![]() , а тогда
, а тогда ![]() . Далее найдем
. Далее найдем ![]() по теореме Пифагора в прямоугольном треугольнике
по теореме Пифагора в прямоугольном треугольнике ![]()
![]() .
.
Пусть ![]() . Тогда
. Тогда ![]() ;
;
![]() .
.
Решим уравнение: ![]() ;
;

![]()
Осталось заметить, что радиус шара равен ![]() , то есть:
, то есть:
![]() .
.
Ответ: ![]()
Шар, вписанный в пирамиду
Шар называется вписанным в пирамиду, если он касается плоскостей всех граней пирамиды (рис. 7).

Рис. 7. Шар, вписанный в пирамиду
В любую треугольную (рис. 8) и любую правильную пирамиду можно вписать шар, причем его центр будет лежать на высоте пирамиды, а точки касания с боковыми гранями – на апофемах (рис. 9).
|
|
|
|
Рис. 8. Шар, вписанный в треугольную пирамиду |
Рис. 9. Шар, вписанный в правильную четырехугольную пирамиду |
Задача №2
Условие: найти радиус шара, вписанного в правильную четырехугольную пирамиду ![]() , сторона основания которой равна 10, а боковое ребро – 13 (рис. 10).
, сторона основания которой равна 10, а боковое ребро – 13 (рис. 10).
|
|
|
|
Рис. 10. Иллюстрация к задаче 2 |
Рис. 11. Треугольник |
Решение
Пусть ![]() – центр шара,
– центр шара, ![]() – центр основания,
– центр основания, ![]() – середина
– середина ![]() ,
, ![]() – середина
– середина ![]() . В силу сформулированного утверждения
. В силу сформулированного утверждения ![]() лежит на
лежит на ![]() . Рассмотрим треугольник
. Рассмотрим треугольник ![]() . По условию расстояния от точки
. По условию расстояния от точки ![]() до
до ![]() ,
, ![]() и
и ![]() должны быть равными – это и есть радиусы шара. Таким образом,
должны быть равными – это и есть радиусы шара. Таким образом, ![]() – просто центр вписанной окружности в треугольник
– просто центр вписанной окружности в треугольник ![]() , радиус этой окружности и надо найти (рис. 11).
, радиус этой окружности и надо найти (рис. 11).
Очевидно, ![]() ,
, ![]() из треугольника
из треугольника ![]() равно 12 (в силу теоремы Пифагора).
равно 12 (в силу теоремы Пифагора).
Тогда ![]() .
.
Значит ![]()
Ответ: ![]() .
.
Заключение
На уроке мы разобрали комбинации шара и пирамиды, а также решили задачи на нахождение радиусов вписанного и описанного шара.
Список литературы
- Атанасян Л.С. и др. Геометрия. Учебник для 10-11 классов.
- Погорелов А.В. Геометрия. Учебник для 10-11 классов.
- Бевз В.Г., Владимирова Н.Г. Геометрия 11 класс.
Домашнее задание
- В правильный тетраэдр с ребром 6 вписана сфера. Найдите радиус сферы.
- В правильный тетраэдр вписана сфера радиуса 5. Найдите радиус сечения этой сферы плоскостью, перпендикулярной высоте тетраэдра и делящей ее в отношении 2:1, считая от вершины тетраэдра.
- Около правильного тетраэдра описана сфера радиуса 5. Найдите длину ребра тетраэдра.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Interneturok.ru (Источник).
- Интернет-портал Interneturok.ru (Источник).
- Интернет-портал Interneturok.ru (Источник).








