Симметрия — соразмерность, соответствие, сходность, порядок в расположении частей. Это слово, как и многие другие математические понятия, произошли от греческих слов.
Смотря на объекты вокруг, мы не раз восклицаем: «Какая симметрия!»
Рис. (1). Симметрия в архитектуре.
Люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре, художестве, строительстве.
Но симметрия широко распространена и в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, морской звезде.
Рис. (2). Симметрия в природе.
Пока рассмотрим две симметрии на плоскости: относительно точки и прямой.
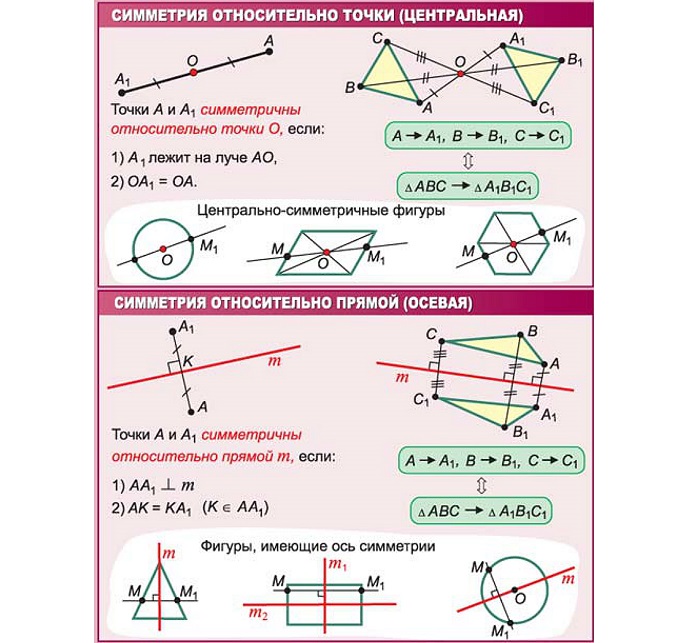
Симметрию относительно точки называют центральной симметрией.
Точки
M
и
M1
симметричны относительно некоторой точки (O), если точка (O) является серединой отрезка
MM1
.
Рис. (3). Центральная симметрия.
Точка (O) называется центром симметрии.
Алгоритм построения центрально-симметричных фигур.
Рис. (4). Треугольники симметричны относительно точки (O).
Построим треугольник
A1B1C1
, симметричный треугольнику (ABC) относительно центра (точки) (O).
1. Для этого соединим точки (A), (B), (C) с центром (O) и продолжим эти отрезки.
2. Измерим отрезки (AO), (BO), (CO) и отложим с другой стороны от точки (O) равные им отрезки
AO=OA1;BO=OB1;CO=OC1
;
3. Соединим получившиеся точки отрезками и получим треугольник
A1B1C1
, симметричный данному треугольнику (ABC).
Фигуры, симметричные относительно некоторой точки, равны.
Фигура симметрична относительно центра симметрии, если для каждой точки этой фигуры симметричная ей точка также лежит на этой фигуре. Такая фигура имеет центр симметрии (фигура с центральной симметрией).
Есть фигуры с центральной симметрией, это, например, окружность и параллелограмм. У окружности центр симметрии — это её центр, у параллелограмма центр симметрии — это точка, в которой пересекаются его диагонали. Есть очень много фигур, у которых нет центра симметрии.
Осевая симметрия
Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Точки
M
и
M1
симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.
Рис. (5). Осевая симметрия.
Алгоритм построения фигуры, симметричной относительно некоторой прямой.
Рис. (6). Треугольники симметричны относительно прямой.
Построим треугольник
A1B1C1
, симметричный треугольнику (ABC) относительно красной прямой.
1. Для этого проведём из вершин треугольника (ABC) прямые, перпендикулярные оси симметрии, и продолжим их дальше на другой стороне оси.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками и получим треугольник
A1B1C1
, симметричный данному треугольнику (ABC).
Фигуры, симметричные относительно прямой, равны.
Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.
Иногда у фигур несколько осей симметрии:
- для неразвёрнутого угла существует единственная ось симметрии — это биссектриса данного угла.
- Для равнобедренного треугольника есть единственная ось симметрии.
- Для равностороннего треугольника — три оси.
- Для прямоугольника и ромба существуют две оси симметрии.
- Для квадрата — целых четыре.
- Для окружности осей симметрии бесчисленное множество — это каждая прямая, которая проходит через центр этой фигуры.
- Есть фигуры без осей симметрии — это параллелограмм и треугольник, все стороны которого различны.
Источники:
Рис. 1 Симметрия в архитектуре. Указание авторства не требуется, 2021-06-02, Архитектура/Здания, бесплатно для коммерческого использования, https://clck.ru/VFC5B.
Рис. 2. Симметрия в природе. Указание авторства не требуется, 2021-06-02, бесплатно для коммерческого использования, https://clck.ru/VFECn.
Рис. 3. Центральная симметрия, © ЯКласс.
Рис. 4. Треугольники симметричны относительно точки O, © ЯКласс.
Рис. 5. Осевая симметрия, © ЯКласс.
Рис. 6. Треугольники симметричны относительно прямой, © ЯКласс.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Координаты на плоскости
- Осевая и центральная симметрии
Осевая симметрия
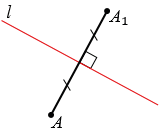
Рассмотрим построение точки, симметричной данной точке А относительно данной прямой 
.
Пусть дана точка А и прямая .
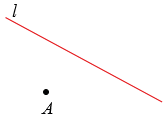
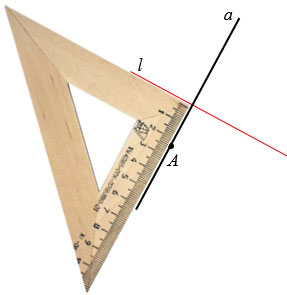
Точку симметричную точке А относительно прямой , можно построить так. Проведем через точку А прямую 
, перпендикулярную прямой . Для этого используем чертежный угольник. Прикладываем чертежный угольник так, как показано на рисунке ниже и проводим прямую через точку А.
Пусть прямые и пересекаются в точке О. Отложим при помощи линейки на прямой отрезок ОА1, равный отрезку ОА.
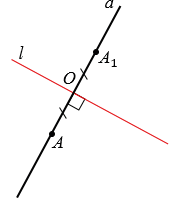
Получаем точки А и А1, которые симметричны относительно прямой .
Также можно построить фигуры, симметричные относительно прямой.
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой .
Пусть дан треугольник АВС и прямая .
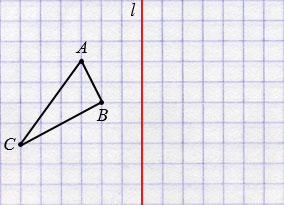
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно прямой (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой .
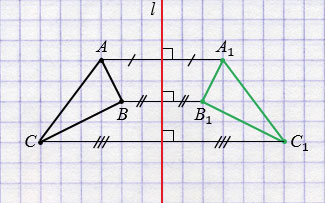
Обратите внимание, любые две фигуры, симметричные относительно прямой, равны.
Если фигура имеет ось симметрии (прямая ) то, все точки этой фигуры, не принадлежащие этой оси, можно разделить на пары симметричных точек.
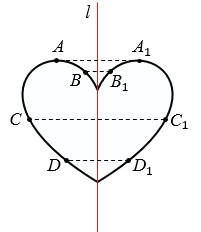
Центральная симметрия
Точки М и М1 называют симметричными относительно точки О, если точка О является серединой отрезка ММ1 (смотри рисунок ниже).
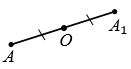
Рассмотрим построение точки, симметричной данной точке М относительно данной точки О.
Пусть даны точки М и О. Точку, симметричную точке М относительно точки О, можно построит так. Проведем луч МО.
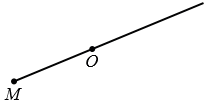
На луче МО отложим отрезок ОN , равный отрезку ОМ.
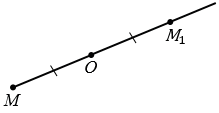
Точки М и М1, которые симметричны относительно точки О.
Также можно построить фигуры, симметричные относительно точки.
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
Пусть дан треугольник АВС и точки О.
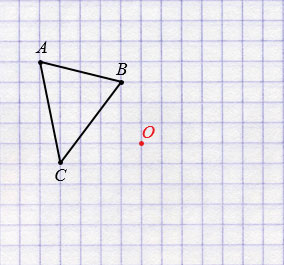
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно точки О (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
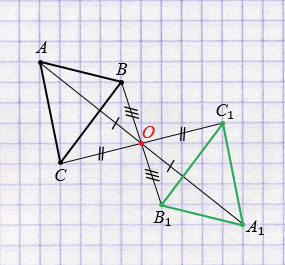
Обратите внимание, любые две фигуры, симметричные относительно точки, равны.
Рассмотрим окружность с центром в точке О. Все точки окружности можно разбить на пары точек, симметричных относительно точки О.
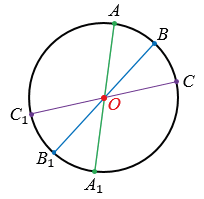
В таком случае говорят, что окружность имеет центр симметрии – точку О.
Также центр симметрии имеют такие фигуры, как отрезок, прямоугольник, эллипс.
Советуем посмотреть:
Перпендикулярные прямые
Параллельные прямые
Координатная плоскость
Координаты на плоскости
Правило встречается в следующих упражнениях:
6 класс
Номер 1247,
Мерзляк, Полонский, Якир, Учебник
Номер 1254,
Мерзляк, Полонский, Якир, Учебник
Номер 1257,
Мерзляк, Полонский, Якир, Учебник
Номер 1259,
Мерзляк, Полонский, Якир, Учебник
Номер 1264,
Мерзляк, Полонский, Якир, Учебник
Номер 1268,
Мерзляк, Полонский, Якир, Учебник
Номер 1270,
Мерзляк, Полонский, Якир, Учебник
Номер 1307,
Мерзляк, Полонский, Якир, Учебник
Номер 1318,
Мерзляк, Полонский, Якир, Учебник
Номер 1334,
Мерзляк, Полонский, Якир, Учебник
Центральная симметрия – самая интересная и познавательная тема в геометрии, которую изучают в начальных классах школы и более тщательно — в 8 — 11 классах. Знания по этой теме обязательно пригодятся ученику в жизни.
Что такое центральная симметрия
Начнём с определения: центральная симметрия – одно из свойств определённой геометрической фигуры, при котором точке В соответствует некая точка В1, находящая в таком же пространственном положении относительно точки С. Точка С лежит на середине отрезка ВВ1. Точка С называется центром симметрии. Это определение соответствует курсу планиметрии.
Центральную симметрию можно построить и в пространстве. В пространстве центральной симметрией называется словно зеркальное отображение какой-либо геометрической фигуры. Она представляет собой две одинаковые фигуры, соответственные точки которых попарно симметричны относительно точки пространства О.
Свойства центральной симметрии
Основные свойства следующие:
1. Центральную симметрию называют движением, при котором соответствующие точки также остаются симметричными, то есть расстояние между ними остаётся прежним.
Посмотрим на рисунок. Треугольники АВС и А1В1С1
симметричны в пространстве относительно точки О. При каком либо преобразовании пространства сохраняются условия: АО=А1О, ВО=В1О, СО=С1О. Значит, картинка остаётся той же.
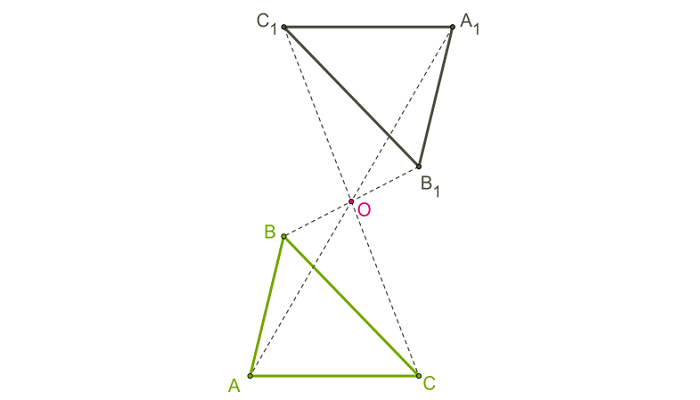
Однако если представить геометрическую фигуру в виде векторов, то при преобразовании пространства эти векторы поменяют свои направления;
2. Центральная симметрия имеет только одну центральную точку, которая является неподвижной при преобразовании пространства;
3. Если прямая проходит через центр симметрии, то она соответствует самой себе, то есть симметрична;
4. Центральная симметрия переводит прямую, не проходящую через центр симметрии, в параллельную ей прямую.
Доказывается это свойство достаточно просто. Для этого нужно построить две параллельные прямые АВ и А1В1 относительно точки О.
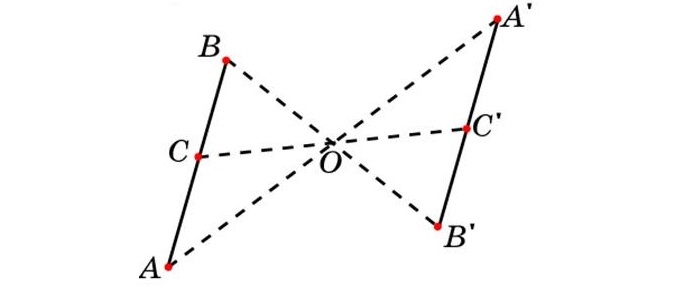
Далее соединяем симметричные точки и получаем отрезки АА1 и ВВ1. Далее легко заметить, что отрезки АО и А1О будут равны. Соответственно равны и отрезки ВО и В1О. Углы, которые образуются при пересечении двумя прямыми точки О также равны.
Значит, треугольники равны по двум сторонам и углу между ними. Следовательно, равны углы А,А1 и В,В1. Значит они являются накрест лежащими при секущих АА1 и ВВ1. Задача решена, АВ и А1В1 параллельны;
5. При центральной симметрии отрезки симметричны отрезкам, лучи симметричны лучам, прямые симметричны прямым.
Примеры фигур, обладающих центральной симметрией
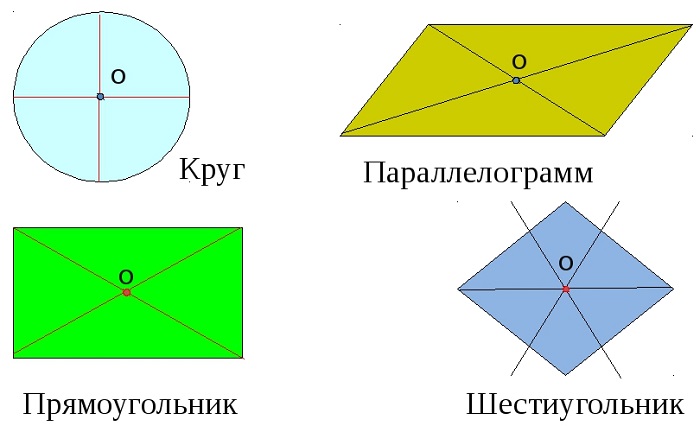
Фигур, как имеющих углы, так и без углов, но при этом обладающих центральной симметрией не так уж мало:
-
параллелограмм;
-
окружность;
-
ромб и квадрат;
-
различные правильные многоугольники.
Интересные факты о центральной симметрии
Вся окружающая нас природа – сплошная центральная симметрия. Многие растения и насекомые обладают центральной симметрией.
Практически у каждого фрукта есть своя симметрия. Например, кокос в разрезе представляет собой окружность с центром в некоторой точке.
Ещё один очевидный пример – бабочка.
Великолепные узоры на её крылышках – четкая и яркая симметрия.
Каждый знает, что видовое разнообразие морских ракушек бесконечно. Наверняка, вы сможете найти несколько как с осевой, так и центральной симметрией.
Великолепные примеры с элементами центральной симметрии можно наблюдать и в архитектуре. Потолки различных храмов и церквей украшаются орнаментами, основой которых является центральная симметрия.
Собор Парижской Богоматери имеет прекрасный, утончённый узор, основанный на центральной симметрии.
Рукодельницы в своих произведениях искусства применяют симметрию, которая заметна в удивительных и затейливых узорах.
Таким образом, центральная симметрия – основа, которая составляет природу, архитектуру и даже иногда музыку. Именно это проявление так радует человеческий глаз при появлении первых снежинок или при знакомстве с сооружениями архитектуры.
Центральная и осевая симметрия
«Симметрия» – слово греческого происхождения. Оно означает соразмерность, наличие определенного порядка, закономерности в расположении частей.
Люди с давних времен использовали симметрию в рисунках, орнаментах, предметах быта.
Симметрия широко распространена в природе. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, мозаике в храме, морской звезде.
Симметрия широко используется на практике, в строительстве и технике. Это строгая симметрия в форме античных зданий, гармоничные древнегреческие вазы, здании Кремля, машинах, самолетах и многом другом. (слайд 4) Примерами использования симметрии являются паркет и бордюр. (смотри гиперссылку об использовании симметрии в бордюрах и паркетах) Рассмотрим несколько примеров, где можно увидеть симметрию в различных предметах, с использованием слайд-шоу (включить значок ).
Определение: Центральная симметрия – это симметрия относительно точки.
Определение: Точки А и В симметричны относительно некоторой точки О, если точка О является серединой отрезка АВ.
Определение: Точка О называется центром симметрии фигуры, а фигура называется центрально-симметричной.
Свойство: Фигуры, симметричные относительно некоторой точки, равны.
Примеры:
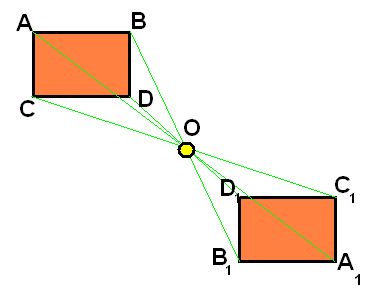
Алгоритм построения центрально-симметричной фигуры
1.Построим треугольник А 1В 1 С 1, симметричный треугольнику АВС, относительно центра (точки) О. Для этого соединим точки А,В,С с центром О и продолжим эти отрезки;
2. Измерим отрезки АО, ВО, СО и отложим с другой стороны от точки О, равные им отрезки (АО=А 1 О 1, ВО=В 1 О 1, СО=С 1 О 1 );
3. Соединим получившиеся точки отрезками А 1 В 1; А 1 С 1; В1 С 1.
Получили ∆А 1 В 1 С 1 симметричный ∆АВС.
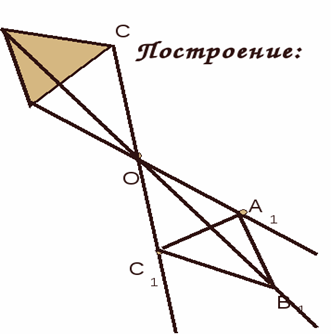
Осевая симметрия – это симметрия относительно проведенной оси (прямой).
Определение: Точки А и В симметричны относительно некоторой прямой а, если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии.
Определение: Осью симметрии называется прямая при перегибании по которой «половинки» совпадут, а фигуру называют симметричной относительно некоторой оси.
Свойство: Две симметричные фигуры равны.
Примеры:
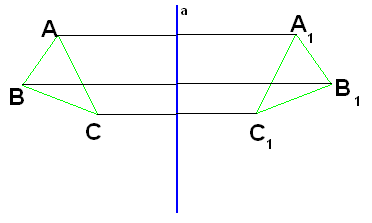
Алгоритм построения фигуры, симметричной относительно некоторой прямой
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой а.
Для этого:
1. Проведем из вершин треугольника АВС прямые, перпендикулярные прямой а и продолжим их дальше.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками А1В1, В1С1, В1С1.
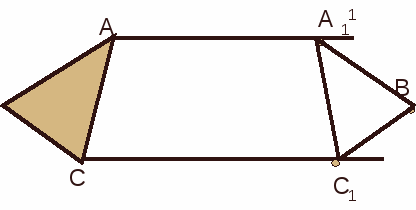
Получили ∆ А1В1С1 симметричный ∆АВС.
Опыты с зеркалами, которые мы проводили на прошлом занятии,
позволили нам прикоснуться к удивительному миру симметрии.
В переводе с греческого слово «симметрия» означает
«соразмерность, пропорциональность, одинаковость в расположении частей».
Посмотрите на кленовый лист, бабочку, снежинку. Их объединяет то,
что они симметричны. Если мы на каждом из рисунков начертим прямую вот таким
образом…
А затем поставим зеркальце вдоль этой прямой на каждом рисунке, то
отражённая в зеркале половинка фигуры дополнит её до целой (такой же, как
исходная фигура).
Поэтому такая симметрия называется зеркальной (или осевой,
если речь идёт о плоскости). Прямая, вдоль которой поставлено зеркало,
называется осью симметрии.
Если симметричную фигуру сложить пополам вдоль оси симметрии, то
её части совпадут.
С симметрией мы постоянно встречаемся в повседневной жизни. Люди
используют симметрию в орнаментах, предметах быта, технике. Издавна человек
использовал симметрию в архитектуре. Древним храмам, башням средневековых
замков, современным зданиям она придаёт гармоничность, законченность. Симметрия
также встречается в природе. Она создаёт ощущение порядка, гармонии, красоты.
Давайте сделаем кляксу. Для этого на лист бумаги капнем чернил.
Сложим лист вдвое, а затем разогнём. Линия сгиба листа является осью симметрии
кляксы.
Получается, что клякса имеет одну (вертикальную) ось симметрии.
А вот у снежинки 6 линий сгиба и все они являются осями симметрии.
У геометрических фигур может быть одна или несколько осей
симметрии, а может и не быть совсем.
Так, прямоугольник обладает двумя осями симметрии, каждая
из которых проходит через середины двух его противоположных сторон. То есть,
вырезав прямоугольник из бумаги и перегнув его по любой из двух осей симметрии,
половинки фигуры совпадут.
Ромб также обладает двумя осями
симметрии. Это прямые, которые содержат его диагонали.
Квадрат имеет четыре оси симметрии.
Две проходят через середины его противоположных сторон. И ещё две – это прямые,
которые содержат его диагонали.
Круг. Его осью симметрии является
любая прямая, которая проходит через его центр, то есть содержит диаметр круга.
А значит, круг имеет бесконечно много осей симметрии
Теперь посмотрите на следующую фигуру. Это произвольный
параллелограмм. У него нет ни одной оси симметрии.
У произвольного треугольника тоже нет осей симметрии.
У равнобедренного треугольника есть одна ось симметрии.
У равностороннего (то есть у правильного) треугольника
– три оси симметрии.
Теперь посмотрите на шестиугольник. У него три оси симметрии,
которые проходят через противоположные вершины, и ещё три оси, которые проходят
через середины противоположных сторон. То есть всего шесть осей симметрии.
Таким образом, мы можем сказать, что круг – «самая
симметричная» фигура из рассмотренных, так как он имеет бесконечно много
осей симметрии.
Сейчас давайте посмотрим на следующие фигуры и выясним, какая из
них лишняя.
Итак, первая фигура напоминает замочную скважину. Она имеет одну
ось симметрии.
Вторая фигура тоже имеет одну ось симметрии.
У третьей фигуры (в виде буквы Т) одна ось симметрии.
У четвёртой тоже одна. А вот пятая фигура не имеет ни одной оси
симметрии. И поэтому она лишняя.
Теперь давайте посмотрим на следующие пять фигур. Что у них
общего?
Первая фигура – круг. Выше мы выяснили, что у круга бесконечно
много осей симметрии. Вторая фигура (в виде стрелки) имеет только одну ось
симметрии. Третья фигура – эллипс. У эллипса две оси симметрии. Четвёртая
фигура имеет одну ось симметрии. Пятая фигура тоже имеет одну ось симметрии. Каждая
фигура имеет хотя бы одну ось симметрии.
На предыдущем занятии мы с вами проводили опыт с двумя плоскими
зеркалами. С помощью составленного из двух зеркал калейдоскопа мы получали
симметричные фигуры.
Давайте изобразим в виде прямых два зеркала под углом друг к
другу. Затем нарисуем в одном из углов некоторую линию и, не пользуясь
настоящими зеркалами, дорисуем её до симметричной фигуры, которая получилась бы
при отражении в зеркалах. Полученная фигура имеет две оси симметрии. Понятно,
что угол ними равен .
Посмотрите на рассмотренные выше фигуры, которые имеют две оси
симметрии. Угол между осями равен .
Если, например, мы поставим зеркала под углом друг к
другу, то линия отразится 5 раз, а полученная фигура будет иметь 3 оси
симметрии.
Давайте научимся точно строить отражение фигуры в зеркале.
Представим, что прямая l – зеркало (или ось симметрии). Изобразим некоторую ломаную и построим
её отражение в зеркале.
Итак, из вершин ,
и
опускаем перпендикуляры на прямую l. Затем продолжаем их «за
зеркало» на такое же расстояние (равное длине соответствующего отрезка).
Получаем точки ,
и
. Соединяем
эти точки. Ломаная является
отражение ломаной .
Можно сказать, что ломаная симметрична
ломаной относительно
прямой l.
Построим с вами треугольник, симметричный треугольнику относительно
прямой l.
Из вершин и
опустим
перпендикуляры на прямую l. Затем продолжим их за прямую l на такое же расстояние
(равное длине соответствующего отрезка). Получим точки и
.
При этом точка осталась на
месте. Она лежит на оси симметрии. Она симметрична сама себе. и
симметричны
относительно прямой l.
А сейчас посмотрите на рисунок.
Давайте выясним, симметрична ли точка точке
относительно
прямой l. Для этого мы соединим точки и
. Затем с
помощью угольника проверим, перпендикулярна ли прямая l отрезку . Перпендикулярна.
Потом с помощью линейки проверим, делит ли прямая l отрезок и
пополам. Делит.
Значит, точки и
симметричны
относительно прямой l.
Кроме симметрии относительно прямой существует ещё симметрия
относительно точки, так называемая центральная симметрия. Она
характеризуется наличием центра симметрии – точки О, которая обладает
определённым свойством. Можно сказать, что точка О является центром
симметрии, если при повороте вокруг точки О на фигура
переходит сама в себя.
Понятие центральной симметрии распространяется и на трёхмерное
пространство.
Проверить, является ли фигура центрально-симметричной или нет,
можно с помощью обычной иголки и кальки. Наложим на нашу фигуру кальку. Затем,
проколов фигуру в предполагаемом центре и обведя её контур, надо повернуть фигуру
на вокруг
иголки. Если фигура «вошла» в свой контур, то она центрально-симметричная.
Сейчас посмотрите на плоские фигуры, которые имеют и центр
симметрии, и оси симметрии.
Это круг. Выше мы сказали, что он имеет бесконечно много
осей симметрии, каждая из которых содержит его диаметр. А вот центром симметрии
круга является его центр.
Квадрат имеет четыре оси симметрии.
Центром симметрии квадрата является точка пересечения его диагоналей.
У шестиугольника шесть осей симметрии. Центром его
симметрии является точка пересечения его диагоналей.
Выше мы сказали, что произвольный параллелограмм не имеет
ни одной оси симметрии. Но он имеет центр симметрии – это точка пересечения его
диагоналей.
А вот, например, равнобедренный треугольник имеет ось
симметрии, но не имеет центра симметрии. То же самое можно сказать и про
пятиугольник, у которого есть оси симметрии, но центра симметрии нет.
