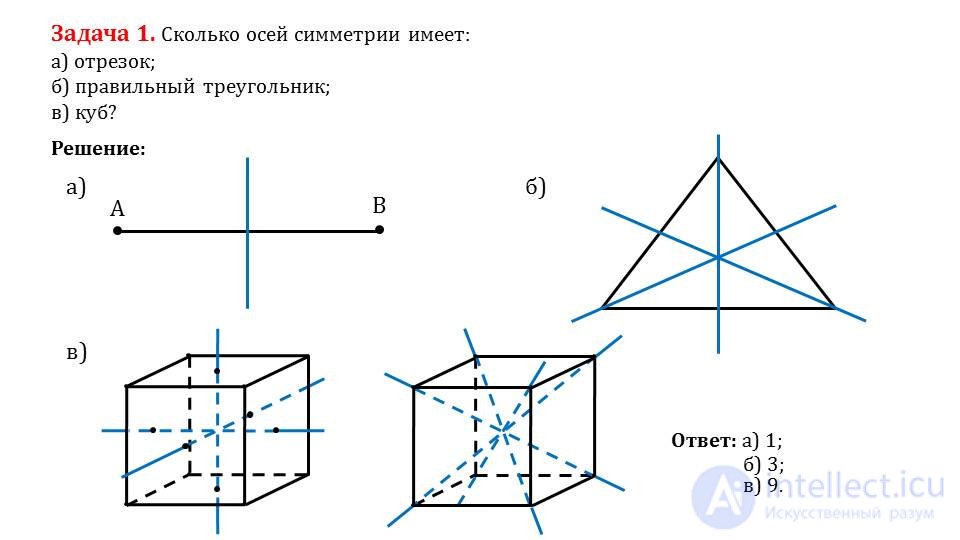
Привет, сегодня поговорим про центральная симметрия параллелепипеда, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
центральная симметрия параллелепипеда, симметрия параллелепипеда, симметрия куба, осевая симметрия параллелепипеда, симметрия многогранников , настоятельно рекомендую прочитать все из категории Стереометрия.
1
симметрия параллелепипеда
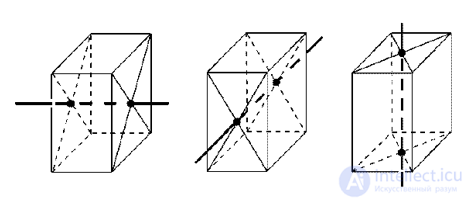
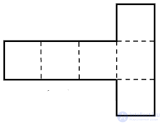
Все диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. Поэтому противоположные вершины параллелепипеда симметричны относительно этой точки. Следовательно, каждый параллелепипед имеет центр симметрии — точку пересечения его диагоналей (рис 1.).
В общем случае осей и плоскостей симметрии параллелепипед не имеет, Прямой, но не прямоугольный параллелепипед всегда имеет ось симметрии — прямую, проходящую через центры симметрии его оснований, и плоскость симметрии, проходящую через середины его боковых ребер.
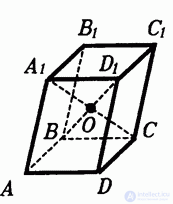
Рисунок 1
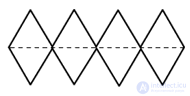
Если основания прямого параллелепипеда — ромбы (но не квадраты), то появляются еще две оси и две плоскости симметрии (Рис 2).
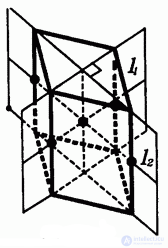
Рисунок 2
Найдите сами элементы симметрии прямоугольного параллелепипеда, среди граней которого нет квадратов.
Если среди граней прямоугольного параллелепипеда есть квадраты, то он является правильной четырехугольной призмой.
Центр симметрии прямоугольного параллелепипеда — точка пересечения диагоналей
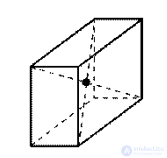
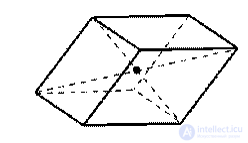
Плоскости симметрии: три плоскости симметрии, проходящие через середины параллельных ребер.
Оси симметрии: три оси симметрии, проходящие через точки пересечения диагоналей противолежащих граней.
2 Симметрия в кубе
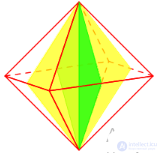
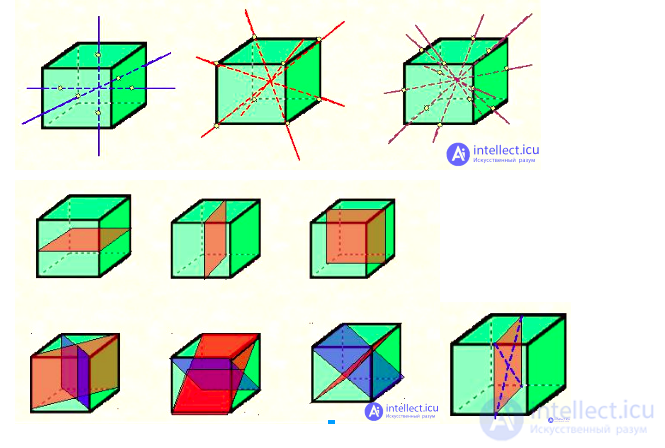
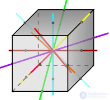
Куб имеет один центр симметрии – точку пересечения его диагоналей. Прямые а и b, проходящие соответственно через центры противоположных граней и середины двух противоположных ребер, не принадлежащих одной грани, являются его осями симметрии. Куб имеет девять осей симметрии. Обратите внимание, все оси симметрии проходят через центр симметрии. Плоскостью симметрии куба является плоскость, проходящая через любые две оси симметрии. Куб имеет девять плоскостей симметрии.

Три плоскости симметрии, проходящие через середины параллельных ребер и шесть плоскостей симметрии , проходящие через противолежащие ребра.
3
центральная симметрия параллелепипеда
Теорема
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.

Доказательство
Рассмотрим любые две диагонали параллелепипеда, например A1A3` и A4A2`. Так как четырехугольники A1A2A3A4 и A2A2`A3`A3 – параллелограммы с общей стороной A2A3, то их стороны A1A4 и A2`A3` параллельны друг другу, следовательно, лежат в одной плоскости. Эта плоскость пересекает плоскости противолежащих граней параллелепипеда по параллельным прямым A1A2` и A4A3`. Следовательно, четырехугольник A4A1A2`A3` – параллелограмм. Диагонали параллелепипеда A1A3` и A2A4` являются диагоналями этого параллелограмма. Поэтому они пересекаются и точкой пересечения O делятся пополам.
Аналогично доказывается, что диагонали A1A3` и A2A4`, а также диагонали A1A3` и A3A1` пересекаются и точкой пересечения делятся пополам . Об этом говорит сайт https://intellect.icu . Теорема доказана.
симметрия многогранников
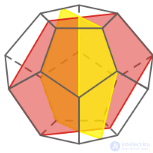
Основной интерес к правильным многогранникам вызывает большое число симметрий, которыми они обладают. Под симметрией (или преобразованием симметрии) многогранника мы понимаем такое его движение в пространстве (например, поворот вокруг некоторой прямой, отражение относительно некоторой плоскости и т.д.), которое оставляет неизменными множества вершин, ребер и граней многогранника.
Рисунок Движение додекаэдра
Иначе говоря, под преобразованием симметрии вершина, ребро или грань либо сохраняет свое исходное положение, либо переводится в исходное положение другой вершины, другого ребра или другой грани. Существует одна симметрия, которая свойственна всем многогранникам. Речь идет о тождественном преобразовании, оставляющем любую точку в исходном положении.
С самым распространенным примером симметрии мы встречаемся в случае прямой правильной n-угольной призмы. Пусть a – прямая, соединяющая центры оснований. Поворот вокруг a на любое целое кратное угла 360/n градусов является симметрией. Пусть, далее, p – плоскость, проходящая посредине между основаниями параллельно им.
Отражение относительно плоскости p(движение, переводящее любую точку A в точку B, такую, что p пересекает отрезок AB под прямым углом и делит его пополам) – еще одна симметрия.
Риунок 10
Таблица 1 – Элементы симметрии правильных многогранников
|
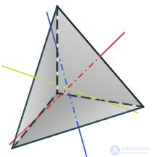
Тетраэдр
|
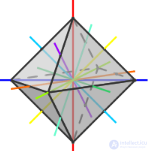
Октаэдр
|
Икосаэдр
|
Гексаэдр (куб)
|
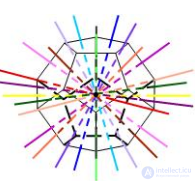
Додекаэдр
|
|
| Количество граней | 4 | 8 | 20 | 6 | 12 |
| количество ребер | 6 | 12 | 30 | 12 | 30 |
| вершин | 4 | 6 | 12 | 8 | 20 |
| Центры симметрии | – | 1 | 1 | 1 | 1 |
| Оси симметрии | 3 | 9 | 15 | 9 | 15 |
 |
 |
 |
 |
 |
|
| Порскости симметрии | 6 | 9 | 15 | 9 | 15 |
 |
|
 |
|
 |
|
| Развертки |  |
 |
 |
 |
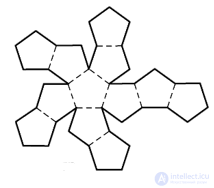 |
Теорема Эйлера Вершины + Грани – Ребра = 2.
Следующий серьезный шаг в науке о многогранниках был сделан в XVIII веке Леонардом Эйлером (1707-1783), который без преувеличения «проверил алгеброй гармонию». Теорема Эйлера о соотношении между числом вершин, ребер и граней выпуклого многогранника, доказательство которой Эйлер опубликовал в 1758 г. в «Записках Петербургской академии наук», окончательно навела математический порядок в многообразном мире многогранников.
Любую симметрию многогранника можно представить в виде произведения отражений. Под произведением нескольких движений многогранника здесь понимается выполнение отдельных движений в определенном заранее установленном порядке. Например, упоминавшийся выше поворот на угол 360/n градусов вокруг прямой a есть произведение отражений относительно любых двух плоскостей, содержащих a и образующих относительно друг друга угол в 180/n градусов. (см. рис 10).
Симметрия, являющаяся произведением четного числа отражений, называется прямой, в противном случае – обратной. Таким образом, любой поворот вокруг прямой – прямая симметрия. Любое отражение есть обратная симметрия.

Рисунок 11
Рассмотрим подробнее симметрии тетраэдра, т.е. правильного многогранника. Любая прямая, проходящая через любую вершину и центр тетраэдра, проходит через центр противоположной грани. Поворот на 120 или 240 градусов вокруг этой прямой принадлежит к числу симметрий тетраэдра. Так как у тетраэдра 4 вершины (и 4 грани), то мы получим всего 8 прямых симметрий. Любая прямая, проходящая через центр и середину ребра тетраэдра проходит через середину противоположного ребра.
Поворот на 180 градусов (полуоборот) вокруг такой прямой также является симметрией. Так как у тетраэдра 3 пары ребер, мы получаем еще 3 прямые симметрии. Следовательно, общее число прямых симметрий, включая тождественное преобразование, доходит до 12. Можно показать, что других прямых симметрий не существует и что имеется 12 обратных симметрий. Таким образом, тетраэдр допускает всего 24 симметрии.
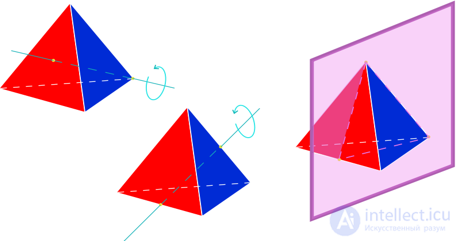
Задачи .
Сколько осей симметрии имеет отрезок, правильный треугольник, куб?
Тест “Правильные многогранники”
1. Сколько существует видов правильных многогранников?
- 13
- 5
- 4
- Много
2. Какие правильные многогранники имеют по 15 осей симметрии и 15 плоскостей симметрии? (несколько ответов)
- Тетраэдр
- Икосаэдр
- Додекаэдр
- Октаэдр
3. Какой из математиков установил соотношения между числом вершин, ребер и граней выпуклого многогранника?
- Платон
- Архимед
- Эйлер
- Кеплер
4. Согласно теории о связи структуры Земли с правильными многогранниками, проекции каких вписанных в земной шар фигур проступают в земной коре? (несколько ответов)
- Икосаэдр
- Гексаэдр
- Додекаэдр
- Октаэдр
5. Кто автор философской картины мира, где главную роль играют правильные многогранники?
- Эйлер
- Кеплер
- Архимед
- Платон
См. также
- понятие симметрии , виды симметрии ,
- симметрия шара , симметрия сферы ,
- симметрии в призме , симметрии в пирамиде ,
- свойство симметрии относительно точки ,
- симметрия относительно прямой , ось симметрии ,
- симметрия относительно точки , центр симметрии ,
- архимедовы тела ,
- тела кеплера – пуансона ,
- многогранники , классификация многогранников ,
- Симметрии в физике
- Суперсимметрия
- Трансляционная симметрия
- Симметрии в биологии
- Асимметрия
- диссимметрии
- сферическая симметрия
- аксиальная симметрия
- радиальная симметрия
- трансляционная симметрия
- двусторонняя (билатеральная) симметрия
- Симметрия в химии
- Анизотропия
- Симметрия в религии и культуре
Понравилась статья про центральная симметрия параллелепипеда? Откомментируйте её Надеюсь, что теперь ты понял что такое центральная симметрия параллелепипеда, симметрия параллелепипеда, симметрия куба, осевая симметрия параллелепипеда, симметрия многогранников
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Стереометрия
Макеты страниц
Все диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. Поэтому противоположные вершины параллелепипеда симметричны относительно этой точки. Следовательно, каждый параллелепипед имеет центр симметрии — точку пересечения его диагоналей (рис. 7.11).
В общем случае осей и плоскостей симметрии параллелепипед не имеет, Прямой, но не прямоугольный параллелепипед всегда имеет ось симметрии — прямую, проходящую через центры симметрии его оснований, и
плоскость симметрии, проходящую через середины его боковых ребер. Если основания прямого параллелепипеда — ромбы (но не квадраты), то появляются еще две оси и две плоскости симметрии (рис. 7.12).
Найдите сами элементы симметрии прямоугольного параллелепипеда, среди граней которого нет квадратов. Если среди граней прямоугольного параллелепипеда есть квадраты, то он является правильной четырехугольной призмой. Симметрия правильных призм рассмотрена в следующем пункте, а симметрия куба — в § 12.

Рис. 7.13
Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Симметрия прямоугольного параллелепипеда
Симметрия прямоугольного параллелепипеда
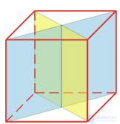
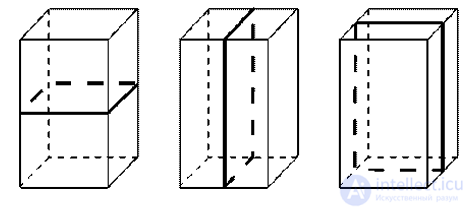
У прямоугольного параллелепипеда, как у всякого параллелепипеда, есть центр симметрии — точка пересечения его диагоналей. У него есть также три плоскости симметрии, проходящие через центр симметрии параллельно граням. На рисунке 416 показана одна из таких плоскостей. Она проходит через середины четырех параллельных ребер параллелепипеда. Концы ребер являются симметричными точками.
Если у параллелепипеда все линейные размеры разные, то у него нет других плоскостей симметрии, кроме названных.
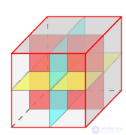
Если же у параллелепипеда два линейных размера равны, то у него есть еще две плоскости симметрии. Это плоскости диагональных сечений, показанные на рисунке 417.
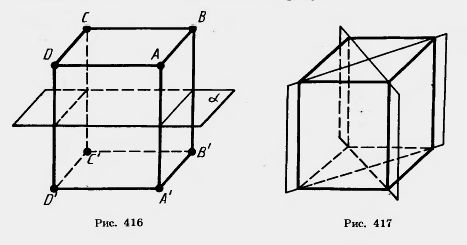
Если у параллелепипеда все линейные размеры равны, т. е. он является кубом, то у него плоскость любого диагонального сечения является плоскостью симметрии. Таким образом, у куба девять плоскостей симметрии.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урокаконспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний – Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.
Разработка – Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
Обновлено: 19.05.2023
Симметрия – это закономерная повторяемость
элементов (или частей) фигуры или какого-либо
тела, при которой фигура совмещается сама с
собой при некоторых преобразованиях
(вращение вокруг оси, отражение в плоскости).
Понятие симметрии включает в себя составные
части – элементы симметрии. Сюда
относятся плоскость симметрии, ось
симметрии, центр симметрии.
3. Симметрия в кубе
Оси симметрии в кубе:
прямые,
проходящие
через
центры
противоположных граней (таких 3) – прямые,
проходящие
через середины противоположных
рёбер(таких 6).
Плоскости симметрии в кубе – плоскости, проходящие через
любые две оси симметрии.
Плоскостей симметрии у куба 9. Проходят они либо через
противоположные ребра (таковых плоскостей 6), либо через
середины противоположных ребер (таких – 3).
Центр симметрии куба точка пересечения его
диагоналей.
Через центр симметрии проходят 9 осей симметрии.
5. Симметрия в параллелепипеде
У прямоугольного параллелепипеда, как у всякого
параллелепипеда, центр симметрии — точка пересечения его
диагоналей, плоскости симметрии ( таких 3), проходящие
через центр симметрии параллельно граням. На рисунке
показана одна из таких плоскостей. Она проходит через
середины четырех параллельных ребер параллелепипеда.
Концы ребер являются симметричными точкам.
6. Симметрия в призме
1. Центр симметрии при четном числе
сторон основания — точка пересечения
диагоналей правильной призмы
2. Плоскости симметрии:
плоскость, проходящая через середины боковых
ребер;
плоскости, проходящие через противолежащие
ребра, при четном числе сторон основания
3. Оси симметрии: при четном числе сторон основания
ось симметрии, проходящая через центры оснований,
оси симметрии, проходящие через точки пересечения
диагоналей противолежащих боковых граней
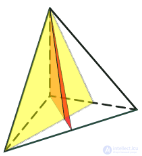
9. Симметрия в пирамиде
Симметрия правильной пирамиды
1. Плоскости симметрии: при четном числе сторон основания
плоскости, проходящие через противолежащие боковые
ребра;
плоскости, проходящие через медианы, проведенные к
основанию противолежащих боковых граней (рис. 1).
2. Ось симметрии: при четном числе сторон основания — ось
симметрии, проходящая через вершину правильной
пирамиды и центр основания (рис. 2).
Рис.1
Рис.2

Тема: Симметрия в кубе, в параллелепипеде, в призме и в пирамиде. Представление о правильных многогранниках.
I. Проверка знаний студентов. Тест по теме “Многогранники и их основные свойства” (15 мин.)
II. Изучение нового материала.
Симметрия: определение и основные понятия.
Симметрия в кубе.
Симметрия в параллелепипеде.
Симметрия в призме.
Симметрия в пирамиде.
Представление о правильных многогранниках.
? Как вы понимаете, что такое симметрия? Где мы можем встретиться с симметрией? Приведите примеры симметрии в природе, технике, архитектуре, быту.
Совершенно верно. С симметрией мы встречаемся в природе, архитектуре, технике, быту. Мы часто видим симметричные творения природы (листья, цветы, птицы, животные) или творения человека (здания, техника) – все то, что окружает нас каждый день. В быту: молотки, рубанки, лопаты, трубы. Мы смотрим на себя в зеркало и видим, что части нашего лица симметричны друг другу. По улицам ездят автомобили, автобусы, правая и левая части которых симметричны. Таким образом, симметрия бывает не только на плоскости (кленовый лист), но и в пространстве (лицо).
Симметрия – это закономерная повторяемость элементов (или частей) фигуры или какого-либо тела, при которой фигура совмещается сама с собой при некоторых преобразованиях (вращение вокруг оси, отражение в плоскости).
Понятие симметрии включает в себя такие понятия, как: ось симметрии, центр симметрии и плоскость симметрии.

1) Ось симметрии – воображаемая ось, при повороте вокруг которой на некоторый угол, фигура совмещается сама с собой в пространстве (
2) Центр симметрии – это точка внутри многогранника, в которой пересекаются и делятся пополам прямые, соединяющие одинаковые элементы многогранника (грани, рёбра, углы) (С).
3) Плоскость симметрии делит многогранник на 2 зеркально равные части (Р).
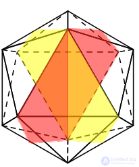
4) Степенью симметрии называется совокупность всех элементов симметрии, которыми обладает данный многогранник. Например, куб обладает высокой степенью симметрии, т.к. в нём присутствуют 3 оси симметрии четвёртого порядка (3, четыре оси симметрии 3 – го порядка (4, шесть осей второго порядка (6 В точке пресечения осей симметрии располагается центр симметрии куба. Кроме того в кубе можно провести 9 плоскостей симметрии (9Р).

(2) Симметрия в кубе.
Кубу свойственны все виды симметрии.
а) Центр симметрии (центр куба) – точка пресечения диагоналей куба.
б) Плоскости симметрии (9): 1) 3 плоскости симметрии, проходящие через середины параллельных ребер; 2) 6 плоскостей симметрии, проходящие через противолежащие ребра.

в) Оси симметрии (13): 1) 3 оси, проходящие через центры противолежащих граней; 2) 4 оси симметрии, проходящие через противолежащие вершины; 3) 6 осей, проходящие через середины противолежащих рёбер.


(3) Симметрия в параллелепипеде.
а) Центр симметрии – точка пересечения диагоналей прямоугольного параллелепипеда.
б) Плоскость симметрии. 3 плоскости симметрии, проходящие через середины параллельных рёбер.

в) Оси симметрии. 3 оси симметрии, проходящие через точки пересечения диагоналей противолежащих граней

(4) Симметрия в призме.
1) Симметрия прямой призмы. Одна плоскость симметрии, проходящая через середины боковых рёбер.

2) Симметрия правильной призмы.
а) Центр симметрии. При чётном числе сторон основания центр симметрии – это точка пересечения диагоналей правильной призмы.

б) Плоскости симметрии: 1) плоскость, проходящая через середины боковых рёбер; 2) при чётном числе сторон основания – плоскости, проходящие через противолежащие рёбра.

1) 2)

в) Ось симметрии: а) при чётном числе сторон основания – ось симметрии проходит через центры оснований; б) оси симметрии, проходящие через точки пресечения диагоналей противолежащих боковых граней.
(5) Симметрия в пирамиде.
а) Плоскости симметрии: при четном числе сторон основания — а) плоскости, проходящие через противолежащие боковые ребра, и б) плоскости, проходящие через медианы, проведенные к основанию противолежащих боковых граней.


б) Ось симметрии: при четном числе сторон основания — ось симметрии проходит через вершину правильной пирамиды и центр основания.
(6) Самостоятельная работа студентов по теме ” Представление о правильных многогранниках”. Задание: заполнить таблицу “Правильные многогранники”.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
ПЛАН ЗАНЯТИЯ №25
Учебная дисциплина: Математика.
Тема: Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Сечения куба, призмы и пирамиды.
а) образовательная: развитие речи, мышления.
б) воспитательная, развивающая: формирование у обучающихся самостоятельности, наблюдательности, трудолюбия, умения сравнивать делать вывод; прививать чувства ответственности и сознательного отношения к изучаемому материалу.
Тип урока: Комбинированный урок.
Метод проведения: Сочетания фронтальной и индивидуальной работы с обучающимися.
Оборудование урока: портативный компьютер, конспект, книги.
Организационный момент: Приветствие группы, проверка дежурства, состояние кабинета, наличие студентов, готовность к занятиям.
Проверка знаний студентов: Проверка наличия и ведения конспектов; проверка домашнего задания; опрос.
Симметрия: определение и основные понятия.
Симметрия в кубе.
Симметрия в параллелепипеде.
Симметрия в призме.
Симметрия в пирамиде.
Представление о правильных многогранниках.
Изучение нового материала: Лекция.
? Как вы понимаете, что такое симметрия? Где мы можем встретиться с симметрией? Приведите примеры симметрии в природе, технике, архитектуре, быту.
Совершенно верно. С симметрией мы встречаемся в природе, архитектуре, технике, быту. Мы часто видим симметричные творения природы (листья, цветы, птицы, животные) или творения человека (здания, техника) – все то, что окружает нас каждый день. В быту: молотки, рубанки, лопаты, трубы. Мы смотрим на себя в зеркало и видим, что части нашего лица симметричны друг другу. По улицам ездят автомобили, автобусы, правая и левая части которых симметричны. Таким образом, симметрия бывает не только на плоскости (кленовый лист), но и в пространстве (лицо).
Симметрия – это закономерная повторяемость элементов (или частей) фигуры или какого-либо тела, при которой фигура совмещается сама с собой при некоторых преобразованиях (вращение вокруг оси, отражение в плоскости).
Понятие симметрии включает в себя такие понятия, как: ось симметрии, центр симметрии и плоскость симметрии.
1) Ось симметрии – воображаемая ось, при повороте вокруг которой на некоторый угол, фигура совмещается сама с собой в пространстве (
2) Центр симметрии – это точка внутри многогранника, в которой пересекаются и делятся пополам прямые, соединяющие одинаковые элементы многогранника (грани, рёбра, углы) (С).
3) Плоскость симметрии делит многогранник на 2 зеркально равные части (Р).
4) Степенью симметрии называется совокупность всех элементов симметрии, которыми обладает данный многогранник. Например , куб обладает высокой степенью симметрии, т.к. в нём присутствуют 3 оси симметрии четвёртого порядка (3, четыре оси симметрии 3 – го порядка (4, шесть осей второго порядка (6 В точке пресечения осей симметрии располагается центр симметрии куба. Кроме того в кубе можно провести 9 плоскостей симметрии (9Р).
(2) Симметрия в кубе.
Кубу свойственны все виды симметрии.
а) Центр симметрии (центр куба) – точка пресечения диагоналей куба.
б) Плоскости симметрии (9): 1) 3 плоскости симметрии, проходящие через середины параллельных ребер; 2) 6 плоскостей симметрии, проходящие через противолежащие ребра.
в) Оси симметрии (13): 1) 3 оси, проходящие через центры противолежащих граней; 2) 4 оси симметрии, проходящие через противолежащие вершины; 3) 6 осей, проходящие через середины противолежащих рёбер.
(3) Симметрия в параллелепипеде.
а) Центр симметрии – точка пересечения диагоналей прямоугольного параллелепипеда.
б) Плоскость симметрии. 3 плоскости симметрии, проходящие через середины параллельных рёбер.
в) Оси симметрии. 3 оси симметрии, проходящие через точки пересечения диагоналей противолежащих граней
(4) Симметрия в призме.
1) Симметрия прямой призмы. Одна плоскость симметрии, проходящая через середины боковых рёбер.
2) Симметрия правильной призмы.
а) Центр симметрии . При чётном числе сторон основания центр симметрии – это точка пересечения диагоналей правильной призмы.
б) Плоскости симметрии: 1) плоскость, проходящая через середины боковых рёбер; 2) при чётном числе сторон основания – плоскости, проходящие через противолежащие рёбра.
в) Ось симметрии : а) при чётном числе сторон основания – ось симметрии проходит через центры оснований; б) оси симметрии, проходящие через точки пресечения диагоналей противолежащих боковых граней.
(5) Симметрия в пирамиде.
а) Плоскости симметрии: при четном числе сторон основания — а) плоскости, проходящие через противолежащие боковые ребра, и б) плоскости, проходящие через медианы, проведенные к основанию противолежащих боковых граней.
б) Ось симметрии: пр и четном числе сторон основания — ось симметрии проходит через вершину правильной пирамиды и центр основания.
(6) Самостоятельная работа студентов по теме ” Представление о правильных многогранниках”. Задание: заполнить таблицу “Правильные многогранники”.
Число граней
Число вершин
Число рёбер
Форма грани
Число граней, сходящихся в одной вершине
Сумма плоских углов при вершине
Подведение итогов урока: Вывод о достижении цели занятия.
1) Что нового я сегодня узнал на уроке?
2) Чему научился на уроке?
3) Что вызвало трудности?
Задание для самостоятельной работы студентов во внеурочное время:
1) конспект урока; 2) изготовить модели правильных многогранников из любого материала: картон, пластмасса, дерево, нитки или др. (развёртки даны в учебнике Атанасян “Геометрия” , 10 – 11 класс); 3) написать мини – сочинение “Геометрия вокруг нас”.

Тема: Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Сечения куба, призмы и пирамиды.
Цели:
а) образовательная: развитие речи, мышления.
б) воспитательная, развивающая: формирование у обучающихся самостоятельности, наблюдательности, трудолюбия, умения сравнивать делать вывод; прививать чувства ответственности и сознательного отношения к изучаемому материалу
Тип урока: Комбинированный урок.
Метод проведения: Сочетания фронтальной и индивидуальной работы с обучающимися.
Оборудование урока: портативный компьютер, конспект, книги.
ХОД УРОКА
1. Организационный момент:
Приветствие класса, проверка дежурства, состояние кабинета, наличие учеников, готовность к занятиям
.2.Актуализация опорных знаний:
“Многогранников вызывающе мало, – написал когда-то Л. Кэролл, – но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук”.
Симметричные тела и предметы состоят из равнозначных, правильно повторяющихся в пространстве частей. Особенно разнообразна симметрия кристаллов. Различные кристаллы отличаются большей или меньшей симметричностью. Она является их важнейшим и специфическим свойством, отражающим закономерность внутреннего строения.
Симметрия – это закономерная повторяемость элементов (или частей) фигуры или какого-либо тела, при которой фигура совмещается сама с собой при некоторых преобразованиях (вращение вокруг оси, отражение в плоскости).
Понятие симметрии включает в себя такие понятия, как: ось симметрии, центр симметрии и плоскость симметрии.
1) Ось симметрии – воображаемая ось, при повороте вокруг которой на некоторый угол, фигура совмещается сама с собой в пространстве (α)2) Центр симметрии – это точка внутри многогранника, в которой пересекаются и делятся пополам прямые, соединяющие одинаковые элементы многогранника (грани, рёбра, углы) (С).
3) Плоскость симметрии делит многогранник на 2 зеркально равные части (Р).
4) Степенью симметрии называется совокупность всех элементов симметрии, которыми обладает данный многогранник. Например, куб обладает высокой степенью симметрии, т.к. в нём присутствуют 3 оси симметрии четвёртого порядка (3 α4), четыре оси симметрии 3 – го порядка (4 α3), шесть осей второго порядка (6 α2). В точке пресечения осей симметрии располагается центр симметрии куба. Кроме того в кубе можно провести 9 плоскостей симметрии (9Р).
Симметрия в кубе.
Кубу свойственны все виды симметрии.
а) Центр симметрии (центр куба) – точка пресечения диагоналей куба.
б) Плоскости симметрии (9):
1) 3 плоскости симметрии, проходящие через середины параллельных ребер;
2) 6 плоскостей симметрии, проходящие через противолежащие ребра.
в) Оси симметрии (13):
1) 3 оси, проходящие через центры противолежащих граней;
2) 4 оси симметрии, проходящие через противолежащие вершины;
3) 6 осей, проходящие через середины противолежащих рёбер.
Симметрия в параллелепипеде.
а) Центр симметрии – точка пересечения диагоналей прямоугольного параллелепипеда.
б) Плоскость симметрии. 3 плоскости симметрии, проходящие через середины параллельных рёбер.
в) Оси симметрии. 3 оси симметрии, проходящие через точки пересечения диагоналей противолежащих граней
Симметрия в призме.
1) Симметрия прямой призмы. Одна плоскость симметрии, проходящая через середины боковых рёбер.
2) Симметрия правильной призмы.
а) Центр симметрии. При чётном числе сторон основания центр симметрии – это точка пересечения диагоналей правильной призмы.
б) Плоскости симметрии:
1) плоскость, проходящая через середины боковых рёбер;
2) при чётном числе сторон основания – плоскости, проходящие через противолежащие рёбра.
в) Ось симметрии:
а) при чётном числе сторон основания – ось симметрии проходит через центры оснований; б) оси симметрии, проходящие через точки пресечения диагоналей противолежащих боковых граней.
(5) Симметрия в пирамиде.
а) Плоскости симметрии: при четном числе сторон основания —
1) плоскости, проходящие через противолежащие боковые ребра,
2) плоскости, проходящие через медианы, проведенные к основанию противолежащих боковых граней.
б) Ось симметрии: при четном числе сторон основания — ось симметрии проходит через вершину правильной пирамиды и центр основания.
4. Самостоятельная работа с по теме ” Представление о правильных многогранниках”.
Задание: заполнить таблицу “Правильные многогранники”.
Определение правильного многогранника Изображение Число граней
(Г) Число вершин
(В) Число рёбер
(Р) Форма грани Число граней, сходящихся в одной вершине Сумма плоских углов при вершине
Тетраэдр – .
Куб (гексаэдр) -.
Октаэдр – .
5.Подведение итогов урока: Вывод о достижении цели занятия.
1) Что нового я сегодня узнал на уроке?
2) Чему научился на уроке?
3) Что вызвало трудности?
Читайте также:
- Конспект урока строчная буква р планета знаний
- Генетическая связь между классами органических соединений 10 класс конспект
- О древнем среднем и новом стихотворении российском конспект
- Вышивка крестом конспект кратко
- Связь между компонентами деления 3 класс конспект урока