Как найти центр симметрии трапеции

Трапеция — это четырехугольник, у которого только две стороны параллельны,
а две другие стороны нет.

Элементы трапеции

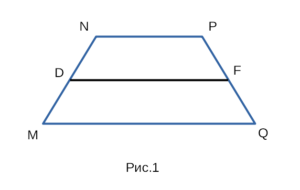
На рисунке 1 изображена трапеция MNPQ, с боковыми сторонами MN и PQ, с основаниями NP и MQ, а также со средней линией DF.

В трапеции две параллельные стороны называются основаниями. 0дна из параллельных сторон называется верхним основанием, а другая параллельная сторона называется нижним основанием. Но как определить, какая из параллельных сторон нижнее основание, а какая верхнее основание? Существует несколько способов это определить. Во-первых, как вы уже наверно догадались, нижнее основание расположено внизу трапеции, а верхнее основание расположено вверху трапеции. Во-вторых, верхнее основание меньше чем нижнее основание, и наоборот нижнее основание больше верхнего основания. C помощью этих двух способов вы можете
легко определить какое основание нижнее а какое верхнее. NP || MQ, NP — верхнее основание, MQ — нижнее основание.

Кроме оснований в трапеции, есть еще две не параллельные стороны. В трапеции эти две не параллельные стороны называются боковыми сторонами. Боковые стороны расположены сбоку от верхнего и нижнего оснований. MN и PQ — боковые стороны.

Отрезок, соединяющий середины боковых сторон называется средней линией трапеции. С средней линией трапеции связано несколько важных формул. Например, достаточно знать длину средней трапеции и одну из сторон основания, чтобы найти другое основание. Средняя линия делит две боковые стороны трапеции на две равных части. DF — средняя линия трапеции, MD = DN, QF = FP.

Центром симметрии трапеции называется середина средней линии трапеции. Центр симметрии
является центром вписанной, и центром описанной окружностей.

Виды трапеции

Также существует несколько видов трапеции. Это равнобедренная и прямоугольная трапеции.

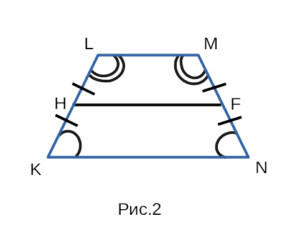
На рисунке 2 изображена равнобедренная трапеция KLMN, с боковыми сторонами KL и MN, с основаниями LM и KN, а также со средней линией HF.

В равнобедренной трапеции боковые стороны равны, углы при основаниях равны. KL = MN, ∠LKN = ∠MNK, ∠KLM = ∠NML.
Чтобы найти среднюю линию в равнобедренной трапеции достаточно знать только одну из боковых сторон.

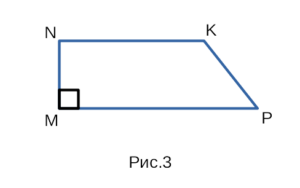
На рисунке 3 изображена прямоугольная трапеция MNKP, с боковыми сторонами MN и KP, с основаниями NK и MP, а также с прямым углом ∠NMP .

В прямоугольной трапеции у одной из боковых сторон есть прямой угол, или же по другом сказать — только одна боковая сторона перпендикулярна одному из оснований.
∠NMP — прямой угол.

Свойства трапеции

1. В трапеции может быть вписанная окружность, лишь в том случае, если сумма длин оснований трапеции равна сумме длин боковых сторон.
2. В трапеции средняя линия делит пополам её основания, и также делит пополам диагонали.
3. В трапеции нижнее и верхнее основания параллельны друг другу.
4. Средняя линия параллельна верхнему и нижнему основанию.
5. В трапеции могут находится только две диагонали. Точка, где пересекаются диагонали лежит на одной прямой.

Признаки трапеции

1. Трапецией является четырехугольник, у которого только две стороны параллельны,
   а две другие стороны нет.
2. Равнобедренной трапецией является трапеция, у которого две боковые стороны равны.
3. Равнобедренной трапецией является трапеция, у которой при любом из оснований углы равны.
4. Прямоугольной трапецией является трапеция, у которой один из углов при основании прямой.

План урока:

Трапеция

Средняя линия трапеции

Прямоугольная и равнобедренная трапеция

Прямоугольник

Ромб

Квадрат

Симметрия

Трапеция

Рассмотрим четырехуг-к, у которого параллельны только две стороны, а две оставшиеся  не параллельны. Такая фигура именуется трапецией.

На рисунке трапеция выглядит следующим образом:

Параллельные стороны именуются основаниями трапеции, а другие две – это боковые стороны.

Обратите особое внимание на то, что одно из оснований всегда больше второго основания. Действительно, если бы основания имели одинаковую длину, то получился бы четырехуг-к, у которого две противоположные стороны и равны, и параллельны. Однако это уже один из признаков параллелограмма, а параллелограмм никак не может быть трапецией.

Иногда полезно представлять трапецию как усеченный треуг-к. Действительно, если в треугольнике провести линию, параллельную одной из сторон и пересекающую две остальные стороны, то она как бы «отсечет» верхушку этого треуг-ка, и получится трапеция. И наоборот, любую заданную трапецию можно достроить до треугольника:

Сумма всех 4 углов трапеции составляет, как и у любого четырехугольника, 360°.

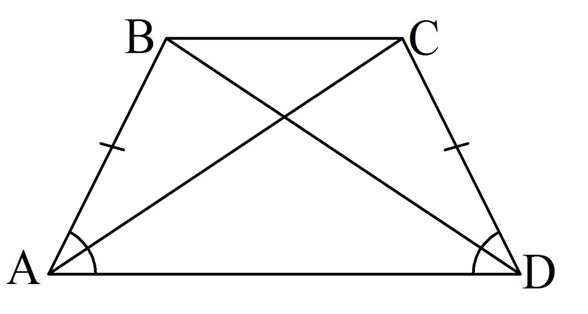
Задание. Известно, что у трапеции АВСD АD||ВС, ∠А = 36°, ∠С = 117°. Найдите∠В и ∠D.

Решение: АВ можно рассматривать как секущую параллельных прямых ВС и АD. Но тогда∠А и ∠В будут являться односторонними, а их сумма будет равна 180°. Отсюда можно найти ∠В:

Аналогично, рассматривая в качестве секущей СD, можно найти и ∠D, который вместе с∠С является односторонним:

Средняя линия трапеции

Если отметить середину каждой из боковых сторон трапеции, а потом соединить эти середины, то получится отрезок, именуемый средней линией трапеции.

Докажем важную теорему, связанную со средней линией:

Для этого изучим трапецию АВСD, у которой боковые стороны – это АВ и CD. Пусть М – середина АВ. Проведем через М прямую, параллельную основаниям, которая пересечет СD в точке N. По теореме Фалеса параллельные друг другу прямые АD, МN и ВС отсекут на прямой СD равные отрезки, то есть СN = ND. Но это означает, что N– середина CD, а тогда MN – средняя линия (согласно ее определению). Естественно, что в трапеции возможно построить только одну среднюю линию, а значит, средняя линия МN параллельна каждому из оснований.

Прямоугольная и равнобедренная трапеция

Существует два частных вида трапеции, обладающих особыми свойствами. Первый из них – это прямоугольная трапеция. Она отличается тем, что один из ее углов равен 90°.

Здесь∠А = 90°. Легко догадаться, что на самом деле если у трапеции хоть один угол составляет 90°, то найдется и ещё один угол, также равный 90°. В данном случае это ∠В. Сумма ∠A и ∠D должна составлять 180°, ведь они односторонние. Именно поэтому из условия

Задание. Основания прямоугольной трапеции имеют длину 10 и 15 см, а один из углов составляет 45°. Вычислите длину ее наименьшей боковой стороны?

Решение:

Пусть основания заданной трапеции – это отрезки АD и ВС, ∠А = 45°, ∠D = ∠C = 90°. Опустим из точки В перпендикуляр ВН на АD:

Очевидно, что ВН||CD, ведь эти отрезки перпендикулярны одной прямой АD. Получается, что в четырехуг-ке НВСD противоположные стороны попарно параллельны, то есть он является параллелограммом. Отсюда вытекает равенство его сторон:

Нашли СD, но является ли этот отрезок именно меньшей боковой стороной трапеции? Для ответа на этот вопрос вернемся к ∆АВН. В нем АВ – это гипотенуза, а потому она заведомо больше катета ВН, то есть больше 5 см. Значит, именно CD – это меньшая боковая сторона.

Ответ: 5 см.

Ещё один особый вид трапеции – равнобедренная трапеция. Она отличается тем, что у неё длины боковых сторон одинаковы.

Равнобедренная трапеция обладает рядом интересных свойств. Начнем с того, что углы при каждом из ее оснований равны.

В итоге мы получили четырехуг-к АВСН, в котором АВ||CН, ВС||АН. Это значит, что он является параллелограммом, и тогда

Отсюда сразу же вытекает и второе свойство равнобедренной трапеции – у неё равные диагонали.

Доказывается этот факт с помощью первого признака равенства треуг-ков:

Действительно, треуг-ки ∆АВD и ∆АСD равны, ведь

Оказывается, есть признаки, которые позволяют определить, является ли трапеция равнобедренной. Сформулируем первый из них:

Для доказательства снова построим в трапеции АВСD такую прямую СН, что СН||АВ:

Тогда

Несколько сложнее доказать другую теорему:

Пусть в трапеции АВCD одинаковы диагонали ВD и АС. Для определенности будем считать, что большее основание – это АD. Опустим из точек В и С перпендикуляры ВЕ и СF на АD:

Ясно, что эти перпендикуляры параллельны друг другу, ведь они перпендикулярны третьей прямой. Тогда в ВСFЕ противоположные стороны параллельны, то есть эта фигура – параллелограмм. Отсюда вытекает, что

BE = CF

Далее рассмотрим ∆ВЕD и ∆АСF. Они оба являются прямоугольными, у них одинаковы гипотенузы (АС = ВD), а также и катеты ВЕ и СF. Значит, эти треуг-ки равны, следовательно,

Задание. Один из углов равнобедренной трапеции составляет 55°. Найдите все остальные углы этой трапеции.

Решение. Проще всего найти ∠D, ведь углы при основании равнобедренной трапеции одинаковы:

Заметим одно важное обстоятельство. Если достроить равнобедренную трапецию до треугольника, продолжив ее боковые стороны, то получится равнобедренный треуг-к:

Действительно, если АВСD – равнобедренная трапеция, то

∠А = ∠D

Пусть продолжения боковых сторон пересеклись в некоторой точке Е. Тогда в ∆АЕD два угла, ∠А и ∠D, окажутся равными, следовательно, ∆АЕD– равнобедренный.

Прямоугольник

Следующим особым четырехугольником является прямоугольник (иногда его сокращенно обозначают как прямоуг-к). Его отличительный признак заключается в том, что все его углы – прямые.

Продемонстрируем несколько прямоугольников:

Очевидно, что у прямоуг-ка противоположные стороны параллельны, ведь они перпендикулярны одной и той же прямой. Следовательно, всякий прямоуг-к одновременно является параллелограммом и обладает всеми его свойствами. Стоит особо отметить, что обратное утверждение неверно – отнюдь не всякий параллелограмм является прямоугольником. Другими словами, прямоугольник – это частный случай параллелограмма, который отличается тем, что его углы составляют 90°.

Из этого вытекает два свойства прямоугольника:

• его противоположные стороны равны;
• точка пересечения его диагоналей является серединой этих самых диагоналей.

Однако есть ещё одно свойство, которое НЕ характерно для остальных параллелограммов.

Доказать это очень просто. Пусть есть прямоугольник АВCD:

Сравним ∆АВD и ∆АСD. Они являются прямоугольными, у них есть общий катет АD, а два других катете, АВ и СD, равны как противоположные стороны прямоугольника. Получается, что рассматриваемые треуг-ники равны, и поэтому равны и их гипотенузы, которые как раз и являются диагоналями прямоугольника.

Оказывается, верна и обратная теорема, которую называют признаком прямоугольника:

Действительно, пусть есть некоторый параллелограмм АВCD, у которого одинаковы диагонали АС и BD.

Противоположные стороны в одном параллелограмме одинаковы:

В итоге все углы АВСD оказываются прямыми, и эта фигура по определению оказывается прямоуг-ком.

Задание. В прямоуг-ке ABCD проведена биссектриса, которая делит сторону СD на отрезки СК и КD длиной 27 и 45 см соответственно. Найдите периметр АВCD.

Решение.Для нахождения периметра необходимо найти длины всех сторон.

Если АК – биссектриса, то

∆КАD является прямоугольным, и мы только что нашли один из его острых углов. Тогда можно найти и 2-ой угол:

Получается, что в ∆АКD два угла равны 45°, значит, он является равнобедренным, и

Мы нашли две смежные стороны прямоугольника, АD и СD. Две другие стороны будут им равны:

Ромб

Следующая особенная фигура – это ромб. Дадим определение ромба:

На рисунке видно, что ромб похож на параллелограмм, и это не случайно. Докажем, что любой ромб является частным случаем параллелограмма. Но прежде заметим, что обратное утверждение неверно – отнюдь не каждый параллелограмм является ромбом.

Для доказательства этого факта проведем диагональ ромба:

В результате получилось два треуг-ка: ∆АВС и ∆АСD. Можно заметить два факта. Во-первых, каждый из этих треуг-ков – равнобедренный, ведь стороны ромба равны. Тогда можно записать равенство углов:

Из равенства треуг-ков вытекает и равенство углов:

Тогда очевидно, что ∠А и ∠С также равны, ведь они состоят из двух равных углов:

В итоге получается, что в ромбе противоположные углы одинаковы. Зная, что все 4 угла в сумме дают 360°, легко найдем сумму каких-нибудь двух смежных углов:

Итак, сумма смежных углов в ромбе равна 180°. Но эти углы можно рассматривать как односторонние. Если их сумма равна 180°, то и соответствующие прямые (в частности, ВС и АD) параллельны. Аналогично доказывается и то, что АВ||CD. Это и значит, что АВСD– параллелограмм.

Продолжим рассматривать построенный нами рисунок, но добавим в него ещё одну диагональ:

Во-первых, мы уже доказали следующее равенство

Из него вытекает, что диагональ АС является биссектрисой для∠А и ∠С. Аналогично и для диагонали ВD можно показать, что и она разбивает ∠В и ∠D пополам. Можно сформулировать следующее свойство ромба:

Далее рассмотрим ∆АВD. Он равнобедренный, а АО является биссектрисой, падающей на основание ВD. Но в равнобедренном треуг-ке такая биссектриса одновременно является высотой, то есть

Получается, что диагонали всякого ромба обязательно пересекаются под прямым углом.

Задание. Длина стороны ромба совпадает с длиной одной из его диагоналей. Определите углы этого ромба.

Решение. Построим рисунок по условию задачи:

Легко заметить, что∆АВС и ∆АСD будут равносторонними. Однако все углы равностороннего треуг-ка равны 60°:

Итак, два угла ромба будут равны 60°, а другие два 120°.

Ответ: 60°; 120°.

Квадрат

Последний особый случай четырехугольника – это квадрат. Эта фигура, которая сразу является и прямоугольником, и ромбом. Естественно, что любой квадрат одновременно является параллелограммом. Дадим определение квадрата:

Свойства квадрата – это совокупность свойств параллелограмма, ромба и прямоуг-ка.Это значит, что его диагонали:

• равны;
• пересекаются под углом 90°;
• точка их пересечения – это середина диагоналей.

Задание. Середины сторон квадрата соединили отрезками. Докажите, что получившаяся фигура также является квадратом.

Решение. Требуется доказать, что фигура, показанная красным цветом, является квадратом:

Так как стороны квадрата одинаковы, то одинаковы и их половины:

Получается, что ∆АМН, ∆МВР, ∆РСК и ∆КНD – прямоугольные, причем у них равны все катеты. Это значит, что, с одной стороны, они являются равнобедренными треуг-ками, а с другой стороны, они равны друг другу. Мы уже знаем, что у равнобедренного прямоугольного треуг-ка углы при основании составляют по 45°, а из равенства треуг-ков вытекает, что

Получается, что у четырехуг-ка МРКН все стороны одинаковы, то есть он является ромбом. Осталось доказать, что все его углы прямые. Рассмотрим, например, ∠РМН. Он в сумме с ∠ВМР и ∠АМН дает 180°, что позволяет вычислить его:

Итак, все углы ромба МРКН прямые, значит, он является квадратом.

Мы видим, что есть множество видов четырехугольников, причем часто одна и та же фигура может относиться сразу к нескольким типам. Для наглядности покажем на одной картинке всю иерархию четырехугольников. Здесь на одном рисунке можно увидеть название всех видов четырехугольников, их форму, также главное свойство, по которым их и определяют:

Симметрия

В заключение рассмотрим также такое важное геометрическое понятие, как симметрия.

В случае, показанном на рисунке,А₁ и А₂ не лежат на b. Если же рассматривается точка, лежащая на b, то она считается симметричной самой себе. На рисунке пары точек А и B, C и D, M и N симметричны относительно b.Для точки же Р нельзя найти парную ей симметричную точку. Поэтому условно считается, что она симметрична сама себе.

Теперь перейдем к такому понятию, как симметричная фигура.

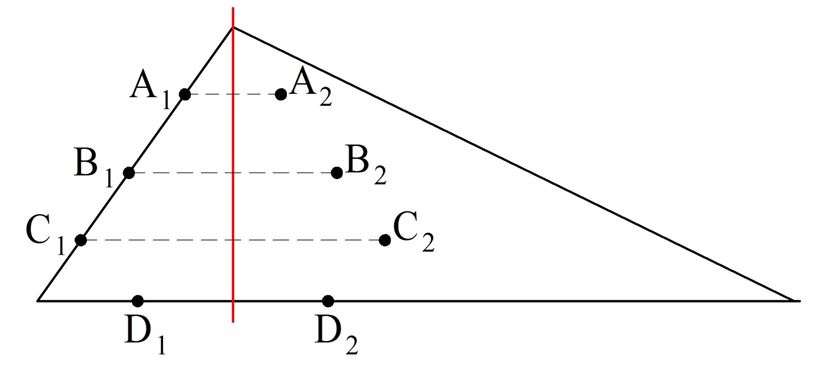
В качестве иллюстрации приведем равнобедренный треуг-к. У него роль оси симметрии играет медиана, проведенная к основанию. Выберем на треугольнике произвольные точки А₁, В₁, С₁ и D₁. Далее отметим симметричные им относительно b точки, которые обозначим как А₂, В₂, С₂ и D₂. Видно, что они также принадлежат треугольнику:

Рассмотрим для иллюстрации и какую-нибудь несимметричную фигуру, например, треугольник с 3 разными сторонами:

Видно, что например, для точка А₁ симметричная ей А₂ НЕ принадлежит треугольнику, поэтому красная линия НЕ является осью симметрии.

Осевая симметрия присуща и многим другим фигурам:

Обратите внимание, что осей симметрии фигуры может быть несколько. У ромба их две (это его диагонали), у квадрата уже четыре (помимо диагоналей добавляются ещё и линии, соединяющие середины его противоположных сторон), а у окружности их и вовсе бесконечно много, так как любой ее диаметр может играть эту роль.

Возможен ещё один случай симметрии:

На приведенном рисунке С – это середина АВ, поэтому А и В симметричны, а точка С для них является центром симметрии.

Снова перейдем от отдельных точек к фигурам.

В частности, центральная симметрия присуща параллелограмму (его центром симметрии будет точка, в которой пересекаются его диагонали), а также окружность. Есть центральная симметрия и у любой прямой, причем в качестве центра симметрии фигуры можно выбрать любую точку, принадлежащую этой прямой:

Симметрия – это не просто умозрительная геометрическая конструкция, она встречается и в реальной жизни. Например, листья многих деревьев обладают осевой симметрией, а зубчатое колесо – центральной симметрией. Интересно, что из 32 выделяемых в царстве животных типов у представителей 28 (это более 99% известных видов) можно выделить правую и левую половину, которые симметричны друг другу. Архитекторы и конструктора при проектировании зданий и машин стремятся придать им симметричную форму, так как в большинстве случаев именно такая форма оказывается оптимальной и экономичной.

Центральная. Осью симметрии является точка в центре тела, относительно которой при всех преобразованиях части тела равны при наложении.

История симметрии

Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.

В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то “центрального огня”, вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.

А философ Платон считал многогранники олицетворением четырех природных стихий:

• тетраэдр – огонь, так как его вершина направлена вверх;
• куб – земля, так как это самое устойчивое тело;
• октаэдр – воздух, нет каких-либо объяснений;
• икосаэдр – вода, так как тело не имеет грубых геометрических форм, углов и так далее;
• образом всей Вселенной являлся додекаэдр.

Из-за всех этих теорий правильные многогранники называют телами Платона.

Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.

Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины “День и ночь”.

Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. “Богатыри”.

Что уж там говорить, симметрия – ключевое понятие для всех деятелей искусства на протяжении многих веков, но в XX веке ее смысл оценили также все деятели точных наук. Точным свидетельством являются физические и космологические теории, например, теория относительности, теория струн, абсолютно вся квантовая механика. Со времен Древнего Вавилона и, заканчивая передовыми открытиями современной науки, прослеживаются пути изучения симметрии и открытия ее основных законов.

Симметрия геометрических фигур и тел

Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.

А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника – также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно – длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.

Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых – бесконечное множество.

У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии – диагонали, а во втором – средние линии. Множество таковых осей только у квадрата.

Симметрия в природе

Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.

А сколько примеров окружает нас постоянно! Это цветы, листья, лепестки, овощи и фрукты, животные и даже соты пчел имеют ярко выраженную геометрическую форму и симметрию. Вся природа устроена упорядоченно, всему есть свое место, что еще раз подтверждает совершенство законов природы, в которых симметрия – основное условие.

Вывод

Нас постоянно окружают какие-либо явления и предметы, например, радуга, капля, цветы, лепестки и так далее. Их симметрия – очевидна, в какой-то степени она обусловлена гравитацией. Часто в природе под понятием “симметрия” понимают регулярную смену дня и ночи, времен года и так далее.

Подобные свойства наблюдаются везде, где есть порядок и равенство. Также и сами законы природы – астрономические, химические, биологические и даже генетические подчинены определенным принципам симметрии, так как имеют совершенную системность, а значит, сбалансированность имеет всеохватывающий масштаб. Следовательно, осевая симметрия – один из основополагающих законов мироздания в целом.

Осевая и центральная симметрия

О чем эта статья:

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.
2. Проводим через точку В прямую, перпендикулярную прямой l.
3. Измеряем расстояния от точек А и В до прямой l.
4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

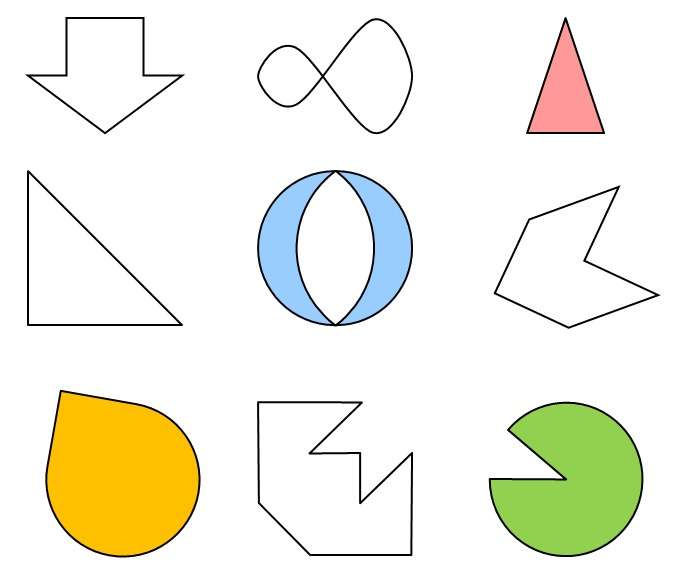
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Осевая симметрия

Осевая симметрия — это симметрия относительно прямой.

Пусть дана некоторая прямая g.

Чтобы построить точку, симметричную некоторой точке A относительно прямой g, надо:

1) Провести из точки A к прямой g перпендикуляр AO.

2) На продолжении перпендикуляра с другой стороны от прямой g отложить отрезок OA1, равный отрезку AO: OA1=AO.

Полученная точка A1 симметрична точке A относительно прямой g.

Прямая g называется осью симметрии.

Таким образом, точки A и A1 симметричны относительно прямой g, если эта прямая проходит через середину отрезка AA1 и перпендикулярна к нему.

Если точка A лежит на прямой g, то симметричная ей точка есть сама точка A.

Преобразование фигуры F в фигуру F1, при котором каждая её точка A переходит в точку A1, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g.

Фигуры F и F1 называются фигурами, симметричными относительно прямой g.

Чтобы построить треугольник, симметричный данному относительно прямой g, достаточно построить точки, симметричные вершинам треугольника, и соединить их отрезками.

Например, треугольники ABC и A1B1C1 симметричны относительно прямой g.

Если преобразование симметрии относительно прямой g переводит фигуру в себя, то такая фигура называется симметричной относительно прямой g, а прямая g называется её осью симметрии.

Симметричная фигура своей осью симметрии делится на две равные половины. Если симметричную фигуру нарисовать на бумаге, вырезать и согнуть по оси симметрии, то эти половинки совпадут.

Примеры фигур, симметричных относительно прямой.

1) Прямоугольник.

Прямоугольник имеет 2 оси симметрии: прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

Ромб имеет две оси симметрии:

прямые, на которых лежат его диагонали.

3) Квадрат, как ромб и прямоугольник, имеет четыре оси симметрии: прямые, содержащие его диагонали, и прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

Окружность имеет бесконечное множество осей симметрии:

любая прямая, содержащая диаметр, является осью симметрии окружности.

Прямая также имеет бесконечное множество осей симметрии: любая перпендикулярная ей прямая является для данной прямой осью симметрии.

Равнобедренная трапеция — фигура, симметричная относительно прямой,перпендикулярной основаниям и проходящей через их середины.

Равнобедренный треугольник имеет одну ось симметрии:

прямую, проходящую через высоту (медиану, биссектрису), проведённую к основанию.

8) Равносторонний треугольник.

Равносторонний треугольник имеет три оси симметрии:

прямые, содержащие его высоты (медианы, биссектрисы).

Угол — фигура, симметричная относительно прямой, содержащей его биссектрису.

Осевая симметрия является движением.

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/osevaya-i-centralnaya-simmetriya

[/spoiler]

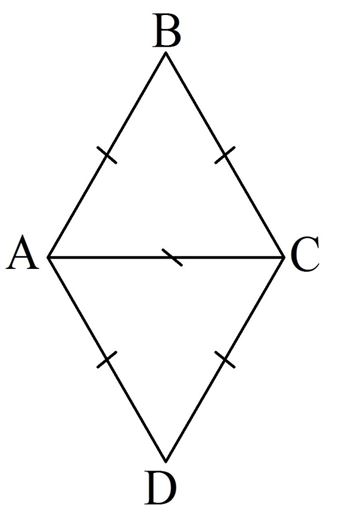
При осевой и центральной симметрии трапеция отображается в трапецию.

1) АВ — ось симметрии, значит отрезок АВ отобразится на себя.

Из точек С и D проведем лучи СК⊥АВ и DH⊥AB.

На этих лучах по другую сторону от прямой АВ отложим отрезки КС₁ = СК и HD₁ = DH.

ABC₁D₁ — искомая трапеция.

2) C — центр симметрии, значит эта вершина отобразится на себя.

Из вершин А, В и D проведем лучи АС, ВС и DC. На них по другу сторону от точки С отложим отрезки

CA₁ = AC, CB₁ = BC и CD₁ = DC.

А₁B₁CD₁ — искомая трапеция.