СПОСОБ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ЦЕНТРА
НАИБОЛЕЕ ОПАСНОЙ ПОВЕРХНОСТИ СКОЛЬЖЕНИЯ
СПОСОБОМ ПОСЛЕДОВАТЕЛЬНОГО ПРИБЛИЖЕНИЯ
Е.1 Центр критической дуги скольжения, проходящей через подошву откоса насыпи находят следующим образом.
1) Предварительно находят точку O1 пересечения двух прямых AO и CB. Прямую AO проводят под углом 25° к средней поверхности откоса (рисунок Е.1). Прямую CB проводят через бровку откоса и точку B, отстоящую от поверхности насыпи на глубину 2H и от подошвы откоса на расстояние 4,5H.
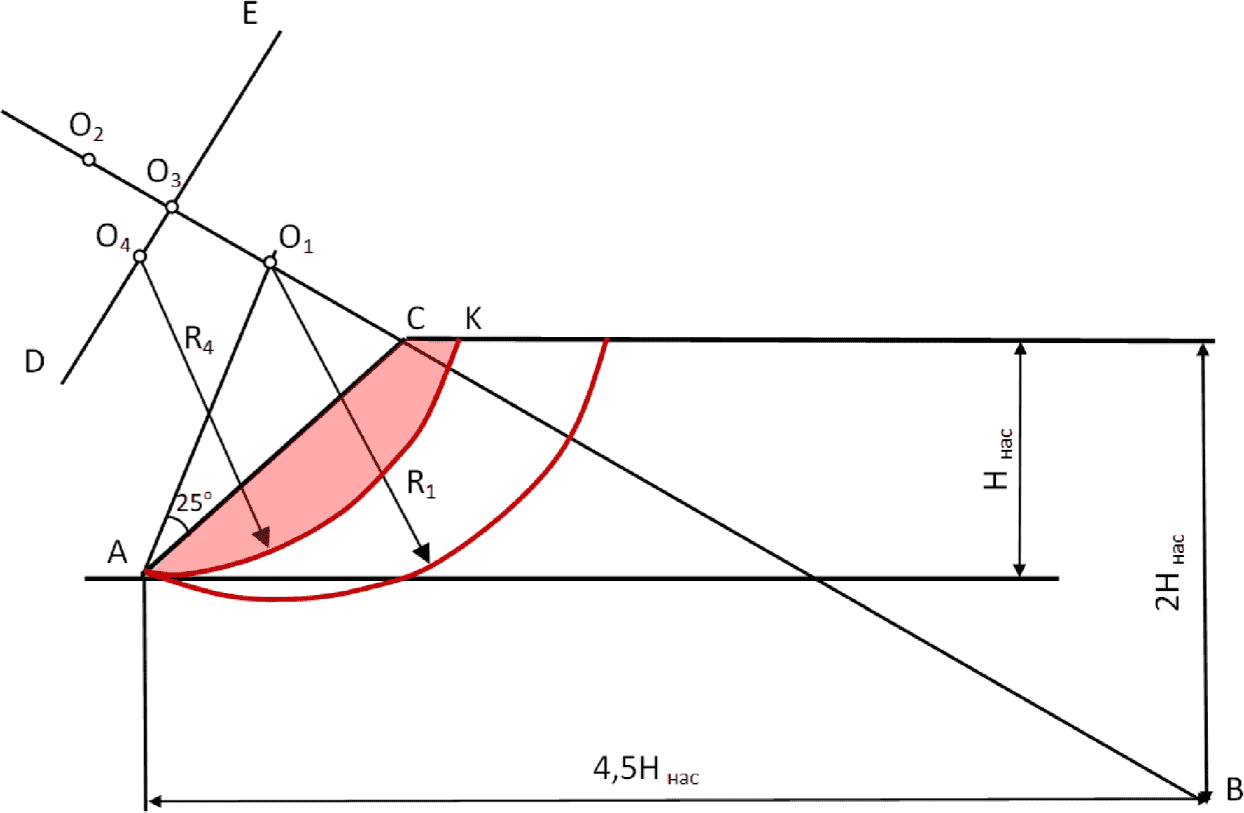
Рисунок Е.1 – Определение местоположения центра критической
поверхности скольжения, проходящей через подошву откоса,
способом последовательного приближения
В первом приближении точка O1 принимается за центр критической кривой скольжения. Проведя из этого центра кривую скольжения, определяют коэффициент запаса для полученного отсека. Далее на прямой CB выбирают еще несколько точек в качестве центров кривых скольжения на расстоянии примерно 0,25Hнас друг от друга и повторяют эти расчеты до тех пор, пока не будет определено положение точки, отвечающей минимальному коэффициенту устойчивости.
Е.2 После нахождения на прямой CB центра наиболее опасной дуги скольжения, которой соответствует минимальный коэффициент запаса устойчивости, необходимо путем ряда аналогичных попыток найти центр наиболее опасной кривой скольжения по прямой DE вправо и влево от центра критической кривой, расположенного на прямой CB.
Е.3 Окончательно за расчетную принимают наиболее опасную кривую скольжения с центром на прямой DE, которой соответствует минимальный коэффициент запаса устойчивости.
Е.4 Центр критической кривой скольжения, проходящий через основание откоса, располагается в зоне между вертикалью и нормалью, проведенными из середины поверхности откоса средней крутизны (рисунок Е.2). Верхняя точка выхода кривой скольжения первоначально принимается на основе предшествующих расчетов, выполненных по п.п. Е.1 – Е.3.
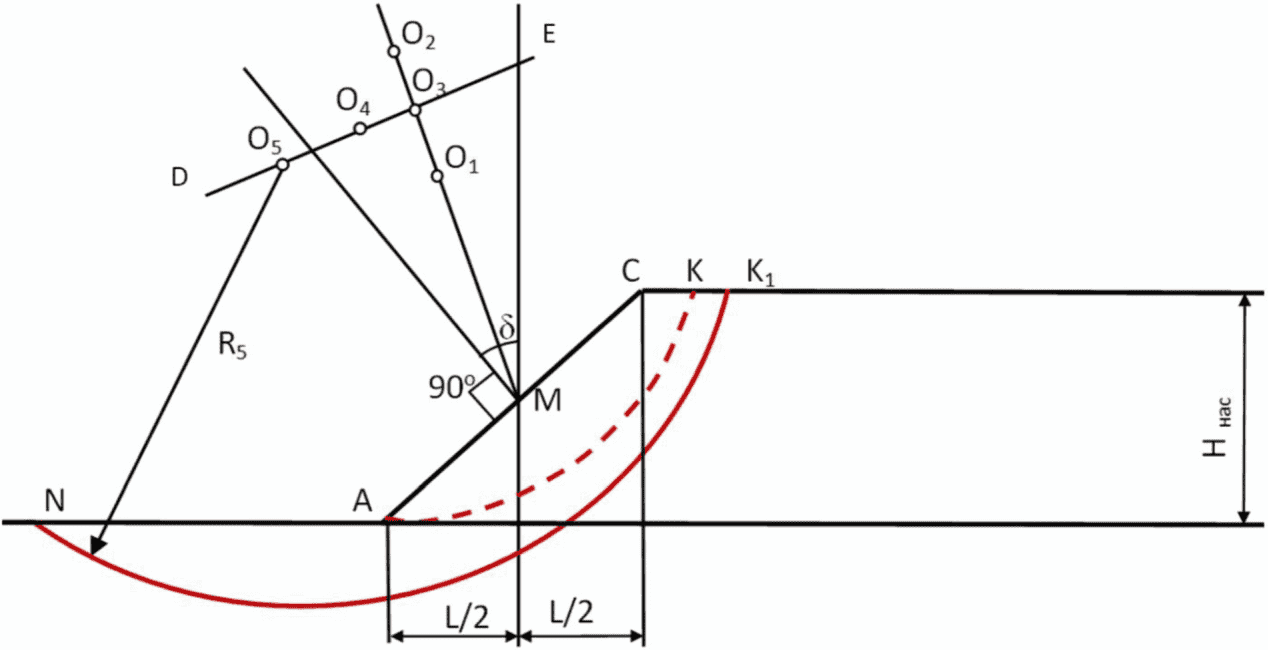
Рисунок Е.2 – Определение местоположения центра критической
поверхности скольжения, проходящей через основание откоса,
способом последовательного приближения
Е.5 В первом приближении этот центр назначают на биссектрисе угла ![]() на расстоянии Hнас от точки M. На продолжении линии O1M через 0,25Hнас откладывают центры для последующих этапов нахождения критической кривой скольжения. Через центр критической кривой скольжения, соответствующей наиболее опасной кривой скольжения, перпендикулярно проводят линию DE, где также через 0,25Hнас откладывают центры возможных критических кривых скольжения для проверочных расчетов.
на расстоянии Hнас от точки M. На продолжении линии O1M через 0,25Hнас откладывают центры для последующих этапов нахождения критической кривой скольжения. Через центр критической кривой скольжения, соответствующей наиболее опасной кривой скольжения, перпендикулярно проводят линию DE, где также через 0,25Hнас откладывают центры возможных критических кривых скольжения для проверочных расчетов.
За расчетный принимают наименьший коэффициент запаса устойчивости, соответствующий критической кривой скольжения, проведенной из центра, расположенного на прямой DE.
Скачать документ целиком в формате PDF
Рассмотрим призму скольжения
Центром вращения «О» и соответственно величиной радиуса R задаются.
Призму скольжения разбивают вертикальными сечениями на ряд отсеков и принимают вес каждого отсека Рi условно приложенным к точке пересечения линии действия веса с соответствующим отрезком дуги скольжения (рис.а). Силы веса раскладывают на направление радиуса вращения (Ni) и ему перпендикулярное (Тi). Затем составляют уравнение равновесия в виде суммы моментов всех сил относительно центра вращения:
![]()
где: L – длина дуги скольжения АС,
φ – угол внутреннего трения грунта,
с – сцепление грунта,
Тi=Рisinφ – сила трения.
В этом уравнении первое слагаемое представляет собою сдвигающий момент, а два других – величину удерживающего момента противоположного направления:

Их отношение составляет коэффициент устойчивости откоса:

В этом выражении величина радиуса вращения R сократилась, а tgφ=f – коэффициент трения грунта по грунту.
Теперь требуется определить какая же кривая скольжения и какая величина коэффициента устойчивости откоса являются истинными? Этот вопрос решается путем последовательных попыток, задаваясь каждый раз различными кривыми скольжения (рис.б) до тех пор, пока не будет найдено такого положения, при котором коэффициент устойчивости имеет минимальное значение («критическая кривая»). Возможно и графическое определение положения центра критической кривой скольжения. Его предложил шведский исследователь Феллениус. С этой целью сначала находят положение центра критической кривой для грунта, не обладающего внутренним трением (φ=0) в зависимости от крутизны откоса:

Тогда таблица углов:

По Феллениусу, центр критической кривой лежит на продолжении прямой ОК, где «О» — центр кривой скольжения для случая φ=0, а «К» — точка на глубине h от подошвы откоса и вправо от нее на расстоянии 4,5h по горизонтальному направлению, где h – высота откосов.
Такое построение справедливо для случая однородного грунта, постоянной крутизны откоса и горизонтальной верхней поверхности. Также следует иметь в виду, что построение Феллениуса не является точным решением вопроса, оно указывает примерную зону расположения центра критической кривой скольжения и нуждается в дальнейшем уточнении путем нескольких дополнительных попыток.
Этот метод впервые был
применен К. Петерсоном в 1916 г. Считается,
что потеря устойчивости откоса может
произойти в результате вращения отсека
грунтового массива относительно
некоторого центра О (рис. 6.5). Поверхность
скольжения в этом случае принимается
проходящей по дуге окружности с радиусом
R. Смещающий массив
рассматривается как недеформируемый
отсек.

Рис. 6.4.
Схема к расчету устойчивости откоса
методом
круглоцилиндрических поверхностей
скольжения
Сущность метода
заключается в определении минимального
коэффициента устойчивости откоса st,
отвечающего заданным условиям и
нагрузкам. Коэффициент st
определяют как отношение суммы
моментов всех сил, удерживающих откос,
относительно центра О к сумме моментов
всех сил, сдвигающих (вращающих) откос,
относительно того же центра.
Расчет устойчивости
откоса методом круглоцилиндрических
поверхностей скольжения производится
в следующей последовательности:
-
Задаются центром
вращения откоса (т.О). -
Проводят через
точку А след круглоцилиндрической
поверхности скольжения радиусом R. -
Призму обрушения
АВС разделяют вертикальными
плоскостями на n
отсеков (обычно от 8 до 10). -
Определяют вес
каждого отсека Pi
и прикладывают его в точке пересечения
вертикали, проходящей через центр
тяжести отсека, с поверхностью скольжения. -
Раскладывают силу
Pi
на нормальную Ni
и касательную Ti
составляющие. -
Определяют
удерживающий и сдвигающий моменты.
Сила
трения в каждом отсеке
Ti’
= Ni
tg
= Pi
cosi
tg,
(6.13)
где i
– угол наклона поверхности скольжения
к горизонту в точке приложения веса
отсека;
– расчетное значение угла внутреннего
трения грунта на поверхности скольжения
отсека.
Удерживающий
момент относительно точки О равен
Муд.
= R Ni
tg
+ R cili
, (6.14)
где R
– радиус поверхности скольжения; с
– расчетное значение удельного сцепления
грунта; i – участок
поверхности скольжения; li
– длина поверхности скольжения в
пределах i – го
участка.
-
Определяют коэффициент
устойчивости откоса st
как отношение суммы моментов
удерживающих сил к сумме моментов
сдвигающих сил относительно центра
О:
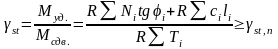
.
(6.15)
Вес отсеков
определяют графически или вычисляют
по значениям углов i.
8. Проводят другие
круглоцилиндрические поверхности с
центрами в разных точках (см. О2…Оn
на рис. 6.4). Для этих поверхностей
рассчитывают коэффициенты устойчивости
и определяют поверхность, которой
соответствует минимальное значение
коэффициента st,min.
Если выполняется условие st,min
st.n,
откос можно считать устойчивым, а если
st,min
< st.n
– неустойчивым.
Пример 6.1
Оценить устойчивость
откоса по заданной круглоцилиндрической
поверхности скольжения. Высота откоса
Н = 6,5 м, угол откоса
= 450 (рис. 6.5).
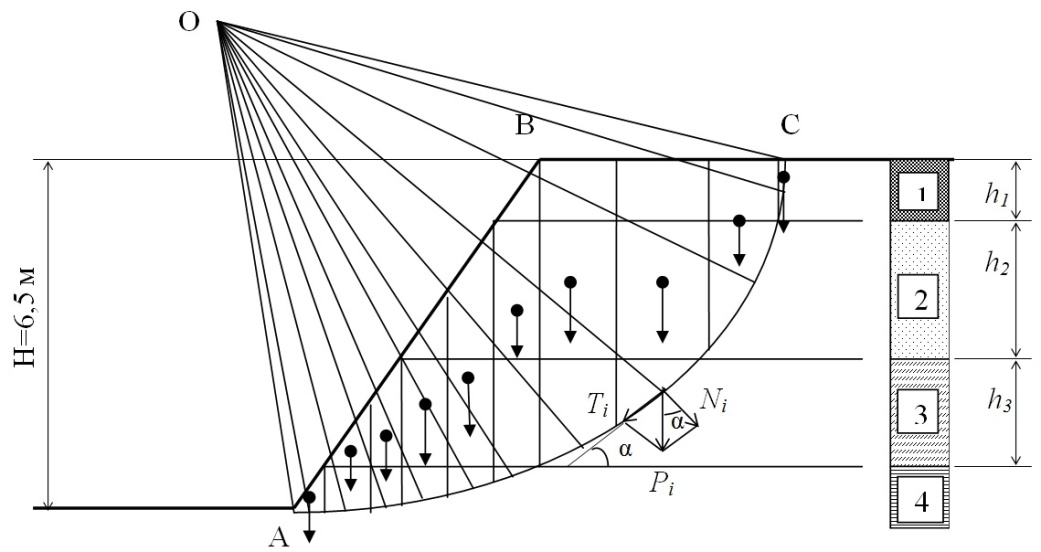
Рис. 6.5. Расчетная
схема откоса к примеру 6.1:
1
–
насыпной грунт; 2 –
песок пылеватый средней плотности
средней
степени водонасыщения; 3 –
супесь пластичная;
4
–
глина полутвердая
Откос сложен
следующими напластованиями грунтов:
1) насыпной грунт, толщина слоя h1
= 1 м; 2) песок пылеватый средней плотности
средней степени водонасыщения, толщина
слоя h2 = 2,6
м, φI
= 270, cI
= 2,7 кПа; 3) супесь пластичная, толщина
слоя h3 = 2,5
м, φI
= 210, cI
= 8,7 кПа; 4) глина полутвердая, толщина
слоя h4 = 4,0
м, φI
= 170, cI
= 45 кПа.
Для
построения цилиндрической поверхности
скольжения выбираем центр вращения О.
Центр вращения находим на пересечении
линий, проведённых с учётом углов ψ =
300 и β = 40°. Через центр вращения О
и точку В на подошве откоса проводим
окружность, которая отсекает объём
грунта с поперечным сечением ABC.
Расчётным является призматический
объём грунта, ограниченный поверхностью
откоса и поверхностью скольжения. Длину
призматического объёма принимаем равной
1м. Выделенную сползающую часть массива
грунта вертикальными плоскостями делим
на 10 элементов. При расчёте ведем запись
промежуточных результатов в табл. 6.1.
Веса
элементов Рi
определяем по формуле Рi=Vi·γcpi.
Центры тяжести каждого элемента определим
графически. Углы наклона поверхности
скольжения к горизонту в точке приложения
веса отсека αi
измеряем транспортиром и их величины
заносим в 5-й столбец табл. 6.1. Пользуясь
полученными данными, раскладываем силы
тяжести каждого из элементов Gi
на нормальные Ni
и касательные составляющие Тi
силы к площадке скольжения каждого из
элементов. Составляющие рассчитываем
по формулам
Ni=Рi
·cosαi
и Тi=Рi·sinαi.
Значения Ni
и Тi заносим
в столбцы 6 и 7 табл. 6.1.
Таблица 6.1
Расчет
устойчивости откоса к примеру 6.1
|
№ эле-мен-та |
Размеры сече-ния, м |
Площадь сечения, м2 |
Вес элемента, Рi |
αi, град |
Ni, кН |
Рi, кН |
град |
Cli, кПа |
li, м |
Cli·li |
Ni·tg кН |
|
1 |
0,3-1 |
0,15 |
2,6 |
67 |
1,03 |
2,44 |
0 |
0 |
1,1 |
0 |
0 |
|
2 |
1,7-3,5 |
3,825 |
71,5 |
54 |
42,04 |
57,87 |
26 |
2,67 |
3 |
8,00 |
20,58 |
|
3 |
1,9-5,2 |
8,265 |
159,1 |
40 |
121,88 |
102,3 |
21 |
8,67 |
2,6 |
22,53 |
46,47 |
|
4 |
1,8-6,2 |
1,026 |
18,3 |
28 |
16,12 |
8,57 |
21 |
8,67 |
2 |
17,33 |
6,15 |
|
5 |
1-5,5 |
5,8 |
103,2 |
20 |
97,01 |
35,32 |
18 |
45,3 |
1,1 |
49,86 |
31,86 |
|
6 |
1,2-4,7 |
6,22 |
123,2 |
14 |
119,5 |
29,80 |
18 |
45,3 |
1,2 |
54,40 |
39,25 |
|
7 |
1,3-3,5 |
5,395 |
108,2 |
7 |
107,36 |
13,19 |
18 |
45,3 |
1,3 |
58,93 |
35,26 |
|
8 |
1,2-2,3 |
3,48 |
70,3 |
0 |
70,3 |
0 |
18 |
45,3 |
1,2 |
54,40 |
23,09 |
|
9 |
2-0 |
2,3 |
46,3 |
7 |
45,91 |
-5,64 |
18 |
45,3 |
2,1 |
95,19 |
15,09 |
|
∑ |
244,0 |
360,64 |
217,75 |
Реактивные усилия
Тuj, действующие на участках
поверхностей скольжения каждого из
элементов, определяются по формуле
Тui=Nitgφli+
cli·li
.
Для
определения составляющих Тui
в столбцы 8 и 9 записываем углы внутреннего
трения φli
и удельные сцепления сli
грунтов, залегающих в пределах
участков поверхности скольжения i-го
элемента.
В
столбец 10 записываем длины участков
поверхности скольжения в пределах i-гo
элемента li.
Данные 11-го и 12-го столбцов суммируем,
а затем полученные суммы складываем
между собой:
ΣТui
=Σ Cli·li+Σ
Ni·tgφli.
Результаты расчёта
анализируем по коэффициенту устойчивости
откоса k:
k=

.
В нашем случае:
ΣТui
= 360,64 + 217,75 = 578,39 кН; ΣТi
= 244,0кН.
st
= 578,39 /244,0 = 2,37 > 1,1,
следовательно, откос
устойчив по выбранной поверхности
скольжения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для того, чтобы проверить откосы насыпи на устойчивость,
необходимо вычислить коэффициент устойчивости ![]() .
.
Расчет ![]() производим
производим
в следующей последовательности:
1. Вычерчиваем на миллиметровке в масштабе 1 : 200
поперечный профиль насыпи. Расчет устойчивости дорожной насыпи ведем на
собственный вес грунта и вес дорожной одежды, нагрузка от веса автомобилей
является дополнительной. Заменяем её на нагрузку эквивалентного слоя грунта.
Толщину слоя грунта вычисляем по формуле:
![]() (2)
(2)
где НГ = 60 кПа – временная нагрузка от гусеничной машины,
соответствующая нормативной нагрузке (давление 60 кН/м гусеницы при ширине
машины 3,3 м); ![]() –
–
ширина машины, м; ![]() –
–
удельный вес грунта насыпи, 17кН/м.
Вычисляем нагрузку эквивалентного слоя грунта по формуле
(2):
![]()
2. Определяем положение центров кривых скольжения, выполняя
следующие построения:
–
из верхней бровки (точка B) откоса проводим прямую под углом 35° к
горизонту;
–
из нижней бровки откоса (точка A) проводим
прямую под углом 26° к линии, соединяющей точки A
и B. На пересечении этой прямой и прямой, проведенной
из точки B, отмечаем точку C;
–
для определения точки D из нижней бровки откоса
откладываем вниз расстояние равное высоте насыпи Нн, затем по
горизонтали в сторону насыпи – 4,5·Нн;
–
соединяем точки D и C
прямой;
–
для получения центра кривой скольжения O из середины отрезка,
соединяющего точки A и N, проводим перпендикуляр до пересечения с продолжением
прямой DC;
–
из центра кривой скольжения O проводим след кругоцилиндрической поверхности радиусом ![]() ,
,
значение которого определяем соответственно по рисункам 3-12;
3. Полученную призму обрушения делим на ряд отсеков. Условно
принимаем точку приложения веса каждого отсека на пересечении дуги скольжения с
линией действия веса отсека. Раскладываем вес каждого отсека на 2 составляющих ![]() – нормальную
– нормальную
к кривой скольжения и ![]() – касательную,
– касательную,
сдвигающую объём грунта: δ – угол наклона отрезков кривой скольжения к
вертикали в пределах каждого отсека.
![]() (3)
(3)
где X – расстояние до вертикального
радиуса, определяемое по рисунку;
R – радиус кривой скольжения.
4. Внося значения ![]() соответственно
соответственно
в таблицы 6-15 принимаем их со знаком «–» если расстояние X отмеряется влево от
вертикали, проходящей через центр кривой скольжения, и со знаком «+» – если
вправо.
5. По рисункам 3-12 вычисляем площадь, а затем и вес каждого
отсека, результаты заносим соответственно в таблицы 6-15.
6. Вычисляем значения N и Т, результаты заносим соответственно в таблицы 6-15.
7. По рисункам 2-11 определяем длины кривых скольжения L и
вычисляем коэффициент устойчивости по формуле:
![]() (4)
(4)
где f – коэффициент, равный 0,45;
c – сцепление грунта равное 1,5
кг/см3.
Расчеты необходимо произвести при прохождении кривой
скольжения через пять точек, в соответствии со схемой, изображенной на рисунке
2.
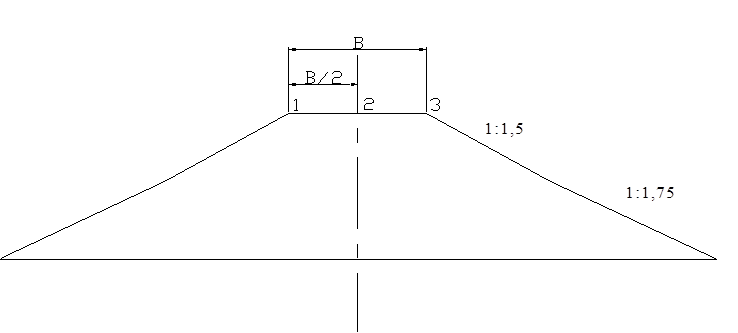
Рисунок 2 – Схема определения положения точек для расчета
коэффициента устойчивости откосов земляного полотна
Произведем расчет коэффициента устойчивости откосов
земляного полотна при двойном заложении откосов (1:1,5 и 1:1,75):
Расчёт устойчивости откосов земляного полотна на ПК 1+70:
Расчет устойчивости откосов при прохождении кривой
скольжения через точку 1 производим в соответствии с рисунком 3.
1. Вычисляем ![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
2. Вычисляем ![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
3. Вычисляем ![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
4. Вычисляем площади частей
по формуле:
![]() , (5)
, (5)
где Ω – площадь
сектора;
A – высота правой грани сектора;
B – высота левой грани сектора;
X – ширина сектора.
C – площадь кругового сегмента.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
5. Вычисляем по формуле:
![]() , (6)
, (6)
где Ω – площадь сектора;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
3. Эвольвентное зубчатое зацепление
3.1. Основной закон зацепления
Этот закон устанавливает связь между геометрией профилей зубьев и условиями передачи движения в зубчатом зацеплении (в более широком смысле – между геометрией элементов высшей пары и условиями передачи движения в механизме с высшей парой).
 Возьмём две центроиды Ц1 и Ц2, принадлежащие колёсам 1 и 2 (рис. 3.1). Эти центроиды касаются друг друга в точке П (прописная греческая буква «пи»), называемой полюсом зацепления.
Возьмём две центроиды Ц1 и Ц2, принадлежащие колёсам 1 и 2 (рис. 3.1). Эти центроиды касаются друг друга в точке П (прописная греческая буква «пи»), называемой полюсом зацепления.
Свяжем с центроидами профили Пр1 и Пр2 так, чтобы они касались друг друга в точке К. Относительная скорость точки К1 профиля Пр1 по отношению к совпадающей с ней точке К2 профиля Пр2, (в данный момент обе точки находятся на нормали n–n в точке K) обозначена на рис.3.1 как Vотн. Докажем следующие два положения: 1). Вектор  перпендикулярен нормали, в противном случае появится составляющая относительной скорости, направленная вдоль неё. Если эта составляющая будет направлена в сторону Пр2, то произойдёт внедрение профиля Пр1 в профиль Пр2, если она будет направлена в обратную сторону, то произойдёт отрыв профилей друг от друга. В обоих случаях высшая пара будет разрушена. Так что данное положение доказано.
перпендикулярен нормали, в противном случае появится составляющая относительной скорости, направленная вдоль неё. Если эта составляющая будет направлена в сторону Пр2, то произойдёт внедрение профиля Пр1 в профиль Пр2, если она будет направлена в обратную сторону, то произойдёт отрыв профилей друг от друга. В обоих случаях высшая пара будет разрушена. Так что данное положение доказано.
2) Вектор  перпендикулярен отрезку КП. Так как полюс П является мгновенным центром поворота центроиды Ц1 относительно центроиды Ц2, то, согласно положению теоретической механики, все точки, связанные с центроидой Ц1, имеют скорости, направленные перпендикулярно отрезку, соединяющему данную точку с центром (полюсом) поворота. Это и служит доказательством перпендикулярности вектора скорости и отрезка КП. Следует также отметить, что полюс зацепления – это не только точка касания центроид, но и точка пересечения контактной нормали профилей с линией центров колёс.
перпендикулярен отрезку КП. Так как полюс П является мгновенным центром поворота центроиды Ц1 относительно центроиды Ц2, то, согласно положению теоретической механики, все точки, связанные с центроидой Ц1, имеют скорости, направленные перпендикулярно отрезку, соединяющему данную точку с центром (полюсом) поворота. Это и служит доказательством перпендикулярности вектора скорости и отрезка КП. Следует также отметить, что полюс зацепления – это не только точка касания центроид, но и точка пересечения контактной нормали профилей с линией центров колёс.
Доказанные положения позволяют сделать следующий вывод. Нормаль к профилям, проведённая в точке их касания, пересекает линию центров колёс в точке, совпадающей с полюсом зацепления, и таким образом делит межосевое расстояние центроид колёс на отрезки, обратно пропорциональные их угловым скоростям,
 .
.
Другими словами, для правильной передачи движения с помощью высшей кинематической пары необходимо обеспечивать такую форму профилей зубьев, при которой нормаль к ним в точке контакта (контактная нормаль) проходила бы через полюс зацепления.
Рекомендуемые материалы
Из этих рассуждений следует также, что полюс зацепления – это не только точка касания центроид, но и точка пересечения контактной нормали с межосевой линией.
Профили, подчиняющиеся основному закону зацепления, называются сопряжёнными.
Следствие 1. Если полюс П занимает неизменное положение на линии центров колёс, то передаточное отношение постоянно, и радиусы центроид также постоянны. Это соответствует круглым зубчатым колёсам. В противном случае колёса некруглые.
Следствие 2. Если полюс П находится между центрами колёс, то они вращаются в противоположные стороны (внешнее зацепление колёс), и передаточное отношение имеет отрицательный знак.
Следствие 3. Если полюс П находится вне отрезка О1О2, (выше или ниже этих центров), то колёса вращаются в одну сторону (внутреннее зацепление колёс).
Следствие 4. Относительная скорость в точке касания профилей по существу является скоростью скольжения профилей зубьев. Чем дальше от полюса находится точка касания профилей, тем больше в ней скорость скольжения. Если в процессе передачи движения точка контакта профилей совпадёт с полюсом, то в этот момент скорость скольжения будет равна нулю.
Существует большое количество профилей зубьев, удовлетворяющих этому закону. При выборе формы профилей руководствуются их технологичностью (простотой изготовления), простотой инструмента и расчетов. Этим требованиям в полной мере отвечает эвольвентное зацепление.
3.2. Эвольвента окружности, её свойства и уравнение
Эвольвента – это траектория точки прямой линии (производящей прямой), перекатывающейся без скольжения по окружности.
Образование эвольвенты можно представить как траекторию, описываемую остриём карандаша, привязанного к концу нити, сматываемой с катушки, установленной своей осью перпендикулярно плоскости листа бумаги.
Свойства эвольвенты
1) Нормаль к эвольвенте является касательной к основной окружности.
2) Центры кривизны эвольвенты лежат на основной окружности, так что основная окружность представляет собой эволюту, т. е. геометрическое место центров кривизны эвольвенты.
 3) Радиус кривизны эвольвенты в данной точке равен отрезку производящей прямой, заключённому между данной точкой эвольвенты и точкой касания производящей прямой с основной окружностью, ρА = AC. В точке начала эвольвенты её радиус кривизны равен нулю, ρA0 = 0.
3) Радиус кривизны эвольвенты в данной точке равен отрезку производящей прямой, заключённому между данной точкой эвольвенты и точкой касания производящей прямой с основной окружностью, ρА = AC. В точке начала эвольвенты её радиус кривизны равен нулю, ρA0 = 0.
4) Радиус кривизны эвольвенты в данной точке равен дуге основной окружности, заключённой между точкой начала эвольвенты и точкой касания этой прямой с основной окружностью, ρA =  C0C.
C0C.
5) Правая и левая ветви эвольвенты симметричны.
6) Все точки эвольвенты лежат снаружи от основной окружности.
Уравнение эвольвенты
Для получения уравнения эвольвенты обратимся к рис. 3.3. Положение произвольной точки Ay эвольвенты в полярной системе координат определяется двумя координатами относительно её начального радиус-вектора OA0 (или OC0):  длиной радиус-вектора Ry и углом θy. Радиус-вектор Ry определим из прямоугольного треугольника OAyCy:
длиной радиус-вектора Ry и углом θy. Радиус-вектор Ry определим из прямоугольного треугольника OAyCy:

Для определения полярного угла θy сначала выразим длину дуги основной окружности через её радиус и центральный угол:

Выразим теперь противолежащий углу αy катет AyCy в ∆OAyCy:

На основании четвёртого свойства эвольвенты имеем

Подставляя в это равенство соответствующие выражения и решая его относительно θy, получаем
 .
.
В этих математических выражениях и на рис. 3.3 угол αy называется профильным углом эвольвенты. Разность между тангенсом какого-либо угла и самим углом называется эвольвентной функцией и обозначается тремя первыми буквами латинского названия эвольвенты involute, т. е. inv, так что окончательно уравнение имеет вид:
θy = invαy.
В математических справочниках приводятся таблицы эвольвентной функции, в которых аргумент αy изменяется от нуля до нескольких десятков градусов.
3.3. Элементы зубчатого колеса
Здесь рассматриваются те элементы колеса, которые относятся к его ободу, где располагаются зубья (рис. 3.4).
Шаг колеса p – это расстояние по делительной окружности между одноимёнными профилями двух соседних зубьев, p = π·m. Шаг включает два параметра – толщину зуба s и ширину впадины e. Если s = e, то имеем колесо с равноделённым шагом, в противном случае имеем колесо с неравноделённым шагом.
Делительная окружность (её радиус  , в зацеплении двух колёс имеет индекс номера колеса):
, в зацеплении двух колёс имеет индекс номера колеса):
– делит зуб на головку и ножку;
– модуль m на этой окружности имеет стандартное значение;
– радиус окружности имеет величину r = 0,5m ;
;
– в точке на делительной окружности профильный угол эвольвенты αy = 20º и обозначается буквой α без индекса.
Основная окружность является базовой для образования эвольвенты (от неё начинается эвольвентная часть зуба). Радиус этой окружности получается из рассмотрения прямоугольного треугольника с углом при вершине O, равным α, и одним из катетов, равным  b, и гипотенузой, равной
b, и гипотенузой, равной  :
:  b =
b =  ·cos α.
·cos α.
Окружность вершин является габаритной окружностью колеса, её радиус определяется формулой
 ,
,
где  – высота головки зуба, причём
– высота головки зуба, причём  . Множитель перед модулем называется коэффициентом высоты головки зуба и равен по величине 1, т. е.
. Множитель перед модулем называется коэффициентом высоты головки зуба и равен по величине 1, т. е.  .
.
Диаметр окружности вершин является диаметром заготовки для изготовления зубчатого колеса.
Окружность впадин ограничивает зуб у основания, её радиус равен
 ,
,
 где
где  – высота ножки зуба, определяемая равенством
– высота ножки зуба, определяемая равенством  , второе слагаемое в скобках называется коэффициентом радиального зазора и имеет величину
, второе слагаемое в скобках называется коэффициентом радиального зазора и имеет величину  .
.
Контур зуба от основной окружности до окружности вершин очерчен эвольвентой, которая сопрягается с окружностью впадин переходной кривой (эквидистантой удлинённой эвольвенты).
3.4. Элементы и свойства эвольвентного зацепления
Отметим прежде всего, что здесь рассматриваются те элементы зацепления, которые имеются именно в зацеплении колёс и исчезают, если колёса вывести из зацепления (рис. 3.5). К этим элементам относятся следующие.
Межосевое расстояние  – это расстояние между центрами колёс O1 и O2. Полюс зацепления П (пи) – это точка касания центроидных окружностей колёс с радусами
– это расстояние между центрами колёс O1 и O2. Полюс зацепления П (пи) – это точка касания центроидных окружностей колёс с радусами  и
и  , которые в эвольвентном зацеплении называются начальными окружностями. Теоретическая линия зацепления N1N2 – это геометрическое место точек мгновенного касания профилей зубьев, отмеченное на неподвижной плоскости. Процесс передачи движения происходит таким образом, что профили одной пары зубьев на протяжении некоторого времени касаются друг друга, т. е. имеют общую нормаль. На основании первого свойства эвольвенты нормаль к ней является касательной к основной окружности, а для двух касающихся друг друга профилей является касательной к обеим основным окружностям. Поэтому для данных профилей контактная нормаль является единственной и лежит на общей касательной к основным окружностям, образуя таким образом прямолинейную линию зацепления. С учётом геометрических размеров конкретных колёс линия зацепления используется для передачи движения только в пределах зоны, заключённой между точками её пересечения с окружностями вершин (рис.3.5). Эта зона называется активной линией зацепления. Её границы на рис. 3.5 отмечены точками H1 и H2.
, которые в эвольвентном зацеплении называются начальными окружностями. Теоретическая линия зацепления N1N2 – это геометрическое место точек мгновенного касания профилей зубьев, отмеченное на неподвижной плоскости. Процесс передачи движения происходит таким образом, что профили одной пары зубьев на протяжении некоторого времени касаются друг друга, т. е. имеют общую нормаль. На основании первого свойства эвольвенты нормаль к ней является касательной к основной окружности, а для двух касающихся друг друга профилей является касательной к обеим основным окружностям. Поэтому для данных профилей контактная нормаль является единственной и лежит на общей касательной к основным окружностям, образуя таким образом прямолинейную линию зацепления. С учётом геометрических размеров конкретных колёс линия зацепления используется для передачи движения только в пределах зоны, заключённой между точками её пересечения с окружностями вершин (рис.3.5). Эта зона называется активной линией зацепления. Её границы на рис. 3.5 отмечены точками H1 и H2.

Угол зацепления  w – это угол между линией зацепления и общей касательной к начальным окружностям, проведённой через полюс зацепления.
w – это угол между линией зацепления и общей касательной к начальным окружностям, проведённой через полюс зацепления.
Сопряжённые (или парные) точки – это точки профилей зубьев, которыми они касаются друг друга на линии зацепления.
Радиальный зазор – это расстояние на межосевой линии между точками пересечения её с окружностью вершин одного колеса и впадин другого колеса.
Свойства зацепления
1) Передаточное отношение постоянно в любой фазе зацепления, так как оно может быть выражено через радиусы основных окружностей. Для доказательства используем подобные прямоугольные треугольники (рис. 3.5)  и
и  и запишем цепочку равенств:
и запишем цепочку равенств:
 .
.
2) Передаточное отношение не зависит от изменения межосевого расстояния  по той же причине, что и в предыдущем случае.
по той же причине, что и в предыдущем случае.
3) Правильное зацепление эвольвентных профилей происходит только в пределах линии зацепления N1N2, так как только в этих пределах контактирующие эвольвентные профили имеют общую нормаль.
4) Эвольвентные колёса одного модуля имеют полную взаимозаменяемость, т. е. могут составить правильное зацепление.
3.5. Методы изготовления
 зубчатых колёс
зубчатых колёс
Метод копирования заключается в том, что профиль зуба колеса повторяет форму профиля инструмента (рис. 3.6), который, в свою очередь, теоретически точно соответствует форме эвольвенты и переходной кривой зуба конкретного колеса. Инструментом могут служить дисковая или пальцевая модульные фрезы, или протяжка. Достоинством метода является возможность применения универсального обоудования (горизонтально- или вертикально-фрезерных станков), оснащенного делительной головкой для точного поворота заготовки на угловой шаг после обработки очередной впадины. Такое оборудование имеется, как правило, в ремонтной службе любого предприятия. К недостаткам следует отнести низкую точность и невысокую производительность. Кроме того, геометрия эвольвенты полностью определяется радиусом основной окружности, зависящей от модуля и числа зубьев, поэтому каждое колесо по существу должно иметь собственный инструмент для нарезания зубьев. Так как это невозможно, то применяют наборы фрез одного модуля из 8 или 15 штук. Каждая фреза набора используется для изготовления нескольких колёс с разными числами зубьев, одному из которых она обеспечивает номинально точную эвольвенту, а другие получают ошибку профиля. Ошибка получается тем больше, чем больше отклоняется число зубьев колеса от номинала. Метод обкатки (огибания) состоит в том, что профиль зуба колеса получается как огибающая ряда последовательных положений профиля инструмента (рис. 3.7).

С точки зрения кинематики движение инструмента относительно ещё ненарезанного колеса с помощью специальной цепи деления станка повторяет то движение, которое осуществляется в зубчатой передаче. Так как инструмент, по существу представляет собой зубчатое колесо с геометрией режущего инструмента, то в процессе нарезания он срезает всё, что попадает в зону движения режущих кромок, а оставшееся и представляет собой зубья колеса. Метод характеризуется высокой точностью, производительностью и, что немаловажно, позволяет инструментом одного модуля изготавливать зубчатые колёса с любым числом зубьев. К недостаткам метода можно отнести необходимость в специальном зубообрабатывающем оборудовании, однако этот недостаток с лихвой компенсируется достоинствами метода.
3.6. Геометрия реечного производящего исходного контура
Реечным производящим исходным контуром (коротко – исходным контуром или инструментальной рейкой) называется профиль зуборезной гребёнки, применяемой для нарезания зубьев на зубострогальном станке, и профиль нормального сечения червячной фрезы, применяемой для нарезания зубьев на зубофрезерном станке. Форма и размеры исходного контура устанавливаются Государственным стандартом. Элементы и размеры исходного контура можно увидеть на рис. 3.8.
Делительная прямая проходит точно посeредине высоты зубьев и делит, таким образом, высоту зуба пополам. По этой прямой шаг исходного контура p = π·m делится на две равные части, толщину зуба s и ширину впадины e, равные половине шага каждая.
Часть контура выше делительной прямой называется головкой, ниже – ножкой исходного контура. Таким образом, делительная прямая делит зуб исходного контура на головку и ножку. Как видно из рис. 3.8, прямолинейная часть профиля мсходного контура заключена между граничными прямыми, параллельными делительной прямой. Эти прямые отстоят от делительной на расстояние  вверх и вниз от неё. Сверху зуб ограничен прямой вершин, отстоящей от граничной прямой головок на величину
вверх и вниз от неё. Сверху зуб ограничен прямой вершин, отстоящей от граничной прямой головок на величину  , снизу он ограничен прямой впадин, отстоящей
, снизу он ограничен прямой впадин, отстоящей
 от граничной прямой ножек на то же расстояние. С учётом отмеченных размеров общая высота зуба исходного контура получается
от граничной прямой ножек на то же расстояние. С учётом отмеченных размеров общая высота зуба исходного контура получается
 .
.
Наклон прямолинейных участков профиля относительно вертикали составляет угол  , который называется углом профиля реечного производящего исходного контура.
, который называется углом профиля реечного производящего исходного контура.
Расстояние по нормали между одноимёнными точками двух соседних зубьев называется нормальным шагом исходного контура  (он равен основному шагу зубчатого колеса pb, поэтому на рис. 3.8 он так и обозначен) и определяется формулой
(он равен основному шагу зубчатого колеса pb, поэтому на рис. 3.8 он так и обозначен) и определяется формулой
 .
.
При изготовлении зубчатого колеса прямолинейная часть профиля исходного контура формирует эвольвенту зуба колеса, а скруглённая часть головки исходного контура формирует переходную кривую на ножке зуба колеса. Рабочая рейка, используемая в реечной передаче, отличается от инструментальной тем, что в ней срезана скруглённая часть на головках зубьев. Тем самым обеспечивается радиальный зазор в передаче, потому что общая высота зуба рабочей рейки равна высоте зуба зубчатого колеса.
При нарезании зубчатого колеса заготовка и инструмент (исходный контур) принудительно движутся относительно друг друга, как колёса в зубчатой передаче, поэтому в зацеплении инструмента и нарезаемого колеса присутствуют все элементы зацепления двух колёс, в том числе и центроиды. Центроидой нарезаемого колеса всегда служит его делительная окружность. Центроида инструмента называется станочно–начальной прямой и может совпадать или не совпадать с делительной прямой. В первом случае получается так называемое нулевое колесо. Если станочно-начальная прямая расположена выше делительной, что соответствует смещению инструмента в сторону от центра колеса, то получается положительное колесо. Такое название связано с тем, что смещение инструмента определяется величиной  , где
, где  называется коэффициентом смещения, и в данном случае он считается положительным. Если станочно-начальная прямая расположена ниже делительной, то получается отрицательное колесо, так как в этом случае коэффициент смещения
называется коэффициентом смещения, и в данном случае он считается положительным. Если станочно-начальная прямая расположена ниже делительной, то получается отрицательное колесо, так как в этом случае коэффициент смещения  считается отрицательным.
считается отрицательным.
3.7. Подрез зуба колеса и его предотвращение
Подрезом зуба называется пересечение траектории точки A. лежащей на граничной прямой головок исходного контура (см. рис. 3.8), с эвольвентой зуба нарезаемого колеса. В результате этого происходит утонение ножки зуба в его опасном сечении при работе на изгиб (рис.3.9) и уменьшение плавности работы передачи из-за сокращения эвольвентной части зуба.
Подрез, как правило, недопустим.  Он наступает при количестве зубьев колеса, которое меньше некоторого значения, называемого минимальным числом зубьев. Для определения этого числа зубьев обратимся к рис. 3.10.
Он наступает при количестве зубьев колеса, которое меньше некоторого значения, называемого минимальным числом зубьев. Для определения этого числа зубьев обратимся к рис. 3.10.
Если число зубьев нарезаемого колеса достаточно велико,  , то конец N’ теоретической линии зацепления при нарезании располагается выше граничной прямой головок инструмента, и подрез отсутствует. Если число зубьев нарезаемого колеса мало
, то конец N’ теоретической линии зацепления при нарезании располагается выше граничной прямой головок инструмента, и подрез отсутствует. Если число зубьев нарезаемого колеса мало  , то конец N” теоретической линии зацепления расположен ниже граничной прямой головок, и подрез есть. Наконец, если граничная прямая головок проходит точно через границу теоретической линии зацепления, то подреза ещё нет, т. е. имеет место некое пограничное состояние. Число зубьев колеса, соответствующее этому состоянию, равно минимальному, т. е.
, то конец N” теоретической линии зацепления расположен ниже граничной прямой головок, и подрез есть. Наконец, если граничная прямая головок проходит точно через границу теоретической линии зацепления, то подреза ещё нет, т. е. имеет место некое пограничное состояние. Число зубьев колеса, соответствующее этому состоянию, равно минимальному, т. е.  . Выразим отрезок KП на межосевой линии двояким образом. С одной стороны он равен
. Выразим отрезок KП на межосевой линии двояким образом. С одной стороны он равен  , с другой, последовательно рассмат-ривая треугольники ПКN и ПОN, имеем
, с другой, последовательно рассмат-ривая треугольники ПКN и ПОN, имеем  .
.

 Приравнивая правую часть полученного выражения к
Приравнивая правую часть полученного выражения к  и, решая новое равенство относительно
и, решая новое равенство относительно  , получаем
, получаем
 .
.
Стандартным параметрам исходного контура соответствует  = 17.
= 17.
 При необходимости изготовления колеса с числом зубьев, меньшем минимального, и предотвращения подреза следует инструментальную рейку сместить от центра колеса на такую величину, при которой её граничная прямая головок пройдёт через точку N линии зацепления (рис. 3.11). Определим необходимую величину смещения. Согласно рис. 3.11 имеем с одной стороны
При необходимости изготовления колеса с числом зубьев, меньшем минимального, и предотвращения подреза следует инструментальную рейку сместить от центра колеса на такую величину, при которой её граничная прямая головок пройдёт через точку N линии зацепления (рис. 3.11). Определим необходимую величину смещения. Согласно рис. 3.11 имеем с одной стороны
 ,
,
и с другой стороны  или
или
 .
.
Так как  , то, приравнивая правые части этих выражений и заменив
, то, приравнивая правые части этих выражений и заменив  на
на  , после несложных преобразований находим искомый коэффициент смещения:
, после несложных преобразований находим искомый коэффициент смещения:
 .
.
Для стандартных размеров исходного контура  , поэтому получаем:
, поэтому получаем:  . Из этой формулы следует, что если число зубьев колеса меньше минимального, то полученный положительный коэффициент смещения означает, что для предотвращения подреза инструмент должен быть смещён в сторону от центра колеса. Если число зубьев колеса больше минимального, то коэффициент смещения получается отрицательным и указывает на допустимое смещение инструмента к центру колеса, при котором не будет подреза.
. Из этой формулы следует, что если число зубьев колеса меньше минимального, то полученный положительный коэффициент смещения означает, что для предотвращения подреза инструмент должен быть смещён в сторону от центра колеса. Если число зубьев колеса больше минимального, то коэффициент смещения получается отрицательным и указывает на допустимое смещение инструмента к центру колеса, при котором не будет подреза.
3.8. Качественные характеристики эвольвентного
зацепления
Коэффициент перекрытия
Коэффициентом перекрытия называется отношение длины активной линии зацепления к основному шагу зубчатого колеса, он обозначается  и определяется отношением
и определяется отношением

 .
.
Передача движения в зубчатом зацеплении происходит таким образом, что, прежде чем предыдущая пара зубьев выйдет из зацепления (из контакта), последующая должна войти в зацепление (в контакт). Чем раньше она вступит в зацепление, тем более плавно работает передача. Количественной характеристикой этого качества и является коэффициент перекрытия, т. е. он, по существу, характеризует плавность работы зубчатой передачи. Обычно величина коэффициента перекрытия заключена между 1 и 2, при этом минимальное значение не должно быть меньше 1,1. Схематически соотношение между длиной активной лини зацепления и основным шагом показано на рис. 3.12. Точка контакта профилей зубьев перемещается вдоль активной линии зацепления от точки H1 к точке H2. Основной шаг короче активной линии зацепления, поэтому в пределах этой линии работают то одна, то две пары зубьев. Если отложить, как показано на рис. 3.12, основной шаг pb от точек H1 и H2, то отрезок H1H2 будет разделён на три части. Две крайние части соответствуют зонам двухпарного зацепления зубьев, а средняя – зоне однопарного зацепления. Чем короче средняя зона, тем плавнее работает зубчатая передача, так как суммарная длина двух крайних участков становится длиннее.
Удельное скольжение
Удельным скольжением называется отношение скорости скольжения профилей в точке их касания к скорости перемещения точки касания по профилю. Этот показатель характеризует износ зубьев в результате трения скольжения их боковых (рабочих) поверхностей. Возьмём точки К1 первого профиля и К2 второго профиля,  совпадающие в данный момент друг с другом (рис. 3.13). В этих точках профили имеют общую касательную t – t, вдоль которой направлены касательные (тангенциальные) составляющие их абсолютных скоростей. В общем случае эти скорости отличаются друг от друга по величине, могут отличаться и по направлению, оставаясь на общей касательной. Разность величин этих скоростей составляет скорость скольжения в контакте зубьев.
совпадающие в данный момент друг с другом (рис. 3.13). В этих точках профили имеют общую касательную t – t, вдоль которой направлены касательные (тангенциальные) составляющие их абсолютных скоростей. В общем случае эти скорости отличаются друг от друга по величине, могут отличаться и по направлению, оставаясь на общей касательной. Разность величин этих скоростей составляет скорость скольжения в контакте зубьев.
Согласно определению, удельное скольжение выразится двумя математическими выражениями, относящимися к разным колёсам:
 и
и  .
.
Для определения тангенциальных составляющих скоростей обратимся к
рис. 3.14. Соединим точку К1 с центром О1 вращения колеса 1 радиусом R1, и точку К2, совпадающую с точкой К1, с центром О2 радиусом R2. Перпендикулярно радиусу R1 в сторону вращения колеса 1 отложим абсолютную скорость точки К1, равную  , и перпендикулярно радиусу R2 в сторону вращения колеса 2 отложим абсолютную скорость точки К2, равную
, и перпендикулярно радиусу R2 в сторону вращения колеса 2 отложим абсолютную скорость точки К2, равную  . Отметим угол β1 между радиусом R1 и перпендикуляром O1N1 к линии зацепления и β2 между радиусом R2 и перпендикуляром О2N2 также к линии зацепления. Спроецируем скорости
. Отметим угол β1 между радиусом R1 и перпендикуляром O1N1 к линии зацепления и β2 между радиусом R2 и перпендикуляром О2N2 также к линии зацепления. Спроецируем скорости  и
и  на линию зацепления N1N2. Линия зацепления направлена по нормали к профилям зубьев, поэтому проекции скоростей на неё являются нормальными составляющими, равными друг другу. Составляющие, направленные перпендикулярно линии зацепления, действуют по касательной к профилям и являются тангенциальными составляющими. Они определяются следующими цепоч-
на линию зацепления N1N2. Линия зацепления направлена по нормали к профилям зубьев, поэтому проекции скоростей на неё являются нормальными составляющими, равными друг другу. Составляющие, направленные перпендикулярно линии зацепления, действуют по касательной к профилям и являются тангенциальными составляющими. Они определяются следующими цепоч-
ками преобразований


 C учётом этого ранее записанные выражения примут следующий вид:
C учётом этого ранее записанные выражения примут следующий вид:
 ,
,  .
.
В этих выражениях буквой К обозначены совпадающие друг с другом точки К1 и К2. Схематический график удельного скольжения показан на рис. 3.15.
 График показывает, что удельное скольжение на головках зубьев меньше чем на ножках, следовательно, ножки изнашиваются интенсивнее, чем головки. Характер износа таков, что чем дальше от полюса в радиальном направлении находится зона профиля, тем больше она изнашивается. В полюсе зацепления износ от скольжения равен нулю, так как эта точка является мгновенным центром поворота одного колеса относительно другого, и точки профилей, попадающие в полюс, имеют радиус относительного вращения вокруг полюса, равный нулю.
График показывает, что удельное скольжение на головках зубьев меньше чем на ножках, следовательно, ножки изнашиваются интенсивнее, чем головки. Характер износа таков, что чем дальше от полюса в радиальном направлении находится зона профиля, тем больше она изнашивается. В полюсе зацепления износ от скольжения равен нулю, так как эта точка является мгновенным центром поворота одного колеса относительно другого, и точки профилей, попадающие в полюс, имеют радиус относительного вращения вокруг полюса, равный нулю.
Коэффициент удельного давления
Коэффициентом удельного давления называется отношение модуля зацепления к приведённому радиусу кривизны профилей зубьев в точке их контакта. Этот коэффициент применяется при расчёте зубьев на контактную прочность. Формула Герца для расчёта контактных напряжений в контакте двух цилиндров имеет вид

где  –нормальное усилие, сжимающее цилиндры,
–нормальное усилие, сжимающее цилиндры,  – приведённый модуль упругости,
– приведённый модуль упругости,  – длина контактной линии цилиндров,
– длина контактной линии цилиндров,  – приведённый радиус кривизны цилиндров.
– приведённый радиус кривизны цилиндров.
Умножив числитель и знаменатель формулы на модуль  , не изменим результат, а формула Герца приобретёт следующий вид
, не изменим результат, а формула Герца приобретёт следующий вид

где  и представляет собой коэффициент удельного давления.
и представляет собой коэффициент удельного давления.
 Приведённый радиус кривизны определяется как величина, обратная приведённой кривизне, равная сумме кривизн контактирующих профилей, т. е.
Приведённый радиус кривизны определяется как величина, обратная приведённой кривизне, равная сумме кривизн контактирующих профилей, т. е.  .
.
На основании свойств эвольвенты радиусы кривизны профилей равны:  и
и , поэтому окончательно формула получится в виде
, поэтому окончательно формула получится в виде
 .
.
Примерный вид графика коэффициента удельного давления в зависимости от положения точки контакта на линии зацепления показан на рис. 3.16.
3.9. Назначение коэффициентов смещения для нарезания зубчатых колёс
Коэффициенты смещения назначаются с целью:
– увеличения изгибной прочности зуба путём увеличения его опасного сечения вблизи основания;
– увеличения контактной прочности зуба путём использования участков эвольвенты, более удалённых от основной окружности;
– выравнивания максимальных удельных скольжений;
– предотвращения подреза малого колеса в передаче;
– увеличения плавности работы передачи путём удлинения активной линии зацепления;
– обеспечения заданного межосевого расстояния;
– обеспечения двухпарного зацепления в полюсе и других целей.
3.10. Расчёт геометрических размеров зубчатых колёс
Исходными данными для расчёта размеров служат: числа зубьев колёс  и
и  , модуль колёс
, модуль колёс  , угол профиля исходного контура
, угол профиля исходного контура  , коэффициенты смещения
, коэффициенты смещения  и
и  , коэффициент высоты головки зуба
, коэффициент высоты головки зуба  и коэффициент радиального зазора
и коэффициент радиального зазора  .
.
Угол зацепления
Формулу для определения угла зацепления приведём здесь без вывода из-за его громоздкости
 .
.
Из этой формулы, в частности, видно, что в нулевой передаче  угол зацепления
угол зацепления  равен углу профиля инструмента
равен углу профиля инструмента  , в положительной передаче
, в положительной передаче 
 , в отрицательной передаче всё наоборот, т.е.
, в отрицательной передаче всё наоборот, т.е.  и соответственно
и соответственно  .
.
Радиусы начальных окружностей и межосевое расстояние
Для вывода формул обратимся к рис. 3.17, на котором показаны необходимые элементы зацепления. Линия зацепления N1N2 образует угол зацепления αw с общей касательной к начальным окружностям радиусов  и
и  , касающимся друг друга в полюсе Π. Опустив перпендикуляры из центров колёс O1 и O2 на линию за
, касающимся друг друга в полюсе Π. Опустив перпендикуляры из центров колёс O1 и O2 на линию за цепления, получаем два прямоугольных треугольника N1O1П и N2O2П с углами при вершинах O1 и O2, равными αw. Из треугольника следует N1O1П
цепления, получаем два прямоугольных треугольника N1O1П и N2O2П с углами при вершинах O1 и O2, равными αw. Из треугольника следует N1O1П  , из треугольника N2O2П–
, из треугольника N2O2П–  . Так как имеют место равенства
. Так как имеют место равенства  ,
,  ,
,  и
и  , а также
, а также  ,
,  , то получаем
, то получаем  и
и  . Вместо радиусов делительных окружностей
. Вместо радиусов делительных окружностей  и
и в эти формулы можно вставить их выражения, записанные ранее, тогда
в эти формулы можно вставить их выражения, записанные ранее, тогда
 ,
,  .
.
Как видно из рисунка, межосевое расстояние равно сумме радиусов начальных окружностей, т. е.  , поэтому
, поэтому
 .
.
Произведение первых двух слагаемых в этой формуле называется делительным межосевым расстоянием. Оно имеет место, когда передача изготавливается нулевой, т. е. когда суммарный коэффициент смещения равен нулю. При этом  , и косинусы сокращаются.
, и косинусы сокращаются.
Радиусы окружностей впадин
При образовании нулевого колеса его центроидой, как всегда, является делительная окружность (рис.3.18), а центроидой инструмента служит его делительная прямая (на рисунке профиль инструмента и его делительная прямая и прямая вершин показаны тонкими линиями). Поэтому радиус  окружности впадин нулевого колеса равен разности
окружности впадин нулевого колеса равен разности  . При смещении инструмента на величину
. При смещении инструмента на величину  радиус окружности впадин увеличивается на эту же величину и приобретает значение
радиус окружности впадин увеличивается на эту же величину и приобретает значение

 .
.
На рис. 3.18 расположение инструмента по отношению к нарезаемому колесу изображено жирными линиями.
Радиусы окружностей вершин
Расчёт радиусов окружностей вершин понятен из рис. 3.19, где представлены те элементы зацепления, которые связаны с этим расчётом. Непосредственно из рисунка видно, что радиус окружности вершин первого колеса равен

 ,
,
радиус окружности вершин второго колеса равен
 .
.
Толщина зуба по делительной окружности
Толщина зуба колеса по делительной окружности определяется шириной впадины инструментальной рейки по станочно-начальной прямой (Рис.3.20), которая при изготовлении колеса перекатывается по его делительной окружности без скольжения.
 Размер S толщины зуба складывается из ширины
Размер S толщины зуба складывается из ширины  впадины инструментальной рейки по её делительной окружности и двух катетов прямоугольных треугольников, заштрихованных на рисунке 3.20, которые расположены на станочно-начальной прямой рейки. Вертикальные катеты этих треугольников равны
впадины инструментальной рейки по её делительной окружности и двух катетов прямоугольных треугольников, заштрихованных на рисунке 3.20, которые расположены на станочно-начальной прямой рейки. Вертикальные катеты этих треугольников равны  , так как они представляют собой величину смещения инструмента от центра колеса при его нарезании, что, по существу, равно расстоянию между делительной и станочно-начальной прямыми. Каждый горизонтальный катет прямоугольного треугольника равен
, так как они представляют собой величину смещения инструмента от центра колеса при его нарезании, что, по существу, равно расстоянию между делительной и станочно-начальной прямыми. Каждый горизонтальный катет прямоугольного треугольника равен  . С учётом этих соображений толщину зуба S можно выразить так
. С учётом этих соображений толщину зуба S можно выразить так
 ,
,
или в окончательном виде, после несложного преобразования
 .
.
Во всех формулах расчёта геометрических размеров зубчатых колёс коэффициенты смещения необходимо подставлять со своими знаками.
Вопросы для самопроверки
1. В чём заключается существо основного закона зацепления?
2. Какие профили зубьев колёс называются сопряжёнными?
3. Что такое эвольвента окружности, производящая прямая?
4. Какими свойствами обладает эвольвента окружности?
5. Что такое эвольвентная функция?
6. Назовите элементы зубчатого колеса, какими линиями очерчивается про- филь зуба?
7. Что называется шагом колеса, модулем, головкой, ножкой зуба?
8. В каком месте измеряется толщина зуба, ширина впадины колеса?
9. Какими свойствами обладает делительная окружность?
10. Что такое коэффициент высоты головки зуба, чему он равен?
11. Какая окружность колеса называется основной?
12. Назовите элементы зацепления пары колёс.
13. Что такое полюс зацепления?
14. Какие окружности колёс называются начальными?
15. Что такое угол зацепления?
16. Что такое линия зацепления, активная линия зацепления?
17. Что такое радиальный зазор, за счёт чего он образуется?
18. Сформулируйте свойства эвольвентного зацепления.
19. Какими методами изготавливают эвольвентные зубья, в чём заключается существо методов? Каковы основные достоинства и недостатки методов?
20. Что такое реечный производящий исходный контур(инструментальная рейка)?
21. Что такое подрез зубчатого колеса?
22. Какое число зубьев считается минимальным, от чего оно зависит?
23. Как предотвратить подрез зубчатого колеса?
24. Что такое коэффициент смещения исходного контура?
25. Какие зубчатые колёса называются нулевыми, положительными и отрицательными?
26. Назовите качественные характеристики эвольвентного зацепления.
Бесплатная лекция: “Дополнение” также доступна.
27. Что называется коэффициентом перекрытия, и что он характеризует?
28. Что такое удельное скольжение, почему возникает скольжение в контакте зубьев?
29. Почему в полюсе зацепления удельное скольжение равно нулю?
30. Что такое коэффициент удельного давления, где он применяется?
31. Для чего назначаются коэффициенты смещения при нарезании зубчатых колёс?
32. Как определяются геометрические размеры зубчатых колёс: угол зацепления, радиусы начальных окружностей, межосевое расстояние, радиусы окружностей впадин, радиусы окружностей вершин и толщина зуба по делительной окружности?

