Как найти центр треугольника по формуле

Центр треугольника

Треугольник — наиболее распространенная форма деталей в сферах машиностроения и строительства. Точка пересечения 3-х медиан считается центром треугольника. На эту точку приходится также центр тяжести и центр симметрии предметов треугольной формы. При разработке дизайнерских, инженерных проектов очень важно точно рассчитать центр тяжести элементов металлической или бетонной конструкции.

Существует несколько понятий центра для треугольника.

Инцентр — точка пересечения его биссектрис. Это — центр описанной около треугольника окружности.

Ортоцентр — точка пересечения его высот.

Центр тяжести,центр масс или центроид (обозн. М) — точка пересечения медиан треугольника.

Рассмотрим треугольник. Определим середины его сторон и соединим их с противолежащими углами. Точка пересечения медиан и будет центром тяжести тр-ка. Медиана делится этой точкой в пропорции 2:1 , (считая от вершины тр-ка).

Как найти центр треугольника

Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.

Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан.

Центр равностороннего треугольника является также центром вписанной и описанной окружности.

Центроид расположен на отрезке, соединяющем ортоцентр и центр описанной окружности. Центроид делит отрезок 2:1.

Быстро найти центр треугольника G можно с помощью онлайн калькулятора. Для этого:

• ввести в поле калькулятора координаты вершин треугольника;
• нажать кнопку Вычислить. Калькулятор вычислит значение центра треугольника G.

Центр тяжести треугольника

Этот онлайн калькулятор находит центроид, или барицентр (центр тяжести) треугольника по координатам его вершин

Центр тяжести (центр масс, барицентр) треугольника для треугольника с равномерно распределённой массой (или в вершинах которого находятся равные массы) находится в центроиде треугольника. Центроидом называется точка пересечения медиан треугольника. Центроид относится к так называемым замечательным точкам треугольника. Например, помимо того, что он является центром тяжести, он также делит каждую медиану в отношении 2:1, считая от вершины, а три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника.

Чтобы вычислить положение центра тяжести по координатам вершин треугольника, достаточно вычислить среднее арифметическое координат вершин по оси x и по оси y, что и делает калькулятор ниже.

Центры тяжести многоугольников и многогранников

Центром тяжести (или центром масс) некоторого тела называется точка, обладающая тем свойством, что если подвесить тело за эту точку, то оно будет сохранять свое положение.

Ниже рассмотрены двумерные и трёхмерные задачи, связанные с поиском различных центров масс — в основном с точки зрения вычислительной геометрии.

В рассмотренных ниже решениях можно выделить два основных факта. Первый — что центр масс системы материальных точек равен среднему их координат, взятых с коэффициентами, пропорциональными их массам. Второй факт — что если мы знаем центры масс двух непересекающихся фигур, то центр масс их объединения будет лежать на отрезке, соединяющем эти два центра, причём он будет делить его в то же отношении, как масса второй фигуры относится к массе первой.

Двумерный случай: многоугольники

На самом деле, говоря о центре масс двумерной фигуры, можно иметь в виду одну из трёх следующих задач:

• Центр масс системы точек — т.е. вся масса сосредоточена только в вершинах многоугольника.
• Центр масс каркаса — т.е. масса многоугольника сосредоточена на его периметре.
• Центр масс сплошной фигуры — т.е. масса многоугольника распределена по всей его площади.

Каждая из этих задач имеет самостоятельное решение, и будет рассмотрена ниже отдельно.

Центр масс системы точек

Это самая простая из трёх задач, и её решение — известная физическая формула центра масс системы материальных точек:

где — массы точек, — их радиус-векторы (задающие их положение относительно начала координат), и — искомый радиус-вектор центра масс.

В частности, если все точки имеют одинаковую массу, то координаты центра масс есть среднее арифметическое координат точек. Для треугольника эта точка называется центроидом и совпадает с точкой пересечения медиан:

Для доказательства этих формул достаточно вспомнить, что равновесие достигается в такой точке , в которой сумма моментов всех сил равна нулю. В данном случае это превращается в условие того, чтобы сумма радиус-векторов всех точек относительно точки , домноженных на массы соответствующих точек, равнялась нулю:

и, выражая отсюда , мы и получаем требуемую формулу.

Центр масс каркаса

Будем считать для простоты, что каркас однороден, т.е. его плотность везде одна и та же.

Но тогда каждую сторону многоугольника можно заменить одной точкой — серединой этого отрезка (т.к. центр масс однородного отрезка есть середина этого отрезка), с массой, равной длине этого отрезка.

Теперь мы получили задачу о системе материальных точек, и применяя к ней решение из предыдущего пункта, мы находим:

где — точка-середина -ой стороны многоугольника, — длина -ой стороны, — периметр, т.е. сумма длин сторон.

Для треугольника можно показать следующее утверждение: эта точка является точкой пересечения биссектрис треугольника, образованного серединами сторон исходного треугольника. (чтобы показать это, надо воспользоваться приведённой выше формулой, и затем заметить, что биссектрисы делят стороны получившегося треугольника в тех же соотношениях, что и центры масс этих сторон).

Центр масс сплошной фигуры

Мы считаем, что масса распределена по фигуре однородно, т.е. плотность в каждой точке фигуры равна одному и тому же числу.

Случай треугольника

Утверждается, что для треугольника ответом будет всё тот же центроид, т.е. точка, образованная средним арифметическим координат вершин:

Случай треугольника: доказательство

Приведём здесь элементарное доказательство, не использующее теорию интегралов.

Первым подобное, чисто геометрическое, доказательство привёл Архимед, но оно было весьма сложным, с большим числом геометрических построений. Приведённое здесь доказательство взято из статьи Apostol, Mnatsakanian “Finding Centroids the Easy Way”.

Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид.

Разобьём данный треугольник на четыре, соединив середины сторон, как показано на рисунке:

Четыре получившихся треугольника подобны треугольнику с коэффициентом .

Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого лежит в точке пересечения его диагоналей (поскольку это фигура, симметричная относительно обеих диагоналей, а, значит, её центр масс обязан лежать на каждой из двух диагоналей). Точка находится посередине общей стороны треугольников №1 и №2, а также лежит на медиане треугольника :

Пусть теперь вектор — вектор, проведённый из вершины к центру масс треугольника №1, и пусть вектор — вектор, проведённый из к точке (которая, напомним, является серединой стороны, на которой она лежит):

Наша цель — показать, что вектора и коллинеарны.

Обозначим через и точки, являющиеся центрами масс треугольников №3 и №4. Тогда, очевидно, центром масс совокупности этих двух треугольников будет точка , являющаяся серединой отрезка . Более того, вектор от точки к точке совпадает с вектором .

Искомый центр масс треугольника лежит посередине отрезка, соединяющего точки и (поскольку мы разбили треугольник на две части равных площадей: №1-№2 и №3-№4):

Таким образом, вектор от вершины к центроиду равен . С другой стороны, т.к. треугольник №1 подобен треугольнику с коэффициентом , то этот же вектор равен . Отсюда получаем уравнение:

Таким образом, мы доказали, что вектора и коллинеарны, что и означает, что искомый центроид лежит на медиане, исходящей из вершины .

Более того, попутно мы доказали, что центроид делит каждую медиану в отношении , считая от вершины.

Случай многоугольника

Перейдём теперь к общему случаю — т.е. к случаю мноугоугольника. Для него такие рассуждения уже неприменимы, поэтому сведём задачу к треугольной: а именно, разобьём многоугольник на треугольники (т.е. триангулируем его), найдём центр масс каждого треугольника, а затем найдём центр масс получившихся центров масс треугольников.

Окончательная формула получается следующей:

где — центроид -го треугольника в триангуляции заданного многоугольника, — площадь -го треугольника триангуляции, — площадь всего многоугольника.

Триангуляция выпуклого многоугольника — тривиальная задача: для этого, например, можно взять треугольники , где .

Случай многоугольника: альтернативный способ

С другой стороны, применение приведённой формулы не очень удобно для невыпуклых многоугольников, поскольку произвести их триангуляцию — сама по себе непростая задача. Но для таких многоугольников можно придумать более простой подход. А именно, проведём аналогию с тем, как можно искать площадь произвольного многоугольника: выбирается произвольная точка , а затем суммируются знаковые площади треугольников, образованных этой точкой и точками многоугольника: . Аналогичный приём можно применить и для поиска центра масс: только теперь мы будем суммировать центры масс треугольников , взятых с коэффициентами, пропорциональными их площадям, т.е. итоговая формула для центра масс такова:

где — произвольная точка, — точки многоугольника, — центроид треугольника , — знаковая площадь этого треугольника, — знаковая площадь всего многоугольника (т.е. ).

Трёхмерный случай: многогранники

Аналогично двумерному случаю, в 3D можно говорить сразу о четырёх возможных постановках задачи:

• Центр масс системы точек — вершин многогранника.
• Центр масс каркаса — рёбер многогранника.
• Центр масс поверхности — т.е. масса распределена по площади поверхности многогранника.
• Центр масс сплошного многогранника — т.е. масса распределена по всему многограннику.

Центр масс системы точек

Как и в двумерном случае, мы можем применить физическую формулу и получить тот же самый результат:

который в случае равных масс превращается в среднее арифметическое координат всех точек.

Центр масс каркаса многогранника

Аналогично двумерному случаю, мы просто заменяем каждое ребро многогранника материальной точкой, расположенной посередине этого ребра, и с массой, равной длине этого ребра. Получив задачу о материальных точках, мы легко находим её решение как взвешенную сумму координат этих точек.

Центр масс поверхности многогранника

Каждая грань поверхности многогранника — двухмерная фигура, центр масс которой мы умеем искать. Найдя эти центры масс и заменив каждую грань её центром масс, мы получим задачу с материальными точками, которую уже легко решить.

Центр масс сплошного многогранника

Случай тетраэдра

Как и в двумерном случае, решим сначала простейшую задачу — задачу для тетраэдра.

Утверждается, что центр масс тетраэдра совпадает с точкой пересечения его медиан (медианой тетраэдра называется отрезок, проведённый из его вершины в центр масс противоположной грани; таким образом, медиана тетраэдра проходит через вершину и через точку пересечения медиан треугольной грани).

Почему это так? Здесь верны рассуждения, аналогичные двумерному случаю: если мы рассечём тетраэдр на два тетраэдра с помощью плоскости, проходящей через вершину тетраэдра и какую-нибудь медиану противоположной грани, то оба получившихся тетраэдра будут иметь одинаковый объём (т.к. треугольная грань разобьётся медианой на два треугольника равной площади, а высота двух тетраэдров не изменится). Повторяя эти рассуждения несколько раз, получаем, что центр масс лежит на точке пересечения медиан тетраэдра.

Эта точка — точка пересечения медиан тетраэдра — называется его центроидом. Можно показать, что она на самом деле имеет координаты, равные среднему арифметическому координат вершин тетраэдра:

(это можно вывести из того факта, что центроид делит медианы в отношении )

Таким образом, между случаями тетраэдра и треугольника принципиальной разницы нет: точка, равная среднему арифметическому вершин, является центром масс сразу в двух постановках задачи: и когда массы находится только в вершинах, и когда массы распределены по всей площади/объёму. На самом деле, этот результат обобщается на произвольную размерность: центр масс произвольного симплекса (simplex) есть среднее арифметическое координат его вершин.

Случай произвольного многогранника

Перейдём теперь к общему случаю — случаю произвольного многогранника.

Снова, как и в двумерном случае, мы производим сведение этой задачи к уже решённой: разбиваем многогранник на тетраэдры (т.е. производим его тетраэдризацию), находим центр масс каждого из них, и получаем окончательный ответ на задачу в виде взвешенной суммы найденных центров масс.

[spoiler title=”источники:”]

http://planetcalc.ru/9363/

http://e-maxx.ru/algo/gravity_center

[/spoiler]

Была ли эта статья полезной?

В этой статье и разберу как нарисовать центр тяжести треугольника и найти его координаты.

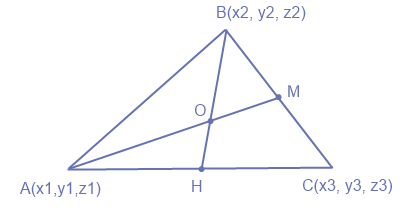
1) Рисуем треугольник ABC
2) Ставим точку M – середина BC
3) Ставим точку H – середина AC
4) Пересечение BH и AM – и есть центр тяжести треугольника ABC
5) Найдем его координаты (координаты точки O

(x_(o), y_(o), z_(o))

)

[x_{0}=frac{x_{1}+x_{2}+x_{3}}{3}, y_{0}=frac{y_{1}+y_{2}+y_{3}}{3}, z_{0}=frac{z_{1}+z_{2}+z_{3}}{3}]

Пример: Найти координаты центра тяжести треугольника с вершинами A(2;3;4), B(3;1;2) и C(4;-1;3). Решение.

Просмотры: 42689 |
Статью добавил: slava191 |
Категория: аналитическая_геометрия

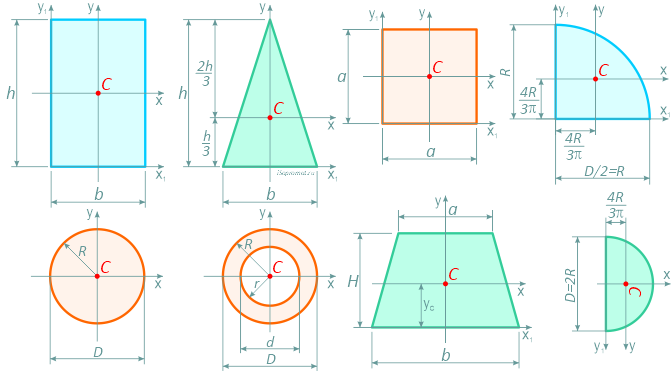
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.

Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
I_x , I_y — осевые моменты инерции сечения относительно главных осей;
I_x1 , I_y1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
I_ρ — полярный момент инерции сечения;
W_x , W_y — осевые моменты сопротивления;
W_ρ — полярный момент сопротивления

Прямоугольник

Прямоугольник высотой h и шириной b.

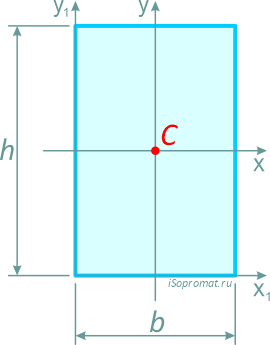
Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.

Площадь

Центральные осевые моменты инерции прямоугольника

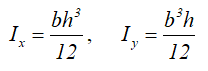
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

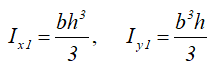
Осевые моменты сопротивления прямоугольного сечения

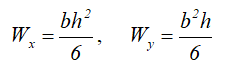
Квадрат

Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.

Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.

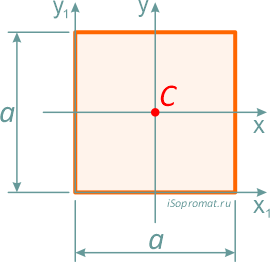
Площадь

Центральные осевые моменты инерции квадрата

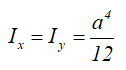
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

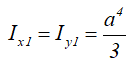
Осевой момент сопротивления квадратного сечения

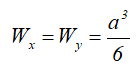
Треугольник равнобедренный

Равнобедренный треугольник высотой h и шириной основания b.

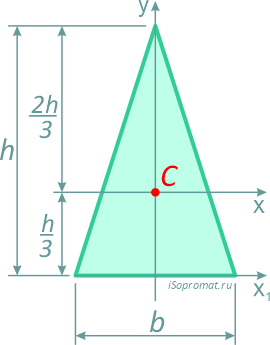
Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.

Площадь

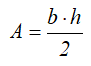
Центральные осевые моменты инерции треугольника

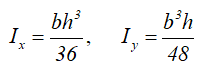
Момент инерции относительно смещенной оси x₁, проходящей через его основание

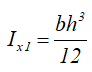
Прямоугольный треугольник

Прямоугольный треугольник высотой h и шириной основания b.

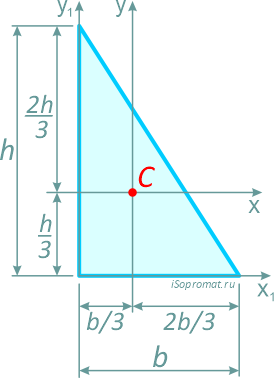
Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.

Площадь

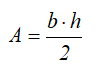
Центральные осевые моменты инерции прямоугольного треугольника

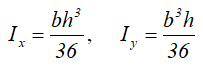
Моменты инерции относительно смещенных осей x₁ и y₁, проходящих через точку, соединяющую его катеты

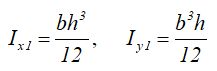
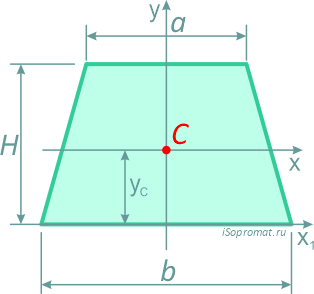
Трапеция

Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.

Площадь трапеции

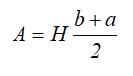
Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:

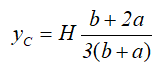
Круг

Круг диаметром D (d) или радиусом R (r)

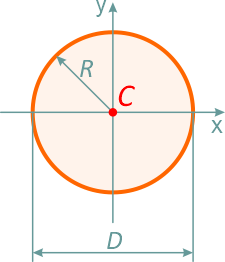
Площадь круга через его диаметр и радиус

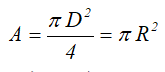
Центральные осевые и полярный моменты инерции круга

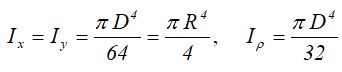
Осевые и полярный моменты сопротивления

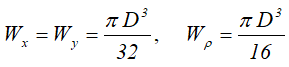
Полукруг

Половина круга диаметром D (d) или радиусом R (r)

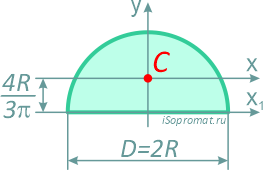
Площадь

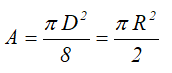
Осевые моменты инерции полукруга

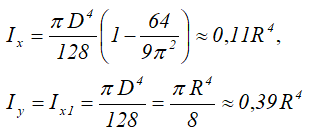
Четверть круга

Четверть круга диаметром D (d) или радиусом R (r)

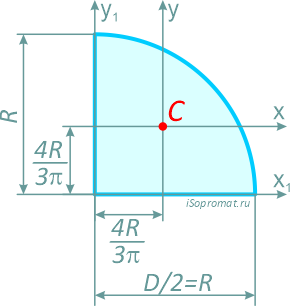
Площадь

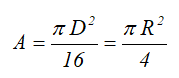
Центральные осевые моменты инерции четверти круга

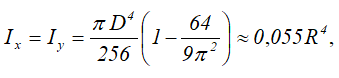
Моменты инерции относительно смещенных осей x₁ и y₁

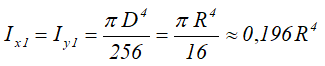
Кольцо

Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)

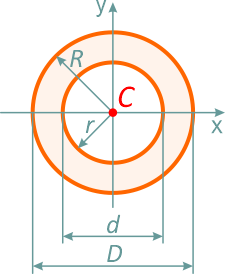
Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.

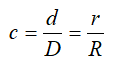
Площадь

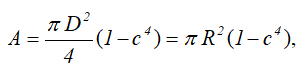
Центральные осевые и полярный моменты инерции кольца

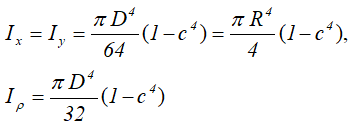
Осевые и полярный моменты сопротивления

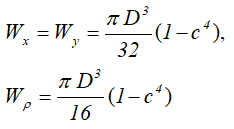
Тонкостенное сечение (труба)

Тонкостенный профиль (сечение трубы) средним радиусом R₀ и толщиной стенки трубы t при R₀>>t

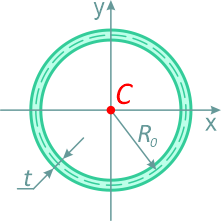
Площадь

Центральные осевые и полярный моменты инерции трубного сечения

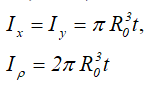
Осевые и полярный моменты сопротивления

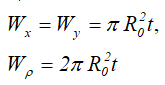
Пример определения координат центра тяжести сложной фигуры:

Другие видео

Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее