Голосование за лучший ответ
Mikhail Levin
Искусственный Интеллект
(614570)
9 лет назад
это точка пересечения серединных перпендикуляров сторон. она же – центр описанной окружности
Ветер переменПросветленный (21839)
4 года назад
Здравствуйте. Правильно я поняла, что это ортоцентр – центр пересечения высот треугольника?
праора
Мудрец
(10512)
9 лет назад
это будет центр описанной вокруг этого треугольника окружности. Этот центр является точкой пересечения серединных перпендикуляров. Короче, найди середины 2 сторон треугольника и от этой середины проведи перпендикуляры, где они пересекутся – там и точка равноудаленная от вершин треугольника
Рустам Искендеров
Искусственный Интеллект
(133392)
9 лет назад
Надо поднять перпендикуляр к плоскости треугольника из точки, указанной тт. Левиным и Ага. Любая точка этого перпендикуляра – ответ.
Кучин Дмитрий
Профи
(647)
5 лет назад
Центр описанной окружности. Пересечение срединных перпендикуляров.
Окружность, описанная около треугольника
Определение окружности, описанной около треугольника
Определение 1. Окружностью, описанной около треугольника называется окружность, проходящей через все три вершины треугольника (Рис.1).
При этом треугольник называется треугольником вписанным в окружность .
Теорема об окружности, описанной около треугольника
Теорема 1. Около любого треугольника можно описать окружность.
Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения серединных перпендикуляров к его сторонам. Проведем отрезки OA, OB и OC. Поскольку точка O равноудалена от точек A, B и C, то OA=OB=OC. Тогда окружность с центром O и радиусом OA проходит через все три вершины треугольника ABC и, следовательно, является окружностью, описанной около треугольника ABC.
Из теоремы 1 следует, что центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника.
Замечание 1. Около любого треугольника можно описать только одну окружность.
Доказательство. Допустим, что около треугольника можно описать две окружности. Тогда центр каждой из этих окружностей равноудален от вершин треугольника и совпадает с точкой O пересечения серединных перпендикуляров сторон треугольника. Радиус этих окружностей равен расстоянию от точки O до вершин треугольника. Поэтому эти окружности совпадают.
Точка равноудалена от сторон треугольника центр окружности
Ключевые слова: основные линии треугольника, медиана, биссектриса, высота, средния линия, серединные перпендикуляры
Рассмотрим произвольный треугольник ABC:
a, b, c – стороны треугольника
$$m_a$$ – медиана к стороне a угла A
$$h_a$$ – высота к стороне a угла A
$$l_a$$ – биссектриса к стороне a угла A
Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.
Свойства медиан треугольника
- Медиана разбивает треугольник на два треугольника одинаковой площади.
- Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
- Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Свойства биссектрис треугольника
- Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
- Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам.
- Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.
Свойства высот треугольника
- В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
- В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
- Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон
- Три высоты в остроугольном треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.
Свойства серединных перпендикуляров треугольника
- Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
- Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника
- Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Точка равноудалена от сторон треугольника центр окружности
554. Докажите, что если центр окружности, описанной около треугольника, принадлежит его высоте, то этот треугольник равнобедренный.
555. Докажите, что если центр окружности, вписанной в треугольник, принадлежит его медиане, то этот треугольник равнобедренный.
556. Докажите, что если центры вписанной и описанной окружностей треугольника совпадают, то этот треугольник равносторонний.
557. Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 7 : 5, считая от вершины треугольника. Найдите стороны треугольника, если его периметр равен 68 см.
558. Периметр треугольника ABC , описанного около окружности, равен 52 см. Точка касания со стороной AB делит эту сторону в отношении 2 : 3, считая от вершины A . Точка касания со стороной BC удалена от вершины C на 6 см. Найдите стороны треугольника.
559. В треугольник с углами 30°, 70° и 80° вписана окружность. Найдите углы треугольника, вершины которого являются точками касания вписанной окружности со сторонами данного треугольника.
560. Окружность, вписанная в равнобедренный треугольник ABC , касается его боковых сторон AB и BC в точках M и N соответственно. Докажите, что MN ‖ AC .
561. Докажите, что если центр окружности, описанной около треугольника, принадлежит его стороне, то этот треугольник — прямоугольный.
562. В треугольник ABC вписана окружность, касающаяся стороны AB в точке M , BС = a . Докажите, что AM = p – a , где p — полупериметр треугольника ABC .
563. К окружности, вписанной в равносторонний треугольник со стороной a , провели касательную, пересекающую две его стороны. Найдите периметр треугольника, который эта касательная отсекает от данного.
564. В равнобедренный треугольник ABC ( AB = BC ) с основанием 10 см вписана окружность. К этой окружности проведены три касательные, отсекающие от данного треугольника треугольники ADK , BEF и CMN . Сумма периметров этих треугольников равна 42 см. Чему равна боковая сторона данного треугольника?
565. В треугольнике ABC отрезок BD — медиана, AB = 7 см, BC = 8 см. В треугольники ABD и BDC вписали окружности. Найдите расстояние между точками касания этих окружностей с отрезком BD .
566. Каждый из углов BAC и ACB треугольника ABC разделили на три равные части (рис. 308). Докажите, что ∠ AMN = ∠ CMN .
567. Пусть вершина угла B недоступна (рис. 309). С помощью транспортира и линейки без делений постройте прямую, содержащую биссектрису угла B .
568. Точки F и O — центры вписанной и описанной окружностей равнобедренного треугольника ABC соответственно (рис. 310). Они находятся на одинаковом расстоянии от его основания AC . Найдите углы треугольника ABC .
Упражнения для повторения
569. Биссектриса угла ABC образует с его стороной угол, равный углу, смежному с углом ABC . Найдите угол ABC .
570. В равнобедренном треугольнике из вершины одного угла при основании провели высоту треугольника, а из вершины другого угла при основании — биссектрису треугольника. Один из углов, образовавшихся при пересечении проведённых биссектрисы и высоты, равен 64°. Найдите углы данного треугольника.
571. На рисунке 311 BC ‖ AD , AB = 3 см, BC = 10 см. Биссектриса угла BAD пересекает отрезок BC в точке K . Найдите отрезки BK и KC .
572. В треугольнике ABC известно, что AB = BC , AM и CK — медианы этого треугольника. Докажите, что MK ‖ AC .
Наблюдайте, рисуйте, конструируйте, фантазируйте
573. В квадрате ABCD вырезали заштрихованную фигуру (рис. 312). Разделите оставшуюся часть квадрата на четыре равные фигуры.
[spoiler title=”источники:”]
http://uztest.ru/abstracts/?idabstract=702368
http://reader.lecta.rosuchebnik.ru/demo/8068/data/Chapter29.xhtml
[/spoiler]
| Центроид треугольника | |
|---|---|
 Медианы и центроид треугольника |
|
| Барицентрические координаты | 1 : 1 : 1 |
| Трилинейные координаты |
 |
| Код ЭЦТ | X(2) |
| Связанные точки | |
| Изогонально сопряженная | точка Лемуана |
| Изотомически сопряженная | она же |
| Дополнительная[es] | она же |
| Антидополнительная[es] | она же |
Центроид треугольника (также барицентр треугольника и центр тяжести треугольника) — точка пересечения медиан в треугольнике[1].
Центроид традиционно обозначается латинской буквой 
Свойства[править | править код]
- Центроид делит каждую медиану в отношении 2:1, считая от вершины.
- Центроид лежит на отрезке, соединяющем ортоцентр и центр описанной окружности, и делит его в отношении 2:1 (см. прямая Эйлера).
- Если в вершины треугольника поместить равные массы, то центр масс (барицентр) полученной системы будет совпадать с центроидом. Более того, центр масс треугольника с равномерно распределённой внутри массой также находится в центроиде.
- Если
— центроид треугольника
то для любой точки
верно равенство
.
- Центроид является точкой, для которой сумма квадратов расстояний до вершин треугольника принимает наименьшее значение (теорема Лейбница).
- Три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника (равной площади).
- Три отрезка прямых, соединяющих середины сторон треугольника с центроидом, разбивают данный треугольник на три равновеликих четырёхугольника (равной площади).
- При изогональном сопряжении центроид переходит в точку Лемуана (в точку пересечения трех симедиан треугольника).
- Построим две прямые, каждая из которых проходит через точку Аполлония и точку Торричелли, отличную от изогонально сопряжённой ей. Такие прямые пересекутся в центроиде треугольника.
- Пусть
— треугольник на плоскости. Окружность, проходящая через центроид и две точки Аполлония треугольника
, называется окружностью Парри треугольника
.
- Три чевианы, проведённые через произвольную точку
внутри треугольника, делят своими концами стороны треугольника на шесть отрезков. Произведение длин трёх из этих шести отрезков, не имеющих общих концов, максимально, если точка
совпадает с центроидом[2].
- Сумма квадратов сторон треугольника равна утроенной сумме квадратов расстояний от центроида до вершин:
.[3]
- и
,
- где
— площадь треугольника.
История[править | править код]
Факт того, что три медианы пересекаются в одной точке, был доказан ещё Архимедом.
Вариации и обобщения. Центроиды в четырёхугольнике[править | править код]
- Центроид (барицентр или центр масс) произвольного четырёхугольника лежит в точке пересечения средних линий четырёхугольника и отрезка, соединяющего середины диагоналей, и делит все три отрезка пополам.
Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершины
- Если во вписанном в окружность четырёхугольнике провести диагональ, а в полученные два треугольника вписать две окружности, затем аналогично поступить, проведя вторую диагональ, тогда центроиды этих четырёх треугольников лежат на одной окружности[5].
- У выпуклого четырёхугольника, вписанного в окружность, «центроид площади» или центр масс его площади Ga, вершинный центроид или центр масс четырёх его вершин Gv и точка пересечения его диагоналей P коллинеарны. Расстояния между этими точками удовлетворяют формуле[6]
См. также[править | править код]
- Барицентр
- Центр тяжести
- Центр масс
- Ортоцентр
- Инцентр
- Замечательные точки треугольника
- Геометрия треугольника
Примечания[править | править код]
- ↑ Е. Смирнова. Планиметрия: виды задач и методы их решений. Элективный курс для учащихся 9—11 классов. — Litres, 2017-09-05. — С. 165. — 417 с.
- ↑ Зетель, 1962, с. 12.
- ↑ Altshiller-Court (1925, pp. 70–71)
- ↑ Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ. Co., 2007
- ↑ Andreescu, Titu & Enescu, Bogdan (2004), 2.3 Cyclic quads, Mathematical Olympiad Treasures, Springer, с. 44–46, 50, ISBN 978-0-8176-4305-8
- ↑ Bradley, Christopher (2011), Three Centroids created by a Cyclic Quadrilateral, <http://people.bath.ac.uk/masgcs/Article141.pdf>
Литература[править | править код]
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 80-81. — ISBN 5-94057-170-0.
- Дм. Ефремов. Новая геометрия треугольника 1902 год
- Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М: Учпедгиз, 1962. 153 с.
- Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble
Четыре замечательные точки треугольника
Замечательные точки треугольника — это точки, расположение которых однозначно определяется треугольником и не зависит от того, в каком порядке рассматривать его стороны и углы.
Всего замечательных точек четыре. Две из них открыл Евклид, вписывая в треугольник окружности, третья, точка пересечения медиан, обнаружена Архимедом. Четвертая, в которой пересекаются высоты треугольника, не упоминалась в трудах Евклида, но описывалась в трудах его современников. Возможно, Евклид и Архимед просто упорядочили и записали доказательства теорем, известных задолго до них.
Особенность замечательных точек в том, что они в любом треугольнике являются пересечением трех линий, при этом их свойства не меняются:
- биссектрисы пересекаются в центре вписанного круга;
- перпендикуляры от середин сторон пересекаются в центре описанного круга;
- высоты пересекаются в ортоцентре, точки, симметричные ортоцентру относительно сторон треугольника, находятся на описанном круге;
- медианы пересекаются в барицентре (он же центроид, или геометрический центр).
В XVIII веке математик Леонард Эйлер, исследуя геометрию треугольников, доказал, что три из этих точек — ортоцентр, барицентр и центр описанного круга — всегда расположены на одной линии. Она называется прямой Эйлера. Точки стали называть «замечательными» или «особенными».
Четыре замечательные точки треугольника
Точка пересечения медиан треугольника
В ней находится центр тяжести однородной треугольной пластины, также она является средним арифметическим положений всех точек треугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
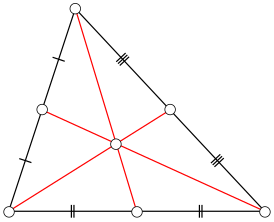
Медианы треугольника пересекаются в его геометрическом центре и делятся в этой точке в отношении 2:1, считая от вершин.
Доказательство
Обозначим точку пересечения медиан О и проведем среднюю линию треугольника (А^1В^1) .
Отрезок (А_1В_1) параллелен (АВ) , поэтому углы 1, 2, 3 и 4 равны друг другу. Таким образом, треугольники (АОВ) и (А_1ОВ_1) подобны по двум углам, и их стороны пропорциональны. (АВ = 2А_1В_1) , значит, (АО = 2А_1О) и (ВО = 2В_1О) , а точка О разделяет медианы на отрезки с отношением 2:1, считая от вершин. Аналогично она делит медиану (СС_1) .
Точка пересечения биссектрис треугольника
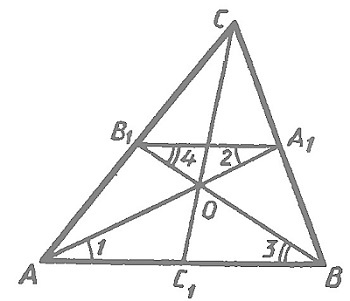
Точка пересечения трех биссектрис расположена на равном расстоянии от всех сторон треугольника и находится в центре вписанного в треугольник круга.
Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
Биссектрисы треугольника пересекаются в одной точке.
Доказательство
Проведем из точки пересечения биссектрис (АА_1) и (ВВ_1) отрезки (ОК) , (ОL) и (ОМ) , перпендикулярные трем сторонам треугольника.
Согласно теореме о равной удаленности точек биссектрисы от сторон угла, ОК = ОМ и ОК = ОL. Соответственно, ОМ = ОL, точка О находится на равном расстоянии от сторон угла АСВ и расположена на биссектрисе. Таким образом, все три биссектрисы пересекутся в одной точке.
Точка пересечения серединных перпендикуляров треугольника
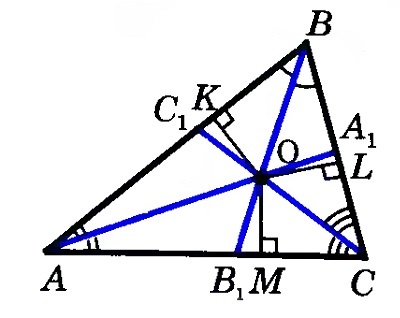
Линии, проходящие через середины сторон треугольника перпендикулярно к ним, пересекаются в центре круга, описанного вокруг треугольника. В остроугольном треугольнике точка пересечения перпендикуляров расположена внутри него, в тупоугольном — снаружи. Если треугольник прямоугольный, точка находится на гипотенузе.
Каждая точка серединного перпендикуляра равноудалена от концов отрезка, к которому он перпендикулярен.
Серединные перпендикуляры от сторон треугольника пересекаются в одной точке.
Доказательство
Изобразим внутри треугольника АВС перпендикуляры m и n, отметим точку их пересечения О.
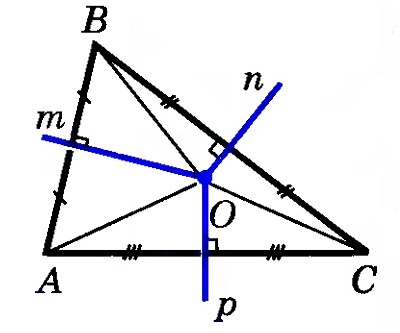
Согласно теореме о равной удаленности серединных перпендикуляров от концов отрезка, ОВ = ОА и ОВ = ОС. Соответственно, ОА = ОС, и точка О находится на одинаковом расстоянии от точек А и С. Таким образом, серединный перпендикуляр р к отрезку АС тоже будет проходить через точку О, и все три перпендикуляра пересекутся в одной точке.
Точка пересечения высот треугольника
Высоты или их продолжения могут пересекаться как внутри треугольника, если он остроугольный, так и вне его, если он тупоугольный. Если треугольник прямоугольный, тогда ортоцентр совпадает с вершиной прямого угла.
Высоты треугольника или их продолжения пересекаются в одной точке.
Доказательство
Изобразим произвольный треугольник (АВС) и прямые (AA_1) , (BB_1) и (СС_1) , содержащие его высоты. Проведем через каждую вершину прямые, параллельные противоположным сторонам треугольника, получив треугольник ( A_2B_2C_2) . Точки А, В и С окажутся серединами его сторон. ( АВ = A_2C = В_2C) , так как эти отрезки являются противоположными сторонами параллелограммов (АВА_2С) и (АВСВ_2) . Соответственно, (С_2А = АВ_2) и (С_2В = ВА_2) .
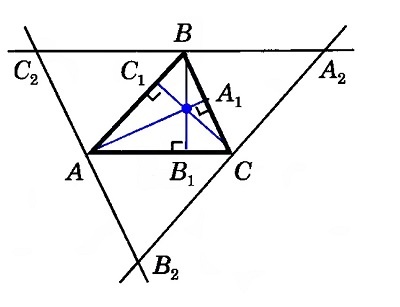
Из построения следует, что отрезок (СС_1) перпендикулярен (А_2В_2) , (АА_1 perp В_2С_2) и (ВВ_1 perp А_2С_2) . Следовательно, прямые (АА_1) , (ВВ_1) и (СС_1) — серединные перпендикуляры сторон треугольника (А_2В_2С_2) , которые пересекутся в одной точке.
Примеры решения задач
Задача 1
Серединные перпендикуляры к сторонам АВ и АС треугольника АВС пересекаются в точке D, лежащей на стороне треугольника ВС. Докажите, что точка D — середина стороны ВС.
Решение
Изобразим треугольник АВС.
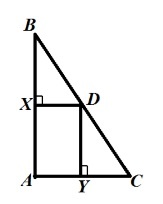
Все серединные перпендикуляры должны пересекаться в одной точке, если два из них уже пересеклись, третий тоже должен проходить через точку D. Таким образом, точка D является основанием третьего серединного перпендикуляра и расположена посередине стороны ВС.
Задача 2
Биссектрисы (AA_1) и (BB_1) треугольника АВС пересекаются в точке D. Найдите углы АСD и ВСD, если известно, что угол АDB составляет (136^circ) .
Решение
Поскольку биссектрисы пересекаются в точке D, луч СD является биссектрисой. Тогда
(angle АСD;=;angle BCD;=;136^circ;-;90^circ;=;46^circ)
Насколько полезной была для вас статья?
Рейтинг: 4.25 (Голосов: 12 )
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Комплексное число — это выражение вида x=a+bcdot i , где a и b — вещественные числа, а i — так называемая «мнимая единица». Если возвести ее в квадрат, получится отрицательное число. Таким образом, она определяется равенством i=sqrt или i^2=-1. Извлечение корня Определение Корнем со степенью n, извлеченным из комплексного числа z называют то число w, у которого n-ая степень равна z и обозначается как sqrt[n]z. Не существует однозначного извлечения корня из комплексного числа, так как он имеет то количество значений, которое равно его степени. Тригонометрическая форма Если число z представлено в тригонометрической форме z=left|zright|cdotleft(cosleft(фright)+isinleft(фright)right), то значения корня n-ой степени находятся по формуле: sqrt[n]z=sqrt[n]cdot(cosleft(fracnright)+isinleft(fracnright)). Где |z| — модуль комплексного числа, ф — аргумент, k — параметр, значения у которого 0,1,2…n-1. Если посмотреть на извлечение корня n-ой степени с точки зрения геометрии, центр окружности с радиусом sqrt[n]z расположен в точке О (0; 0), а все полученные значения, расположенные на ней, образуют правильный n-угольник (как это представлено на чертеже выше). Алгебраическая форма Если из данного числа z нужно извлечь корень n-ой степени, а он представлен в алгебраической или показательной форме, необходимо выполнить извлечение по пунктам: Представить число в тригонометрической форме: вычислить модуль left|zright| и аргумент (ф). Полученные значения применить в тригонометрической форме: z=left|zright|cdotleft(cosleft(фright)+isinleft(фright)right). Извлечь корни по формуле, приведенной выше. Алгоритм вычисления квадратного и кубического корня Задача на кубический корень Задача: Извлечь кубический корень sqrt[3]z, где z=frac12+frac12cdot i в алгебраической форме. Решение: Вспомним, что тригонометрическая форма записи комплексного числа выглядит так: z=left|zright|cdotleft(cosleft(фright)+isinleft(фright)right). По условию мы знаем, что a=frac12 и b=frac12. Можем вычислить исходное значение комплексного числа: r=sqrt=sqrt=sqrt=frac1. Теперь посчитаем аргумент исходного комплексного числа: ф=arg(z)=arctanleft(fracright)=arctanleft(1right)=fracpi4. Далее подставим значения в тригонометрическую форму записи и получим: z=frac2cdotleft(cosleft(fracpi4right)+isinleft(fracpi4right)right). Мы знаем, что корнем n-ой степени некоторого числа z=left|zright|cdotleft(cosleft(фright)+isinleft(фright)right) является комплексное число, определяемое следующим равенством: sqrt[n]z=sqrt[n]cdot(cosleft(fracnright)+isinleft(fracnright)). Воспользуемся этой формулой: Для k=0: w_1=sqrt[3]z=sqrt[3]>cdotleft(cosleft(fracpiright)+icdotsinleft(fracpiright)right). Для k=1 будет справедливо уравнение: w_2=sqrt[3]z=sqrt[3]>cdotleft(cosleft(frac3right)+icdotsinleft(frac3right)right)=sqrt[3]>cdotleft(cosleft(frac4right)+icdotsinleft(frac4right)right). Для k=2: w_3=sqrt[3]z=sqrt[3]>cdotleft(cosleft(frac3right)+icdotsinleft(frac3right)right)=sqrt[3]>cdotleft(cosleft(fracright)+icdotsinleft(fracright)right). Задача на квадратный корень Задача: Извлечь корень sqrt z для заданных комплексных чисел в показательной форме: z=3cdot e^. Решение: Определим значение модуля и аргумента в тригонометрической форме записи: z=left|zright|cdotleft(cosleft(фright)+isinleft(фright)right): r=3, ф=fracpi3. Подставляем ф в равенство: z=3cdotleft(cosleft(fracpi3right)+isinleft(fracpi3right)right). Воспользуемся формулой sqrt[n]z=sqrt[n]cdot(cosleft(fracnright)+isinleft(fracnright)). Для k=0 справделиво уравнение: w_1=sqrt z=sqrt3cdotleft(cosleft(fracpi6right)+isinleft(fracpi6right)right); Для k=1: w_2=sqrt z=sqrt3cdotleft(cosleft(frac2right)+isinleft(frac2right)right)=sqrt3cdotleft(cosleft(frac6right)+isinleft(frac6right)right).
Ход урока
1. Проверить решение задачи № 24 по записям (с пробелами), сделанными на доске до начала урока.
Решение задачи № 24 Пусть АВα (рис. 166).
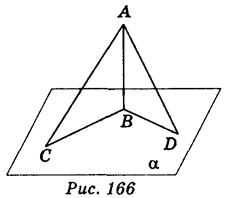
1) ВС = 40 см, BD =. ; пусть AD = х см, тогда АС=. С ΔАВ D : АВ2 = х2 -122 = х2 — 144. Из ΔАВС АВ2. Тогда х2 — 144 = (х + 26)2 — 402; 52х=. ; х =15. Следовательно, AD=. AC = 41 см.
2) BD=. BC=7 см; пусть А D =. тогда AC = 2х см.
С ΔАВ D AB2=. Из Δ АВС АВ2 = 4х2 — 49.
Тогда х2 — 1 = . ; 3х2 = . ; х2 = 16. Отсюда х = . ; следовательно, AD =. AC = 2·4 = 8 (см).
Ответ. 1) 15 см и 41 см; 2) 4 см и 8 см.
2. Математический диктант.
МО — перпендикуляр к плоскости ОАВ; AOB = 90° (рис. 167); МА и МВ — наклонные.
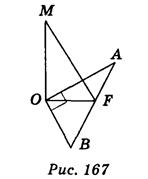
Вариант 1 — МО = 1 см, ОА = 3 см, MB = см;
вариант 2 — МЕ = 1 см, ОВ = 4 см, МА = см. Пользуясь рисунком, найдите:
1) длину неизвестной наклонной; (2 балла)
2) длину неизвестной проекции наклонной; (2 балла)
3) длину отрезка АВ; (2 балла)
4) расстояние от точки В до середины отрезка АВ; (2 балла)
5) расстояние от точки М до середины отрезка АВ; (2 балла)
6) расстояние от точки А до плоскости ЯЗЫКОВ. (2 балла)
Ответ. Вариант 1.1) см; 2) см; 3) см; 4) см; 5) см; 6) 3 см.
Вариант 2. 1) см; 2) 3 см; 3) 5 см; 4) 2,5 см; 5) см; 6) 3 см.
II. Восприятие и осознание нового материала
Свойство точки, равноудаленной от вершины многоугольника
Если через центр окружности, описанной вокруг многоугольника, проведено прямую, перпендикулярную к плоскости многоугольника, то каждая точка этой прямой равноудалена от вершин многоугольника.
Доведение
Пусть ABCD — четырехугольник, вокруг которого описана окружность с центром в точке О, и OS(ABC). Докажем, что SA = SB = SC = SD (рис. 168).
ΔASO = ΔBSO = ΔCSO = ΔDSO (за двумя катетами: SO — общая, АО = BO = CO = DO).
Из равенства треугольников следует, что SA = SB = SC = SD.
Если некоторая точка равноудалена от вершин многоугольника, то основание перпендикуляра, опущенного из данной точки на плоскость многоугольника, совпадает с центром окружности, описанной вокруг многоугольника.
Доведение
Пусть ABCD — данный четырехугольник, для точки S пространства SA = SB = SC = SD и SOАВС. Докажем, что точка О — центр окружности, описанной вокруг ABCD (рис. 168). ΔASO = ΔBSО = ΔCSO = ΔDSO (по гипотенузой и катетом: SO — совместный, AS = BS = CS = DS — по условию). Из равенства треугольников следует, что АО = BO = CO = DO, т.е. точка О — центр окружности, описанной вокруг четырехугольника ABCD.
Далее следует напомнить формулы для нахождения радиуса круга, описанного вокруг некоторых многоугольников, с помощью данной настенной таблицы.
1. ABC = 90°; МА = MB = МС (рис. 169). Опустите из точки М перпендикуляр на плоскость АВС.
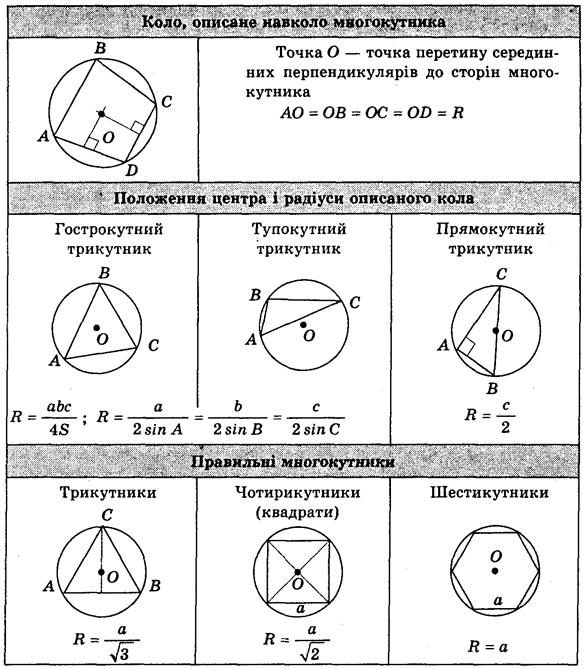
2. ABCD — квадрат, АВ = 4 см, МА = MB = MC = MD = 5 см (рис. 170). Найдите расстояние от точки М до плоскости АВС.
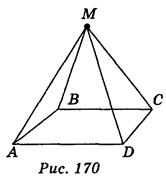
3. АВ = ВС = АС = 5 см; МА = MB = MC = 13 см (рис. 171). Найдите расстояние от точки М до плоскости АВС.
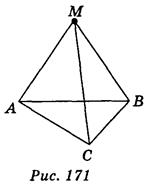
4. ABCD — квадрат, SO( ABC ), SO = 2см, АВ = 4 см (рис. 172). Найдите расстояние от точки S до вершин квадрата.
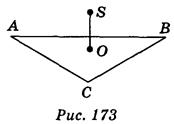
5. Δ АВС — правильный; точка О — центр треугольника; АВ = 3см; SO(АВС); SO = см (рис. 173). Найдите расстояние от точки 5 до вершин треугольника АВС.
6. Задача 21 из учебника (с. 35).
7. Задача 20* из учебника (с. 35).
III. Домашнее задание
Задачи № 6, 17-19 (с. 34-35).
IV. Подведение итога урока
Вопрос к классу
1) Какое свойство имеют точки, которые лежат на перпендикуляре, проведенном к плоскости многоугольника через центр окружности, описанной вокруг многоугольника?
2) Где находятся точки, равноудаленные от вершин некоторого многоугольника?
3) Через центр О правильного шестиугольника ABCDEF проведем перпендикуляр SO к плоскости АВС (рис. 174). Укажите, какие из приведенных утверждений правильные, а какие — неправильные:
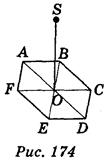
а) расстояния от точки S до вершин шестиугольника ABCDEF разные;
б) угол OAS равен углу OCS;
в) если ОА = 1 cm, SO = 1 см, то SA = cm;
г) если SO = OB, то OSB = 60°.
4) Расстояния от точки S до всех вершин прямоугольника ABCD равны, точка О — точка пересечения диагоналей АС и BD прямоугольника ABCD. Укажите, какие из приведенных утверждений правильные, а какие — неправильные:
Четыре замечательные точки треугольника
В треугольнике есть так называемые четыре замечательные точки: точка пересечения медиан. Точка пересечения биссектрис, точка пересечения высот и точка пересечения серединных перпендикуляров. Рассмотрим каждую из них.
Точка пересечения медиан треугольника
О пересечении медиан треуголника: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.
Доказательство.
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 1).
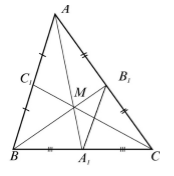
Рисунок 1. Медианы треугольника
По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $angle ABB_1=angle BB_1A_1, angle BAA_1=angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда
Аналогично доказывается, что
Точка пересечения биссектрис треугольника
О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.
Доказательство.
Рассмотрим треугольник $ABC$, где $AM, BP, CK$ его биссектрисы. Пусть точка $O$ — точка пересечения биссектрис $AM и BP$. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).
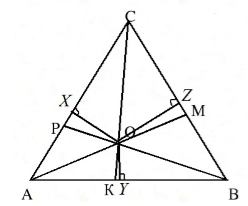
Рисунок 2. Биссектрисы треугольника
Готовые работы на аналогичную тему
Для доказательства нам потребуется следующая теорема.
Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
По теореме 3, имеем: $OX=OZ, OX=OY$. Следовательно, $OY=OZ$. Значит точка $O$ равноудалена от сторон угла $ACB$ и, значит, лежит на его биссектрисе $CK$.
Точка пересечения серединных перпендикуляров треугольника
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Доказательство.
Пусть дан треугольник $ABC$, $n, m, p$ его серединные перпендикуляры. Пусть точка $O$ — точка пересечения серединных перпендикуляров $n и m$ (рис. 3).
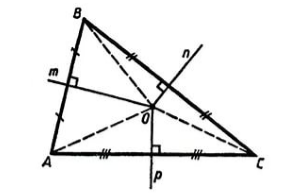
Рисунок 3. Серединные перпендикуляры треугольника
Для доказательства нам потребуется следующая теорема.
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.
По теореме 3, имеем: $OB=OC, OB=OA$. Следовательно, $OA=OC$. Значит точка $O$ равноудалена от концов отрезка $AC$ и, значит, лежит на его серединном перпендикуляре $p$.
Точка пересечения высот треугольника
Высоты треугольника или их продолжения пересекаются в одной точке.
Доказательство.
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник $A_2B_2C_2$ (рис. 4).
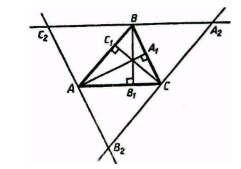
Рисунок 4. Высоты треугольника
Так как $AC_2BC$ и $B_2ABC$ параллелограммы с общей стороной, то $AC_2=AB_2$, то есть точка $A$ — середина стороны $C_2B_2$. Аналогично, получаем, что точка $B$ — середина стороны $C_2A_2$, а точка $C$ — середина стороны $A_2B_2$. Из построения мы имеем, что $_1bot A_2B_2, _1bot A_2C_2, _1bot C_2B_2$. Следовательно, $_1, _1, _1$ — серединные перпендикуляры треугольника $A_2B_2C_2$. Тогда, по теореме 4, имеем, что высоты $_1, _1, _1$ пересекаются в одной точке.
Пример задачи на использование 4 замечательных точек треугольника
Серединные перпендикуляры к сторонам $AB$ и $AC$ треугольника $ABC$ пересекаются в точке $D$ стороны $BC$. Докажите, что
а) точка $D$ — середина стороны $BC$.
б) $angle A=angle B+angle C$
Решение.
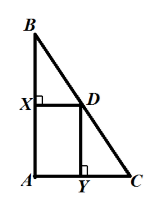
а) По теореме 4, все серединные перпендикуляры пересекаются в точке $D$. Следовательно, $D$ — основание серединного перпендикуляра к стороне $BC$. Значит точка $D$ — середина стороны $BC$.
б) Так как $X$ и $D$ — середины сторон, то $XD$ — средняя линия треугольника. Тогда, по теореме о средней линии треугольника $XD||AC$. Значит,$angle A=angle DXB$, как соответственные углы. Значит, $angle A=^0$. Тогда$angle B+angle C=^0-angle A=^0-^0=^0=angle A$
Окружность, описанная около треугольника
Окружность называют описанной около треугольника, если все вершины треугольника расположены на окружности.
Её центр равноудалён от всех вершин, то есть должен находиться в точке пересечения серединных перпендикуляров к сторонам треугольника.
Следовательно, около любого треугольника можно описать окружность, так как серединные перпендикуляры к сторонам пересекаются в одной точке.

Для остроугольного треугольника центр окружности находится в треугольнике.
Другая ситуация с прямоугольным и тупоугольным треугольниками.


Окружность, вписанная в треугольник
Окружность называют вписанной в треугольник, если все стороны треугольника касаются окружности.
Её центр равноудалён от всех сторон, то есть должен находиться в точке пересечения биссектрис треугольника.
Следовательно, в любой треугольник можно вписать окружность, так как биссектрисы треугольника пересекаются в одной точке.

Так как биссектрисы углов треугольника всегда пересекаются внутри треугольника, то для всех треугольников центр вписанной окружности находится в треугольниках.
Равносторонний треугольник
Обрати внимание!
У равностороннего треугольника совпадают биссектрисы, медианы и высоты, то есть, эти отрезки являются также серединными перпендикулярами. Это значит, что центры описанной и вписанной окружности совпадают.
Радиус описанной окружности
Радиус вписанной окружности
, где (h) — высота треугольника.
Если дана сторона треугольника (a), то
h=a32
.
Поэтому
r=a36
.
Прямоугольный треугольник
Радиус описанной окружности
, где (c) — гипотенуза.
Радиус вписанной окружности
, где (p) — полупериметр.
Произвольный треугольник
Радиус описанной окружности
, где
α
— угол, противолежащий стороне (a);
.
Радиус вписанной окружности
, где (p) — полупериметр.


