Пример. Определить координаты центра
тяжести сечения, составленного из
прокатных профилей, как показано
на рис. 6, а. Сечение состоит из двутавровой
балки № 33,
швеллера № 27, двух уголков 90х56х6 и листа
сечением 12х180 мм.
Решение: 1 Разобьем
сечение на прокатные профили и
обозначим их 1,
2, 3, 4, 5.
-
Пользуясь табл.
2, 3 и 4 прил. I,
укажем центры
тяжести каждого
профиля и
обозначим их С1
C2,
C3,
С4
и С5. -
Выберем систему осей координатных. Ось
у совместим с
осью симметрии, а ось х
направим
перпендикулярно
оси у и
проведем через центр тяжести двутавровой
балки. -
Выпишем формулы для определения
координат центра
тяжести сечения:
хс=0,
так как ось у
совпадает с
осью симметрии;
![]()
Учитывая,
что А2=Аз,
а также, что у2
= уз, получим
![]()
Определим площади и координаты
центров тяжести отдельных
профилей проката, используя сечение и
табл.
2, 3 и 4 прил. I:
А1
=35,2 см2;
А2
= А3
=
8,54 см2;
А4
= 53,8см2;
А5=
1,2
·18
= 21,6
см2;
у1
= hдв//2
+ dшв
– z0(шв)
= 33/2 + 0,6 – 2,7=14,63 см
у2
=у3=
hдв//2
+ dшв
– bшв
+ z0(уг)
= 33/2 + 0,6 – 9,5 + 1,28=8,88 см
у4
= 0, так
как ось х проходит через центр тяжести
двутавра;
у5
= – (hдв//2
– δлиста//2)=
![]()
= – 17,1 см.
Подставим
полученные значения в формулу для
определения
ус:
ус
=
![]() см
см
укажем положение
центра тяжести сечения С (рис.6, а)
Проверка
решения. Проведем
ось х
по
нижней грани листа
(рис. 6, б).
Площади
профилей останутся теми же,
а координаты центров тяжести изменятся:
у1
=
δлиста
+ hдв
+ dшв
— z0(шв)
= 1.2 + 33 + 0,6 —
2,47 = 32,33 см;
у2
= δлиста
+ hдв
+ dшв
– bшв
— z0(уг)
= 1,2
+ 33 + 0,6 — 9,5+
1,28 = 26,58 см;
у2
= у3
= 26,58 см;
у4=
δлиста
+ hдв/2
=
1.2 + 33/2 = 1,2 +16,5 = 17,7 см;
у5=
δлиста
/ 2 =
1,2/2 = 0,6 см.
Определим
положение центра тяжести в новой системе
координат
ус=![]()
см
Р азность
азность
между координатами тяжести должна быть
равна расстоянию
между осями х в
первом и во втором решении:
20,3 —
2,33= 33/2 + 1,2
откуда 17,7 см
= 17,7 см.
Ответ:
ус
=
2,33 см, если ось х
проходит
через С4,
и ус
= 20,03
см, если ось х
проходит
по нижней грани

Рис.6
Пример.
Определить положение центра тяжести
(сечения,
состоящего из простых геометрических
фигур, (рис.
7,а).
Решение:
1. Разобъем
сечение на пять фигур: два
прямоугольника,
два треугольника и круг (рис. 7,б). Они
обозначены 1, 2,
3, 4, 5
2. Укажем
центры тяжести простых фигур С1,
С2,
Сз,
С4,
С5
в (рис.
7,
б).
3. Выберем
систему координат. Ось
х
проведем
через центр
тяжести С2
прямоуголь-ника, а ось у
совместим
с осью
симметрии сечения.
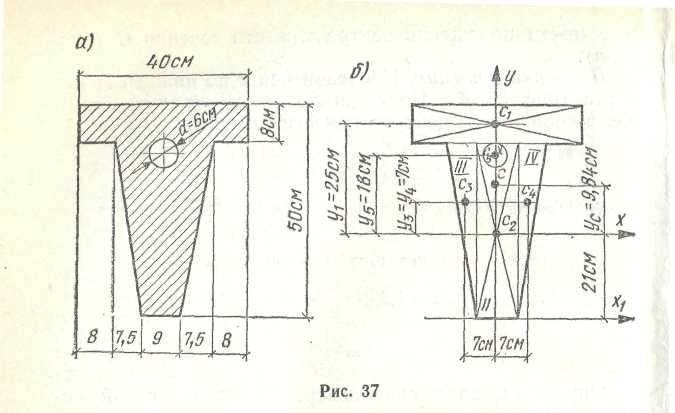
Рис.7
4.
Определим
координаты центра тяжести сечения.
Координаты
хс=0,
так
как ось у
совпадает
с осью симметрии.
Координату ус
определим
по формуле
![]()
Используя
прил. II,
определим площади фигур и координаты
центров тяжести:
А1
= 40 · 8 = 320 см2;
у1
=![]() см;
см;
А2=9
·42 = 378 см2,
у2=0
А3=А4=![]() см2;
см2;
у3=у4=2/3
· 42 – ½ · 42 = 28 – 21 = 7 см
А5=![]() см2;
см2;
у5=21
– 3= 18 см
Подставим
числовые значения в формулу для
определения ус:
ус=
![]()
см
Для
проверки решения ось Х1
можно
провести по нижней
грани сечения. В этом случае ус
= 30,84 см. Поскольку
30,84—21=9,84 см, то решение верно.
Ответ:
ус=9,84
см, если ось х
проходит
через С2.
Задание
для расчетно-графической работы 3. Задача
1. Определить
положение центра тяжести сечения,
состоящего из профилей проката,
по данным одного из вариантов, показанных
на рис. 8.
Задача
2. Определить положение центра тяжести
сечения, состоящего
из простых геометрических фигур, по
данным одного из вариантов,
показанных на рис. 9




Рис.8




Рис.9
Практическая работа № 4
а) Построение эпюр продольных сил,
нормальных напряжений для ступенчатого
бруса, а также определение перемещения
свободного конца бруса;
б) Расчет на прочность: проверочный
расчет, проектный расчет, определение
допускаемой нагрузки.
Пример. Построить
эпюры продольных сил и нормальных
напряжений
для бруса по рис. 10, а.
Решение. Делим брус по
длине на три участка (/, //, ///). Проведя
произвольное сечение 1 — 1 на участке
I, отбросим верхнюю часть бруса
и рас-

Рис.10
смотрим равновесие
нижней части (рис. 10, б),
на которую
действуют внешняя сила Р1
= 24кН и искомая
продольная сила N1.
Составляем
уравнение равновесия:
ΣΥ = — N1
+ P1
= 0, откуда N1
= P1==24
кН.
Продольная сила N1
на участке 1
постоянна и
является растягивающей (направлена
от рассматриваемого сечения). Проводим
сечение 2—
2 на
участке // и
рассматриваем равновесие нижней
отсеченной части (рис. 10, в),
на которую
действуют внешние силы Р1 и
Р2 и искомая продольная сила N11.
Составляем уравнение
равновесия:
ΣΥ = – N11
+ Р1
+ Р2
= 0,
откуда NII
= P1
+ P2
= 24 + 24 = 48 кН.
В сечениях
участка II
продольная
сила также растягивающая.
Наконец, проведя
сечение 3 — 3,
получаем, что
на нижнюю отсеченную часть
действуют три внешние силы Р1,
Р2
и Р3
и искомая
продольная сила NIII
(рис. 10, г).
Составляем
уравнение равновесия:
ΣΥ= -NIII
+ Р1
+ Р2
+ Р3
= 0, откуда NIII
=24 + 24+ 12 = 60 кН.
По полученным
величинам продольных сил строим их
эпюру (рис. 10, д). Положительные
ординаты эпюры откладываем вправо
от оси (базиса) эпюры. Нормальные
напряжения определяем по формуле σ
= N/
F:
на участке I
σ1
=
![]()
60·106
Н/м2=
60 МН/м2;
на
участке II
σII
=
![]()
120-106
Н/м2=
120 MH/м2
на участке III
σIII
=![]()
150 · 106
Н/м2=
150 МН/м2.
По
полученным данным строим эпюру нормальных
напряжений (рис. 10, е).
Определить перемещение свободного
конца бруса можно используя закон Гука:
![]()
Задание для
расчетно-графической работы № 4. Построить
эпюры продольных
сил и нормальных напряжений для
ступенчатого бруса, определить перемещение
свободного конца бруса
по данным одного из вариантов, показанных
на рисунке 11. и таблицы
2.
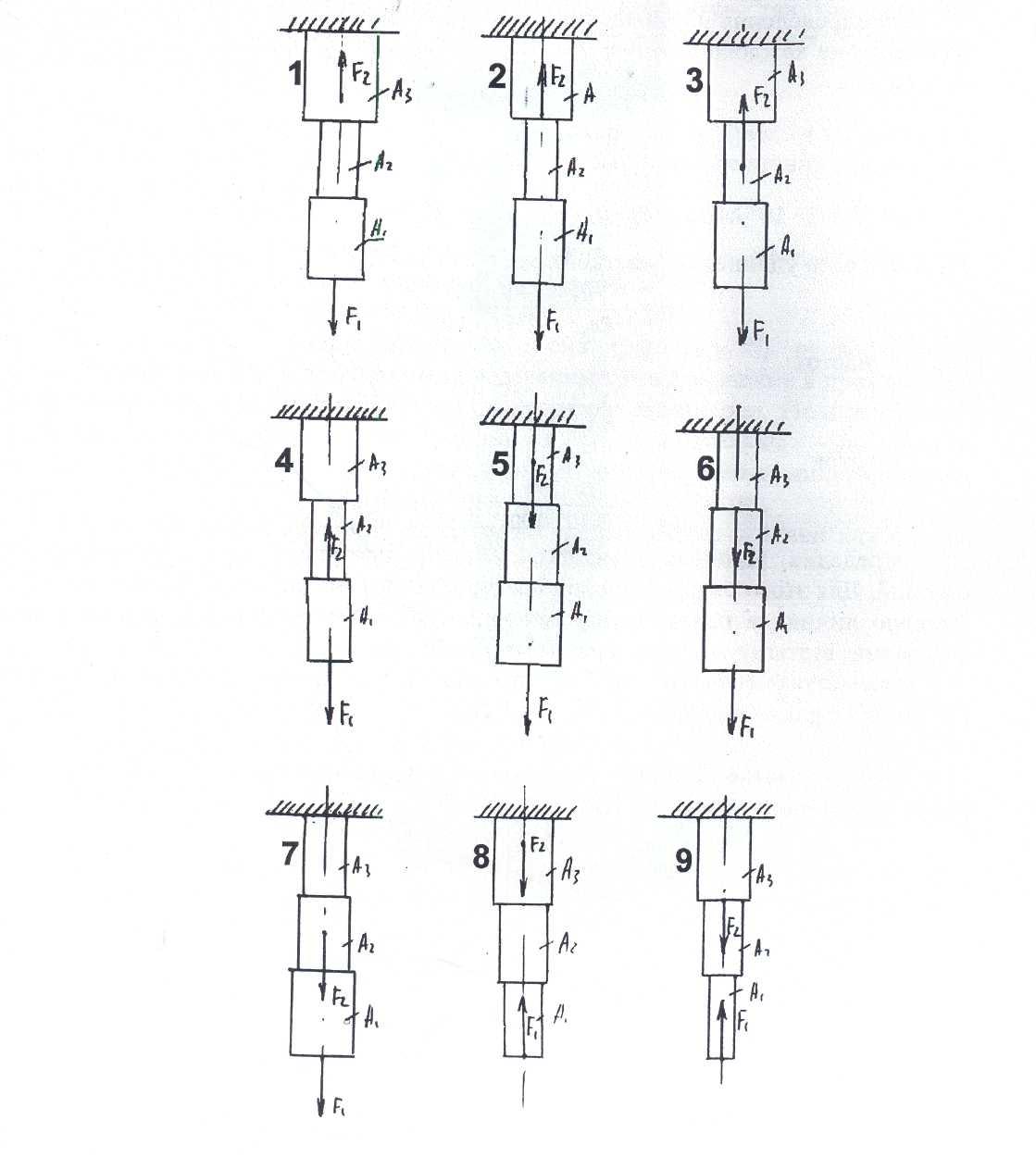


Рис.11
Таблица 2
|
№ п/п |
Вариант |
А1 см2 |
А2 см2 |
А3 см2 |
i F1 кН |
F2 кН |
№ пп |
Вариант |
A1 см2 |
А2 см2 |
А3 см2 |
F1 кН |
F2 кН |
|
1 |
1 |
8 |
6 |
14 |
18 |
20 |
1 |
1 |
7 |
5 |
13 |
16 |
18 |
|
2 |
2 |
6 |
4 |
12 |
20 |
12 |
2 |
2 |
8 |
6 |
16 |
18 |
14 |
|
3 3 3 |
3 |
4 |
2 |
8 |
40 |
50 |
3 |
3 |
6 |
4 |
10 |
30 |
40 |
|
4 |
4 |
6 |
4 |
12 |
16 |
24 |
4 |
4 |
8 |
6 |
10 |
24 |
16 |
|
5 |
5 |
16 |
12 |
8 |
28 |
38 |
5 |
5 |
15 |
10 |
6 |
30 |
20 |
|
6 |
6 |
12 |
10 |
6 |
30 |
40 |
6 |
6 |
16 |
14 |
12 |
40 |
30 |
|
7 |
7 |
8 |
6 |
4 |
30 |
20 |
7 |
7 |
10 |
8 |
6 |
20 |
30 |
|
8 |
8 |
2 |
4 |
6 |
25 |
40 |
8 |
8 |
4 |
6 |
8 |
30 |
35 |
|
9 |
9 |
2,5 |
6 |
8 |
20 |
18 |
9 |
9 |
3 |
7 |
10 |
25 |
30 |
|
10 |
10 |
4,5 |
6 |
8 |
18 |
24 |
10 |
10 |
5 |
8 |
12 |
25 |
30 |
|
11 |
11 |
2 |
16 |
14 |
14 |
32 |
11 |
11 |
4 |
12 |
10 |
16 |
40 |
|
12 |
12 |
4,2 |
6,4 |
5 |
26 |
18 |
12 |
12 |
4 |
6 |
4,5 |
20 |
25 |
|
13 |
13 |
3 |
5 |
4 |
30 |
20 |
13 |
13 |
4 |
6 |
5 |
25 |
15 |
|
14 |
14 |
4 |
12 |
8 |
35 |
40 |
14 |
14 |
6 |
16 |
11 |
40 |
35 |
|
15 |
15 |
16 |
6 |
12 |
25 |
15 |
15 |
15 |
14 |
5 |
10 |
15 |
25 |
|
16 |
16 |
14 |
8 |
12 |
20 |
12 |
16 |
16 |
12 |
10 |
11 |
18 |
16 |
|
17 |
17 |
12 |
6 |
8 |
30 |
25 |
17 |
17 |
14 |
8 |
12 |
25 |
30 |
|
18 |
18 |
14 |
6 |
10 |
25 |
30 |
18 |
18 |
16 |
6 |
12 |
20 |
40 |
|
19 |
19 |
12 |
4 |
6 |
30 |
40 |
19 |
19 |
14 |
5 |
8 |
35 |
20 |
|
20 |
20 |
10 |
6 |
8 ‘ |
24 |
36 |
20 |
20 |
12 |
4 |
6 |
34 |
22 |
|
21 |
21 |
18 |
14 |
16 |
40 |
50 |
21 |
21 |
20 |
16 |
18 |
35 |
30 |
|
22 |
22 |
12 |
10 |
8 |
40 |
60 |
22 |
22 |
14 |
12 |
10 |
60 |
40 |
|
23 |
23 |
10 |
6 |
4 |
35 |
55 |
23 |
23 |
12 |
8 |
6 |
20 |
40 |
|
24 |
24 |
12 |
6 |
3 |
25 |
45 |
24 |
24 |
18 |
12 |
10 |
30 |
25 |
|
25 |
25 |
3 |
5 |
9 |
20 |
5 |
25 |
25 |
4 |
6 |
12 |
18 |
40 |
|
26 |
26 |
6 |
5 |
6 |
10 |
15 |
26 |
26 |
12 |
6 |
12 |
12 |
20 |
|
27 |
27 |
7 |
9 |
6 |
12 |
14 |
27 |
27 |
10 |
14 |
8 |
20 |
8 |
|
28 |
28 |
4 |
6 |
8 |
10 |
16 |
28 |
28 |
6 |
8 |
12 |
12 |
25 |
|
29 |
29 |
6 |
8 |
5 |
7 |
9 |
29 |
29 |
10 |
18 |
8 |
14 |
18 |
|
30 |
30 |
8 |
10 |
6 |
4 |
8 |
30 |
30 |
12 |
14 |
8 |
10 |
12 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В этой статье посмотрим, как определяются координаты центра тяжести сложной фигуры — состоящей из простых. В задачах по сопромату часто приходится находить положение центра тяжести составных сечений, для дальнейшего вычисления моментов инерции и т. д.
Также часто, при изучении теоретической механики, студентам предлагается решить подобную задачу, и найти центр тяжести какой-нибудь фигуры.
Условие задачи
Предлагаю рассмотреть следующую фигуру:

В сопромате принято заштриховывать сечения тонкими линиями, вот так:

В своих же уроках я буду использовать заливку. Так, штриховка не будет мешать наносить обозначения.
Разбивка сложной фигуры на простые
Как видишь, сечение состоит из прямоугольника, прямоугольного треугольника, четверти круга, а также имеет круглый вырез:

Отметим центры тяжести (С1, С2, С3, С4) каждой отдельной фигуры, с учётом справочной информации.
Открой эту страничку, и пока не закрывай, она нам ещё понадобится!

Покажем вспомогательные оси (x0, y0) для всего сечения, которые будем использовать для нахождения положения центра тяжести (C):

Как определить положение центра тяжести?
Чтобы определить координату центра тяжести сечения, например, вертикальное расстояние от оси x0 до центра тяжести сечения (yc):

Нужно статический момент сечения относительно этой вспомогательной оси (x0) разделить на площадь всего сечения (A):

Площадь всего сечения (A) найти просто – это алгебраическая сумма площадей всех фигур:

Статический момент сечения, относительно вспомогательной оси будет равен алгебраической сумме статических моментов каждой фигуры (с учётом знака):

где Ai – площадь отдельной фигуры;
yi – расстояние от центра тяжести отдельной фигуры до вспомогательной оси (x0).
Координата центра тяжести (xc), находится аналогично:

Определение площади сечения
Для начала предлагаю сделать самое простое, используя формулы, указанные на этой странице, найти площадь всего сечения (A):


Как видишь, круглый вырез, нужно учесть с «минусом», что очевидно.
Определение расстояний от вспомогательных осей до центров тяжести отдельных фигур
Найдём расстояния от вспомогательных осей (x0, y0) до центров тяжести отдельных фигур, опять же, используя нашу шпаргалку:

Определение статических моментов
Определяем статические моменты сечения относительно вспомогательных осей (x0, y0):


Важно! Статические моменты могут быть и отрицательными.
Определение координат центра тяжести
И, наконец, определяем положение центра тяжести всего сечения (C):

Покажем центр тяжести всего сечения (C):

Если остались какие-то вопросы по данному уроку, можешь смело задавать их в комментариях. Также, другие уроки, на сайте – ssopromat.ru, по определению геометрических характеристик, можешь найти здесь.

Пример решения задачи по расчету координат положения центра тяжести (центра масс) сложного сечения методом разбиения на простые фигуры.
Задача
Определить координаты центра тяжести сложного сечения.

Другие примеры решений >
Помощь с решением задач >
Пример решения
Подробный пример определения координат центра тяжести сложного плоского сечения в нашем коротком видео:
Другие видео
Разбиваем заданную фигуру на простые, для которых легко можно рассчитать площадь и положение центра тяжести:
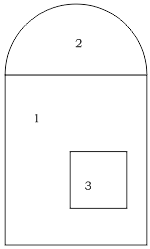
В данном случае это:
1 — прямоугольник;
2 — полукруг;
3 — квадрат.
Площадь всей фигуры составляет:
A=A1+A2-A3
Задаем систему координат, и показываем центры тяжести каждой из простых фигур:
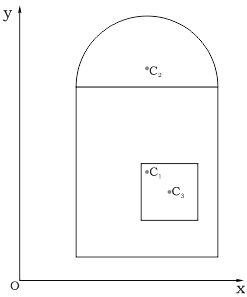
Определив расстояние от осей x и y до соответствующих центров тяжести элементарных фигур:
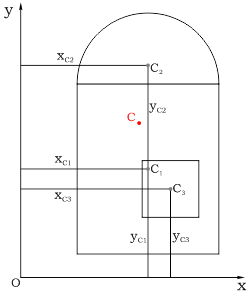
Рассчитываем положение центра тяжести C всей фигуры сложного сечения:
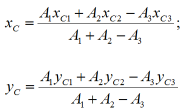
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату





Центр изгиба
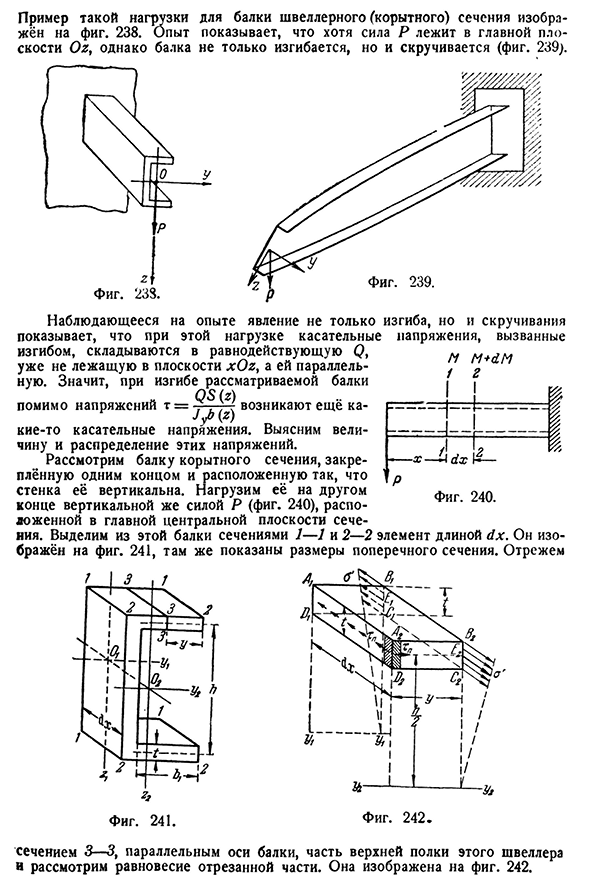
- Центр изгиба. При изучении случая плоского изгиба балок мы предположили, что все внешние силы находятся в одной из главных инерционных плоскостей балок. Возьмем балку с симметричным поперечным сечением (например, прямоугольник) и посмотрим, что произойдет, если приложить усилие к плоскости, параллельной основной плоскости симметрии, и приложить нагрузку(рис. 237). Для этой балки усилие Р прикладывается к концу стержня OiO в плоскости торца балки и закрепляется на нем. При
приложении к центру тяжести двух равных и прямо противоположных сил р О конца, мы видим, что балка изгибается в плоскости главной оси Оз силой Р, и чтобы избежать скручивания сразу стирается на чертеже, а момент Р*О^О и сила вытянутой прямоугольноподобной балки поперечного сопротивления недостаточны, необходимо приложить силу Р, чтобы опыт показал, что на практике этого не происходит при размещении балки симметричного поперечного сопротивления на плоскости симметричного поперечного сечения.
Загрузка луча с фокусом на плоскость главной оси, которая не является осью симметрии,
Людмила Фирмаль
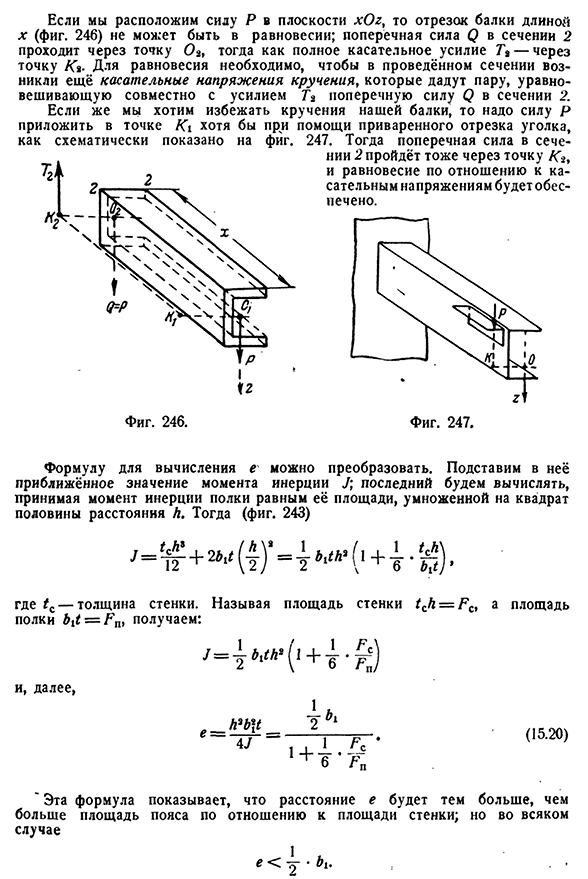
несколько отличается. Центр Сгиба 319 Пример такой нагрузки для канала (желоба) секционной балки показан на рисунке. 238 опыт показывает, что сила Р находится в главной плоскости Od, но балка не только согнута, но и скручена(рис. 239). М м+ДМ Фигура. 240. п dx2 Явление изгиба, а также скручивания, наблюдаемое в эксперименте, — это тангенциальное напряжение, вызванное изгибом под этой нагрузкой, но изгиб балки, которая считается уже не лежащей на плоскости движения, не то же самое, что изгиб балки посредством. «<?5(Д) Помимо напряжения Т=7 -х, есть несколько
касательных напряжений. Рассмотрим величину и распределение этих напряжений. Рассмотрим балку желоба, закрепленную на одном конце и расположенную так, чтобы ее стенки были вертикальными. Нагрузка на другой конец с той же силой Р(рис. 240), расположенный на главной центральной грани секции. Выберите из этого пучка отрезок 1-1 и 2-2 длины элемента dx. Это показано на рисунке. Размеры поперечного сечения 241 показаны в том же месте. Резать Фигура. 241. Участок 3-3, параллельный оси балки, является частью
- верхней полки этого канала и учитывает равновесие срезаемой части. Это показано на рисунке. 242.320 касательное напряжение балки и главное напряжение [глава XV В терминах aibtcidi и A2B2C2D2 этого элемента нормальная сила на площади aibicidi больше суммы эффективных площадей aibicidi; поэтому для выбранных элементов AIBICIDI напряжение TP больше суммы нормальных сил. dlala2d2 Сумма напряжений та должна уравновешивать разницу между нормальными силами. РНТ ДХ = Н2 — Через секцию El lBlClDl — ’ показано среднее напряжение на конце полки, соответствующее среднему напряжению в точке (рис. 242). Затем В точке 2 Значение нормального напряжения, действующего на 2b2c242i, т. е.
напряжение » через Е2 Или Здесь значение напряжения a равно h ’~J ’ 2 ″ И так оно и есть., .. М+ДМ ч< = —— — ^ Тайлер. Дж Точно так же М ч, 7 ′ 2 * Один. Привет 1 1 1 Т1^ ’ второй И так оно и есть.. . AG AG dM h Тя ФД х=п я — — — ж — — — — 2ты, (15.18) Согласно характеристикам пары тангенциальных напряжений, если TP присутствует в участке a lA2D2Dl, то такая же величина в точке ребра A2B2C2D2 участка A и обратный знак 242 тангенциального напряжения). (Следует помнить, что масштаб рисунка искажен: отрезок DtD2=^dx очень мал, а отрезок A2B2=y-конечная величина. Таким образом, участок 2-2 точек верхней полки действует на тангенциальное напряжение TL, направленное горизонтально, которое изменяется по закону прямой по y(фиг. Двести сорок три): Qх т н~~2ДЖ г’ Точно так же показано, что то же самое напряжение действует в противоположном направлении, в точке нижней полки. Тангенциальное напряжение
TP, действующее на каждую полку, дает суммарную результирующую силу, которую
Людмила Фирмаль
можно рассчитать следующим образом. Сила, действующая на затененную область t dy (рис. 243): dTt-rnt dy=Q j y, t dy -,,§ 961 центр кривизны 321 Чтобы суммировать все такие силы、: Отчет Эти усилия проиллюстрированы на рисунке. В дополнение к касательному напряжению 244, вертикальное касательное напряжение действует вдоль поперечного сечения: СМО(£) Дж * б(з) * ) Все выводы настоящего пункта можно считать достаточно точными при условии, что толщина станка и полки составляет менее 1: 20 от соответствующего второго размера. Например, при определении положения силы та необходимо также учитывать вертикальные тангенциальные силы полок. Условный график распределения этих напряжений показан на рисунке. 245. Соответствующая сила считается равной боковой силе Q с достаточной точностью и добавляется к результирующей силе GA, приложенной к центру
тяжести стенки c a(рис. 244); поэтому вертикальное тангенциальное давление полки игнорируется(по сравнению с тангенциальным давлением стенки). Фигура. 244. Полная система тангенциальных сил, состоящая из силы Ha и пары сил 7, может быть заменена одной силой Ha, приложенной в точке k b на расстоянии e от центра тяжести стенки CA. 7 пары плеч измеряются расстоянием h(рис. 243 и 244). Чтобы определить расстояние e, обнулите сумму трех силовых моментов в точках/b_Qт * б * t_h Ha4JQ » 4 с * (15.19) Таким образом, при изгибе канала, помимо центра тяжести сечения, помимо обычного напряжения t, существует еще тангенциальное напряжение TP. Суммируя все эти напряжения, центр тяжести сечения Ot и точка/C2, так называемый центр изгиба (иногда
называемый центром жесткости или центром среза), 322-тангенциальное направление валков и основное напряжение[гл. XV Когда сила P помещается на плоскость xozy, отрезок балки длиной x(рис. 246) она не может быть уравновешена; поперечная сила Q секции 2 проходит через точку O2, в то время как полная тангенциальная сила G2 проходит через точку / C2. Для равновесия необходимо, чтобы в проводящей части все еще существовало тангенциальное напряжение кручения, которое уравновешивается вместе с поперечной силой Q сечения T2. Если мы хотим избежать скручивания нашей балки, нам нужно приложить силу p в точке Ki с помощью, по крайней мере, углового сварного сегмента, как показано на рисунке 247.- Фигура. 246. NII2 также проходит через
точку 7Q, обеспечивая равновесие по касательному напряжению. Фигура. 247. Можно преобразовать формулу для вычисления E. подставим в нее приближение момента инерции J; последний принимает момент инерции полки равным ее площади, умноженной на половину расстояния L в квадрате двести сорок три.) Где же толщина стен? Когда вы называете стеной зона ТЖ-ФЗ и шельфе бит=ПВ: В дальнейшем, 4 с — (15.20 )) Эта формула показывает, что чем больше площадь пояса, тем большее расстояние е связано с площадью стенки. 1 на тему » Доброе утро, Америка.»§ 9 7] выбор поперечного сечения балки при допустимой нагрузке 323 В секции двутаврового типа при изгибе под действием боковых сил в поясе возникает горизонтальное тангенциальное напряжение (рис. 248). Однако из-за симметрии секций эти напряжения взаимно
уравновешиваются внутри каждой полки, и центр изгиба совпадает с центром тяжести секции. Совпадение центра тяжести и Центра изгиба сечения происходит, когда сечение имеет две оси симметрии или центр антисимметрии (z-образный). Кроме того, из формул (15.18) и (15.19) следует, что кручение балки в нагрузке в основной плоскости, которая не находится в плоскости симметрии, связано с наличием в поперечном сечении поперечных сил. Однако в тонкостенных стержнях асимметричного профиля(см. главу XXX) скручивание балок может происходить при отсутствии боковых сил. Практическая значимость этого явления достаточно велика. Таким образом, положение рабочей поверхности внешних сил вне центра изгиба может вызвать значительные деформации в этих балках. Однако следует помнить, что для возникновения этих
дополнительных напряжений должна иметь место торсионная деформация (довольно значительная деформация), так как более точные исследования показывают, что в некоторых случаях кручение балки таких профилей сопровождается появлением дополнительных нормальных напряжений и иногда достигает значительных величин. Таким образом, наличие соединения, соединяющего балку с соседними конструктивными элементами и предотвращающего кручение, даже если плоскость внешних сил не совпадает с плоскостью центра изгиба, необходимо учитывать эти дополнительные факторы. П р и М Е Р69. Канал № 40 изогнут концентрацией, расположенной
в плоскости, параллельной стенке. Определите расстояние от оси стенки этой плоскости, если необходимо исключить кручение балки. Рабочая поверхность усилия должна проходить через линию Центра изгиба. Расстояние этой линии от оси стенки определяется по формуле (15.20) ч * б * т е = ~эй — Наш профиль (см. таблицу в приложении IX) — b-d= 1 1 5 — 8 = == 107 ммч=400-13. 5=386,5 мм; J=15220смH38. 65а• 10,72 • 1,35 4 • 15220 То есть плоскость нагрузки должна проходить вне сечения Hq на расстоянии e=3,8 см от оси стенки.
Смотрите также:
- Примеры решения задач по сопромату

