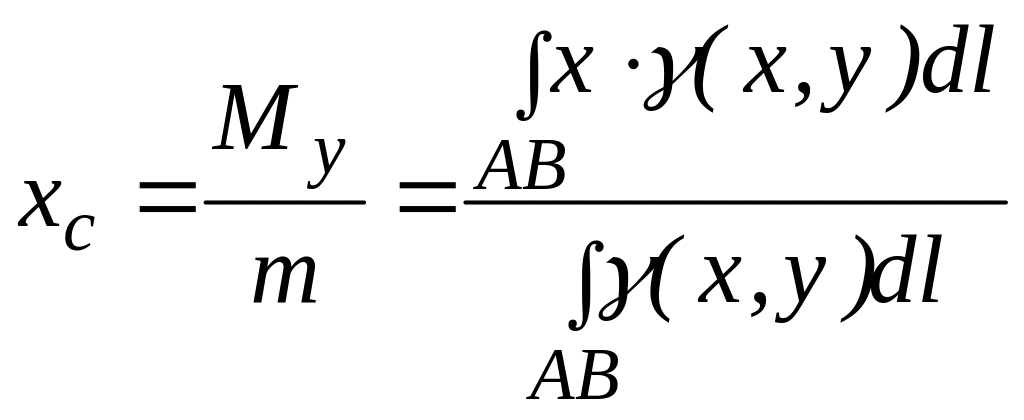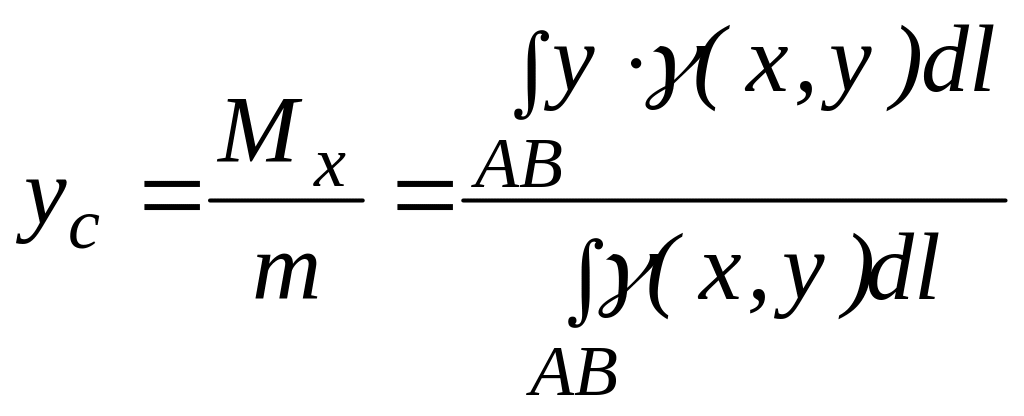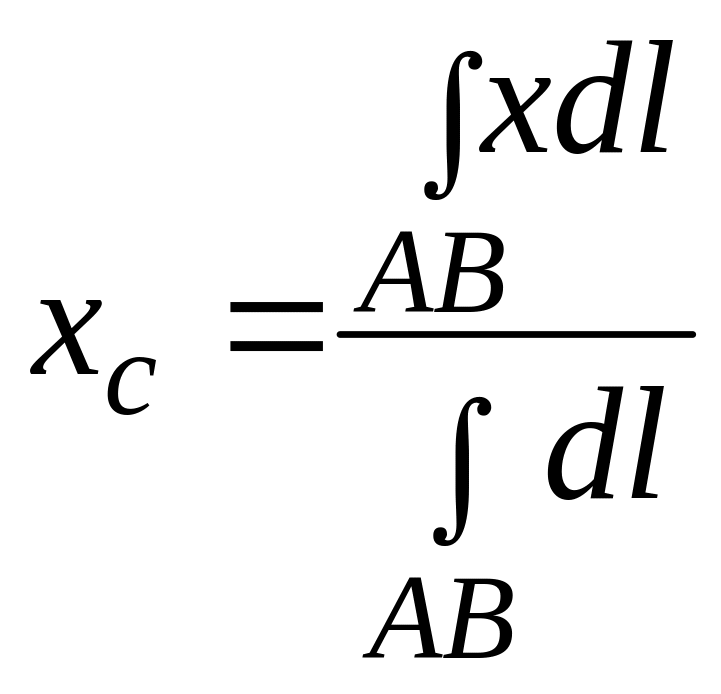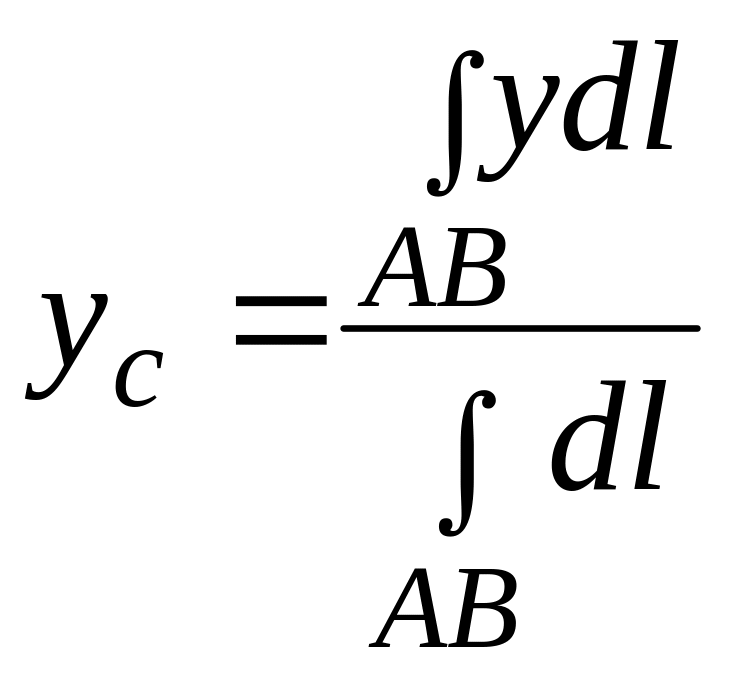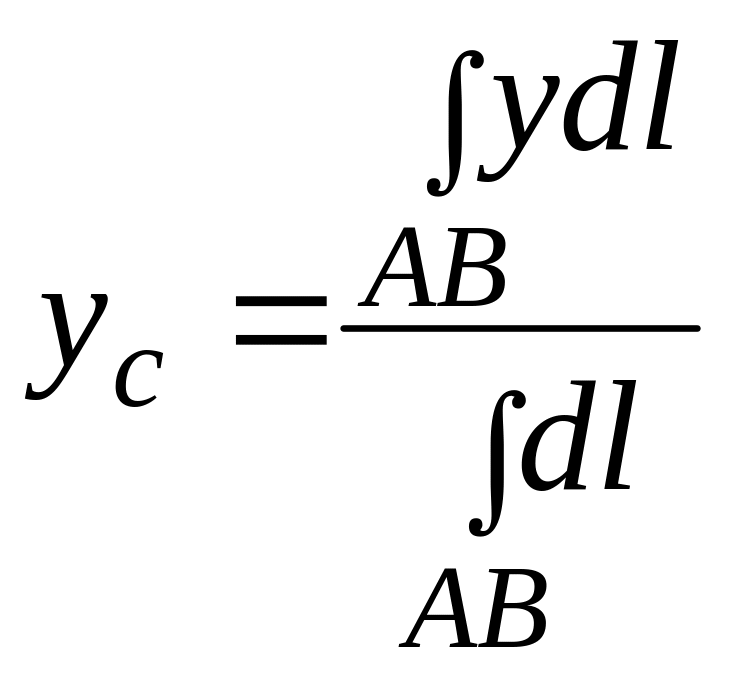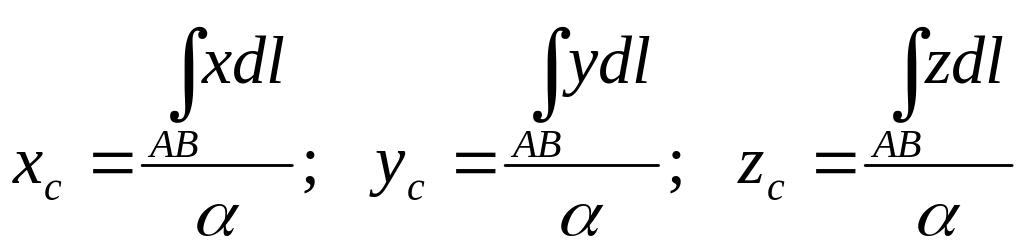Как найти центр тяжести циклоиды - Сайт, где вы сможете решить свои вопросы

Предварительно изучите по учебнику Г. М. Фихтен-гольца главу XII, п° 206, 207. При решении задач рекомендуется помнить, что если кривая расположена симметрично относительно некоторой прямой, то центр тяжести кривой лежит на этой прямой.

592. Найти центр тяжести дуги цепной линии:

содержащейся между точками, для которых х = — а х = а.

Решение. Так как рассматриваемая дуга расположена симметрично относительно оси Oyt то центр тяжести дуги лежит на оси Oy и, следовательно,Найдем ординату, пользуясь формулой

Так как

и, следовательно,

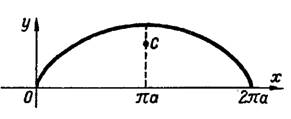
593. Найти центр тяжести одной арки циклоиды:

Решение. Так как арка циклоиды расположена симметрично относительно прямой х = па, то центр тяжести дуги циклоиды лежит на этой прямой и, следовательно,

Ордината центра тяжести будет: ? ( ~ е [а I а

Ц – – Ie _L_£

1 a(e*~-)Ja 2 f

I = Jt а.

Найдем ординату центра тяжести по формуле:

Длина дуги одной арки циклоиды равна 8а (см. задачу

Найдем ординату центра тяжести:

594. Найти центр тяжести дуги кривой»

содержащейся между точками, для которых Решение. Найдем

(см. задачу 491).

Найдем абсциссу центра тяжести:

3 + 2 In 2

Найдем ординату центра тяжести:

595. Найти центр тяжести однородной треугольной пластинки.

3 (3 + 2 In 2)

Решение. Разбиваем данную пластинку прямыми, параллельными одной из сторон, на бесконечно тонкие полоски. Центр тяжести каждой полоски находится в ее середине и лежит, таким образом, на медиане, а следовательно, и центр тяжести всей треугольной пластинки лежит на этой медиане. Так как это рассуждение применимо к любой стороне, то центр тяжести треугольника находится в точке пересечения его медиан.

Тот же результат получаем вычислением. Площадь полоски, отстоящей на расстояние х от данной стороны

Ь, равна dS = —(h—х) А я, где А —высота, опущенная h

на эту сторону, а Дл; — ширина полоски, следовательно, расстояние центра тяжести от этой стороны равно: н н

I*= — [ xdS — Г— (h—х) xdx =

SJ bh J h 9

A1 2 3 J I о 3 Таким образом, центр тяжести треугольника находится на расстоянии, равном — высоты от соответствующей

стороны, т. е. в точке пересечения его медиан, ибо это— е&инственная точка, обладающая таким свойством.

596. Найти центр тяжести площади, ограниченной осью Ox и одной полуволной синусоиды

Решение. Так как площадь одной полуволны синусоиды расположена симметрично относительно прямой

, то центр тяжести лежит на этой прямой и, сле

довательно, . Ордината центра тяжести находится

по формуле

Так как

то

Итак, центр тяжести данной площади находится в точке

597. Найти координаты центра тяжести площади, ограниченной параболами

Решение. Данные параболы, пересекающиеся в точках О (0, 0) и А (а; а), ограничивают площадь, расположенную симметрично относительно биссектрисы Следовательно, центр тяжести данной площади лежит на биссектрисе, а отсюда

Так как площадь ограничена двумя кривыми

и, то абсцисса центра тяжести площади на-

ходится по формуле:

найдем:

точке

598. Найти центр тяжести площади, ограниченной осью абсцисс и одной аркой циклоиды:

Таким образом, центр тяжести площади находится в

Решение. Данная площадь расположена симметрично относительно прямой, следовательно, центр тяжести ее находится на этой прямой и отсюда

Найдем ц по формуле. Площадь S данной

фигуры была вычислена (см.Задачу 467):Сле

довательно,

Центр тяжести данной площади находится в точке

599. Пользуясь теоремой Гюльдена, вычислить поверхность тора, образованного вращением круга радиуса а вокруг оси, расположенной в его плоскости и отстоящей от центра его на расстояние

Решение. Так как длина данной окружности равна , а длинаокружности, описанной центром тяжести ее, равна, то поверхность тора по первой теореме Гюльдена равна:

600. Пользуясь теоремой Гюльдена, вычислить объем и боковую поверхность прямого кругового конуса.

Решение. Боковая поверхность конуса с высотой, образующейИ радиусом основанияПолучается при вращении гипотенузы длинойВокруг катета длиной. Центр тяжести гипотенузы находится на ее середине и

удален от оси вращения на. Поэтому по первой теореме Гюльдена боковая поверхность равна:

Площадь треугольника равна, центр тяжести его, находясь на пересечении медиан, отстоит от катета А на расстояние, равноеВысоты, опущенной на этот катет, т. е., следовательно, по второй теореме Гюльдена объем конуса равен:

601. На цилиндре, имеющем 6 см в диаметре, кругом вдоль поверхности вырезан канал, имеющий поперечным сечением равносторонний треугольник со стороной в 0,5 сж. Вычислить объем срезанного материала.

Решение. Искомый объем есть объем тела, получаемого при вращении равностороннего треугольника со стороной в 0,5 см вокруг оси, параллельной основанию и удаленной от него на 3 ел, причем вершина лежит между основанием и осью (рис. 26).

Высота треугольника равна

площадь его равна

Расстояние центра тяжести от оси ОС = OA — AC =

(AC равно

высоты). По второй теореме Гюльдена имеем:

602. Длина одной арки циклоиды

РавнаА поверхность, образуемая вращением ее вокруг оси Oxt равна. Вычислить поверхность, образуемую вращением той же арки циклоиды вокруг касательной в верхней ее точке.

Решение. Пусть— расстояние центра тяжести от оси Oxi тогда по первой теореме Гюльдена:

, откуда

Наибольшая ордината кривой соответствуетИ рав

на 2а, причем касательная в этой точке параллельна оси Ох следовательно, расстояние центра тяжести от этой

касательной равно

Таким образом, искомая поверхность, образуемая’ вращением той же арки циклоиды вокруг касательной в верхней ее точке равна:

603. Найти центр тяжести дуги, составляющей четверть окружности радиусаРасположенной в первом квадранте.

604. Найти центр тяжести расположенной в первом квандранте дуги гипоциклоиды x = acosst, у = a sin31.

605. Найти центр тяжести половины площади эллипса, опирающейся на большую ось.

606. Найти центр тяжести площади, заключенной

– L – L. L между параболой х2 – J – у2 = а 2 и осями координат.

607. Найти центр тяжести плоской фигуры, ограниченной кривой at/2 = Jc3 и прямой х = а {а > 0).

608. Найти центр тяжести площади, ограниченной кривыми

у = ах3, х = а, у = 0.

609. Найти центр тяжести площади, ограниченной эллипсом jc2 -)- 4у2 = 4 и окружностью х2– у2 = 4 и расположенной в первом квадранте.

610. Найти центр тяжести фигуры, ограниченной замкнутой кривой у2 = ах3 — х*.

< Предыдущая		Следующая >

Источник

Координаты центра тяжести
Центром тяжести совокупности материальных точек называется центр параллельных сил тяжести, приложенных в этих точках.
Для материальной дуги плоской кривой прямоугольные координаты центра тяжести С определяются формулами

$x_{C}=frac{m_{y}}{m}=frac{int_{(A)}^{(B)}delta xdl}{int_{(A)}^{(B)}delta dl},: y_{C}=frac{m_{x}}{m}=frac{int_{(A)}^{(B)}delta ydl}{int_{(A)}^{(B)}delta dl}; ; ; (1)$

где — масса дуги ; $m_{x}$ и $m_{y}$ — статические моменты этой дуги относительно осей и ; delta (M) — линейная плотность распределения массы в точке M(x,y) дуги; — дифференциал дуги; (A) и (B) обозначают значения выбранной переменной интегрирования в точках и .

Если материальная дуга является однородной, то формулы (1) упрощаются: постоянная delta выносится за знаки интегралов и сокращается.

Рис.1

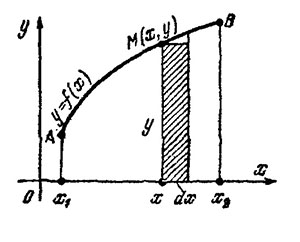
Для материальной однородной криволинейной трапеции, прилежащей к оси (см. рис. 1),

$x_{C}=frac{int_{a}^{b}xydx}{int_{a}^{b}ydx};; y_{C}=frac{int_{a}^{b}y^{2}dx}{2int_{a}^{b}ydx}.; ; ; (2)$

Центр тяжести однородной материальной линии или фигуры, имеющей ось симметрии, лежит на этой оси.

Пример 1. Найти центр тяжести четверти окружности $x^{2}+y^{2}=a^{2}$ , расположенной в первом квадранте, если в каждой ее точке линейная плотность пропорциональна произведению координат точки.
Решение. Из уравнения окружности найдем затем :

$2x+2yy'=0;; y'=-frac{x}{y};$

$dl=sqrt{1+(y')^{2}}dx=sqrt{1+frac{x^{2}}{y^{2}}}dx=sqrt{frac{y^{2}+x^{2}}{y^{2}}}dx=frac{a}{y}dx.$

Далее вычислим интегралы, содержащиеся в формулах (1), полагая, согласно условию, delta =kxy :

$int_{(A)}^{(B)}delta xdl=int_{0}^{a}kxycdot xcdot frac{a}{y}dx=kaint_{0}^{a}x^{2}dx=frac{ka}{3}x^{3} left.begin{matrix} \ \ end{matrix}right| _{0}^{a}=frac{ka^{4}}{3},$

$int_{(A)}^{(B)}delta ydl=kaint_{0}^{a}xydx=kaint_{0}^{a}xsqrt{a^{2}-x^{2}}dx=frac{ka}{2}int_{a}^{0}(a^{2}-x^{2})^{frac{1}{2}}d(a^{2}-x^{2})=frac{ka}{3}(a^{2}-x^{2})^{frac{3}{2}} left.begin{matrix} \ \ end{matrix}right| _{a}^{0}=frac{ka^{4}}{3},$

$int_{(A)}^{(B)}delta dl=kaint_{0}^{a}xdx=frac{ka}{2}x^{2} left.begin{matrix} \ \ end{matrix}right| _{0}^{a}=frac{ka^{3}}{2}.$

Подставляя значения интегралов в формулы (1), получим

$x_{C}=y_{C}=frac{2}{3}a.$

Очевидно, найденная точка не лежит на данной дуге, а расположена ниже ее.

Пример 2. Найти центр тяжести однородной арки циклоиды (рис.2)

x=a(t-sin t),; y=a(1-cos t).

Решение. Данная однородная дуга симметрична относительно прямой x=pi a . Поэтому центр тяжести дуги лежит на этой прямой, т. е. $x_{C}=pi a$ . Для определения $y_{C}$ найдем дифференциал дуги циклоиды

$dl=sqrt{x^{2}+y^{2}}dt=sqrt{a^{2}(1-cos t)^{2}+a^{2}sin^{2}t}dt=2asin frac{t}{2}dt$

Рис.2

и вычислим интегралы, содержащиеся во второй из формул (1):

$I_{1}=int_{(A)}^{(B)}delta ydl=2delta a^{2}int_{0}^{2pi }(1-cos t)sin frac{t}{2}dt=$

$=2delta a^{2}left ( int sin frac{t}{2}dt-int cos tsin frac{t}{2}dt right ) left.begin{matrix} \ \ end{matrix}right| _{0}^{2pi }=2delta a^{2}left { 2int sin frac{t}{2}dfrac{t}{2}-frac{1}{2}int left [ sin frac{3}{2}t+sin left ( -frac{t}{2} right ) right ]dt right } left.begin{matrix} \ \ end{matrix}right| _{0}^{2pi }=$

$=2delta a^{2}(-3cos frac{t}{2}+frac{1}{3}cos frac{3}{2}t) left.begin{matrix} \ \ end{matrix}right| _{0}^{2pi }=frac{32}{3}delta a^{2}.$

$I_{2}=int_{(A)}^{(B)}delta dl=2delta aint_{0}^{2pi }sin frac{t}{2}dt=-4delta acos frac{t}{2} left.begin{matrix} \ \ end{matrix}right| _{0}^{2pi }=8delta a.$

По формуле (1), $y_{C}=frac{4}{3}a.$

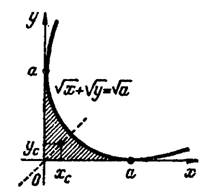
Пример 3. Найти центр тяжести однородной фигуры (пластинки), ограниченной параболой sqrt{x}+sqrt{y}=sqrt{a} и осями координат.

Рис.3

Решение. Данная однородная фигура симметрична относительно биссектрисы первого координатного угла (рис. 3), поэтому $x_{C}=y_{C}$ .
Вычислим интегралы, содержащиеся в первой из формул (2):

$I_{1}=int_{a}^{b}xydx=int_{0}^{a}x(a^{frac{1}{2}}-x^{frac{1}{2}})^{2}dx=int_{0}^{a}(ax-2a^{frac{1}{2}}x^{frac{3}{2}}+x^{2})dx=left ( frac{1}{2}ax^{2}-frac{4}{5}a^{frac{1}{2}}x^{frac{5}{2}}+frac{1}{3}x^{3} right ) left.begin{matrix} \ \ end{matrix}right| _{0}^{a}=frac{a^{3}}{30}.$

$I_{2}=int_{a}^{b}ydx=int_{0}^{a}x(a^{frac{1}{2}}-x^{frac{1}{2}})^{2}dx=int_{0}^{a}(a-2a^{frac{1}{2}}x^{frac{1}{2}}+x)dx=frac{a^{2}}{6}.$

Следовательно, $x_{C}=y_{C}=frac{I_{1}}{I_{2}}=frac{a}{5}.$

Источник

Пусть
на плоскости хоу
задана кривая АВ,
в каждой
точке которой определена непрерывная
функция f(х,
у) двух
независимых переменных х
и у.
Рассмотрим
криволинейный интеграл I
рода (по длине дуги) от этой функции по
кривой АВ.
Он обозначается

,
кривая АВ
называется кривой интегрирования, А
– начальной,
а В – конечной
точками интегрирования. Из определения
криволинейного интеграла первого рода
следует, что он не зависит от направления
кривой АВ,
т.е.:

Если АВ – пространственная кривая, то
криволинейным интегралом первого рода,
распространенным на эту кривую называется
интеграл вида:

где
функция f(х,
у, z)
– функция
трех независимых переменных, которая
определена и непрерывна в каждой точке
кривой АВ.

Масса
m
материальной кривой, имеющей плотность
(х,
у, z)
равна криволинейному интегралу первого
рода от функции (х,
у, z)
по пространственной кривой АВ,
т.е.:

.
(3.16)

В
этом состоит физический (механический)
смысл криволинейного интеграла первого
рода.

Если
масса распределена непрерывно вдоль
дуги плоской кривой АВ
с плотностью функции 
= (х,
у) в каждой
точке кривой, то статические моменты
М_х
и М_у
дуги
относительно координатных осей ОХ
и ОУ
соответственно
определяются по формулам:

;

.
(3.17)

Моменты
инерции этой дуги относительно
координатных осей ОХ
и ОУ
соответственно равны:

;

.
(3.18).

Координаты
центра тяжести дуги АВ
вычисляются по формулам:

;
(3.19)

.
(3.20)

Если
кривая однородна, то плотность функции
(х,
у) = const,
поэтому формулы (3.19) и (3.20) примут вид:

,
(3.21)

где

– длина дуги АВ.

Если
плоская гладкая кривая АВ
задана параметрическими уравнениями
вида х = х(t);
у = у(t),
причем, существуют непрерывные производные
х_t
и у_t,
где параметр
t
применяется
на дуги АВ
в пределах


t

.

Тогда

и криволинейный интеграл выражается
через определенный по формуле:

.
(3.22)

Если
кривая АВ
задана уравнением у
= у(х); где а

х 
b,
то

.
(3.23);

Рассмотрим
теперь случай пространственной гладкой
кривой АВ.
Пусть ее параметрические уравнения
имеют вид:

х
= х(t);
у = у(t);
z = z(t);
причем существуют непрерывные производные
х_t,
у_t
и z_t.
Предположим, что параметр t
изменяется
в пределах 

t

.

Тогда
справедлива формула:

.
(3.24)

Криволинейный
интеграл от функции f(х,
у)
по дуге, заданной уравнением в полярных
координатах r
= r(),
где 



,
вычисляется
с помощью формулы:

.
(3.25)

Задача
3.3.
Вычислить

,
где АВ
часть окружности х²
+ у²
= R²,
лежащая в
I
четверти.

Решение.
Выразим из
уравнения окружности явно ординату у
через абсциссу х,
получим

(в первой четверти у

0).

Найдем

и подставим в выражения

;

По
формуле (3.23)
получим:

Ответ:

.

Задача
3.4.

Найти
центр тяжести полуокружности х²
+ у²
= R²,
лежащей в
верхней полуплоскости, а также ее момент
инерции относительно оси ОХ
(плотность
считать равной единице).

Решение.
Центр тяжести
дуги кривой определяется по формуле
(3.20). Из соображений симметрии следует,
что он находится на оси ОУ.
Поэтому х_с
= 0.

,
где

,
так как это длина полуокружности.

Для
вычисления числителя дроби воспользуемся
параметрическими уравнениями окружности:
x
= R
cos
t;
y
= R
sin
t.

Тогда

.

;

Ответ:
х_с
= 0,

.

Задачи
для самостоятельного решения

Задача
3.5.
Найти
координаты центра тяжести одной арки
циклоиды: x
= a(t
– sin
t),
y
= a(1
– cos
t),
0 
t

2.

(Считать
плотность равной единице).

Указание.
Воспользоваться
формулами (3.22).

Учитывая
симметрию, заключаем, что абсцисса
центра тяжести х_с
= а.

;

Ответ:
х_с
= а;

Задача
3.6.
Найти массу
участка кривой у
= ln
x
от точки с абсциссой

до точки с абсциссой

,
если плотность в каждой точке равна
квадрату ее абсциссы.

Указание.

;

Ответ:

Задача
3.7.

Определить
центр тяжести дуги астроиды x
= a
cos³t,
y
= a
sin³t,
лежащий в
первой четверти

.
Плотность считать равной единице.

Ответ:

Определение
криволинейного интеграла

второго рода
и его механический смысл

Рассмотрим
задачу, приводящую к понятию криволинейного
интеграла второго рода. Эта задача о
вычислении работы переменной силы при
перемещении материальной точки вдоль
некоторой кривой.

Предположим,
что при движении по кривой АВ
материальная точка М переходит из
положения А в положение В. Во
время движения на точку М действует
сила

=

(x,
y, z),
заданная своими проекциями P,
Q, R
на координатные оси OX,
OY и OZ,
т.е.

= P(x, y, z)

+ Q(x, y, z)

+ R(x, y, z)
.
(3.26)

Найдем работу Е
силы

при данном перемещении точки.

Если бы перемещение
точки М было прямолинейным, а
действующая сила

– постоянной (по величине и направлению),
то работа Е этой силы, по известной
формуле из физике, была бы равна скалярному
произведению вектора на вектор перемещения

,
т.е. Е =(
,

).
Однако особенность задачи состоит в
том, что перемещение точки является
криволинейным, а действующая сила
переменной . Разобьем кривую АВ на
части (элементарных дуг) точками М₀,
М₁, М₂,…, М_n_-1,
M_n
где M₀совпадает с А, а M_n
– с точкой В. Обозначим диаметр
разбиения через d.
На каждой дуге выберем производную
точку

(
,

,

)
и найдем в ней значение силы

=
(P_к, Q_к,
R_к),
где P_к = P
(
,

),
Q_к= Q(
,

),
R_к=
R(
,

).
Предположим, что сила сохраняется
постоянной в точках дуги и под ее действие
точка перемещается на каждом элементарном
участке не по дуге, а по хорде, соединяющей
точки М_к-1, M_к(к
= 1, 2, …, n).
Используя формулу для вычисления
скалярного произведения через проекции
силы и векторы перемещения, получим
приближенное значение работы на каждом
элементарном участке дуги

Е_к 
P (
,

)x_к
+ Q(
,

)y_к
+ R(
,

)z_к,

x_к
= x_к –
x_к-1, y_к
= y_к –
y_к-1, z_к
= z_к –
z_к-1, а x_к, y_к,
z_к,
координаты точки M_к

(к = 1, 2, …, n).

Суммируя полученные
частичные работы, найдем приближенно
полную работу силы

при перемещении точки М вдоль кривой
АВ

E


P
(
,

)x_к
+ Q(
,

)y_к
+

+ R(
,

)z_к].

(3.27)

За работу E
силы

при перемещении материальной точки
вдоль кривой АВ примем предел суммы
(3.27) при стремлении диаметра разбиения
к нулю, т.е.

E
=

P
(
,

)x_к
+ Q(
,

)y_к
+ R(
,

)z_к].

Перейдем к
определению криволинейного интеграла
второго рода.

Пусть в пространстве
OXYZ задана
непрерывная, гладкая кривая АВ и
функция P(x,
y, z)
на этой кривой. С помощью точек М₀,
М₁, М₂,…, M_n
в направлении от А и В разобьем
на n дуг производные
длины. На каждой дуге М₀,
М_к-1, M_к
выберем производную точку

(
,

,

)
и найдем в ней значение функции P(
,

)
. Для каждой элементарной дуги
вычислим произведение P(
,

)x_к,
где x_к
– проекция дуги М_к-1, M_к
на ось ОХ, т.е. x_к
= x_к –
x_к-1,
где x_к и x_к-1соответственно абсциссы конца и
начала хорды М_к-1, M_к.
Просуммируя полученные произведения,
получим

P
(
,

)x_к.
(3.28)

Суммы вида (3.28)
называются интегральными суммами
второго рода для функции P(x,
y, z),
соответствующими разбиению {M_к}
кривой АВ (относительно координаты
х) с отмеченными точками

(
,

,

определение.
Предел интегральных сумм вида (3.28) при
d

0 (n
),
если он существует и не зависит от
способа разбиения кривой АВ
на частные дуги и выбора точек

,
называется криволинейным интегралом
второго рода по координате х
и обозначается

(x,
y, z)dx , т.е.

(x,
y, z)dx =

P
(
,

)x_к
. (3.29)

Аналогично
определяются криволинейные интегралы
по координатам y
и z,
их обозначают

(x,
y, z)dy и

(x,
y, z)dz , беря
для функции

Q(x,
y,
z)
проекции y_к
на ось ОY,
а для R(x,
y,
z)
проекции
z_к
на ось
ОZ.

Определение.
Сумма трех интегралов

(x,
y, z)dx,

(x,
y, z)dy,

(x,
y, z)dz называется
общим криволинейным интегралом второго
рода (по координатам) и обозначается

(x,
y, z)dx =
(x,
y, z)dy +
(x,
y, z)dz.
(3.30)

Если
P,
Q,
R
– проекции силы

на координатной оси, то из формулы (3.27)
следует, что общий криволинейный интеграл
второго рода выражает работу этой силы
на пути АВ,
т.е.

E
=

(x,
y, z)dx +
(x,
y, z)dy +
(x,
y, z)dz (3.31)

В
этом состоит физический смысл
криволинейного интеграла второго рода.

Замечание
1. Если кривая
АВ
лежит в плоскости ХОY
и функции P(x,y)
и Q(x,y)
не зависят от z,
то криволинейные интегралы второго
рода имеют вид

(x,
y)dx + Q(x, y)dy.
(3.32)

Замечание
2. В отличие
от криволинейного интеграла первого
рода криволинейный интеграл второго
рода меняет свое значение на противоположное
при изменении направления кривой АВ,
т.е.

(x,
y, z)dx = –
(x,
y, z)dx

В
самом деле, если изменить направление
обхода кривой, то изменятся знаки
проекций x_к
в сумме (3.28), значит и сама сумма, и ее
предел.

Замечание
3. Криволинейный
интеграл второго рода обладает всеми
свойствами криволинейного интеграла
первого рода, за исключением одного: он
меняет знак на противоположный при
изменении направления обхода кривой.

Замечание
4. В случае,
когда кривая АВ
– замкнутая (т.е. точка В
совпадает с точкой А)
употребляется обозначение

(M)dx
+ Q(M)dy
+ R(M)dz.

В
случае, когда кривая АВ
замкнутая, за положительное направление
обхода принимается такое, при котором
область, лежащая внутри этого контура
остается слева по отношению к точке,
совершающей обход.

Теорема:
Если функции P(x,
y, z), Q(x,
y, z), R(x,
y, z) непрерывны,
или имеют конечное число разрывов
первого рода вдоль непрерывной кривой
АВ,
имеющей конечную длину, то криволинейные
интегралы

(x,
y, z)dx,

(x,
y, z)dy,
(x,
y, z)dz, а

следовательно
и криволинейный интеграл

dx
+ Qdy
+ Rdz
существуют.

Вычисление
криволинейного интеграла второго рода

Пусть
гладкая кривая АВ
задана параметрическими уравнениями
х= х(t),
y=y(t),
z=z(t),
причем изменению t
от 
до 
соответствует
движение точки по кривой от А
до В
(не обязательно, чтобы 
было меньше ).
Тогда

=

. (3.33)

Аналогичные
формулы имеют место и для интегралов
по координатам y
и z.
Выпишем формулу для вычисления общего
интеграла второго рода

+Q(x,y,z)dy+R(x,y,z)dz=

=
+Q(x(t),y(t),z(t))y(t)+

+R(x(t),y(t),
z(t))z(t)
] dt. (3.34)

Если
АВ
– кривая, расположенная, например, в
плоскости ХОУ,
то формула (3.34) в этом случае примет вид

=
+

+Q(x(t),y(t),z(t))y(t)
+ R(x(t),y(t),z(t))z(t)dt.
(3.35)

Для
плоской гладкой кривой у
= у(х), где а
х 
b,
заданной явным уравнением, получим

=
.
(3.36)

Задача
3.8. Вычислить
криволинейный интеграл

,
где АВ
– одни виток винтовой линии

х=
cos
t,
у = sin
t,
z
= 2t
от точки А
(1,0,0) до точки
В (1,0,4).

Решение.
Вдоль дуги АВ
параметр t
изменяется от 0
до 2.
Тогда, используя формулу (3.24),
получим

=

=

=
=
.

Задача
3.9. Вычислить
криволинейный интеграл

вдоль
кривой у=х³
от точки А
(1,1)до
точки В(2,8).Решение.
По формуле (3.26) получим

Связь
между криволинейными интегралами

первого
и второго рода.

Пусть
АВ
– направленная пространственная кривая
с началом А
и концом В,
тогда все касательные к АВ
также являются направленными прямыми.
Обозначим углы, которые образует
касательная к АВ
с осями ОХ,
ОУ, ОZ
соответственно ,

и .
Очевидно,
что эти углы являются функциями координат
x,y,z
точки касания М.

Выделим
из АВ
элементарную дугу dl,
и будем считать ее прямолинейной. Значит
dl
–это вектор с проекциями dx,
dy,
dz,
направленный так же, как и кривая АВ.
Следовательно, dx
= cos

dl,
dy
= cos
dl,
dz
= cos
dl.

Тогда
общий интеграл второго рода выразится
через интеграл первого рода по формуле

=

.
(3.37)

По
формуле (3.37) осуществляется переход от
криволинейного интеграла первого рода
к интегралу второго рода.

Формула
Остроградского – Грина.

Рассмотрим
на плоскости ХОУ
компактную фигуру Ф,
ограниченную замкнутой гладкой (или
кусочно – гладкой) кривой A.

Пусть
функции Р(х,у)
и Q(х,у)
непрерывны вместе со своими частными
производными

на компактной фигуре Ф.Тогда
имеет место формула

=
,
(3.38)

которая
называется формулой Остроградского-Грина.
Она устанавливает связь между двойным
интегралом по некоторой плоской области
и криволинейным по контуру, ограничивающему
эту область, играет фундаментальную
роль в векторном анализе.

Докажем
справедливость формулы (3.38). Рассмотрим
в плоскости ХОУ
выпуклую в
направлении обеих осей фигуру Ф,
ограниченную замкнутым контуром А,
состоящим из двух кривых

у
= у₁(х)
и у = у₂(х),
где у₁(х)

у₂(х),

Рис.
3.2

а

х 
b
(рис. 3.2). Так как по условию Р(х,у)
и Q(х,у)
непрерывно дифференцируемые функции
на Ф,
то существует

,
который можно преобразовать следующим
образом

=

=

=
.

(3.39)

Если
взять в качестве параметра х
и записать параметрическое уравнения
кривой АDВ
в виде х = х,
у = у₂(х),
а кривой АСВ
– в виде х =
х, у = у₁(х),
то используя ранее выведенные формулы,
получим

;
.

(3.40)

Подставляя
выражение (3.40) в (3.30) и учитывая свойства
криволинейных интегралов, имеем

.
(3.41)

Аналогично
можно доказать, что

.
(3.42)

Вычитая
(3.41) из (3.42), получим формулу

(в
предположении, что обход контура А
осуществляется
против часовой стрелки). Формула (3.38)
доказана для выпуклой фигуры Ф.

Однако
она справедлива и для всякой замкнутой
области, которую можно разбить на
конечное число выпуклых фигур.

Замечание.
При доказательстве формулы (3.36)
рассматривалась область Ф,
ограниченная одним замкнутым контуром
(односвязная). Можно доказать, что
формула Остроградского-Гаусса остается
справедливой и для многосвязной области,
ограниченной не одним, а несколькими
не связанными друг с другом контурами
(многосвязной).

Геометрические
и механические приложения

криволинейных
интегралов

Криволинейные
интегралы имеют широкие приложения в
геометрии, механике и физике. Ограничимся
рассмотрением только некоторых из них.
Площадь плоской области

Используя
формулу Грина (3.38), выведем формулы для
вычисления площади фигуры Ф
с помощью криволинейного интеграла.

Если
функции Р(х,у)
= -у, а Q(х,у)=0,
то

и формуле
(3.38) примет вид

.
Откуда S
= –
.
(3.43)

Аналогично,
полагая Р(х,
у) = 0, Q(х,
у) = х, получим

S
= –

(3.44)

При
Р(х, у) = -1/2 у;
Q
(х, у) = 1/2 х,
имеем

S
= 1/2
.

Задача
3.10. Найти
площадь S
плоской фигуры, ограниченной эллипсом

.

Решение.
Параметрические уравнения эллипса
имеют вид x
= а соs
t,
y
= b
sin
t,
где 0
t

2.

По
формуле (3.44) находим

S=
=

.

Координаты центра
масс материальной кривой

Для определения
координат центра масс материальной
кривой АВ, если известна линейная
плоскость распределения массы (М)
в каждой ее точке М, используются
формулы

,
(3.45)

где
M
=

-масса
кривой АВ.

Если
кривая АВ
однородна, то есть 
= const,
то формулы (3.45) упрощаются

.
(3.46)

где

=

–кривой
АВ.

Задача
3.11. Вычислить

,
где АВ –
первая четверть окружности х²
+ у²
= R²,
пробегаемая
против часовой стрелки.

Решение.
Из уравнения окружности выразим у
через х.

Получим

,
так как в первой четверти у

0, то

;

Учитывая,
что интегрирование ведется против
часовой стрелки х
изменяется от R
до 0.

По
формуле (3.29)
получим:

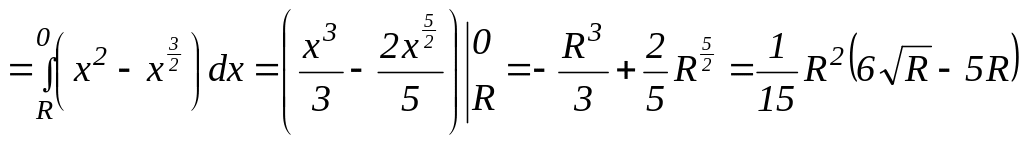
Ответ:

Задача
3.12. Вычислить
криволинейный интеграл,

где АВ один
виток линии х
= cos
t,

y
= sin
t,
z
= 2t
от точки
А(1, 0, 0)
до В(1, 0, 4).

Решение.
Очевидно,
что вдоль дуги
АВ параметр
t
изменяется
от 0
до 2.
По формуле
(3.28), получим

Ответ:

Задачи
для самостоятельного решения

Задача
3.13. а) Вычислить

,
где АВ – дуга
параболы у
= х²
от точки х
= 0 до точки
х = 2;

б)
Вычислить
,
где АВ та
же дуга.

Ответ:
а)

;
б)

.

Задача
3.14.
Вычислить

,
где АВ

1)
отрезок прямой, соединяющий точки А(2,
3) и В(3,
5);

2)
дуга параболы у
= х²(0

х 
2);

3)
дуга параболы у=х²,
соединяющая точки С(0,0)
и D(4,2).

Ответ:
1)
;
2)
;
3)
.

Задача
3.15. Вычислить:

;

где
L
одна из линий, соединяющих точки О(0,
0) и А(2,
2).

отрезок
ОА;
парабола

;
парабола

;
кубическая
парабола
ломанная
ОСА,
где С(2, 0).

Решение.

Уравнение
прямой на которой лежит отрезок ОА
у = х, поэтому
dy
= dx.
Заменим в подынтегральном выражении
у
на х, а
dy
на
dx,
получим:

Из
уравнения кривой

следует, что dy
= xdx.

Заменяя
в подынтегральном выражении у
на

,
а dy
на
хdx,
получим, что

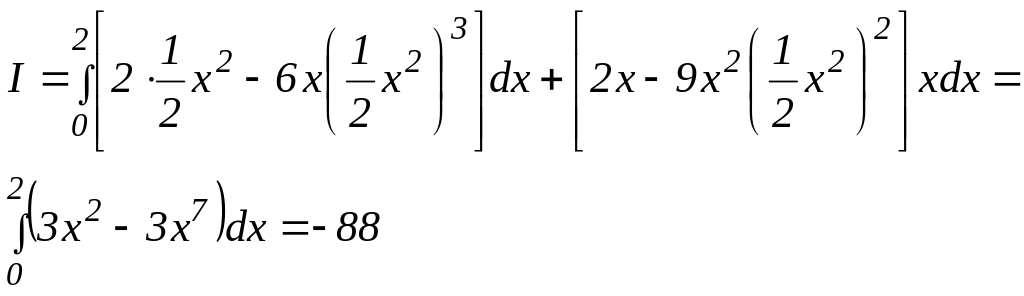
Так
как уравнение линии

,
то dx
= ydy.
Заменим в подынтегральном выражении
х, на

,
а dx
на ydy,
получим, учитывая, что у
изменяется от 0
до 2.

Убедиться
самостоятельно, что I
= – 88.
Вычислим
этот интеграл по ломанной ОСА,
состоящий из отрезка ОС
оси ОХ и
отрезка СА
прямой Х =
2.

В
этом случае на отрезке ОС:
у = 0, dy
= 0. На отрезке
СА: х = 2, dх
= 0, а у
изменяется
от 0
до 2,
так как

Итак,
по какой бы из указанных кривых,
соединяющих точки (0,
0) и (2,
2), мы не
вычисляли этот интеграл, оказывается,
что он равен одному и тому же числу.
Иначе говоря, величина этого интеграла
не зависит от пути интегрирования.

Ниже
будет указано условие, которому должно
удовлетворять подынтегральное выражение
Р(х,у)dx
+ Q(x,y)dy
в криволинейном интеграле второго
рода, чтобы интеграл не зависел от пути
интегрирования, соединяющего эти точки.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
30.04.2022655.36 Кб144.doc
#
#
#
#
#
#
#
#
#

Источник

Статические моменты и координаты центра тяжести

Вычисление статических моментов и координат центра тяжести кривой

а) Пусть материальная точка массы отстоит от оси ell на расстоянии . Статическим моментом этой точки относительно оси ell называют число . Статическим моментом системы материальных точек A_1,A_2,ldots,A_n , расположенных по одну сторону от оси ell , массы которых равны m_1,m_2,ldots,m_n , а расстояния от оси ell равны d_1,d_2,ldots,d_n называют число

$S_{ell}= sumlimits_{k=1}^{n}m_kd_k,.$

Если же эти точки расположены по разные стороны от оси, то для точек, находящихся по одну сторону оси, расстояния берутся положительными, а для точек по другую сторону от оси — отрицательными.

Поэтому если точки A_1,A_2,ldots,A_n расположены на координатной плоскости,

A_k=A_k(x_k;y_k) , то $S_x=sumlimits_{k=1}^{n}m_ky_k,,~~ S_y=sumlimits_{k=1}^{n}m_kx_k,,$

где S_x — статический момент относительно оси и S_y — относительно оси .

б) Рассмотрим теперь случай, когда масса равномерно распределена по некоторой кривой Gamma или по некоторой области lambda . Будем считать, что плотность распределения равна единице. Тогда масса дуги численно равна ее длине, а масса области — ее площади.

Начнем со случая кривой линии Gamma , задаваемой уравнением y=f(x),~a leqslant x leqslant b , причем предположим, что функция f(x) непрерывна и неотрицательна.

Как обычно, разобьем отрезок [a;b] на части точками a=x_0<x_1< ldots<x_n=b и обозначим через m_k и M_k наименьшее и наибольшее значения функции f(x) на отрезке $[x_k;x_{k+1}]$ , Этому разбиению соответствует разбиение дуги Gamma на части $gamma_0,ldots, gamma_{n-1}$ (рис. 60). Из физических соображений ясно, что статический момент S_k части gamma_k относительно оси абсцисс заключен между m_kell_k и , где ell_k —длина этой части, ell_k=ell(gamma_k) (напомним, что мы положили линейную плотность дуги равной единице). Таким образом,

Разбиение отрезка на части точками

m_kcdotell_k leqslant S_k leqslant M_kcdotell_k . Поэтому $sumlimits_{k=0}^{n-1} m_kell_k leqslant S_x leqslant sumlimits_{k=0}^{n-1}M_kell_k$ , то есть

$sumlimits_{k=0}^{n-1}m_k intlimits_{x_k}^{x_{k+1}} sqrt{1+(y')^2},dx leqslant S_x leqslant sumlimits_{k=0}^{n-1}M_k intlimits_{x_k}^{x_{k+1}} sqrt{1+(y')^2},dx,.$

Так как на отрезке $[x_k;x_{k+1}]$ выполняется неравенство

$m_kcdot sqrt{1+(y')^2} leqslant ycdot sqrt{1+(y')^2} leqslant M_kcdot sqrt{1+(y')^2},,$

то в тех же границах, что и S_x , заключен интеграл $intlimits_{a}^{b} ysqrt{1+(y')^2},dx$ . Значит,

$S_x= intlimits_{a}^{b}ysqrt{1+(y')^2},dx,.$

(1)

Этот интеграл обозначают также следующим образом: $intlimits_{Gamma}y,dell$ или $intlimits_{0}^{ell}y,dell$ .

Физики обычно заменяют проведенное рассуждение более коротким. Они берут “бесконечно малый участок дуги” dell . Его статический момент равен y,dell . А статический момент всей дуги равен сумме элементарных статических моментов, т. е. $intlimits_{a}^{b} y,dell$ . Преимуществом этого вывода является его наглядность. Однако в нем не определено, что такое “бесконечно малый участок дуги”, или как еще говорят, “элемент дуги”. При уточнении этого понятия мы вновь приходим к более длинному выводу, изложенному ранее. В дальнейшем для краткости изложения мы будем использовать принятый в физике метод рассуждений. С его помощью сразу выводим, что

$S_y=intlimits_{a}^{b}xsqrt{1+(y')^2},dx= intlimits_{0}^{ell}x,dell,.$

(2)

Как формула (1), так и формула (2) верны и в случае, когда кривая Gamma пересекает оси координат.

в) Введем понятие центра тяжести.

Определение. Центром тяжести тела называется такая точка , что если в ней сосредоточить всю его массу, то статический момент этой точки относительно любой оси будет равен статическому моменту всего тела относительно той же оси.

Обозначим через и eta расстояния центра тяжести кривой от осей ординат и абсцисс.

Тогда, пользуясь определением центра тяжести кривой, получим:

$S_x= ellcdoteta= intlimits_{0}^{ell}y,dell,;qquad S_y=ellcdotxi= intlimits_{0}^{ell}x,dell,.$

Разрешая полученные равенства относительно и eta , найдем координаты центра тяжести плоской кривой Gamma:

$xi=frac{1}{ell} intlimits_{0}^{ell} x,dell,;qquad eta=frac{1}{ell} intlimits_{0}^{ell}y,dell,.$

Замечание. Если кривая расположена симметрично относительно некоторой прямой, то центр тяжести такой кривой находится на этой прямой.

Это замечание позволяет в некоторых случаях упростить нахождение координат центра тяжести плоской кривой.

Пример 1. Найти статический момент полуокружности относительно диаметра.

Решение. Выберем систему координат так, чтобы центр окружности совпал с началом координат, а диаметр, относительно которого мы ищем статический момент, совпал с осью . Тогда статический момент полуокружности относительно диаметра выразится формулой

$S_x=intlimits_{0}^{ell} y,dell$ , где $dell=sqrt{1+(y')^2},dx$ — дифференциал дуги кривой y=f(x) .

В выбранной системе координат уравнение полуокружности запишется так: $y=sqrt{R^2-x^2}$ . Тогда

$y'=-frac{x}{sqrt{R^2-x^2}},~~1+(y')^2= frac{R^2}{R^2-x^2}$ и потому $dell=frac{R,dx}{sqrt{R^2-x^2}}$ .

Следовательно,

$S_x=intlimits_{-R}^{R}! sqrt{R^2-x^2}cdot frac{R,dx}{sqrt{R^2-x^2}}= 2R intlimits_{0}^{R}dx= 2R^2.$

Пример 2. Найдем центр тяжести четверти окружности x^2+y^2=4 , расположенной в первом квадранте.

Решение. Данная кривая расположена симметрично относительна биссектрисы первого координатного угла, следовательно, центр тяжести этой кривой лежит на биссектрисе, а потому xi=eta . Достаточно найти только $xi=frac{1}{ell} intlimits_{0}^{ell} x,dell$ .

Вычисление проще провести, перейдя к параметрическим уравнениям окружности. Так как ее радиус равен двум, то для четверти окружности имеем:

$begin{cases}x=2cos{t},,\ y=2sin{t},,end{cases} 0 leqslant t leqslant frac{pi}{2},.$

Отсюда находим, что $x'_t=-2sin{t},~ y'_t=2cos{t}$ и

$dell= sqrt{(x'_t)^2+(y'_t)^2},dt= sqrt{4sin^2t+4cos^2t},dt= 2,dt,.$

Поскольку длина ell четверти данной окружности равна $frac{1}{4}cdot 2picdot2=pi$ , то

$xi=frac{1}{pi} intlimits_{0}^{2pi} 2cos{t}cdot2,dt= left.{frac{4}{pi} sin{t}}right|_{0}^{pi/2}= frac{4}{pi},.$

Вычисление статических моментов и координат центров тяжести плоских фигур

Найдем статический момент прямоугольника со сторонами и ell относительно стороны . Разобьем этот прямоугольник на элементарные прямоугольники, имеющие стороны и (рис. 61). Масса элементарного прямоугольника равна его площади k,dy (напомним, что по предположению плотность распределения массы равна единице). Поэтому элементарный статический момент равен ky,dy , а статический момент всего прямоугольника равен

Разбиение прямоугольника на элементарные прямоугольники

$intlimits_{0}^{ell} ky,dy= left.{frac{k}{2},y^2}right|_{0}^{ell}= frac{kell^2}{2},.$

(1)

Теперь уже легко найти статический момент криволинейной трапеции, ограниченной сверху кривой y=f(x) , где f(x) — непрерывная и неотрицательная функция на отрезке [a;b] , снизу осью абсцисс, а с боков прямыми x=a,~ x=b .

Разобьем криволинейную трапецию на элементарные прямоугольники, основание каждого из которых равно и высота . Статический момент такого прямоугольника относительно оси абсцисс по формуле (1) равен $frac{y^2}{2},dx$ , а потому статический момент всей криволинейной трапеции равен $frac{1}{2}intlimits_{a}^{b} y^2,dx$ . В случае, когда не выполняется предположение о неотрицательности функции y=f(x) , эту формулу надо заменить такой:

$S_x=frac{1}{2} intlimits_{a}^{b} y|y|,dx$

(части фигуры, расположенные ниже оси абсцисс, дают отрицательный вклад в S_x ).

Поскольку по предположению плотность равна единице, то масса криволинейной трапеции равна ее площади, т. е. интегралу $intlimits_{a}^{b} |y|,dx$ , а потому ордината центра тяжести этой трапеции выражается формулой

$eta=frac{intlimits_{a}^{b} y|y|,dx}{2 intlimits_{a}^{b} |y|,dx},.$

Нетрудно найти и статический момент криволинейной трапеции относительно оси ординат. Для этого достаточно заметить, что расстояние элементарного прямоугольника от этой оси равно . Поэтому его статический момент равен x|y|,dx , а статический момент всей трапеции выражается формулой

$S_y=intlimits_{a}^{b} x|y|,dx$ . Следовательно, абсцисса центра тяжести выражается так: $xi=frac{intlimits_{a}^{b} x|y|,dx}{intlimits_{a}^{b} |y|,dx}$ .

Пример 3. Найти статический момент (относительно оси ) фигуры, ограниченной осью абсцисс и одной аркой циклоиды:

$begin{cases}x=a(t-sin{t}),\ y=a(1-cos{t}),end{cases} 0leqslant tleqslant2pi,.$

Решение. Так как параметр одной арки циклоиды изменяется от до 2pi , то

$begin{aligned}S_x&= frac{1}{2} intlimits_{0}^{2pi} a^2(1-cos{t})^2a(1-cos{t}),dt= frac{a^3}{2} intlimits_{0}^{2pi} (1-cos{t})^3,dt=\ &= left.{frac{a^3}{2}! left[t-3sin{t}+ frac{3}{2}! left(t+frac{1}{2} sin2tright)- left(sin{t}-frac{1}{3} sin^3tright)right] }right|_{0}^{2pi}=\ & =frac{a^3}{2}! left(2pi+frac{3}{2}cdot 2piright) = frac{5}{2},pi a^3.end{aligned}$

Пример 4. Найти центр тяжести фигуры, ограниченной осью и одной полуволной синусоиды y=sin{x} .

Решение. Так как фигура под полуволной синусоиды расположена симметрично относительно прямой $x=frac{pi}{2}$ , то центр тяжести лежит на этой прямой и, следовательно, $xi=frac{pi}{2}$ . Ордината eta центра тяжести находится по формуле $eta=frac{1}{2S} intlimits_{0}^{pi} y^2,dx$ .

Так как $S=intlimits_{0}^{pi} sin{x},dx= Bigl.{-cos{x}}Bigr|_{0}^{pi}=2$ , то $eta=frac{1}{4} intlimits_{0}^{pi}sin^2x,dx = frac{pi}{8}$ .

Итак, центр тяжести данной фигуры находится в точке $left(frac{pi}{2}; frac{pi}{8}right)$ .

Пример 5. Найти центр тяжести фигуры, ограниченной осью абсцисс и одной аркой циклоиды $begin{cases}x=a(t-sin{t}),\ y=a(1-cos{t}).end{cases}$ .

Решение. Данная фигура расположена симметрично относительно прямой x=pi a , следовательно, центр тяжести ее находится на этой прямой, и потому xi=pi a . Найдем eta по формуле $eta=frac{1}{2S} intlimits_{a}^{b} y^2,dx$ .

Площадь данной фигуры была вычислена раньше, она равна 3pi a^2 . Следовательно,

$eta=frac{1}{6pi a^2} intlimits_{0}^{2pi} a^3(1-cos{t})^3,dt= frac{5}{6},a,.$

Центр тяжести данной фигуры находится в точке $left(pi a; frac{5}{6},aright)$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Статические моменты и координаты центра тяжести

Вычисление статических моментов и координат центра тяжести кривой

Вычисление статических моментов и координат центров тяжести плоских фигур

Вам также может понравиться

Как найти частника для ремонта квартиры

Как найти кнопку эксель

Как по разному можно составить число 3 ответ

Добавить комментарий Отменить ответ