как найти центр тяжести экспериментально?
Ученик
(151),
закрыт
12 лет назад
ValKo
Высший разум
(112944)
12 лет назад
У “объемного” тела (типа камня) центр тяжести находится внутри, поэтому “найти” его затруднительно.
У плоской фигуры центр тяжести можно найти следующим образом:
Подвесить фигуру за какую-то точку и с помощью отвеса провести линию.
Подвесить фигуру за другую точку и с помощью отвеса провести линию.
Пересечение линий и укажет центр тяжести.
Лучше поделать опыт несколько раз и взять “среднюю” между точками пересечения.
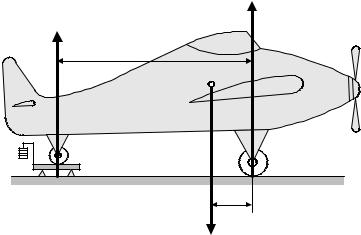
Другим возможным способом экспериментального определения центра тяжести является метод взвешивания. Устанавливают весы поочередно под опоры тела и определяют силы реакций опор. Затем составляют уравнение моментов относительно центра
|
тяжести и находят его положение. |
157 |
|
RA |
||
|
RB |
l |
|
|
C |
||
|
B |
A |
|
|
a |
||
|
P |
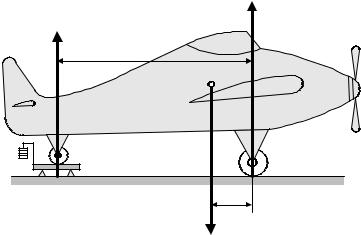
Для определения координаты центра тяжести приме- няют экспериментальный способ. Поставив колесо В на платформу весов, определяют взвешиванием силу давления колеса на платформу. Тем самым мы найдём численное значение силы реакции опорной поверх- ности в точке В – RB. Таким же способом находим
значение силы реакции поверхности в точке А – RA.
158
|
RA |
||
|
RB |
l |
|
|
C |
||
|
B |
A |
|
|
a |
||
|
P |
Применяют теорему Вариньона, в соответствии с которой сумма моментов сил относительно точки С
равна нулю:
RAa RB (l a) 0,
откуда следует
|
a |
RBl |
||
|
. |
|||
|
R |
A |
R |
|
|
B |
159
Центр тяжести (центр масс):
Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.
Центр тяжести – геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.
На каждую точку тела в поле сил тяжести действует сила, а на все тело – равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.
Центр масс (центр инерции) – точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе внешние силы.
При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.
Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.
При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, – параллельными.
Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.
Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.
Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.
Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.
Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.
1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О – середине стержня.
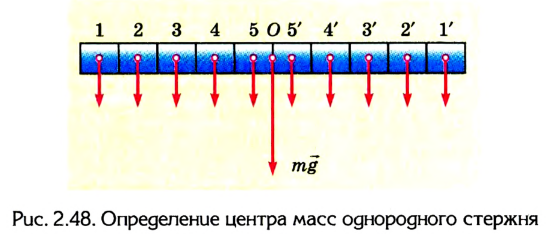
Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.
Центр тяжести однородного стержня расположен в середине стержня.
2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).
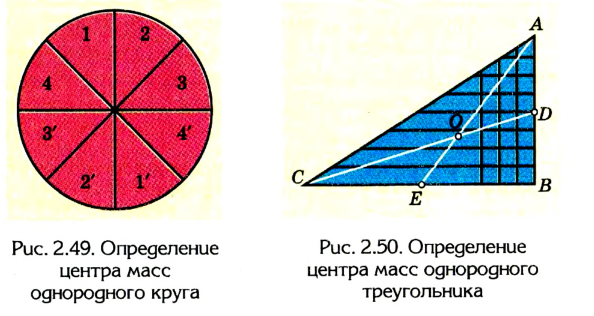
Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.
Центр тяжести однородного круга совпадает с его центром.
Центр тяжести однородного треугольника находится в точке пересечения его медиан.
3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.
Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.
4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).
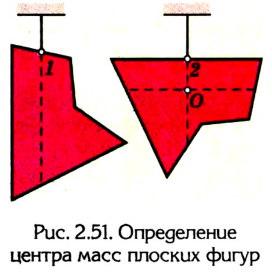
Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.
Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.
Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.
- Заказать решение задач по физике
Центр тяжести тела и центр масс тела
Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.
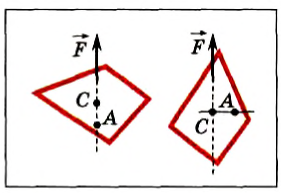
Рис. 151
Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.
Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m1 и m2, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:
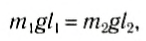
или
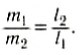
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:
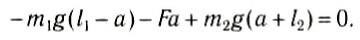
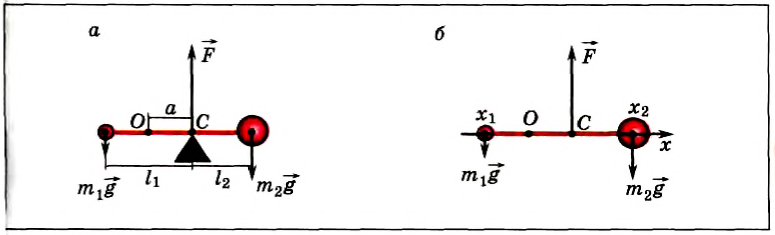
Рис. 152
Поскольку F=(m1 + m2)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.
Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х1, хс и х2. Запишем условие моментов относительно точки О:
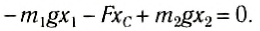
Отсюда
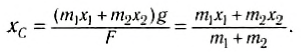
При выводе этой формулы было использовано значение силы F = (m1 + m2) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии хс, определенном формулой (2).
Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.
Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.
Если произвольное тело можно разбить на n элементов, массы которых m1, m2…, mn, и если известны координаты центров масс этих элементов x1, x2…, xn относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:
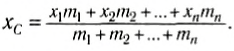
Естественно, что такие же соотношения можно записать и для ус и zc. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m1 = 2m2). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C1) и линейки (C2).
Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х1 = 0, y1 =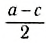 , а координаты центра масс линейки:
, а координаты центра масс линейки: 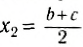 , y2 = 0 .
, y2 = 0 .
По формуле (3): .
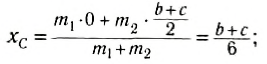
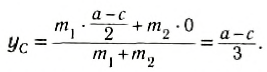
Таким образом, центр масс угольника находится вне тела.
Главные выводы:
- Центр тяжести — точка, в которой приложена сила тяжести.
- Центр масс симметричных однородных тел находится в их геометрическом центре.
- Координаты центра масс тела можно вычислить по формуле (3).
- Импульс тела в физике
- Замкнутая система в физике
- Реактивное движение в физике
- Освоение космоса – история, этапы и достижения с фотографиями
- Международная система единиц СИ
- Математика – язык физики
- Законы Ньютона в физике
- Гравитационные силы в физике
Ленинградская область
Выборгский район
МОУ «Вещевская СОШ»
 |
|||||
|
Работу выполнили учащиеся 11 класса:
|

![]()
u Цель исследования:
• экспериментально определить центр тяжести
плоских фигур, изготовленных учащимися.
u Задачи исследования:
• подготовка к ЕГЭ по физике;
• углубленное изучение темы «Центр тяжести» из
раздела «Статика»;
• раскрытие творческих способностей учащихся;
• поиск информации в сети Интернет;
• применение компьютерных технологий при
оформлении исследовательской работы;
• овладение технологией проектной деятельности.
Введение.
Понятие о центре тяжести было впервые изучено
примерно 2200 лет назад греческим геометром Архимедом, величайшим математиком
древности. С тех пор это понятие стало одним из важнейших в механике, а также
позволило сравнительно просто решать некоторые геометрические задачи.
Первым открытием Архимеда в механике было введение понятия центра
тяжести, т.е. доказательство того, что в любом теле есть единственная
точка, в которой можно сосредоточить его вес, не нарушив равновесного
состояния. Архимед решил ряд задач на нахождение центров тяжести различных
геометрических фигур: треугольника, параллелограмма, окружности и др., а также
упомянул о существовании фигур, у которых центр тяжести находится извне, например,
кольцо.конуса
В дальнейшем Герон и Папп приводят со ссылкой на Архимеда
доказательство существования центра тяжести. Герон предваряет теорему фразой,
относящейся к рассмотрению Архимедом идеализированных «физико-математических»
тел (метод абстракции). Герон пишет: «Никто не отрицает, что о наклонении и
отклонении в действительности говорят только о телах. Если же мы говорим о
плоских или телесных (объемных) фигурах, что некоторая точка является их
центром поворота и центром тяжести, то это достаточно разъяснено Архимедом».
Эта фраза подтверждает, что замена тел их теоретическими моделями была в науке
новшеством, введенным Архимедом. В современности модель материальной точки
просто необходима при решении многих физических задач.
Понятие центра тяжести в школьном курсе обучения
физике даётся в начале седьмого класса, а на определение центра тяжести
отводится всего один урок в десятом классе. Этих знаний не достаточно для
изучения темы «Статика» при подготовке к ЕГЭ. Этим мотивируется выбор темы
нашего дальнейшего исследования.
Ø Определение центра тяжести формулируется так: «…центром тяжести некоторого тела является некоторая расположенная
внутри него точка, обладающая тем свойством, что если за нее мысленно подвесить
тяжелое тело, то оно останется в покое и сохранит первоначальное положение».

Ø Доказательство существования центра тяжести также основано на мысленном уравновешивании
тела. В нем тело мысленно помещают на горизонтальную прямую, являющуюся
основанием вертикальной плоскости: «Если какое-нибудь обладающее весом тело
положить на прямую так, чтобы оно полностью рассекалось продолжением
упомянутой плоскости, то оно может иногда занять такое положение, что будет
оставаться в покое… Если затем переставить груз так, чтобы он касался
прямой другой своей частью, то можно при поворачивании дать ему такое
положение, что он, будучи отпущен, останется в покое… Если снова вообразить
плоскость продолженной, то она разделит груз на две взаимно
уравновешивающиеся части и пересечется с первой плоскостью… Если бы эти
плоскости не пересеклись, то те же самые части были бы и уравновешивающимися и
неуравновешивающимися, что нелепо».
Гипотеза.
Чтобы экспериментально определить центр тяжести плоской
фигуры, нужно подвесить её за некоторую точку А и провести через эту точку
вертикальную прямую АС по отвесу. В положении равновесия центр тяжести должен
лежать на вертикали АС, иначе сила тяжести имела бы момент относительно оси,
проходящей через точку подвеса, и этот момент вызывал поворот тела. Затем
подвесить тело за некоторую точку В и вновь провести вертикальную прямую ВD, на которой также должен лежать центр тяжести.
Следовательно, он находится в точке О пересечения прямых АС и ВD.
 |
Центр тяжести
геометрической фигуры (по Архимеду).
Центром тяжести круга – это точка пересечения его
диаметров.

Центр тяжести треугольника – это точка пересечения
его медиан.



Существуют фигуры, у которых центр тяжести
находится вне фигуры.
Например, кольцо.

Проведённый эксперимент.
|
Правильность определения центра тяжести проверяется
|
|||
 |

Фигуры, изготовленные учащимися.
(творческие работы)

Проведение эксперимента.
 |
|||||
 |
|||||
 |

Исследовательская задача.
Имеется однородный
диск радиусом 12 сантиметров. На сколько сместится центр тяжести этого диска,
если из него вырезать круг радиусом 6
см так, чтобы вырезанный круг касался окружности диска.

Дано:
Решение:
R1=
12 см
![]()
![]() R2= 6 см
R2= 6 см
х = ?
Обозначим центр диска
точкой О, центр вырезанного круга точкой А, точку касания двух окружностей В и
центр полученной фигуры точкой С. Искомое расстояние х есть нечто иное как
отрезок ОС. ОА = R1/2 по построению.
При определении
положения центра тяжести диск с вырезом формально можно считать как сплошной
диск массы m1,
на который наложен диск радиуса R2, имеющий отрицательную массу – m2, равную по модулю массе вырезанной части. Очевидно, что центр тяжести
диска (т. С) лежит на продолжении прямой ОВ, соединяющей центры диска и выреза.
Равенство моментов сил тяжести, действующих на положительную и отрицательную
массы, относительно оси, проходящей через точку С, даёт
m1gx = m2g(x + R/2)
Учитывая, что m1 = π R12σ и m2 = πR22 σ, где σ –
масса единицы площади диска, находим искомое расстояние: х = R22 R1/2(R12 – R22).
Откуда, х = 2 (см).
Ответ: смещение составляет
2 см.
Проведя
экспериментальное определение центра тяжести фигуры, получаем совпадение
результатов решения и эксперимента.
 |
|||
 |
|||
Выводы:
Проведенный эксперимент полностью подтвердил гипотезу
опытного определения центра тяжести плоских фигур.
Источники информации:
1. Тихомирова С.А,
Яворский Б.М. Физика 10 класс. – М.: Мнемозина, 2008.
2. Атанасян Л.С.,
Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7-9 класс. – М.: просвещение, 2006.
3. Сайт «Википедия».
4. Задачи по физике
для поступающих в вузы. Бендриков Г.А., Буховцев Б.Б., Керженцев В.В., Мякишев
Г.Я. – М.: Физматлит, 1995.
Оглавление:
1. Цель и задачи
исследования ………………………………………..2
2. Введение
……………………………………………………………..3
3. Определение центра
тяжести ………………………………………4
4. Гипотеза
………………………………………………………………5
5. Центр тяжести
геометрической фигуры (по Архимеду) ………….6
6. Проведенный
экспнримент …………………………………………7
7. Фигуры,
изготовленные учащимися ……………………………….8
8. Проведение
эксперимента …………………………………………..9
9. Исследовательская
задача ………………………………………….10
10. Выводы
……………………………………………………………..11
11. Источники
информации ………………………………………… 12
