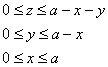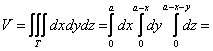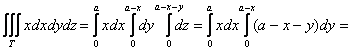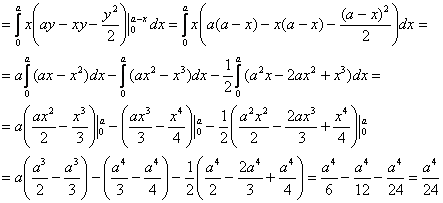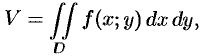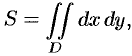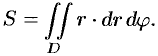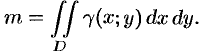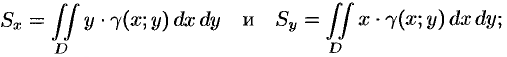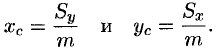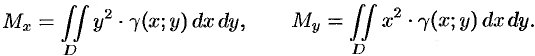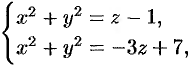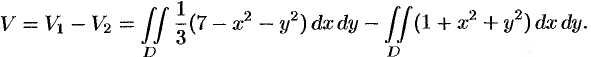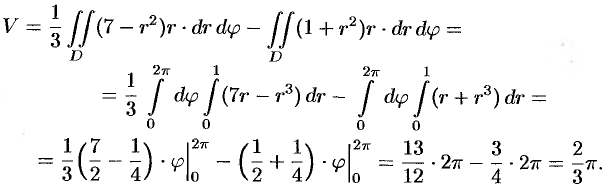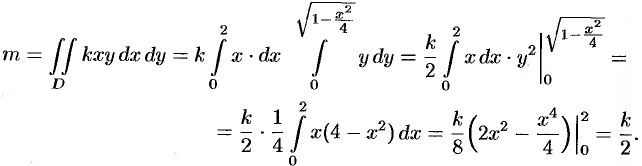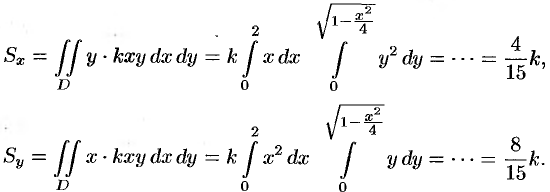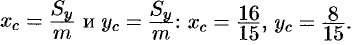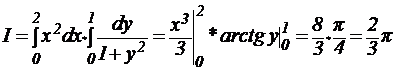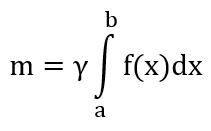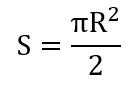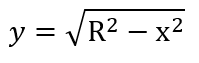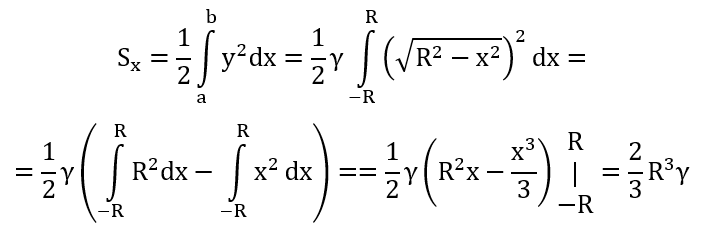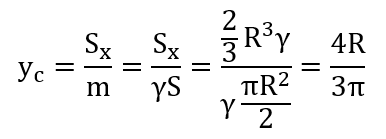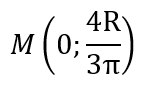2.6.2. Центр тяжести тела
Подобно тому, как задача о вычислении центра тяжести плоской фигуры решалась с
помощью двойного интеграла, задача об отыскании центра тяжести тела
решается аналогичным способом – с помощью тройного интеграла.
Что такое центр тяжести тела, довольно удачно объяснил ещё Архимед. Если тело подвесить на нить за центр тяжести,
то оно будет сохранять равновесие в любом положении (как бы мы его предварительно ни повернули). В известной степени это не
реализуемо (таки центр тяжести внутри тела), но зато очень понятно. И вполне в стиле древнегреческого учёного, который просил
дать ему точку опоры, чтобы с помощью рычага перевернуть Землю.
Центр тяжести неоднородного тела
рассчитывается по формулам:
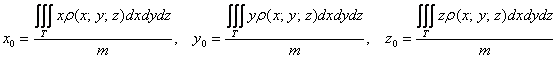
– функция плотности тела, а
– масса тела.
Если же тело однородно (стеклянное, оловянное, пластмассовое и т.д.), то формулы упрощаются. Так как плотность постоянна, и масса
– есть произведение плотности на объём, получаем:
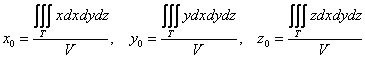
.
Для центра тяжести однородного тела справедливы следующие утверждения:
– если у тела есть центр симметрии, то он является центром тяжести (простейший пример – центр шара);
– если у тела существует линия симметрии, то центр тяжести обязательно принадлежит данной линии;
– если у тела есть плоскость симметрии, то центр тяжести непременно лежит в этой плоскости.
Как видите, практически полная аналогия с центром тяжести плоской фигуры.
Ну и, само собой, не могу не порадовать вас тематической задачей:
Пример 42
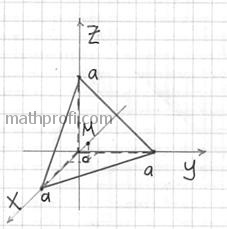
Найти центр тяжести однородного тела, ограниченного поверхностями ,
. Выполнить чертежи данного тела и его проекции на плоскость
.
Решение: искомое тело ограничено координатными плоскостями и плоскостью , которую в целях последующего построения удобно представить в
отрезках: . Выберем «а» за единицу
масштаба и выполним трёхмерный чертёж:
На чертеже уже поставлена готовая точка центра тяжести, однако, пока мы её не знаем.
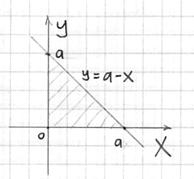
Проекция тела на плоскость очевидна, но, тем не менее, напомню, как её найти аналитически – ведь такие
простые случаи встречаются далеко не всегда. Чтобы найти прямую, по которой пересекаются плоскости нужно решить систему, составленную из их уравнений:
Подставляем значение в 1-е
уравнение системы: и получаем
уравнение «плоской» прямой:
Для взятия грядущих интегралов выберем «классический» порядок обхода тела:
Координаты центра тяжести
тела
вычислим по формулам:
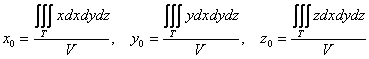
– объём данного тела. И понеслась песня:
1) Сначала вычислим объём тела. Его, кстати, можно узнать заранее, пользуясь известной задачей геометрии об объёме
тетраэдра. Объём тетраэдра равен 1/6-й объёма прямоугольного параллелепипеда, построенного на его трёх смежных рёбрах. В нашем
случае параллелепипед представляет собой куб с ребром «а», а посему: .
Осталось аккуратно провести штатные вычисления:
В примерах с громоздкими преобразованиями рекомендую записывать решение «столбиком» – меньше шансов запутаться:

в средний интеграл)
, и дело за тремя тройными
интегралами:
2) Вычислим «иксовый» интеграл, …и местечка у меня тут не хватает, поэтому решение в столбик отменяется:
Таким образом, «иксовая» координата центра тяжести: 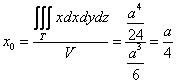
Учитывая симметрию тела, две другие координаты должны получиться такими же. Теперь ошибочный финал практически исключён! И
я вам предлагаю рассчитать самостоятельно, после чего можно записать красивый ответ.
…А вы, наверное, не так давно и представить себе не могли, что окажетесь в эпицентре такого кошмара =)


| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже показано (п. 53.2), объем цилиндрического тела находится по формуле
где 
Площадь плоской фигуры
Если положить в формуле (53.4) 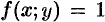
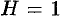




или, в полярных координатах,
Масса плоской фигуры
Как уже показано (п. 53.2), масса плоской пластинки 
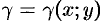
Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры 

а координаты центра масс фигуры — по формулам
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы 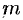
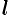
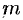
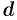
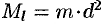

Момент инерции фигуры относительно начала координат — по формуле 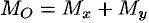
Замечание. Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
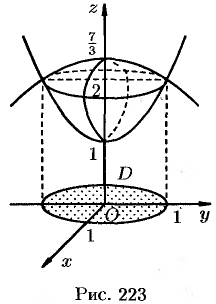
Пример №53.3.
Найти объем тела, ограниченного поверхностями 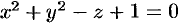
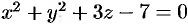
Решение:
Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему
находим уравнение линии их пересечения: 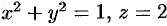
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг 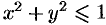
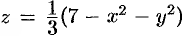
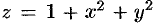
Переходя к полярным координатам, находим:
Пример №53.4.
Найти массу, статические моменты 
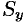
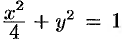
Решение:
По формуле (53.6) находим массу пластинки. По условию, 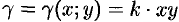
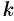
Находим статические моменты пластинки:
Находим координаты центра тяжести пластинки, используя формулы
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
Пусть на плоскости Oxy дана
система материальных точек ,
, …,
с массами
координаты центра
тяжести в данном случае будут определяться по формулам

Центр
тяжести плоской линии
Пусть
задана кривая АВ уравнением ,
, и пусть эта кривая представляет собой материальную
линию.
Координаты центра
тяжести данной линии

Центр
тяжести плоской фигуры.
Пусть данная фигура,
ограниченная линиями ,
,
,
, представляет собой материальную плоскую фигуру.
Координаты центра
тяжести такой фигуры
Пример:
Вычислить
координаты центра масс однородной плоской фигуры, ограниченной линиями и
Координаты центра
тяжести такой фигуры
Данное значение координаты можно получить
из соображений симметрии.
Кратные и криволинейные интегралы
№ 1.Вычислить двойной интеграл по указанному прямоугольнику D:
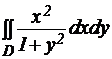
0≤x≤2, 0≤y≤1.
Преобразуем двойной интеграл в повторный. Пределы интегрирования известны, поэтому
Повторный интеграл свелся к произведению двух независимых друг от друга интегралов, поскольку результат вычисления внутреннего интеграла есть число.
№ 2.Вычислить двойной интеграл по области G, ограниченной указанными линиями:

Изобразим область интегрирования G.
Так как прямая y=x и парабола y=½x² пересекаются в точках O(0;0) и A(2;2), то область G определяется системой неравенств:
Теперь вычислим искомый интеграл I:

Интеграл был найден методом интегрирования по частям.
№ 3.Вычислить криволинейный интеграл:
1) , где L – дуга параболы
y2=2x, заключенная между точками (2;2) и (8;4). Найдем дифференциал дуги dl для кривой . Имеем

.
Следовательно, данный интеграл равен
.
2) , где L – окружность
x2+y2=a·x (a>0).
Введем полярные координаты x=r·cos(φ), y=r·sin(φ). Тогда, так как x2+y2=a·x, уравнение окружности примет вид r2=a·r·cos(φ), т.е. r=a·cos(φ), а дифференциал дуги
При этом φ∈[-π/2; π/2]. Следовательно, 
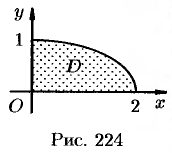
№ 4. Двойной интеграл выражает площадь области G. Вычислить площадь области G, если она ограниченна линиями:
y2=2x и y=x.
Имеем . Направление, или порядок интегрирования выберем так, как указано на чертеже:

Сначала определим координаты точки пересечения прямой и параболы:

Проекция области G на ось Oy есть отрезок [0;2]. Таким образом,
Центр тяжести однородной плоской фигуры
Пусть областью D плоскости xOy является материальная пластинка, масса которой распределяется с поверхностной плотностью p=f(x,y). Тогда масса M этой пластинки вычисляется по формуле
(1)
Координаты точки C(xc,yc), являющейся центром тяжести этой пластинки, определяются по формулам


Если поверхностная плотность p постоянна (пластинка однородна), то из формулы (2) следует:


где S – площадь области D.
Пример. Найти координаты центра тяжести однородной плоской фигуры, ограниченной параболой y=x2-2x-1 и прямой y=x-1 (рис.).
Решение
Вычислим площадь S данной фигуры с помощью двойного интеграла: .
Парабола и прямая пересекаются в точках A(0,-1) и B(3,2). Область D определяется неравенствами 0≤x≤3, x2-2x-1≤y≤x-1.
Тогда
Вычислим статистические моменты Mx и My пластинки относительно осей Ox и Oy:

Следовательно, ,

– центр тяжести данной фигуры.
Skip to content
matematicus.ru
matematicus включает разделы – высшая математика, аналитическая геометрия в пространстве и на плоскости, теория вероятностей, Arduino, Android Studio, Excel, программирование, программы, Windows, ошибки, таблицы, формулы, примеры, физика, химия
Координаты центра тяжести плоской фигуры
Координаты центра тяжести плоской фигуры находятся из выражений: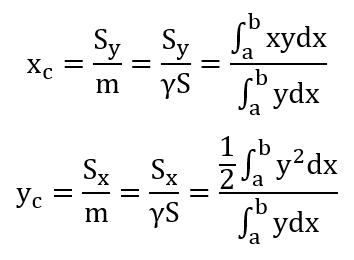
тогда координаты центра тяжести плоской фигуры (приложение интеграла) определяются по формуле:
γ — const
Пример
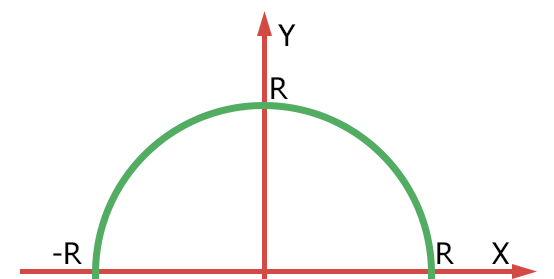
Найти координаты центра тяжести полуокружности
Решение
Площадь полукруга определяется по формуле:
Уравнение полуокружности имеет вид:
Найдем Sx:
Отсюда находим yc:
Таким образом, центра тяжести полуокружности имеет координаты:
1680