В этой статье посмотрим, как определяются координаты центра тяжести сложной фигуры — состоящей из простых. В задачах по сопромату часто приходится находить положение центра тяжести составных сечений, для дальнейшего вычисления моментов инерции и т. д.
Также часто, при изучении теоретической механики, студентам предлагается решить подобную задачу, и найти центр тяжести какой-нибудь фигуры.
Условие задачи
Предлагаю рассмотреть следующую фигуру:

В сопромате принято заштриховывать сечения тонкими линиями, вот так:

В своих же уроках я буду использовать заливку. Так, штриховка не будет мешать наносить обозначения.
Разбивка сложной фигуры на простые
Как видишь, сечение состоит из прямоугольника, прямоугольного треугольника, четверти круга, а также имеет круглый вырез:

Отметим центры тяжести (С1, С2, С3, С4) каждой отдельной фигуры, с учётом справочной информации.
Открой эту страничку, и пока не закрывай, она нам ещё понадобится!

Покажем вспомогательные оси (x0, y0) для всего сечения, которые будем использовать для нахождения положения центра тяжести (C):

Как определить положение центра тяжести?
Чтобы определить координату центра тяжести сечения, например, вертикальное расстояние от оси x0 до центра тяжести сечения (yc):

Нужно статический момент сечения относительно этой вспомогательной оси (x0) разделить на площадь всего сечения (A):

Площадь всего сечения (A) найти просто – это алгебраическая сумма площадей всех фигур:

Статический момент сечения, относительно вспомогательной оси будет равен алгебраической сумме статических моментов каждой фигуры (с учётом знака):

где Ai – площадь отдельной фигуры;
yi – расстояние от центра тяжести отдельной фигуры до вспомогательной оси (x0).
Координата центра тяжести (xc), находится аналогично:

Определение площади сечения
Для начала предлагаю сделать самое простое, используя формулы, указанные на этой странице, найти площадь всего сечения (A):


Как видишь, круглый вырез, нужно учесть с «минусом», что очевидно.
Определение расстояний от вспомогательных осей до центров тяжести отдельных фигур
Найдём расстояния от вспомогательных осей (x0, y0) до центров тяжести отдельных фигур, опять же, используя нашу шпаргалку:
Определение статических моментов
Определяем статические моменты сечения относительно вспомогательных осей (x0, y0):


Важно! Статические моменты могут быть и отрицательными.
Определение координат центра тяжести
И, наконец, определяем положение центра тяжести всего сечения (C):

Покажем центр тяжести всего сечения (C):

Если остались какие-то вопросы по данному уроку, можешь смело задавать их в комментариях. Также, другие уроки, на сайте – ssopromat.ru, по определению геометрических характеристик, можешь найти здесь.
Download Article
Download Article
The center of gravity (CG) is the center to an object’s weight distribution, where the force of gravity can be considered to act. This is the point where the object is in perfect balance, no matter how turned or rotated around that point.[1]
If you want to know how to calculate the center of gravity of an object, then you have to find the weight of the object: and any objects on it, locate the datum, and plug the known quantities into the equation for calculating the center of gravity. If you want to know how to calculate the center of gravity, just follow these steps.
Calculator
-
1
Calculate the weight of the object. When you’re calculating the center of gravity, the first thing you should do is to find the weight of the object. Let’s say that you’re calculating the weight of a see-saw that has a weight of 30 lbs. Since it’s a symmetrical object, its center of gravity will be exactly in its center if it’s empty. But if the see-saw has people of different weights sitting on it, then the problem is a bit more complicated.[2]
-
2
Calculate the additional weights. To find the center of gravity of the see-saw with two children on it, you’ll need to individually find the weight of the children on it.[3]
The first child has a weight of 40 lbs. and the second child’s is 60 lbs.
Advertisement
-
1
Choose a datum. The datum is an arbitrary starting point placed on one end of the see-saw.[4]
You can place the datum on one end of the see-saw or the other. Let’s say the see-saw is 16 feet long. Let’s place the datum on the left side of the see-saw, close to the first child. -
2
Measure the datum’s distance from the center of the main object as well as from the two additional weights. Let’s say the children are each sitting 1 foot away from each end of the see-saw.[5]
The center of the see-saw is the midpoint of the see-saw, or at 8 feet, since 16 feet divided by 2 is 8. Here are the distances from the center of the main object and the two additional weights form the datum:- Center of see-saw = 8 feet away from datum.
- Child 1 = 1 foot away from datum
- Child 2 = 15 feet away from datum
Advertisement
-
1
Multiply each object’s distance from the datum by its weight to find its moment. This gives you the moment for each object. Here’s how to multiply each object’s distance from the datum by its weight:
- The see-saw: 30 lb. x 8 ft. = 240 ft. x lb.
- Child 1 = 40 lb. x 1 ft. = 40 ft. x lb.
- Child 2 = 60 lb. x 15 ft. = 900 ft. x lb.
-
2
Add up the three moments. Simply do the math: 240 ft. x lb. + 40 ft. x lb. + 900 ft. x lb = 1180 ft. x lb. The total moment is 1180 ft. x lb.
-
3
Add the weights of all the objects. Find the sum of the weights of the seesaw, the first child, and the second child. To do this, add up the weights: 30 lbs. + 40 lbs. + 60 lbs. = 130 lbs.
-
4
Divide the total moment by the total weight. This will give you the distance from the datum to the center of gravity of the object. To do this, simply divide 1180 ft. x lb. by 130 lbs.
- 1180 ft. x lb. ÷ 130 lbs = 9.08 ft.
- The center of gravity is 9.08 feet from the datum, or measured 9.08 feet from the end of the left side of the see-saw, which is where the datum was placed.
Advertisement
-
1
Find the center of gravity in the diagram. If the center of gravity you found is outside of the system of objects, you have the wrong answer.[6]
You may have measured the distances from more than one point. Try again with just one datum.- For example, for people sitting on a seesaw, the center of gravity has to be somewhere on the seesaw, not to the left or right of the seesaw. It does not have to be directly on a person.
- This is still true with problems in two dimensions. Draw a square just large enough to fit all of the objects in your problem. The center of gravity must be inside this square.
-
2
Check your math if you get a tiny answer. If you picked one end of the system as your datum, a tiny answer puts the center of gravity right next to one end. This can be the right answer, but it’s often the sign of a mistake. When you calculated the moment, did you multiply the weight and distance together? That’s the correct way to find the moment. If you accidentally added them together instead, you’ll usually get a much smaller answer.
-
3
Troubleshoot if you have more than one center of gravity. Every system only has a single center of gravity. If you find more than one, you might have skipped the step where you add all the moments together. The center of gravity is the total moment divided by total weight. You do not need to divide each moment by each weight, which only tells you the position of each object.
-
4
Check your datum if your answer is off by a whole number. The answer to our example is 9.08 ft. Let’s say you try it and get the answer 1.08 ft., 7.08 ft, or another number ending in “.08.” This most likely happened because we chose the left end of the seesaw as the datum, while you chose the right end or some other point an integer distance from our datum. Your answer is actually correct no matter which datum you choose! You just need to remember that the datum is always at x = 0. Here’s an example:
- The way we solved it, the datum is at the left end of the seesaw. Our answer was 9.08 ft, so our center of mass is 9.08 ft from the datum at the left end.
- If you pick a new datum 1 ft from the left end, you get the answer 8.08 ft for the center of mass. The center of mass is 8.08 ft from the new datum, which is 1 ft from the left end. The center of mass is 8.08 + 1 = 9.08 ft from the left end, the same answer we got before.
- (Note: When measuring distance, remember that distances to the left of the datum are negative, while distances to the right are positive.)
-
5
Make sure all your measurements are in straight lines. Let’s say you see another “kids on the seesaw” example, but one kid is much taller than the other, or one kid is hanging underneath the seesaw instead of sitting on top. Ignore the difference and take all your measurements along the straight line of the seesaw. Measuring distances at angles will lead to answers that are close but slightly off.
- For seesaw problems, all you care about is where the center of gravity is along the left-right line of the seesaw. Later, you might learn more advanced ways to calculate the center of gravity in two dimensions.
Advertisement
Add New Question
-
Question
Why do we calculate centers of gravity?
Danoyachtcapt
Top Answerer
Center of gravity (CG) is very important, especially in aircraft and other vehicles like cars and trains. The Vehicle has to be designed so the CG is within certain limits so the vehicle will be well-balanced while in motion.
-
Question
I have to find the center of gravity for a 1310 mm length MS Steel. How can I go about doing that?
Balance it on a knife edge and record the position by marking the edge. Then, turn the object approx. 30 degrees and re-balance it on the knife edge. Record the position by marking the edge — you should now have 2 intersecting lines, and the intersection point will give you the center of gravity.
-
Question
Why is the determination of the center of gravity necessary, and where might I apply it in real life?
It’s more useful in certain sports and careers. If you are an engineer, you don’t want whatever you’re building to be off center. In sports such as gymnastics, it’s easier to do harder moves if you know where your center of balance is.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
To find the distance a person needs to move to balance the see-saw over the fulcrum, use the formula: (
weight moved
) / (
total weight
) = (
distance CG moves
) / (
distance weight is moved
). This formula can be rewritten to show that the distance the weight (person) needs to move equals the distance between the CG and the fulcrum times the weight of the person divided by the total weight. So the first kid needs to move
-1.08ft * 40lb / 130lbs =
-.33ft or -4in. (toward the edge of the see-saw). Or, the second kid needs to move
-1.08ft * 130lb / 60lbs =
-2.33ft or -28in. (toward the center of the see-saw).[7]
-
The definition for center of gravity of a general mass distribution is (∫ r dW/∫ dW) where dW is the differential of weight, r the position vector and the integrals are to be interpreted as Stieltjes integrals over the entire body. They can however be expressed as more conventional Riemann or Lebesgue volume integrals for distributions that admit a density function. Starting with this definition all properties of CG including the ones used in this article may be derived from properties of Stieltjes integrals.
-
To find the CG of a two dimensional object, use the formula Xcg = ∑xW/∑W to find the CG along the x-axis and Ycg = ∑yW/∑W to find the CG along the y-axis. The point at which they intersect is the center of gravity.
Thanks for submitting a tip for review!
Advertisement
-
Trying to blindly apply this mechanical technique without understanding the theory may result in errors. Understand the laws/theories behind it first.
Advertisement
References
About This Article
Article SummaryX
To calculate the center of gravity of 2 objects on a see-saw, first identify the weight of each separate object. Choose a starting point, or datum, on one end of the see-saw and measure its distance from the center and each object. Find each object’s moment by multiplying the distance by the object’s weight, then add up the 3 moments. Add up the weights of the objects and divide the total moment by the total weight to get the datum’s distance from the center of gravity. For examples and ways to check your answer, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,422,390 times.
Did this article help you?
И. В. Богомаз. Механика
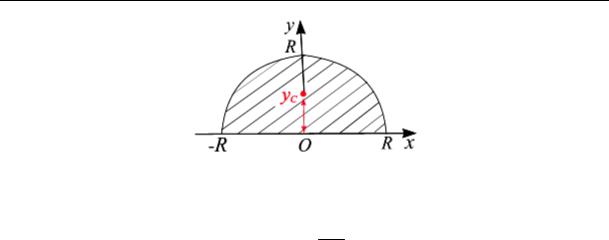
Рис. 5.7
Центр тяжести полукруга yC = 43Rπ .
Метод разбиения на части. Некоторые тела сложной формы можно разбить на части, положение центра тяжести которых известно. В таких случаях центр тяжести составного тела вычисляют по формуле
|
n |
n |
|||
|
∑Ai xi |
∑Ai yi |
|||
|
x = |
i=1 |
, y = |
i=1 |
. |
|
C |
A |
C |
A |
|
Здесь A = ∑Ai – площадь сечения; xi, yi – центр тяжести i-го сечения; Ai – площадь i-го сечения.
Пример 5.1. Вычислить координаты центра тяжести однородного сечения, составленного из двух прямоугольников (рис. 5.8). Размеры прямоугольников показаны на рис. 5.8 в см.
Решение. Разбиваем сечение на два прямоугольника (линии разреза показаны пунктиром) и проводим оси координат (рис. 5.8).
Вычислим координаты центров тяжести и площадь каждого из прямоугольников:
|
x =1cм, |
x = 4 см, |
|||
|
1 |
2 |
|||
|
y1 = 4 см, |
y2 = 9 см, |
|||
|
А = 2 8 =16cм2 |
; |
А =8 2 =16см2. |
||
|
1 |
2 |
112
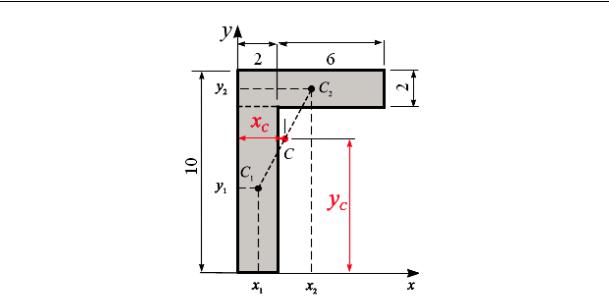
5. Центр тяжести
Рис. 5.8
Площадь всего сечения
|
3 |
|||||||
|
А= ∑Аk = А1 + А2 =16 +16 = 32 см2. |
|||||||
|
Тогда |
k=1 |
||||||
|
x1 A1 + x2 A2 |
= 1 16 + 4 16 = 80 = 2,5см; |
||||||
|
x |
= |
||||||
|
С |
A |
32 |
32 |
||||
|
y |
= |
y1 A1 + y2 A2 |
= 4 16 +9 16 = 64 +144 = 6,5см. |
||||
|
С |
A |
32 |
32 |
||||
Положение центра тяжести совпадает с точкой С {2,5; 6,5}
(рис. 5.7).
Метод отрицательных площадей. В данном методе вырезан-
ные сечения заменяют отрицательными площадями. Проиллюстрируем этот метод на примере сечения.
Пример 5.2. Задано сечение (рис. 5.9, а). Дано: R = 6 см. Вычислить центр тяжести сечения.
Решение. Разобьем сечение на простые фигуры: дополним квадрат – сечение 1, полукруг – сечение 2 и четверть круга – сечение 3 (рис. 5.9, б). За вспомогательную систему координат выберем стороны квадрата: Oxy. Вычислим площадь и координаты центров тяжести каждого сечения.
113
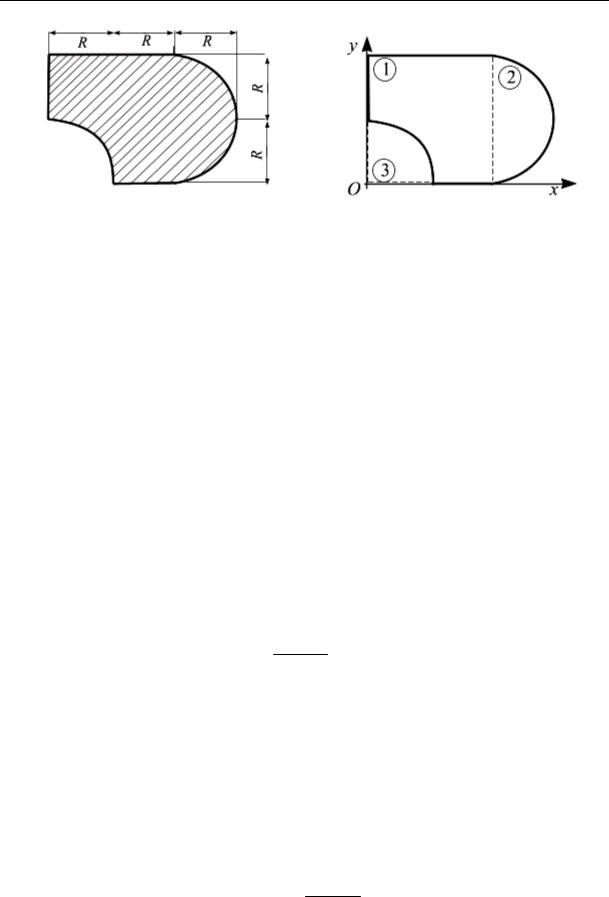
И. В. Богомаз. Механика
Рис. 5.9
Имеем (рис. 5.10) 1. Квадрат:
A1 = 2R 2R = 4R2 = 4 62 = 4 36 =144 см2;
x1 = R = 6 см; y1 = R = 6 см.
2. Полукруг:
A2 = πR2 2 = 3,142 62 = 56,52 см2;
x2 = 2R + 43Rπ = 2 6 + 343,146 =12 + 2,55 =14,55см;
y2 = R = 6 см.
3. Четверть круга:
A3 = − πR4 2 = −3,144 62 = −28,26 см2; xC = yC = 43Rπ = 3 43.146 = 2,6 см.
114
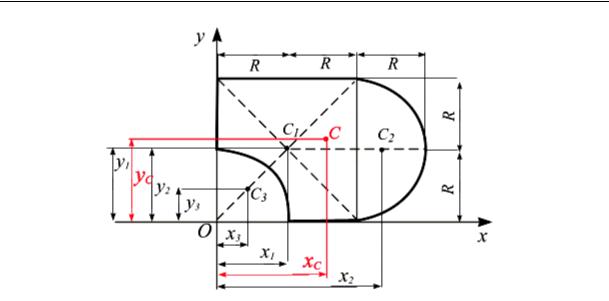
5. Центр тяжести
Рис. 5.10
|
Итак, |
|||||
|
x |
= x1 A1 + x2 A2 + x3 A3 |
= 6 144 +14,55 56,52 −2,6 28,26 = |
|||
|
С |
A1 + A2 + A3 |
144 |
+56,52 −28,26 |
||
|
= 864 +822,37 −73,5 |
= 9, 4см; |
||||
|
172, 26 |
|||||
|
y |
= y1 A1 + y2 A2 + y3 A3 = 6 144 +6 56,52 −2,6 28,26 = |
||||
|
С |
A1 + A2 + A3 |
144 |
+56,52 −28,26 |
||
|
= 864 +339,12 −73,5 |
= 6,6см. |
||||
|
172, 26 |
Положение центра тяжести совпадает с точкой С {9,4; 6,6}
(рис. 5.11).
Статические моменты. Статические моменты сечения Sx и Sy определим, как сумму произведений элементарных площадей dAi на кратчайшее расстояния до осей Ox, Oy соответственно (рис. 5.11), т. е.
S x = ∑Ai yi → Sx = ∫y dA, Sy = ∑Ai xi → Sy = ∫x dA.
A A
115

И. В. Богомаз. Механика
Рис. 5.11
Статические моменты имеют размерность см3 или м3.
При параллельном переносе осей (Oxy → O1x1 y1 ) значения ста-
тических моментов изменяются и могут иметь как положительное, так и отрицательное значение. Следовательно, существует ось, относительно которой статический момент равен нулю.
Ось, относительно которой статический момент равен нулю, называется центральной. Точка пересечения центральных осей совпадает с точкой центра тяжести сечения.
Координаты центра тяжести тела через статические моменты будут вычисляться следующим образом:
|
x |
= |
Sy |
= ∑Ai xi →, |
y |
= |
Sx |
= ∑Ai yi . |
|
C |
A A |
C |
A |
A |
|||
Пример 5.3. Для заданного несимметричного поперечного сечения, составленного из швеллера № 20 и неравнополочного уголка № 10/6,5 (рис. 5.12), найти положение центральных осей.
Рис. 5.12
116

I – момент инерции;
5. Центр тяжести
Решение. Из сортамента выберем геометрические характеристики швеллера № 20 и неравнополочного уголка № 10/6,5 (табл. 5.1) и построим чертеж в масштабе (рис. 5.13).
Таблица 5.1
Сталь горячекатаная. Швеллеры. Сортамент (ГОСТ 8240–89)
|
I – момент инерции; |
||||||||
|
h – высота швеллера; |
z0 – расстояние от оси y до на- |
|||||||
|
b – ширина полки |
ружной грани стенки; |
|||||||
|
А – площадь поперечного сече- |
||||||||
|
ния |
||||||||
|
Номер |
Размеры, |
|||||||
|
швел- |
мм |
А, см2 |
Ix, см4 |
Iy, см4 |
x0, см |
|||
|
лера |
h |
b |
||||||
|
20 |
200 |
76 |
23,4 |
1530 |
134 |
2,3 |
Уголки стальные горячекатаные неравнополочные. Сортамент (ГОСТ 8510–86)
В – ширина
большей полки; z0 – расстояние от оси y до наружной b – ширина грани стенки;
меньшей полки А – площадь поперечного сечения
|
Но- |
Разме- |
|||||||
|
мер |
ры, мм |
А, см2 |
Ix, см4 |
Iy, см4 |
Ixy, см4 |
x0, см |
||
|
угол- |
В |
b |
||||||
|
ка |
||||||||
|
10/6,5 |
200 |
65 |
15,67 |
155,52 |
51,68 |
51,18 |
2,3 |
Для вычисления положения центра тяжести заданного сечения за вспомогательные оси примем центральные оси швеллера C1x1y1
(рис. 5.13).
Вычислим координаты центра тяжести сечения осей C1x1y1:
|
y |
= ∑Sxi |
= |
S1x1 |
+ S2x1 |
= |
А1 уС1 + А2 уС2 |
= |
0 +15,67 6,63 |
= 2,66; |
||||||||
|
A1 |
+ A2 |
А1 + А2 |
23,4 +15,67 |
||||||||||||||
|
C |
∑Ai |
||||||||||||||||
|
х |
= |
∑Sуi = |
S1у1 + S2 у1 |
= |
А1 хС1 + А2 хС2 |
= |
0 +15,67 (−3,94) |
= −1,58. |
|||||||||
|
23,4 +15,67 |
|||||||||||||||||
|
C |
∑Ai |
A1 + A2 |
А1 + А2 |
117
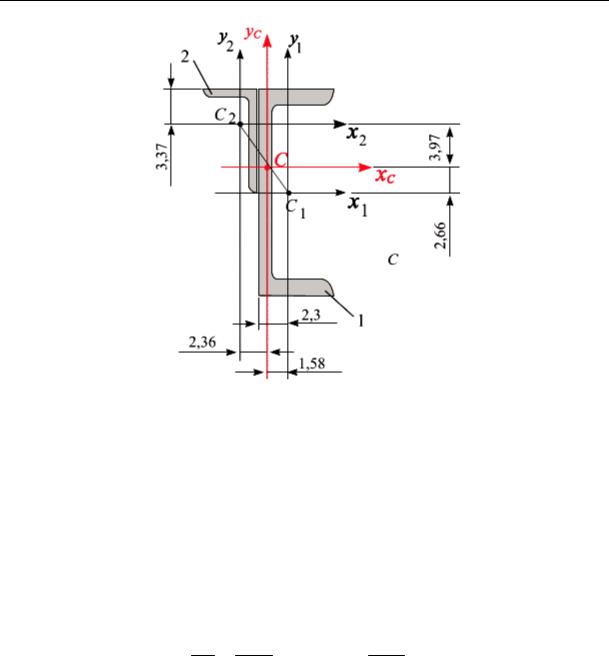
И. В. Богомаз. Механика
Рис. 5.13
Откладываем на схеме координаты точки центра тяжести сечения С{xC , yC }. Координаты центра тяжести сечения «легли» на отре-
зок С1С2, соединяющий центры тяжести частей (профилей), составляющих заданное сечение. Проверим правильность расчета. Соотношение отрезков должно быть равно соотношению площадей. Измеряем отрезки С1С и С2С, уточняем правильность соотношения
A2 = C1C →15,67 = C1C = 0,67.
A1 C2C 23,4 C2C
Проводим центра центральные оси CxCyC (рис. 5.13).
118
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Загрузить PDF
Загрузить PDF
Центр тяжести – это точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю. То есть это такая точка, в которой система находится в идеальном равновесии независимо от того, как система повернута или вращается вокруг этой точки. Чтобы найти центр тяжести системы, необходимо определить массу основного объекта и массу тел, входящих в систему, найти точку отсчета и подставить эти значения в формулу.
-
1
Определите вес основного объекта. Чтобы найти центр тяжести, сначала необходимо определить вес основного объекта. Например, рассмотрим качели-доску (качели-балансир) массой 12 кг. Таким образом, вес качелей равен 120 Н (Р=mg, где P – вес, m – масса, g – ускорение свободного падения, приблизительно равное 10 м/с2). Так как такие качели представляют собой симметричный объект, его центр тяжести находится точно по центру (когда на качелях никого нет). Но если на качелях сидят дети разной массы тела, задача усложняется.[1]
-
2
Определите дополнительные веса. Чтобы найти центр тяжести качелей с двумя детьми, необходимо определить вес каждого ребенка. Предположим, что масса тела первого ребенка равна 16 кг, а второго – 24 кг. Таким образом, вес первого ребенка равен 160 Н, а второго – 240 Н.
Реклама
-
1
Выберите точку отсчета. Точкой отсчета является любая точка, которая находится на одном (любом) конце доски. Предположим, что длина доски равна 5 м. Поместите точку отсчета на левой стороне доски возле первого ребенка.
-
2
Измерьте расстояние от точки отсчета до центра основного объекта и до дополнительных тел. Допустим, дети сидят на расстоянии 50 см от каждого конца доски. До центра доски 2,5 м (5/2=2,5). Вот расстояния от точки отсчета до центра основного объекта и двух дополнительных тел:
- Центр доски находится на расстоянии 2,5 м от точки отсчета.
- Первый ребенок находится на расстоянии 0,5 м от точки отсчета.
- Второй ребенок находится на расстоянии 4,5 м от точки отсчета.
Реклама
-
1
Перемножьте вес каждого тела и его расстояние до точки отсчета. Так вы найдете момент силы для каждого тела. Вот как умножить расстояние до каждого тела на его вес:
- Доска: 120 Н х 5 м = 600 Н х м.
- Первый ребенок: 160 Н x 0,5 м = 80 Н х м.
- Второй ребенок: 240 Н x 4,5 м = 1080 Н x м.
-
2
Сложите найденные значения. Сложение: 600 + 80 + 1080 = 1760 Н х м. Суммарный момент равен 1760 Н x м.
-
3
Сложите веса всех объектов. Найдите сумму веса качелей, веса первого ребенка и веса второго ребенка. Сумма: 120 Н + 160 Н + 240 Н = 520 Н.
-
4
Разделите суммарный момент на суммарный вес. Так вы найдете расстояние от точки отсчета до центра тяжести системы. В нашем примере разделите 1760 Н х м на 520 Н.
- 1760 Н х м / 520 Н = 3,4 м
- Центр тяжести находится на расстоянии 3,4 м от точки отсчета или на расстоянии 3,4 м от левого конца доски, где находится точка отсчета.
Реклама
-
1
Нарисуйте схему системы и отметьте на ней центр тяжести. Если найденный центр тяжести находится вне системы объектов, вы получили неверный ответ. Возможно, вы измерили расстояния от разных точек отсчета. Повторите измерения.
- Например, если на качелях сидят дети, центр тяжести будет где-то между детьми, а не справа или слева от качелей. Также центр тяжести никогда не совпадет с точкой, где сидит ребенок.
- Эти рассуждения верны в двумерном пространстве. Нарисуйте квадрат, в котором поместятся все объекты системы. Центр тяжести должен находиться внутри этого квадрата.
-
2
Проверьте математические вычисления, если вы получили маленький результат. Если точка отсчета находится на одном конце системы, маленький результат помещает центр тяжести возле конца системы. Возможно, это правильный ответ, но в подавляющем большинстве случаев такой результат указывает на ошибку. Когда вы вычисляли моменты, вы перемножали соответствующие веса и расстояния? Если вместо умножения вы сложили веса и расстояния, вы получите гораздо меньший результат.
-
3
Исправьте ошибку, если вы нашли несколько центров тяжести. Каждая система имеет только один центр тяжести. Если вы нашли несколько центров тяжести, скорее всего, вы не сложили все моменты. Центр тяжести равен отношению «суммарного» момента к «суммарному» весу. Не нужно делить «каждый» момент на «каждый» вес: так вы найдете положение каждого объекта.
-
4
Проверьте точку отсчета, если ответ отличается на некоторое целое значение. В нашем примере ответ равен 3,4 м. Допустим, вы получили ответ 0,4 м или 1,4 м, или другое число, оканчивающееся на «,4». Это потому, что в качестве точки отсчета вы выбрали не левый конец доски, а точку, которая расположена правее на целую величину. На самом деле, ваш ответ верен, независимо от того, какую точку отсчета вы выбрали! Просто запомните: точка отсчета всегда находится в положении x = 0. Вот пример:
- В нашем примере точка отсчета находилась на левом конце доски и мы нашли, что центр тяжести находится на расстоянии 3,4 м от этой точки отсчета.
- Если в качестве точки отсчета выбрать точку, которая расположена на расстоянии 1 м вправо от левого конца доски, вы получите ответ 2,4 м. То есть центр тяжести находится на расстоянии 2,4 м от новой точки отсчета, которая, в свою очередь, находится на расстоянии 1 м от левого конца доски. Таким образом, центр тяжести находится на расстоянии 2,4 + 1 = 3,4 м от левого конца доски. Получился старый ответ!
- Примечание: при измерении расстояния помните, что расстояния до «левой» точки отсчета отрицательные, а до «правой» – положительные.
-
5
Расстояния измеряйте по прямым линиям. Предположим, на качелях два ребенка, но один ребенок намного выше другого, или один ребенок висит под доской, а не сидит на ней. Проигнорируйте такую разницу и измерьте расстояния по прямой линии доски. Измерение расстояний под углами приведет к близким, но не совсем точным результатам.
- В случае задачи с качелями-доской помните, что центр тяжести находится между правым и левым концами доски. Позже вы научитесь вычислять центр тяжести более сложных двумерных систем.
Реклама
Советы
- Чтобы найти расстояние, на которое должен переместиться ребенок, чтобы сбалансировать качели-доску относительно точки опоры, используйте формулу: (перемещаемый вес)/(общий вес) = (расстояние движения центра тяжести)/(расстояние движения веса). Эту формулу можно переписать так: расстояние, на которое должен переместиться ребенок = (расстояние между центром тяжести и точкой опоры х вес ребенка)/(общий вес). Поэтому первому ребенку нужно переместиться на -0,9*160/520 = -0,28 м или -28 см (к концу доски), а второму ребенку нужно переместиться на -0,9*520/240 = -1,95 м или -195 см (к концу доски).
- Если нужно найти центр тяжести двумерного объекта, используйте формулу Xcg = ΣxW/W, чтобы найти центр тяжести вдоль оси X, и Ycg = ΣyW/ΣW, чтобы найти центр тяжести вдоль оси Y. Точка, в которой они пересекаются, является центром тяжести.
- Определение центра тяжести общего распределения масс: (∫ r dW/∫ dW), где dW – дифференциал веса, r – радиус-вектор, а интегралы должны интерпретироваться как интегралы Стилтьеса по всему телу. Но эти интегралы могут быть выражены как более общие интегралы (по плотности) Римана или Лебега для распределений, допускающих функцию плотности. Начиная с этого определения, все свойства центра тяжести (включая те, которые описаны в этой статье) могут быть получены из свойств интегралов Стилтьеса.
Реклама
Предупреждения
- Не пытайтесь применить описанные здесь методы, не поняв теорию. В противном случае вы получите неверный результат.
Реклама
Об этой статье
Эту страницу просматривали 52 569 раз.



























