Приведем пример
определения центра массы тела методом разделения его на отдельные тела, центры
масс которых известны.
Пример 1. Определить координаты центра массы однородной
пластины (рис.9). Размеры заданы в миллиметрах на рисунке 9.
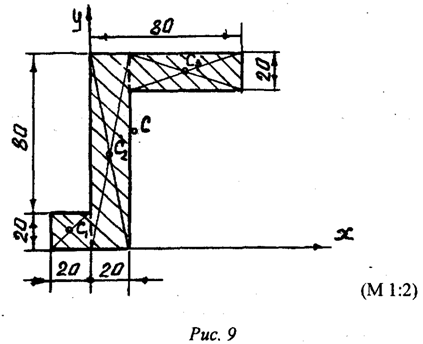
Решение: Показываем оси координат ![]() и
и
![]() . Разбиваем пластину на части,
. Разбиваем пластину на части,
которые образованы тремя прямоугольниками. Для каждого прямоугольника проводим
диагонали, точки пересечения которых ![]() и
и![]() определяют положения центров массы
определяют положения центров массы
каждого прямоугольника. В принятой системе координат несложно найти значения
координат этих точек. А именно:
![]() (-1;
(-1;
1), ![]() (1;5),
(1;5),![]() (5;9).
(5;9).
Площади каждого тела соответственно равны:
![]() ;
; ![]() ;
;
![]() .
.
Площадь всей пластины равна:
![]() .
.
Для определения
координат центра массы заданной пластины применяем выражения (21). Подставим
значения всех известных величин в данном уравнении, получим
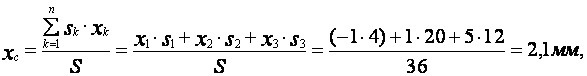
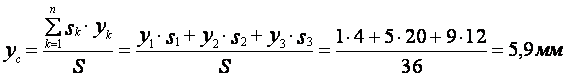 .
.
Согласно полученных
значений координат центра массы пластины укажем точку С на рисунке. Как видно,
центр массы (геометрическая точка) пластины находится за ее пределами.
Способ дополнения. Этот способ есть частичным случаем способа
разделения. Он может применяться к телам, которые имеют вырезы (пустоты).
Причем, без вырезанной части, положение центра массы тела известно. Рассмотрим
например применение такого метода.
Пример 2. Определить положение центра массы веса круглой
пластины радиусом R, в которой есть вырез радиусом r (рис.10). Расстояние ![]() .
.
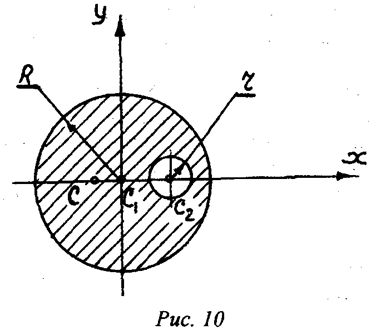
Решение: Как видим, из рис.10 центр массы пластины лежит на
оси симметрии пластины, то есть на прямой ![]() ,
,
поскольку эта прямая есть осью симметрии. Таким образом, для определения
положения центра массы этой пластины необходимо определить только одну
координату ![]() , поскольку вторая координата
, поскольку вторая координата ![]() будет расположена на оси симметрии и
будет расположена на оси симметрии и
уравновешивает нулевые. Покажем оси координат ![]() ,
, ![]() . Примем, что
. Примем, что
пластина складывается из двух тел – из полного круга (как будто без выреза) и
тела, которое как будто выполнено с вырезом. В принятой системе координат
координаты ![]() для указанных тел будут равны:
для указанных тел будут равны: ![]() .Площади тел равны:
.Площади тел равны: ![]() ;
; ![]() .
.
Общая площадь всего тела будет равна разнице между площадями первого и
второго тела, а именно
![]() .
.
Теперь,
для определения неизвестной координаты центра массы заданной пластины
применяем первое уравнение выражения (21). Подставим значения всех известных
величин в это уравнение, получаем
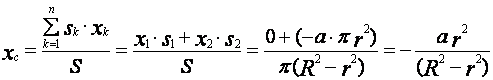 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Метод
симметрии. При
определении центров тяжести широко
используется
симметрия тел. Для однородного тела,
имеющего плоскость
симметрии, центр тяжести находится в
плоскости симметрии.
Для однородного тела, имеющего ось или
центр симметрии, центр
тяжести находится соответственно на
оси симметрии или в центре
симметрии.
Метод
разбиения на части. Некоторые
тела сложной формы можно
разбить на части, центры тяжести которых
известны. В таких случаях
центры тяжести сложных фигур вычисляются
по общим формулам,
определяющим центр тяжести, только
вместо элементарных
частиц тела берутся его конечные части,
на которые оно разбито.
Пример
1. Определить
координаты центра тяжести однородной
пластины,
показанной на рис. 7.3. Все размеры показаны
на рисунке в сантиметрах.
Решение.
Проводим
оси координат и разбиваем пластину на
три прямоугольника
(линии разреза показаны пунктиром).
Вычислим координаты
центров тяжести каждого из
прямоугольников и их площади:
![]()
![]()
![]()
![]()
.
Площадь
всей фигуры
![]()
.
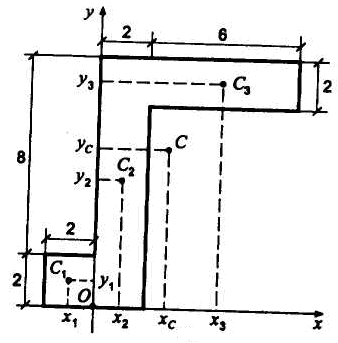
Рис.
7.3
Тогда,
![]()
,
![]()
.
Найденное
положение центра тяжести совпадает с
точкой С
и показано
на рис. 7.3.
Метод
отрицательных масс.
Проиллюстрируем этот метод на плоской
фигуре.
Пример
2. Определить положение центра тяжести
круглой пластины радиусом R
с вырезом радиуса r
(рис. 7.4). Расстояние
![]()
.
Решение.
Центр тяжести пластины лежит на линии
![]()
– на оси симметрии. Проводим оси
координат, как показано на рис. 7.4.
Для
нахождения координаты
![]()
дополняем площадь пластины
![]()
до полного круга, затем вычитаем из
полученной площади площадь вырезанного
круга
![]()
.
Тогда
![]()
![]()
![]()
.
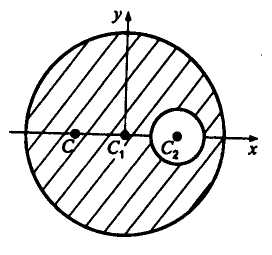
Рис.
7.4
Положение центра
тяжести вычислим по формуле
![]()
Найденный
центр тяжести лежит левее точки
.
4 Центры тяжести простейших тел
Дуга
окружности.
Центр тяжести находится на оси симметрии
дуги, которую примем за ось координат
Ох
(рис. 7.5). Координату центра тяжести дуги
АВ
вычисляем по формуле
![]()
.
(а)
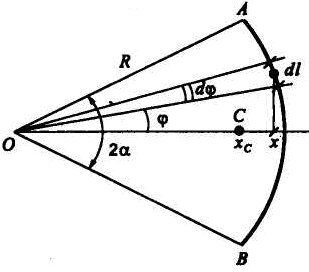
Рис.
7.5
Дуга
окружности АВ,
равная L,
определяется радиусом R
и стягиваемым ее центральным углом
2а
В рассматриваемом случае
![]()
.
Подставляя эти
значения в формулу (а), получим
![]()
.
Таким
образом,
![]()
.
Центр
тяжести полукруга.
Центр тяжести полукруга радиуса R
(pис. 7.6) находится на оси симметрии,
которую примем за ось Оу.
Координату центра тяжести полукруга
вычислим по формуле
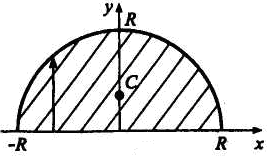
Рис.
7.6
![]()
.
В
рассматриваемом случае
![]()
.
Имеем:
![]()
.
Подставляя
эти значения в формулу для вычисления
центра тяжести
полукруга
![]()
,
получим:
Таким
образом,
![]()
.
5 Статические моменты и центр тяжести
Рассмотрим
плоскую фигуру площадью А
и
ограниченную некоторой
кривой (рис. 7.7) в прямоугольной системе
координат. Примем
плотность тела
![]()
,
т.е. тогда масса
любой части тела будет измеряться
ее площадью. Это всегда подразумевается,
когда говорят о статических
моментах. Выделим в плоскости фигуры
элемент площади dA
с
координатами х
и
у
(pис.
7.7) и определим статические
моменты плоской фигуры, как
взятые по всей площади А
суммы
произведений
элементарных площадей dA
на
их расстояния х
и
у
до
осей Ох
и
Оу.
Итак,
статические моменты плоской
фигуры определяются как
![]()
.
(7.9)
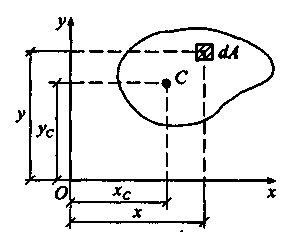
Рис.
7.7
Статические
моменты обычно выражаются в см3
или м3.
При
параллельном переносе осей значения
статических моментов
не остаются постоянными, а изменяются
и могут иметь как положительное,
так и отрицательное значение. Следовательно,
существует
ось, относительно которой статический
момент равен нулю.
Ось,
относительно которой статический момент
равен нулю, называется
центральной.
Точка
пересечения центральных осей является
центром тяжести
сечения.
Если
известны статические моменты площади
фигуры относительно
координатных осей, то координаты ее
центра тяжести можно определить
по формулам
![]()
,
(7.10)
где
А
–
площадь сечения.
Пример
3.
Вычислить
центр тяжести плоской фигуры, изображенной
на рис. 7.8.
Размеры
сечения на рисунке даны в сантиметрах.
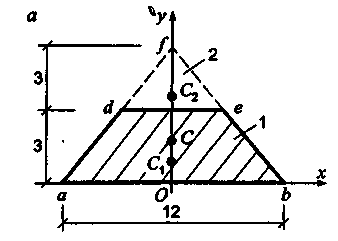
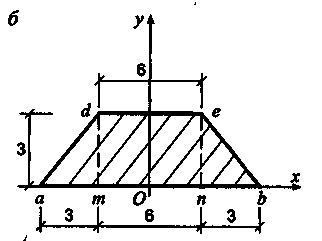
Рис.
7.8
Решение.
Сечение
имеет ось симметрии. Поэтому определяем
только
координату
пользуясь
методом разбиения на части. Дополним
трапецию до треугольника abf
u
рассмотрим
заданное сечение, состоящее из
треугольников abf
(часть
1) и def
(часть
2) (рис. 7.8). При
вычислении статического момента площадь
треугольника def
следует
брать со знаком «минус», так как этот
треугольник является дополнением
к заданному сечению (трапеции).
Вычислим
центр тяжести по формулам (7.9).
Определим
статический момент трапеции относительно
оси Ох.
![]()
![]()
.
Площадь сечения
![]()
.
Тогда
![]()
.
Статический
момент
![]()
можно также определить как сумму
статических
моментов составляющих ее частей
относительно той же оси
Ох.
Для
этого разобьем трапецию на два одинаковых
треугольника
amd
(часть
1) и пbе
(часть
2) и прямоугольник mden
(часть
3) (рис. 7.8,
б)
и вычислим
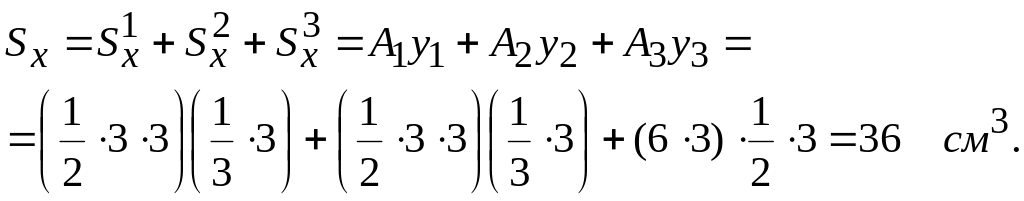
Координата
центра тяжести
имеет
положительное значение, т.
к.
![]()
и, следовательно, должна быть отложена
по оси Оу
вверх.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Пример решения задачи по определению координат положения центра тяжести тонкой однородной симметричной пластины методом отрицательных площадей.
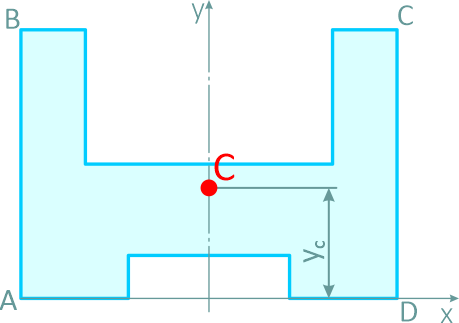
Задача
Определить положение центра тяжести тонкой однородной пластинки, имеющей ось симметрии (рисунок 2.6).
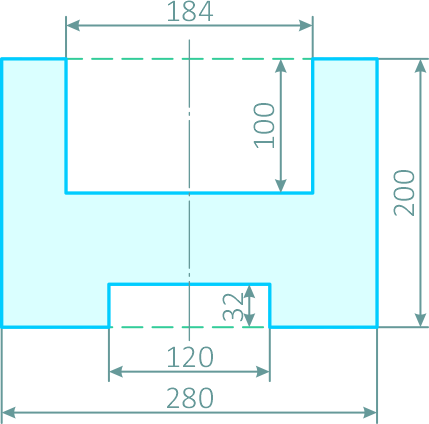
Рисунок 2.6
Другие примеры решений >
Помощь с решением задач >
Решение
Пример определения координат центра тяжести для несимметричных фигур рассмотрен в нашем коротком видео:
Другие видео
Пластина симметрична, т.е. имеет ось симметрии, на которой находится центр тяжести. Совместим с осью симметрии ось y, а ось x – с нижним краем пластинки (абсцисса центра тяжести плоской фигуры xC= 0).
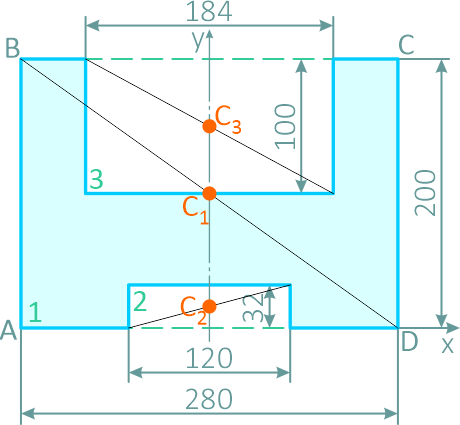
Дополнив пластинку до прямоугольника ABCD, разобьем ее на три части. Определим площади каждой части в см2 и координаты их центров тяжести в см:
S1= 28∙20 = 560 см2; C1(0;10);
S2= 12∙3,2 = 38,4 см2; C2(0;1,6);
S3= 18,4∙10 = 184 см2; C3(0;15).
Определим ординату центра тяжести плоской фигуры с помощью метода отрицательных площадей:
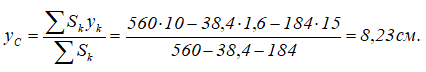
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Приложения кратных интегралов в механике
Краткая теория
Масса и статистические моменты пластики
Если
– область плоскости
, занятая пластинкой, и
– поверхностная плотность пластики в точке
, то масса
пластинки и ее статистические моменты
и
относительно осей
и
выражаются двойными интегралами:
Если
пластика однородна, то
Координаты центра тяжести пластики
Если
– центр тяжести пластики, то
где
– масса пластинки и
– ее статистические моменты относительно осей
координат.
Моменты инерции пластики
Моменты
инерции пластинки относительно осей
и
соответственно равны:
Момент инерции пластики относительно
начала координат:
Полагая
, получаем геометрические моменты инерции плоской
фигуры.
Масса тела, занимающего область
![]() и статистические моменты тела относительно
и статистические моменты тела относительно
координатных плоскостей
где
– плоскость тела в точке
Координаты центра тяжести
Если тело
однородно, то формулах для координат центра тяжести можно положить
.
Моменты инерции относительно
осей координат
Полагая в
этих формулах
, получаем геометрические
моменты инерции тела.
Примеры решения задач
Задача 1
Вычислить
массу материальной пластины, занимающей область
плоскости
, если поверхностная
плотность
и границы области
заданы уравнениями.
Решение
Сделаем
чертеж области
:
Искомая
масса материальной пластины:
Ответ:
Задача 2
Найти
статистический момент фигуры, ограниченной линиями
и
относительно оси абсцисс.
Решение
Сделаем
чертеж:
Статистический
момент относительно оси
:
Ответ:
Задача 3
Вычислить
координаты центра масс однородной
материальной пластины
, ограниченной данными
линиями:
Решение
Сделаем
чертеж:
Масса
пластинки:
Статистические
моменты:
Искомые
координаты центра масс:
Ответ:
.
Задача 4
Вычислить массу тела
, ограниченного заданными поверхностями
-плотность в
точке
.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Изобразим
тело на рисунке:
С боков
тело будет ограничено цилиндром
и плоскостями
. Сверху плоскостью
Проекция на плоскость
:
Ответ:
Задача 5
Найти
момент инерции однородного шара
с массой
относительно оси
.
Решение
Момент
инерции относительно оси
можно найти по формуле:
Шар
однородный, поэтому плотность:
Перейдем
к сферическим координатам:
Получаем:
Ответ:
Техническая механика. Помогите решить билет.
Сергей Рябинин
Ученик
(125),
на голосовании
2 года назад
1. Как определить центр тяжести тонкой однородной пластины, составленной из
простых геометрических фигур.
2. Чистый сдвиг. Условие прочности и жесткости при чистом сдвиге.
3.Определите диаметр вала, который передает крутящий момент Т=0,3кНм на
прямозубую цилиндрическую шестерню редуктора диаметром d=112 мм. Для
схемы принять l1=25мм, l2=30мм, l3=50мм.
Голосование за лучший ответ
Nanalia Tuzina
Мудрец
(10741)
2 года назад
1) Разбить пластину на простые детали, найти их площади и центры тяжести. Построить оси ОХ и ОУ и найти расстояния от центров тяжести до осей и по формуле найти координаты ЦТ пластины.
